Describing one- and two-neutron halos in effective field theory

Abstract

In this paper, the recent work our group has undertaken on effective field theory (EFT) analyses of experimental data pertaining to one- and two-neutron halo nuclei is discussed. The cases of ¹⁹C and ⁸Li (one-neutron halos) and ²²C (two-neutron halo) are considered. For ¹⁹C and ⁸Li electromagnetic processes, such as Coulomb dissociation and radiative capture are considered. In the ²²C system the way in which the measured matter radius can be used to derive constraints on the two-neutron separation energy of this very neutron-rich system is shown. In each case the ‘Halo EFT’ ability to correlate different experimental observables with one another, in a model-independent manner, and up to an accuracy that is determined by the separation of scales in the halo system is shown.

1 Introduction

Effective field theory (EFT) enables a model-independent, systematically improvable treatment of systems in which a separation of scales exists. Halo nuclei are amenable to an EFT description, because the typical distances occupied by neutrons in a nuclear halo, R _halo, are much larger than the size of the nuclear core, R _core. Halo EFT is thus built on the scale hierarchy R _core≪R _halo. Physical observables in this EFT are expressed as expansions in powers of R _core/R _halo. For nuclei, in which the halo consists of a single neutron it is a simple extension of the EFT for shallow s-wave bound states developed in, e.g., [1–4] – indeed, from the Halo-EFT point of view the deuteron is the lightest halo nucleus, with R _core set by the pion Compton wavelength. In the context of few-nucleon systems such an EFT treatment, based on nucleon degrees of freedom interacting via short-range potentials, has been successfully applied not just to the A=2 system, but also to A=3 and A=4 [5–7].

Halo systems beyond A=4 can be treated in an analogous fashion, in which a tightly-bound nuclear core is employed as one degree of freedom. The core is structureless in the leading-order (LO) Halo-EFT Lagrangian, and so the theory is designed to treat reactions in which core structure is not resolved, i.e., momenta are k≲1/R _core. Given reasonable values for R _core, this means that we are restricted to systems with neutron separation energies of 1 MeV or less, but within that domain an EFT treatment that links phenomena across different halos is possible. The formalism was extended to bound states and low-energy resonances of p-wave character in [8]. It has now been applied to numerous halo systems including ⁵He [8], ⁸Li [9], ¹⁵C [10], and a variety of two-neutron (2n) halos [11,12].

In [13] we applied this theory to the one-neutron (1n) halo ¹¹Be. This nucleus is particularly interesting because it has both a shallow s-wave (1/2⁺) and a shallow p-wave (1/2⁻) bound state. In Halo EFT these bound states are generated by zero-range forces, and thus have (reduced) wave functions

$$ u_{0}(r)=A_{0} \exp(-\gamma_{0} r), \quad u_{1}(r)=A_{1} \left(1 + \frac{1}{\gamma_{1} r}\right) \exp(-\gamma_{1} r) $$

(1)

with $\gamma _{0,1}=\sqrt {2 m_{R} S_{1n}}$ being the binding momentum of the neutron in the 1/2^+,− state and A _0,1, the corresponding asymptotic normalization coefficient (ANC). At leading order (LO), the ANC (A ₀) is fixed to be $\sqrt {2 \gamma _{0}}$, and so there are three free parameters in the theory at LO: γ ₀, γ ₁, and A ₁. Data on the energy levels of ¹¹Be fix the first two, and the third was determined using the sizeable and well-measured B(E1) of the 1/2⁺ to 1/2⁻ transition in ¹¹Be. In future this parameter could perhaps be extracted from ab-initio calculations (see §3). Once these three parameters were fixed we could predict the Coulomb dissociation spectrum of ¹¹Be at next-to-leading order (NLO) in Halo EFT. At that order, an additional parameter associated with the ANC (A ₀) is introduced. It can be adjusted to obtain a good description of the low-energy dB(E1)/dE spectrum [13].

While the zero-range wave functions (1) are the starting point for the Halo EFT expansion, expressions are systematically corrected to include the piece of the dissociation (or capture) which takes place at distances where the expressions (1) do not apply, r∼R _core. For Coulomb dissociation of ¹¹Be this piece of the matrix element is parametrically suppressed by (R _core/R _halo)². Thus, the dominant effect of dissociation at distances ∼R _core appears one order beyond that to which the computation was carried out in [13] at N ²LO there is an unknown low-energy constant (LEC) in the Halo EFT photodissociation amplitude, which can only be determined using the data on E1 transitions in ¹¹Be.

Section 2 describes the recent results from a similar treatment of the s-wave 1n halo ¹⁹C. Fitting the N ²LO EFT amplitude for the Coulomb dissociation of ¹⁹C to experimental data allows accurate values to be extracted for the n ¹⁸C effective-range parameters [14]. Such treatments are similar to those based on effective-range theory (e.g., [15]), but offer the added benefit of a systematic EFT expansion which permits estimation of the error associated with the neglected terms.

The reaction ⁷Li+n→⁸Li+γ involves capture of a neutron into a p-wave halo state. There have been many attempts to describe this process theoretically, mainly driven by its relation to a key process in the chain of solar neutrino production reactions, ⁷Be+p→⁸B+γ. An accurate EFT description of these A = 8 radiative captures becomes difficult as several inputs are already required at LO. Section 3 describes one way to deal with the issue: the use of ANCs obtained in ab-initio calculations as input to Halo EFT. The resulting predictions for capture reactions agree with the data to within the expected accuracy of a LO calculation in the EFT [16].

Two-neutron halos are discussed in §4. A recent measurement by Tanaka et al of the r.m.s. matter radius of ²²C gives $\langle {r_{m}^{2}} \rangle ^{1/2}=5.4 \pm 0.9$ fm [17]. Here how the halo EFT predicts a universal correlation between the matter radius and the two-neutron separation energy of s-wave 2n halos, such as ²²C is shown. Applying this universal relation to ²²C and including estimates of higher-order EFT corrections in a treatment where ²⁰C is an inert core, we have put constraints on the poorly-known values of the ²²C two-neutron separation energy and n ²⁰C virtual-state energy using the experimental datum [18]. Finally, §5 offers a few concluding remarks.

2 Coulomb dissociation of ¹⁹C

The ¹⁸C ground state has J ^π=0⁺, while the ground state of ¹⁹C is now understood to be 1/2⁺ and has a one-neutron separation energy of ≈500 keV. This is significantly less than the one-neutron separation energy of ¹⁸C: S _1n (¹⁸C)=4.2 MeV. ¹⁹C is thus, a candidate for an s-wave neutron-halo state: it has a reasonable separation of scales, with the expansion parameter R _core/R _halo expected to be ≈0.4.

In [14] we have derived the dipole transition strength, B(E1), for the excitation of ¹⁹C to the ¹⁸C+n continuum. We found [10]

$$ \frac{\mathrm{d}B(E1)}{e^{2} \mathrm{d}E}= \frac{12}{\pi^{2}}\frac{\mu^{3}}{M^{2}}Z^{2} \frac{\gamma_{0}}{1-r_{0}\gamma_{0}}\frac{p^{3}}{\left({\gamma_{0}^{2}}+p^{2}\right)^{4}}, $$

(2)

where r ₀ is the effective range of the n ¹⁸C interaction. Up to the accuracy of the calculation of [14], r ₀ is related to the ANC (A ₀) by

$$ {A_{0}^{2}}=\frac{2 \gamma_{0}}{1-\gamma_{0} r_{0}}. $$

(3)

At LO in the EFT r ₀ = 0 and eq. (2) is universal, i.e., it applies to any s-wave 1n halo at LO, and, indeed, to the dissociation of any shallow s-wave quantum bound state. Effects of the finite range of the ¹⁸C–n interaction appear at orders beyond leading, and are manifest in eq. (2) through the effective range parameter r ₀. In the case of ¹⁹C, p-wave final-state interactions are strongly suppressed, they do not appear until N ³LO in the EFT expansion (cf. the case of ¹¹Be). Short-distance (∼ R _core) pieces of the capture matrix element occurs only at N ⁴LO [19].

Therefore, by combining eq. (2) and a reaction theory that relates dB(E1)/dE to the Coulomb dissociation cross-section (see, e.g., [20] for a full procedure and [14] for a summary), we can predict the Coulomb dissociation cross-section at N ²LO in the EFT. In practice we have fitted the input parameters γ ₀ and r ₀ to the data on the differential angular and differential energy cross-sections for Coulomb dissociation of ¹⁹C from [21] and [22]. In figure 1 we show these data along with the best fits. In each of the panels the dashed lines are fits to just the data shown in that panel. The solid line is the combined fit. The agreement is very good, and extends beyond the fit region E < 1 MeV.

Figure 1

(a) Angular distribution of the differential cross-section for $S_{1n}({}^{19}\mathrm {C})=540$ keV (dashed line) and $S_{1n}({}^{19}\mathrm {C})=575$ keV (solid line) (data from [21]). (b) Relative energy spectrum of the differential cross-section at $S_{1n}({}^{19}\mathrm {C})=580$ keV (dashed line) and $S_{1n}({}^{19}\mathrm {C})=575$ keV (solid line) (data from [22]) (figure taken from [14]).

The best fit to the combined data set yields r ₀/a=0.33 for the ratio of ¹⁸C–n effective range to scattering length. This is a more accurate value for the EFT expansion parameter than our initial estimate R _core/R _halo≈0.4. Therefore, in addition to the statistical errors, all the parameters determined above have a relative error of ${r_{0}^{3}}/a^{3}=0.036$. The EFT extraction gives values of S _1n (¹⁹C), a, and r ₀ of (575±55(stat.)±20(EFT)) keV, (7.75±0.35(stat.)±0.3(EFT)) fm, and $(2.6^{+0.6}_{-0.9}(\mathrm {stat.})\pm 0.1(\text {EFT}))$ fm, respectively. Note that uncertainties in the reaction theory must be assessed separately [23].

The width of the longitudinal momentum distribution predicted by EFT using these parameters also agrees well with the experimental data of Bazin et al [24]. The success of this description affirms the dominance of the s-wave configuration of the valence neutron.

3 Threshold neutron capture on ⁷Li

Halo EFT was applied to the A=8 capture process ⁷Li(n,γ)⁸Li in [9]. The neutron and ⁷Li core were the degrees of freedom used in the LO calculation. Four parameters were needed as input and in ref. [9] a combination of capture and scattering length data and model assumptions were used to fix them.

In [16] we pursued an alternative strategy. We used ANCs from ab-initio calculations to fix several EFT parameters. We also incorporated the bound excited state of ⁷Li (⁷Li ^∗ hereafter) as an additional degree of freedom in the EFT. The high-energy scale in our EFT can then be associated with the breakup energy of ⁷Li→t+⁴He. From the binding energy of ⁸Li with respect to the ⁷Li–n threshold, 2.03 MeV, we obtain a nominal expansion parameter ∼ 0.5. However, the result we ultimately find for the p-wave effective range in n ⁷Li scattering suggests a more convergent expansion.

There are two different incoming spin channels S _i =2,1 in this process. As spin does not participate in the E1 transition the ANCs for each ⁸Li state is considered (⁸Li and ⁸Li^∗) with respect to both the n ⁷Li spin channels. This necessitates the computation of four ANCs, results of which are given in table 1. These were obtained via variational Monte Carlo calculations using the Argonne v18 NN potential and UIX 3N force [25]. Overall, the agreement with the experimental data of [26] is remarkable. The inclusion of the excited state of ⁷Li as an extra degree of freedom signifies the need of the ANC of both ⁸Li and ⁸Li^∗ in ⁷Li ^∗+n channels. Those three ANCs have not been determined experimentally, but can be computed by the methods discussed in [25]. From the ANCs and Halo EFT formulae that relate them to scattering parameters, we find an effective ‘range’ for n ⁷Li scattering in the channel where ⁸Li occurs at r ₁ = −1.43 fm⁻¹.

Table 1 ANCs (fm^−1/2) for different channels. The $\tilde {C}_{(X)}$ represents ANCs of the bound excited state of ⁸Li. The first row gives the variational Monte Carlo ⁷Li+n ANCs reported in [25] and the second row shows measurements by Trache et al.

With the input parameters fixed, we can predict the capture to the ground state of ⁸Li. The scattering length in the ⁵ S ₂ n ⁷Li channel is significantly larger than R _core, and so the EFT mandates resummation of the initial-state interactions in that channel (see figure 2). In contrast, the scattering length in the ³ S ₁ channel is ‘natural’ (i.e., a∼R _core) and so initial-state interactions in that channel only appear at NLO. The nominal accuracy of the LO cross-section prediction, which is shown in figure 3, is ≈40%. The central value of the threshold cross-section is below the average data, but within the expected size of higher-order corrections. In fact, because at NLO there are increases in the ANCs used in the EFT calculation, we expect the NLO Halo-EFT result for the cross-section to be higher than the LO prediction..

Figure 2

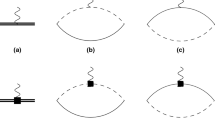
Tree and loop diagrams for neutron capture to ⁸Li and ⁸Li^∗. The solid line represents the neutron, the dashed line the ⁷Li core, and the thick solid line ⁸Li (or ⁸Li^∗). The two left-most diagrams are LO for two initial total spin S _i = 2 and S _i =1 channels. The dominant components in the initial state are ⁵ S ₂ and ³ S ₁ but d-wave components also contribute in the left diagram. The black blob corresponds to the scattering of the incoming particles in the s-wave. The sum of the two right-most diagrams is finite, as a result of current conservation [9,13]. For these two diagrams only the S _i =2 channel occurs at LO. Perturbative initial-state scattering effects in the S _i =1 channel enter at NLO. With the ⁷Li fields in the loop changed to ⁷Li^∗ fields, these diagrams represent the first dynamical effect of core excitation that takes place (it occurs at NLO). Detailed discussions can be found in [16] (figures from [16]).

Figure 3

Total cross-section vs. neutron laboratory energy and various data (for details of data, see [16]). ‘cal’ is our LO results, while ‘1.4cal’ and ‘0.6cal’ are the LO results multiplied by 1.4 and 0.6, to indicate our LO theory uncertainty (figure taken from [16])

We can also compute the fraction of the capture that proceeds from the initial S _i = 2 state. We find

$$\begin{array}{@{}rcl@{}} \frac{\sigma[(S_{i}=2)\rightarrow 2^{+}]}{\sigma(\rightarrow 2^{+})} = 0.93(2), \end{array} $$

(4)

where the uncertainty comes from the higher-order effects in the EFT. In [27] (see also [28]), a lower bound of 0.86 for the ratio on the left-hand side of eq. (4) has been reported. Our result is certainly consistent with that constraint. In contrast, the EFT calculation in [9] assumed equal n ⁷Li coupling strengths in ³ P ₂ and ⁵ P ₂ channels and consequently failed to satisfy the experimental lower bound.

As for the branching ratio for capture to the ground state, we find that near threshold the ratio is σ(→2⁺)/σ=0.88, with the remaining 12% going to the excited (1⁺) state in ⁸Li. This ratio is largely controlled by the excited- and ground-state ANCs, but is also affected by the initial-state (rescattering) effect due to the large (∼ R _halo) s-wave scattering length in the S _i = 2 channel. In [29], the branching ratio is measured to be 0.89±0.01 for thermal neutrons. The authors of [30] also recorded the same value at 20 to 70 keV. Both these measurements are in excellent agreement with our result.

We have subsequently extended this approach to describe the isospin-mirror reaction ⁷Be+p→⁸B + γ. The Halo EFT is even more convergent in this reaction, because the ⁸B ground state is shallower than that of ⁸Li. For centre-of-mass energies below 400 keV, the resulting description of the astrophysical S-factor is already quite accurate at LO [31].

4 The matter radius of ²²C

Recently, Tanaka et al measured the reaction cross-section of ²²C on a hydrogen target and, using Glauber calculations, deduced a ²²C r.m.s. matter radius of 5.4±0.9 fm [17]. Their measurement implies that the two valence neutrons in ²²C preferentially occupy the 1s _1/2 orbital and are weakly bound [17]. This conclusion is supported by the data on high-energy two-neutron removal from ²²C [32]. As ²¹C is unbound [33], it suggests that ²²C is an s-wave Borromean halo nucleus with two neutrons orbiting a ²⁰C core.

EFT was applied to 2n halo nuclei in [11], and equations that describe the core–neutron–neutron bound state were derived. These are the (homogeneous) Faddeev equations for this three-body system. The equations require two-body subsystem amplitudes as input. To solve the Faddeev equations an ultraviolet cut-off, Λ, needs to be applied to the integrals. A neutron–neutron–core contact interaction, H(Λ), is then required to cancel the dependence of physical observables on Λ [34]. Once H(Λ) is fixed to an experimental datum, the Faddeev components are independent of the cut-off Λ for momenta ≪Λ. The resulting theory displays a discrete scale invariance which is related to the Efimov effect [35]. With the Faddeev components in hand, the three-body wave function can be reconstructed and a number of different form factors obtained in the usual way (see [11,18] for details).

Because proper renormalization of this problem requires a three-body force at LO, the inputs to the equations describing an s-wave 2n halo are the energies of the neutron–core resonance/bound state, E _nc, and the nn virtual state, as well as the binding energy, B, of the halo nucleus [35a]. All other properties of the nucleus are predicted (at LO accuracy) once these (together with the core-neutron mass ratio A) are specified.

In [18], we used this methodology to compute the function that describes the mean-square matter radius of an arbitrary Borromean 2n halo. We then specialized that result to ²²C. The connection between the binding energy and several low-energy properties of ²²C, including the r.m.s. matter radius has been explored in a three-body model by Ershov et al [36]. Yamashita and collaborators investigated such correlations in halo nuclei earlier in 2004 [37] (see also [38] for a review). In 2011, Yamashita et al [39] attempted to apply EFT to analyse the experiment of [17]. However, as discussed in [18], an additional assumption in [39] renders the results of Yamashita et al model-dependent—in contrast to the rigorous, model-independent LO-EFT results we discussed here.

From the form factors computed via reconstruction of the nnc wave function, we extract the mean-square radii that describe the quantum-mechanical arrangement of this system. In particular, the mean-square matter radius of a two-neutron halo in the point-like core approximation, $\langle {r_{0}^{2}} \rangle$, can be expressed in terms of such radii as

$$ \langle {r_{0}^{2}} \rangle = \frac{2(A+1)^{2}}{(A+2)^{3}} \langle r_{n-nc}^{2} \rangle +\frac{4A}{(A+2)^{3}} \langle r_{c-nn}^{2} \rangle. $$

(5)

At LO in halo EFT, the quantity $mB\langle {r_{0}^{2}}\rangle$ depends on all the variables featuring in the Faddeev equations: E _{n n} , E _{n c} , B, and A, but, a being dimensionless, it can only be a true function of dimensionless ratios of these four parameters. Thus it is convenient to define the function f(E _{n n} /B,E _{n c} /B;A) as [37]

$$ mB\langle {r_{0}^{2}}\rangle \equiv f \left(\frac{E_{nn}}{B},\frac{E_{nc}}{B};A\right). $$

(6)

The function f can be calculated for any value of A, but, to be specific, figure 4 shows a three-dimensional plot of f(E _{n n} /B,E _{n c} /B;20) in the (E _{n n} /B,E _{n c} /B) plane. The disagreement with the results of [39] is 15% in the limit E _{n n} =E _{n c} =0 and appears to be worse at finite values of E _{n c} and E _{n n} .

Figure 4

$f \left (E_{nn}/B,E_{nc}/B;20\right )$ vs. $\left (E_{nn}/B,E_{nc}/B\right )$.

Figure 4 gives the results required to set a model-independent constraint on the binding energies of ²¹C and ²²C. First, though, we must account for the fact that, when applied to this system, Halo EFT only reliably predicts the difference between the ²²C matter radius and that of ²⁰C. We account for the finite spatial extent of the core by including that effect in the expression for the mean-square matter radius of the two-neutron halo:

$$ \langle r^{2} \rangle = \langle {r_{0}^{2}} \rangle+\frac{A}{A+2}\langle r^{2} \rangle_{\text{core}}. $$

(7)

Here 〈r ²〉_core is the mean-square radius of the core, which is obtained from the ²⁰C r.m.s. radius of (2.98±0.05) fm measured by Ozawa et al [40]. In subsequent calculations, the value of E _{n n} obtained from a _{n n} =(−18.7±0.6) fm [41] is also used.

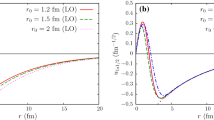
To calculate the breakdown scale of the EFT, Λ₀, we approximate the range of the neutron–core interaction by the size of the ²⁰C r.m.s. radius, i.e., we take ${\Lambda }_{0} \approx 1/\sqrt {\langle r^{2} \rangle _{^{20}\mathrm {C}}}$. We then estimate the relative error of the calculation by $\sqrt {mE_{nn}}/{\Lambda }_{0}$, $\sqrt {2mE_{nc}}/{\Lambda }_{0}$ or $\sqrt {2mB}/{\Lambda }_{0}$, whichever is the largest. In figure 5 we plot the sets of (B, E _{n c} ) values that cover the 1- σ range of Tanaka et al’s value – $\sqrt{\langle r^{2} \rangle}=$ 4.5, 5.4 and 6.3 fm – in each case with a theoretical error band assigned. Since Yamashita et al obtained a LO matter radius that is too large for a given binding energy, their constraints on the maximum possible value of B are about 20% weaker than the value obtained in this study.

Figure 5

Plots of $\sqrt {\langle r^{2} \rangle }$ = 5.4 fm (blue dashed), 6.3 fm (red solid), and 4.5 fm (green dotted), with their theoretical error bands in the (B,E _{n c} ) plane (figure taken from [18]).

Figure 5 shows that, regardless of the value of the ²¹C virtual energy, Tanaka et al’s experimental result puts a model-independent upper limit of 100 keV on the 2n separation energy of ²²C. The recent experimental finding of Mosby et al [42] that there is no low-energy resonance in the ²¹C system puts significant tension into this analysis, suggesting that ²²C is bound by less than 20 keV (1- σ, combined EFT, and experimental errors).

Following [11], we can also construct a region in the (B,E _{n c} ) plane within which an excited Efimov state in ²²C could occur. The Efimov-excited-state-allowed and r.m.s.-radius-constraint regions do not overlap for a n ²⁰C virtual energy larger than a keV (see [18]). Thus, while we cannot categorically rule out the existence of an Efimov state in ²²C, we can say that the ²¹C system would need to be tuned very close to the unitary limit in order for an Efimov state to be present. Again, the results of [42] suggest that this is not the case, and so it appears highly doubtful that Efimov physics is realized in the ²²C nucleus. This is in accord with the conclusion of [43], where the three-body equations were solved for a variety of 2n halos assuming separable potentials for the nn and n–core interactions, and it was found that Borromean halo nuclei such as ²²C are less likely to provide realizations of the Efimov effect than the 2n halos where the corresponding 1n halo is also bound (e.g., ²⁰C).

5 Conclusion

Halo EFT is based on the premise that quantum systems which are loosely bound share universal features. This quantum universality has proven to be a very powerful way to correlate results in nuclear physics, atomic physics, and hadron physics [7,44]. In halo nuclei we have seen that there are universal formulae for, e.g., the E1 dissociation of an s-wave halo (eq. (2)) and the matter radius of an s-wave 2n halo. These encode correlations between experimental observables which occur purely because these are quantum bound states in which the particles spend most of their time outside the range of the interparticle potential. The resulting universal correlations should persist in 3n and 4n halos.

Of course, the applicability of a clustered description of these nuclei has long been recognized, and the degrees of freedom and general philosophy of EFT treatments of these reactions are the same as those in R-matrix and potential-model calculations. All such ‘cluster models’ use some data to fix parameters and then attempt to predict other observables. But the EFT’s systematic expansion provides a quantitative estimate of the uncertainty at each order of approximation and a framework to improve accuracy.

As ab-initio calculations improve in power, accuracy, and scope one might question why any of these processes should not be computed directly. Part of the answer lies in the large separation of scales involved in such first-principles calculation: in the case of radiative proton capture on ⁷Be the E1 integral must be carried out to 200 fm, and no ab-initio calculation should be used to describe physics on all scales from ≈1.5 fm to such a large distance. Indeed, much of any (low-energy) ab-initio reaction calculation amounts to an indirect treatment of the collective motion of clusters through and around Coulomb and centrifugal barriers, and so halo EFT can profitably be combined with ab-initio calculations. We are seeking to extend the LO calculations of captures in the A=8 system to higher order, and we anticipate that additional information from ab-initio calculations will be needed if we want to continue to use the EFT to make predictions based largely on ab-initio input. Halo EFT has also been applied to ⁶He [12,45] and this appears to be an excellent meeting ground for ab-initio calculations and Halo EFT – although in that case the formalism to make the connection remains to be worked out.

The combined insights gained from ab-initio calculations and Halo EFT will continue to illuminate the fascinating physics of the quantum few-body systems known as halo nuclei. In combination with data from existing and new facilities – particularly from facilities with unstable beams – this promises to significantly enhance our understanding of the interplay of nuclear dynamics and nuclear binding close to the drip line.