1 Introduction

The stability and oscillations of a gas bubble suspended in a liquid under the influence of an acoustic driving pressure field in the ultrasonic frequency range have been the subject of discussion in a large body of the scientific literature [1–14]. Studies on the system have been made from different viewpoints coming from its diverse applications and occurrences. Ultrasound is routinely used in medical ultrasonography including echocardiography, lithotripsy, phacoemulsification, in treatment of cancer and for dental cleansing. Other significant applications of ultrasonic forcing of fluids in which studies of bubble dynamics and cavitation become very important are in sonochemistry, sonoluminescence, ultrasonic cleaning of materials, waste water treatment and in focussed energy weapons. Cavitation events involving violent collapse of micron-sized bubbles in the fluid can cause immense damage to the surfaces they are in contact with. Studies of cavitation events in pumps, turbines, surfaces exposed to hydrodynamic flow, etc., continue to be of immense interest in industries and in technological designs of devices.

Rayleigh’s study of bubble cavitation was motivated by the need to understand and explain the damage to ships’ propellers [1]. Under ultrasonic forcing, the behaviour of a bubble in a fluid depends heavily upon its ambient radius and the amplitude and frequency of the driving sound field. Thus, the bubble can show regular oscillatory behaviour which can be periodic or it can show highly irregular oscillations which are chaotic and of unpredictable amplitude. For applications where damage caused on surfaces due to bubble cavitation can be disastrous, such as in medicine, it is desirous to operate the sonic device in a ‘safe’ regime, and/or to be able to have control over the bubble’s motion. Often in biological systems, it is known that bubbles in fluids can be electrostatically charged. Studies of the dynamics governing the oscillations, growth and collapse of charged bubbles are therefore of immense relevance because of their prevalence in diverse applications and situations. Experimental and theoretical work on the presence of charge on gas bubbles in fluids goes back to, e.g., the work of McTaggart, Alty and Akulichev [9,10,16,17], and more recently to the work of Shiran and Watmough and Atchley [11,12,18]. None of these, though, has addressed the issue of dynamics of a charged bubble under ultrasonic forcing.

It is interesting to know what effect the presence of electric charge on the bubble would have and see if the motion of such a charged bubble forced by ultrasound would vary significantly from that of an electrically neutral bubble in a fluid. This, especially becomes of practical significance when we are looking at cavitation phenomena in fluids in real life, be it in the context of cavitation in mechanical systems or in the case of bubbles in fluids in living tissue in a medical context. Grigor’ev and Zharov [15] have reported some studies on the stability of the equilibrium states of a charged bubble. In this paper, we report some studies on the dynamics of a charged bubble in a liquid (which we take to be water) when ultrasound is incident on it. We assume that heat transfer across the bubble takes place adiabatically, and the gas is a monatomic ideal gas. We therefore take the polytropic constant Γ=5/3.

The extremely nonlinear nature of the system, and the presence of a large number of parameters do not facilitate a straightforward analysis and it becomes essential to take the aid of numerical methods to get an understanding of the dynamics governing the observed behaviour.

In §2 we discuss briefly the nature of the radial dynamics of a charged bubble. Starting with a modified Rayleigh–Plesset equation, we obtain the time-series of the bubble radius as also of its radial velocity and temperature. We also calculate the phase portrait of the bubble, under different pressure regimes.

In §3 we discuss the pressure thresholds that influence bubble dynamics; we introduce the expansion–contraction ratio ζ which we had introduced in [23] that enables us to locate the presence of the Blake and upper transient threshold pressures easily when plotted as a function of the driving pressure amplitude P s . The effects of driving frequency ω and charge on ζ are demonstrated in the present work.

The influence of P s and ω on the bubble dynamics are investigated in detail in §4. We obtain an expression for the minimum charge required on a bubble for radial oscillations to occur at some velocity c 1, as also an expression for the dependence on the forcing pressure amplitude P s of the maximum forcing frequency ω H at which an uncharged bubble will oscillate with velocity c 1.

We then obtain, in §5, the bifurcation diagrams for the system with driving frequency as the control parameter, and also the bifurcation diagram with charge as the control parameter. We observe that the presence of charge on the bubble advances period-doubling bifurcations with driving frequency as the control parameter. Increasing P s causes the advancement of period-doubling and halving bifurcations for charged as well as uncharged bubbles, and bands of chaotic behaviour are observed at large P s . Largest Lyapunov exponents for the charged bubble have been calculated and plotted across large frequency ranges.

The effect of charge and driving frequency on the maximal temperature are discussed in §6. We note that the pressure regime in which the bubble is being forced (whether P s is above or below the upper transient threshold pressure) determines the frequency dependence of the temperature, and we obtain rough limits on the maximum charge a bubble may carry depending on its ambient radius.

We conclude the paper with a summary of the results in §7.

2 Radial dynamics of the charged bubble

In real-life situations, bubbles in fluids often have some electric charge sticking to them. This has been seen in the case of gas bubbles in various liquids as well as for cavitation events in water. In this paper, we adapt the procedures for describing cavitation and forced bubble oscillations (that has a long and extensive literature), to include the presence of charge.

Description of ultrasonically forced bubble motion in a fluid has been made through the Rayleigh–Plesset equation [1–3] and its variants [5,6,8,13,14,19–22] modified to take into account the compressibility of the fluid or various other factors. Proceeding as we did in our earlier work [23], we further modify the form of the Rayleigh–Plesset equation for the evolution in time of the bubble radius R(t) employed by Parlitz et al [19] to include the presence of a constant charge Q on the bubble as follows [15]:

$$\begin{array}{@{}rcl@{}} &&\left(\left(1-\frac{\dot{R}}{c}\right)R +\frac{4\eta}{c\rho}\right)\ddot{R}=\frac{1}{\rho}\left(P_{0} -P_{v}+\frac{2\sigma}{R_{0}} -\frac{Q^{2}}{8\pi\epsilon {R_{0}^{4}}}\right)\\ &&\times\left(\frac{R_{0}}{R}\right)^{3{\Gamma}}\left(1+\frac{\dot{R}}{c}(1-3{\Gamma})\right) -\frac{\dot{R}^{2}}{2}\left(3-\frac{\dot{R}}{c}\right)\\ &&+\frac{Q^{2}}{8\pi\rho\epsilon R^{4}}\left(1-\frac{3\dot{R}}{c}\right)-\frac{2\sigma}{\rho R} -\frac{4\eta}{\rho}\left(\frac{\dot{R}}{R}\right)\\ &&-\frac{1}{\rho}(P_{0}-P_{v}+P_{s}\;\text{sin}(\omega t))\left(1+\frac{\dot{R}}{c}\right) -\frac{R}{\rho c}P_{s}\omega\; \text{cos}(\omega t), \end{array} $$
(1)

where R 0 denotes the ambient equilibrium radius of the bubble, P 0 is the static pressure and P v =2.34 kPa, is the vapour pressure of the gas. We denote by P s and ω=2π ν, respectively (ν being the driving frequency), the amplitude and angular frequency of the ultrasound forcing field. We consider water to be the liquid surrounding the bubble, and having density ρ=998 kg/m3, viscosity η=10−3 Ns/m2, surface tension σ=0.0725 N/m, and the velocity of sound in the liquid c=1500 m/s, P 0=101 kPa, Γ is the polytropic index and 𝜖=85𝜖 0, where 𝜖 0 is the vacuum permittivity.

The modified Rayleigh–Plesset equation can be simplified and rewritten in dimensionless form [23] as

$$\begin{array}{rcl} &&\left(1-\frac{\dot{r}}{c_{*}}\right)r\ddot{r} + F\ddot{r}+\frac{\dot{r}^{2}}{2}\left(3 -\frac{\dot{r}}{c_{*}}\right) \\[4pt] && = H\left(1-P_{*v}+M\right)\left(\frac{1}{r}\right)^{3\Gamma}\left(1+\frac{\dot{r}}{c_{*}}(1-3\Gamma)\right) \\[4pt] && \quad+\frac{C}{r^{4}}\left(1-\frac{3\dot{r}}{c_{*}}\right)-S\frac{1}{r}-Fc_{*}\left(\frac{\dot{r}}{r}\right) \\[4pt] &&\quad -H\left(1-P_{*v}+P_{*s}\sin(\tau)\right)\left(1+\frac{\dot{r}}{c_{*}}\right)-H\frac{rP_{*s}}{c_{*}}\cos(\tau), \end{array} $$
(2)

where r=R/R 0, τ=ω t, P ∗v =P v /P 0, P ∗s =P s /P 0 and the overdot here corresponds to differentiation with respect to τ, and where the following dimensionless constants have been used:

$$\begin{array}{@{}rcl@{}} &&c_{*}=\frac{c}{R_{0}\omega}, \quad F=\frac{4\eta}{\rho R_{0} c}, \quad H=\frac{P_{0}}{{R_{0}^{2}}\omega^{2}\rho},\\ &&M=\frac{1}{P_{0}}\left(\frac{2\sigma}{R_{0}}-\frac{Q^{2}}{8\pi\epsilon {R_{0}^{4}}}\right),\\ &&C=\frac{Q^{2}}{8\pi\epsilon {R_{0}^{6}}{\omega}^{2}\rho};\quad S=\frac{2\sigma}{\rho {R_{0}^{3}}\omega^{2}}. \end{array} $$

We have employed the dimensionless form of the equations for obtaining their numerical solutions. In all the expressions that follow, and in the numerical results shown in graphs, we have rescaled the quantities by the appropriate factors and displayed only the dimensional form for a physical understanding of the magnitudes of the quantities involved.

The presence of charge Q counters the effect of surface tension, reducing its effective value, and induces several interesting changes to the dynamics of bubble oscillations. In a previous work [23], we had obtained for the charged bubble, the Blake threshold and radius and also some results for the upper transient threshold for cavitation. In the following sections, we describe some interesting consequences of the presence of charge on a bubble.

As the bubble expands and contracts, the surface charge density decreases or increases, respectively. The presence of charge lowers the surface tension and for submicron-sized bubbles, dominates over it, influencing the minimum and maximum values of the radius and the maximum velocities achieved by the bubble, and changing its point of collapse. A charged bubble achieves higher temperatures within it than an uncharged one, the collapse of the bubble being more violent in the charged case.

The above results indicate that since the bubble oscillations are more energetic for the charged bubble, the temperature attained by the gas within the bubble during its oscillations would be higher as well. To confirm this, we calculate the temperature using eq. (3) [20].

$$ T(t) = T(0)\left(\frac{{R_{0}^{3}} - h^{3}}{R^{3} - h^{3}}\right)^{\Gamma -1}, $$
(3)

where h is the van der Waals hard core radius for the gas, h=R 0/8.86 for argon [22]. This equation is obtained under the assumption that there is no exchange of heat from the gas to its surroundings, that the system is essentially adiabatic.

This assumption is not strictly true, as in reality the equation of state of the gas enclosed within the bubble can be either adiabatic or isothermal, depending upon the rate of collapse of the bubble and whether or not the various relaxation time-scales permit thermal diffusion to occur, to and from the bubble. We use the expression in order to get an idea of the magnitudes achievable by the temperature in the presence of charge. To better visualize the effect that the amplitude of the forcing pressure P s and charge Q have on the bubble dynamics, we consider a bubble being driven at 20 kHz, i.e., the lower limit of the ultrasonic spectrum. Even in this lowest ultrasonic regime, the time-series of bubble radius, radial velocity, and temperature all show enhancement in values due to charge. Moreover, P s crucially determines the dynamics of the bubble as illustrated in figures 1 and 2. We have considered three values of P s : P s =1.0P 0, 1.12P 0 and 1.2P 0. These pressures are, respectively, below the Blake threshold P Blake, at the upper transient pressure threshold P tr, and above P tr. As can be seen, the pressure regime in which the bubble dynamics occurs, crucially determines the behaviour. At P s = 1.0P 0, T max≈370 K, the uncharged bubble temperature being marginally less than that for the charged bubble (Q=0.38 pC); for P s =P tr=1.12P 0, T max goes upto about 1520 K for the charged bubble and about 1320 K for the uncharged case; and for P s = 1.2P 0, T max shoots up still further. These temperatures vary by orders of magnitude and spell out the importance of P s and Q.

Figure 1
figure 1

(A) Time-series of R. (B) Phase portrait (R vs. \(\dot R\)), for R 0=5 μm and bearing charge Q=0 (blue line) and Q=0.38 pC (red line), P s = (a) 1.0P 0, (b) 1.12P 0, (c) 1.2P 0. Amplitudes of R, \(\dot {R}\) are larger; the phase portrait spans a larger space for the charged bubble than for the uncharged case.

Full size image
Figure 2
figure 2

Time-series of temperature (in K) plotted as a function of time for R 0=5 μm at driving frequency ν = 20 kHz, and bearing charge Q=0 (blue line) and Q = 0.38 pC (red line) for three values of P s : (a) 1.0P 0, (b) 1.12P 0, (c) 1.2P 0. Temperatures T are larger for the charged bubble than for the uncharged case.

Full size image

3 Pressure thresholds

The Blake threshold determines the pressure threshold beyond which an acoustically forced bubble undergoes drastic expansion. After the Blake threshold and preceding the onset of bubble collapse following a larger threshold known as the upper transient threshold, P tr, the bubble is essentially in an unstable regime.

Depending upon whether the amplitude of the applied acoustic forcing pressure is greater or lesser than P tr, the response of the bubble to the frequency of the applied pressure wave varies drastically.

At low amplitudes of the forcing pressure (i.e., P s < P tr), increasing driving frequency causes a proportional increase in the bubble’s maximum radial velocity v max. This happens upto some critical value of the frequency for that P s after which v max rises more steeply but accompanied with large oscillations.

At larger amplitudes of the forcing pressure, with P s approaching the value of the Blake and upper transient threshold pressures, the situation is different. v max first decreases with increasing driving frequency upto a frequency ω hc, after which v max rises with frequency but with large oscillations. As could be expected from the above observations, a similar observation can be made regarding the maximum temperature T max of the gas inside the bubble.

A useful graphical illustration of the transient threshold pressures, i.e., of the Blake threshold (P Blake) and the upper transient threshold (P tr) pressures, can be obtained by plotting ζ=(R max−R 0)/(R 0−R min) as a function of the amplitude of driving pressure. This quantity ζ, which we call the expansion–contraction ratio, conveniently shows the location of both the Blake and the upper transient thresholds. Both these thresholds cannot be identified easily at the same time from, for example, a plot of R max/R min as a function of applied pressure amplitude. In figure 3, the points of inflection of the curves correspond to the Blake threshold pressures for the respective R 0 values. The effect of charge is clearly seen in reducing the threshold pressure as compared to the charged case. The upper transient threshold cannot be easily pinned down from this plot. While the Blake threshold is indicative of the threshold of the expansive growth of the bubble, the upper transient threshold demarcates where the violent collapse of the bubble occurs. A plot of ζ vs. P s for different values of R 0 as shown in figure 4 shows a rise of the curve till it peaks (at P s =P Blake) followed by a trough or well (at P s =P tr) before rising up steeply for higher P s (this has been discussed in some detail in our earlier work [23]). At pressures between P Blake and P tr, the bubble is in an unstable regime. This also explains the presence of large fluctuations or oscillations in the velocity vs. frequency plots at such intermediate pressures. The presence of charge shifts the threshold pressures to lower values. With increasing ambient radius R 0, ζ loses its distinctive peak–valley appearance gradually.

Figure 3
figure 3

Plots of \(R_{\min }\) (a) and \(R_{\max }/R_{\min }\) (b) as functions of P s for different values of ambient radius (for Q=0 and Q=0.4 pC) at 20 kHz forcing frequency.

Full size image
Figure 4
figure 4

(a) Plot of \(\zeta = (R_{\max } - R_{0})/(R_{0} - R_{\min })\) as a function of forcing pressure amplitude P s and R 0 at 20 kHz. (b) shows the locations of the Blake threshold pressure and the upper transient threshold pressure on the ζ– P s curve. Increasing bubble charge shifts the curve down and to the left, while increasing driving frequency decreases the steepness of the curve and flattens it.

Full size image

The maximum radius attainable by the bubble gradually increases with charge for a given driving frequency [23]. This can be understood from the fact that the presence of charge on the bubble decreases the effective surface tension. This causes the bubble to expand more easily in the negative pressure field. A casual reading might give rise to the observation that by the same argument, the minimum radius reached by the bubble would likewise follow a similar trend, with R min for a charged bubble having a larger value than that of a neutral bubble. However, this is not so. It should be borne in mind that R min is influenced by the maximal velocity the bubble is able to reach. The greater the velocity, the smaller the R min that it collapses to. Hence, perhaps counter-intuitively, charged bubbles undergoing forced oscillations, will achieve smaller values of R min than electrically neutral bubbles.

Thus, presence of charge leading to greater bubble expansion, in turn results in the bubble collapse being much more rapid and violent, shrinking the bubble volume more than in the case of the uncharged bubble. This can be seen in figure 3a, where the minimum radius, R min, reached by the bubble at the moment of collapse is plotted as a function of the driving pressure P s and R 0 for the charged and uncharged bubble. As was shown in greater detail in our earlier work [23], R min reduces with increasing Q.

4 Influence of amplitude and frequency of driving pressure field

The maximum radial velocity of the bubble attained during its collapse or contracting phase depends also on the driving frequency, the charge present on the bubble, as well as on the amplitude of the driving pressure wave, as also on the initial radius R 0 of the bubble in its quiescent state. Figure 5 shows the plots of the maximal radial velocity as functions of the driving frequency (a) and pressure P s (b). Several interesting features are evident from the figures.

Figure 5
figure 5

Maximum velocity vs (a) driving frequency, plotted at seven different P s values and for zero and non-zero values of charge; the P s =1.12P 0 curves (number 6, darkest (Q=0 black line) and just above that (Q=1 pC, dark green line)) correspond to the upper transient threshold pressure P tr (for R 0 = 5 μm) and clearly demarcate distinct behaviour for P s >P tr and P s < P tr. (b) \(v_{\max }\) vs. P s for different frequencies for R 0 = 5 μm, at five different driving frequencies (20–40 kHz, increasing from left to right), for zero (∙) and non-zero (Q=0.4 pC, triangle) charge.

Full size image

The behaviour of v max above P s = P tr is different from that below it. The plots shown are for a bubble of R 0 = 5 μm for which P tr = 1.12P 0. Figure 5a shows that at P s < P tr, v max increases as a function of driving frequency ν while for P s > P tr figure 5b, it decreases. Increasing the driving frequency induces instability by producing large-amplitude oscillations.

For a given magnitude of pressure amplitude P s , the magnitude of charge present influences the dynamical regime of the bubble. If the driving angular frequency of the applied pressure wave is ω at a certain pressure amplitude, for bubble oscillations to occur with some maximal radial velocity \(\dot {R} = c_{1}\), the charge present on the bubble should have some minimum magnitude Q=Q min(ω). At low frequencies, even an uncharged bubble might oscillate at that velocity. However at higher frequencies, if charge Q < Q min, the radial bubble velocity would be smaller than c 1. This is because as frequency increases, the bubble does not get sufficient time to complete its expansion, so that its subsequent collapse occurs with a smaller radial velocity than if expansion to a greater size had been reached. The presence of charge reduces the surface tension and encourages expansion to larger radial dimension and the consecutive, more violent collapse to a smaller radius.

The change in Q min(ω) with ω shows a bifurcation in the parameter space which is clear from figure 6. This transition from zero to non-zero Q min occurs at an angular frequency ω H . For P s = 1.35 P 0 and R 0=5 μm, this transition frequency has the value ω H = 23 kHz. The magnitude of Q min varies with driving frequency as

$$ Q_{\min} \approx a(\omega - \omega_{H})^{b}, $$
(4)

where the prefactor a has appropriate dimensions and depends on the value of the initial ambient bubble radius R 0, and b≈0.25.

Figure 6
figure 6

\(Q_{\min }\) vs. frequency ω: isovelocity plots (v≈1500 m/s) for (a) R 0=5 μm, P s =1.35P 0 (\(Q_{\min }\) is given in pC, ω in kHz). (b) Schematic illustrating the nature of the iso-velocity plot, \(Q_{\min } \sim (\omega - \omega _{H})^{0.25}\). (c) Plot showing the dependence of ω H on P s for different values of R 0 (curves 2–7 correspond to the corresponding R 0 values in μm). (d) Plot illustrating variation of dω H /dP s with R 0.

Full size image

We could attempt to give a simple explanation for the frequency dependence of Q min. We could argue that for a given value of constant maximal radial velocity c 1, the kinetic energy of the bubble would scale as the electrostatic contribution ∼Q 2/R min, so that Q 2∼a 2 c 1 R min, a 2 being a prefactor with appropriate dimensions. Since for high applied pressures (i.e., for P s above the Blake threshold pressure or of the order of or above the upper transient threshold pressure) we know that the minimum bubble radius scales as the 2/5th power of the driving frequency R min∝ω 2/5, it would follow that Q 2∝c 1 ω 2/5 so that Q∝ω 0.2, which is close but not equal to the observed exponent of 0.25. Hence, this argument, while it serves to give a lower bound for Q min, is insufficient.

Proceeding more systematically therefore, we start by making a linearization of the Rayleigh–Plesset equation. Proceeding along the lines of [5], the driving sound pressure is introduced through a small perturbation α, so that the total external field P ext can be written as

$$ P_{\text{ext}} = P_{0}(1-\alpha \cos\omega t). $$
(5)

The bubble oscillations R(t) about the equilibrium radius R 0 can then be expressed as

$$ R = R_{0}(1 + x(t)), $$
(6)

where x(t) is a small quantity of order α. Substituting this equation in the Rayleigh–Plesset eq. (1) and linearizing it, we get

$$ \ddot x + \beta \dot x + {\omega_{0}^{2}} x = - F_{\text{ext}}, $$
(7)

where the damping coefficient β and natural frequency of oscillation ω 0 of the bubble are given by

$$\begin{array}{@{}rcl@{}} \beta &=& \frac{1}{\rho c R_{0}\left(1 + {(4\eta}/{c\rho R_{0}}\right))}\left(4\phi/{R_{0}^{5}} + \frac{3Q^{2}}{8\pi\epsilon {R_{0}^{4}}} + \frac{4\eta c}{R_{0}}\right), \\[4pt] {\omega_{0}^{2}} &=& \frac{1}{\rho {R_{0}^{2}}\left(1 + {(4\eta}/{c\rho R_{0}}\right))}\left(5\phi/{R_{0}^{5}} -\frac{2\sigma}{R_{0}} + \frac{4Q^{2}}{8\pi\epsilon {R_{0}^{4}}}\right). \end{array} $$
(8)

Here only terms linear in x and its derivatives have been retained and \(\phi / {R_{0}^{5}}\) is the equilibrium gas pressure in the bubble defined by

$$ \frac{\phi}{{R_{0}^{5}}} = \left( P_{0} - P_{v} + \frac{2\sigma}{R_{0}} - \frac{Q^{2}}{8\pi\epsilon {R_{0}^{4}}}\right) . $$
(9)

The particular situation of looking for conditions where the radial velocity is constant is thus implicitly satisfied. In eq. (7), F ext is given by

$$\begin{array}{@{}rcl@{}} F_{\text{ext}} &=& -P_{s} \frac{\left( 1 + ({{R_{0}^{2}}\omega^{2}}/{c^{2}}) \right)^{{1}/{2}} } {\left( {R_{0}^{2}} + ({4\eta R_{0}}/{c\rho}) \right)} \\ &~&\times \cos \left( \omega t - \arctan \left(\frac{c}{R_{0}\omega}\right) \right) \\ &\approx& -P_{s} \frac{\left( 1 + ({{R_{0}^{2}}\omega^{2}}/{c^{2}}) \right)^{{1}/{2}} } {\left( {R_{0}^{2}} + ({4\eta R_{0}}/{c\rho}) \right)}\cos \left(\omega t -\frac{\pi}{2}+ \frac{R_{0}\omega}{c}\right), \end{array} $$
(10)

where in arriving at the last line of eq. (10), use has been made of the fact that (R 0 ω/c)≪1. Scaling the time as \(\hat t = \omega _{0} t \) for convenience, eq. (7) can be solved exactly. Dropping the hat (\(\hat {}\)) over t for convenience of notation in all of the following, the steady-state part of the solution is found to be

$$\begin{array}{@{}rcl@{}} x &=&-\frac{P_{s}\left( 1 + ({{R_{0}^{2}}\omega^{2}}/{c^{2}}) \right)^{{1}/{2}} } {\rho\left( {R_{0}^{2}} + ({4\eta R_{0}}/{c\rho}) \right)} \frac{1}{{({\omega_{0}^{2}}-\omega^{2})}^{2} + \omega^{2}\beta^{2}}\\ ~&~&\times \left(({\omega_{0}^{2}}-\omega^{2})\cos\left(\frac{\omega}{\omega_{0}}t+\theta\right) + \omega\beta\sin\left(\frac{\omega}{\omega_{0}}t+\theta\right)\right), \end{array} $$
(11)
$$\begin{array}{@{}rcl@{}} v &=& \dot x =-\frac{P_{s}\left( 1 + ({{R_{0}^{2}}\omega^{2}}/{c^{2}}) \right)^{{1}/{2}} } {\rho\left( {R_{0}^{2}} + ({4\eta R_{0}}/{c\rho}) \right)}\frac{\omega}{\omega_{0}} \frac{1}{{({\omega_{0}^{2}}-\omega^{2})}^{2} + \omega^{2}\beta^{2}}\\ ~&~&\times \left(-({\omega_{0}^{2}}-\omega^{2})\sin\left(\frac{\omega}{\omega_{0}}t+\theta\right) + \omega\beta\cos\left(\frac{\omega}{\omega_{0}}t+\theta\right)\right), \end{array} $$
(12)

where 𝜃 denotes the phase.

Combining eqs (11) and (12) we obtain

$$ \frac{\omega^{2}}{{\omega_{0}^{2}}}x^{2} + v^{2} = \frac{\omega^{2}}{{\omega_{0}^{2}}} \frac{{P_{s}^{2}}}{{R_{0}^{4}}\rho^{2}{(1+({4\eta}/{c\rho R_{0}}))}^{2}}\ \frac{1}{\left({({\omega_{0}^{2}}-\omega^{2})}^{2} + \omega^{2}\beta^{2}\right)}. $$
(13)

Again, using eq. (6) to rewrite x=R/R 0−1, and \(v=\dot R/R_{0}\) in eq. (13), we obtain after some algebra an equation for ω:

$$ \omega^{4} + \frac{K}{\rho^{2}{R_{0}^{4}}{\left(1+({4\eta}/{c\rho R_{0}})\right)}^{2}}\omega^{2} + \frac{G^{2}}{\rho^{2}{R_{0}^{4}}{\left(1+({4\eta}/{c\rho R_{0}})\right)}^{2}} = 0, $$
(14)

where

$$\begin{array}{@{}rcl@{}} G &=& 5(P_{0}-P_{v})+\frac{8\sigma}{R_{0}}-\frac{Q^{2}}{8\pi\epsilon {R_{0}^{4}}}, \\ K &=& -\frac{2{R_{0}^{2}}}{c^{2}}(c^{2}\rho + P_{0}-P_{v})G + \frac{{R_{0}^{2}}}{c^{2}}{\left (\frac{4\eta c}{R_{0}}-(P_{0}-P_{v})\right)}^{2} \\ ~&~&-\frac{{R_{0}^{6}}{P_{s}^{2}}\rho \left(1+({4\eta}/{c\rho R_{0}})\right)} {\left[ \rho {R_{0}^{4}}\left(1+({4\eta}/{c\rho R_{0}})\right)(R^{2}-2RR_{0}+{R_{0}^{2}})+G{\dot R}^{2} \right]}. \end{array} $$
(15)

This leads to the following expression for ω:

$$\begin{array}{@{}rcl@{}} \omega &=& \frac{1}{\rho {R_{0}^{2}}\left(1+({4\eta}/{c\rho R_{0}})\right)} \\ &~&\times {\left[-K \pm {\left(K^{2}-4\rho^{2}{R_{0}^{4}} {\left(1+\frac{4\eta}{c\rho R_{0}}\right)}^{2} G^{2}\right)}^{1/2} \right]}^{1/2}. \end{array} $$
(16)

After a careful look at each of the term in this equation, we find that the dominant contribution of Q to dω/dQ occurs as a cubic term:

$$ \frac{\mathrm{d}\omega}{\mathrm{d}Q} \sim a_{3} Q^{3}, $$
(17)

a 3 being a prefactor with appropriate dimensions. Integrating both sides of this equation between the limits corresponding to Q=0 and Q gives

$$ \omega-\omega_{H} \sim a_{3} Q^{4}, $$
(18)

where ω H is the frequency for the bubble with zero charge at which \(\dot {R}_{\max } = c_{1}\), so that

$$ Q \sim a_{3}^{\prime}{{(\omega-\omega_{H})}^{1/4}}, $$
(19)

(the prefactor \(a_{3}^{\prime }\) having appropriate dimensions), reproducing eq. (4) that was obtained from an analysis of the numerical results shown in the plots in figure 6. Hence, it is very easy to predict the minimum charge Q min required on a bubble at a given applied pressure amplitude for attaining some particular value of the bubble’s radial velocity, once ω H is known.

There is another interesting feature to be noted in this transition. The value of the frequency ω H depends on the magnitude of the amplitude P s of the driving pressure wave. Indeed, for a given ambient bubble radius R 0, ω H takes the simple linear form

$$ \omega_{H} = b_{1} + b_{2} P_{s}, $$
(20)

where b 1 and b 2 vary with R 0. This can be seen clearly from the plot (figure 6c). A further functional dependence of b 2 on R 0, i.e., of the slope dω H /dP s on R 0, is also found (figure 6d), and is of the form

$$ \frac{\mathrm{d}\omega_{H}}{\mathrm{d}P_{s}} \sim R_{0}^{-0.9}. $$
(21)

The maximal charge, Q max, which a bubble can carry, is bounded by the fact that beyond a value Q h of the charge, bubble dimensions may reduce to below the value of the van der Waals hard core radius for the gas enclosed, which is physically untenable.

Hence, the value of Q h , the physically feasible maximal limit to the charge the bubble may carry, will be less than Q max for a particular R 0. Moreover, it depends as well on the amplitude of the forcing pressure P s , with Q h decreasing with increasing P s and also with decreasing driving frequency. Figure 7 shows plots of Q h as a function of P s for three different driving frequencies, for R 0=2 μm. Below a certain value of P s , Q h becomes nearly independent of frequency as well as P s .

Figure 7
figure 7

Q h as a function of P s for a bubble of R 0=2 μm for three different values of driving frequencies ν. The value of P s at which Q h =0, increases with increasing frequency. The physically reachable region is the area below the curve corresponding to \(R_{\min }>h\). The region above the curve corresponds to the (unphysical) regime where \(R_{\min }<h\).

Full size image

5 Bifurcation diagrams

That the driving frequency influences the bubble dynamics is unquestionable. Techniques of dynamical systems theory have been used for long in the literature to understand bubble stability under variation of parameters (see e.g., [19,24–27]. Parlitz et al [19] have, in their work, extensively investigated the frequency bifurcation diagrams for the bubble radius at various values of the driving amplitude pressure, P s .

In figures 8–11 we have shown the bifurcation diagrams for the maximum radial amplitude R max of the given time-series of the bubble, with the driving frequency as the control parameter for R 0=1.45 μm,2 μm and 5 μm for uncharged and charged bubbles.

Figure 8
figure 8

Bifurcation diagram of a bubble oscillator with driving frequency as the control parameter, and for R 0 = 2 μm and (top): P s = 1.2P 0 (i.e., P s < P tr), and (bottom): P s = P tr=1.3P 0. Q = 0 in (a) and (c), and Q = 0.2 pC in (b) and (d).

Full size image
Figure 9
figure 9

Bifurcation diagram with respect to driving frequency of a bubble oscillator with R 0 = 2 μm and P s = 1.4P 0 for an uncharged bubble (a) and having charge Q = 0.2 pC (b). (Note that P s >P tr.)

Full size image
Figure 10
figure 10

Bifurcation diagram with respect to driving frequency of a bubble oscillator with R 0 = 5 μm for Q = 0.8 pC. The driving pressure P s = 1.4P 0 (here, P s > P tr). Successive images (clockwise from top left) show magnification of preceding insets showing period doubling and chaos.

Full size image
Figure 11
figure 11

Bifurcation diagram of a bubble oscillator with driving frequency as the control parameter for a smaller bubble. R 0 = 1.45 μm and P s = 1.4P 0. (a) Q = 0 and (b) Q = 0.1 pC.

Full size image

The bifurcation diagrams for various sets of parameters are constructed by sampling the time-series after making sure the transients have decayed, for every time period T = 1/ν of the external acoustic driving pressure elapsed. These sample points are precisely the points of intersection of the trajectories in phase plane with the Poincare cross-section, and the orbit formed by the points represents the Poincare map. The bifurcation diagram is then constructed by plotting the sampled points calculated for a range of values of the control parameter (frequency or charge) and then plotting it with the control parameter on the horizontal axis and the sampled points on the vertical axis.

In the response curves where period-doubling bifurcations occur, the branches always merge back to give period-1 oscillations.

The presence of non-zero charge on the bubble advances the period-doubling bifurcations with the driving frequency as the control parameter. This is demonstrated in the bifurcation diagrams of figures 8 and 9. For an uncharged bubble with ambient radius R 0 of 2 μm at a driving pressure of 1.2 P 0, period doubling is first seen at around 720 kHz for the uncharged bubble, while the presence of 0.2 pC charge advances it to about 600 kHz (figures 8a, b). We observe that there are no chaotic regimes present at least till driving frequencies of 1000 kHz for low driving pressures such as these.

Figures 8–10 show that increasing the external pressure P s also has the effect of advancing the succession of period-doubling–period-halving bifurcations both for the charged as well as for the uncharged systems. For instance, at 1.3 P 0 (figures 8c, d), the first period-doubling bifurcation occurs at a forcing frequency of approximately 320 kHz, followed by period-halving bifurcation at 350 kHz leaving period-1 oscillations, whereas on introducing charge Q = 0.2 pC, the first period-doubling bifurcation makes its appearance much earlier, at about 295 kHz, only to merge back to period-1 oscillations through a period-halving bifurcation at 315 kHz. As one increases the driving frequency further, one observes the occurrence of a sequence of period-doubling–period-halving bifurcations.

It should be noted that the chaotic regions make their appearance at the upper transient threshold pressure P tr (which for an uncharged bubble of R 0 = 2 μm is 1.3P 0), and become more prominent for P s > P tr (figure 9). At large driving pressures, bands of chaotic regimes are present at high values of the forcing frequency, in agreement with observations of time-series data. This is shown in figure 9 for P s = 1.4P 0: chaotic behaviour is seen to be present even at around 270–300 kHz for charged and uncharged bubbles.

In figure 10 the sequence of period-2 and period-1 oscillations generated is shown for a slightly larger bubble, with R 0 = 5 μm and bearing charge Q = 0.8 pC, driven at pressure amplitude P s = 1.4P 0.

From these observations and other plots (not shown here) we deduce that the maximal radial amplitude of the bubble of a given equilibrium radius R 0 shows chaotic behaviour as a function of the driving frequency ν, for P s ≥P tr at large values of ν. It was shown in [23] that P tr = 1.12P 0 for R 0 = 5 μm and P tr = 1.3P 0 for R 0 = 2 μm for the uncharged bubble.

For smaller frequencies, such as in the sonoluminescent regime, the presence of charge does not appear to introduce period-doublings in the system. However, the effect of charge in bringing about drastic changes in the bubble stability is more pronounced for smaller values of R 0. This is demonstrated in figures 11a, b for a bubble with R 0=1.45 μm and driving pressure amplitude P s of 1.4P 0.

The presence of 0.1 pC charge on the bubble (figures 11b) induces a period-doubling bifurcation at a driving frequency of 880 kHz followed in quick succession by a period-halving bifurcation at 1040 kHz. These are absent for an uncharged bubble (figure 11a).

To get a clearer picture of the dynamics, largest Lyapunov exponents λ max have been calculated for ambient bubble radius 5 and 1.45 μm, and plotted respectively in figures 12 and 13. These correspond respectively to the parameter values and frequency ranges considered in the bifurcation diagrams in figures 10 and 11b.

Figure 12
figure 12

Largest Lyapunov exponents for a bubble oscillator of ambient radius R 0 = 5 μm, Q = 0.8 pC and P s = 1.4P 0, calculated across driving frequencies ranging from 35 to 400 kHz, shown with the corresponding section of the bifurcation diagram in figure 10.

Full size image
Figure 13
figure 13

Largest Lyapunov exponents for a bubble oscillator of ambient radius R 0 = 1.45 μm, Q = 0.1 pC and P s = 1.4P 0, calculated across driving frequencies ranging from 500 to 1100 kHz, shown with the corresponding section of the bifurcation diagram in figure 11b.

Full size image

The figures show positive values where chaotic dynamics occur. The dips in figure 12 correspond precisely to the windows of stable periodic oscillations. Figure 13 shows negative values of Lyapunov exponents showing stable periodic behaviour and reducing to zero at the points of bifurcation. In fact, λ max vanishes at the bifurcation points located at 509, 622, 798, 897 (period-doubling bifurcation) and 1049 kHz (period-halving bifurcation).

In figure 14 we obtain the bifurcation diagram of a bubble of R 0 = 2 μm driven by sonic pressure amplitude of 1.4P 0 and frequency 300 kHz with charge as the control parameter. The choice of 300 kHz for the driving frequency has been made using the bifurcation diagram with frequency as the parameter (figure 9), where the system is just beginning to get chaotic at this frequency. In figure 14 we see an interesting non-chaotic region centred around Q=0.125 pC with period-doubling and period-halving cascades. While constructing the bifurcation diagrams, care has been taken to ensure that we work only within the range of charges permissible for a bubble of a given ambient radius.

Figure 14
figure 14

Bifurcation diagram of a bubble oscillator with charge Q as the control parameter and with R 0 = 2 μm, P s = 1.4P 0 and ν = 300 kHz. Non-chaotic windows are seen, and the most prominent one centred around Q = 0.125 pC.

Full size image

6 The collapsing bubble: Frequency and charge dependence of temperature

Investigating the maximum temperature as a function of the driving frequency, we obtain the interesting result that there exist two distinct domains of behaviour of T max depending upon the amplitude of the driving pressure, P s .

At lower pressures, i.e., for P s < P tr (e.g., for P s = 1.1P 0, R 0 = 5 μm), T max increases with driving frequency. However, as this value of P s falls in the vicinity of the transient threshold in the unstable regime (figure 4a), we would expect T max to show large oscillations with frequency, as is also seen in figure 15a.

Figure 15
figure 15

Maximum temperature T max vs. ν for different values of charge Q at (a) P s = 1.1P 0 (lower/medium pressure, P s < P tr) and (b) P s =1.25P 0 (high pressure, P s > P tr); the contrasting behaviour above and below P tr can be seen.

Full size image

At higher pressures, i.e., for P s > P tr (e.g., for P s = 1.25P 0, R 0 = 5 μm), the maximal temperature’s frequency dependence is the opposite, with T max decreasing uniformly with increasing frequency, showing oscillatory behaviour (figure 15b). T max shows a frequency dependence of the form

$$ T_{\max} = a_{4} \times (\nu - a_{5})^{-4/5}, $$
(22)

a 4 and a 5 being constants with appropriate dimensions. This is understood by recalling that the temperature is obtained from

$$ T = T(0) \left(\frac{{R_{0}^{3}} - h^{3}}{R^{3} - h^{3}}\right)^{2/3}, $$
(23)

for Γ = 5/3. Making the approximation that (h/R 0)3 < 1 and also that (h/R)3 < 1 is sufficiently small at most values of R, we can approximate eq. (23) by

$$ T \approx T(0){R_{0}^{2}} / R^{2}. $$
(24)

Since at regimes at or near the Rayleigh collapse, R(t)∼ω 2/5, it immediately follows that

$$ T(t) \propto \omega^{-4/5}. $$
(25)

Values of T max at lower pressures are less than that at higher pressures. Temperature T max rises steeply with pressure P s after some critical value of the pressure that equals the upper transient pressure threshold. Temperature calculations have also been reported by Wu and Roberts [28] and Yasui [29] giving high magnitudes of the temperature. The presence of charge serves to reduce the pressure at which the maximum temperature T max is reached. As seen in figure 5b, increasing the driving frequency shifts the curves to the right, i.e., the same maximal bubble velocity v max that is obtained at some driving frequency ω 1 for a pressure amplitude P s 1, is reached for a higher frequency ω 2>ω 1 only at a higher pressure P s 2>P s 1. Figures 5b and 16, where v max vs. P s , P tr vs. Q and T max vs. Q plots, respectively are shown for R 0=5 and 2 μm for charged and uncharged bubble at different driving frequencies, illustrate the effect of driving frequency and charge on bubble velocity, temperature and the location of the upper transient pressure threshold.

Figure 16
figure 16

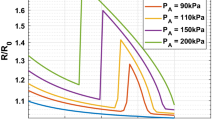
(a) P tr decreases with increasing Q over all driving frequencies. At a given charge, higher driving frequencies imply higher P tr. (b) The P tr–Q curves when scaled by P tr at Q=0, P tr 0, all fall on a master curve obeying eq. (26). (c) \(T_{\max }\) vs. Q curves plotted at a pressure equal to the corresponding upper transient threshold value P tr for that particular value of Q, all fall nearly on the same curve. Plots are for R 0=2 μm.

Full size image

The regime of large fluctuations and drastic increases and decreases in T max correspond to the region of competing dynamics between the explosive expansion subsequent to the Blake threshold and the violent implosion at the upper transient pressure threshold. This competing influence is reflected also in figure 5a for the dependence of the maximum radial bubble velocity on the applied frequency. There, as mentioned in §4, v max decreases with frequency for P s >P tr and increases with frequency for P s < P tr. The time-scales involved in the collapse and expansion being different, lead to sudden fluctuations in radial velocity and thereby in the temperatures attained within the bubble. The competition in time-scales is also reflected in the saw-tooth like curves characteristic of relaxation oscillations in figure 15. The occurrence of multistability is therefore indicated. Further investigations on the structure of possible basins of attraction are underway and will be reported elsewhere.

The net effect of charge is to raise the possible T max for a bubble in comparison to the uncharged bubble. A comparative plot of T max reached at the upper transient threshold pressure P tr as a function of charge Q is shown for a few values of the driving frequency ν in figure 16. The temperature T max increases with charge Q for all forcing frequencies.

The value of P tr (for a given bubble charge, Q) increases with ν. P tr at a given driving frequency decreases with increasing Q. The dependence of P tr on Q over all frequencies can be captured by a normalized plot of P tr/P tr 0 against Q, where P tr 0 is the upper transient threshold pressure at zero charge, for a given frequency. This yields a master curve approximately obeying a relation of the form

$$ P_{\text{tr}}= \frac{{P_{\text{tr}}}_{0}}{1 + 0.794 Q^{2}}, $$
(26)

as seen in figure 16b. The maximal value of temperature T max reached in a driven oscillating bubble, at the corresponding, respective P tr (which varies with ν and Q), over all values of charge Q, seems almost independent of the driving frequency ν, as shown in figure 16c.

At higher pressures, beyond the upper transient threshold pressure, bubble velocities become larger and of the order of c. We argue that the maximal kinetic energy \(\frac {1}{2}M{\dot {R}}^{2} \approx \frac {1}{2}Mc^{2}\) would approximately equal the dominant electrostatic contribution to the potential energy Q 2/(4π 𝜖 R 0), so that using \(M = 4\pi {R_{0}^{3}}\rho /3\), we get \(Q^{2} \sim {R_{0}^{4}}\). This argument is independent of the driving frequency at which the bubble is being forced. At a sufficiently high charge Q max, a bubble of ambient radius R 0 will collapse to the same minimum radius R min, independent of the driving frequency of the forcing pressure amplitude. However, this Q max value will typically be greater than Q h , the upper bound imposed on charge Q by the physically realistic requirement that R min does not go below the van der Waals hard-core radius. Thus, while this results in Q h being the greatest, physically realistic value of charge that a bubble can carry, we can still read off the value of a larger Q=Q max from R min vs. Q plots at high driving pressures, by identifying Q at which frequency independence of the curves sets in and all the curves for different driving frequencies converge to the same R min. More detailed discussions of R min dependencies are included in our earlier work [23], and we do not show the plots here.

Hence a comparative estimate of this maximal charge a bubble can carry, Q max, for two different values of the initial bubble radius R 0, say, R 0 a and R 0 b , would be obtained from

$$ \left(\frac{{R_{0}}_{a}}{{R_{0}}_{b}}\right)^{2} \sim \left(\frac{{Q_{\max}}_{a}}{{Q_{\max}}_{b}}\right), $$
(27)

(for larger bubbles, of order O(μm) and above). This is essentially a statement that the maximal surface charge density a bubble can carry is approximately same regardless of its initial ambient radius for micrometer and larger bubble radius, given that all other system parameters such as the surface tension, pressure conditions, viscosity, etc. remain unchanged, while the influence of the effective surface tension (including the correction for charge present) is predominant in the submicron range. Indeed, for submicron and at very small bubble sizes where the surface tension and charge terms become just comparable, we would have instead (comparing electrostatic energy with surface tension or elastic energy) \(Q^{2}/R_{0}\sim k{R_{0}^{2}} = m{\omega _{b}^{2}} {R_{0}^{3}}\), with \(k = m{\omega _{b}^{2}}\) being an effective spring constant, ω b some natural frequency and m the oscillator mass, so that on substituting for \(m= (4/3)\pi \rho {R_{0}^{3}}\), we get

$$ \left(\frac{{R_{0}}_{a}}{{R_{0}}_{c}}\right)^{3} \sim \left(\frac{{Q_{\max}}_{a}}{{Q_{\max}}_{c}}\right)^{2} $$
(28)

for two different values of the initial bubble radius R 0, R 0 a and R 0 c .

That such a non-rigorous approach cannot give any accurate numbers, is obvious. Nonetheless, it is useful in giving rough estimates of the maximal charge that the bubble can carry, in the absence of a constraint such as that imposed by the van der Waals hard-core radius.

A comparison of the values so obtained in this rough and ready way to that obtained from the numerical results is given in table 1 for three different values of ambient bubble radius R 0, at P s =1.35P 0.

Table 1 \(Q_{\max }\) ratio from eq. (27) (through R 0 ratio) compared with numerical values of \(Q_{\max }\) from the data.
Full size table

7 Conclusions

The presence of charge on a bubble suspended in a fluid influences the bubble’s oscillations under ultrasonic forcing, and some of the aspects of the dynamics have been addressed in this paper, taking the polytropic constant Γ=5/3 which governs the equation of state for adiabatic heat transfer. A dimensionless constant ζ which we introduced in an earlier work [23] helps us to clearly identify the Blake threshold and the upper transient threshold P tr for acoustic cavitation. We use this to understand the influence of driving pressure P s and frequency ν of the applied ultrasonic field on the bubble oscillations. The presence of charge reduces the effective surface tension on the bubble walls so that its maximum radius R max attained during the expansion phase is larger than when it is uncharged; similarly, the minimum bubble radius R min during collapse is much smaller in magnitude when the bubble is charged. The charged bubble undergoes a more violent collapse, achieving far higher temperatures in its interior in comparison with the uncharged one. We find that when P s < P tr, the maximum temperatures T max achieved in the bubble increase with increasing ν and charge. For P s >P tr, T max obeys a power-law decrease with respect to ν, with an exponent of −4/5. The power-law behaviour is also obtained analytically through scaling arguments near the regime of Rayleigh collapse.

Bifurcation diagrams of the maximal radial amplitude of the bubble as a function of the driving frequency show the presence of chaotic regimes for P s ≥P tr for any given ambient bubble radius at fairly large driving frequencies. The route to chaos is through period-doubling followed by period-halving bifurcations. The effect of charge is to always advance these bifurcations. At the lower end of the ultrasound spectral range, for instance, in the sonoluminescent regime, the presence of charges do not appear to induce any period doublings.

Consistent with the fact that the presence of charge has a greater dominating effect over surface tension on bubbles of smaller equilibrium radii [23], the bifurcation diagrams demonstrate that the effect of charges in drastically changing bubble stability is more pronounced for smaller bubbles.

We also obtain the bifurcation diagram of the maximal radial amplitude at any given P s as a function of charge at large driving frequency. Here too, period doublings and period halvings are seen interspersed with large chaotic regimes. The Lyapunov exponents calculated across a vast range of frequencies also make clear the underlying periodicities and chaotic dynamics of the bubble.

We analytically estimate the minimum charge Q min required on a bubble at a given magnitude of applied pressure to attain a certain value c 1 of the bubble radial velocity. We find that this is related by a simple power-law to the driving frequency of the acoustic wave. We show that above a critical frequency ω H , uncharged bubbles necessarily have to oscillate at velocities below c 1. The calculations are reproduced numerically also. Further, we show that ω H depends upon P s .