Early thermal evolution and planetary differentiation of the Moon: A giant impact perspective

Abstract

The Moon is a unique planetary body with low bulk metallic iron content and a core–mantle–crust structure. Multiple observations contraindicate the cogenetic, capture, and fission hypotheses for the origin of the Moon and suggest a cataclysmic origin. This strengthens the giant impact hypothesis as the most plausible hypothesis for the formation of the Moon. Although the giant impact hypothesis has been rigorously studied for a vast range of scenarios, the uncertainty remains regarding the most plausible one. In addition, the early thermal evolution and planetary-scale differentiation from the giant impact perspective are poorly understood. Several unresolved issues exist, such as the initial average temperature of accreting moonlets, the depth of the initial magma ocean, the role of convection, and the cooling and iron-core formation timescales. We present a novel lunar model for the early thermal evolution, convective magma ocean evolution, and core-mantle differentiation based on the giant impact hypothesis to access some of these uncertainties. This model numerically incorporates the features associated with local Rayleigh numbers for convection, the gravitational energy released by planetary-scale differentiation, and the numerical dependencies of physical and thermodynamical quantities on parameters like depth, temperature, pressure, density, viscosity, and crystal mass fraction. In order to have an early iron-core formation, the accreting moonlets should have a minimum temperature of 1900 K. This can serve as a stringent constraint on the giant impact models if the core was formed early through Stokes' flow. This implies a ≥1000 km deep fully molten initial magma ocean which cooled down to rheological critical temperature profile over hundred thousand years.

Research highlights

• 1. Local Rayleigh numbers in convection yield cooling timescales of 0.01–0.1Ma.

• 2. Temperature of accreting moonlets ≥ 1900 K is required for early core formation.

• 3. A ~1000 km deep initial lunar magma ocean is capable of early core formation.

• 4. Early core-formation leads to fully molten core, potent for producing geomagnetism.

1 Introduction

The Moon is a unique planetary body with a low bulk density of ~3346 kg m⁻³ (Williams et al. 2014) and a tiny iron-core of 330 km radius that constitutes ~1.5% of the bulk mass fraction (Weber et al. 2011; Williams et al. 2014). The Moon and Earth have similar isotopic compositions of oxygen (Spicuzza et al. 2007), chromium (Lugmair and Shukolyukov 1998), silicon, titanium (Zhang et al. 2012), and tungsten (Kruijer and Kleine 2017; Melosh 2014; Touboul et al. 2015). Further, the ratio of the orbital angular momentum of the satellite to the total angular momentum of the planet-satellite system is extraordinarily-high for the Earth–Moon system compared to the majority of the other planet-satellite systems in the solar system, viz., Jupiter, Saturn, Uranus, Neptune, and Mars. These observations substantially rule out the feasibility of the cogenetic, capture, and fission hypotheses for the origin of the Moon (e.g., reviews, Canup 2004; Stevenson 1987). Furthermore, the depletion of volatiles like K, Na, and Zn (Taylor et al. 2006) suggests formation of the Moon in a cataclysmic event (Canup et al. 2015). However, recent studies indicate the Moon is comparatively less volatile than the earlier estimates (Saal et al. 2008; Hauri et al. 2015). Consequently, the giant impact hypothesis remains the only plausible hypothesis for the formation of the Moon.

The canonical giant impact hypothesis (Hartmann and Davis 1975; Cameron and Ward 1976) deals with an oblique collision of a Mars-sized body ‘Theia’ with the early Earth. The two bodies are considered to have differentiated into the core-mantle structure before the impact, thereby resulting in the merger of the planetary iron cores (Salmon and Canup 2014) subsequent to the collision. The hypothesis has been rigorously simulated numerically in many subsequent studies (e.g., Benz et al. 1986; Stevenson 1987; Canup and Asphaug 2001; Canup 2004, 2012; Ćuk and Stewart 2012; Salmon and Canup 2014; Canup et al. 2015; Barr 2016; Lock et al. 2018). The chronological records of the Earth and Lunar samples indicate the giant impact event took place within the first ~30 to 100 million years of the solar system formation (Elkins-Tanton et al. 2011; Touboul et al. 2015; Kruijer and Kleine 2017).

The canonical giant impact models draw a large portion of disk material from the impactor. These models provide angular momentum of the order of present-day angular momentum of the Earth–Moon system. On the other hand, in the non-canonical models, the head-on collision of a comparatively large or small impactor is considered. As a result, these models draw most of the material from the surface of the Earth. In addition, these models produce comparatively compact disks, with a large part inside the Roche limit and an angular momentum two to three times that of the present-day angular momentum of the Earth–Moon system (Ćuk and Stewart 2012; Salmon and Canup 2014).

Several mechanisms have been proposed for the removal of the additional angular momentum from the system. For example, Ćuk and Stewart (2012) suggested the removal of excess angular momentum tidally when the Moon enters in evection resonance with the Sun. Wisdom and Tian (2015) and Tian et al. (2017) have shown that evection resonance suggested by Ćuk and Stewart (2012) removes too much angular momentum and gets destabilised by overheating the Moon. They also proposed a limit cycle of the evection resonance that removes excess angular momentum without overheating the Moon. Ćuk et al. (2016) proposed another mechanism where the additional angular momentum is shed off tidally during the Laplace plane transition. In addition, this mechanism also attempts to explain the lunar orbital inclination. This causes weak tidal heating of 10¹⁴–10¹⁵ W for several Myr after a few initial Myr.

The canonical models require chemical equilibration between the hot Earth and the orbiting disk via vapour cloud to satisfy the isotopic similarities (e.g., Lugmair and Shukolyukov 1998; Spicuzza et al. 2007; Zhang et al. 2012; Melosh 2014; Touboul et al. 2015) between the Earth and the Moon. However, the equilibration of titanium isotopes would require a temperature above 3000 K for more than a year after collision (Pahlevan and Stevenson 2007; Melosh 2014). On the other hand, the non-canonical models require the capture of the Moon into the evection resonance with the Sun at a slower pace to effectively shed off the extra angular momentum of the Earth–Moon system (Salmon and Canup 2014). Because only the material inside the Roche-interior disk is continuously churned by tidal forces, the chemical equilibration of titanium for Roche-exterior material may not be feasible in canonical models, leaving about half of the lunar material as chemically distinct from the Earth (Melosh 2014; Salmon and Canup 2014).

In both scenarios, the simulations have indicated that the Moon rapidly accreted around 40% of its mass from the Roche-exterior disk within a matter of few days. After several tens of years, the Roche-interior disk expanded beyond the Roche limit. The expansion resulted in the disk being cooled down, and the formation of new moonlets initiated. These newly formed moonlets either got accreted on the young Moon or scattered, based on the recoil velocity and the Earth–Moon distance as the proto-Moon proceeded away from the Earth. After ~200 years from the giant impact, the accretion became inefficient due to higher eccentricities of the moonlets (Salmon and Canup 2014).

A new model has been proposed in the form of a recently conceptualised planetary structure, referred to as ‘Synestia’ (Lock and Stewart 2017), as an intermediate state between giant impact and formation of the Moon in contrast to an orbiting disk in the conventional models (Lock et al. 2018). These models utilise impact scenarios with higher angular momentum that exceed the corotation limit. The excess angular momentum can be shed off via one or more mechanisms discussed earlier, like in the case of non-canonical models. In the models based on Synestias, the dynamics of synestias effectively equilibrate the materials of the impactor and target at a specific temperature and pressure (Lock and Stewart 2017). Synestias extending beyond Roche limit provide chemical equilibration with Roche-exterior matter (Lock and Stewart 2017; Lock et al. 2018). The cooling timescales of Synestia are also proposed to be around 10–1000 years (Lock et al. 2018).

While the giant impact hypotheses have been rigorously studied, the early thermal evolution and differentiation of the Moon are poorly understood. A few attempts have been made to analyse the early evolution of the Moon (e.g., Elkins-Tanton et al. 2011; Suckale et al. 2012; Sahijpal and Goyal 2018; Maurice et al. 2020) based on the giant impact event. Elkins-Tanton et al. (2011) have numerically studied a magma ocean that fractionates with 100% efficiency and convectively cools at a rate fully controlled by surface radiation. Suckale et al. (2012) considered the crystal residency times in a convective magma ocean, where surface radiation controlled the cooling rate. Sahijpal and Goyal (2018) numerically studied the thermal evolution of the early Moon with several convective cooling rates. Maurice et al. (2020) studied the late evolution of the magma ocean and the core. However, there still remain many uncertainties regarding the initial stages of evolution. These include issues related to accreting moonlets’ initial average temperature, the depth of the initial magma ocean, the role of convection and the cooling and core formation timescales.

Here, we present a set of novel numerical models for the planetary-scale differentiation and evolution of the early Moon to derive insights into the gaps in our understanding of the early Moon. Contrary to the models by Sahijpal and Goyal (2018), hereafter referred to as SG18, the models presented here are more realistic in numerically implementing the detailed science related to thermal evolution and differentiation. The numerical modelling is performed based on a versatile novel code developed in ‘Python’ language, using ‘NumPy’ and ‘SciPy’ packages, contrary to SG18 in ‘Fortran’ language that had numerical limitations in the complete realisation of the various processes related to thermal evolution and differentiation. We have perhaps for the first time numerically incorporated local Rayleigh numbers to study the radial variation of convection in 1-D (one-dimensional) full-scale planetary models and the heating due to the gravitational energy released during planetary-scale differentiation apart from the impact-induced accretional heating. Several novel features have been incorporated in our present lunar models by considering the dependencies of physical quantities on several parameters like depth, temperature, pressure, density, viscosity, and crystal mass fraction.

2 Methods

A two-component thermal model for the differentiation of the Moon is developed with metals and silicates as the major components.

2.1 Energy conservation equation

We simulated the thermal evolution of the Moon using a modified heat conduction equation for the one-dimensional representation of a spherically symmetric body using equation (1). The body represents the Moon during its growth and evolution. The values and expressions of the various physical quantities are listed in table 1.

Table 1 List of the adopted values, numerical ranges, expressions, and symbols for the various physical parameters used in simulations and the manuscript. Quantities are in SI units unless specified otherwise.

$$\rho {C}_{p}\frac{\partial T}{\partial t}=\frac{1}{{r}^{2}}\frac{\partial }{\partial r}\left[\left({k}_{{\rm lat}}+{k}_{{\rm rad}}\right){r}^{2}\frac{\partial T}{\partial r}+{k}_{{\rm conv}}{r}^{2}\left(\frac{\partial T}{\partial r}-{\left(\frac{\partial T}{\partial r}\right)}_{S}\right)\right]+{E}_{g},$$

(1a)

Using, ${k}_{{\rm eff}}={k}_{{\rm lat}}+{k}_{{\rm rad}}+{k}_{{\rm conv}}, {k}_{{\rm conv}}=\left(Nu-1\right)\times {k}_{{\rm lat}}, {H}_{S}={k}_{{\rm conv}}{\left(\frac{\partial T}{\partial r}\right)}_{S}$, we get:

$$\rho {C}_{p}\frac{\partial T}{\partial t}={k}_{{\rm eff}}\frac{{\partial }^{2}T}{\partial {r}^{2}}+\frac{\partial {k}_{{\rm eff}}}{\partial r}\frac{\partial T}{\partial r}+\frac{2{k}_{{\rm eff}}}{r}\frac{\partial T}{\partial r}-\frac{2{H}_{S}}{r}-\frac{\partial {H}_{S}}{\partial r}+{E}_{g} .$$

(1b)

A novel Python code was written to solve this equation numerically. Here, ρ is the bulk density, C_p is the effective specific heat, T is the evolving temperature, k_lat is the thermal conductivity due to phonons, k_rad is the thermal conductivity due to photons, k_conv is the equivalent thermal conductivity due to convection, k_eff is the effective thermal conductivity, Nu is the Nusselt number, E_g is a source term for the gravitational energy released during planetary-scale differentiation. All of these parameters evolve in r and t. The radial distance r is from the centre, and the time t is measured from the giant impact event at the time of onset of the Moon’s accretion.

The term $(\frac{\partial T}{\partial r}-{\left(\frac{\partial T}{\partial r}\right)}_{S})$ represents super-adiabatic thermal gradients. In the present models, we have incorporated the terms, ∂T/∂r and ∂k_eff/∂r, which were not incorporated in SG18. In SG18, the term ∂T/∂r was neglected on the basis that it is significant only for a few spatial grids close to the centre due to 1/r dependence. However, we assert that it is also essential in our detailed models, in spatial grids with ∂T/∂r ≫ ∂²T/∂r². The term ∂k_eff/∂r becomes significant because incorporating the local convection effects, as discussed later, in computing k_eff has resulted in a considerable spatial variation of its value.

There is a considerable variation in conductivity among silicate glass/liquid and crystalline phases, and the extent of crystallisation is not perfectly known. The values incorporated here are representative of silicate glasses. We have also incorporated thermal conduction by optical transfer, which was not considered in SG18. The effective thermal conductivity was computed using the equation, k_eff = Nu × k_lat+k_rad, which includes the thermal conduction, k_lat, the optical conduction, k_rad, and the thermal convection, Nu. Nusselt number, Nu is assumed to be one outside the convection zones. A detailed description of computing Nusselt number, Nu, is provided in subsection 2.6.

2.2 Numerical scheme

We used a classical-explicit approach for the finite-difference method to solve the equation (1). The entire Moon was radially partitioned into 1737 spatial grids with the block-centred partitioning scheme defined by δ_r: 0 = r_1/2 < r_3/2 < … < r_n−1/2 < r_n+1/2 = R with grid-size, Δr = 1 km, grid position, r_i = (i −1/2) Δr, where i ∈ [1,1737]. In the scheme, ith grid-layer spans space bounded by [(i−1) Δr, iΔr]. A group of spatial grids is occasionally referred to as a layer in the text. The assumed spherical symmetry yields ∂f/∂r|_r=0 = 0, where f is any spherically symmetric physical quantity. This defines the boundary condition at the centre. Another boundary condition at the surface was set up in the form of fixed surface temperature.

Within the initial 0.1 years, we added the first 1280 spatial grids, and in the subsequent 199.9 years, we added the remaining 457 grids (Salmon and Canup 2014). During the accretion, the surface temperature was dictated by impact-induced heating and the initial energy from giant impact (see subsection 2.3). After the accretion, the surface temperature was fixed at an ambient temperature of 250 K. It is essential to mention that we fixed only the surface (r = R) temperature to 250 K, while allowing the temperature of the last 1737th grid-layer (r = R – Δr/2) to evolve freely. Figure 1 shows the approximate free evolution of the temperature of the last 1737th grid-layer (r = R – Δr/2) in our numerical models. In the SG18, the impact heating was not incorporated whenever the surface temperature rose above 1625 K due to the assumption related to thermal relaxation. However, as a significant improvement, we completely relaxed this assumption in the present work, thereby allowing the temperature to rise due to impact heating beyond the earlier limit defined for thermal relaxation. This makes the present thermal models more realistic in terms of the realisation of thermal evolution of the Moon, especially during the convective magma ocean cooling.

Figure 1

Temporal evolution of temperature of 1737th grid-layer (surface layer) 0.5 km below the surface.

In the simulations, we fixed a spatial resolution of 1 km. We varied the temporal resolution with an adaptive approach. This has several advantages over our earlier approach (SG18), where it was fixed. We considered four distinct criteria for defining the upper limit of the temporal step. These are based on:

• (i) half of the basic courant criteria defined by Δr²/κ_{eff, max}/4,

• (ii) minimum of 2ρC_pk_eff/(2k_eff/r + ∂k_eff/∂r)² over complete spatial range to satisfy the additional stability criterion required by term ∂T/∂r.

• (iii) half of the minimum time taken by any metallic parcel to move by a distance equal to spatial grid size computed by Δr/v_max/2,

• (iv) a static minimum temporal resolution.

to a minimum of these four was taken as the temporal step. The temporal step was recalculated using equation (2) after each computational step.

$$\Delta t={\rm min}\left\{\frac{\Delta {r}^{2}}{4{\kappa }_{{\rm eff},{\rm max}}} ,{\rm min}\left\{\frac{2\rho {C}_{{p}}{k}_{{\rm eff}}}{{\left(\frac{2{k}_{{\rm eff}}}{r} +\frac{\partial {k}_{{\rm eff}}}{\partial r}\right)}^{2}}\right\},\frac{\Delta r}{2{v}_{{\rm max}}} , {\Delta t}_{{\rm next}},\Delta {t}_{m}\right\}.$$

(2)

Here, v_max is the descend velocity of the fastest molten metallic blob during differentiation and Δt_next is the time remaining for the accretion of the next spatial grid, or time remaining for the next predefined output time, and Δt_m is 100 years. The timestep varied from ~1 minute to 100 years in the simulations.

2.3 Heat sources

Heat energy in the Moon primarily came from the initial heat energy (remnant of energy from Giant Impact), impact-induced heating, heating by gravitational energy release due to planetary differentiation, and radiogenic heating.

2.3.1 Initial heat energy and impact-induced heating

During the formation period of the Moon, while adding ith grid-layer, we compute the temperatures at the surface (r = i×Δr) and that of ith grid-layer (r = (i−1/2)×Δr) by h-parameter using the equation, T(r) = hgr/C_p + T_ini (Kaula 1979; Sahijpal and Goyal 2018). Here, T_ini is the initial average temperature of the accreting moonlets subsuming the remnant heat energy of Giant Impact, and g is the local acceleration due to gravity. This equation implies the conversion of kinetic energy at escape velocity to the heating of the surface grid, with an efficiency of impact-induced heating defined by the h-parameter at any instant of lunar accretion.

2.3.2 Heating by gravitational energy release due to planetary differentiation

The planetary-scale differentiation leads to a decrease in total gravitational potential energy. This energy is dissipated as heat in the moving molten metallic blobs and their surroundings (Solomon 1979; Desch et al. 2009; Ricard et al. 2009; Šrámek et al. 2010; Neveu et al. 2015). This gravitational energy released due to planetary differentiation is incorporated into the models in a manner that is neither time-averaged nor space-averaged. The gravitational energy released by each descending parcel between the specific spatial grids was calculated at each time step, and added to the heat-conduction equation (1) as a source term. The source term was computed by equation (3)

$${E}_{g}=\frac{{\rm Energy \, released}}{{\rm Volume }\times {\rm time}}=\frac{{\Delta {m}_{i}g}_{i}\Delta r}{{{V}}_{{i}}\Delta t}=\frac{\left({M}_{i+1\to i}-{M}_{i\to i-1}\right)\left({\rho }_{M}-{\rho }_{Si}\right)}{{\rho }_{M}} \frac{{g}_{i}\Delta r}{{{V}}_{{i}}\Delta t}.$$

(3)

Here, M_i+1→i denotes the molten metallic mass moved from the spatial grid ‘i+1’ to ‘i’ in time Δt, g_i defines the local gravity, V_i is the volume of grid-layer, and Δm_i is mass gain by ith grid-layer.

2.3.3 Radiogenic heating

The late formation of the Moon deprived it from the short-lived radionuclide, ²⁶Al, which is a potent heat source (Sahijpal et al. 1995; Sahijpal and Goyal 2018). On the other hand, the long-lived radionuclides (⁴⁰K, ^235,238U, ²³²Th) could not provide significant global heating for the timespan considered in this study. Based on our calculations, we estimate that radiogenic heating due to homogeneously distributed long-lived radionuclides could make a total increase of the order of 10⁻¹ K in the timespan of 2 Myr (million years). This makes the effect of heating due to long-lived nuclides negligible in the present two-component model. Therefore, radiogenic heating is not incorporated in the present models.

2.4 The chemical composition and thermodynamic properties

In SG18, we had assumed a modified H-chondritic composition to represent lunar material. The values used for the various parameters like solidus, liquidus, specific heat, etc., were also of H-chondrites. However, in the present models, we adopted a composition to match the Moon’s composition better and computed parameters more suitable for the Moon. Lunar Primitive Upper Mantle (LPUM) composition was used to represent the bulk silicates in the Moon (Longhi 2006; Elardo et al. 2011). Several options are available for the bulk silicate compositions in the literature, e.g., LPUM, Taylor Whole Moon (TWM), O’Neill (ON), and the versions thereof. TWMs represent compositions enriched with alumina, whereas LPUM compositions represent alumina similar to the terrestrial primitive upper mantle. ON contains terrestrial refractory concentration but with a lower Mg-number (Charlier et al. 2018). Recently, the estimates of composition are further improved by making use of igneous crystallisation programs, e.g., Lin et al. (2017), Charlier et al. (2018), Rapp and Draper (2018). The choice of composition in this study does not advocate for a particular composition. Instead, the LPUM composition was chosen because of the availability of data that is more compatible to implement in our two-component models. Recent improved compositions like Rapp and Draper (2018) were not utilised because consistency cannot be ensured while incorporating fractional crystallisation into the two-component model. For the bulk metallic content, we considered a composition defined by the mole fraction of 0.15 for FeS in the Fe–FeS assemblage (Antonangeli et al. 2015; Morard et al. 2018). In SG18, we did not consider the density-dependent pressures. However, in the present models, we computed the depth-dependent pressures as a function of the continuously evolving density profile. In the present models, we have incorporated latent heat by modifying the effective specific heat capacity during melting and solidification, whereas in SG18, the latent heat was only included during melting.

Figure 2 shows the depth-dependent pressures for three cases: (i) Differentiated 1737 km Moon, (ii) Homogeneous 1737 km Moon, and (iii) Homogeneous 1280 km Moon (0.1 years). The internal pressures clearly rise sharply with accretion, and the differentiation results in an increase in the pressure of core-region by up to 15%.

Figure 2

The radial profile of depth-dependent internal pressures. The solid curve shows a fully accreted Moon that is differentiated into the core-mantle structure. The dotted curve represents a fully accreted but homogeneous Moon. The dashed curve shows a partially accreted (40% by mass) homogeneous Moon.

Figure 3 shows the liquidus, solidus, the rheological transition (i.e., 40% melting of the pure component) temperatures of (a) silicates and (b) metals for (i) differentiated 1737 km Moon, (ii) homogeneous 1737 km Moon, and (iii) homogeneous 1280 km Moon (0.1 years). These temperatures are computed using equations given in table 1 (Elardo et al. 2011) and pressures shown in figure 2. Rheological transition temperature (40% melting) was computed assuming linear melting between solidus and liquidus. Our simulations allowed the hydrostatic pressure and transition temperature to evolve freely according to the prevailing density profile.

Figure 3

Depth-dependent phase-transition temperatures. The radial profile of the various phase transition temperatures for (a) silicates and (b) metals. In each panel, the solid curve shows a fully accreted Moon differentiated into core-mantle structure; the dotted curve shows a fully accreted but homogeneous Moon. The dashed curve shows a partially accreted (40% by mass) homogeneous Moon.

2.5 Metal-silicate segregation through Stokes' flow and rheological properties

Because of the unavailability of data and the complicated mixing effects, the contributions of metals were neglected while calculating viscosity. Therefore, the viscosity parameters were computed to conform to LPUM composition irrespective of the metallic fraction in a specific spatial grid. In SG18, the crystal-fraction dependency of the viscosity of partial melt was used only to estimate the Nusselt number's maximum value. However, in present models, the crystal-fraction dependence of viscosity is incorporated numerically into the model itself and considered in all viscosity-dependent processes.

In SG18, we used a constant descent velocity for the molten iron blobs for the planetary differentiation processes. However, we incorporated Stokes' velocity using the equation, v = (2/9η)Δρga², for metal blobs falling through the rheological liquid in our present models. There exist significant uncertainties in the size of the molten metallic iron blobs because the iron blobs may pass through each other due to differential velocities and can merge to form more giant blobs. Further, these blobs have a maximum stable size that depends upon the viscosity of the underlying material. Therefore, we dynamically varied the molten metallic iron blob size from 0.001 m (Solomatov 2015) to 1 m based on the increase in the metallic content. The iron-blob size was further limited by the maximum stable size. The maximum stable size for iron-blobs is considered as 0.014 η^0.32 (Qaddah et al. 2019). In some models, we varied the blob size from 0.05 m instead of 0.001 m to study the lower bound’s effect. We have not incorporated the inhibition of Stokes' flow by convective turbulence (discussed in later sections).

At every timestep, a volume ΔV_i was exchanged between consecutive grid-layers i and i+1. The grid-layer i receive the metallic mass of volume ΔV_i from grid-layer i+1, and grid-layer i+1 receives the silicate mass of volume ΔV_i from grid-layer i. The process was performed for each consecutive pair of grid layers. Therefore, each layer gained metals from the layer above it, lost metals to the layer beneath it, gained silicates from the layer beneath it, and lost silicates to the layer above it at every timestep. The volume exchange was limited to half of the grid volume to provide an accessible pathway to moving parcels. The exchange volume, ΔV_i, was computed using equation (4):

$$\Delta {V}_{i}={\rm min}\left({V}_{m,i}\frac{v\Delta t}{\Delta r}, {V}_{s,i-1},\frac{{V}_{i}}{2} \right).$$

(4)

Here, V_m,i is the volume occupied by metals in grid-layer i, V_s,i−1 is the volume occupied by silicates in grid-layer i−1, V_i is the volume grid-layer i, v is the Stokes' velocity, Δt is timestep, and Δr is grid-size.

2.6 Convection

Convection is the trickiest part of full-scale planetary thermal models in terms of numerical treatment. Incorporating convection using ab-initio methods is not computationally feasible. However, some scaling laws are available using Rayleigh numbers and Nusselt numbers (Neumann et al. 2014; Solomatov 2015). An averaged Rayleigh number can be computed by using equation (5)

$$Ra=\frac{\alpha g\rho {L}^{3}\Delta T}{\kappa \eta }=\frac{\alpha g{\rho }^{2}{C}_{p}{L}^{3}\Delta T}{k\eta }.$$

(5)

Here, L is the characteristic length of the convection zone, and ΔT is the super-adiabatic temperature difference between the top and bottom boundary of the convection zone across its characteristic length. In averaged Rayleigh number approach, the average values of α, g, ρ, κ, C_p, k and η, over the convection zone are used for computing Rayleigh number. In this approach, the thickness of the convection zone is taken as the characteristic length of the convection zone.

Nusselt number, Nu can be computed using equations (6 and 7) adapted from Solomatov (2015).

In soft turbulence regime (1418 < Ra < Ra_H) (Solomatov 2015):

$$Nu=0.089\, R{a}^{1/3}.$$

(6)

In hard turbulence regime (Ra > Ra_H)

$$Nu=C {Ra}^{\beta } {{Pr}}^{\gamma }{\lambda }^{\delta } ; \,\, Pr=\frac{\eta }{\rho \kappa }=\frac{\eta {C}_{p}}{k}.$$

(7)

Here, Ra_H = 4×10⁷ (Heslot et al. 1987; Castaing et al. 1989). The constants β and γ depend on the value of the Prandtl number, Pr. For Pr < 1, β = 1/4 and γ = 1/7, whereas for Pr > 1, β = 2/7 and γ = 0 (Verzicco and Camussi 1999; Silano et al. 2010). As in our models, Pr is always above unity, and we chose λ = 1 (Solomatov 2015), the equation (7) simplifies to equation (8):

$$Nu=0.205 {Ra}^{2/7} .$$

(8)

Here, we have computed constant C to ensure that the value of Nu is continuous at Ra_H.

The above approach does not consider local effects inside convection zones. To elaboratively incorporate all the local dependencies like density, gravity, thermal diffusivity, viscosity, thermal gradients, and characteristic length. α, g, ρ, κ and η can be readily replaced by their local values in equation (5). The parameters L and ΔT need special treatment due to their non-local behaviour. While ΔT is not a local variable, ΔT/L can be easily replaced by a local variable (∂T/∂r)−(∂T/∂r)_S. We replaced L with the distance of the grid-layer i from the nearest boundary of the convection zone. This may not be the best option, e.g., another choice based on the geometric mean of distances from both boundaries of the convection zones to the grid-layer seems to be comparatively better. However, this requires a drastic drop in temporal step size in most models to the limit of computational feasibility. Therefore, we could not incorporate a formulation based on geometric mean. Our adopted approach of replacing L caused a mismatch between the averaged Rayleigh number and the average of the Rayleigh number computed from local values. We incorporated the parameter N_local = 80 and derived equation (9) for the nearest boundary case to remove this discrepancy.

$$Ra={N}_{{\rm local}}\frac{\alpha g\rho {L}^{4}}{\kappa \eta }\left(\frac{\partial T}{\partial r}-{\left(\frac{\partial T}{\partial r}\right)}_{S}\right)={N}_{{\rm local}}\frac{\alpha g{\rho }^{2}{C}_{p}{L}^{4}}{k\eta }\left(\frac{\partial T}{\partial r}-{\left(\frac{\partial T}{\partial r}\right)}_{S}\right).$$

(9)

Although this approach has not been tested against ab-initio convection models to our knowledge, we deem this approach more suitable. This is because of its consistency with the averaged approach described above than other local parametrisations available in the literature. We favoured consistency over ab-initio tested local parametrisations because averaged Rayleigh number approach has been experimentally tested. In contrast, other local parametrisations are mostly tested using ab-initio models to our knowledge.

We redefined the convection zones at each simulation time step by verifying the conditions, ∂T/∂r < (∂T/∂r)_S and ϕ_l > 0.4. These conditions represent the scenarios where the negative thermal gradients are super-adiabatic, and the magma is rheologically liquid. Such redefined convection zones were further redefined twice at each step by verifying Nu > 1 to avoid including a region where convection is practically off.

3 Results

The giant impact is considered to have produced a swarm of moonlets with high initial average temperatures. At high initial temperatures (> 1800 K), during the secondary accretion stage (i.e., subsequent to 40% accretion by mass), the accreting moonlets could be already differentiated prior to their accretion, thereby yielding large molten iron blobs. These descending blobs can fragment in their downward descent until they attain a stable size (Qaddah et al. 2019). This is contrary to the formulations based on the fixed minimum size of iron-blobs. This could theoretically enhance the efficiency of the metal-silicate segregation. In order to study the effect of this phenomenon, we run 40 test simulations with T_ini = (1700, 1800, 1900, 2000) K and minimum size (a_min) of (0.001, 0.01, 0.02, 0.05, 0.1, 0.5, 1.0, 10.0, 100.0, 1000.0) m of the descending molten metallic iron blobs during differentiation, and a value of 0.1 for the impact heating parameter (h) to constrain the optimum values of a_min. To assess the influence of a_min on the extent of metal-silicate differentiation, we computed the moment of inertia from density profile at the end of t = 2 Myr, and is shown in figure 4. The moment of inertia is minimum for a_min = 0.05 m and maximum for 0.001 m. Therefore, we selected these two blob sizes to run the final models.

Figure 4

The moment of inertia of lunar models (t = 2 Myr) at several sizes of iron-blobs, a_min with h = 0.1. Colours represent several initial temperatures of accreting moonlets, T_ini. Moment of Inertia of the fully differentiated and homogeneous Moon is shown in black.

We performed final simulations for models with T_ini in the range of (1800, 1900, 2000, 2100) K, a_min in range of (0.001, 0.05) m, and h in range of (0.01, 0.1, 0.5). All the simulations were run for the initial 2 Myr after the giant impact. The list of the models, along with their details, is provided in table 2. The evolution of all the models is converted into video form (Supplementary videos 1–18). Supplementary videos can be viewed at a predefined speed or by moving the cursor to a specific time.

Table 2 List of models with the respective set of parameters, figures, and videos.

3.1 Thermal evolution of the Moon

Figures 5–6 shows the thermal evolution of the Moon. Figure 5 shows the radial thermal profile, whereas figure 6 shows the corresponding effective thermal diffusivities representing the extent of convection. The timings are marked in forest-green colour, at which the Nusselt number is at peak value, and in dark-bluish colour, at which the convection is active in the majority of the magma ocean. We note that the change in the size of the descending molten iron blobs on account of gravity does not significantly affect thermal evolution. Therefore, only the models with a_min = 0.05 m are shown.

Figure 5

Radial thermal profiles for the initial 2 million years of the evolution of the Moon of the models with the accreting moonlets’ initial temperature of 1800, 1900, 2000, and 2100 K with the time measured (in years) from the time of giant impact event (a–k). In panel (a–d) shows thermal profiles for h = 0.01, (e–h) for h = 0.1, and (i–k) for h = 0.5. Panel (l) shows the thermal profile of all the models after 2 Myr from the Giant Impact event. In panel (l) initial average temperature of the accreting moonlets, T_ini and the h-parameter are represented by the colours and line styles, respectively. The thermal profiles in (i) green and (ii) dark-bluish colour correspond to a specific time at which (i) the Nusselt Number is at its peak value and (ii) the whole magma ocean is convective, respectively (a–k). In all the panels, the value of a_min is 0.05 m; however, the profiles do not vary significantly at other values too.

Figure 6

Radial profiles of Nusselt Number for the initial 2 million years of the evolution of the Moon of the models with the accreting moonlets’ initial temperature of 1800, 1900, 2000, and 2100 K with the time measured (in years) from the time of giant impact event. Panels (a–d) shows profiles for h = 0.01, (e–h) for h = 0.1, and (i–k) for h = 0.5. The profiles in (i) green and (ii) dark-bluish colour correspond to a specific time at which (i) the Nusselt Number is at its peak value and (ii) the whole magma ocean is convective, respectively. In all the panels, the value of a_min is 0.05 m; however, the profiles do not vary significantly at other values too.

As of now, the h-parameter is poorly constrained. In the thermal models of Mars and Mercury, the h-parameter is adopted to be 0.1 (Bhatia and Sahijpal 2016, 2017). However, its value for the Moon is arguable. Because the Moon got accreted rapidly within 200 years compared to Mars and Mercury, the shedding away of the impact energy between subsequent impacts through thermal radiation could be inefficient due to insufficient time, thereby indicating the possibility of a higher value of the h-parameter. However, due to the high value of T_ini, the splashing of inner molten parts of accreting moonlets and the target body, which are at a higher temperature than their surfaces, results in higher energy loss. Therefore, the value of the h-parameter remained arguable in the presence of two mutually negating effects. We ran models for a conservative value of 0.1 (figures 5e–h, 6e–h), a higher value of 0.5 (figures 5i–k, 6i–k), and a lower value of 0.01 (figures 5a–d, 6a–d). The thermal evolution of all the models with a_min = 0.05 m has been shown on the same scale in Supplementary video 19.

In the absence of radiogenic heating, an inverted (positive) thermal gradient is set up during the accretion as expected in the h-parameter approach (figure 5). Subsequent to accretion, the surface temperature is set at an ambient temperature of 250 K. A negative thermal gradient slowly starts to develop from the lunar surface due to heat losses. As the negative gradient establishes, the convection starts off in the specific region. Then, the convection gradually extends towards the centre with time, thereby paving the way for the inner regions to lose energy. The Nusselt number reaches its peak value in ~10³ years (figure 6). After reaching a maximum depth in ~10^3–4 years, convection starts to recede as the temperature approaches the convection cut-off temperature at 40% bulk melting. The convection disappears on timescales of the order of 10⁵ years. After the liquid state convection ends, the heat transfer takes place through heat conduction in our simulation. Figure 5(l) shows the final thermal profile at the end of 2 Myr after the Giant Impact event. The part of the Moon (excluding pure metallic layers) that was rheologically liquid at the end of the accretion (200 years) cools to approximately 40% bulk melting temperatures. However, the timescales for the same vary a little. In none of our models, the metallic iron-core could achieve solidus temperatures.

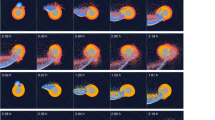
Figure 7(a–r) shows the evolution of melt fraction for all models, whereas figure 7(s) shows the scales for the same. The most noticeable difference in melt fraction profile is actuated by T_ini and h-parameter, whereas a_min makes a lesser effect on the radial profile of melt fraction. As we move on the time axis (represented as angular axis), the melt fraction of the inner layers is reduced by increasing hydrostatic pressure due to accretion over the initial 200 years. The central area with a high melt fraction is the lunar core (figure 7f–r). Blue rings are metallic shells with high melt fractions (figure 7a–e). After 200 years, the surface starts to cool, generating negative thermal gradients paving the way for convection. The convective cooling process begins from the surface side and reaches maximum depth in a few thousand years. After 10^3–4 years, the melt fraction falls to ~0.4 except for the metallic layers. There is only a little change subsequently till 2 Myr.

Figure 7

Radial profiles of melt fraction for the initial 2 million years of the evolution of the Moon of the models with the accreting moonlets’ initial temperature of 1800, 1900, 2000, and 2100 K with the time measured (in years) from the time of giant impact event (a–r). The radial axis shows the distance from the centre, and the angular axis represents the time from the giant impact. Axis scales are shown in panel (s). Columns of panel represent the distinct initial average temperature of the accreting moonlets and rows of the panels represent the combination of distinct values for h-parameter and a_min. The colour map is greyscale compatible and can be viewed by printing in greyscale if colours are not distinct for some type of colour-blindness.

Some bulk parameters were computed using the radial profiles of various physical quantities from the raw output of simulations, and their temporal evolution is shown in figure 8. Figure 8(a) shows the temporal evolution of mass-averaged temperature, T_av of the whole Moon. During the initial 200 years, T_av increases on account of impact-induced heating. Afterwards, T_av decreases rapidly due to convection for 10^3–4 years. This is followed by slow convection for order of timescales in the range of 10⁵ years, resulting in a less steep fall in T_av. The final T_av does not differ significantly among models irrespective of the early conditions. Figure 8(b) shows the evolution of the melt fraction of the bulk Moon. Initially, it falls for 200 years on account of an increase in hydrostatic pressures caused by accretion. Afterwards, it rapidly decreases for 10⁴ years due to rapid cooling by convection. Figure 8(c) shows the evolution of radial thickness of the outermost rheologically liquid zone, whereas figure 8(d) shows the evolution of the rheologically liquid mass fraction of the bulk Moon. For the initial 200 years, the radial thickness increases by accretion of more rheologically liquid layers for higher temperature, T_ini of 2100 K, and decrease for lower temperatures due to the reduction of the melt fraction of inner layers below 0.4 by a change in hydrostatic pressures. For T_ini = 2000 K and h = 0.5, the increase is followed by a decrease due to competition between the two effects. After 200 years, it remains almost constant for 10⁴ years during rapid convection. From 10⁴ to 2×10⁵ years, the radial thickness decreases due to a decrease in melt fraction of convective layers below 0.4. The evolution of rheologically liquid mass fraction is similar except for the initial 200 years because this being a ratio is unaffected by the addition of accreting mass. Figure 8(e) shows the evolution of radial thickness of convective zones, and figure 8(f) shows the evolution of the fraction of lunar mass under convection. For the initial 200 years, convection does not start due to high surface temperature caused by rapid accretion. Afterwards, the negative thermal gradients begin to form from the surface side and expand inwards. This results in the expansion of the convection zone for the next 10^3–4 years. Thereafter, it starts contracting on account of cooling and recession of convection. Figure 8(g) shows the evolution of the mass-averaged Nusselt number, whereas figure 8(h) shows the product of the Nusselt number and mass under convection. These parameters represent the rapidity and effectiveness of the convection. Their values maximise within initial 1000–3000 years except for T_ini = 2000 K and h = 0.5, for which the process takes several thousands of years. Both start declining afterwards.

Figure 8

Temporal evolution of several computed bulk-parameters. Temporal evolution of mass-averaged lunar temperature (a), total lunar melt fraction (b), outermost rheologically-liquid zone (c), the rheologically-liquid mass fraction (d), the thickness of convective zones (e), the fraction of lunar mass in convection zones (f), mass-averaged Nusselt number (g), and the sum of products of Nusselt number and mass (h) with the time measured (in years) from the time of giant impact event. The results at a_min = 0.001 m are almost identical to that at a_min = 0.05 m and hence, are not plotted. In all panels, initial average temperature of the accreting moonlets, T_ini is represented by colours, and h-parameter is represented by line styles.

3.2 Metal-silicate segregation through Stokes' flow

Figure 9 shows the metal-silicate segregation and formation and evolution of the metallic iron-core for different models. Figure 9(s) shows the axis scales for figure 9(a–r). At T_ini = 1800 K, only metallic shells are formed, and no iron-core forms for any value of h or a_min (figure 9a–e). At T_ini = 1900 K, small iron-core form for a_min = 0.05 m with varying extent of segregation for distinct values of h (figure 9f, g, j), whereas a very thick metallic shell with a small undifferentiated core beneath it forms for a_min = 0.001 m (figure 9h–i). At T_ini = 2000 K, comparatively larger iron-core form with varying extent of segregation for distinct values of h or a_min (figure 9k–o). At T_ini = 2100 K, nearly complete iron-core form for a_min = 0.05 m (figure 9p–r). It may be noted that size of the incomplete core increase with an increase in T_ini.

Figure 9

Radial profiles of metal fraction for the initial 2 million years of the evolution of the Moon of the models with the accreting moonlets’ initial temperature of 1800, 1900, 2000, and 2100 K with the time measured (in years) from the time of giant impact event (a–r). The radial axis shows the distance from the centre, and the angular axis represents the time from the giant impact. Axis scales are shown in panel (s). Columns of the panels represent the distinct initial average temperature of the accreting moonlets and rows of the panels represent the combination of distinct values for h-parameter and a_min. The colour map is greyscale compatible and can be viewed by printing in greyscale if colours are not distinct for some type of colour-blindness. The white colour represents the complete absence of metallic content.

Figure 9(a, f, k, p) can be compared with figure 9(b, g, l, q) and (e, j, o) to analyse the effect of impact-induced heating on metal-silicate segregation. Figure 9(c, h, m) can also be compared with figure 9(d, i, n). It can be seen that higher efficiency of impact-induced heating results in rapid and enhanced metal-silicate segregation. However, this alone cannot complete the process of segregation. To analyse the effect of the size of iron blobs, we compare figure 9(b, g, l, q) with figure 9(c, h, m, r) and figure 9(d, i, n) with figure 9(e, j, o). The extent and speed of metal-silicate segregation are higher for a_min = 0.05 m than for 0.001 m.

We computed the moment of inertia from radial density profiles. Moment of inertia can be treated as a good proxy for evaluating the extent of metal-silicate segregation. Figure 10(a) shows the evolution of the moment of inertia in our models. During the accretionary phase, the moment of inertia decreases due to rapid differentiation until the increasing hydrostatic pressures substantially increase viscosity by reducing melt-fraction. Afterwards, the moment of inertia increases for the rest of the accretionary period. This increase is caused by the accumulation and trapping of metallic content above and inside layers of increasing viscosity. In models with a_min = 0.001 m, the moment of inertia decreases again for the next few tens to a few hundred years for continued fast segregation that is already completed in models with a_min = 0.05 m. Afterwards, the segregation process becomes extremely slow and does not produce any significant change in the moment of inertia. On comparison, we find that the extent of segregation is in ascending order of the selected (h, a_min) parametric combinations of (0.1, 0.001 m), (0.01, 0.05 m), (0.1, 0.05 m), (0.5, 0.001 m) and (0.5, 0.05 m).

Figure 10

Temporal evolution of moment of inertia (a), average velocity of metallic content for T_ini = 1800 K (b), T_ini = 1900 K (c), T_ini = 2000 K (d), and T_ini = 2100 K (e), for distinct values of h-parameter and a_min with the time measured (in years) from the time of giant impact event.

Figure 10(b–e) shows the mass-averaged velocity of molten metallic content during its downward descend. For the initial ~200 years, the metallic content is descending at a rapid average velocity >1 km year⁻¹. The average velocity gradually falls afterwards to 10⁻⁷ km year⁻¹ for a_min = 0.001 m and rapidly for a_min = 0.05 m. Segregation at this small velocity continues for a few tens of thousands of years, after which the segregation stops completely.

3.3 Depth of initial magma ocean

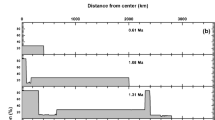
Figure 11 presents the depth estimates of the initial magma ocean as a function of T_ini with different extents of the bulk silicate melt percentage. A fully molten magma ocean is defined by ϕ =1.0, whereas a rheologically liquid magma ocean is defined by ϕ > 0.4. A rheologically solid magma ocean could have extended up to the lunar centre depending on T_ini and the h-parameter. It is difficult to impose stringent constraints on the depth of the magma ocean on the basis of numerical simulation. Our simulations suggest that early core formation through Stokes' flow require either T_ini > 2000 K (for a_min = 0.001 m) or T_ini > 1900 K (for a_min = 0.05 m). T_ini > 1900 K produces an initial magma ocean that is fully molten up to ~770 km and rheologically liquid up to ~1055 km. T_ini > 2000 K produces an initial magma ocean that is fully molten up to ~1000 km and rheologically liquid up to ~1280 km. Several studies have found a fully molten magma ocean up to 1000 km consistent with the crustal thickness (Elkins-Tanton et al. 2011; Suckale et al. 2012). Therefore, an incomplete core can easily form early with a 1000 km deep fully molten magma ocean consistent with the crustal thickness.

Figure 11

Depth of initial magma ocean. Depth of fully molten initial magma ocean is shown with solid lines, whereas the depth of rheologically liquid magma ocean is shown with dashed lines. A fully molten magma ocean is defined by ϕ = 1.0, and a rheologically liquid magma ocean is defined by ϕ > 0.4. The different colours represent distinct values of the h-parameter.

4 Discussion and conclusions

Prior to the present work, the incorporation of local Rayleigh numbers in full-scale planetary models for early evolution had remained a formidable task due to enormous computational costs and numerical instabilities. Further, the inherent time-sequential nature of the models has deprived these models of massively parallel computing capabilities. This has prevented earlier studies from incorporating several dependencies of physical quantities in numerical simulations. Here, we presented a suite of models that incorporate the formulation based on local Rayleigh numbers and the gravitational energy released during segregation, besides several other improvements. The scope of the present work is the thorough study of the early two million years after the Giant Impact event. Therefore, the solid-state convection, the melt extraction due to compaction, and metal silicate segregation through Rayleigh–Taylor instability and large diapirs were not incorporated.

The major features of the study are listed hereunder:

• (1) The key issue addressed in the present work is to constrain the initial average temperature of the accreting moonlets. Our simulations predict it to be ≥1900 K. This implies a more stringent constraint on the giant impact hypothesis. This is a significant revision compared to our earlier estimates (≥1600 K) from a model that was based on the simplistic treatment of convection (Sahijpal and Goyal 2018).

• (2) Further, based on our rigorous convective treatment, we propose the timescales for cooling the convective magma ocean to the critical rheological temperature in the range of ~10^4–5 years. Here the convective cooling is much more rapid during the initial 10⁴ years. Afterwards, the speed of convective cooling declines for the next 10⁵ years before halting entirely. This happens due to increasing viscosities as the melt fraction nears the rheologically critical melt fraction, 0.4. Earlier estimates were 10^3–4 years from a model based on the simplistic treatment of convection (Sahijpal and Goyal 2018).

• (3) The majority of the metal-silicate segregation through Stokes' flow in the rheologically-liquid magma ocean takes place during the initial 10^2–3 years. In order to complete core formation in multiple models, other processes like Rayleigh–Taylor instability or flow of large diapirs through rheologically-solid mantle are required. However, this can occur only at timescales larger than that are analysed in this study.

• (4) An initial average temperature of 1900–2000 K of the accreting moonlets required for early core-formation produced a <1000 km fully molten magma ocean, which is consistent with earlier studies (Elkins-Tanton et al. 2011; Suckale et al. 2012).

• (5) In all the numerical models where the metallic iron-core is formed, the iron-core is fully molten at the end of the initial 2 Myr. This would cause an internally driven lunar geomagnetism when the iron snow starts falling due to solidification of the iron core (Breuer and Moore 2015) at a later time. There is evidence for an internally driven strong lunar geomagnetic field that existed between at least 4.25 and 3.56 Gyr ago (Cisowski et al. 1983; Weiss and Tikoo 2014; Tikoo et al. 2017). Although constraining a timescale for such a lunar geomagnetic field is out of scope for the present study, a more detailed analysis in the future can shed light on this matter.

• (6) The majority of metal-silicate segregation through Stokes' flow occurs before convection spreads to all of the magma ocean. Therefore, inhibition of Stokes' flow due to convective turbulence could not significantly affect metal-silicate segregation.

• (7) These models have not incorporated tidal heating. Tidal heating can substantially heat up the Moon when caught up in an evection resonance with the Sun because the extent of heating may surpass the convective cooling rates (Ćuk and Stewart 2012; Tian et al. 2017). This heating can cause the incomplete metal-silicate segregation to complete and enlarge the cooling timescales.

• (8) We have not considered heliocentric impacts in these models. Jackson and Wyatt (2012) suggested that a large amount of material from the giant impact event can escape to heliocentric orbits. This debris later re-accrete on Earth, Moon, and Venus over the next tens to hundreds of million years (Jackson and Wyatt 2012). Besides this, the leftover planetesimals also accreted over similar time periods. These include the Late Veneer and Late Heavy Bombardment (Gomes et al. 2005; Mojzsis et al. 2019). The impactors on heliocentric orbits efficiently cool down to ambient temperatures much before being re-accreted due to larger timescales and smaller sizes. Therefore, such impactors could not heat further the already hotter Moon, at least globally. Instead, the phenomenon would assist in cooling down the Moon. In a Moon with a conductive lid, the impactors of sufficient sizes will puncture the holes and push the parts of colder crust into the magma ocean resulting in the cooling of the magma ocean. The magma that reaches the surface through the crust's punctured holes will quench by losing heat through thermal radiation (Gupta and Sahijpal 2010; Perera et al. 2018). In a Moon without a conductive lid, the impactor will splash the hotter material from deeper parts of the magma ocean. This will transiently increase the active surface area to cool by thermal radiation, besides stirring the magma ocean.

• (9) Roy et al. (2014) suggested that the Moon cools faster than the Earth due to the larger surface to volume ratio. A brighter Earthshine from the hotter Earth will result in asymmetrically high ambient temperature on the nearside of the tidally locked young Moon. Incorporating the longitudinally asymmetrical surface temperature is out of the scope of the present 1-D model. The nearside ambient temperature can be approximated by 250+T_E/1.19/√D. Here, T_E is the Earth's surface temperature. D is the Earth–Moon distance in multiples of Earth-radius, R_⊕. At T_E = 2000 K and D = 3 R_⊕, this results in a nearside temperature of 1220 K in comparison to the farside temperature of 250 K. This hemispheric temperature gradient will result in slower cooling on the nearside than the farside.