Universality in bio-rhythms: A perspective from nonlinear dynamics

Abstract

Bio-rhythms are ubiquitous in all living organisms. A prototypical bio-rhythm originates from the chemical oscillation of intermediates or metabolites around the steady state of a thermodynamically open bio-chemical reaction network with autocatalysis and feedback and is often described by minimal kinetics with two state variables. It has been shown that notwithstanding the diverse nature of the underlying bio-chemical and bio-physical processes, the associated kinetic equations can be mapped into the universal form of the Liénard equation which admits of mono-rhythmic and bi-rhythmic solutions. Several examples of bio-kinetic schemes are examined to illustrate this universality.

1 Introduction

In a chemical reaction we deal with conversion of a set of reactants into a set of products. This is guided by the laws of thermodynamics which assure us that for this conversion to happen, the free energy change between the final stable and the initial metastable states of the reaction must be negative. Furthermore, the kinetics of the reaction, in general, are monotonic in nature. However, there is a class of chemical reactions occurring in cells of living organisms which are characterized by autocatalysis and feedback of the reaction intermediates. The kinetics of the intermediates are often observed to be non-monotonic. Under certain conditions, one may encounter oscillation of the concentration of the intermediates or metabolites (Murray 1989; Epstein and Pojman 1998). The very idea of chemical oscillation, however, was not well accepted by the chemistry community in the early days of development of this field for nearly 50 years from the 1920s (Epstein and Pojman 1998). The primary reason was the traditional wisdom that a chemical reaction cannot oscillate around an equilibrium state like the bob of a pendulum since the positive slopes of oscillation violate the second law of thermodynamics. The riddle was finally resolved with the advent of nonlinear chemical dynamics, when it was realized that an intermediate of a chemical reaction can oscillate around a steady state which lies far away from the unique equilibrium state of the reaction. The stability properties of the steady states are the guiding factors of the chemical oscillations (Murray 1977; Strogatz 1994; Jordan and Smith 2007). Chemical oscillation is therefore a far-from-equilibrium phenomenon.

Chemical oscillations or the oscillations of intermediates of a bio-chemical reaction network characterized by autocatalysis and feedback lie at the heart of bio-rhythms (Goldbeter and Berridge 1996). Bio-rhythms are ubiquitous characteristics of all living organisms. The periodic conversion of sugar to alcohol or glycolysis, which is fundamental for the metabolism of a cell, is one of the first bio-chemical oscillations observed in the mid-sixties of the last century (Higgins 1964; Sel’kov 1968). Since then a large number of bio-chemical oscillators have been discovered in reaction networks, associated with various biological processes, e.g., membrane potential oscillation (time period 10 ms–10 s) (Barnett and Larkman 2007; Bean 2007; V-Ghaffari et al. 2016), cardiac rhythms (1 s) (Źebrowski et al. 2007; Gois and Savi 2009; Thanom and Loh 2011; Ryzhii and Ryzhii 2014), muscle contraction (seconds–hours) (Shimizu and Yamada 1975; Meyrand and Marder 1991; Smith and Stephenson 2009), $\hbox {Ca}^{+2}$ oscillations (second–minutes) (Woods et al. 1986; Berridge et al. 1988; Shangold et al. 1988; Berridge and Irvine 1989; Goldbeter et al. 1990), glycolytic oscillation (1 min–1 h) (Higgins 1964; Sel’kov 1968; Goldbeter and Lefever 1972; Tornheim and Lowenstein 1975; Decroly and Goldbeter 1982; Tornheim 1988; Goldbeter and Berridge 1996; Kar and Ray 2003; Yaney and Corkey 2003; Goldbeter 2017), insulin secretion (minutes) (Goldbeter and Berridge 1996; Kar and Ray 2005), cell cycle (30 min–24 h) (Prestige 1972; John 1981; Tyson 1991; Gérard and Goldbeter 2012), circadian rhythms (24 h) (Pittendrigh and Victor 1957; Pavlidis 1967; Winfree 1967; Gonze et al. 2002; Reppert and Weaver 2002; Leloup and Goldbeter 2004; Gonze et al. 2005; Sen et al. 2008; Gonze 2011; Oda and Friesen 2011), ovarian cycle (weeks–months) (Goldbeter and Berridge 1996), to name a few. Because of the involvement of the law of mass action for each of the primary steps of the chemical reaction kinetics in a complicated network as dictated by a proposed reaction mechanism, the underlying model for a bio-chemical process, in general, is extremely complex since a large number of intermediates or metabolites actively participate in the kinetics. Based on the appropriate separation of time scales one may eliminate a number of variables to arrive at a minimal model for the process. This minimal model for bio-chemical oscillation must be comprised of at least two variables. As expected these model equations with two phase space variables are of widely different forms. A question is: is there any underlying universality in these models of bio-chemical oscillation from the perspective of nonlinear dynamics? Or, in other words, do they belong to a specific class of oscillators known in physical sciences? The object of this article is to address this question. We show that, notwithstanding the diversity of the underlying bio-chemical processes and of the associated two variable autonomous kinetic equations, these models meet on a common theoretical ground. They can be cast in the form of a Liénard equation. This oscillator is well known for over a century in physical sciences, particularly in many oscillating circuits in the development of radio and vacuum tube technologies, and vibrating strings and musical instruments in acoustics (Strutt 1877; van der Pol 1920; van der Pol 1922; Strogatz 1994; Jordan and Smith 2007). In what follows in the subsequent sections we first present a general formalism for mapping the two variable kinetic equations in the form of a Liénard equation which admits of limit cycle solutions describing the bio-rhythms. A related issue was discussed earlier in some of our publications (Ghosh and Ray 2014, 2015; Saha and Gangopadhyay 2017; Saha et al. 2019, 2020). Here we stress the aspect of universality and introduce a classification scheme for the Liénard master equation in three major families. The universality of the Liénard equation is examined in several examples for illustration.

The outline of the article is as follows: In section 2 we discuss the mathematical conditions for mapping the general two variable kinetic equations into the Liénard equation which has been classified further in three distinct families. In sections 3, 4, and 5 we illustrate each family of the Liénard system with specific examples. The review is concluded in section 6.

2 Biochemical oscillator as a Liénard oscillator

2.1 The reduction scheme

We consider here a set of autonomous kinetic equations for a thermodynamically open system with two variables,

$$\begin{aligned} \frac{dx}{dt}&= a_0+a_1 x+a_2 y+f(x,y), \nonumber \\ \frac{dy}{dt}&= b_0+b_1 x+b_2 y+g(x,y), \end{aligned}$$

(1)

where x(t) and y(t) are, for example, concentrations of metabolites or populations of intermediates in chemical, biological or ecological processes (Murray 1977; Murray 1989; Strogatz 1994; Epstein and Pojman 1998). $a_i,b_i$ for $i=0,1,2$ are all real parameters expressed in terms of the appropriate kinetic constants. Our aim here is to show that equations (1) for oscillatory kinetics can be cast into the form that describes a Liénard oscillator well known in physical and mathematical sciences of nonlinear dynamics. Let ($x_s, y_s$) be the fixed point of the system and f(x, y) and g(x, y) are the nonlinear functions of x and y. The linear terms have been taken out explicitly from the kinetic functions on the right hand side of equation (1). This is a bit advantageous for the methodology that is being followed here to take care of the linear shift of the steady states to the origin along with the linear transformation of the variables.We begin by shifting of the steady state ($x_s, y_s$) to the origin (0, 0) with the help of a linear transformation from the variables (x, y) to a new set $(\xi , u)$ so that $\xi _s=0,~u_s=0$. This linear transformation can be chosen by introducing $\xi =\beta _0+\beta _1 x+\beta _2 y$ with $\beta _0=-(\beta _1 x_s+\beta _2 y_s),$ i.e., $\xi =\beta _1 (x-x_s)+\beta _2 (y-y_s)$ such that ${\dot{\xi }}=u$. $\beta _1,\beta _2$ are the constants that make the new steady state at the origin, $\xi _s=0$, $u_s=0$. u is expressed as $u=\alpha _0+\alpha _1 x+\alpha _2 y$; $\beta _i$, $\alpha _i$ for $i=0,1,2$ are all real constants which can be expressed in terms of system parameters ($g=\mu f$ holds, where $\mu$ depends on $\beta$). From the inverse transformation we easily obtain the expressions for x and y as given by

$$\begin{aligned} x&=\frac{\alpha _2 \left( \beta _0-\xi \right) +\beta _2 \left( u-\alpha _0\right) }{\alpha _1 \beta _2-\alpha _2 \beta _1}=L(\xi ,u), \nonumber \\ y&=\frac{\alpha _1 \left( \xi -\beta _0\right) +\beta _1 \left( \alpha _0-u\right) }{\alpha _1 \beta _2-\alpha _2 \beta _1}=K(\xi ,u), \end{aligned}$$

(2)

provided that $\alpha _1 \beta _2-\alpha _2 \beta _1 \ne 0$. Differentiating ${\dot{\xi }}=u$ with respect to the independent variable t, we obtain

$$\begin{aligned} \ddot{\xi }&= {\dot{u}} =\alpha _1{\dot{x}}+\alpha _2{\dot{y}}\nonumber \\&= \alpha _1 \lbrace a_0+a_1 L(\xi ,{\dot{\xi }})\nonumber \\&\quad+a_2 K(\xi ,{\dot{\xi }})+\varphi (\xi ,{\dot{\xi }})\rbrace \nonumber \\&\quad+\alpha _2 \lbrace b_0+b_1 L(\xi ,{\dot{\xi }})+b_2 K(\xi ,{\dot{\xi }})+\phi (\xi ,{\dot{\xi }})\rbrace , \end{aligned}$$

(3)

where $L(\xi ,{\dot{\xi }})=c_1 \xi +c_2{\dot{\xi }}+c_{L}$ and $K(\xi ,{\dot{\xi }})=c_3 \xi +c_4{\dot{\xi }}+c_{K}$ with $\begin{bmatrix} c_1 &{} c_2 &{} c_{L}\\ c_3 &{} c_4 &{} c_{K} \end{bmatrix}$ = $\frac{1}{\alpha _1 \beta _2-\alpha _2 \beta _1}$ $\begin{bmatrix} -\alpha _2 &{} \beta _2 &{} \alpha _2 \beta _0-\alpha _0 \beta _2\\ \alpha _1 &{} -\beta _1 &{} \alpha _0 \beta _1-\alpha _1 \beta _0 \end{bmatrix}$. The functions $\varphi$ and $\phi$ can be expressed as a power series expansion as

$$\begin{aligned} \varphi (\xi ,{\dot{\xi }})=\sum _{n,m=0}^{\infty } \varphi _{nm} \xi ^n {\dot{\xi }}^m ~\quad\text{and}\quad ~ \phi (\xi ,{\dot{\xi }})=\sum _{n,m=0}^{\infty } \phi _{nm} \xi ^n {\dot{\xi }}^m, \end{aligned}$$

(4)

with $\phi (\xi ,{\dot{\xi }})=\mu \varphi (\xi ,{\dot{\xi }})$, as the functions f and g are related through $\mu$ by $g=\mu f$, $\mu \in {\mathbb {R}}$. Substitution of equation (4) in  (3) yields

$$\begin{aligned} \ddot{\xi }&= \alpha _1 a_0+\alpha _1 a_1(c_1 \xi +c_2 {\dot{\xi }}+c_{L})+\alpha _1 a_2(c_3 \xi +c_4 {\dot{\xi }}+c_{K})\nonumber \\&\quad+(\alpha _1+\mu \alpha _2) \sum _{n,m=0}^{\infty } \varphi _{nm} \xi ^n {\dot{\xi }}^m \nonumber \\&\quad+\alpha _2 b_0+\alpha _2 b_1(c_1 \xi +c_2 {\dot{\xi }}+c_{L})\nonumber \\&\quad+ \alpha _2 b_2(c_3 \xi +c_4 {\dot{\xi }}+c_{K}), \rm{i.e.}, \nonumber \\ \ddot{\xi }&= A_{00}+\left( A_{10}+\sum _{n>1} A_{n0} \xi ^{n-1}\right) \xi \nonumber \\&\quad+ \left( A_{01}+\sum _{n>0} A_{n1} \xi ^n +\sum _{n\ge 0} \sum _{m>1} A_{nm} \xi ^n {\dot{\xi }}^{m-1}\right) {\dot{\xi }}, \end{aligned}$$

(5)

where $\alpha _1 a_0+\alpha _2 b_0+(\alpha _1+\mu \alpha _2) \varphi _{00}+(\alpha _1 a_1 +\alpha _2 b_1) c_{L}+(\alpha _1 a_2 +\alpha _2 b_2) c_{K}=A_{00}=0$ (by definition of a zero fixed point of $\xi$), $A_{10}=\alpha _1(a_1 c_1+a_2 c_3)+\alpha _2 (b_1 c_1+b_2 c_3)+(\alpha _1+\mu \alpha _2) \varphi _{10}$, $A_{01}=\alpha _1(a_1 c_2+a_2 c_4)+\alpha _2 (b_1 c_2+b_2 c_4)+(\alpha _1 +\mu \alpha _2) \varphi _{01}$, $A_{n0}=(\alpha _1+\mu \alpha _2) \varphi _{n0}$, $A_{n1}=(\alpha _1+\mu \alpha _2) \varphi _{n1}$ and $A_{nm}=(\alpha _1+\mu \alpha _2) \varphi _{nm}$, where indices follow the values as given in the summation over $m,n \in {\mathbb {Z}}^+$. Equation (5) then looks like

$$\begin{aligned} \ddot{\xi }+F(\xi ,{\dot{\xi }}) {\dot{\xi }} +G(\xi )=0, \end{aligned}$$

(6)

where the functions $F(\xi ,{\dot{\xi }})$ and $G(\xi )$ are given by

$$\begin{aligned} F(\xi ,{\dot{\xi }})&= -\left[ A_{01}+\sum _{n>0} A_{n1} \xi ^n +\sum _{n\ge 0} \sum _{m>1} A_{nm} \xi ^n {\dot{\xi }}^{m-1}\right] , \nonumber \\ G(\xi )&= -\left[ A_{10}+\sum _{n>1} A_{n0} \xi ^{n-1} \right] \xi . \end{aligned}$$

(7)

Equation (6) is the well-known equation called the Liénard equation. This master equation forms the basis of the rest of the treatment in this article.

2.2 Limit cycle, center and Liénard families

Summarizing the above discussions we now note that the oscillatory dynamics that governed the kinetic equations (1) in two variables can be cast into the form of a Liénard equation of form (6), if there exists a linear transformation of the variables (x, y) to $(\xi ,u)$ such that ${\dot{\xi }}=u$. The construction of this linear transformation is system-specific and is illustrated in the examples in three subsequent sections. The main advantage of such a description is that it is easy to identify the external forcing term $G(\xi )$ and the nonlinear dissipation term $F(\xi ,{\dot{\xi }})$ in equation (6). Depending on the nature of $F(\xi ,{\dot{\xi }}),$ the periodic solutions of equation (6) are of two types: limit cycle type and the periodic solution at the center type. We first discuss the associated conditions for these solutions.

Case I.   If $F(\xi ,{\dot{\xi }})$ and $G(\xi )$ are continuously differentiable functions and satisfy the following conditions (i) there exists $a>0$ such that $F(\xi ,{\dot{\xi }})>0$ where $\xi ^2+{\dot{\xi }}^2>a^2$; (ii) $F(0,0)<0$ (hence $F(\xi ,{\dot{\xi }})<0$ in the neighbourhood of the origin); (iii) $G(0)=0$, $G(\xi )>0$ when $\xi >0$ and $G(\xi )<0$ when $\xi <0$; (iv) $g(\xi )=\int _0^\xi G(u) du \rightarrow \infty \,\, \text{as} \,\, ~\xi \rightarrow \infty$, then the system has, at least, one unique stable limit cycle around the origin in the $(\xi ,{\dot{\xi }})$ phase plane. For $F(0,0)>0$ the limit cycle becomes unstable. The proof of this theorem is given in Jordan and Smith (2007). $G(\xi )$, an odd function, acts as a restoring force which tends to reduce any displacement. $F(\xi ,{\dot{\xi }})$, on the other hand, is a nonlinear dissipative function which acts as a pumping term (negative damping) when the displacement or velocity is very small and as a damping term when the displacement or velocity becomes large. This implies that the large oscillations get damped while the small oscillations are forced up so that the system asymptotically settles down on an unique isolated trajectory in phase plane.

Case II.   The condition for the existence of the periodic solution at a center is $F(0,0)=0$. It can be shown from the linear stability analysis that there is a relation between F(0, 0) and the eigenvalues of the stability matrix $\lambda _{\pm }$ with $F(0,0)=-2Re(\lambda _{\pm })$.

We now classify the periodic solutions arising out of our master equation (6). The basis of this classification is the nature of the polynomial functions in $F(\xi ,{\dot{\xi }})$ and $G(\xi )$. Each polynomial is governed by the kinetics of the underlying model as illustrated in the following sections. We consider the three major families.

(a) Liénard family.   We return to equation (7) and rewrite $F(\xi ,{\dot{\xi }})=F_L(\xi ,{\dot{\xi }})$ and $G_L(\xi )=-\left[ A_{10}+\sum _{n>1} A_{n0} \xi ^{n-1} \right]$. Equation (6) then assumes the following form

$$\begin{aligned} \ddot{\xi }+F_L(\xi ,{\dot{\xi }}) {\dot{\xi }} +G_L(\xi )\xi =0. \end{aligned}$$

(8)

We shall discuss several kinetic schemes under this category in section 3.

(b) Rayleigh family.   If the coefficients of the polynomials in $F(\xi ,{\dot{\xi }})$ and $G(\xi )$ in equation (7) are such that $A_{nm}=0$, for $n\ge 2$ for any m, there is a unique steady state $\xi _s=0$ of the dynamics controlled by a restoring force linear in $\xi$; equation (6) then reduces to

$$\begin{aligned} \ddot{\xi }+F_R({\dot{\xi }}) {\dot{\xi }} +G_R({\dot{\xi }})\xi =0, \end{aligned}$$

(9)

where

$$\begin{aligned}&F_R({\dot{\xi }})=-\left[ A_{01}+\sum _{m>1} A_{0m} {\dot{\xi }}^{m-1}\right] ,~~~ G_R({\dot{\xi }}) =-\left[ A_{10}+\sum _{m>0} A_{1m} {\dot{\xi }}^{m}\right] . \end{aligned}$$

(10)

For the limit cycle to be an admissible periodic solution of equation (9), the condition (i) in Case I has to be modified as $F(0)<0$.

The class of kinetic equations satisfying the form (9) may be termed as a member of the Rayleigh family. We digress a little to reflect on its genesis in the Rayleigh oscillator.

Rayleigh (Strutt 1877) treated the problem of oscillation in the context of the vibration of string and musical instruments by introducing a velocity-dependent force component into the standard linear dissipative oscillator

$$\begin{aligned} m \ddot{\xi }(t)=-a_0 {\dot{\xi }}(t) -a_1 \xi (t)+a_2 {\dot{\xi }}(t), \end{aligned}$$

(11)

where $a_0$ is the coefficient of linear friction, $a_1$ is the coefficient of elasticity, and $a_2$ is the coefficient of the velocity-dependent force component. If $a_0>a_2$, the oscillation gets damped. For $a_2 > a_0,$ the oscillation diverges exponentially with time. The addition of a forcing term of the form $\alpha ' {\dot{\xi }}^3, \alpha '>0$ can act in such a way that it is directed opposite to the velocity so that the last equation takes the form

$$\begin{aligned} \ddot{\xi }(t)+\alpha {\dot{\xi }}(t)+\alpha ^{'} {\dot{\xi }}^3+\omega ^2 \xi =0, \end{aligned}$$

(12)

where the redefined parameters are $\alpha =(a_2-a_0)/m$, and $\omega ^2=a_1/m$ as well as a new one, $\alpha ^{'}.$

Rayleigh showed that if $\alpha$ and $\alpha ^{'}$ are of opposite signs the dynamical system can exhibit self-sustained oscillation, i.e., a limit cycle. If the restoring force $\omega ^2 \xi$ is velocity-dependent, then the generalization of the Rayleigh oscillator takes the form (9), where

$$\begin{aligned} F_R({\dot{\xi }})&=(\alpha +\alpha ' {\dot{\xi }}^2) ~\quad\text {and} \quad ~ G_R({\dot{\xi }}) = \frac{a_1({\dot{\xi }})}{m}, \end{aligned}$$

(13)

In section 4 we discuss two bio-kinetic schemes that correspond to this Rayleigh family.

(c) Extended Liénard family. We now return to our master equation (6). Rearranging the terms in the polynomial functions $F(\xi ,{\dot{\xi }})$ and $G(\xi )$ by taking care of the summation over n in $A_{nm,}$ we have

$$\begin{aligned} F_E(\xi ,{\dot{\xi }})&= -\left[ A_{01}+\sum _{n>0} A_{n1} \xi ^n +\sum _{n\ge 0(\ne 1)} \sum _{m>1} A_{nm} \xi ^n {\dot{\xi }}^{m-1}\right] , \nonumber \\ G_E(\xi ,{\dot{\xi }})&= -\left[ A_{10}+\sum _{n>1} A_{n0} \xi ^{n-1} \right] +\left[ \sum _{m>1} A_{1m} {\dot{\xi }}^{m} \right] . \end{aligned}$$

(14)

This leads us to an extended form of the Liénard equation which carries a velocity-dependent restoring force $G_E(\xi ,{\dot{\xi }})\xi$ nonlinear in displacement.

$$\begin{aligned} \ddot{\xi }+F_E(\xi ,{\dot{\xi }}) {\dot{\xi }} +G_E(\xi ,{\dot{\xi }})\xi =0. \end{aligned}$$

(15)

This form of the extended Liénard equation has been utilized to describe two bio-kinetic schemes of chemical oscillations in section 5. Before concluding this section a pertinent point must be stressed. We note that the scheme of mapping an arbitrary set of two-variable kinetic equations into a Liénard form rests on the linearity of the transformation of variables. The scheme fails if the kinetic equations are devoid of any linear term.

3 Liénard family

In this class of bio-kinetic schemes we consider two bio-rhythms in glycolytic oscillations, pigmentation of fish model and substrate depletion in enzymes arising out of limit cycles. The ecological model of Lotka–Volterra is also shown to belong to this family but admits a periodic solution at the center.

3.1 Glycolysis: Limit cycle

Glycolysis (Higgins 1964; Sel’kov 1968; Goldbeter and Lefever 1972; Tornheim and Lowenstein 1975; Decroly and Goldbeter 1982; Tornheim 1988; Goldbeter and Berridge 1996; Yaney and Corkey 2003) is the fundamental metabolic process of respiration in both aerobic and anaerobic pathways whereby glucose is converted into pyruvic acid. Glucose is found in the blood as a result of the breakdown of carbohydrates into sugars. It enters the cells through specific transporter proteins from outside the cell into the cell’s cytosol which contains all the glycolytic enzymes.

Oscillations occur in a number of enzymatic systems as a result of feedback regulation. The influence of Michaelis–Menten kinetics on the oscillatory behaviour in enzyme systems is investigated in the activity of phosphofructokinase (PFK) in glycolysis. The model for the PFK reaction is based on a product-activated allosteric enzyme reaction coupled to enzymatic degradation of the reaction product. The Michaelian nature of the product decay term markedly influences the period, amplitude and waveform of the oscillations. The earliest model of oscillatory PFK dynamics is due to Higgins (1964), who explained glycolytic oscillations in yeast with the activation of PFK by one of its products, fructose-1,6-bisphosphate (FBP). The model of Goldbeter and Lefever (1972) based on yeast glycolysis takes care of the activation by the other product, ADP. With the availability of experimental data it became clear that glycolytic oscillations in muscle primarily depend on PFK activation by FBP (Tornheim and Lowenstein 1975; Tornheim 1988; Yaney and Corkey 2003). Based on experiments on yeast they proposed the following dynamics:

$$\begin{aligned} &\frac{d \alpha }{d t}= v-\sigma _M \phi (\alpha , \gamma ), \nonumber \\ &\frac{d \gamma }{d t}= q \sigma _M \phi (\alpha , \gamma )-k_s \gamma ;\\& \phi (\alpha , \gamma ) = \frac{\alpha (1+\alpha ) (1+\gamma )^2}{L+(1+\alpha )^2 (1+\gamma )^2}\,. \end{aligned}$$

(16)

The variables $\alpha$ and $\gamma$ are basically the substrate and the product, respectively, v is the substrate injection rate, $q, L \,\, \text{and}\,\, ~k_s$ are the system parameters. This mathematical model of the bio-chemical glycolytic process has been very useful to understand metabolism in yeast cell showing mono-rhythmicity.

3.1.1 Mono-rhythmicity

The kinetic properties are complemented by the mathematical analysis of Sel’kov (1968) and related models. A simplified form for the oscillatory glycolysis in closed vessels by Merkin-Needham-Scott (MNS) (Merkin et al. 1986) is given by

$$\begin{aligned} {\dot{x}}&= -x+(a+x^2) y,\nonumber \\ {\dot{y}}&= b-(a+x^2) y. \end{aligned}$$

(17)

The variable x is the concentration of ADP (adenosine di-phosphate) and y is that of F6P (fructose-6-phosphate). The phosphofructokinase step considered by Sel’kov’s model and its MNS-generalization considers the ATP to ADP transition accompanying fructose-6-phosphate (F6P) to fructose-1,6-diphosphate (F1,6DP). The parameter b means ATP influx and a is the rate of non-catalyzed side-steps (a side-process, which needs to be taken into account for consideration of the closed vessel (Merkin et al. 1986)). The fixed point of the system is at $x_s=b,y_s=\frac{b}{a+b^2}.$ It is a stable focus for a given parameter range and an unstable focus for others. The crossover from stable to unstable focus takes place on the boundary curve which is a locus of points in the a−b plane where a Hopf bifurcation occurs, i.e., the fixed point for those values of (a, b) is a center which satisfies the equation $(a+b^2)^2 +(a-b^2)=0$.

In order to characterize the oscillatory dynamics hidden in the above kinetic model we need to have it under the Liénard umbrella. As per the reduction scheme we transform the system of equations into a single second-order homogeneous differential equation. Expressing $\xi =(x-x_s)+(y-y_s)$ such that

$$\begin{aligned} {\dot{\xi }}&= u, \end{aligned}$$

(18)

we have $u=b-x=x_s-x$. Here x, y can be expressed as

$$\begin{aligned} x = (b-u) \quad \text {and}\quad y=(\xi +\frac{b}{a+b^2}+u). \end{aligned}$$

(19)

Differentiation of equation (18) with respect to time and subsequent elimination of x and y gives the form of $G_L$ and $F_L$ as follows:

$$\begin{aligned} \ddot{\xi }+F_L(\xi ,{\dot{\xi }}) {\dot{\xi }}+G_L(\xi )\xi =0, \end{aligned}$$

(20)

where

$$\begin{aligned}& F_L(\xi ,{\dot{\xi }})= (a+b^2)+\frac{(a-b^2)}{(a+b^2)}-2 b \xi +\left( \frac{b}{a+b^2}-2 b\right) {\dot{\xi }}+\xi {\dot{\xi }}+{\dot{\xi }}^2~~ \nonumber \\ & \quad \text {and} \,\,G_L(\xi )= (a+b^2). \end{aligned}$$

(21)

Thus the glycolytic oscillator belongs to the Liénard family. Note that all the conditions for a Liénard system are satisfied for appropriate choice of a and b. The condition for existence of a stable limit cycle is $F_L(0,0)<0$, i.e.,

$$\begin{aligned} (a+b^2)+\frac{(a-b^2)}{(a+b^2)}<0. \end{aligned}$$

(22)

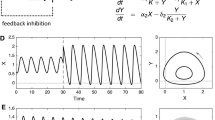
In figure 1a we present the bifurcation diagram in (a, b) parameter space. Figure 1b depicts the limit cycle for the red-dot point $(a=0.11,~b=0.6)$ in the Hopf region.

Figure 1

Mono-rhythmic glycolytic model (equation 20). (a) The bifurcation diagram (shaded area — stable limit cycle; unshaded area — unstable limit cycle) in the parameter space (a, b) showing the oscillatory and the steady state regions. (b) The corresponding phase space plot in Liénard space for the red-dot point $(a=0.11,~b=0.6)$ of (a) in the oscillatory region.

3.1.2 Bi-rhythmicity

In 1984 Goldbeter and co-authors (Decroly and Goldbeter 1982) extended their bio-chemical model to accommodate bi-rhythmicity and proposed a modified scheme.

$$\begin{aligned} & \frac{d \alpha }{d t}= v-\sigma _M \phi (\alpha , \gamma )+\frac{\sigma _i \gamma ^4}{K^4+\gamma ^4}\nonumber \\ & \frac{d \gamma }{d t}= q \sigma _M \phi (\alpha , \gamma )-k_s \gamma -\frac{q \sigma _i \gamma ^4}{K^4+\gamma ^4};\\ & \phi (\alpha , \gamma )=\frac{\alpha (1+\alpha ) (1+\gamma )^2}{L+(1+\alpha )^2 (1+\gamma )^2} \end{aligned}$$

(23)

Here the additional nonlinearity arises as a function of the product variable $\gamma$.

Motivated by the requirement of additional nonlinearity as considered in the above model we envisage a similar but simpler scheme. To this end we refer to equation (20) which can be rewritten as

$$\begin{aligned} \ddot{\xi }+\left( F(0,0)-2 b \xi +c_1 {\dot{\xi }}+\xi {\dot{\xi }}+{\dot{\xi }}^2\right) {\dot{\xi }}+\omega ^2\xi =0, \end{aligned}$$

(24)

where $F(0,0)=\omega ^2+\frac{\omega ^2-2b^2}{\omega ^2},\,\,c_1=\frac{b}{\omega ^2}-2 b, \,\,\omega =\sqrt{(a+b^2)}$. After rescaling time $\tau \rightarrow \omega t$, we have

$$\begin{aligned} \ddot{\xi }+\epsilon \left( k_0-k_1 \xi +k_2 {\dot{\xi }}+k_3\xi {\dot{\xi }}+k_4{\dot{\xi }}^2\right) {\dot{\xi }}+\xi =0, \end{aligned}$$

(25)

where $\epsilon =\frac{|F(0,0)|}{\omega }~(0<\epsilon \ll 1),\,\,k_0=\frac{F(0,0)}{|F(0,0)|}=+1 \,\,\, \text {or} \,\, -1,~k_1=\frac{2b}{|F(0,0)|},~k_2=\frac{\omega c_1}{|F(0,0)|},~k_3=\frac{\omega }{|F(0,0)|},~k_4=\frac{\omega ^2}{|F(0,0)|}.$

To observe the bi-rhythmicity in the Sel’kov model, we need to add the minimal nonlinearity. The detailed recipe for designing such types of bi-rhythmic or tri-rhymic models is given in detail in Saha et al. (2020). We add $-\alpha \xi ^4+\beta \xi ^6$ (the other way can be $-\alpha {\dot{\xi }}^4+\beta {\dot{\xi }}^6$) in the damping force function.

$$\begin{aligned} \ddot{\xi }+\epsilon \delta \left( k_0-k_1 \xi +k_2 {\dot{\xi }}+k_3\xi {\dot{\xi }}+k_4{\dot{\xi }}^2-\alpha \xi ^4+\beta \xi ^6\right) {\dot{\xi }}+\xi =0. \end{aligned}$$

(26)

Here $\alpha$ and $\beta$ are positive constants. $\delta$ is a smallness parameter that controls the strength of nonlinear dissipation. Making use of the Krylov–Bogoliubov perturbation method it is possible to construct (Saha et al. 2020) the amplitude-phase dynamics of the model and locate various regions of $(\alpha ,\beta )$ space for the given parameter values (a, b) specifying the mono-rhythmic region.

Figure 2

Bi-rhythmic Sel’kov model (equation 26). (a) Bifurcation diagram (shaded area — bi-rhythmic; unshaded area — mono-rhythmic) in parameter region space $(\alpha ,\beta )$. (b) Phase space plots in Liénard space for $a=0.11,~b=0.6,\alpha =84.9417~\,\text {and}~\,\beta =82.6841$ (red dot in a) where continuous lines show the stable limit cycles and the dotted line refers to the unstable limit cycle dividing the basin of attractions. Here $\epsilon =0.0903122$ and $\delta =0.8$.

Upon choosing $(\alpha ,~\beta )$ values from the region, i.e., (84.9417,  82.6841) of figure 2a we demonstrate bi-rhythmicity in figure 2b. The phase plots show the unstable cycle in between the inner and the outer cycles, dividing the basin of attractions of the two stable cycles. Equation (26) therefore is an extended Sel’kov model in the Liénard form that describes the essential features of the bi-rhythmicity in glycolysis.

3.2 Lotka–Volterra model: Center

Predators and prey can influence the evolution of one another. Predicting the outcome of populations of the species due to their interactions is of interest to biologists trying to understand how communities are structured and sustained in course of time. The Lotka–Volterra (Murray 1989; Strogatz 1994) model was proposed in the 1920s describes the predator–prey (or herbivore–plant, or parasitoid–host) dynamics in their simplest case with one predator population and one prey population. It shows characteristic oscillations in the population size of both predator and prey, with the peak of the predator’s oscillation lagging slightly behind the peak of the prey’s oscillation. This oscillation is shown to have a center. If this prey population is x and the predator population is y, then the equations are given by

$$\begin{aligned} {\dot{x}}(t)&= \alpha x -\beta x y, \nonumber \\ {\dot{y}}(t)&= -\gamma y+\delta x y, \end{aligned}$$

(27)

with $\alpha ,\beta ,\gamma ,\delta >0$. The two fixed points are ($x_s = 0, y_s =0$) and ($x_s = \frac{\gamma }{\delta }, y_s =\frac{\alpha }{\beta }$), where the first one is a saddle point (which is not of any interest in the present context) and the latter one gives a center solution obtained from standard linear stability analysis. To obtain the Liénard form of the above system, let us set $\xi =\delta (x-x_s)+\beta (y-y_s)$ so that ${\dot{\xi }}=\alpha \delta x-\beta \gamma y=u$. This gives $x=\frac{{\dot{\xi }}+\gamma \xi }{(\alpha +\gamma )\delta }+\frac{\gamma }{\delta }$ and $y=\frac{-{\dot{\xi }}+\alpha \xi }{(\alpha +\gamma )\beta }+\frac{\alpha }{\beta}\,.$ After taking time derivative upon ${\dot{\xi }}$, we have

$$\begin{aligned} \ddot{\xi }+\left( \frac{\alpha -\gamma }{\alpha +\gamma } \xi -\frac{1}{\alpha +\gamma } {\dot{\xi }}\right) {\dot{\xi }}+ \alpha \gamma \xi +\frac{\alpha \gamma }{\alpha +\gamma } \xi ^2&=0, \end{aligned}$$

(28)

where $F_L(\xi ,{\dot{\xi }})=a_1 \xi +a_2 {\dot{\xi }}$ with $a_1=\frac{\alpha -\gamma }{\alpha +\gamma }$ and $a_2= - \frac{1}{\alpha +\gamma }.$ It is to be noted that $G_L(\xi )$ contains nonlinearity with $G_L(\xi )=\omega ^2+a_3 \xi,$ where $\omega =\sqrt{\alpha \gamma }$ and $a_3=\frac{\alpha \gamma }{\alpha +\gamma }.$ Here, $F(0,0)=0$, which implies that the periodic oscillation is not a limit cycle but is at a center. The periodic solution is plotted in figure 3 for the parameter values as shown in the figure.

Figure 3

Center oscillation (equation 28). Phase space plot of the Lotka–Volterra systems showing a center for the parameter values $\alpha =\beta =\gamma =\delta =1$.

3.3 Pigmentation of fish model

The colouration of a fish (Aragón et al. 1998; Barrio et al. 1999; Barrio et al. 2009; Singh et al. 2016; Scarabotti et al. 2020) is primarily due to three pigments, erythrin (red), melanin (black), and xanthin (yellow), which occur in different cells called chromatophores. Because of its importance in developmental biology, fish skin colouration has been widely studied. Mathematical modelling of fish skin patterning first predicted the existence of morphogens and helped to elucidate the mechanisms of pattern formation. The catfishes of the genus Pseudoplatystoma offer themselves as good model candidates for these studies. They present labyrinths, closed loops (or cells), alternate spots and stripes, only spots and their combinations. The basic model is a two-component, nonlinear reaction–diffusion system that presents a rich variety of bifurcations. A variant is an activator–inhibitor model with pentagonal symmetry developed by Maini and collaborators (Aragón et al. 1998; Barrio et al. 1999) for understanding pigmentation of fish pattern. An interesting feature of the associated chemical kinetics is that it contains, in addition to linear and cubic terms, also quadratic terms. The governing equations are given by

$$\begin{aligned} {\dot{x}}&= \alpha x \left( 1-r_1 y^2\right) +y \left( 1-r_2 x\right) \nonumber \\ {\dot{y}}&= \beta y \left( \frac{x y \left( \alpha r_1\right) }{\beta }+1\right) +x \left( \gamma +r_2 y\right) \end{aligned}$$

(29)

where x and y are the dimensionless concentrations of activator and inhibitor chemical species. The parameters are $\alpha , \beta , \gamma , r_1, r_2$. Following Barrio et al. (1999) $\gamma = -\alpha$ is set for the present purpose. The fixed point of the system is at $x_s=0,y_s=0$. If we suppose $\xi =(x-x_s)+(y-y_s)$ such that

$$\begin{aligned} {\dot{\xi }}=u, \end{aligned}$$

(30)

then we have $u=(1+\beta ) y$. Here x, y can be expressed as

$$\begin{aligned} x=\xi -\frac{u}{1+\beta } \quad \text {and} \quad y=\frac{u}{1+\beta }\,. \end{aligned}$$

(31)

Differentiating equation  (30) with respect to time and eliminating x and y gives the Liénard form

$$\begin{aligned} \ddot{\xi }+F_L(\xi ,{\dot{\xi }}) {\dot{\xi }}+G_L(\xi )\xi =0, \end{aligned}$$

(32)

where

$$\begin{aligned} & F_L(\xi )= -(\alpha +\beta )-r_2 \xi +\frac{r_2}{1+\beta }{\dot{\xi }}-\frac{\alpha r_1}{1+\beta }\xi {\dot{\xi }}+\frac{\alpha r_1}{(1+\beta )^2}{\dot{\xi }}^2 \nonumber \\ & \quad \text {and}\,\, G_L(\xi )= \alpha (1+\beta ). \end{aligned}$$

(33)

The condition for the existence of a stable limit cycle is

$$\begin{aligned} (\alpha +\beta )>0. \end{aligned}$$

(34)

Equation  (34) gives the bifurcation condition. The bifurcating diagram is shown in figure 4a in $(\alpha ,\beta )$ parameter space for the set of parameter values as mentioned in the figure. Figure 4b illustrates a representative limit cycle oscillation in phase space for the red-dot point $(\alpha = 0.5815,\beta =-0.1508)$ shown in figure 4a.

Figure 4

Pigmentation of fish model (equation 32). (a) Bifurcation diagram (shaded area — stable limit cycle; unshaded area — unstable limit cycle) in parameter region space $(\alpha ,\beta )$ for $r_1=0.02\,~\text {and}~\,r_2=0.2$. (b) Phase space plot in Liénard space for the red-dot point $(\alpha = 0.5815,\beta =-0.1508)$ in (a).

3.4 Substrate depletion model

The important enzyme cycling kinetic parameters (Robinson and Tiedje 1983; Waley 1993; Fall et al. 2002; Srividhya and Schnell 2006), K_cat and K_m, represent the maximal enzyme turnover rate and substrate concentration-dependence of enzyme activation, respectively. They are responsible for an enzyme’s performance, specificity, efficiency and proficiency. The calculation of K_cat and K_m values from intrinsic rate constants requires knowledge of the reaction mechanism since K_cat and K_m are the composites of the elementary reaction constants.

The simplest oscillatory mechanism is probably the linear pathway where the species Y is converted into a species X by an enzyme that is activated by its product. Hence, the production of X is autocatalytic; the reaction speeds up as [X] increases, until the substrate Y is depleted so much that the reaction ceases. The two-component oscillator based on autocatalysis assumes that product-binding to regulatory sites is highly cooperative, so that one may neglect the fraction of enzyme with only one product molecule bound.

An interesting example of substrate–product enzyme kinetics was proposed in Fall et al. (2002). The governing equations are:

$$\begin{aligned} {\dot{x}}&= a-x y^2 \nonumber \\ {\dot{y}}&= \epsilon -b y+x y^2 \end{aligned}$$

(35)

where x and y are the dimensionless concentrations of chemical species. The parameters are $a, b, \epsilon > 0$. It may be considered that as substrate x is needed for the production of product y, but as y increases it inhibits the substrate’s reaction rate. So, it is referred to as a ‘substrate depletion system’. The fixed point of the system is at $x_s=\frac{a b^2}{(a+\epsilon )^2},y_s=\frac{a+\epsilon }{b}.$ If we put $\xi =(x-x_s)+(y-y_s)$ such that

$$\begin{aligned} {\dot{\xi }}=u, \end{aligned}$$

(36)

then we have $u=a+\epsilon -b y$. Here x, y can be expressed as

$$\begin{aligned} x=\xi +\frac{{\dot{\xi }}}{b}+\frac{a b^2}{(a+\epsilon )^2}\quad\text {and}\quad y=\frac{a+\epsilon -u}{b}. \end{aligned}$$

(37)

Differentiating equation (36) with respect to time and eliminating x and y results in the Liénard equation,

$$\begin{aligned} \ddot{\xi }+F_L(\xi ,{\dot{\xi }}) {\dot{\xi }}+G_L(\xi )\xi =0, \end{aligned}$$

(38)

where

$$\begin{aligned} & F_(\xi )= \frac{(a+\epsilon )^2}{b^2}-b \frac{a-\epsilon }{a+\epsilon }-2 \frac{a+\epsilon }{b}\xi \nonumber \\&\quad+\frac{a b^3-2 (a+\epsilon )^3}{b^2 (a+\epsilon )^2}{\dot{\xi }}+\frac{1}{b}\xi {\dot{\xi }}\nonumber \\&\quad+\frac{1}{b^2} {\dot{\xi }}^2\nonumber \\ & \quad \text {and} \,\,G_(\xi )= \frac{(a+\epsilon )^2}{b}. \end{aligned}$$

(39)

The condition for the existence of a stable limit cycle is

$$\begin{aligned} \frac{(a+\epsilon )^2}{b^2}-b\frac{a-\epsilon }{a+\epsilon }<0\,. \end{aligned}$$

(40)

The bifurcation diagram in (a, b) parameter space is shown in figure 5a. The limit cycle in the Liénard plane is shown in figure 5b for the red-dot point $(a = 0.86,b=2.33)$ shown in figure 5a.

Figure 5

Substrate depletion model (equation 38). (a) Bifurcation diagram (shaded area — stable limit cycle; unshaded area — unstable limit cycle) in (a, b) space for $\epsilon =0.1$. (b) Phase space for the red-dot point $(a = 0.86,b=2.33)$ shown in (a).

4 Rayleigh family

In this category of the Liénard system we discuss two model bio-kinetic schemes, one for bacterial respiration and the other for the cell cycle.

4.1 Bacterial respiration model

During respiration (Fairén and Velarde 1979; Slonczewski and Foster 2013) bacteria oxidize food materials present in the cytoplasm to obtain energy. Most bacteria using the free oxygen of the atmosphere or oxygen dissolved in the liquid environment are called aerobes or aerobic bacteria. However, there is a class of bacteria which is able to live and multiply in the absence of free oxygen. In fact they perish in the presence of free oxygen. Respiration of these bacteria is accomplished by the secretion of certain oxidizing enzymes to bring about breakdown of foods. The amount of energy available from this type of respiration is much less than when free oxygen is used.

A model for respiration in a bacterial culture was proposed by Fairén and Velarde (1979). Here the dynamics is considered for concentration levels of nutrient and oxygen denoted by x and y, respectively, as given by the following two equations:

$$\begin{aligned} {\dot{x}}&= B-x-\frac{xy}{1+q x^2} \nonumber \\ {\dot{y}}&= A-\frac{xy}{1+q x^2}; A, B, q>0. \end{aligned}$$

(41)

The fixed point of the system is at $x_s=B-A,y_s=\frac{A}{B-A}+q A (B-A)$. If we set $\xi =-(x-x_s)+(y-y_s)$ so that

$$\begin{aligned} {\dot{\xi }}&= u, \end{aligned}$$

(42)

we have $u=A-B+x=x-x_s$. Here x, y can be expressed as

$$\begin{aligned} x=u+x_s=u+B-A \quad\text {and}\quad y=\xi +u+ys=\xi +u+\frac{A}{B-A}+q A (B-A). \end{aligned}$$

(43)

Differentiating equation (42) with respect to time and eliminating x and y we obtain the Liénard equation in Rayleigh form

$$\begin{aligned} \ddot{\xi }+F_R({\dot{\xi }}) {\dot{\xi }}+G_R({\dot{\xi }})\xi =0, \end{aligned}$$

(44)

where

$$\begin{aligned} F_R({\dot{\xi }})= \frac{1}{T}\left[ (B-A)\{1-q(2 A-B)\}+\frac{B}{B-A}\right. \nonumber \\ \quad \left. +(1-3 q A+2 q B){\dot{\xi }}+q{\dot{\xi }}^2 \right] \nonumber \\ \text {and}\,\, G_R({\dot{\xi }})= \frac{1}{T}\left[ B-A+ {\dot{\xi }}\right] ; \quad T=1+q(B-A+{\dot{\xi }})^2. \end{aligned}$$

(45)

The condition for existence of a stable limit cycle is

$$\begin{aligned} \frac{(B-A)\{1-q(2 A-B)\}+\frac{B}{B-A}}{1+q(B-A)^2}<0. \end{aligned}$$

(46)

The bifurcation condition (46) is illustrated in (A, B) parameter space in figure 6a, where the shaded region denotes the oscillatory region. In figure 6b we have depicted the oscillatory dynamics in a phase space plot corresponding to the red-dot point $(A = 5.588,B = 7.758)$ lying in the Hopf region in figure 6a.

Figure 6

Rhythmic bacterial respiration model (equation 44). (a) Bifurcation diagram (shaded area — stable limit cycle; unshaded area — unstable limit cycle) in parameter space (A, B) with $q=1.$ (b) Phase space plot in Liénard space for the red-dot point $(A = 5.588,B = 7.758)$ of (a).

4.2 Cell cycle model

During cell division, microtubules position the chromosomes in a common plane after breakdown of the nuclear envelope before they segregate such that each daughter cell receives a full copy of the genetic material (Prestige 1972; John 1981; Tyson 1991; Gérard and Goldbeter 2012). For this, the microtubules arrange themselves in a bipolar structure called a spindle. Microtubules emanate from two microtubules organizing centers with their plus ends pointing away from the centers. Some microtubules connect to chromosomes at a structure denoted as the kinetochore, whereas other microtubules reach out to the cell cortex or interdigitate maintaining spindle integrity. This dynamic assembly of microtubules and motors is prone to oscillations probed by laser ablation of structural elements and theoretical models for obtaining a quantitative understanding of the oscillation mechanisms and is an important area of investigation.

Based on the interaction between two proteins cdc2 and cyclin, Tyson (1991) proposed a minimal model for the cell division cycle. The governing equations are

$$\begin{aligned} {\dot{x}}&= b(y-x)(\alpha +x^2)-x \nonumber \\ {\dot{y}}&= c-x. \end{aligned}$$

(47)

Here, x denotes the active form of a cdc2-complex and y refers to the total cyclin concentration (monomer and dimer). The parameters $b\gg 1$ and $\alpha \ll 1$ are fixed and they satisfy $8 \alpha b < 1$. c is an adjustable parameter. The fixed point of the system is at $x_s=c,y_s=c+\frac{c}{b (\alpha +c^2)}$. If we put $\xi =y-y_s$ so that

$$\begin{aligned} {\dot{\xi }}=u, \end{aligned}$$

(48)

we have $u=c-x$. Here x, y can be expressed as

$$\begin{aligned} x=c-u \;\text {and}\,~ y=\xi +ys. \end{aligned}$$

(49)

Differentiating equation (48) with respect to time and eliminating x and y we obtain the Liénard form of the Rayleigh family,

$$\begin{aligned} \ddot{\xi }+F_R({\dot{\xi }}) {\dot{\xi }}+G_R({\dot{\xi }})\xi =0, \end{aligned}$$

(50)

where

$$\begin{aligned} F_R({\dot{\xi }})= b (\alpha +c^2)+\frac{\alpha -c^2}{\alpha +c^2} + c \left( \frac{1}{\alpha +c^2}-2 b\right) {\dot{\xi }}+b {\dot{\xi }}^2 \nonumber \\ \text {and} \\ G_R({\dot{\xi }})= b (\alpha +c^2)-2 b c {\dot{\xi }}+b {\dot{\xi }}^2. \end{aligned}$$

(51)

The condition for existence of a stable limit cycle is

$$\begin{aligned} b (\alpha +c^2)+\frac{\alpha -c^2}{\alpha +c^2}<0. \end{aligned}$$

(52)

In figure 7a and b we have presented the bifurcation diagram and the limit cycle on the Liénard plane, respectively, for the set of parameter values as mentioned in figure 7.

Figure 7

Cell cycle model (equation 50). (a) Bifurcation diagram (shaded area — stable limit cycle; unshaded area — unstable limit cycle) in $(b,\alpha )$ space for $c=0.2$. (b) Phase space plot in Liénard space for the red-dot point $(b = 1.577,\alpha = 0.0163)$ of (a).

5 Extended Liénard family

Here we consider two diverse types of bio-rhythms, circadian oscillation in the sleep–wake cycle and $\hbox {Ca}^{2+}$ oscillation controlling intracellular signals.

5.1 Circadian model

The circadian model describes the sleep–wake cycle of all living organisms including cyanobacteria, fungi, plants, and mammals (Pittendrigh and Victor 1957; Pavlidis 1967; Winfree 1967; Gonze et al. 2002; Reppert and Weaver 2002; Leloup and Goldbeter 2004; Gonze et al. 2005; Sen et al. 2008; Gonze 2011; Oda and Friesen 2011). Circadian rhythms are driven by a self-sustained oscillator with a period of about 24 h and are based on a gene regulatory network of interacting feedback loops. This clock acts on all physiological and behavioural levels, allowing a living organism to anticipate daytime changes so as to organize its resources in an effective way and relies on repetitive synchronization with an environmental zeitgeber (timer), the most important one being the periodic change between daylight and darkness in the course of the day–night cycle. Pittendrigh and co-workers (1959) (Pittendrigh and Victor 1957; Pittendrigh and Bruce 1959) in a series of experiments on zeitgebers reported the complex dynamics of the phase of the overt rhythm in Drosophila. Here we consider the oscillator model that explains the main features of the complex behavioural results of these experiments (Pavlidis 1967). The model has recently been utilized to describe the two-oscillator circadian rhythms entrained by two environmental cycles (Oda and Friesen 2011). The oscillator simulated by the Pittendrigh–Pavlidis equations are given by

$$\begin{aligned} {\dot{x}}&= x-c y-b y^2+d-L+\frac{1}{1+100 x^2};\\L&=A~\rm{sin}(\omega t) \nonumber \\ {\dot{y}}&= x-a y, \end{aligned}$$

(53)

where x and y are the state variables; a, b, c, d are the parameters for the autonomous system. L is a periodic function with a 12 h time period for light and dark. These equations were developed earlier for studies of the oscillator controlling the eclosion rhythm in Drosophila and later on employed even for mammalian circadian rhythms (Oda et al. 2000; Oda and Friesen 2002; Schwartz et al. 2009).

The fixed point of the above system, say $(x_s,~y_s)$, can be solved analytically by solving ${\dot{x}}={\dot{y}}=0$. If we suppose $\xi =(y-y_s)$ so that

$$\begin{aligned} {\dot{\xi }}&= u, \end{aligned}$$

(54)

then we have $u=x-a y$. Here x, y can be expressed as

$$\begin{aligned} x={\dot{\xi }} + a (y_s + \xi ) \quad \text {and} \quad y=\xi +y_s. \end{aligned}$$

(55)

Differentiation of equation (54) with respect to time and further elimination of x and y gives the Liénard extended form

$$\begin{aligned} \ddot{\xi }+F_E(\xi ,{\dot{\xi }}) {\dot{\xi }}+G_E(\xi ,{\dot{\xi }})\xi =-L \end{aligned}$$

(56)

where

$$\begin{aligned} F_E(\xi ,{\dot{\xi }})&= \frac{1}{T}\left[ 100 a \left( a^2-3 a+2 c\right) y_s^2\right. \nonumber \\&\quad+200 a b y_s^3-200 a d y_s+a-1\nonumber \\&\quad+100 \left( \left( 2 a^2-3 a+c\right) y_s+b y_s^2-d\right) {\dot{\xi }}\nonumber \\&\quad\left. +100 (a-1){\dot{\xi }}^2 \right] \\ \text {and} \nonumber \\ G_E(\xi ,{\dot{\xi }})&= \frac{1}{T}\left( -100 a^3 \xi ^2+100 a^2 \xi (\xi (b \xi +c)-d)+2 y_s \right. \nonumber \\&\quad\left( 200 a^2 b \xi ^2-50 a^2 (3 a \xi -3 c \xi +2 d)+b\right) \nonumber \\&\quad-300 a^2 y_s^2 (a-2 b \xi -c)+400 a^2 b y_s^3\nonumber \\&\quad\left. -a+b \xi +c\right) \end{aligned}$$

(57)

$$\begin{aligned}&+ \frac{1}{T}\left( 100 a \left( \xi \left( a^2-3 a+2 b \xi +2 c\right) +2 y_s \right. \right. \nonumber \\&\quad\left. \left. \left( a^2-3 a+3 b \xi +2 c\right) +6 b y_s^2-2 d\right) \right) {\dot{\xi }}\nonumber \\&\quad+\frac{1}{T} 100 \nonumber \\&\quad\left( 2 a^2-3 a+b \xi +2 b y_s+c\right) {\dot{\xi }}^2\nonumber \\ T&= 100 (a (y_s+\xi )+{\dot{\xi }})^2+1\nonumber \\&\quad-y_s^2 \left( b-100 a^2 d\right) -100 a^2 b y_s^4\nonumber \\&\quad+100 a^2 (a-c) y_s^3+(a-c) y_s+d+1=0 \end{aligned}$$

(58)

Equation (56) is the extended Liénard oscillator driven by a periodic forcing L(t) zeitgeber (timer). The condition for the existence of a stable limit cycle obtained from $F(0,0)<0$ is

$$\begin{aligned} \frac{100 a \left( a^2-3 a+2 c\right) y_s^2+200 a b y_s^3-200 a d y_s+a-1}{100 a^2 y_s^2+1}<0 \end{aligned}$$

(59)

In figure 8a we have illustrated the bifurcation diagram in (a, c) parameter space for fixed values of b and d. The limit cycles in absence and presence of forcing on the Liénard plane are shown in figure 8b and c, respectively, for the red-dot point in the Hopf region in figure 8a.

Figure 8

Circadian Rhythm (equation 56). (a) Bifurcation diagram (shaded area — stable limit cycle; unshaded area — unstable limit cycle) in (a, c) parameter space for $b=0.3\,~\text {and}~\,d=0.5$. (b and c) Phase space plots in Liénard space for the red-dot point $(a =0.85,c=0.8)$ for $L=0$ and $L=2~\rm{sin}(12~\it{t})$, respectively.

5.2 Ca²⁺ model

Calcium ions ($\hbox {Ca}^{2+}$) are highly important messengers which control intracellular signalling molecules in numerous cellular processes like cell growth, division, motility, and apoptosis and various cell functions such as muscle contraction, gene regulation, etc. $\hbox {Ca}^{2+}$ oscillation was first observed in the 1980s (Woods et al. 1986; Berridge et al. 1988; Shangold et al. 1988; Berridge and Irvine 1989; Goldbeter et al. 1990). It is well known that the oscillations may arise spontaneously or due to receptor stimulation. The time periods of these bio-rhythms range from seconds to minutes, depending on cell type or stimulus level while the oscillations depend on interacting positive and negative regulatory feedbacks. We refer to Goldbeter et al. (1990) for the detailed mechanism of the pathways of how the G-protein-coupled receptor induces production of $IP_3$ (inositol 1,4,5 tri-phosphate) by activation of PLC (phospholiphase) and how $IP_3$ in turn, binds to the receptor channels $(IP_3Rs)$ at the intracellular ion $\hbox {Ca}^{2+}$ ion stores to induce $\hbox {Ca}^{2+}$ release.

A model for calcium oscillation proposed by Goldbeter et al. (1990) is based on the dynamics of the concentration levels of nutrient and oxygen denoted by z and y, respectively, governed by the following two equations:

$$\begin{aligned} {\dot{z}}&= v_0+v_1 \beta -v_2+v_3+k_f y-k z \nonumber \\ {\dot{y}}&= v_2-v_3-k_f y; v_2=v_{m2}\frac{z^2}{k_2^2+z^2},~v_3=v_{m3}\frac{y^2}{k_r^2+y^2} \frac{z^4}{k_a^4+z^4} \end{aligned}$$

(60)

As the system involves high powers of state variables and a large number of parameters, it is very difficult to deal with the analytical expressions particularly the fixed point. A simple way out of this difficulty is to fix the parameter set (Goldbeter et al. 1990), i.e., $v_0=k_f=k_2=1,~k=10,~v_1=7.3,~v_{m2}=65, ~v_{m3}=500,~k_a=0.9,~k_r=2,\beta =0.301$, and determine the fixed point of the system numerically as $(z_s,~y_s)=(0.31973,~2.03702)$. If we now put $\xi =(z-z_s)+(y-y_s)$ as before such that

$$\begin{aligned} {\dot{\xi }}=u, \end{aligned}$$

(61)

we have $u=3.1973-10 z$. Following the procedure as worked out before z, y can then be expressed as

$$\begin{aligned} z=0.31973 - 0.1 u \quad \text {and} \quad y=2.03702 + 0.1 u + \xi . \end{aligned}$$

(62)

Differentiating equation (61) with respect to time and subsequently eliminating z and y we have the extended Liénard form

$$\begin{aligned} \ddot{\xi }+F_E(\xi ,{\dot{\xi }}) {\dot{\xi }}+G_E(\xi ,{\dot{\xi }})\xi =0, \end{aligned}$$

(63)

where

$$\begin{aligned} F_E(\xi ,{\dot{\xi }})&= \frac{1}{T}[0.000011 {\dot{\xi }}^8+0.00460749 {\dot{\xi }}^7+0.0973646 {\dot{\xi }}^6\nonumber \\&\quad-0.761579 {\dot{\xi }}^5 +10.0822 {\dot{\xi }}^4\nonumber \\&\quad+92.5724 {\dot{\xi }}^3-2267.75 {\dot{\xi }}^2\nonumber \\&\quad+9800.28 {\dot{\xi }}-1207.43]~~ \\ & \text {and}~~\nonumber \\ G_E(\xi ,{\dot{\xi }})&= \frac{1}{T}[734.69 \xi ^2+5820.03 \xi +0.00023 {\dot{\xi }}^8\nonumber \\&\quad+(0.0013 \xi +0.087884) {\dot{\xi }}^7\nonumber \\&\quad+\left( 0.001 \xi ^2+0.416172 \xi +0.0763332\right) {\dot{\xi }}^6\nonumber \\&\quad+ \left( -0.0191838 \xi ^2-8.13284 \xi -10.0753\right) {\dot{\xi }}^5\nonumber \\&\quad+\left( 0.253341 \xi ^2+115.739 \xi +287.902\right) {\dot{\xi }}^4\nonumber \\&\quad+ \left( -1.93262 \xi ^2-917.09 \xi -3068.61\right) {\dot{\xi }}^3\nonumber \\&\quad+\left( 14.2622 \xi ^2+3335.26 \xi +12700.1\right) {\dot{\xi }}^2+\nonumber \\&\quad\left( -57.0338 \xi ^2-4075.47 \xi -15855.8\right) {\dot{\xi }}\nonumber \\&\quad+17504.1];\nonumber \\ T&= (1. {\dot{\xi }}^2-6.3946 {\dot{\xi }}+110.223) \left( (0.31973\, -0.1 {\dot{\xi }})^4\right. \nonumber \\&\quad\left. +0.6561\right) \left( (1. \xi +0.1 {\dot{\xi }}+2.03702)^2+4\right). \end{aligned}$$

(64)

The condition for existence of a stable limit cycle is guaranteed since

$$\begin{aligned} F(0,0)=\frac{-1207.43}{598.733}=-2.01665<0. \end{aligned}$$

(65)

In figure 9 we illustrate the variation of $\xi$ and ${\dot{\xi }}$ with time for the $\hbox {Ca}^{2+}$ oscillation.

Figure 9

Model for $\hbox {Ca}^{2+}$ oscillation (equation 63). The figure represents the time series plots in extended Liénard space that depict $\hbox {Ca}^{2+}$ oscillations for the set of parameter values as mentioned in the text ($\xi$ vs. time, continuous line; ${\dot{\xi }}$ vs. time, dashed line).

6 Conclusion

We now summarize the main conclusion of this study. The bio-oscillators in two state variables giving rise to bio-rhythms over a wide range, in general, are Liénard oscillators irrespective of their genesis in biology. This has been shown in a general mathematical setting and illustrated in terms of several examples, after a classification of three major families of the Liénard system. Except the case of pigmentation of fish model, all the biochemical models considered here for illustration of the three families are based on experimental kinetic data which corroborate well with the theoretical predictions of the models.

Depending on the specificity of the situations the oscillators can be classified into distinct families. Each family is specified by a characteristic nonlinear damping function and a forcing term. Since a Liénard equation allows mono-rhythmic or multi-rhythmic limit cycle solutions in addition to a periodic solution at the center for appropriate parameter space, the present formulation opens up wider possibilities when the parameters of the corresponding systems are tuned appropriately. This aspect of multi-periodicity has been demonstrated in the case of glycolysis. Apart from universality, there are other features of this scheme. First, the conspicuous feature of a limit cycle and a center in terms of the nonlinear damping function at the origin F(0, 0) is made clear. Second, by casting the bio-kinetic equations in the form of a Liénard equation with identification of the nonlinear damping and forcing terms, the general methods of perturbation theory like the Lindstedt–Poincaré technique (Strogatz 1994; Jordan and Smith 2007), etc., or more generally, the Renormalisation Group Technique (Sarkar et al. 2010) can be used to calculate the higher-order corrected frequency analytically so that the direct dependence of the bio-rhythm on the system parameters can be understood quantitatively. Third, one may also initiate a systematic search for new models as variants of already known models of a given family of Liénard systems. To this end a case has been illustrated in section 3.1 whereby a mono-rhythmic Sel’kov model is transformed into a bi-rhythmic type by adding nonlinearity in the damping force function $F(\xi ,{\dot{\xi }})$. For a tri-rhythmic variant one may add further terms $\xi ^8, \xi ^{10}$ and lower the value of $\delta$ in an appropriate way.

Before concluding, two pertinent points are in order. First, in this scheme of mapping the kinetic equations in Liénard form it is necessary that at least one of the equations must contain a linear term. If neither of the two equations contains a linear term, the linear transformation cannot be constructed by inspection of the equations and the method fails. Such an occurrence is, of course, a rare occasion in chemical dynamics. Second, the applicability of the method to kinetic equations with more than two variables depends on how effectively one can reduce the number of phase space variables to two by appropriate elimination of the fast variables. Complications may arise in biological systems in the presence of positive and/or negative feedback loops with delays. The time delays are used to simplify the complex reactions with many intermediates. They are, in general, related to kinetic parameters, such as rate constants, steady state concentrations, etc., of the intermediates. The direct extension of the present scheme to transform the delay differential equations into the Liénard form needs modification. A recipe based on the Taylor expansion used earlier (Epstein and Pojman 1998) may be implemented. The Taylor expansion of a delay term, say $x(t-\tau ),~\tau$ being the delay time, generates successive terms of the order of delay. A fourth-order expansion was shown to be reasonably good with higher derivatives of x(t). This results in an increase of the number of variables. These multivariate systems can be related to two variable systems by projection of the system on the centre manifold and adiabatic elimination of the fast variables (Das and Ray 2013) appropriately identified after the projection. However, if the separation of the underlying time scales of a multivariate system is too blurry, the scheme fails. Finally we conclude with a remark that the universality of bio-rhythms as demonstrated from the perspective of nonlinear dynamics forms a bridge between two worlds—the domain of biology and the world of physical science of vibration of strings and musical instruments.