1 Introduction

The nature of dark matter (DM) and dark energy (DE), which is supposed to constitute more than 95% of the energy density of the universe, is still uncertain. DM is supposed to be in the form of unknown weakly interacting massive particles. The manner in which the velocities vary with radius gives the distribution of mass in the galaxy. A solid disk would rotate such that the velocity increases linearly with radius. If the mass is concentrated at the centre, the velocity decreases with the square root of the radius (Keplerian case). A flat rotation curve, that is, one in which the velocity is constant over some range of radii, implies that the mass is still increasing linearly with radius. Most galactic rotation curves have two regions. The inner region indicates that the velocity increases linearly with radius near the centre, while the other (outer) region indicates a constant (or gradually rising) velocity rotation in the outer parts. The typical rotation curve of galaxies is given in Figure 1, where \(r_{\mathrm{max}} \) is the distance from the galactic centre beyond which the rotation curve flattens out.

Now, for a distance \(r\ll r_{\mathrm{max}} \) (i.e., close to the galactic centre), for a constant density (\(\rho _{0} )\), the mass is given by \(M\left( r \right) =\frac{4}{3}\pi r^{3}\rho _{0} \), which gives the velocity as \(v=\left( {\frac{4}{3}\pi G\rho _{0} } \right) ^{1/2}r\), i.e., a velocity varying linearly with distance up to a certain distance \(r_{\mathrm{max}} \), which is in agreement with the observation (i.e., region I of the rotation curve of the galaxy (cf. Figure 1)). For \(r\gg r_{\mathrm{max}} \) (i.e., in the region II of the rotation curve of the galaxy), the velocity becomes constant. This flat rotation curve indicates nonluminous matter (dark matter) holding the galaxy together.

Several experiments to detect DM, that is, six times more abundant than baryonic matter, have yielded no positive results so far. Results from PandaX-II dark matter experiment reported that no DM candidates have been observed (Tan et al. 2016). Even the upgraded XENON1T has set most stringent limits on DM interaction cross-section but detection still remains elusive (Aprile et al. 2017).

Another unsolved mystery in cosmology is that 70% of the energy density of the universe is unaccounted for. The dimensionless quantity, i.e., the deceleration parameter which measures the cosmic acceleration of the universe’s expansion is given by \(q_{0} =-\frac{\ddot{R} R}{R^{2}}=\frac{{\Omega }_{M}}{2}-{\Omega }_{{\Lambda }} \), where \({\Omega }_{M} =\rho _{M} /\rho _{\mathrm{c}} \) and \({\Omega }_{{\Lambda }} =\rho _{{\Lambda }} /\rho _{\mathrm{c}} \), \(\rho _{M} \) and \(\rho _{{\Lambda }} \) are the densities of matter and DE respectively, R is the scale factor, and \(\rho _{\mathrm{c}} =\frac{3H_{0}^{2} }{8\pi G}\) is the critical density, where \(H_{0} \) is the present Hubble constant (for cosmological constant \({\Lambda }\), \(\rho _{{\Lambda }} =\frac{{\Lambda }c^{2}}{8\pi G})\). The negative value of \(q_{0} \), deduced from the measurements of Type Ia supernovae (Perlmutter et al. 1999; Riess et al. 1998) indicates an accelerated expansion of the universe with a repulsive gravity and negative pressure. By measuring their flux with redshift, \(q_{0}\) is determined to be −0.55. This together with the fact that the universe is flat (from cosmic microwave background radiation (CMBR)) gives (Ade et al. 2016) \({\Omega }_{M} \approx 0.316\), which includes both baryonic and DM, and \({\Omega }_{{\Lambda }} \approx 0.684\), i.e., in some exotic form which is dubbed dark energy (Sivaram 2009).

Fig. 1
figure 1

Rotation curve of a typical galaxy.

Full size image

Various models for DE have been proposed, out of which the simplest is the cosmological constant originally introduced by Einstein in 1917 as an addition to his theory of general relativity (GR). Though the cosmological constant as DE is supported by many observations, it has two major problems. One being the problem of fine tuning and the other is the coincidence problem, i.e., why are the matter and vacuum energy densities approximately equal at the present epoch? As there has been no direct detection of DM (in two decades) and the nature of DE is unclear, alternate models for DM and DE need to be taken seriously (Arun et al. 2017, 2018).

2 Modification of Newtonian dynamics

One such alternative picture, the Modification of Newtonian Dynamics (MOND) was initially proposed as an alternative to account for the flat rotation curves of spiral galaxies, without invoking DM in the halo by Milgrom (1983a, b). The theory required an ad hoc introduction of a fundamental acceleration \(a_{0} \approx 10^{-8}\, \text{ cm }/\text{ s }^{2}\). When the acceleration approaches \(a_{0} \), the Newtonian law giving the field strength is modified as

$$\begin{aligned} a=\frac{\left( {GMa_{0} } \right) ^{1/2}}{r}, \end{aligned}$$
(1)

where a is the acceleration, r is the radial distance and M is the central mass. This gives a constant velocity, i.e., flat rotation curve for the galaxies, with the constant velocity, \(v_\mathrm{c} \), at the galactic outskirts given by

$$\begin{aligned} v_\mathrm{c} =\left( {GMa_{0} } \right) ^{1/4}. \end{aligned}$$
(2)

These results can also be arrived at by considering a minimum acceleration given by de Sabbata and Sivaram (1993):

$$\begin{aligned} a_{\mathrm{min}} =\frac{GM}{r_{\mathrm{max}}^{2} }. \end{aligned}$$
(3)

Here \(r_{\mathrm{max}} \) is the radius of the structure corresponding to the minimum acceleration and it sets the limit for the size of large scale structures, which follows from equation (3) as

$$\begin{aligned} r_{\mathrm{max}} =\left( {\frac{GM}{a_{\mathrm{min}} }} \right) ^{1/2}. \end{aligned}$$
(4)

Substituting for \(r_{\mathrm{max}} \) (from Equation (4)) in the usual expression for the velocity of stars in the galactic outskirts, we have

$$\begin{aligned} v_\mathrm{c}^{2} =\frac{GM}{r_{\mathrm{max}} }=\frac{GM}{\sqrt{\frac{GM}{a_{\mathrm{min}} }} }. \end{aligned}$$
(5)

From Equation (5), we get

$$\begin{aligned} v_\mathrm{c} =\left( {GMa_{\mathrm{min}} } \right) ^{1/4}. \end{aligned}$$
(6)

This velocity is independent of r beyond \(r_{\mathrm{max}} \), which is consistent with observation. In the case of the Milky Way, this constant velocity from Equation (6) is \(\sim \)300 km/s which is the same order as that observed. For clusters of galaxies, such as Virgo (\(M\approx 1.25\times 10^{15}M_{\odot } )\) and Coma (\(M\approx 7\times 10^{14}M_{\odot } )\) clusters, the velocity (from Equation (6)) is found to be \(\sim \)1500 km/s which is again in accordance with what is observed.

This is same as the velocity in the galactic outskirts as proposed by MOND (i.e., Equation (2)), where the minimum acceleration \(a_{\mathrm{min}}\sim a_{0} \). Equation (4) sets constraints on the size of large scale structures such as galaxies, clusters and super clusters, i.e., \(r_{\mathrm{max}} =\left( {\frac{GM}{a_{\mathrm{min}} }} \right) ^{1/2}\). The size constraint from Equation (4) closely matches with observations, as can be seen in Table 1.

Table 1 Observed and calculated sizes of clusters and superclusters.
Full size table

These constraints on the size of large scale structures are seen to be within the observed scales for smaller clusters such as Virgo cluster, Omega Centauri, etc. In the case of larger structures, like the superclusters, there is an order difference in the limit set by Equation (4) and the observed sizes. This could be due to disparity in observation where the outermost structures of these superclusters may not be bound to them (Rebecca et al. 2018).

It was also discussed in recent papers that the requirement that the attractive gravitational binding self-energy density of large scale structures (such as galaxies, clusters, super clusters, etc.) should at least be equal to the background repulsive DE density which implies a mass–radius relation of the type (Sivaram et al. 2013; Sivaram & Arun 2012, 2013)

$$\begin{aligned} \frac{M}{r^{2}}=\frac{c^{2}}{G}\sqrt{{\Lambda }} \approx 1\,\text{ g }/\text{ cm }^{2} \end{aligned}$$
(7)

for the observed value of \({\Lambda }\sim 10^{-56}\,\text{ cm }^{-2}\), where M and r correspond to mass and radius of these various structures. This relation holds true for primeval galaxies as well as those at present epoch as shown in Rebecca et al. (2018). This relation can also be obtained by rearranging Equation (3), i.e.,

$$\begin{aligned} \frac{M}{r_{\mathrm{max}}^{2} }=\frac{a_{\mathrm{min}} }{G}\approx 1\, \text{ g }/\text{ cm }^{2}\quad , \end{aligned}$$
(8)

where the minimum acceleration is \(a_{\mathrm{min}}\sim 10^{-8}\,\text{ cm }/\text{ s }^{2}\).

3 Modifications of Newtonian gravity

The flat rotation curves can also be explained by considering Modifications of Newtonian Gravity (MONG). By adding a gravitational self-energy term to the Poisson’s equation, we get

$$\begin{aligned} \nabla ^{2}\phi +K\left( {\nabla \phi } \right) ^{2}=4\pi G\rho , \end{aligned}$$
(9)

where \(\phi \left( {\sim \frac{GM}{r}} \right) \) is the gravitational potential and the constant \(K\sim G^{2}/c^{2}\). The gravitational self-energy density is given by \(K\left( {\nabla \phi } \right) ^{2}\), and also contributes to the gravitational field along with the matter density \(\rho \). For small values of the density \(\rho \) (for e.g., at the outskirts of galaxies), we have

$$\begin{aligned} \nabla ^{2}\phi +K\left( {\nabla \phi } \right) ^{2}=0. \end{aligned}$$
(10)

The solution of this equation yields

$$\begin{aligned} \phi ={K}'\mathrm{ln}\frac{r}{r_{\mathrm{max}}}, \end{aligned}$$
(11)

where \({K}'=\frac{GM}{r_{\mathrm{max}}}\) is a constant. This gives the force of the form

$$\begin{aligned} F=\frac{K''}{r}, \end{aligned}$$
(12)

where \(K''=\left( {GMa_{\mathrm{min}} } \right) ^{1/2}\), which is again a constant. The balance of the centripetal force and gravitational force then gives

$$\begin{aligned} \frac{v^{2}}{r}=\frac{K''}{r}. \end{aligned}$$
(13)

Thus Equation (13) implies the independence of v on r (i.e., flat rotation curve \(v^{2}=K''\), which is a constant) for larger distances from the centre of the galaxy (i.e., for \(r>r_{\mathrm{max}} )\). For DE given by the cosmological constant \(\Lambda \), the Newtonian modification is

$$\begin{aligned} \nabla ^{2}\phi -\Lambda c^{2}=0. \end{aligned}$$
(14)

Including both gravitational self-energy and DE densities, the Poisson’s equation now takes the form

$$\begin{aligned} \nabla ^{2}\phi +K\left( {\nabla \phi } \right) ^{2}-\Lambda c^{2}=0. \end{aligned}$$
(15)

The general solution (for the potential \(\phi \)) can be written as

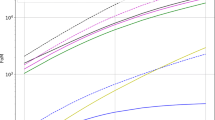
$$\begin{aligned} \phi =\frac{GM}{r}+{K}'\mathrm{ln}\frac{r}{r_{\mathrm{max}}}+\Lambda r^2c^2. \end{aligned}$$
(16)

We now make use of this general solution for different regimes of interest in the galaxy structure. Where matter density dominates, i.e., \(r<r_{\mathrm{max}} \), \(\phi \approx \frac{GM}{r}\) (solution of \(\nabla ^{2}\phi =4\pi G\rho )\) which gives a velocity varying linearly with distance. For \(r>r_{\mathrm{max}} \), \(\left( {\nabla \phi } \right) ^{2}\) term dominates, and \(\phi \) goes as \({K}'\mathrm{ln}\frac{r}{r_{\mathrm{max}}}\), (giving a constant velocity) accounting for the DM (solution of \(\nabla ^{2}\phi +K\left( {\nabla \phi } \right) ^{2}=0)\). For \(r\gg r_{\mathrm{max}} \), \(\phi \) goes as \(\Lambda r^{2}c^{2}\), DE dominates (i.e., the cosmological constant term). The above are the boundary conditions. In the case of the Milky Way, the velocity flattens out beyond \(\sim 2\, \mathrm{kpc}\), which is what is obtained from the above results, which is plotted in Figure 2. Other galaxies also show similar typical rotation curves, with MONG matching with observation.

Fig. 2
figure 2

Galaxy rotation curve (for Milky Way) from modified Newtonian gravity.

Full size image

4 Modification of relativistic gravity

The relativistic theory of MOND gives a new theory called Tensor–Vector theory (TeVe theory (Bekenstein 2004)) like MORG—Modification of Relativistic Gravity. These theories have severe constraints from CMBR anisotropy and lensing. In TeVe theories, vector and scalar fields are also present in addition to tensor fields. In \(f\left( R \right) \) theories, we replace Einstein’s action \(\smallint R\sqrt{-g} \text{ d }^{4}x\) by a function of curvature \(f\left( R \right) \), i.e., \(\smallint f\left( R \right) \sqrt{-g} \text{ d }^{4}x\). Here R is the curvature scalar and g is the determinant of the metric tensor \(g_{\upmu \upnu } \). This gives the field equations

$$\begin{aligned} {f}'(R)R_{\upmu \upnu }-\frac{1}{2}g_{\upmu \upnu }f(R)=\frac{8\pi G}{c^4}T_{\upmu \upnu }, \end{aligned}$$
(17)

where prime denotes derivative with respect to R, \(R_{\upmu \upnu } \) is the Ricci tensor, \(T_{\upmu \upnu } \) is the energy-momentum tensor, as in the usual GR notation. \(f\left( R \right) \) theories are not equivalent to TeVe theories (they do not have a vector field), however \(f\left( R \right) \) theories with suitable transformations can be put in the form of scalar–tensor theories (Sivaram & Campanelli 1992).

The idea of minimum field strength can be extended to GR by incorporating a minimum curvature, even in the absence of matter, since in GR, curvature and field strength are equivalent. A possible function \(f\left( R \right) \) involving a minimum curvature \(R_{\mathrm{min}} \) can have the form

$$\begin{aligned} f\left( R \right) =\frac{R}{\left( {1-\frac{aR_{\mathrm{min}} }{R}} \right) }, \end{aligned}$$
(18)

where a is a dimensionless constant that can be constrained by observation. Here we have modified the usual action so as to include a minimum curvature, \(R_{\mathrm{min}} )\). So we have the field equations

$$\begin{aligned} \frac{2R_{\upmu \upnu } }{\left( {1-\frac{aR_{\mathrm{min}} }{R}} \right) ^{2}}-\frac{R_{\upmu \upnu } }{\left( {1-\frac{aR_{\mathrm{min}} }{R}} \right) }=\frac{8\pi G}{c^{4}}T_{\upmu \upnu }. \end{aligned}$$
(19)

Equation (18) need not be a unique function of the curvature. The motivation for choosing this function \(f\left( R \right) \) (given by Equation (18)) is to obtain the usual field equations in the limit of \(R_{\mathrm{min}} \) tending to zero, as in GR there is no minimum limit to curvature, i.e., when \(R_{\mathrm{min}} \rightarrow 0\), Equation (19) becomes \(R_{\upmu \upnu } =\frac{8\pi G}{c^{4}}T_{\upmu \upnu } \). This is one of the simplest possibilities.

If \(R\gg R_{\mathrm{min}} \), it reduces to the usual GR (for local scales). On expanding Equation (18), we get

$$\begin{aligned} f\left( R \right) =R+aR_{\mathrm{min}} +a^{2}\frac{R_{\mathrm{min}}^{2} }{R}+\cdots \end{aligned}$$
(20)

(we arrive at Equation (20) by expanding the action \(f\left( R \right) \) in Equation (18) in powers of \(\frac{aR_{\mathrm{min}} }{R}\), as \(\frac{aR_{\mathrm{min}} }{R}\ll 1)\).

The first term represents GR, the second term is a background minimal curvature, which is now equivalent to \({\Lambda }\) (the cosmological constant), which shows the presence of DE. The higher order terms can be neglected since the minimum curvature (which is identified as the cosmological constant), \(R_{\mathrm{min}} ={\Lambda }=10^{-56} \ \text{ cm }^{-2}\) is quite small. When the decreasing curvature of the expanding universe approaches \(R_{\mathrm{min}} \), DE dominates, as at the present epoch.

The above action leads to GR with a constant minimum background curvature (equivalent to a cosmological constant) in the limit when curvature of the expanding universe tends to the minimum value. Here we do not have an ad hoc cosmological constant, fine-tuned to the present epoch. As is well known, the Newtonian limit will now be

$$\begin{aligned} \nabla ^{2}\phi -R_{\mathrm{min}} c^{2}=0. \end{aligned}$$
(21)

So in Equation (15), how does the \(\left( {\nabla \phi } \right) ^{2}\) (that gives rise to MOND) arise? So for this we have to consider the corresponding energy-momentum tensor (self-energy of the gravitational field) which is given by

$$\begin{aligned} T_{00} =K\left( {\nabla \phi } \right) ^{2}, \end{aligned}$$
(22)

where \(\phi \) is the gravitational potential, \(T_{00} \) is the time (static) component of the energy-momentum tensor, and K is the same constant as in Equation (9).

With this, on the RHS of the Einstein equation we will have an extra contribution to the metric tensor, i.e., \(T_{00} =K\left( {\nabla \phi } \right) ^{2}\). This gives a correction term to the metric of the order (Sivaram & Arun 2011; Sivaram et al. 2016) of

$$\begin{aligned} \frac{G^{2}M^{2}}{c^{4}r^{2}}=K\left( {\nabla \phi } \right) ^{2}. \end{aligned}$$
(23)

With this, the Newtonian limit now becomes

$$\begin{aligned} \nabla ^{2}\phi +K\left( {\nabla \phi } \right) ^{2}-R_{\mathrm{min}} c^{2}=0 \end{aligned}$$
(24)

which is same as Equation (15) above.

5 Similarity to the DGP model

In the DGP model (Dvali et al. 2000), which is a popular model as an alternative to DE, where gravity leaks off a 4D Minkowski-brane into 5D space-time and on small scales, gravity is bound to the 4D brane giving Newtonian gravity. The Hubble expansion evolves as

$$\begin{aligned} H^{2}-\frac{H}{R_\mathrm{C} }=\frac{8\pi G}{3}\rho _{\mathrm{m}} . \end{aligned}$$
(25)

The crossover scale \(R_{\mathrm {C}} \) separates 5D and 4D regimes and \(\rho _{\mathrm{m}} \) is the matter density. This scale \(\sim 1/H_{0} \) (\(H_{0} \) is the present Hubble constant), and generates late-time acceleration. Here in our model, we have \(R_{\mathrm{C}} \approx R_{\mathrm{min}} \), hence

$$\begin{aligned} H^{2}-\frac{H}{R_{\mathrm{min}} }=\frac{8\pi G}{3}\rho _{\mathrm{m}.} \end{aligned}$$
(26)

Again, locally \(R\gg R_{\mathrm{min}} \), hence the higher-order terms of \(R_{\mathrm{min}} \) can be neglected. The present model is similar to the DGP model, without the extra dimension.

6 Summary and conclusion

The introduction of a minimum acceleration in Newtonian dynamics leads to a MOND-like scenario. Similarly, the introduction of a minimum curvature in GR leads naturally to a term equivalent to a cosmological constant. So by postulating separately a minimal field strength (equivalent to minimal curvature) and a minimal acceleration, we are able to get a model to account for the observed evidence for both DM and DE.

The postulate of minimal acceleration leads to MOdified Newtonian Dynamics (MOND) and MOdified Newtonian Gravity (MONG), whereas the postulate of a minimal curvature leads to MOdified Relativistic Gravity (MORG). The modified action with its consequences connecting these postulates are given by Equations (17)–(19). Postulating limits to physical constants has previously also led to new physics. For instance, a postulated minimum action, \(\hslash \), led to quantum mechanics and a maximum light speed limit, c, led to special relativity. In this scenario, we are able to avoid introduction of DM and an ad hoc fundamental acceleration (to account for DM), since it naturally follows from the minimal acceleration. As shown, this minimal acceleration modifies the Kepler’s law and gives a constant rotation velocity above a distance \(r_{\mathrm{max}} \), as follows from Equation (6). This gives an alternate to DM and is equivalent to MOND as shown.

To deal with DE, we separately postulate a minimal curvature, which involves modifying the GR action. In GR, there is no minimal curvature. As the Universe expands, its curvature decreases and approaches this minimal curvature, \(R_{\mathrm{min}} \). This is equivalent to having a cosmological constant term dominating and giving rise to DE. So these two separate postulates give rise to flat rotation curve and dark energy, dominated by a cosmological constant. DE could also arise through extended gravity models as emphasised in Corda (2009), which will lead to similar consequences.