1 Introduction

The study of accretion-powered millisecond pulsars was inaugurated in the 1970s by the discovery of the 4.8 s X-ray pulsations from Centaurus X-3 (Cen X-3) (Giacconi et al. 1971). Over a period of time, Cen X-3 showed peculiar spectral structures and was found to be a source of variable energy emissions. Thereafter, observations of shorter period pulsations (1.2 s) were observed from Hercules X-1 (Her X-1) (Tananbaum et al. 1972) and on the millisecond-scale, a 2.494 ms pulsation was observed for SAX J1808.4-3658 (in ’t Zand et al. 2001). Because of this rapid period change, pulsars are both theoretically and observationally puzzling astronomical objects in ascertaining their spin periods (Camenzind 2007). They are believed to be old, rapidly rotating neutron stars which have been spun up or recycled back as radio pulsars through accretion of matter from a companion star in a close binary system (Alpar et al. 1982; Bhattacharya & van den Heuvel 1991; Wijnands & van der Klis 1998).

Accretion powered MSPs (APMSPs) are known to have magnetic surface field of the order of 10\(^8\)–10\(^9\) G (Backer et al. 1982), which is less than that of a typical X-ray pulsar. Consequently, the ionized gas in the pulsar magnetosphere is brought into corotation closer to the stellar surface (Psalts & Chakrabarty 1999) and is channeled along field lines to the polar caps, releasing its potential and kinetic energy, mostly in X-rays (Shapiro & Teukolsky 2004). As a result of the energy released, the accretion disc temperature reaches such a high temperature that gas pressure is far less than radiation pressure. They therefore behave uniquely when the accreting plasma is threaded by the stellar magnetic field (Wijnands 2004; Naso & Miller 2010, 2011; Tessema & Torkelsson 2011; Naso et al. 2013).

Firstly, APMSPs were observed to exhibit kilohertz quasi-periodic oscillations (kHz QPOs) (van der Klis et al. 1996) as well as millisecond coherent pulsations (“burst oscillations”) (Wijnands 2004; Bildsten et al. 2006), providing evidence for weak magnetic neutron stars. Secondly, in the Tessema and Torkelsson (2011) (hereafter TT11) dynamo model, they found out that the accretion disc in APMSPs is truncated at a larger radius, thus increasing the lever arm between the edge of the disc and the neutron star, resulting into enhanced torques. Also, Naso et al. (2013) indicated that some regions of the disc around MSPs, outward of the corotation radius (rotating more slowly than the neutron star), were found to contribute to spinning up the neutron star. These findings are crucial in explaining the large spin changes that have been observed in some of the APMSPs such as SAX J1808.4-3658 (Wijnands & van der Klis 1998; Chakrabarty & Morgan 1998), XTE J1751-305 (Markwardt et al. 2002) and XTE J1814-338 (Haskell & Patruno 2011).

In a strong magnetic \((B \gtrsim 10^{11})\) G accreting neutron star model (Ghosh & Lamb 1979a), the star-disc interaction region consists of two distinct parts: the outer broad transition zone and the inner transition zone. In the former region, the angular velocity is Keplerian, and the effective viscous stress is dominant compared to the magnetic stress associated with the twisted field lines. The magnetic stresses in this region attempt to force the disc material into corotation with the neutron star, and this results into spin-down torques (Ghosh & Lamb 1978). This torque was re-assessed by Wang (1987) to give a more realistic result than in Ghosh and Lamb (1979a). According to Ghosh and Lamb (1979b), the other part of the disc is narrow and it is where matter is brought into corotation with the neutron star, having magnetic stress dominating over viscous stress. This region plays a significant role leading to different observational properties of X-ray pulsars (Yi et al. 1997). According to TT11, these local divisions of the accretion disc cannot suit the observed properties of weakly magnetized \((B \lesssim 10^{11})\) G fast rotating MSPs.

A compelling model of disc accretion around MSPs was suggested by TT11 with an internal dynamo. The dynamo is a result of a physical phenomena in the accretion disc, with the ability of enhancing the magnetic torques exerted on the neutron star (Tessema & Torkelsson 2010). Like in the Shakura and Sunyaev (1973) model, the TT1 model divides the disc into three regions, depending on matter interactions with the stellar magnetic fields. The inner region experiences stronger magnetic stresses which affect angular momentum transport than in the outer region, which is predominantly affected by viscous stresses (Ghosh & Lamb 1978). Additionally, besides the thermal instability and radiation pressure instability, the dissipation associated with plasma motion across the magnetosphere makes the region to have a different accretion flow rate from other regions (Pringle 1981). To sum it all, the TT1 model considered the outer region as dominated by gas pressure and free-free opacity, the middle region with gas pressure and electron scattering opacity, while in the inner region radiation pressure dominates over the gas pressure with electron scattering as the main source of opacity. The corresponding suitable flow rates were set to \(0.012\times 10^{14} \, {\text {kg}}\,{\text {s}}^{-1}\) for outer, and \(0.12\times 10^{14} \, {\text {kg}}\,{\text {s}}^{-1}\) and \(1.5\times 10^{14} \, {\text {kg}}\,{\text {s}}^{-1}\) for middle and inner regions respectively in the same model.

The TT11 results show that the dynamo action exerts different torques in the three regions and these are capable of explaining spin variations in MSPs. However, in the TT11 model, pressure gradient force (PGF) effects in the equation of motion were not considered. In a pioneering study on the effect of PGF for a disc around a black hole, Hoshi and Shibazaki (1977) showed that the PGF alters the structure of a disc. Pressure gradients in an accretion disc result from internal stresses caused by the surrounding streaming fluid (Frank et al. 2002). Recently, Habumugisha et al. (2018) modified the Hoshi and Shibazaki (1977) model by considering a dynamo model around a magnetized neutron star, and showed that the resulting PGF torque couples with viscous torque to provide an enhanced spin-down torque. In this paper, we extend the quasi-Keplerian model of Habumugisha et al. (2018) to study the quasi-Keplerian model for a weakly magnetized object, taking care of PGF, and then apply the model to explain the observed spin variations in APMSPs.

In the next section, we present the basic equations to describe the disc’s time-independent dynamical phenomena. In Section 3, we discus quasi-Keplerian accretion disc micro-physics. Sections 4 and 5 are dedicated for theoretical and numerical results respectively, Section 6 is for discussion of torque exerted on MSPs. Finally, in Section 7, we present the conclusion of our findings.

2 Basic model equations

The interaction between a star and an accretion disc is best described by employing either spherical coordinates (Elsner & Lamb 1977; Ghosh & Lamb 1978) or cylindrical coordinates (Ghosh & Lamb 1979a, b). For the dynamics of a quasi-Keplerian model, we consider cylindrical polar coordinates (\(R,\,\phi ,\,z\)) with matter inflow assumed to lie very close to the plane \(z = 0\) and we modify the angular velocity, \(\Omega ^{\prime}_k\) as

$$\begin{aligned} \Omega ^{\prime}_k=v_\phi /R. \end{aligned}$$
(1)

Here \(v_\phi \) is the modified azimuthal velocity, which is expressed as (Campbell 1987)

$$\begin{aligned} v_\phi = \xi \sqrt{\frac{GM}{R}}, \end{aligned}$$
(2)

where G is Newton’s gravitational constant, M is the mass of the central object and \(\xi \) is a quasi-Keplerian parameter assumed to lie in the range \(0<\xi \le 2\) (Hoshi & Shibazaki 1977) and it is the range used in this study. This inequality depicts that for a physical meaning, \(\xi =1\) Keplerian motion is regained while for large values of \(\xi \) (\(\xi>>1\)) the disc is distorted and the shape of the disc is slim (Abramowicz et al. 1988). We consider a thin, axisymmetric \((\partial /\partial \phi =0)\), and steady \((\partial /\partial t=0)\), accretion disc with a non-relativistic viscous flow, i.e.,

$$\begin{aligned} v_o/c<<1. \end{aligned}$$
(3)

Here c is the speed of light and \(v_o=l/\jmath \) is a characteristic electromagnetic (or plasma) speed, while l and \(\jmath \) are a typical length and time scales. This is a fundamental assumption of magnetohydrodynamics in a way that the speeds are non-relativistic. Some authors have considered models consisting of relativistic flows (e.g. Rezzolla et al. 2014; Bakala et al. 2010; Petri 2013, 2014) and recently, a general relativistic simulation was extended to APMSPs (Parfrey & Tchekhovskoy 2017) in a bid to obtain convincing explanation of high energy emissions observed in astronomical environments. However, many other authors working on magnetized accretion follow this approach (e.g. Ghosh & Lamb 1978, 1979a, b; Pringle 1981; Wang 1987; Campbell 1987, 1992; Pringle 1992; Wang 1995; Lai 1998) because it yields results that have been known over time to explain observable phenomenon.

In this study, we used the same basic equations as in Habumugisha et al. (2018) for conservation of mass, momentum and energy in an accretion disc. Integrating vertically, the mass conservation yields

$$\begin{aligned} {\dot{M}}=-2\pi R \int _{-H}^{+H} \rho v_R\, {\text {d}}z= -2\pi R \Sigma v_R, \end{aligned}$$
(4)

where \({\dot{M}}\) is the accretion rate, \(\Sigma =\int _{-H}^{+H} \rho \, {\text {d}}z\) is the surface density, \(\rho \) is the density, H is the half-disc thickness and \(v_R\) is the radial velocity. Here we note that \({\dot{M}}\) is a constant for a steady disc (Bondi 1952) and basically depends on three parameters; R, \(v_R\) and \(\Sigma \).

Following the basic equation manipulation in Habumugisha et al. (2018), the three components of momentum equation are:

  1. (i)

    radial component

    $$\begin{aligned} \frac{\partial \Pi }{\partial R}&= -\Sigma \left[ v_R\frac{\partial v_R}{\partial R}-\frac{v_\phi ^2}{R}\right] - \frac{ \Sigma GM}{R^2} \nonumber \\&\quad + \left[ \frac{B_zB_R}{\mu _0}\right] _{z=-H}^{z=+H}, \end{aligned}$$
    (5)
  2. (ii)

    azimuthal component

    $$\begin{aligned} \Sigma \left[ v_R\frac{\partial (Rv_{\phi })}{\partial R}\right]&= R \left[ \frac{B_z B_\phi }{\mu _0}\right] _{z=-H}^{z=+H} \end{aligned}$$
    (6)
    $$\begin{aligned}&+\frac{1}{R}\frac{\partial }{\partial R} \left[ R^3(\nu \Sigma ) \frac{\partial }{\partial R}\left( \frac{v_{\phi }}{R}\right) \right] , \end{aligned}$$
    (7)
  3. (iii)

    and vertical component

    $$\begin{aligned} P(R)&= \int _{-H}^{+H}\frac{\rho GM}{(R^2+z^2)^{\frac{3}{2}}}\,{\text {d}}z \nonumber \\&\quad -\int _{-H}^{+H}\rho \left[ v_R\frac{\partial v_z}{\partial R}+ v_z\frac{\partial v_z}{\partial z}\right] \,{\text {d}}z. \end{aligned}$$
    (8)

Here, \(B_R, B_\phi , B_z\) and \(v_R, v_\phi , v_z\) are the radial, azimuthal and vertical components of the magnetic field \({\mathbf{B }}\) and velocity \({\mathbf{v }}\) respectively, \(\Pi =\int _{-H}^{+H}P{\text {d}}z\) with P(R) as the pressure, \(\mu _0\) is the permeability of free space and \(\nu \) is the kinematic viscosity. The kinematic viscosity \(\nu \) is expressed as (Shakura & Sunyaev 1973),

$$\begin{aligned} \nu =\alpha _{\text {ss}}c_s H, \end{aligned}$$
(9)

where \(\alpha _{\text {ss}}\) is a constant showing the strength of viscosity and \(c_s=(P/\rho )^{1/2}\) is the isothermal sound speed.

The vertical field component, \(B_{z}\) (Wang 1987) and the radial field component, \(B_{R}\) (Lai 1998) are stated as

$$\begin{aligned} B_{z}=-\frac{\mu }{R^3} \end{aligned},$$
(10)

and

$$\begin{aligned} B_{R}=-\frac{B_z}{R}\left( \frac{v_R}{\Omega ^{\prime}_k}\right) , \end{aligned}$$
(11)

with \(\mu \) as the magnetic dipole moment of the neutron star. There are two components of \(B_\phi \): the shear component and the dynamo component. The sheared component \(B_{\phi , {\text {shear}}}\) is given in terms of the modified \(\Omega ^{\prime}_k\) as

$$\begin{aligned} B_{\phi , {\text {shear}}}=-\gamma B_z \left[ 1-\left( \frac{\Omega _s}{\Omega ^{\prime}_k}\right) \right] . \end{aligned}$$
(12)

In Equation (12), \(\Omega _s\) is the angular velocity of the star, while \(\gamma \gtrsim 1\) is a dimensionless parameter usually defined as the quotient when radial distance R is divided by the vertical velocity shear length scale (Ghosh & Lamb 1979a). Thus, from Equations (2), (10) and (12), we obtain

$$\begin{aligned} B_{\phi , {\text {shear}}}=\frac{\gamma \mu }{R^3} \left[ 1-\frac{1}{\xi }\left( \frac{R}{R^{\prime}_{\text {co}}}\right) ^{3/2}\right] . \end{aligned}$$
(13)

In this model \(R^{\prime}_{\text {co}}=\xi ^{2/3}R_{\text {co}}\) is the quasi-Keplerian corotation radius, where \(R_{\text {co}}\) is the usual corotation radius expressed as (Tessema & Torkelsson 2010)

$$\begin{aligned} R_{\text {co}}=\left( \frac{GM P^2_{\text {spin}}}{4\pi ^2}\right) ^\frac{1}{3}=1.5\times 10^6 P_{\text {spin}}^{\frac{2}{3}} M_1^{\frac{1}{3}}, \end{aligned}$$
(14)

where \(P_{\text {spin}}=2\pi /\Omega _s\) is the spin period of the star, \(M_1\) is the ratio of mass of the accretor (M) to solar mass (\(M_\odot \)), i.e., \(M_1 = M/M_\odot \). The component \(B_{\phi , {\text {dyn}}}\) arising due to dynamo action, is expressed as (Tessema & Torkelsson 2011)

$$\begin{aligned} B_{\phi , {\text {dyn}}}=\epsilon (\alpha _{\text {ss}}\mu _0\gamma _{\text {dyn}}P(R))^{\frac{1}{2}}, \end{aligned}$$
(15)

where \(\epsilon \) is a factor which describes the direction of the magnetic field and \(\gamma _{\text {dyn}}=B_\phi /B_R\) (Torkelsson 1998) is the azimuthal pitch. As usual, \(\gamma _{\text {dyn}}\) signifies the rate of recconnection and amplification of toroidal field (Campbell 1999). In reference to the standard model, we use the value of \(\alpha _{\text {ss}} = 0.01\) (Shakura & Sunyaev 1973) and \(\gamma _{\text {dyn}} = 10\) while \(-1 \le \epsilon \le +1\) (Brandenburg et al. 1995). These basic equations are not explicit in the parameters comprising them. Therefore, we need to identify some accretion disc micro-physics.

3 Accretion disc micro-physics

With accretion disc micro-physics, we mean such parameters as: opacity, temperature, equation of state, pressure and scale height. These quantities were first used by Bardeen and Petterson (1975) in order to understand disc alignment in the centres of active galactic nuclei. Here the rationale of these micro-physics is to obtain a complete structure of a quasi-Keplerian disc and thereby explain the dynamics of accretion driven pulsars.

3.1 Opacity and temperature

In an optically thick accretion disc, the rate at which energy is deposited in the disc per unit area by dissipative process, e.g. viscous dissipation, must be equal to the rate at which the disc can radiate this energy away per unit area (Pringle 1981).

The energy balance has (Frank et al. 2002)

$$\begin{aligned} {\mathbf{v }}\cdot {\mathbf{f }}_\nu =\nabla \cdot {\mathbf{F }}_{\mathbf{rad }}, \end{aligned}$$
(16)

where \({\mathbf{f }}_\nu \) is the viscous force and \({\mathbf{F }}_{\mathbf{rad }}\) is the radiative energy flux. Thus a balance between radiative losses and viscous dissipation gives a relation between temperature and radial distance along the disc. For a quasi-Keplerian disc approximation, the total dissipated power per unit surface area is equal to the radiation flux. This is the required energy equation that can relate most of the physical quantities (refer to Frank et al. (2002) for details of derivation for a Keplerian case)

$$\begin{aligned} \frac{9}{8}\xi ^2\nu \Sigma \frac{GM}{R^3}=\frac{4}{3}\frac{\sigma T^4_c}{\tau }, \end{aligned}$$
(17)

where \(\sigma \) is the Stefan Boltzmann constant and \(\tau \) is the optical depth of the disc defined as (Shapiro & Teukolsky 2004)

$$\begin{aligned} \tau =\frac{1}{2}\Sigma \kappa =\frac{1}{2}\Sigma (\kappa _{\text {es}}+\kappa _{\text {ff}}), \end{aligned}$$
(18)

where \(\kappa \) is the opacity with \(\kappa _{\text {es}}\) as the electron scattering opacity and \(\kappa _{\text {ff}}\) as the free–free opacity. Here \(\kappa _{\text {es}}=0.40 \, {\text {cm}}^2 \, {\text {g}}^{-1}\) and using Kramer’s law \(\kappa _{\text {ff}}=\kappa _0\rho T_c^{-3.5} \, {\text {cm}}^2 \, {\text {g}}^{-1} \, {\text {K}}^{-3.5}\). The constant \(\kappa _0=5\times 10^{24}\) for our astronomical environment i.e. accretion disc around magnetized neutron stars (Frank et al. 2002). Thus, from Equations (17) and (18), the temperature at mid-plane of the disc can be expressed as

$$\begin{aligned} T_c^4=\frac{27}{32\sigma }\xi ^2\rho H(\kappa _{\text {es}}+\kappa _{\text {ff}})(\nu \Sigma )\frac{GM}{R^3}. \end{aligned}$$
(19)

The temperature \(T_c\) is the typical disc interior temperature that is related to the disc total pressure P through density \(\rho \) at \(z\approx 0\) (the temperature at the mid-plane of the disc).

3.2 Pressure and vertical scale height

The total pressure P of the disc material is, essentially, the sum of thermal gas pressure (\(\sim T_c\)) and radiation pressure (\(\sim T_c^4\)), expressed as (Shakura & Sunyaev 1973)

$$\begin{aligned} P(\rho ,T_c)=\left( \rho \frac{k_{\text {B}} T_c}{{\bar{\mu }}m_p}+\frac{4\sigma T^4_c}{3c}\right) , \end{aligned}$$
(20)

where \(k_{\text {B}}\) is Boltzmann constant, \({\bar{\mu }}\) is the mean molecular weight, and \(m_p\) the mass of a proton. Since there is no flow in the vertical direction i.e. \(v_z=0\), the vertical hydrostatic equilibrium must hold. Therefore, the pressure at the mid-plane of the disc is obtained from Equation (8) as

$$\begin{aligned} P(R)=\rho \left( \frac{GM}{R^3}\right) H^2. \end{aligned}$$
(21)

Radial angular momentum transport is due to the \(R-\phi \) plane of the turbulent stress tensor (Campbell 1992). The viscous stress (force per unit area) \(f_{R\phi }\) exerted in the \(\phi \) direction by the fluid element at R on neighboring elements at \(R+{\text {d}}R\), is related to the Maxwell stress tensor and is given as (Frank et al. 2002)

$$\begin{aligned} f_{R\phi }=\frac{3}{4}\xi (\nu \Sigma )\left( \frac{GM}{R^3}\right) ^\frac{1}{2}H^{-1}. \end{aligned}$$
(22)

According to the Shakura and Sunyaev (1973) \(\alpha \)-parameterization, the pressure P(R) in Equation (21) is related with stress in Equation (22) to get

$$\begin{aligned} f_{R\phi }=\alpha _{\text {ss}}P(R). \end{aligned}$$
(23)

The density \(\rho \) of the gas in a quasi-Keplerian disc is thus obtained as

$$\begin{aligned} \rho =\frac{3}{4}\frac{\xi (\nu \Sigma )}{\alpha _{\text {ss}}H^3}\left( \frac{GM}{R^3}\right) ^{-\frac{1}{2}}. \end{aligned}$$
(24)

Equating Equations (20) and (21), yields the vertical scale height as

$$\begin{aligned} H=\left( \frac{k_{\text {B}} T_c}{{\bar{\mu }}m_p}+\frac{4\sigma T^4_c}{3c\rho }\right) ^{\frac{1}{2}}\left( \frac{R^3}{GM} \right) ^ {\frac{1}{2}}. \end{aligned}$$
(25)

This implies that in a quasi-Keplerian model around a fast rotator, H will have different local solutions i.e., outer, middle and inner regions depending on \(T_c\).

  1. (1)

    The outer and middle regions are dominated by gas pressure, albeit the outer region has free-free interaction while in the middle region electron scattering is the main source of opacity, then \(\left( \frac{k_{\text {B}} T_c}{{\bar{\mu }}m_p}>>\frac{4\sigma T^4_c}{3c\rho }\right) \). Therefore from Equation (25), the outer and middle regions have H(R) expressed as

    $$\begin{aligned} HO(R)&= HM(R) \nonumber \\&= \left( \frac{k_{\text {B}} T_c}{{\bar{\mu }}m_p} \right) ^ {\frac{1}{2}}\left( \frac{R^3}{GM} \right) ^ {\frac{1}{2}}. \end{aligned}$$
    (26)
  2. (2)

    Inner region is dominated by radiation pressure and electron scattering opacity. As a result \(\left( \frac{k_{\text {B}} T_c}{{\bar{\mu }}m_p}<<\frac{4\sigma T^4_c}{3c\rho }\right) \) and

    $$\begin{aligned} HI(R)= \left( \frac{4\sigma T^4_c}{3c\rho } \right) ^ {\frac{1}{2}}\left( \frac{R^3}{GM} \right) ^ {\frac{1}{2}}. \end{aligned}$$
    (27)

It can be noted that both the outer and the middle regions are independent of \(\rho \), while in the inner region \(H \propto (T^2_c/\sqrt{\rho })\). Accordingly the temperatures build up for radiation pressure to overcome gas pressure in the inner region (Shakura & Sunyaev 1973). These Equations (26) and (27) help to get the local disc solutions for a quasi-Keplerian model.

4 Theoretical results

In this section, we present the theoretical results for global and local disc solutions. Of interest also is the local pressure gradient solution.

4.1 Global and local disc solutions

On simplifying Equation (7) using Equations (10)–(15), we get a single first order differential equation showing rate at which material flows for a quasi-Keplerian accretion disc around MSP as

$$\begin{aligned} (\nu \Sigma )^{\prime}&= \frac{{\dot{M}}}{6\pi R}-\frac{(\nu \Sigma )}{2 R} \nonumber \\&\quad - \epsilon \xi ^{-1} \left( \frac{4\mu ^2 \gamma _{\text {dyn}}}{3\mu _0 H}(\nu \Sigma )\right) ^{\frac{1}{2}} (GM)^{-\frac{1}{4}}R^{-\frac{9}{4}} \nonumber \\&\quad -\xi ^{-1}\frac{4\mu ^2\gamma }{3\mu _0} (GM)^{-\frac{1}{2}}R^{-\frac{9}{2}} \left[ 1- \xi ^{-1}\left( \frac{R}{R^{\prime}_{\text {co}}}\right) ^{\frac{3}{2}}\right] . \end{aligned}$$
(28)

We notice that in Equation (28), \((\nu \Sigma )\rightarrow {\dot{M}}/3\pi \) as \(R\rightarrow \infty \) giving a boundary condition. At this stage, it is convenient to introduce a dimensionless rate of mass flow and radial length variables \(\Lambda \) and r respectively, so that

$$\begin{aligned} \Lambda&= \frac{(\nu \Sigma )}{{\dot{M}}}, \end{aligned}$$
(29)
$$\begin{aligned} r&= \frac{R}{R_A}. \end{aligned}$$
(30)

Here r is a dimensionless radial coordinate and \(R_A\) is the Alfvén radius, which is a characteristic radius at which the disc plasma is channeled along the stellar magnetic fields (Wang 1987). \(R_A\) is expressed as

$$\begin{aligned} R_A&= \left( \frac{2\pi ^2 \mu ^4}{GM{\dot{M}}^2\mu _0^2}\right) ^{\frac{1}{7}} \nonumber \\&= 1.4\times 10^4M_1^{-\frac{1}{7}} {\dot{M}}_{14}^{-\frac{2}{7}}\mu _{16}^{\frac{4}{7}}\,{\text {m}}, \end{aligned}$$
(31)

where \({\dot{M}}\) is the rate of accretion, \(\mu _{16}\) is the stellar magnetic dipole moment in units of \(10^{16}\) T m\(^3\) and \({\dot{M}}_{14}\) is the accretion rate in units of \(10^{14}\) kg s\(^{-1}\). Re-writing Equation (28) in terms of \(\Lambda \) and r we get

$$\begin{aligned} \Lambda ^{\prime}&= \frac{1}{6\pi r}-\frac{\Lambda }{2 r} - \frac{\epsilon }{\xi } \nonumber \\&\quad\left( \frac{4\mu ^2 \gamma _{\text {dyn}}}{3\mu _0 H{\dot{M}}}\Lambda \right) ^{\frac{1}{2}} (GM)^{-\frac{1}{4}}R_A^{-\frac{5}{4}}r^{-\frac{9}{4}} \nonumber \\&\quad - \frac{1}{\xi }\frac{4\mu ^2\gamma }{3\mu _0{\dot{M}}} (GM)^{-\frac{1}{2}}R_A^{-\frac{7}{2}}r^{-\frac{9}{2}} \nonumber \\&\quad \left[ 1- r^{\frac{3}{2}}\left( \frac{\omega _s}{\xi }\right) \right] , \end{aligned}$$
(32)

where \(\Lambda ^{\prime}={\text {d}}\Lambda /{\text {d}}r\) and \(\omega _s\) is a fastness parameter expressed as (Elsner & Lamb 1977):

$$\begin{aligned} \omega _s&= \left( R_A/R_{\text {co}}\right) ^{\frac{3}{2}} \nonumber \\&= 0.36M_1^{-\frac{5}{7}} {\dot{M}}^{-\frac{3}{7}}_{14} \mu _{16}^{\frac{6}{7}}\left( \frac{4.8\,{\text {ms}}}{P_{\text {spin}}}\right) , \end{aligned}$$
(33)

where \(P_{\text {spin}}\) is the spin period of the central object, measured in milliseconds (ms). The global solution (Equation (32)) is important in this study because some of the local structural equations and pressure gradient force are dependent on it.

The quasi-Keplerian model of Habumugisha et al. (2018), for a disc surrounding a magnetized neutron star dealt with the gas dominated outer region of the disc. It was found that the disc behavior is indistinguishable in the outer region irrespective of the spin period for both Keplerian and quasi-Keplerian. This is because the outer region is slowly rotating as compared to the inner region. Therefore, it is prudent to focus on the inner and middle regions of the disc.

In the middle region, we have gas pressure \(P_g\gg \) radiation pressure \( P_r\,{\text {but}}\,\kappa _{\text {es}}\gg \kappa _{\text {ff}}\) and on using Equation (29) and (30) in Equation (26) we have

$$\begin{aligned} HM(r)&= \left[ \left( \frac{k_{\text {B}}}{m_p{\bar{\mu }}}\right) ^{\frac{2}{5}}\left( \frac{81\kappa _{\text {es}}}{128\sigma \alpha _{\text {ss}} } \right) ^ { \frac{ 1 }{ 10 } } \left( \frac{GM}{(rR_A)^3}\right) ^{-\frac{7}{20}}\right] \nonumber \\&\quad({\dot{M}}\Lambda )^{\frac{1}{5}}. \end{aligned}$$
(34)

Carefully using the definitive equations (Equation (15)) for \(B_{\phi , {\text {dyn}}}\) and Equations (17) to (24) for \(\Sigma \), \(T_c\), \(P_c\), \(\rho _c\) and \(\tau \), with Equations (29), (30) and (34), we obtain the disc structure equations as

$$\begin{aligned} \Sigma&= \frac{3}{2\alpha _{\text {ss}}} \left( \frac{m_p{\bar{\mu }}}{k_{\text {B}}}\right) ^{\frac{4}{5}}\left( \frac{81\kappa _{\text {es}}}{128\sigma \alpha _{\text {ss}} } \right) ^ { -\frac{ 1 }{ 5 } }\nonumber \\&\quad \left( \frac{GM}{R^3}\right) ^{\frac{1}{5}} (\nu \Sigma )^\frac{3}{5}\xi ^{\frac{2}{5}}. \end{aligned}$$
(35)

The mid-plane temperature is obtained as

$$\begin{aligned} T_c&= \left( \frac{m_p{\bar{\mu }}}{k_{\text {B}}}\right) ^{\frac{1}{5}}\left( \frac{81\kappa _{\text {es}}}{128\sigma \alpha _{\text {ss}} } \right) ^ { \frac{ 1 }{ 5 } }\nonumber \\&\quad \left( \frac{GM}{R^3}\right) ^{\frac{3}{10}}(\nu \Sigma )^\frac{2}{5} \xi ^{\frac{3}{5}}. \end{aligned}$$
(36)

The pressure, density and the optical depth of the disc are respectively,

$$\begin{aligned} P&= \frac{3}{4\alpha _{\text {ss}}}\left( \frac{m_p{\bar{\mu }}}{k_{\text {B}}}\right) ^{\frac{7}{5}}\left( \frac{81\kappa _{\text {es}}}{128\sigma \alpha _{\text {ss}} } \right) ^ { -\frac{ 1}{10}} \nonumber \\&\quad \left( \frac{GM}{R^3}\right) ^{\frac{17}{20}}(\nu \Sigma )^\frac{4}{5}\xi ^{\frac{7}{10}}, \end{aligned}$$
(37)
$$\begin{aligned} \rho&= \frac{3}{4\alpha _{\text {ss}}}\left( \frac{m_p{\bar{\mu }}}{k_{\text {B}}}\right) ^{\frac{6}{5}} \left( \frac{81\kappa _{\text {es}}}{128\sigma \alpha _{\text {ss}} } \right) ^ { -\frac{ 3}{10}}\nonumber \\&\quad \left( \frac{GM}{R^3}\right) ^{\frac{11}{20}}(\nu \Sigma )^\frac{2}{5}\xi ^{\frac{1}{10}}, \end{aligned}$$
(38)
$$\begin{aligned} \tau&= \frac{3}{\alpha _{\text {ss}}}\left( \frac{m_p{\bar{\mu }}}{k_{\text {B}}}\right) ^{\frac{4}{5}}\left( \frac{81\kappa _{\text {es}}}{128\sigma \alpha _{\text {ss}} } \right) ^ { -\frac{ 1}{5}}\nonumber \\&\quad \left( \frac{GM}{R^3}\right) ^{\frac{1}{5}}(\nu \Sigma )^\frac{3}{5}\xi ^{\frac{2}{5}}. \end{aligned}$$
(39)

Finally, we obtained the magnetic field generated by the internal dynamo as

$$\begin{aligned} B_{\phi , {\text {dyn}}}&= \left( \frac{3\mu _0\gamma _{\text {dyn}}}{4}\right) ^{\frac{1}{2}}\epsilon \left( \frac{m_p{\bar{\mu }}}{k_{\text {B}}}\right) ^{\frac{7}{10}} \left( \frac{81\kappa _{\text {es}}}{128\sigma \alpha _{\text {ss}}}\right) ^{-\frac{1}{20}}\nonumber \\&\quad \left( \frac{GM}{R^3}\right) ^{\frac{17}{40}} (\nu \Sigma )^{\frac{2}{5}} \xi ^{\frac{7}{10}}. \end{aligned}$$
(40)

On further simplifying this set of equations and substituting for \(m_p\), \(k_{\text {B}}\), G, \(\kappa _{\text {es}}\) and \(\sigma \), we have

$$\begin{aligned} \Sigma&= 7.1\times 10^5{\bar{\mu }}^{\frac{4}{5}}\alpha _{\text {ss}}^{-\frac{4}{5}} M_1^{\frac{2}{7}}{\dot{M}}_{14}^{\frac{27}{35}}\mu _{16}^{-\frac{12}{35}}\nonumber \\&\quad \Lambda (r)^ {\frac{3}{5}} r^{-\frac{ 3}{5}}\xi ^{\frac{2}{5}}\,{\text {kg}}\,{\text {m}}^{-2}, \end{aligned}$$
(41)
$$\begin{aligned} T_c&= 1.8\times 10^{8}{\bar{\mu }}^{\frac{1}{5}}\alpha _{\text {ss}}^{-\frac{1}{5}}M_1^{\frac{3}{7}} {\dot{M}}_{14} ^{\frac{23}{35}} \mu _{16}^{-\frac{18}{35}} \nonumber \\&\quad \Lambda (r)^ {\frac{2}{5}} r^{-\frac{9}{10}}\xi ^{\frac{3}{5}}\,{\text {K}}, \end{aligned}$$
(42)
$$\begin{aligned} P_c&= 3.1\times 10^{15}{\bar{\mu }}^{\frac{2}{5}}\alpha _{\text {ss}}^{-\frac{9}{10}}M_1^{\frac{17}{14}} {\dot{M}}_{14} ^{\frac{107}{70}} \mu _{16}^{-\frac{51}{35}} \nonumber \\&\quad \Lambda (r)^ {\frac{4}{5}} r^{-\frac{51}{20}}\xi ^{\frac{7}{10}}\,{\text {N}}\,{\text {m}}^{-2}, \end{aligned}$$
(43)
$$\begin{aligned} \rho _c&= 2.1\times 10^3{\bar{\mu }}^{\frac{6}{5}}\alpha _{\text {ss}}^{-\frac{7}{10}}M_1^{\frac{11}{14}} {\dot{M}}_{14} ^{\frac{61}{70}} \mu _{16}^{-\frac{33}{35}} \nonumber \\&\quad \Lambda (r)^ {\frac{2}{5}} r^{-\frac{33}{20}}\xi ^{\frac{1}{10}}\,{\text {kg}}\,{\text {m}}^{-3}, \end{aligned}$$
(44)
$$\begin{aligned} \tau&= 1.4\times 10^{4}{\bar{\mu }}^{\frac{13}{10}}\alpha _{\text {ss}}^{-\frac{4}{5}}M_1^{\frac{2}{7}} {\dot{M}}_{14}^{\frac{8}{35}} \mu _{16}^{\frac{12}{35}} \nonumber \\&\quad \Lambda (r)^ {\frac{3}{5}} r^{-\frac{3}{5}}\xi ^{\frac{2}{5}}, \end{aligned}$$
(45)
$$\begin{aligned} B_{\phi , {\text {dyn}}}&= 6.2\times 10^4\epsilon \gamma _{\text {dyn}}^{\frac{1}{2}}{\bar{\mu }}^{\frac{1}{5}}\alpha _{\text {ss}}^{\frac{1}{20}} M_1^ {\frac{17}{28}}{\dot{M}}_{14}^{\frac{107}{140}} \mu _{16}^{-\frac{51}{70}}\nonumber \\&\quad \Lambda (r)^ {\frac{2}{5}} r^{-\frac{51}{40}}\xi ^{\frac{7}{10}}\,{\text {T}}. \end{aligned}$$
(46)

Similarly for the inner region we have \(P_g\gg P_r\,{\text {but}}\,\kappa _{\text {es}}\gg \kappa _{\text {ff}}\) with

$$\begin{aligned} HI(R)=\left[ \frac{ 9\kappa _ {\rm {es}} }{ 8c} \right] ({\dot{M}}\Lambda ), \end{aligned}$$
(47)

and the disc structure equations are

$$\begin{aligned} \Sigma&= 94 \alpha _{\text {ss}}^{-1} M_1^{-\frac{5}{7}}{\dot{M}}_{14}^{-\frac{10}{7} }\mu _{16}^{\frac{6}{7}}\nonumber \\&\quad \Lambda (r)^ {-1} r^{\frac{ 3}{2}}\xi ^{-3}\,{\text {kg}}\,{\mathrm{m}}^{-2}, \end{aligned}$$
(48)
$$\begin{aligned} T_c&= 1.9\times 10^{7}\alpha _{\text {ss}}^{-\frac{1}{4}}M_1^{\frac{5}{28}} {\dot{M}}_{14} ^{\frac{3}{28}} \mu _{16}^{-\frac{3}{14}} \nonumber \\&\quad r^{-\frac{3}{8}}\xi ^{-\frac{1}{4}}\,{\text {K}}, \end{aligned}$$
(49)
$$\begin{aligned} P_c&= 3.6\times 10^{13}\alpha _{\text {ss}}^{-1}M_1^{\frac{5}{7}} {\dot{M}}_{14} ^{\frac{3}{7}} \mu _{16}^{-\frac{6}{7}} \nonumber \\&\quad r^{-\frac{3}{2}}\xi ^{-1}\,{\text {N}}\,{\mathrm{m}}^{-2}, \end{aligned}$$
(50)
$$\begin{aligned} \rho _c&= 3.1\times 10^{-3}\alpha _{\text {ss}}^{-1}M_1^{-\frac{5}{7}} {\dot{M}}_{14} ^{-\frac{17}{7}} \mu _{16}^{\frac{6}{7}} \nonumber \\&\quad \Lambda (r)^ {-2}r^{\frac{3}{2}}\xi ^{-5}\,{\text {kg}}\,{\mathrm{m}}^{-3}, \end{aligned}$$
(51)
$$\begin{aligned} \tau&= 1.9\alpha _{\text {ss}}^{-1}M_1^{-\frac{5}{7}}{\dot{M}}_{14} ^{-\frac{10}{7}} \mu _{16}^{\frac{6}{7}}\Lambda (r)^ {-1} r^{\frac{3}{2}}\xi ^{-3}, \end{aligned}$$
(52)
$$\begin{aligned} B_{\phi , {\text {dyn}}}&= 6.7\times 10^3\epsilon \gamma _{\text {dyn}}^{\frac{1}{2}}\alpha _{\text {ss}}^{\frac{1}{20}} M_1^{\frac{5}{14}} \nonumber \\&\quad {\dot{M}}_{14}^{\frac{3}{14}} \mu _{16}^{-\frac{3}{7}} r^{-\frac{3}{4}}\xi ^{-\frac{1}{2}}\, {\text {T}}. \end{aligned}$$
(53)

Apart from the toroidal magnetic field,

$$\begin{aligned} B_{\phi , {\text {shear}}}&= -3.7\times 10^{3} \gamma M_1^{3/7}{\dot{M}}_{14}^{6/7} \nonumber \\&\quad \mu _{16}^{-5/7}(1-\xi ^{-1}\omega _sr^{3/2})r^{-3}\,{\text {T}}, \end{aligned}$$
(54)

the rest of the structural equations change as we transit through the disc regions. However, \(B_{\phi , {\text {shear}}}\) will only vanish when \(\xi =\omega _s\).

4.2 Pressure gradient local solutions

The effect of the surrounding fluid on the ring of the disc is obtained by adopting the \(\alpha \)-parametrization of Shakura and Sunyaev (1973). Thus, considering the dominant terms of Equation (5) without loss of generality, we can drop the term \(v_R \partial v_R/\partial R\) to obtain

$$\begin{aligned} \frac{\partial \Pi }{\partial R} =\Sigma \left( \frac{v_\phi ^2}{R} - \frac{ GM}{R^2}\right) . \end{aligned}$$
(55)

Using Equation (2) and the pressure-density relation in Equation (24) in Equation (55), it is easy to show that

$$\begin{aligned} \frac{\partial \Pi }{\partial R} = \frac{3}{2}(\xi ^2-1)\alpha _{\text {ss}}^{-1} (\nu \Sigma )(GM)^{\frac{1}{2}} R^{-\frac{1}{2}}H^{-2}. \end{aligned}$$
(56)

Equation (56) is the pressure gradient equation expressed in terms of \(\Lambda \). For \(\xi =1\), the PGF is zero, a state which corresponds to the Keplerian fashion. As the disc deviates from this state, the azimuthal velocity is faster and the disc material becomes more dense for \(\xi >1\). A reverse situation occurs when \(\xi <1\) (slower and less dense). Further, because of H in Equation (56), it indicates that there are separate local solutions for a disc around a MSP. Consequently, using Equations (26) and (27) in Equation (56), the pressure gradient in the middle region is

$$\begin{aligned} \frac{\partial \Pi }{\partial R}\bigg |_{\text {middle}} = 2.2\times 10^{22} (\xi ^2-1) \Lambda (r)^{\frac{3}{5}} r^{-\frac{21}{10}}, \end{aligned}$$
(57)

and the inner region is

$$\begin{aligned} \frac{\partial \Pi }{\partial R}\bigg |_{\text {inner}} = 5.6\times 10^{15} (\xi ^2-1) \Lambda (r)^{-1} r^{-\frac{1}{2}}. \end{aligned}$$
(58)

Comparing Equations (57) and (58), pressure gradient (\(\partial \Pi /\partial R \)), is \(\propto \Lambda ^{+0.6} \) in the middle region while \(\partial \Pi /\partial R \propto \Lambda ^{-1} \) in the inner region. This implies that for a given \({\dot{M}}\) (flow rate), PGF grows faster in the inner region than in the middle region. The inner region is known to be hot, where characteristic emissions originate from and the observed X-ray flux changes can be attributed to PGF influence. This layout gives a basis to find the numerical solution of a quasi-Keplerian accretion disc.

5 Numerical results

In a quasi-Keplerian model for a disc around MSP, we consider a neutron star with a mass \(M=1.4M_\odot \) and a magnetic moment of \(10^{16}\) T m\(^{3}\) which is accreting at an average flow rate of \(10^{14}\) kg s\(^{-1}\) (Shapiro & Teukolsky 2004). Other parameters considered are \(\alpha _{\text {ss}}=0.01\), \(\gamma =1 \) (Shakura & Sunyaev 1973), \(\gamma _{\text {dyn}}=10\) (Brandenburg et al. 1995) and \( -0.1 \le \epsilon \le +0.1\), a factor which describes the direction of the magnetic field (Tessema & Torkelsson 2011). Further we consider a spin period of 4.8 milliseconds and vary the quasi-Keplerian parameters \(\xi \) from \(0.1 \,{\text {to}}\, 1.5\) as justified in \(\S \)2. This allows for a heuristic analysis of quasi-Keplerian disc dynamics.

The disc is expected to show transition from the outer region to the middle region at a point where electron scattering is equal to the free–free scattering \((\kappa _{\text {es}}=\kappa _{\text {ff}})\) and middle to inner when gas pressure is balanced by radiation pressure \((P_g=P_r)\). Using the boundary condition that \(\Lambda \simeq 1/3 \pi \) as \(r \rightarrow \infty \), the transition radius from the middle region to the inner region is given by

$$\begin{aligned} r_{\text {MI}}=13{\bar{\mu }}^{\frac{8}{21}}M_1^{\frac{10}{21}} {\dot{M}}_{14} ^{\frac{22}{21}} \mu _{16}^{-\frac{4}{7}}, \end{aligned}$$
(59)

while the transition radius from the outer region to the middle region is given by

$$\begin{aligned} r_{\text {OM}}=49 {\bar{\mu }}^{-\frac{1}{3}}M_1^{\frac{10}{21}} {\dot{M}}_{14} ^{\frac{20}{21}} \mu _{16}^{-\frac{4}{7}}. \end{aligned}$$
(60)

In Table 1, we present the different accretion rates (\(1.2\times 10^{12}\) kg s\(^{-1}\) for outer, \(1.2\times 10^{13}\) kg s\(^{-1}\) for middle, \(1.5\times 10^{14}\) kg s\(^{-1}\) for inner) (Shakura & Sunyaev 1973) and corresponding Alfvén radius, fastness parameter and transition radii (outer-middle (\( r_{\text {OM}}\)) and middle-inner (\( r_{\text {MI}}\))).

Table 1 Accretion rates and corresponding Alfvén radius, fastness parameter and transition radii (outer-middle (\(r_{\text {OM}}\)) and middle-inner (\( r_{\text {MI}}\))).
Full size table

The numerical solution for Equation (32) with \(\epsilon = 0.1\), 0.05, 0, −0.05 and −0.1 has two kinds of solutions at the inner edge of the accretion disc, depending on the kind of inflow. These cases are: case D and case V. The former occurs when

$$\begin{aligned} \Lambda =0, \end{aligned}$$
(61)

i.e., the curve crosses the r-axis. In this case we see that the corresponding \(\rho \) and \(T\longrightarrow 0\) at the inner edge. In the latter case, (case V)

$$\begin{aligned} \Lambda \ne 0 \quad {\text {or}}\quad \frac{{\text {d}}}{{\text {d}}r}\left( r^3\Lambda \frac{{\text {d}}\Omega }{{\text {d}}r}\right) =0, \end{aligned}$$
(62)

i.e., when the curve does not cross the r-axis. The difference between these boundary conditions is that for case D to arise, viscosity does not contribute to driving the accretion (Shakura & Sunyaev 1973) while in case V, the inflow at the inner edge of the accretion disc is driven completely by the transfer of excess angular momentum from the accreting matter to the stellar magnetic field (Wang 1995). Basing on this comparison, we discuss separate numerical local solutions and effect of pressure gradient force in the next sub sections.

5.1 Inner region \((1<r_{\text {MI}})\)

In Figure 1, we present graphs of \(\Lambda (r)\) and \({\text {d}}/{\text {d}}r(\Lambda \sqrt{r})\) for a choice of \(\xi = 0.8\), 1.0 and 1.2. It can be observed that in Figure 1(c), when \(\xi =1\) (Keplerian motion), the solution is similar to that of TT11 where we have only case V \((\Lambda \ne 0)\) solution. This can be verified using Figure 1(d) where \({\text {d}}/{\text {d}}r(\Lambda \sqrt{r})\) is plotted against r. But when we consider the quasi-Keplerian case, it is found that when \(\xi >1\) in Figure 1(e), we also obtain all our solutions as case V (confirm with Figure 1(f)). Only one case D solution (see Figure 1(a)) appears when \(\xi <1 \). Still from Figure 1, we observe an interesting display where the position of the inner edge is shifted further inwards when \(\xi >1\) (Figure 1(e)) and outwards when \(\xi <1\) (Figure 1(a)). Besides the parameter \(\xi \), in the inner region, the dynamo parameter (\(\epsilon \)) has a significant effect in determining the location of the inner edge of the disc as it was the case for the TT11 model. The dynamo generated magnetic field by the dynamo are shown with \(\epsilon =-0.1\) dotted, \(\epsilon =-0.05\) dot-dashed, \(\epsilon =0\) black solid, \(\epsilon =0.05\) long-dashed and \(\epsilon =0.1\) dashed. According to Naso et al. (2013), the complex dynamics of the inner region converts matter into an intense hot, completely ionised plasma, that interacts with the weak magnetic field to produce spinning up of the MSPs.

Figure 1
figure 1

Variation of dimensionless rate of mass flow, \(\Lambda (r)\) and d/dr\((\sqrt{r}\Lambda )\) with radial distance for a neutron star within the inner region. The magnetic field generated by the dynamo are shown as follows: \(\epsilon =-0.1\) – dotted, \(\epsilon =-0.05\) – dot-dashed, \(\epsilon =0\) – black solid, \(\epsilon =0.05\) – long-dashed and \(\epsilon =0.1\) – dashed.

Full size image

5.2 Middle region (\(r_{\text {MI}}<1<r_{\text {OM}}\))

The middle region is characterized by gas pressure, being greater than radiation pressure, but opacity is due to electron scattering (refer to TT11). Assuming a flow rate of \({\dot{M}} = 1.2 \times 10^{13}\) kg s\(^{-1}\) (Shapiro & Teukolsky 2004), we obtain the numerical solutions in Figure 2 for the middle region using Equation (32) for dynamo parameters \(\epsilon = 0.1,\, 0.05, \,0,\, -0.05\,{\text {and}}\, -0.1\). From Figure 2(c), we have one case D solution for \(\xi =1.0\). For clarity, see Figure 2(d) where \({\text {d}}/{\text {d}}r(\Lambda \sqrt{r})\) is plotted against r. Another case D solution is obtained for \(\xi =1.2\) (refer to Figure 2(e)). This result corresponds to the dynamo parameter \(\epsilon =-0.1\). When \(\xi =0.8\), the solution of Equation (32) provides two case D solutions (see Figure 2(a)). This has a consequence on the total torque for this region as the viscous torque, \(N_{\text {visc}}\) vanishes (\(N_{\text {visc}}=0\)) for every case D. This case gives a chance for pressure gradient torque to have a significant contribution to the total torque exerted on a MSP (Habumugisha et al. 2018).

Figure 2
figure 2

Variation of dimensionless rate of mass flow, \(\Lambda (r)\) and d/dr\((\sqrt{r}\Lambda )\) with radial distance for a neutron star within the middle region. The magnetic field generated by the dynamo are shown as follows: \(\epsilon =-0.1\) – dotted, \(\epsilon =-0.05\) – dot-dashed, \(\epsilon =0\) – black solid, \(\epsilon =0.05\) – long-dashed and \(\epsilon =0.1\) – dashed.

Full size image

5.3 Effect of pressure gradient force

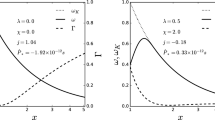
To analyse the effect of PGF, we plot the solution of local PGF (\(\partial \Pi /\partial R\)) using Equations (57) and (58). For middle region, we obtained Figures 3(a) and (b) while for inner region we have Figures 3(c) and (d). In general, for \(\xi >1\), we have a positive PGF (see Figures 3(b) and (d)) and a negative PGF when the azimuthal quasi-Keplerian coefficient \(\xi \) is \(<1\) (see Figures 3(a) and (c)). The pressure gradient in the inner region is greater than that in the middle region and so are the corresponding torques. Details of various torques exerted on MSPs are discussed in Section 6.

Figure 3
figure 3

Pressure gradient force (\(\partial \Pi /\partial R\)) as a function of radial distance for a neutron star within the middle region (top panel) and inner region (bottom panel). The magnetic field generated by the dynamo are shown as follows: \(\epsilon =-0.1\) – dotted, \(\epsilon =-0.05\) – dot-dashed, \(\epsilon =0\) – black solid, \(\epsilon =0.05\) – long-dashed and \(\epsilon =0.1\) – dashed.

Full size image

6 Torques on MSP in a quasi-Keplerian disc

To obtain the torque acting on a MSP, we use a simple approach,

$$\begin{aligned} N(R)=\int _{R_{i}}^{R_{\text {out}}} 2\pi R F(R) {\text {d}}R\, {\text {N}}\,{\mathrm{m}}, \end{aligned}$$
(63)

where N(R) is the torque and F(R) is the force. Using Equation (55) the torque contribution from the pressure gradient force is

$$\begin{aligned} N_{\text {pgf}}=- 2\pi \int _{R_{i}}^{R_{\text {out}}}\Sigma (\xi ^2-1)\frac{ GM}{R}\, {\text {d}}R, \end{aligned}$$
(64)

while the other torques are as follows:

  1. (i)

    the material torque

    $$\begin{aligned} N_{\text {adv}}(R_i)=\xi {\dot{M}}\sqrt{GMR_i}\, {\text {N}}\,{\mathrm{m}}, \end{aligned}$$
    (65)
  2. (ii)

    the viscous torque

    $$\begin{aligned} N_{\text {visc}}(R_i)=- 3\pi \xi (\nu \Sigma ) (GMR_i)^\frac{1}{2}\, {\text {N}}\,{\mathrm{m}}, \end{aligned}$$
    (66)
  3. (iii)

    the dynamo torque

    $$\begin{aligned} N_{\text {dyn}}(R_i)&= \int _{R_{i}}^{R_{\text {out}}} \frac{4\pi }{\mu _0} [B_z (B_{\phi , {\text {dyn}}})]R^2\,{\text {d}}R\, {\text {N}}\,{\mathrm{m}}, \end{aligned}$$
    (67)
  4. (iv)

    and the shear component of the magnetic field yields a torque

    $$\begin{aligned} N_{\text {shear}}(R_i)&= \int _{R_{i}}^{R_{\text {out}}} \frac{4\pi }{\mu _0}\nonumber \\&\quad [B_z (B_{\phi , {\text {shear}}})]R^2\,{\text {d}}R\, {\text {N}}\,{\mathrm{m}}. \end{aligned}$$
    (68)

Equations (65) and (66) represents the material and viscous torques on the neutron star respectively, while Equations (67) and (68) are the magnetic torques. Here we note that both \(N_{\text {adv}}\) and \(N_{\text {visc}}\) are directly proportional to the term \(\xi {\dot{M}}\); \({\dot{M}}=\nu \Sigma /\Lambda \). Thus a change in \(\xi \) or \({\dot{M}}\) will affect the magnitude of the torque. Infact, the resulting PGF torque couples with viscous torque (when \(\xi < 1\)) to provide a spin-down torque and a spin-up torque (when \(\xi > 1\)) (Habumugisha et al. 2018).

We can further simplify Equations (64)–(68) to obtain the local torque solutions as

$$\begin{aligned} N_{\text {adv}}I&= 2.4\times 10^{26}\xi M_1^{\frac{3}{7}}{\dot{M}}_{14}^{\frac{6}{7}}\mu _{16}^{\frac{2}{7}}\Lambda r_i^{\frac{1}{2}}|_{r_{A}}^{r_{\text {MI}}}, \end{aligned}$$
(69)
$$\begin{aligned} N_{\text {adv}}M&= 1.9\times 10^{25}\xi M_1^{\frac{3}{7}}{\dot{M}}_{14}^{\frac{6}{7}}\mu _{16}^{\frac{2}{7}}\Lambda r_i^{\frac{1}{2}}|_{r_{\text {MI}}}^{r_{\text {OM}}}, \end{aligned}$$
(70)
$$\begin{aligned} N_{\text {visc}}I&= -2.3\times 10^{27}\xi M_1^{\frac{3}{7}}{\dot{M}}_{14}^{\frac{6}{7}}\mu _{16}^{\frac{2}{7}}\Lambda r_i^{\frac{1}{2}}|_{r_{A}}^{r_{\text {OM}}}, \end{aligned}$$
(71)
$$\begin{aligned} N_{\text {visc}}M&= -1.8\times 10^{26}\xi M_1^{\frac{3}{7}}{\dot{M}}_{14}^{\frac{6}{7}}\mu _{16}^{\frac{2}{7}}\Lambda r_i^{\frac{1}{2}}|_{r_{\text {MI}}}^{r_{\text {OM}}}, \end{aligned}$$
(72)
$$\begin{aligned} N_{\text {shear}}&= 1.2\times 10^{26}M_1^{\frac{3}{7}}{\dot{M}}_{14}^{\frac{6}{7}}\mu _{16}^{\frac{2}{7}}\left[ 1-2\frac{\omega _s}{\xi }r_i^{\frac{3}{2}} \right] , \end{aligned}$$
(73)
$$\begin{aligned} N_{\text {pgf}}I&= 4.2\times 10^{22}(\xi ^2-1) \alpha _{\text {ss}}^{-1} M_1^{\frac{2}{7}}{\dot{M}}_{14}^{-\frac{10}{7}}\nonumber \\&\quad \mu _{16}^{\frac{6}{7}}\Lambda ^{-1} r_i^{-\frac{1}{2}}|_{r_{A}}^{r_{\text {OM}}}, \end{aligned}$$
(74)
$$\begin{aligned} N_{\text {pgf}}M&= -4.1\times 10^{26}(\xi ^2-1) \alpha _{\text {ss}}^{-\frac{4}{5}}{\bar{\mu }}^{\frac{4}{5}} M_1^{\frac{51}{35}}{\dot{M}}_{14}^{\frac{32}{35}}\nonumber \\&\quad \mu _{16}^{-\frac{22}{35}}\Lambda ^{\frac{3}{5}} r_i^{-\frac{3}{5}}|_{r_{\text {MI}}}^{r_{\text {OM}}}, \end{aligned}$$
(75)
$$\begin{aligned} N_{\text {dyn}}I&= 9.6\times 10^{26}\epsilon \gamma _{\text {dyn}}^{\frac{1}{2}} M_1^{\frac{5}{14}}{\dot{M}}_{14}^{\frac{3}{14}}\mu _{16}^{\frac{4}{7}} r_i^{-\frac{3}{4}}|_{r_{A}}^{r_{\text {MI}}}. \end{aligned}$$
(76)
$$\begin{aligned} N_{\text {dyn}}M&= 6.5\times 10^{27} \epsilon \gamma _{\text {dyn}}^{\frac{1}{2}} \alpha _{\text {ss}}^{\frac{1}{20}}{\bar{\mu }}^{\frac{1}{5}} M_1^{\frac{17}{28}} \nonumber \\&\quad {\dot{M}}_{14}^{\frac{107}{140}} \mu _{16}^{\frac{19}{70}} \Lambda ^{\frac{2}{5}} r_i^{-\frac{51}{40}}|_{r_{\text {MI}}}^{r_{\text {OM}}}, \end{aligned}$$
(77)

The total torque exerted on the neutron star \(N_T\) can be expressed in terms of the inner edge position \(r_{\text {in}}\) as

$$\begin{aligned} N_T(r_{\text {in}})&= N_{\text {pgf}}+N_{\text {adv}}+N_{\text {visc}}+N_{\text {dyn}} \nonumber \\&\quad +N_{\text {shear}}\, {\text {N}}\,{\mathrm{m}}. \end{aligned}$$
(78)

The values of individual terms in Equation (78) are shown in Table 2.

Table 2 Net torque on a neutron star evaluated at \(R_{\text {in}}\).
Full size table

6.1 Comparison with observed results

The spin variation is related to torque by

$$\begin{aligned} {\dot{\nu }}_{13} = \frac{N_{T}}{2\pi I_{38}}\,{\text {Hz}}\,{\mathrm{s}}^{-1}, \end{aligned}$$
(79)

where \({\dot{\nu }}_{13}\) is the spin derivative in units of \(10^{-13}\) Hz s\(^{-1}\) and \(I_{38}\) is the moment of inertia of the neutron star measured in \(10^{38}\) kg m\(^2\). Several accretion driven pulsars have been observed with changing spin frequencies e.g. SAX J1808.4-3658 (Chakrabarty & Morgan 1998) and XTE J1814-338 (Haskell & Patruno 2011). Specifically, SAX J1808.4-3658, was reported by Bildsten et al. (2006) to have spin variations, \({\dot{\nu }}_{13}\) between \(-7.6 \times 10^{-14}\) and \(4.4 \times 10^{-13}\) Hz s\(^{-1}\) while Hartman et al. (2008) noted \({\dot{\nu }}_{13}\lesssim 2.5\times 10^{-14}\) Hz s\(^{-1}\). Other objects include among others: XTE J1751-305 which has a frequency of 435 Hz and a pulse-frequency derivative of \({<}3 \times 10^{-13}\) Hz s\(^{-1}\) while XTE J0929-314 has a frequency of 185 Hz and a pulse-frequency derivative of \((-9.2 \pm 0.4) \times 10^{-14}\) Hz s\(^{-1}\) (see Wijnands (2004) for a review of these objects). Using Equation (79), it is interesting to note that these spin-up/down frequencies for MSPs are comparable to our model values in Table 2. We therefore argue that the observed spin variations are catered for in a quasi-Keplerian model when the disc is transiting to and from Keplerian flow.

7 Conclusion

We have modeled the structure of a quasi-Keplerian dynamo powered accretion disc surrounding a MSP. Our model shows that the PGF arising from the deviation of the disc from the Keplerian motion has significant contribution to the net torque exerted on the MSP. The resulting torque due to PGF was found to couple to the viscous torque (when \(\xi < 1\)) to provide a spin-down torque and a spin-up torque (when \(\xi > 1\)) by coupling with the advective torque. The total torque shows change of sign (reversals) that result in spin variations of the same order as those observed in MSP (e.g. see the paper of Bildsten et al. (2006) or Hartman et al. (2008) for details on MSPs). We thus believe that the PGF can trigger tilting of an accretion disc though in a different way from how viscous torques were found by Pringle (1992) for a steady Keplerian disc. This study therefore, provides a contribution to the theoretical understanding of the dynamics of quasi-Keplerian discs surrounding magnetized neutron stars.