Observations and physics of prompt emission of gamma ray bursts

Abstract

Gamma ray bursts (GRBs) are the brightest explosions known to occur in the Universe. For the last several decades, they have been extensively observed and studied using both space as well as ground based observatories. In this review, the observational breakthroughs made till date, the techniques of observation and analyses of obtained data, temporal and spectral properties of the observed prompt emission of GRBs including polarisation, as well as the various theoretical models adopted to explain them are discussed.

1 Introduction

During the summer of 1967, American military satellites named Vela 3 and Vela 4 detected some strong gamma ($\gamma$) ray signals from unidentified sources. The information about the discovery of these transient events of gamma ray emission called as gamma ray bursts (GRBs) were declassified and published in 1973 (Klebesadel et al. 1973). Thus began the extraordinary era of observations and study of gamma ray bursts using various space based telescopes. GRBs are extremely intense flashes of gamma rays observed for a short duration at an average rate of nearly one event per day. These events are extremely bright and outshines the entire gamma ray sky including our Sun. Just for comparison, the typical energy doled out during this small period of time of a few seconds is of the order of $10^{48} - 10^{55} \, {\mathrm{erg}},$ which is nearly equivalent to what our Sun would have emitted over its entire lifetime (10 billion years). Such huge energies were otherwise known to be only produced in catastrophic events relating to the death of a star known as the supernova.

One of the challenges in detecting GRB is its localisation in the sky. This requires a detector which has an all sky field of view and can provide directional information as to from which part of the sky the flash has originated. In 1991, the Burst and Transient Spectrometer Experiment (BATSE) on board Compton Gamma Ray Observatory (CGRO) was launched by National Aeronautics and Space Administration (NASA) to study GRBs, in the energy range 20–2000 keV (Fishman 2013). It consisted of eight detector modules, where each module, as shown in Fig. 1, consisted of a Large Area Detector (LAD) made of two sodium iodide (NaI) scintillation detectors which were developed for high sensitivity and directional response, and a spectroscopy detector (SD) for energy coverage and resolution. These eight modules were placed such that they were parallel to the eight faces of a regular octahedron whose primary axes aligned with the coordinate axes of the spacecraft. The GRB triggering occurred when the count rate in at least two of the eight LAD detectors crossed a statistical significant threshold of 5.5 $\sigma$ above the background rate. The observations continued until 4th June 2000, when NASA removed CGRO from its orbit, thereby completing 9 successful years, during which BATSE detected 2704 GRBs.

Fig. 1

A schematic diagram of one of the eight detector modules of the BATSE instrument is shown above. The positions of the various detectors (LAD, SD and charged particle detector) along with the instrument auxiliaries are marked on it (NSSTC 2018).

One of the key observation results of BATSE was that the all sky map of GRB localisations showed that GRBs are isotropically distributed, thus coming from all parts of the sky (Fig. 2). This indicated that GRBs are coming from the cosmos. The light curves of the GRBs were found to be very unique and diverse in nature (Fig. 3) (Fishman et al. 1994). Some light curves were very spiky, some were single broad pulses, other times, they were multiple pulses, sometimes with well defined quiescent periods in between, and some being very erratic. This highly diverse nature and the non-repetitiveness of the event make GRBs very difficult to be put together in a common framework of understanding.

Fig. 2

The all sky map of the localisations of the 2704 GRBs detected by BATSE in its entire lifetime is shown above. The different colours refer to the different fluence of the recorded GRBs (HEASARC 2012).

The major breakthrough in observations came in 1997, when the Italian Dutch satellite BeppoSAX, observed the first afterglow of a fading X-ray source nearly 4–6 h after the detection of GRB 970228 (Costa et al. 1997) in the same localisation. This triggered a multi-wavelength observational campaign resulting in the observation of optical afterglow (Galama et al. 1997) from the source, however no spectroscopic redshift could be obtained. The associated host galaxy was found to be at a redshift of $z \sim 0.695$. The first spectroscopic measurement of the redshift of GRB was made for the burst GRB 970508 at $z = 0.8349 \pm 0.0002$, thereby confirming that GRBs originated at cosmological distances (Pian et al. 1998).

The study of the T90¹ duration of the bursts detected by BATSE showed a bimodal distribution peaking at 0.3 s and 30 s (Kouveliotou et al. 1993) (Fig. 4a). A dip was found between the two peaks of the distribution at around $T90 \sim 2 \, {\mathrm{s}}$. GRBs were, thus, classified into two subsets with bursts having duration less than 2 s known as short GRBs and those with duration greater than 2 s known as long GRBs. The hardness ratio (HR) estimate of taking the ratio of observed counts in higher energy channel (100 -300 keV) to lower energy channel (50 -100 keV) also showed two centres of clustering when plotted against T90 (Kouveliotou et al. 1993), see Fig. 4b. The average HR of short GRBs was found to be $\sim 0.7$, which is larger than that of long GRBs which was $\sim 0.4$. This tells us that short GRBs tend to have higher energetic photons in comparison to long GRBs.

Fig. 3

A typical sample of GRB light curves of varied variety as detected by the BATSE instrument is shown. Figure is taken from Fishman et al. (1994).

The next major advancement in observations happened with the launch of the multi-wavelength satellite, Niel Grehels Swift observatory (Gehrels & Swift collaboration 2004), on 20th November 2004. It consists of three main instruments: Burst Alert Telescope (BAT; Barthelmy et al. 2005) which has large field of view of nearly 2 steradians, detecting in the energy range 15–150 keV and on board computes positions of the bursts within an arcminute accuracy; X-ray Telescope (XRT; Burrows et al. 2005) is capable of doing pointed follow up observations of the afterglow of the GRBs, providing higher accuracy on the GRB positions as well as images and spectra in the energy range 0.3 –10 keV; and UV/Optical Telescope (UVOT; Roming et al. 2005) also do follow up pointed observations of the GRB afterglow in the ultraviolet and optical energy range of 170–600 nm, thereby providing 0.5 arcs accuracy of the GRB position as well as the possibility of the determination of the redshift for the bright UV/optical observations. With the BAT detection, Swift could autonomously repoint the spacecraft such as to bring the burst location within the field of view of XRT within $\sim 90 \, \mathrm{s}$. This swiftness in follow up resulted in the breakthrough of the first detection of a X-ray afterglow of short GRBs for the burst GRB050509B (Castro-Tirado et al. 2005). Thus, confirming that short GRBs also originate from cosmological distances. Swift detects nearly 100 GRBs per year. The sample of GRBs with known redshifts have increased considerably post the launch of Swift. The average redshift of short and long GRB population is around 0.6 and 2 respectively (Le & Dermer 2007; Coward 2009; Le & Mehta 2017). The farthest redshift measured till now for GRBs are $z=8.26$ (spectroscopic measurement) for GRB090423A (Chary et al. 2009) and $z =9.2$ (photometry) for GRB090429B (Cucchiara et al. 2011).

Fig. 4

(a) The T90 distribution of the GRBs reported in the first BATSE GRB catalog is shown above. A bi-modality in the distribution is clearly visible with the division at $\mathrm{T90} \sim 2\, {\mathrm{s}}$. (b) The plot of T90 vs hardness ratio is shown. Two centres of clustering can be observed, which are marked by dashed lines. Figures are taken from Kouveliotou et al. (1993).

Fig. 5

(a) The orientations and positions of all the 11 NaI detectors (marked as 0-11) and two BGO detectors (marked as 12 and 13) present in the Fermi GBM instrument are shown (Meegan et al. 2009). (b) A schematic figure of the Fermi LAT instrument is shown (Atwood et al. 2009).

On 11th June 2008, Fermi satellite was launched which provided an unprecedented wide energy range of 8 keV to 300 GeV to observe the GRB emission. This is achieved by two main instruments onboard: Gamma ray Burst Monitor (GBM; Meegan et al. 2009), which includes 12 sodium iodide (NaI) scintillators detecting in the energy range 8 keV - 900 keV and two bismuth gallium oxide (BGO) scintillators detecting in the energy range 200 keV to 40 MeV. The placement and orientation of the detectors can be seen in Fig. 5. GBM thus observes the entire sky except the earth occulted region. It detects nearly 250 GRBs per year. The Large Area Telescope (LAT) is a particle detector providing measurement up to $\sim 300\, \mathrm{GeV}$ (Atwood et al. 2009). The LAT is placed such that it faces upwards away from the earth and scans the entire sky within 2 orbits. In case of strong detection, Fermi autonomously repoints the LAT to the burst location within a few hours. LAT detects nearly 10 GRBs per year. BGO energy range overlaps with the NaI detector at lower energies and with LAT detector at higher energies. This enables joint spectral analysis of GRB emission spanning nearly 7 decades of energy.

There are many other observatories which are also contributing to the detection of GRBs. They are listed as follows:

• (i) Konus Wind: The instrument Konus onboard the Wind satellite, launched on 1st November 1994, detects GRBs within the energy range 10–770 keV (Golenetskii et al. 1998). It detects nearly 120 GRBs per year.

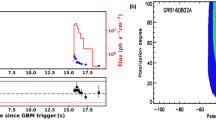
• (ii) INTEGRAL: The International Gamma-Ray Astrophysics Laboratory (INTEGRAL) was launched on 17th October 2002 and detects in the energy range 3 keV– 10 MeV (Bošnjak et al. 2014). It detects nearly 8 GRBs per year. Such low number is due to its small field of view ($\sim 0.1$ steradians). It also provides the opportunity of polarisation measurement within the observed energy band. Polarised emission was detected for the burst GRB 041219A (Götz et al. 2014).

• (iii) CALET: The CALET Gamma-ray Burst Monitor (CGBM) onboard the CALET mission on the International Space Station (ISS) was launched on 19th August 2015 and is observing in the energy range 7 keV –20 MeV (Yamaoka et al. 2013; Cherry 2014).

• (iv) ASTROSAT: The Cadmium Zinc Telluride Imager (CZTI) onboard the ASTROSAT mission was launched on 28th September 2015 and observes in the energy range 10 keV–100 keV (Rao et al. 2017; Bhalerao et al. 2017; Singh et al. 2014). It also has polarisation detection capability in the energy range 100 - 400 keV (Chattopadhyay et al. 2017).

• (v) POLAR: It is a detector for the measurement of polarisation of the GRB photons in the energy range 50– 500 keV. It was launched on 15th September 2016 (Kole 2018).

A GRB event can be divided into two main parts: the prompt emission consisting of the gamma ray emission produced immediately for a few seconds, and the afterglow phase which includes emission from gamma rays to radios extending over a longer period of time. The bimodality in the T90 distribution of the prompt $\gamma -$ ray emission, lead to the hypothesis that short and long GRBs have different progenitors such that long GRBs are a result of the core collapse of massive stars and short GRBs are produced as a result of the merger of binary neutron stars or a neutron star and a black hole. For long GRBs, this hypothesis was confirmed when a supernova was detected coincidently, both spatially and temporally with GRB 030329A (Stanek et al. 2003; Kawabata et al. 2003; Mazzali et al. 2003; Langer et al. 2008). Recently, with the coincident detection of gravity waves measured by LIGO along with short GRB 170817A, confirms the hypothesis that at least a fraction of the short GRBs are produced from the merger of binary neutron stars (Abbott et al. 2017a, b).

In this review, I will be focussing on the observational, spectral analysis results and their related modelling of the emission mechanism in the prompt emission of long GRBs observed by Fermi.

2 Key characteristics of the GRBs

Nearly five decades of study of GRBs, have enabled us to understand a few important characteristics of this event with significant confidence (Mészáros 2006), whereas the understanding regarding the radiation mechanism, process of acceleration of particles, launch of jet etc remain still inconclusive. Some of the key characteristics that have been inferred about the GRB are:

Compact source: the observed fastest variability, $t_\mathrm{v}$, in the light curves is of the order of a few milliseconds. This suggests that the central engine is a very compact source of radius, $\sim c \, t_\mathrm{v} = 10^{6} - 10^{7} \, \mathrm{cm}$, which can be either a stellar mass black hole ($5 - 10 \, M_{\odot }$) or a magnetar.

Relativistic outflow: if the outflow is non-relativistic and the observed huge amount of energy is deposited in this small compact region would have resulted in photon–photon annihilation producing electron–positron pairs. Thus, photons of energy above 1 MeV (pair production threshold energy) would not be observed. This is referred to as the compactness problem. However, since photons of energy as high as a few GeV are observed, requires that the outflow is moving at relativistic velocities wherein the emission is beamed towards the observer such that the photons now move relatively more radial to each other as a result lowering the scattering cross section for pair production. This phenomenological argument leads to the inference that the outflow produced in the GRB is relativistic.

Jetted outflow: the observed high energy flux integrated over time result in total isotropic energy, $E_{\gamma , \mathrm{iso}}$, comparable to the solar rest mass energy ($\sim 10^{54}\, \mathrm{erg}$). On the other hand, a supernova, emits a total energy of the order of $10^{51}\, \mathrm{erg}$ which is only $10^{-3}$ th of the solar rest mass. This issue could be resolved if we assume the outflow is ejected in the form a jet with an opening angle, $\theta _j$, rather than isotropically, which then brings down the total energy to $\sim E_{\gamma , \mathrm{iso}} \, \theta _j^2$, which is now more consistent with that of a core collapse supernova. The observational evidence of a jet has been obtained by the breaks observed in the X-ray and optical/IR afterglow light curves (Racusin et al. 2009; Kobayashi & Zhang 2003; Castro-Tirado et al. 1999).

3 Observation, data analysis and statistics

In this section, I will discuss the technique of observation, data analysis and statistics, particularly relevant for X-ray and $\gamma$-ray astronomy (Vianello et al. 2015; Arnaud et al. 1999).

Process of observation: An observation by a telescope includes detecting photons and measuring their properties such as energy, directionality etc. In this process, the signal from the source ($\mathcal {S}$) under study is convolved with the response of the detector ($\mathcal {R}$) as well as the noise ($\mathcal {N}$) to obtain the observed counts/ data. The noise in the data are mainly of two types: (i) the Poisson noise inherent to the observation, and (ii) noise which can be characterised as the background such as detector noise, photons coming from sources other than the source of our interest etc.

Response of an instrument is characterised by how the true energy (E) and position (P) of the source is related to the reconstructed energy, e and position, p in the detector. In other words, it tells us about the probability an incoming photon of energy, E, and position, P, would be reconstructed to be energy, e and position, p in the detector. A spread in the reconstructed energy is obtained such that $e \ne E$, which is referred to as the energy dispersion, characterised by the function, $\mathcal {D}( E,e)$. Similarly, a spread in the position of the source reconstructed in the detector is obtained such that $p \ne P$. This is characterised by the function, $\mathcal {P}( E,p,P)$ and is referred to as the Point source spread function. In addition to these factors, response function also includes the geometric cross section of the detector that is exposed to the incoming radiation from the sky at position, P, multiplied by the efficiency at E known as the effective area ($\mathrm{cm}^2$) of the detector, characterised by the function, $\mathcal {A}( E,P)$. Thus, the response of a detector can be summarised as

$$\begin{aligned} \mathcal {R}( e,p,E,P) = \mathcal {A}( E,P) \, \times \, \mathcal {D}( E,e) \, \times \, \mathcal {P}( E,p,P) \end{aligned}$$

(1)

Typically, what an instrument measures is counts of photons detected in various spatial and energy bins/channels ($I \equiv (i,j)$, where i, j gives the count of spatial and energy bins respectively) of finite size, thereby giving a differential flux of photons ($\mathcal {C}$) in terms of $\mathrm{cm}^{-2} \, \mathrm{s}^{-1} \, \mathrm{keV}^{-1} \, \mathrm{sr}^{-1}$. Thus, the observed spectrum is related to the emission from the source by

$$\begin{aligned} \mathcal {C}( I) = \int \, \mathcal {S}( E) \mathcal {R}( I, E) \, { d}E \end{aligned}$$

(2)

where $\mathcal {S}( E)$ is the actual spectrum of the source, and $\mathcal {R}( I, E)$ is the response of the instrument. This detected counts is a random variable including the above-mentioned noise factors.

Data analysis: The aim of the analysis of the obtained data is to extract the information about the source ($\mathcal {S}$). For a given observation, in order to conduct data analysis, three main files are required: (i) Data file: It contains the information of how many photons were detected in each energy channel; (ii) Background file: This contains information about the background photons (photons from other sources in the background of our source) detected in each energy channel; and (iii) Instrument response file: It contains the discretised information of the instrument response in the form of a matrix defined by the energy ranges. The background and data files are used to obtain the background subtracted count rate i.e the observed spectrum, $\mathcal {C}( I)$ of the source. Then, from the above equation 2, one finds that $\mathcal {S}$ can be obtained if the $\mathcal {R}( I, E)$ is inverted. Unfortunately, the inverse of response function is found to be non-unique and unstable to small changes in the observed counts, $\mathcal {C}$. Thus, a practical method, known as forward folding technique is adopted. In this method, a model function, $\mathcal {M}( E)$ with parameters, $m=\{m_1,m_2...m_n\}$ where n=total number of parameters of the model, is assumed for the source $\mathcal {S}( E)$ and substituted in the equation 2. This gives the predicted count spectrum for a given model, $\mathcal {C}_{ m}( I)$, which is then compared with the observed counts spectrum. The comparison is ascertained by the quantity called as the likelihood function, which is given as

$$\begin{aligned} \mathcal {L}(\mathcal {C}|\mathcal {M}, m) = \prod _{I} P_{ f}( c_{I}|e_{I}) \end{aligned}$$

(3)

where $P_f$ is the probability function describing the probability to obtain the observed counts, $c_{I}$, provided the expected value is $e_{I}$ for a given model and its parameters. Thus, the likelihood function gives a measure of the probability to obtain the observed data, $\mathcal {C}$ if the assumed model, $\mathcal {M}( E)$ with its given set of parameters, m, are true. The parameters of the model function are varied until the likelihood function is maximised, such that the model fits best to the data. For computational convenience, the minimisation of the negative of the logarithm of the likelihood function, $-log(\mathcal {L})$ is done. If $P_f$ is a Gaussian distribution, then $2\, \times$ log-likelihood is equivalent to $\chi ^2$ statistic.

In case of X-ray/$\gamma -$ray observations, there may not be enough number of photons detected in each bin always. Thus, the assumption that photon count in each bin is drawn from a normal distribution is no more valid. In such a case, the general usage of $\chi ^2$ statistics, defined as

$$\begin{aligned} \chi ^2 = \sum \limits _{I} \frac{(c_{I} - e_{I})^2}{\sigma ^2_{I}}, \end{aligned}$$

(4)

becomes undefined. In such scenarios, it is better to use the general maximum likelihood estimation methodology, where the $P_f$ can be any form of distribution. Note, the $\sigma _{I}$ includes the error in source as well as background added in quadrature, where both the source and background data follow Gaussian distributions.

In the Fermi gamma ray burst data analysis, it is generally observed that high energy photons are less in number, therefore statistics such as $\chi ^2$ cannot be used. If both the source as well as the background data follow a Poisson distribution, a background subtracted spectrum cannot be used in the likelihood equation as mentioned above, since difference of two Poisson variables is not equal to another Poisson variable. In such a case, a likelihood combining both the source and background data are defined such that a statistic called as Cstat is obtained. If the source is assumed to follow a Poisson distribution and the background data follows a Gaussian distribution, then the likelihood function is defined such that the statistic thereby obtained is known the Pgstat. For more details please refer Arnaud et al. (1999).

Goodness of fit: In the next step of analysis, we have to determine if the model fitted to the data is good or not. First step would be to look at the residuals of the fit, which is given by $c_{ I} - e_{ I}$. The observed source spectrum is a sum of the source emission + noise. Thus, if the assumed model function, $\mathcal {M}$, is similar to the actual source emission, then the resultant residuals should be just noise, which would be random variations about zero. If the residuals show any particular pattern or deviations from zero in any direction, for e.g. wavy structures etc, see upper panel of Fig. 6, we can conclude that the assumed model function is incorrect. However, if the residuals appear random with no particular deviation patterns, see lower panel of Fig. 6, we can say that the assumed model is consistent with the data. It is worth recognising that we can always reject a model with certainty, however, we can never be absolutely sure about a model. Instead we can only claim a model to be consistent with the observed data at certain level of confidence. The determination of this level of confidence is known as the ’goodness of fit’.

Fig. 6

Residuals obtained for the fit of model 1 and model 2 to the same data set of a GRB observed by Fermi are shown in upper and lower panels respectively. The residuals obtained for the model 1 have a wavy structure, whereas the residuals of the model 2 are more random around zero, which tells us that model 1 is a better model for the observed data.

In $\chi ^2$ statistics, the goodness of fit is determined by the parameter known as the reduced $\chi ^2$ defined by

$$\begin{aligned} \bar{\chi ^2} = \frac{\chi ^2}{d_f} \end{aligned}$$

(5)

where $d_f$ is degree of freedom. If $\bar{\chi ^2} \gg 1$ means that the fit has not been able to model data properly, in other words the error variance ($\sigma _I$) has been underestimated. If $\bar{\chi ^2} < 1$, it means the model is over-fitting the data such that the $\sigma _I$ is overestimated. If $\bar{\chi ^2} = 1$, then the model matches the data consistently within the errors.

In case of Cstat or Pgstat, their obtained value from the fit does not give us any measure of the goodness of fit, as the value depends on the number of bins (I) and values of the data points. Thus, in order to assess the goodness of fit, one has to perform Monte Carlo simulations of the spectra based on the best fit model and create a distribution of the statistic. Then note where the obtained statistic of the fit lie on the corresponding cumulative distribution plot, thereby giving the level of confidence at which the best fit to the data is obtained.

Model comparison: When we have two different models that can fit the data well, then we need to choose which model among them is better. According to Occam’s Razor idea of less complex model with a few number of parameters and that reduces the value of the statistic, is generally accepted as the better model. However, this can be more quantified by the methodology of hypothesis testing. Wherein first two exclusive hypothesises are defined such as the null hypothesis ($H_0$) which is the simpler model that is to be rejected and the alternate hypothesis ($H_1$) is another model that is different and more complex than the $H_0$. First, fit the data with both the models, $H_0$ and $H_1$, then obtain the corresponding statistics and note the difference between the statistics, say $\Delta \,\mathrm{Cstat}^{*}$. Using the Monte Carlo method, simulate a large number of datasets based on $H_0$, then fit each simulated dataset with both the $H_0$ and $H_1$ models, and calculate the difference in statistics for each case. Thus, build a cumulative probability density plot of the $\Delta \,\mathrm{Cstat}$. Note the value of probability, p, of the actual $\Delta \,\mathrm{Cstat}^{*}$ on this plot. $(1-p)$ gives the level of confidence of obtaining any value $> \Delta \,\mathrm{Cstat}^{*}$. If the prescribed level of acceptance of the alternate model, $H_1$ is decided at say $95\%$, then if the value of $(1-p) \ge 95\%$, we can reject the $H_0$ at a confidence level of $\ge 95\%$.

Confidence limits of parameters: Once we have the best fit model to the data and its best fit parameters, it is now necessary to estimate what are the confidence intervals of the fit parameter values. Lets consider $\alpha$ is our parameter of interest whose confidence interval needs to be determined. The remaining parameters of the model are kept frozen and $\alpha$ is varied between its hard limits to obtain different values of the statistic. For a given significance, $s_g$, the region of confidence is defined as (Avni 1976)

$$\begin{aligned} \mathrm{Cstat}_{\mathrm{s}_{\mathrm{g}}} = \mathrm{Cstat}_\mathrm{min} + \Delta (\mathrm{d}_\mathrm{f}, \mathrm{s}_\mathrm{g}). \end{aligned}$$

(6)

The value of $\Delta$ depends only on the number of parameters, thus e.g., for a significance of 0.68 and number of parameter be 1, $\Delta = 1$, ; see Table 1 in Avni 1976 for more details. Thus, the $68\%$ confidence limits of $\alpha$ is given by the values limiting the change in the best fit minimum statistic by the $\Delta = 1$ on its either side.

Fig. 7

(a) The $\nu F_{\nu }$ plot of the Band function and synchrotron physical model fitted to the data of GRB081110A are shown in orange and green solid lines respectively. (b) The $\nu F_{\nu }$ plot of the 2 blackbodies + power law and synchrotron physical model + blackbody, fitted to the data of GRB110920A are shown in pink and green solid lines respectively. In both the figures, the respective shaded regions represent the uncertainty in the shape of the model, corresponding to $68\%$ confidence level. Figures are taken from Iyyani et al. (2016).

As I conclude this section, I would like to bring to attention a few points of caution before we delve into various spectral models of GRB spectrum and their physical interpretations. Since the basic method of extracting the information about the source spectrum is via forward folding technique, wherein it is based on the assumed model for the source, our obtained results can be biased towards our assumption. Also, there can be different models that can give equally good fits to data. This in turn can result in different values of spectral peak, spectral slopes etc. As an example in Fig. 7a, a $\nu F_{\nu }$ plot of the two different models, Band function and synchrotron fitted to the same observational data are shown in orange and green respectively. The shaded region shows the uncertainty in the shape of the model. The full width half maximum of the $\nu F_{\nu }$ peak of the Band function was found to be small such that it was inconsistent with synchrotron emission. However, we find that a direct synchrotron emission model can also equally fit the observed data well. Thus, the inference made from an empirical function was invalidated. In Fig. 7b, another example where the models of Comptonisation (pink) and blackbody + synchrotron (green), fitted to the same data for GRB110920A are shown. One can clearly see that both models find two different shapes for the spectrum.

Thus, the modelling and interpretation of the observed data remains valid under the specific assumption of the model one has used. The empirical models may not be sufficient to test the viability of proposed physical models as shown above. Therefore, in order to test various theoretical models, one should always opt for direct fitting of the physical model to the data which would give a reliable measure of its feasibility.

4 Spectral observations

GRB spectrum in general look non-thermal and is mostly modelled using a phenomenological function called as the ‘Band function’ named after the scientist David Band who used this function in Band et al. (1993). The Band function is described by a power law with an exponential cutoff at lower energies and a simple power law at the higher energies, which are smoothly joined at a peak parameterised as ‘$E_\mathrm{peak}$’. The photon flux, N ($\hbox {photons/cm}^{2}\hbox {/s/keV}$) is given by

$$\begin{aligned} {\begin{matrix} N(E) =&{} A \, \left( \frac{E}{100}\right) ^{\alpha } \, \mathrm exp\left[ \frac{-E}{E_0}\right] &{} \, if \, E < E_0 \, (\alpha - \beta ) \\ &{} A\, \left[ \frac{(\alpha - \beta ) E_0}{100}\right] ^{\alpha - \beta } \left( \frac{E}{100}\right) ^{\beta } \mathrm{exp}[-(\alpha -\beta )] &{} \, if \, E > E_0 \, (\alpha - \beta ) \end{matrix}} \end{aligned}$$

(7)

where $\alpha$ is the low energy power law index, $\beta$ is the high energy power law index, $E_0$ is the break energy such that spectral peak, $E_\mathrm{peak} = (2+\alpha ) \, E_0$, and A is the normalisation. Being an empirical function, Band function alone does not provide us any direct information about the physical process giving rise to the observed radiation. However, several inferences can be made by comparing the values of the obtained spectral indices ($\alpha , \beta$) and $E_\mathrm{peak}$ to the various expected spectra from physical processes like synchrotron emission, inverse Compton scattering and emission from photosphere, etc.

Apart from Band function, there are several other empirical functions which are used to analyse the GRB data, such as

• (i) Simple power law: The function is defined by just two parameters

  $$\begin{aligned} N(E) = A\left( \frac{E}{E_\mathrm{piv}}\right) ^{\lambda } \end{aligned}$$

  (8)

  where $\lambda$ is the power law spectral index and $E_\mathrm{piv}$ is generally kept constant at 100 keV.

• (ii) Comptonised Model: It is a power law with an exponential cutoff,

  $$\begin{aligned} N(E)= A \left( \frac{E}{E_\mathrm{piv}}\right) ^{\lambda } \, \mathrm{exp}\left[ -\frac{(\lambda +2) \, E}{\hbox {E}_\mathrm{peak}}\right] \end{aligned}$$

  (9)

• and (iv) Smoothly Broken Power Law (SBPL): This model gives a more flexible curvature between the power laws modelling the low and high energy spectra (Ryde 1999; Kaneko et al. 2006). It is given by

  $$\begin{aligned} N(E) = A \left( \frac{E}{E_\mathrm{piv}}\right) ^{b} \, 10^{a-a_\mathrm{piv}} \end{aligned}$$

  (10)

where

$$\begin{aligned}&a = m\, \Delta \, ln\left( \frac{e^q + e^{-q}}{2}\right) ,\\&a_\mathrm{piv} = m \, \Delta \, ln\left( \frac{e^{q_\mathrm{piv}} + e^{-q_\mathrm{piv}}}{2}\right) , \\&q = \frac{\mathrm{log}(\hbox {E/E}_\mathrm{b})}{\Delta }, \, q_\mathrm{piv} = \frac{\mathrm{log}(\hbox {E}_{\mathrm{piv}}/\hbox {E}_{\mathrm{b}})}{\Delta }, \\&m = \frac{\lambda _2 - \lambda _1}{2},\, b = \frac{\lambda _2 + \lambda _1}{2}. \end{aligned}$$

where $\lambda _1$ and $\lambda _2$ are the low and high energy power law indices, $E_b$ is the break energy in keV and $\Delta$ gives the break scale as a measure of decades of energy, which is independent of the power law indices in contrast to the Band function, thus giving more flexibility to the model.

The distribution of the spectral indices of the low and high energy spectrum and $E_\mathrm{peak}$ obtained for the GRB spectra observed by Fermi GBM, using the best fit models are shown in Fig. 8 (Gruber et al. 2014).

Fig. 8

The distribution of the parameters: (a) low energy index, (b) high energy index and (c) $E_\mathrm{peak}$, obtained for the GRBs observed by Fermi as reported by Gruber et al. (2014) are shown. In Fermi GRB spectral catalog, a GOOD model is defined such that its each parameter has a relative error on its determined values such as $\alpha$ is 0.4, $\beta$ is 1.0 and $E_\mathrm{peak}$ is 0.4. A BEST sample is further defined such that among these GOOD models, which represent the data best which is determined by model comparison. In the above figures, the BEST fit parameter distribution (gray histogram) obtained for the GRB spectra are shown and in respective coloured dashed lines the constituent models are also shown. Figures are taken from Gruber et al. (2014).

Some of the key spectral features and questions that are being addressed in the study of the radiation mechanism of GRBs, are the following:

(i) :

Soft and hard low energy spectrum: The low energy power law index distribution is found to peak at $-0.8$, (Fig. 8a). This is inconsistent with fast cooling synchrotron emission whose expected $\alpha = -1.5$ but is consistent with slow cooling synchrotron emission whose $\alpha =-0.67$. It was recently shown by Burgess et al. (2015) that when a slow cooling synchrotron emission spectrum is modelled using a Band function, the corresponding $\alpha$ that is obtained = $-0.8$ instead of $-0.67$. Thus, the line of death of synchrotron emission is actually at $\alpha = -0.8$, which makes a larger fraction of observed GRBs to be incompatible with synchrotron emission. The thermal emission spectrum of a blackbody is expected to have an $\alpha = +1$, which is again inconsistent with majority of the observations. However, the distribution of the $\alpha$ ranges from soft to hard ($\alpha =-3$ to $+0.5$) values (Fig. 8a). Thus, the challenge for any underlying radiation process is to explain both the hard as well as soft sub-peak spectra.

(ii) :

Narrow clustering of $E_\mathrm{peak}$values: The spectral peak, $E_\mathrm{peak}$, is found to have a very narrow distribution peaking between a few hundreds of keV for long GRBs (Fig.  8c). This is however not naturally expected in case of non-thermal process like synchrotron emission where the peak, $E_\mathrm{peak} \propto \Gamma \, \gamma _\mathrm{el}^2\, B$ where $\Gamma$ is the bulk Lorentz factor of the outflow, $\gamma _\mathrm{el}$ is the electron Lorentz factor and, B is the magnetic field intensity, and thus, their combinations can have a wider range of values. On the other hand, in the process of thermalisation it is more likely to have similar $E_\mathrm{peak}$ values in GRB spectra, as the peak is determined by the temperature of the thermalised plasma which is related to the total luminosity of the burst which ranges between $10^{50 - 53}$ erg/s.

(ii) :

Hardness –intensity correlation: The key motivation behind studying various correlations between different observables of the GRB spectrum was to eventually use GRBs as a standard candle as similar to supernova Type Ia. A positive correlation between $E_\mathrm{peak}$ and luminosity of the burst, $L \propto E_\mathrm{peak}^{\gamma }$, where $\gamma \sim 1.5 - 1.7$, is observed (Golenetskii et al. 1983; Kargatis et al. 1994). Later, a correlation between the redshift (z) corrected peak with the total isotropic energy of the burst was studied. A correlation such as $E_\mathrm{peak} (1+z) \propto E_{iso}^{\gamma }$, where $\gamma \sim 0.5$ was obtained and it became known as ’Amati correlation’ (Amati et al. 2002, 2009; Amati 2006). However, there have been several arguments that the wide scatter observed in the data points cannot assure the presence of any underlying correlation between the studied parameters. Thus, a better understanding of the scatter in the data is required before the correlations can be used as a cosmological tool. Several other correlations also exist, please refer Pe’er (2015); Kumar & Zhang (2015).

(iii) :

Region of emission: It is key to understand where in the outflow the cooling of the electrons occur because this can be crucial in determining by what radiation process the electrons cool and thereby the resulting spectrum. Also, the microphysics involved in the shock acceleration of the electrons is far from being understood.

(iv):

High radiative efficiency: The radiation efficiency estimated for the prompt emission by several studies Racusin et al. (2009), Cenko et al. (2010)) is found to be high, ranging between $20\% - 95\%$. This is a challenge for the existing models of dissipation mechanism and radiation processes to justify these high values.

(v):

Temporal spectral evolution: The temporal study of the spectra of a given GRB via time resolved spectral analysis, indicates significant variation and evolution pattern within a single pulse of emission. These changes have to be related to the dynamics of the outflow which in turn need to be explained within the proposed physical models for GRB.

In addition to the above observations, some of the key spectral features identified by Fermi are the following:

(i) :

Detection of GeV photons: With the LAT instrument, high energy photons of a few GeV have been detected for several GRBs. In some cases, for e.g in GRB 090510 such photons are observed along with the low energy GBM emission. But in many cases like 090902B (Abdo et al. 2009a), 100724B (Vianello et al. 2018), 130427A (Ackermann et al. 2014) etc, such high energetic photons are observed after the GBM emission has ended. The highest energy photon observed till date is of 95 GeV in case of GRB 130427A at $\mathrm{T0}+244 \, \mathrm{s}$. Similarly, photon of energy 33 GeV has been detected for GRB 090902B at time $\mathrm{T0} + 82\, \mathrm{s}$, where $\mathrm{T0}$ is the trigger time of the GRB.

(ii):

Delayed onset and extended high energy emission: Emission above $100 \, {\mathrm{MeV}}$ observed by Fermi LAT have shown a delayed onset in comparison to the lower MeV emission observed by GBM (Castignani et al. 2014). At the same time, this emission extended much further even after the end of GBM pulse for $\sim 100$ to 1000s. For e.g. in case of short GRB 090510A, the LAT emission started $\sim 0.7 s$ after the GBM trigger and continued until 200 s. The highest energy photon detected was 31 GeV. Similarly, in case of long GRB 080916C, a delayed onset of LAT emission after 5 s was observed and the emission continued until 560 s while the GBM emission lasted only for 40 s (Abdo et al. 2009b).

(iv):

Multiple spectral components (or Band model crisis): The brightest GRBs observed by Fermi show that a single component like a Band function alone cannot effectively model the entire emission (Ackermann et al. 2013). Sometimes, additional components like a blackbody function at lower energies (e.g GRB 110721A, Axelsson et al. 2012; 100724B, Guiriec et al. 2011), a power law extending from low to high energies (e.g GRB 090902B, Abdo et al. 2009a; Ryde et al. 2010, 2011; GRB 110920A, Iyyani et al. 2015) or a power law with an exponential cutoff (e.g GRB 090926A, Ackermann et al. 2011) and sometimes multiplicative exponential cutoff at higher energies are required (GRB 100724B, GRB 160905A, Vianello et al. 2018). In case of bright GRBs, the photon statistics is higher enabling to capture finer spectral features during the analysis, however, in less bright GRBs, the low photon statistics results in modelling a more averaged out spectrum where the finer features of the spectrum are smoothed out and thereby the Band function gives a reasonable good fit.

(v):

Spectral width of the GRBs: In a recent study done by Axelsson & Borgonovo (2015), the width of the Band function fitted to the GRB spectra were analysed. The spectral width was defined as the logarithm of the ratio of the energies bounding the full width half maximum (FWHM) of the $\nu F_{\nu }$ plot of the best fit Band function model to the data.

$$\begin{aligned} W = log_{10}\left( \frac{E_2}{E_1}\right) \end{aligned}$$

(11)

where $E_1$ and $E_2$ are the lower and upper limits of the FWHM of the Band function $\nu F_{\nu }$ peak. The distribution of the W obtained for long and short GRBs are shown in the Fig. 9. Spectral width peaks at $\sim 1$ for long GRBs and at $\sim 0.8$ for short GRBs. This is much narrower and inconsistent with the widths of the spectrum from fast cooling synchrotron emission ($W = 1.6$) and slow cooling synchrotron emission ($W = 1.4$) from a power law of index = $-2$, and Maxwell–Boltzmann electron distributions respectively. At the same time, this is much wider than a blackbody spectrum whose width, $W =0.54$.

Fig. 9

The distribution of the spectral width parameter, W obtained for both short (blue) as well long (pink) GRBs are shown. The solid blue line marks the W = 0.92, obtained for synchrotron emission from mono-energetic electrons. The dashed line marks the blackbody spectral width, $W=0.54$, dotted line marks the width of the slow cooling synchrotron emission from Maxwell- Boltzmann electron distribution, and dash dot line marks the width of fast cooled synchrotron emission. Figure is taken from Axelsson & Borgonovo (2015).

5 Fireball model framework

5.1 Baryonic fireball model

The most popular framework within which most of the modelling of the GRB physics is done is the relativistic fireball model (Cavallo & Rees 1978; Mészáros 2006). The basic dynamics involved in the case of classical baryonic dominated fireball model is described below.

As the core of the massive star collapses or NS-NS/ NS-BH merges, a compact object like a stellar mass black hole (BH) or a magnetar is formed. This is followed by the accretion of the debris formed around the compact object resulting in the release of huge amount of energy. A large fraction of this gravitational energy is dissipated in the form of gravitational waves and neutrinos. A small portion of the energy forms a fireball of radius, $r_0$, temperature, $T_0$ (energy, $E_0$), and mass $M_0$ comprising of baryons, electrons–positrons and gamma ray photons. This baryonic fireball eventually is the source of the electromagnetic energy observed from this event. The highly dense fireball, at this stage is optically thick to photons. The radiation luminosity of the fireball is of the order of $10^{50-52}\, \mathrm{erg/s}$ which is much larger than the Eddington luminosity $\sim 10^{38} \, \mathrm{erg/s}$, as a result, the fireball starts to expand adiabatically from the nozzle radius of the jet, $r_0$. During the process, the internal energy is converted into the kinetic energy of the plasma. Thus, the total energy density of the plasma at any radius is

$$\begin{aligned} \mathcal {U}( r) = \mathcal {U}_{\gamma }( r) +\mathcal {U}_{ k}( r) \end{aligned}$$

(12)

where $\mathcal {U}_{\gamma }( r) = E\, n_{\gamma } = a T'^4 ( r)$ is the photon energy density, where E is the average energy of the photon, $n_{\gamma }$ is the number density of the photons in the lab frame, a is the radiation constant and $T' (r)$ is the comoving temperature of the plasma²; $\mathcal {U}_{ k}( r) = \Gamma n\, m_e\, c^2$ is the kinetic energy density, where $\Gamma$ is the local Lorentz factor of the outflow, n is the electron number density, $m_e$ is the mass of the electron and c is the speed of light. Deep inside the outflow, where the radiation is dominant, $E=\Gamma kT' = \mathrm{constant}$. Thus,

$$\begin{aligned} T' \propto \Gamma ^{-1} \end{aligned}$$

(13)

The comoving energy density can be defined as

$$\begin{aligned} \mathcal {U}'_{\gamma } = n'_{\gamma } E' = aT'^4 \end{aligned}$$

(14)

where $n'_{\gamma } = L/(\Gamma \, kT_0\, 4\pi \,r^2\, \beta c)$, where L is the burst luminosity, $\beta = v/c$ where v is the velocity of the plasma and $E' = kT'$. This results in

$$\begin{aligned} T'^3 \propto \Gamma ^{-1} \, r^{-2} \end{aligned}$$

(15)

Using equation 13 in equation 15 gives

$$\begin{aligned} T' \propto r^{-1} \end{aligned}$$

(16)

which in turn implies $\Gamma \propto r$. Thus, by conservation of energy as the outflow expands, the plasma gains kinetic energy at the expense of the decrease in comoving internal energy per particle. The bulk Lorentz factor of the outflow cannot increase beyond the initial internal energy per particle, $\eta = E_0/M_0 \,c^2$. This is achieved when the internal energy becomes equal to the kinetic energy of the plasma at the radius, $r_{\mathrm{s}} = \eta r_0$, known as the saturation radius. Beyond this radius, the outflow coasts with the constant Lorentz factor, $\Gamma = \eta$ and the kinetic energy dominates. Above $r_{\mathrm{s}}$, following equation 15, we find the co-moving temperature of the outflow to decay as

$$\begin{aligned} T'&\propto r^{-2/3} \end{aligned}$$

(17)

$$\begin{aligned} T'(r)&= \frac{T_0}{\eta } \left( \frac{r}{r_s}\right) ^{-2/3} \end{aligned}$$

(18)

where the factor $(r/r_s)^{-2/3}$ corresponds to the adiabatic cooling the photons undergo in the coasting phase till the radius, r.

5.1.1 Photospheric emission:

As the outflow expands, at one point the density of the outflow becomes small such that the opacity to photons become equal to unity. The radius at which the photons gets decoupled from the plasma is known as the photosphere, $r_\mathrm{ph}$. In a relativistically expanding plasma, the electron travels a relative distance, $\beta \, \mathrm{cos}\theta \, \mathrm{ds}$, in the direction of the photon motion while the photon moves a distance, ds, where $\theta$ is the angle between the photon and electron’s direction of motion. Thus, the optical depth for a photon to escape from a position r in the outflow towards infinity along the radial direction is given by

$$\begin{aligned} \tau (r) = \int _r^{\infty }(1-\beta \mathrm{cos}\theta ) \, n \, \sigma _T \, ds \end{aligned}$$

(19)

where $\sigma _T$ is the Thompson cross section. In a relativistic outflow, due to aberration of light most of the photons propagate almost radially in the direction of the electrons such that $\theta =0$. As $\tau$ decreases to unity, the photospheric radius, $r_\mathrm{ph}$ is given by

$$\begin{aligned} r_\mathrm{ph} = \frac{L \sigma _T}{8 \pi m_p c^3 \Gamma ^2 \eta } \end{aligned}$$

(20)

assuming $\Gamma$ is constant which is valid for $r \, > \, r_s$.

The emission at the photosphere is expected to be a blackbody as the photons produced in the explosion get thermalised by undergoing large number of Compton scatterings with the electrons before it gets decoupled from the plasma at the photosphere. However, it was shown by Beloborodov (2011), that only in the radiation dominated regime i.e accelerating phase of the outflow where $\Gamma \propto r$, the solution of the radiative transfer gives an exact blackbody spectrum from the photosphere. Whereas in the matter dominated regime i.e in the coasting phase, where the thermal radiation cools adiabatically before it gets released at the photosphere, the observed spectrum cannot be an exact blackbody (Rayleigh-Jeans slope of $\alpha = +1$) but would be slightly broader such that $\alpha = +0.4$. This is irrespective of whether any subphotospheric heating happens or not.

5.1.2 Internal shocks:

The observed non-thermal gamma ray emission requires some manner in which the dominant kinetic energy of the burst gets converted back into photons. While the central engine is active, it is possible that different shells with different densities and energies are produced, thereby resulting in different terminal Lorentz factors. In such a scenario, the shells with high Lorentz factor crashes into the slow moving preceding shell creating shocks by dissipating the differential Lorentz factor (or kinetic energy) of the two shells. The resulting shocks are then capable of accelerating electrons to very high energies by Fermi mechanism. Eventually, the energised the electrons cool by radiating via various emission processes like synchrotron, or inverse Compton scattering. This mechanism of dissipating the kinetic energy of the outflow is known as internal shocks (Rees & Mészáros 1994; Sari & Piran 1997; Kobayashi et al. 1997; Daigne & Mochkovitch 1998). This process can naturally explain the rapid variability observed in the GRB light curves where each such spike can be related to an internal shock. However, internal shock mechanism suffers from low efficiency problem. Consider two consecutively emitted shells of mass $m_1$ and $m_2$ with Lorentz factors $\Gamma _1$ and $\Gamma _2$ respectively such that $\Gamma _2 > \Gamma _1$. Assuming that these shells undergo inelastic collision, the efficiency of the kinetic energy dissipation is given by (Kobayashi et al. 1997)

$$\begin{aligned} \epsilon = 1-\frac{(m_1 +m_2)\, \Gamma _m}{m_2 \Gamma _2 + m_1 \Gamma _1} \end{aligned}$$

(21)

where $\Gamma _m = \sqrt{(m_1\Gamma _1 + m_2\Gamma _2)/(m_1/\Gamma _1 + m_2/\Gamma _2)}$ is the Lorentz factor of the merged shell that is formed after collision. High efficiency can be achieved only if the colliding shells have near equal masses and large difference in Lorentz factors. However such high contrast in Lorentz factors are not expected in the GRB outflow. The estimate of the observed radiation efficiency of the burst further involves factors such as efficiency in accelerating the electrons in the shocks, efficiency of the electrons to convert its energy to photons and finally, the efficiency involving the sensitivity of the detectors in detecting this radiation. Thus, in the internal shock model, the overall radiation efficiency expected is very low of $\sim 1-10\%$ (Mochkovitch et al. 1995; Kobayashi et al. 1997; Kumar 1999; Panaitescu et al. 1999; Guetta et al. 2001), which is inconsistent with the observations which exhibit high radiative efficiency of $\sim 20 -90\%$ (Lloyd-Ronning & Zhang 2004; Ioka et al. 2006; Zhang et al. 2007; Racusin et al. 2009; Cenko et al. 2010).

5.2 Poynting dominated fireball

As the core of the star collapses it is likely to first form a fast rotating proto-neutron star known as the magnetar, before it eventually collapses into a blackhole after a span of few seconds (MacFadyen et al. 2001; Heger et al. 2003). Magnetar as the central engine has also been observationally motivated by instances like long duration of plateau phase observed in the afterglow, which can be explained by the late time energy injection coming from the spin down of the magnetar (Zhang et al. 2006; Rowlinson et al. 2013; Stratta et al. 2018). Even though the process of jet launching is still inconclusive, our limited understanding until now requires strong magnetic fields to produce highly collimated outflows via mechanisms like Blandford -Znajek (Blandford & Znajek 1977; Komissarov 2001) and Blandford -Payne (Blandford & Payne 1982). In such scenarios, magnetic dominated outflows can be expected (Usov 1994; Katz 1997; Mészáros & Rees 1997; Zhang and Yan 2011), which have a different evolutionary dynamics in comparison to a baryon dominated outflow.

A simple model of the dynamics of a Poynting dominated outflow is discussed below (Drenkhahn 2002). The total luminosity of the burst can be defined, $L = L_k + L_p$ where $L_k = \Gamma \dot{M} c^2$ is the kinetic energy luminosity and $L_p = (B^2/8\pi ) 4\pi r^2 \beta c$ is the Poynting flux luminosity where B is the magnetic field intensity. The magnetisation parameter, $\sigma _0$ is defined as

$$\begin{aligned} \sigma _0 = \frac{L_p}{L_k}. \end{aligned}$$

(22)

The magnetic fields anchored to the rotating central engine change their polarity on a scale of $\lambda \sim 2\pi c/\Omega$, where $\Omega$ is the angular frequency of the rotating central engine. This change in polarity lead to the reconnection of the field lines which result in the dissipation of the magnetic energy. The reconnection rate is assumed to remain constant at a fraction, $\epsilon$, of the Alfvén speed. This accelerates the outflow, thereby converting into the kinetic energy of the outflow such that

$$\begin{aligned} \Gamma = \eta _\mathrm{p} \left( \frac{r}{r_s}\right) ^{1/3} \end{aligned}$$

(23)

where $\eta _\mathrm{p}$ is the terminal Lorentz factor. Thus, here the acceleration of the outflow is more gradual in comparison to the radiation dominated scenario. The total luminosity can be rewritten as

$$\begin{aligned} L = (1+\sigma _0) \Gamma _0 \dot{M} c^2 \end{aligned}$$

(24)

where $\Gamma _0 = \sqrt{\sigma _0}$ is the Lorentz factor of the outflow at the Alfvénic radius where the magnetisation, $\sigma _0 \gg 1$. Thus, the mass ejection rate is $\dot{M} \sim L/ \sigma _0^{3/2} c^2$. The outflow reaches its terminal velocity when $L_k \gg L_p$, such that $L = L_k$. Thus, the maximum Lorentz factor is given by

$$\begin{aligned} \eta _\mathrm{p} = \sigma _0^{3/2}. \end{aligned}$$

(25)

The saturation radius, $r_s$ where this is achieved is given by $r_s = r_0 \, \sigma _0^3$. In such a scenario, the photospheric radius is found to be

$$\begin{aligned} r_\mathrm{ph} = 6 \times 10^{11} \frac{L_{52}^{3/5}}{(\epsilon \Omega )_3^{2/5} \sigma _2^{3/2}} cm \end{aligned}$$

(26)

While considering the above dynamics, it is also key to note that our understanding of the physics of the magnetic reconnection is limited and its study is still an open issue, therefore many assumptions are involved in the above estimations.

6 Emission models

The two main competing radiation models are of optically thin synchrotron emission and the photospheric emission.

6.1 Synchrotron emission

Synchrotron emission is produced when relativistic electrons gyrate through the magnetic fields (Rybicki & Lightman 1986). In internal shocks as well as in magnetic reconnections, the energetic electrons produced in the relativistic shocks radiate their energy in the presence of magnetic fields. This simple and straightforward process has been widely used to explain the GRB prompt emission (Rees & Mészáros 1992; Tavani 1996; Papathanassiou & Mészáros 1996; Pilla & Loeb 1998; Sari et al. 1998; Piran 1999; Kumar & McMahon 2008; Beniamini & Piran 2013; Beniamini & Giannios 2017; Beniamini et al. 2018).

In a relativistic shock produced in a plasma of particle density, n and Lorentz factor, $\Gamma$, the electrons are assumed to be accelerated to a power law distribution such that

$$\begin{aligned} N(\gamma _e) d\gamma _e \propto \gamma _e^{-p} d\gamma _e \end{aligned}$$

(27)

where $\gamma _e$ is the electron Lorentz factor, p is the power law index. The minimum Lorentz factor, $\gamma _m$ of the power law distribution is given by

$$\begin{aligned} \gamma _m = \epsilon _e \left( \frac{p-2}{p-1}\right) \frac{m_p}{m_e} \Gamma . \end{aligned}$$

(28)

where $\epsilon _e$ is the fraction of the dissipated energy that energises the electrons, $m_p$ and $m_e$ is mass of proton and electron respectively. A fraction, $\epsilon _B$, of the dissipated energy generates magnetic fields of strength,

$$\begin{aligned} B = (32\, \pi \, m_p \, \epsilon _B \, n)^{1/2} \, \Gamma \,c. \end{aligned}$$

(29)

The observed peak of the synchrotron emission is given by

$$\begin{aligned} E_\mathrm{sync} = \frac{\Gamma }{(1+z)} \frac{3}{4} \frac{h \, q B}{ \pi \, m_e c} \gamma _\mathrm{el}^2 \end{aligned}$$

(30)

where q and $m_e$ is the charge and mass of the electron. The total observed flux is estimated to be

$$\begin{aligned} F_\mathrm{sync} =\frac{\sigma _T c \Gamma ^2 \gamma _\mathrm{el}^2 B^2 N_e}{24 \pi ^2 d_L^2} \end{aligned}$$

(31)

where $N_e$ is the total number of radiating electrons. The radiative cooling time is given by

$$\begin{aligned} t_\mathrm{cool} = \frac{6 \pi m_e c}{\sigma _T B^2 \Gamma \gamma _\mathrm{el} (1+\mathcal {Y})} \end{aligned}$$

(32)

where $\mathcal {Y}$ is the Compton $\mathcal {Y}$ parameter. Comparing the cooling time of the electrons to the dynamical time, the time electrons take to cross the shocked region, $t_\mathrm{dyn} = R/ (2\Gamma ^2 c)$, there are two different cases of cooling. If $t_\mathrm{cool} < t_\mathrm{dyn}$, then the electrons radiate their energy efficiently. This is referred to as the fast cooling synchrotron emission. Such a radiation spectrum consists of three segments: a power law such that $P_{\nu } \propto \nu ^{1/3}$ in the range, $\nu < \nu _{c}(\gamma _c)$, where $\gamma _c$ is the electron Lorentz factor corresponding to $t_\mathrm{cool}$ and $\nu _{c}$ is known as the cooling frequency, a second power law segment of $P_{\nu } \propto \nu ^{-1/2}$ between the range, $\nu _c$ and $\nu _m$, and the third power law segment, $P_{\nu } \propto \nu ^{-p/2}$ in the range $\nu > \nu _m$; see upper panel of Fig. 10. If $t_\mathrm{cool} > t_\mathrm{dyn}$, then the electrons do not lose their energy within the dynamical time and is referred to as slow cooling synchrotron emission. Such a radiation spectrum again consists of three segments consisting of a power law, $P_{\nu } \propto \nu ^{1/3}$ when $\nu < \nu _m$, a second power law, $P_{\nu } \propto \nu ^{-(p-1)/2}$ when $\nu _m<\nu < \nu _c$ and a third power law segment, $P_{\nu } \propto \nu ^{-p/2}$, when $\nu > \nu _c$; see lower panel of Fig. 10.

Fig. 10

Upper and lower panels show the fast and slow cooling synchrotron spectra respectively. Synchrotron self absorption (SSA) plays a key role below frequency, $\nu _a$. Figure is taken from Sari et al. (1998).

Thus, in the photon spectrum, the low energy power law index for a fast cooling synchrotron emission is given by $\alpha = -3/2$ and for the slow cooling synchrotron emission, $\alpha = -2/3$, which is referred to as the ‘line of death’ of synchrotron emission because any spectral index harder than this value cannot be explained by synchrotron emission. There is a significant fraction of observed GRB spectra, whose $\alpha > -0.67$ which pose a challenge for synchrotron emission models (Fig. 8a). However, it has been recently shown by Burgess et al. (2018), that when an idealised synchrotron emission, properly including the time dependent cooling of electrons, is considered, can successfully fit GRB spectra possessing either soft or hard $\alpha$ values, even those violating the ‘line of death’.

With increasing number of afterglow measurements, it is found that the prompt emission process in GRBs is radiation efficient (Racusin et al. 2009; Cenko et al. 2010). This is in contrast with the slow cooling synchrotron emission models, where most of the electrons do not cool. Also, in case of non-cooled electron distribution, it is inferred that only a small fraction of the electrons in the shocked region is accelerated to very large Lorentz factors such that $\gamma _m \ge 10^5 - 10^6$. Such high $\gamma _e$ is difficult to be achieved within internal shocks, where the electrons would be only mildly relativistic and $\gamma _m$ is expected to $m_p/m_e = 1836$ (Bošnjak et al. 2009). High radiation efficiency requires the process to be fast cooling synchrotron emission. However, in Burgess et al. (2014), where synchrotron emission model was directly fitted to the data, one of the key results was that the observed GRB spectrum is inconsistent with fast cooling synchrotron emission as the fast cooling spectrum possess a wide spectral peak ($\nu F_{\nu }$ peak) in contrast to the narrow spectral width of the data.

Thus, the above simple synchrotron emission models cannot self consistently explain the observed non-thermal emission in GRBs. Several alternatives as well as modifications have been proposed for the synchrotron emission.

(i) :

Decaying magnetic field: In the above discussed scenario, the magnetic field strength was assumed to remain constant with time and radius throughout the shocked region. However, it was initially proposed by Pe’er & Zhang (2006) that magnetic fields can decay with time on small scales of length. This model has been further studied in Uhm & Zhang (2014), Zhang et al. (2016). They find that in order to explain a GRB spectrum of $\alpha = -0.8$, a rapid increase in electron injection rate is required. This in turn means that even though in the beginning the electrons are in the fast cooling regime, because of the rapid decay of magnetic fields resulting in increased number of energised electrons. Thus, dominant emission is obtained from electrons radiating in low magnetic field strength. This eventually produces a spectrum similar to slow cooled synchrotron spectrum, whose major drawback is the low radiative efficiency.

(ii) :

Marginally fast cooling: In this scenario, the minimum electron Lorentz factor is considered to be $\gamma _c \le \gamma _m$ in contrast to the requirement of $\gamma _c \ll \gamma _m$ in case of a typical fast cooling synchrotron emission. The spectral peak would be formed at $\nu _{c,eff}$ such that the low energy power law index is $-2/3$ even when the electrons cool fast (Daigne et al. 2011; Beniamini et al. 2018). Such scenario requires a lot of fine tuning in order to keep $\gamma _c \le \gamma _m$ such as low magnetic field and large bulk Lorentz factor of the outflow.

(iii) :

Re-acceleration/ slow heating: The possibility of re-acceleration of the radiating electrons such that they are accelerated on a timescale smaller than the radiative cooling time is considered. In such a case, the electrons appear to remain uncooled even when the electrons cool efficiently. However, such a mechanism of trapping the radiating electrons in order to continuously reaccelerate them, is not known to exist in baryonic shocks, where the accelerated electrons leave the shocked region and cool off undisturbed (Ghisellini & Celotti 1999), see also Kumar & McMahon (2008). Whereas possibilities such as extended shock scenario has been discussed in Pilla & Loeb (1998), Medvedev & Loeb (1999). However, such possibilities exist within magnetic dominated outflow as discussed in Asano & Terasawa (2009), Murase et al. (2012), Beniamini & Piran (2014).

(iv) :

External shocks: External forward shocks are created when the outflow crashes into the circum-burst medium (Mészáros & Rees 1993; Panaitescu & Mészáros 1998; Chiang & Dermer 1999; Dermer et al. 2000). Here the resultant shocks are relativistic due to the large differential kinetic energy of the colliding materials and therefore can explain the large inferred electron Lorentz factors from observations. This process, however, produces smooth $\gamma -$ ray pulses and cannot account for short -time variability of a few milliseconds, as observed in many GRBs (Dermer & Mitman 1999; Kobayashi et al. 1997; Sari & Piran 1997).

(v) :

Synchrotron self Compton (SSC): Here the low energy synchrotron photons are up scattered to higher energies by the energetic electrons via inverse Compton scattering (Panaitescu & Mészáros 2000; Stern & Poutanen 2004; Nakar et al. 2009). One of the concerns in this model is that a second scattering can give photons of TeV energies which can severely strain the energy budget of the GRB (Piran et al. 2009).

(vi) :

Synchrotron self absorption (SSA): At low frequencies, the relativistic electrons can absorb the synchrotron photons produced by other electrons in the same magnetic field. This process is generally adopted to explain the steep low energy power law slopes. However, the SSA is likely to occur at infra-red or optical frequencies and at the same time requires huge magnetic fields strengths (Granot et al. 2000; Lloyd & Petrosian 2000).

(vii) :

Radiation from hadrons: The shocks that accelerate leptons can equally accelerate the hadrons present in the outflow to high energies. In that case, the resultant energetic protons can then radiate via proton synchrotron emission (Waxman 1995; Böttcher & Dermer 1998; Totani 1998; Asano et al. 2009). In this context, GRBs are expected to be sources of high energy cosmic rays and thereby of ultra-relativistic neutrinos (Waxman & Bahcall 1997; Zhang et al. 2018; Wang et al. 2018). However, until now this hypothesis has never been confirmed yet as no neutrinos have been detected from a GRB (Icecube Collaboration et al. 2012). On the other hand, the radiation efficiency of hadrons is less in comparison to leptons as the cross- section for the synchrotron radiation is $\sim (m_e/m_p)^2$.

6.2 Photospheric emission

As discussed above, non-thermal emission models involving internal shocks face difficulties in explaining many observed features such as hard low energy spectral slopes, high radiative efficiency etc. These naturally lead to the quest of alternate models that could resolve these issues. Among them, the photospheric emission models have gained extensive popularity recently. Photospheric emission is inherently expected within a fireball model explanation of the relativistic jet emerging from the collapse of the stellar core. A thermalised emission of a blackbody spectrum is expected from the photosphere. Thus, the GRB spectra observed by CGRO BATSE instrument were analysed using a hybrid model defined as combination of blackbody and a non-thermal component like power law or Band function.

Fig. 11

The detected blackbody temperature, kT, (black/circles) evolves as a broken power law and the normalisation of the blackbody, $\mathcal {R}$ (blue/squares) evolves in the form of an increasing power law. These values are detected for the GRB110721A. This is similar to the previous thermal behaviours observed in BATSE GRBs. Figure is taken from Iyyani et al. (2013).

Several GRBs were successfully analysed with the hybrid model (Ryde & Pe’er 2009). The thermal component was identified to show some recurring behaviours across different GRBs. The temperature, T and flux, $F_\mathrm{BB}$, were found to show a broken power law behaviour with time, see Fig. 11. The temperature of the blackbody, T showed either a constant or mildly decreasing trend before the break with a power law index of $-0.07 \pm 0.19$ and decayed faster after the break with a power law of index, $-0.68 \pm 0.24$. The thermal flux evolution exhibited a power law index, $-0.63 \pm 0.66$ before the break, and after the break the flux decays with time with a spectral index, $-2.07 \pm 0.75$.

The normalisation of the blackbody is parameterised as $\mathcal {R} \equiv ( F^\mathrm{obs}_\mathrm{BB}/ (\sigma \, T^{4}))^{1/2}$. It represents the transverse size of the region emitting thermal emission which is the photosphere. Therefore, within a single burst, the temporal evolution of $\mathcal{{R}} \propto r_{ph}/\Gamma$ (Pe’er et al. 2007). It shows a recurring behaviour of an increasing power law see Fig. 11 and sometimes remains constant with time, either throughout a pulse of emission or the burst duration. In some cases, it was noted that $\mathcal {R}$ shows a break in the power law behaviour after some time by either becoming constant or by decreasing with time, after the break. A constant $\mathcal {R}$ with time indicates that the transverse size of the photosphere remains constant with time. On the other hand, an increasing $\mathcal {R}$ indicates that with time one is observing larger part of the photosphere. If the photospheric radius, $r_{ph}$ remains constant, then an increasing $\mathcal {R}$ suggests the Lorentz factor of the outflow is decreasing with time, thereby increasing the cross section of the photosphere from where the emission is received. If $\Gamma$ remains constant, then it would indicate that the $r_{ph}$ increases with time due increased luminosity of the burst (equation 20).

Fig. 12

A schematic representation of two types of the photospheric emission models are shown: (a) Two emission zone model and (b) One emission zone model. $r_0$, $r_s$, $r_\mathrm{ph}$ and $r_d$ are the nozzle radius of the jet, saturation radius, photospheric radius and the radius of dissipation respectively.

In the BATSE era of observations, there were five bursts, GRB 930214, 941023, 951228, 971127, 990102, whose spectra could be best modelled with a blackbody function alone (Ryde 2004). In the Fermi observations until now, there have been just two such cases: GRB 101219B (Larsson et al. 2015) and 100507 (Ghirlanda et al. 2013), also see Ryde et al. (2017). The observation of a pure thermal component is highly challenging for different GRB emission models because as discussed in section 5.1.1. Thermal emission expected from the photosphere formed in the coasting phase would be a broadened blackbody such that the low energy power law index, $\alpha = + 0.4$ instead of $\alpha = +1$. An exact blackbody is expected only from the photosphere formed in the accelerating phase. In such a scenario, the kinetic energy of the burst is minimum and therefore any afterglow emission cannot be expected which however has been observed for some of these bursts.

During BATSE observations, it was observed in certain cases that the power law of the hybrid model had an increasing trend indicating that the peak of the spectrum lies beyond the energy window of the instrument (Ryde & Pe’er 2009; González et al. 2009). In Fermi observations, because of the wider available energy range, the non-thermal emission could be modelled by a Band function instead of a power law. This enabled to constrain the spectral peak which is found to be at a few ${\mathrm{MeV}}$. For example, in GRB 110721A, the spectrum was best modelled using the blackbody + Band function (Axelsson et al. 2012). The highest spectral peak energy of $15 \pm 2 \, {\mathrm{MeV}}$ was measured. The blackbody temperature followed the typical broken power law behaviour, whereas the Band function, $E_{\mathrm{peak}}$, evolved smoothly as a power law with time. Similarly, the time integrated spectrum of GRB100724B was modelled using a combination of blackbody function of $kT \sim 40 \, \mathrm{keV}$ and Band function with a spectral peak at $2500 \, {\mathrm{MeV}}$ (Guiriec et al. 2011), also see Vianello et al. (2018). In this model, the blackbody function forms only a small part of the entire spectrum and is seen as a shoulder to the main spectral peak. Here the non-thermal emission can be interpreted as the synchrotron emission expected in internal shocks happening in the optically thin region of the outflow. With that perspective of modelling, several other GRBs have also been found to show similar spectrum in Burgess et al. (2014), Preece et al. (2014), where the Band function was replaced by the actual synchrotron emission model. This spectral model of a combination of thermal and non-thermal component is referred to as the two emission zone model (Fig. 12).

In such a scenario, no dissipation of the kinetic energy of the burst occurs below the photosphere and the photosphere is expected to form in the coasting phase. The observed thermal emission is, thus, expected to be slightly modified at the lower energies due to both geometrical as well as radial effects of the photosphere in the relativistic outflow. The broadened blackbody spectrum is referred to as the multicolour or modified Planck spectrum (Beloborodov 2011). However, in the spectral analysis, we use generally a pure thermal function. This is practically sufficient when the non-thermal emission is highly dominant and therefore, with the thermal function what we are able to capture in the analysis is only the peak of the blackbody emission and not it entire spectral shape, thereby masking these relativistic effects.

In this physical picture, the various spectral shapes can be explained by the relative strength of these two components that is given by the ratio,

$$\begin{aligned} \frac{L_\mathrm{NT}}{L_\mathrm{th}} \le \epsilon _d \, \epsilon _e \left( \frac{r_\mathrm{ph}}{r_{\mathrm{s}}}\right) ^{2/3} \end{aligned}$$

(33)

where $L_\mathrm{NT}$ and $L_\mathrm{th}$ is the observed non-thermal and thermal luminosities respectively, $\epsilon _d$ is the fraction of the kinetic energy of the burst (or the Poynting flux) that is dissipated and $\epsilon _e$ is the fraction of the dissipated energy that energies the electrons (Ryde & Pe’er 2009). If $r_\mathrm{ph}$ lies closer to $r_s$, then a strong thermal component can be expected in the spectrum. But if $r_\mathrm{ph}$ forms further away from $r_s$, then the thermal emission is expected to be weak as it has undergone significant adiabatic cooling.

6.2.1 Subphotospheric dissipation

Rees & Mészáros (2005) suggested that it is possible to have oblique and collimation shocks within the outflow as the jet pierces through the stellar material. This can result in continuous or localised dissipation of the kinetic energy of the burst in regions even before the outflow reaches its photosphere. The scenario of localised dissipation occurring below the photosphere was discussed in Pe’er and Waxman (2004), Pe’er & Waxman (2005). The high energetic electrons cool rapidly by synchrotron radiation or via inverse Compton scattering of the incoming thermal photons coming from the initial explosion. The electrons eventually achieve a quasi-steady state with a quasi-Maxwellian distribution. The non-thermal radiation produced at the dissipation site cannot easily escape the outflow as it is optically thick. The emission undergoes a number of Compton scatterings with this electron distribution, which results in the modification of the spectra. If the dissipation occurs at large optical depths ($\tau > 100$), then the non-thermal radiation produced at the site, gets thermalised completely before it escapes from the photosphere, and the spectral peak would be now regulated at a higher temperature ($\sim 1 \, \mathrm{MeV}$). However, if the dissipation occurs at lower or moderate optical depths then enough time is not available for the non-thermal photon field to thermalise. The inverse Compton scattering of the seed thermal photons result in a two temperature plasma and therefore, in such scenarios, spectrum such as that of a ’top-hat’ shape, emerges from the photosphere. Thus, the photospheric emission need not be thermal in nature. This model is referred to as the one emission zone model. In such dissipative photospheric models, the dominant part of the prompt emission spectra extending from keV to MeV is modelled to come from the photosphere itself (Ahlgren et al. 2015). For example GRB 110920A, was best modelled using a quasi thermal Comptonisation model, that was empirically defined by two blackbodies, and a power law (Iyyani et al. 2015). The low energy blackbody represented the seed thermal component and the high energy blackbody temperature represented the Comptonised peak. The power law required could be a part of the Comptonsiation model or may be representing any emission coming from the optically thin region of the outflow. This can become more clear if one does direct modelling of the spectrum with the physical model of Comptonisation.

In Beloborodov (2010), a mechanism of collisional dissipation is considered to extract the kinetic energy of the burst. The GRB jet outflow is considered to contain comparable number of neutrons and protons. As the outflow expands and approaches the coasting phase, the jet develops into a two fluid state, where the neutrons and protons achieve different terminal Lorentz factors. This results in a drag within the outflow causing nuclear collisions between the neutron and proton fluids producing electron -positron pairs whose energy is converted into radiation before they get thermalised with the plasma. In contrast to internal shocks, here the dissipation is not confined to the shock front instead it spreads across the volume of the jet. This kind of continuous radial dissipation leading up to the photosphere results in smearing out of any spectral breaks, eventually producing a smooth spectrum like a Band function. Thus, in subphotospheric dissipation scenario, the observed shape of the photospheric spectrum indicates the type of profile the subphotospheric dissipation mechanism possess.

GRB 090902B was an intense burst observed at a redshift of $z = 1.8$. The entire emission of the burst could be divided into two main epochs. In the first epoch the spectrum was modelled by a very narrow Band function such that $\alpha = +0.3$ and $\beta = -4$, whereas in the second epoch, the spectral shape became broader such that $\alpha = -0.6$ and $\beta = -2.5$. Thus, the burst evolved from something close to a Planck function to a broader spectrum with time. Therefore, this burst has been considered as a typical example of subphotospheric dissipation scenario (Ryde et al. 2010, 2011; Pe’Er et al. 2012). This broadening of the spectrum was also suggestive of the effects of geometry of the viewing angle of the GRB jet on the emission from the photosphere (Pe’er 2008).

Photospheric emission models do have a few drawbacks like it cannot explain the very high GeV emission. However, the delayed onset of these high energy emission suggests a different emission radius, therefore, along with the subphotospheric dissipation model, we need to evoke some optically thin non-thermal emission models as well in order to explain these GeV emissions (Ryde et al. 2010).

6.2.2 Geometrical broadening

In a spherically symmetric outflow, it was shown by Goodman (1986), in a one dimensional (radial) approach, that the emission of GRB from relativistic outflow is a broadened blackbody. Later, Abramowicz et al. (1991) showed that in a relativistic spherically symmetric outflow due to the variation of the optical depth based on the viewing angle, the shape of the photosphere becomes concave and symmetric around the line of the sight of the observer. In Pe’er (2008), the probability of the last scattering position of the photons from the entire emitting volume was studied which gave an expression for the photospheric radius,

$$\begin{aligned} r_\mathrm{ph} \propto \frac{\theta ^2}{3} + \frac{1}{\Gamma ^2} \end{aligned}$$

(34)

where $\theta$ is the angle measured from the line of sight of the observer. When $\theta = 0$ i.e when the emission is dominantly coming along the LOS, there the photospheric radius would be minimum equivalent to the expression given in equation 20. But when $\theta >0$ on either side of the LOS of the observer, the photospheric radius becomes larger. Thus, the observed photosphere across the LOS attains a concave shape (Fig. 13). This is very much similar to the ‘limb darkening’ effect observed in the sun, but here it is observed in a relativistic outflow. Beloborodov (2011) however, came to a similar result via solving the radiative transfer equation in the relativistic limit. He termed the photosphere as ‘fuzzy photosphere’ because of the distribution in the values of radii and angles that represent the last scattering position of the photons escaping the plasma.

Fig. 13

The last scattering position of the photons are shown in terms of both $\theta$ and radius, $r/r_0$ where $r_0$ is constant present in the equation 34. Figure is taken from Pe’er (2008).

Several hydrodynamic simulations regarding the jet (non-spherical outflow) propagation through the star (Zhang et al. 2003b; Morsony et al. 2007; Mizuta et al. 2011), show that the emerging jet have an angular structure for the Lorentz factor of the outflow. With this motivation, Lundman et al. (2013) studied the propagation of photons within an optically thick, steady, axisymmetric jet while considering a Lorentz factor structure for the jet as given by

$$\begin{aligned} \Gamma (\theta ) = \Gamma _0 \, \left( 1+\left( \frac{\theta }{\theta _j}\right) ^{2p}\right) ^{-1/2}, \end{aligned}$$

(35)

where $\Gamma _0$ is the maximum value of the Lorentz factor and $\theta _j$ is the jet opening angle. They found that the thermal emission from the photosphere was significantly broadened such that $\alpha = -1$. This could be achieved in case of narrow jets $(\theta _j \le 1/\Gamma _0)$ for any viewing angles, and in case of wide jets $(\theta _j \ge 5/\Gamma _0)$ when viewed such that $\theta _v \sim \theta _j$.

Fig. 14

For the burst 110721A, (a) the Lorentz factor, $\Gamma$ was found to decrease monotonously with time from 1000 to 100, whereas, (b) the nozzle radius of the jet, $r_0$ increases and reaches a peak at $2.5\, \mathrm{s}$ and then tends to decrease. The red circle and blue star mark the respective values for redshifts, $z =3.5$ and $z=0.38$ respectively. Figures are taken from Iyyani et al. (2013).

6.2.3 Dynamics of the outflow

Thermal emission in contrast to optically thin non-thermal emissions is more deterministic as it originates from the photosphere. Therefore, identifying the blackbody component in the spectrum enables to determine properties of the outflow as well. In Pe’er et al. (2007) a methodology to determine the parameters of the outflow characterised by nozzle radius of the jet, $r_0$ and Lorentz factor of the outflow, $\Gamma$ is given.

To begin the calculations, one needs to know if the photosphere is formed in the coasting or accelerating phase of the outflow. This can be determined by equating the photospheric radius to the saturation radius in the expression

$$\begin{aligned} \mathcal {R} = \left( \frac{\hbox {F}_{\mathrm{BB}}}{\sigma \hbox {T}^4}\right) ^{1/2} = \zeta \frac{(1+\hbox {z})^2 }{\hbox {d}_\mathrm{L}} \frac{\hbox {r}_{\mathrm{ph}}}{\Gamma }, \end{aligned}$$

(36)

where $\zeta$ is a numerical factor of order of unity, thereby obtaining the critical Lorentz factor, $\eta ^*$ to be

$$\begin{aligned} \eta ^* = \frac{r_{s} \zeta (1+z)^{2}}{\mathcal{{R}} \hbox {d}_{\mathrm{L}}} \end{aligned}$$

(37)

If $\eta < \eta ^*$, then photosphere forms in the coasting phase and otherwise in the accelerating phase.

In the coasting phase, the photospheric radius is given by equation (20) and substituting it in equation (36) gives the expression for Lorentz factor, $\Gamma \equiv \eta$

$$\begin{aligned} \Gamma = \left( \zeta (1+z)^2 \, d_L \frac{Y F_\mathrm{tot}}{2m_p c^3 \mathcal {R}}\right) ^{1/4} \end{aligned}$$

(38)

where Y is the ratio of observed $\gamma -$ ray luminosity to the total burst luminosity and $F_\mathrm{tot}$ is the total observed $\gamma -$ ray energy flux. Including the relation between co-moving temperature ($T'$) and observed temperature, T (equation (18)) in the equation (36), we can deduce the expression for the nozzle radius of the jet to be

$$\begin{aligned} r_0 = \phi \frac{d_L}{(1+z)^2} \left( \frac{F_\mathrm{BB}}{\epsilon _\mathrm{BB} Y F_\mathrm{tot}}\right) ^{3/2} \mathcal {R}\, \Gamma _0 \end{aligned}$$

(39)

where $\phi$ is a numerical factor of order unity, $\epsilon _\mathrm{BB}$ is the fraction of the burst l luminosity that is thermalised at the radius, $r_0$ and $\Gamma _0$ is the Lorentz factor of the outflow at $r_0$.

The time resolved spectral analysis of GRBs allows to determine the temporal variation in the spectral properties. Based on the blackbody component that was detected in the time resolved spectra of the GRBs, time dependent variation of the outflow parameters were studied in Iyyani et al. (2013), Preece et al. (2014), Iyyani et al. (2016), Larsson et al. (2011), Guiriec et al. (2013). The two important results of the study are the following: (i) Lorentz factor, $\Gamma$ of the outflow was found to decrease monotonously with time across a GRB pulse of emission (Fig. 14a). This could be related to either a decrease in the burst luminosity or an increase in the baryonic mass of the outflow with time. (ii) The nozzle radius of the jet was also found to increase from close to the event horizon of the black hole or magnetar surface ($10^6 - 10^ 7 \, \mathrm{cm}$) to a radius of $10^9 - 10^{10}\, \mathrm{cm}$ which is close to the expected surface core of a Wolf–Rayet progenitor star (Fig. 14b). This rise could be due to increased dissipation and efficient photon production occurring in the region below the thermalisation radius as oblique/collimation shocks are created as the jet pierces through the star. Beyond the stellar core, there is no further collimation shocks, thereby causing the $r_0$ to not increase any further, instead decrease or remain nearly steady.

If the photosphere forms in the accelerating phase ($\eta > \eta ^*$), then the corresponding estimates of the outflow parameters are given as follows

$$\begin{aligned} \eta&= \left( \frac{\phi \sigma _T}{6 m_p c^3 \mathcal{{R}}}\right) ^{1/4} d_L^{1/4} (1{+}z)^{1/2} \frac{YF_\mathrm{tot}}{(YF_\mathrm{tot}{-}F_\mathrm{BB})^{3/4}}, \end{aligned}$$

(40)

$$\begin{aligned} r_\mathrm{ph}&= \left( \frac{\sigma _T \mathcal{{R}}^3}{6m_pc^3 \phi ^3}\right) ^{1/4} \frac{d_L^{5/4} (YF_\mathrm{tot}{-}F_\mathrm{BB})^{1/4}}{(1{+}z)^{3/2}}, \end{aligned}$$

(41)

$$\begin{aligned} \Gamma _\mathrm{ph}&= \left( \frac{\phi \sigma _T}{6 m_p c^3 \mathcal{{R}}}\right) ^{1/4} d_L^{1/4} (1{+}z)^{1/2} (YF_\mathrm{tot} {-}F_\mathrm{BB})^{1/4}, \end{aligned}$$

(42)

see Bégué & Iyyani (2014) for more details. Above discussed estimates of outflow parameters are valid when the outflow is baryonic dominated. However, it is also possible to have a Poynting (magnetic) dominated outflow or may be a hybrid outflow with significant contribution from both baryonic as well as magnetic constituents to the jet. In such a scenario, the possible estimates of the outflow parameters are discussed in Gao & Zhang (2015).

There are several other techniques that are used to estimate or place limits on the Lorentz factor of the outflow. They are as follows: (i) The common method is to use the highest energy observed photon (e.g GeV photons) to place a lower limit on $\Gamma$. The method basically assumes that both the GeV as well as the MeV emission originates from the same region in the outflow, and thereby use the condition of what minimum $\Gamma$ is required to prevent $\gamma -$ ray pair attenuation thereby leading to the observation of GeV photons (Lithwick & Sari 2001). However, this gives estimates of very large Lorentz factor $\Gamma > 1000$ (Abdo et al. 2009a, b). (ii) As a remedy to the assumption made in the above case, in Zhao et al. (2011), Zou et al. (2011), Hascoët et al. (2012), they considered that GeV and MeV emission came from different regions in the outflow and then estimated the values of $\Gamma$, which were found to be lower than the previous case. (iii) An estimate of $\Gamma$ is also made from the deceleration timescale of the forward shock which can be related to the peak of the optical or X-ray afterglow light curves. Unfortunately, this method is not always applicable as afterglow is not always observed and in some cases by the time X-ray observations start the peak of the light curve would have been crossed, thereby giving only upper limits on the $\Gamma$ (Sari & Piran 1999; Molinari et al. 2007; Liang et al. 2010). (iv) In Zhang et al. (2003), an estimate of $\Gamma$ is obtained by constraining the forward and reverse shock components in the early optical afterglow emission. (v) In Zou & Piran (2010), they assess the contribution of forward shock emission during the observation of prompt emission, by looking at the deep minima/ dips between the various peaks observed in the prompt emission light curves. This assessment gives an upper limit on $\Gamma$.

Thus, the outflow parameters of the GRB jet are inferred based on different model assumptions.

7 Polarisation

Inspite of the extensive observations and theoretical modelling of GRB emission, many key questions regarding jet composition, radiation mechanism, geometry of the jet structure etc still remain elusive. In the previous section, we discussed about the emission models that are employed to explain the observed GRB radiation. Currently, there exists degeneracy between these various emission models in the explanation of GRB spectra. Therefore, it is important to devise a way forward that can break this degeneracy as well. One key way is to directly analyse the GRB spectrum using the proposed physical models rather than by using any empirical function. However, this process can be computationally very intensive as well as time consuming. Therefore, there exists a need to have more constraining observables from observations such as polarisation measurements of GRBs, which can be crucial to further our understanding about GRBs.

Table 1 List of GRBs and their polarisation fractions reported till to date are shown.

The polarisation property of the incoming X-ray or $\gamma -$ ray radiation is yet to be well studied observationally. Several attempts of $X-$ ray and $\gamma -$ ray polarimetry measurement of GRBs have been made using instruments like Compton imaging Telescope (COMPTEL) (Schönfelder et al. 1993; Lei et al. 1996) and BATSE (Paciesas et al. 1989; McConnell et al. 1996) instruments onboard CGRO, Ramaty High-Energy Solar Spectroscopic Imager (RHESSI) (McConnell et al. 2002), Imager on Board the INTEGRAL Satellite (IBIS) (Forot et al. 2007) and Spectrometer on INTEGRAL (SPI) (Chauvin et al. 2013; Kalemci et al. 2004) onboard INTEGRAL, GAmma-ray Polarimeter (GAP) onboard IKAROS, Cadmium Zinc Telluride Imager (CZTI) (Rao et al. 2017) onboard Astrosat, and POLAR (Kole 2018). Among them, GAP and POLAR are the only instruments which have been specifically designed to measure gamma ray burst polarisation in the energy range $70-300$ keV and $50 -500$ keV respectively. Since May 2014, GAP instrument is only partially in observation mode and therefore, there has been no observations reported since then. Recently, CZTI instrument has made polarisation measurements of several GRBs since its launch in September 2015. The pixellated nature of the instrument enables its usage for Compton polarimetry (Vadawale et al. 2015, 2018; Chattopadhyay et al. 2014).

In Table 1, GRBs whose polarisation measurement has been reported till to date are listed. Until now, most of the observations suffer from limited statistical significance, thereby preventing us from making any coherent conclusion about the GRB radiation process. the estimates of the polarisation fraction hint towards high values.

7.1 Technique of polarisation measurement

In the high energy range of keV - MeV, where most of the GRB photons are detected, Compton scattering is the dominant means of photon interaction. In Compton scattering, the photons tend to scatter at right angles to the incident electric field vector. Thus, once the direction of scattered photon is recognised, one can infer the direction of the incident electric field vector. Therefore, the challenge of any instrument is to measure the azimuthal distribution of the scattering photons. This is achieved by determining the energies of both the scattered photon as well as the scattered electron. This thereby requires the polarimeter to consist of two main detectors where the first detector acts as the scattering detector and the second detector acts as the calorimeter where the full energy of the scattered photon is absorbed (Lei et al. 1997). The locations of both the detectors and the direction of incoming $\gamma -$ rays give the direction of scatter. The identification of these Compton scattered events require a definition of coincidence timing where two detector elements trigger within a small window of time. Smaller coincidence windows can rule out false selections in case of bright events. Thus, the aim of the Compton polarimeter is to measure the azimuthal distribution of the Compton scattered photons in the detector plane. Since the polarisation properties are estimated from these Compton events, the statistical significance of the result basically depends on how many such events are identified during the observation. The Klein-Nishina cross section of the Compton scattering is given by

$$\begin{aligned} \frac{d \sigma }{d \Omega } = \frac{r_0*^2}{2} \left( \frac{E'}{E_0}\right) ^2 \left( \frac{E_0}{E'} +\frac{E'}{E_0} - 2 \mathrm{sin}^2 \theta \mathrm{cos}^2 \phi \right) \end{aligned}$$

(43)

where $E_0$ and $E'$ is the energy of the incident and scattered photons respectively, which are related by

$$\begin{aligned} \frac{E'}{E_0} = \frac{1}{1+\left( \frac{E_0}{mc^2}\right) (1-\mathrm{cos}\theta )} \end{aligned}$$

(44)

where $\theta$ is the Compton scatter angle from the incident direction, and $\phi$ is the azimuthal scatter angle measured between the plane of scattering (detector plane) and the plane containing the incident direction of the photon and the polarisation vector. For a given $\theta$, the scattering cross section is minimum at $\phi =0$ and is maximum at $\phi =90^{\circ }$. In other words, the photons tend to scatter in a direction perpendicular to the polarisation vector. If incident radiation is polarised, then the distribution of scattered photons about $\phi$ would be non-uniform and modulated as $\mathrm{cos}^2 \phi$.

After including the geometrical corrections based on the corresponding distribution obtained for an unpolarised radiation, the measured azimuthal count rate of scattered photons is modelled by the function

$$\begin{aligned} C(\phi ) = A \, \mathrm{cos}\left( 2 \left( \phi - \phi _0 +\frac{\pi }{2}\right) \right) + \mathrm{B} \end{aligned}$$

(45)

where $\phi _0$ is the polarisation angle, A and B are constants which corresponds to $(C_{max} - C_{min})$ and $(C_{max}+ C_{min})$ respectively, where $C_{max}$ and $C_{min}$ are the maximum and minimum of the modulation curve. Thus, the modulation factor of the polarised emission is given by

$$\begin{aligned} \mu =\frac{A}{B} \end{aligned}$$

(46)

Finally, to get the measure of the polarisation of the source, modulation factor ($\mu _{100}$) for a 100$\%$ polarised source of the same intensity as that of our source of interest, coming from the same direction in the sky is measured in the instrument. This is generally done by Monte Carlo simulations. This gives the measure of polarisation fraction to be

$$\begin{aligned} {\mathrm{PF}} = \frac{\mu }{\mu _{100}} \end{aligned}$$

(47)

The minimum detectable polarisation (MDP) defines the sensitivity of the instrument towards polarisation for a given source of count rate, $C_{s}$, instrumental background, $C_{bkg}$, instrument systematics parameterised in $\mu _{100}$ and observation time, t, is given by

$$\begin{aligned} \mathrm{MDP(\%)} = \frac{4.29}{\mu _{100} \hbox {C}_\mathrm{s}} \sqrt{\frac{2(C_{s} + C_{bkg})}{t}} \end{aligned}$$

(48)

Non-trivial systematic effects are produced when the GRBs are observed off axis to the detector which can result in false modulation signatures in the data. Even for an unpolarised signal, a positive modulation is expected in the detector (Muleri 2014). Therefore, proper pre-fight calibrations, detailed Monte Carlo simulations taking into account the instrument asymmetries, proper choice of coincidence events etc, as well as strong signal to noise ratio of the event are essential for a credible measurement of GRB polarisation. Thus, GRB polarisation measurement is highly challenging.

7.2 Theoretical predictions of different emission models

Synchrotron emission is inherently linearly polarised in nature. With respect to GRBs, two different scenarios are considered. Firstly, the synchrotron emission is expected to be produced by the relativistic electrons which are cooling within a globally ordered magnetic fields which is likely to originate from the central engine. Magnetic fields anchored to a rotating central engine is generally expected to result in a dominant toroidal magnetic field component (i.e magnetic field lines are perpendicular to the direction of expansion) at larger distances. In such a case there exists a symmetry of field lines across the jet axis. So, polarisation is observed when an anisotropic configuration is achieved. This can be attained when GRB jet is wide (i.e $\Gamma \theta _j > 1$), has a top-hat profile and is viewed off the jet axis (i.e $q >0$).

For a Band function like spectrum, the local polarisation degree (or maximum measurable polarisation degree) is given by

$$\begin{aligned} \mathrm{PF}_0^\mathrm{sync}&= (\alpha + 1)/(\alpha + 5/3) \, \hbox {for x } < (\alpha - \beta ) \end{aligned}$$

(49)

$$\begin{aligned}&= (\beta + 1)/(\beta + 5/3) \, \hbox {for x } > (\alpha - \beta ) \end{aligned}$$

(50)

where $x = E/E_{break}$. The measured polarisation degree, however, depends on the geometry of how much part of the emitting region (parameterised by $y_j = \theta _j/(1/\Gamma )$), as well as how the jet is viewed (parameterised by $q = \theta _v/\theta _j$). Thus, the measurable polarisation degree, $\mathrm{PF}$, in the energy range [E1, E2] is calculated by integrating the local polarisation degree over the geometrical parameters of $y_j$ and q, see Toma et al. (2009) for more details. This results in the observed polarisation fraction to be less than $\mathrm{PF}_0^\mathrm{sync}$ . In a highly ordered magnetic field, a slow and fast cooling synchrotron emission of $\alpha = -2/3$ and $-3/2$ gives $\mathrm{PF}_0^\mathrm{sync} = 50\% \, \mathrm{and} \, 70\%$, and a measurable polarisation of $\mathrm{PF} = 40\% \, \mathrm{and} \, 60\%$ when $0<q<1$ and $y_j=1$ respectively (Granot 2003).

Secondly, synchrotron emission is also expected to be produced in internal shocks where the magnetic field orientations are random on a scale less than the plasma skin depth (Medvedev & Loeb 1999). As a result, within the jet cone, around the line of sight of the observer, the emission is expected to be symmetric even when $q > 0$, thereby resulting in low polarisation fraction. Here, high polarisation fraction can be obtained only when the symmetry of emission around the line of sight is broken. This happens when the observer views the jet either along or outside the jet edge. This results in strong asymmetry in emission within the view cone of $1/\Gamma$ which results in net polarisation of $\mathrm{PF} \sim 40\%$ when $q >1$, $y_j=1$, $\alpha = -0.2$, and $\beta = 1.2$ (Toma et al. 2009).

Inverse Compton scattering (Compton drag, CD) is an alternate radiation mechanism advocated for GRB emission. Here also there is a symmetry of local polarisation angles around the line of sight of the observer, thereby resulting in null polarisation along the jet axis as well as within the jet cone. This radiation mechanism, thus, also requires an off axis viewing of the jet in order to break the symmetry of emission within the view cone to result in a net polarisation fraction $>0$. The local polarisation degree is given by

$$\begin{aligned} {\mathrm{PF}}_0^\mathrm{CD} = \frac{1-\mathrm{cos}^2 \theta }{1+\mathrm{cos}^2 \theta }. \end{aligned}$$

(51)

Here the local polarisation degree has no dependence on the frequency/energy. For $y_j=1$ and $q>0$, a polarisation fraction of $\mathrm{PF} \sim 70\%$ is achieved (Toma et al. 2009).

Emission from the photosphere is dominated by scattering of photons from electrons. It was shown by Beloborodov (2011) that if the co-moving photon field possess some anisotropy then the scattered emission observed will be polarised. Thus, it was found that in a radiation dominated regime (i.e accelerating phase) the emission from the photosphere is a blackbody and is not expected to be polarised. However, in a matter dominated regime (i.e coasting phase), the co-moving photon field close to the photosphere was found to achieve an anisotropic distribution which thereby can result in polarised emission. However, it is key to note that if the detector is unable to spatially resolve the source (which is generally the case), the net polarisation is expected to be low or null, because of the symmetry of emission that exists around the line of sight. Thus, in photospheric emission also, polarised emission can be expected if the jet emission is viewed off axis, thereby breaking the symmetry. It was shown by Lundman et al. (2014) that photospheric emission can attain a maximum polarisation fraction of $\mathrm{PF} \sim 40\%$ in case of a structured wide jet when viewed off axis.

Recently, it was shown by Lundman et al. (2018) that in case of photospheric emission with subphotospheric dissipation produces polarised emission only at lower energies, much below the spectral peak where the emission is . At the same time, polarisation of the spectral peak is not expected as it is formed at high optical depths where the co-moving photon field is highly isotropic. Thus, in this model, measured polarisation fraction has anti-correlation with energy. For example, in case of GRB160802A, CZTI detected a high polarisation fraction of $85 \pm 30\%$ in the energy range 100-400 keV (Chand et al. 2018). The spectral analysis of the first episode of the GRB found a Band function fit to the data with parameters $\alpha > -0.67$ and a spectral peak of $200-400$ keV. Hard $\alpha$ values ruled out the possibility of optically thin synchrotron emission. Thus, the spectrum was best explainable using subphotospheric dissipation model. However, the spectral peak, which was well constrained within the energy window of CZTI showed such high polarisation which is not expected within this model. Combining both spectral and polarisation measurements of the GRB, it was more plausible that the jet whose emission was due to subphotospheric dissipation was viewed along the boundary of the jet with its emission dropping drastically along its edge. Thus, the observed polarisation was due to observing geometry rather than due to the intrinsic emission process. This observation was thus in line with Waxman (2003), where it was suggested that in case of a top hat jet a high polarisation can be expected when viewed along the jet edge which can produce strong asymmetry in emission within the viewing cone.

When there would be enough number of polarisation measurements, collectively these data can be a diagnostic for the radiation process. As shown in Toma et al. (2009), a differentiation can be observed between the trends in PF versus spectral peak of the GRBs and possible values of PF for different radiation processes. Thus, polarisation can be the constraining observable that can help identify the different emission process as well as the jet geometry of a GRB.

8 Summary and conclusions

Ever since their discovery in 1967, GRBs have been extensively studied, however, it largely remains a mystery until today. Having said that over the last few decades, we have gathered a lot of information regarding the prompt and afterglow spectra of GRBs via both space and ground based observatories. At the same time various theoretical models have been developed in depth to understand these spectra.

GRB spectrum was generally modelled using a Band function alone, which was reasonable to certain extent provided the limited energy window and sensitivity of the observations that were made using BATSE. With the launch of Fermi and Niel Grehels Swift observatories and co-ordinated multi-wavelength observations, there have been an unprecedented improvement in spectral data coverage over wider energy range as well as in improved localisation and determination of redshifts of GRBs. This has certainly enhanced our knowledge base about the variety that exists in both spectrum as well as light curves of the GRBs. This eventually has lead to multi-component spectral analysis, thereby suggesting that Band function alone is not sufficient to model the GRB spectra. Thus, Band function may be just a general representative of an overall shape of GRB spectrum where the spectral features are not evident due to poor photon statistics. This has triggered several theoretical endeavours to explain these observed spectral shapes and features.

Most important advancement has also come in our understanding that a simple optically thin synchrotron emission model face difficulties to explain the GRB spectrum self-consistently. This has lead to consider more realistic physical models of synchrotron emission such as including time dependent cooling of electrons (Burgess et al. 2018) as well as decaying magnetic fields (Uhm & Zhang 2014; Zhang et al. 2016), which have been shown to explain most of the observed GRB spectra. On the other hand, this has also lead to renewed interest in different types of photospheric emission models. It readily solves or alleviates many of the problems that non-thermal emission models face such as radiation efficiency, hard spectral slopes, etc. At the same time the photospheric models cannot explain very high energy emission such as those observed in GeV energy range, which requires some form of non-thermal emission mechanism. Thus, a hybrid model which is a combination of both photospheric as well optically thin non-thermal models have been used to explain the data. Currently, we are at a juncture where degeneracy has come between various emission model explanations, which needs to be broken. A way forward is to conduct direct testing of the proposed physical models to the data instead of approximate empirical functions (Burgess et al. 2014; Ahlgren et al. 2015). However, this can be very time consuming as well as computationally intensive. At the same time, proposed physical models should have clear predictions which can be tested against observations.

Another important advancement is the attempt of polarisation measurement of GRB emission via instruments like INTEGRAL, GAP, CZTI and POLAR. There has been no statistically significant observation made till to date due to poor statistics and insufficient understanding of the instrument systematics. However, in future with dedicated polarimetric instruments for GRBs, it is more likely to make some credible measurements which will be crucial in narrowing down the possible emission models.

With the advent of multi-messenger astronomy such as the historic detection of gravity waves coincident to short GRB170817A (Abbott et al. 2017a), as well as detection of neutrinos from a flaring blazar (Keivani et al. 2018), have brought the study of GRBs more into the limelight of high energy astrophysics. Even though the progenitor of short GRBs are merging compact objects in contrast to long GRBs, the radiation physics of both prompt and afterglow are expected to be remain the same. GRBs being the most energetic explosions known to occur in the Universe, are therefore considered to be potential sources or sites where ultra-relativistic cosmic rays and neutrinos are produced (Samuelsson et al. 2018). However, there has been no successful detection made yet. The better understanding of radiation physics and correspondingly the correlations between intensity and spectral peak can enable GRBs to become standard candles to understand cosmology as well.

Thus, the study of gamma ray burst is at a most exciting epoch where the event can be studied just not across the different wavelengths of electromagnetic spectrum, but even by different carriers of information like gravity waves and neutrinos. This is definitely promising to unlock the mystery regarding the prompt emission as well as shed light on related physics issues such as acceleration process, stellar evolution, etc., in the coming decade.