1 Introduction

Interactive design and manufacturing as a novel paradigm can integrate user expectations in the product development process, allowing the designer to interact with the virtual product and its environment [1]. Interactive product design is a major economic and strategic issue in innovative products generation. It allows a better definition of the design problem and, finally, it introduces the phase of specification definition. The designers and manufacturing engineers usually attempt to find an optimal design to reach the product with high quality at the minimum cost. Process tolerance design can be carried out as an interactive design tool which plays an important rule on the cost and quality of products.

In manufacturing processes, processed dimensions are often deviated from nominal values vary within specific intervals. Tolerances can be specified to control the actual dimensions of processed features within allowable variation zones [2]. In process tolerance design, manufacturing engineers and process planning experts determine the manufacturing processes, the machine tools, the fixtures, and process tolerances [1]. Many researchers have done considerable researches on the optimal tolerance allocation based on the least-cost tolerancing issue [3,4,5,6]. In these studies, the manufacturing cost has been considered as the cost function of optimal tolerance design problems. In the literature, the several cost- tolerance relationships have been reported [6]. Jeang [7] presented a method to allocate optimal tolerances of a mechanical assembly by minimizing the total cost by using the response surface methodology (RSM) approach on the experimental data. Choi et al. [8] presented an approach for the optimal tolerance design by minimizing a combined single objective optimization problem including the cost and the Taguchi’s loss functions. Prabhaharan et al. [9] proposed a method to allocate the optimal tolerances based on the minimum cost and shifting the nominal dimensions to the less sensitive portion. Based on the proposed method, a continuous Ants colony algorithm has been used as an optimization tool. Wang et al. [10] proposed an optimal tolerance allocation methodology based on the fuzzy concept. Etienne et al. [11] proposed a method to allocate the functional tolerances for providing the best ratio between functional performances and manufacturing cost based on a genetic algorithm. According to this method, the process selection is carried out by a constraint satisfaction algorithm. Wu et al. [12] presented a method for minimization of the manufacturing costs subject to the geometrical requirements based on the Monte Carlo simulations and the genetic algorithm approaches. Mao et al. [13] presented a method to the robust design of tolerances design established upon the minimum cost of manufacturing. The corresponding constraints are related to select suitable manufacturing processes. Huang and Zhang [14] presented a minimized cost based method for robust design of tolerances of the mechanisms with joint clearances through the Taguchi method. Khodaygan et al. [15] introduced a method for tolerance analysis and allocation mechanical assemblies with all types of dimensional tolerances established upon on the fuzzy theory and small degrees of freedom concepts. Shen et al. [16] proposed a method for optimal product and tolerance design in terms of the quality loss function through a linear model. González and Sánchez [17] presented a method for the concurrent optimization of design centering and tolerances which it takes into account the correlations of the variables due to the manufacturing process. Lee and Kwon [18] proposed a conservative multi-objective optimization for considering design robustness and tolerances based on the signal to noise (S/N) and design of experiment concepts. Din et al. [19] proposed a CAD-based approach for tolerance allocation to individual part dimensions to achieve specified tolerances on the assembly dimensions. In this method, the sensitivities of product dimensions are estimated by varying the parameters in the CAD model. Khodaygan and Movahhedy [20] presented an evolutionary based approach for the robust tolerance design of mechanical assemblies through a multi-objective optimization formulation. They (2014) proposed a method to extend the conventional process capability for developing a computational tool for analysis of the functional quality of a mechanical product [21]. Based on the proposed indices which have been called functional process capability indices, a statistics-based process capability analysis method can be used to estimate the ability of a manufacturing process for meeting the functional requirements of a mechanical system. Etienne et al. [22] proposed a method for the key indicators assessment to the relevance of variation management in the product development. According to this method, tolerances are optimized for balancing the quality level of the product and the production cost.

The interactive design approach is a process which contains the cognitive or physical interactions between the designers and the virtual/physical product at corresponding environments and human–computer interactions in all steps of the design process from customer’s needs to the final real physical product. Products result from a complex design process that involves knowledge across the technical, economic, social and corporate objectives [23]. Interactive product design is a major economic and strategic issue in innovative products generation. In interactive design, the creation of a product is considered by three factors: the experts’ knowledge, the end-user satisfaction and the realization of functions [24]. Interactive and integrated design approaches by supplying efficient solutions from an analysis of cognitive or physical interactions can be used as a great helpful tool for designers [25]. Design methods such as evolutionary approaches and optimization are improved to help designers. In other words, the latest developments in product design and simulation, computer-aided design, and computer-aided process planning and computer aided tolerancing are related to the need for industrial agility [25]. The designers and manufacturing engineers usually attempt to find an optimal solution to reach the product with maximum quality and the minimum cost. In today’s competitive environment, the need to produce the part with better quality and low cost is necessary. This leads to conquering of the target market and the satisfaction of customers [24].

The computer aided tolerance design is a computational approach, not only as a simply checking tool in downstream stages but also as a powerful tool for interactive and responsive designs can be used in the early stages of the design and manufacturing process. The cognitive or physical interactions between the real physical and the virtual objectives and human-computer interactions at several steps of the optimal process tolerance design can be efficiently integrated within the proposed CAD-based method. The proposed method as a computer aided design tool can be interactively used to support the engineering analysis through determining the optimal process tolerances for minimization of manufacturing cost and maximization the product quality by optimal planning the manufacturing processes at the early stage of the design.

In this paper, a new method to allocate the optimal process tolerances of the mechanical is presented. The manufacturing cost and product quality are usually considered as conflicting objectives. According to the proposed method, the optimal process tolerances of components are allocated through a multi-objective optimization problem where the process capability function and the overall manufacturing cost should be simultaneously optimized. To derive the proper objective functions in terms of the individual process capabilities, the new formulations for describing the process capability and manufacturing functions are proposed. After formulating the optimal tolerance allocation procedure in a multi-criteria optimization problem, the NSGA-II algorithm is used for solving it. Consequently, the best solution from all of the feasible alternatives in the Pareto front can be selected from Shannon‘s entropy-based TOPSIS. According to this method, the decision making the procedure to select the best solution from the optimal Pareto front is automatically carried out without the need to determine the criteria weightings. Based on the proposed method, determining the optimal process tolerances of the virtual model in the design stage to reach a real production with higher quality and the lower cost can be an effective approach to success in the competitive environment of manufacturing companies.

The paper is organized as follows; In Sect. 2, the main steps of the proposed approach are presented in details. In Sect. 3, to illustrate the capability of the proposed method into optimal process tolerance design, a case study is considered. Finally, the paper followed by the conclusions in Sect. 4.

2 The proposed interactive optimal process tolerance design method

Generally, in the product design, the analysis, simulation, and optimization of the product are carried out as key operations to find the optimal design which satisfies the functional and customer’s requirements [26]. In the interactive design, the creation of a product can be considered by three factors: the experts’ knowledge, the end-user satisfaction and the realization of functions [27].

In general, tolerance design should be interactively carried out through a computerized process. Optimal tolerance design approaches usually be failed because that the sequence of the manufacturing processes must be planned prior to the tolerance design. In order to overcome this weakness, the interactive tolerance design can be used for the computer aided process planning. Since the proposed algorithm can be simply automated for use within CAD/CAM software, based on the human–computer interactions, it can be utilized as a useful interactive tool in the design stage for multi-objective optimal tolerance design. Based on the interactive tolerance design, product designers will not have to redraw components of the mechanical assembly or redesign geometrical features and dimensional characteristics. By optimally allocating the process tolerances of the virtual product model in the design stage, the quality and cost of the real product can be simultaneously optimized. Therefore, the interactive computer-aided tolerance design can be used as an efficient strategy to satisfy the design, manufacturing, and assembly requirements and customer’s needs in today’s concurrent engineering environment.

To demonstrate the position of the proposed optimal tolerance design method as an interactive approach in the product development design procedure, Fig. 1 is presented. The cognitive or physical interactions between the designers and the virtual product and human–computer interactions in all steps of the tolerance design process from the customer’s needs to the final real physical product are shown in Fig. 1. Also, the key roles of the experts’ knowledge, the end-user satisfaction and the realization of functions in the interactive optimal tolerance design and the computer-aided decision making during the product development procedure are illustrated in Fig. 1.

Fig. 1
figure 1

The main interactions between real physical and the virtual objectives in the proposed method as an interactive design approach

Full size image

In this section, the algorithm of the proposed method to optimal process tolerance design of the mechanical systems is introduced. Generally, the proposed method can be presented in the following steps:

  • Step 1 Extracting the design function from the CAD model

  • Step 2 Formulating the process capability function in terms of individual process indices

  • Step 3 Formulating the manufacturing cost function in terms of individual process indices

  • Step 5 Formulating the optimal tolerance allocation as a multi-objective optimization problem

  • Step 6 Solving the multi-criteria optimization problem by the NSGA II method

  • Step 7 Automated decision making for selecting the best tolerances from the optimal Pareto front

The main steps of the proposed algorithm are described in details as follows;

2.1 Extracting the design function from the CAD model

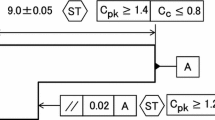
In the first step of the optimal process tolerance design algorithm, the designer should specify the functional and the design variables. The design specifications usually are dependent on the inherent characteristics of the system. Therefore, the dimensional and geometrical deviations of the effective variables due to several sources can directly affect the functionality of a mechanical system. Generally, in a mechanical system, the variables that can be independently varied and their variations should be controlled by individual tolerances in the allocation procedure, are considered as the processed dimensions (\(\mathrm {x}\)). In Fig. 2, the individual parts of a wheel assembly (see Fig. 3) and the processed dimensions with dimensional and geometric tolerances are shown. On the other hand, variables which are dependent on the system functionality and their variations are related to tolerances of the design variables can be considered as the functional specification (\(\mathrm {y}\)). For example in Fig. 3, the vertical distance of shaft axial with respect to the base (the datum A in Fig. 2) of the wheel assembly is considered as the functional specification (\(\mathrm {y}\)) and its tolerance can be investigated as a functional or assembly tolerance (\(t_{y}\)).

Fig. 2
figure 2

The individual parts and the processed dimensions with dimensional and geometric tolerances

Full size image
Fig. 3
figure 3

The wheel assembly and its functional variable

Full size image

Generally, the design function as a mathematical relationship that relates the functional variable(s) to the design variables can be parametrically extracted from CAD model (virtual environment of software) in the implicit or explicit form. In some cases, it can be straightforwardly derived from the 2D sketch. But, in some cases, it may be obtained from a complex iterative approach such as Monte Carlo simulations. However, it can be generally described in explicit form as follows:

$$\begin{aligned} y=f(x_{1},\ldots ,x_{n}) \end{aligned}$$
(1)

where \(x_{i}\) indicate ith design variable as the random variable and y is functional variable. The mean of the functional variable (y) can be obtained from

$$\begin{aligned} \mu _{y}=f(\mu _{x_{i}},\ldots ,\mu _{x_{n}}) \end{aligned}$$
(2)

where \(\mu _{x_{i}}(i=1,\ldots ,n)\) and \(\mu _{y}\) are mean values of the random variables and the functional variable, respectively. The target value of the functional variable (\(T_{y}\)) can be individually specified as a design or customer’s requirement (from the real world) or can be estimated based on the target values of design variables (\(T_{x_{i}}\)) in the computational environment. Based on the obtained design function, the target of functional variable (y) can be computed as follows

$$\begin{aligned} T_{y}=f(T_{x_{i}},\ldots ,T_{x_{n}}) \end{aligned}$$
(3)

where \(T_{x_{i}}(i=1,\ldots ,n)\) and \(T_{y}\) are the target values of the effective random variables and the functional variable, respectively.

To perform a linearized error analysis, the function f, usually called the design function, is linearized about the nominal values of the variables, using Taylor’s series expansion. The partial derivatives of the contributor \(\partial f/\partial x_{i}\) are the sensitivity factors can be determined from the design function.

Similar to the target value of the functional variable, the lower and upper specifications of the functional variable can be individually specified as a design or customer’s specifications or may be computed based on the lower and upper specifications of design variables. Since the lower and upper specifications of independent variables according to the sign of sensitivity coefficient of independent variables as processed dimensions (\(x_{i}\)) can affect the lower and upper specifications of the functional variable (y), respectively, the lower and upper specifications of the functional variable can be computed based on the lower and upper specifications and the sign of sensitivities of the effective variable (\(x_{i}\)) as follows

$$\begin{aligned} {{\textit{USL}}}_{y},{{\textit{LSL}}}_{y}= & {} y((\left( {{\textit{USL}}}_{1}+{{\textit{LSL}}}_{1} \right) \nonumber \\&\pm \, {{ sign}}\left( \frac{\partial f}{\partial x_{1}} \right) \left( {{\textit{USL}}}_{1}-{{\textit{LSL}}}_{1} \right) )/2,\ldots ,\nonumber \\&(\left( {{\textit{USL}}}_{n}+{{\textit{LSL}}}_{n} \right) \pm {{ sign}}\left( \frac{\partial f}{\partial x_{n}} \right) \nonumber \\&\times \left( {{\textit{USL}}}_{n}-{{\textit{LSL}}}_{n} \right) )/2) \end{aligned}$$
(4)

where \({\textit{LSL}}_{y}\) and \({\textit{USL}}_{y}\) are the lower and upper specifications of the functional variable (y), respectively. \({{ sign}}\left( \partial f/\partial x_{i} \right) \) indicates the sign of sensitivity coefficient of ith design variable (\(\partial f/\partial x_{i})\).

After linearization, both worst-case and statistical analysis can be used [28]. Many experiments and manufacturing processes rely on assumption of the normal distribution. In practice, the assumption of normality is a reasonable one to make in the tolerance design procedure. Assuming that the component feature dimensions are independent and normally distributed, The Taylor series expansion of the nonlinear functional function yields

$$\begin{aligned} {\upsigma }_{y}=\left\{ \sum \limits _{i=1}^n \left\{ \left( \frac{\partial f}{\partial x_{i}} \right) {\upsigma }_{i} \right\} ^{2} \right\} ^{1 / 2} \end{aligned}$$
(5)

where \({\upsigma }_{y}\) is the standard deviation of the functional dimension and \({\upsigma }_{i}\) is standard deviation of the ith component dimension as \(x_{i}\) and \(\partial f/\partial x_{i}\) is the sensitivity of y to the contributor \(x_{i}\).

The proposed method is capable of handling the mechanical assemblies with linear and non-linear assembly functions for allocating optimal process tolerances. However, as the major limitation of the proposed method, its efficiency is contingent upon the assumption of normality and independence of component tolerances.

2.2 Formulating the process capability function in terms of individual process indices

In general, the process capability index compares the natural variability of a process. Process capability indices (PCIs) are extensively used to determine whether a process is capable of producing objects within customer specification limits or not. Process capability analysis has always been a very important engineering decision tool in practice. The index \(C_{\textit{pmk}}\) alerts the user when the process variance increases and the process mean deviates from its target value [29]. The index \(C_{\textit{pmk}}\) is defined as

$$\begin{aligned} \mathrm {C}_{\textit{pmk}}=\frac{d-\left| \mu -m \right| }{3\left\{ \sigma ^{2}+{(\mu -T)}^{2} \right\} ^{1 / 2}} \end{aligned}$$
(6)

\(m=({\textit{LSL}}+{\textit{USL}})/2\) is the mid-point between the lower and the upper specification limits and \(d=({\textit{LSL}}-{\textit{USL}})/2\) is the half specification width, and \({\textit{LSL}}\) and \({\textit{USL}}\) are the lower and upper specification limits of the functional requirement y, respectively.

The sample process standard deviation based on process capability index \(C_{\textit{pmk}}\) can be written as

$$\begin{aligned} S_{\textit{pmk}}^{2}=\left( \frac{d-\left| \mu -m \right| }{3C_{\textit{pmk}}} \right) ^{2}-{(\mu -T)}^{2} \end{aligned}$$
(7)

The sample process standard deviation (Eq. 7) can be substituted into the statistical model relation (Eq. 5). Therefore, the sample process standard deviation of functional parameters based on individual process capability indices (\(C_{{\textit{pmk}}_{i}})\) can be written as

$$\begin{aligned}&S_{{\textit{pmk}}_{y}}\nonumber \\&\quad =\sum \limits _{i=1}^n \left\{ \left( \partial f/\partial x_{i} \right) ^{2}\left( \left( \frac{d_{i}-\left| \mu _{i}-m_{i} \right| }{3\,{C_{\textit{pmk}}}_{i}} \right) ^{2}-{(\mu _{i}-T_{i})}^{2} \right) \right\} ^{1 / 2}\nonumber \\ \end{aligned}$$
(8)

According to Eq. 6, the functional process capability \(\mathrm {C}_{{\textit{pmk}}_{y}}\) can be written as

$$\begin{aligned} \mathrm {C}_{{\textit{pmk}}_{y}}=\frac{d_{y}-\left| \mu _{y}-m_{y} \right| }{3\left\{ S_{{\textit{pmk}}_{y}}^{2}+{(\mu _{y}-T_{y})}^{2} \right\} ^{1 / 2}} \end{aligned}$$
(9)

where \(\mu _{y}\) and \(T_{y}\) are the mean and the target of the functional variable, determined by the Eqs. 3 and 4, respectively, \(m_{y}=({{\textit{LSL}}}_{y}+{{\textit{USL}}}_{y})/2\) is the mid-point between the lower and the upper specification limits and \(dy=(USLy+LSLy)/2\) is the half specification width, and \({\textit{LSL}}_{y}\) and \({\textit{USL}}_{y}\) are the lower and upper specification limits of the functional variable (y), respectively.

Substituting Eqs. 2, 3, 4 and 8 into Eq. 9, the functional process capability \(C_{{\textit{pmk}}_{y}}\) can be rewritten as follows;

$$\begin{aligned} \mathrm {C}_{{\textit{pmk}}_{y}}=\frac{d_{y}-\left| y(\mu _{1},..,\mu _{n})-m_{y} \right| }{3\left\{ \sum \nolimits _{i=1}^n {\left\{ {\left( \frac{\partial f}{\partial x_{i}}\right) }^{2}\left[ \left( \frac{d_{i}-\left| \mu _{i}-m_{i} \right| }{3C_{{\textit{pmk}}_{i}}} \right) ^{2}-{(\mu _{i}-T_{i})}^{2} \right] \right\} +{(y(\mu _{1},..,\mu _{n})-y(T_{1},..,T_{n}))}^{2}} \right\} ^{1 / 2}} \end{aligned}$$
(10)

For including the systematic tolerance of the manufacturing processes due to several factors such as the tool wear, the shift value (\(\Delta _{i}\)) of mean value (\(\mu _{i}\)) from the corresponding target (\(T_{i}\)) can be defined as below;

$$\begin{aligned} {\Delta _{i}=\mu }_{i}-T_{i}\qquad i=1,\ldots ,n \end{aligned}$$
(11)

Therefore, mean values can be written in terms of target and shift values (i.e. \(\mu _{i}=T_{i}+\Delta _{i})\), the process capability function (Eq.) can be rewritten as follows;

$$\begin{aligned} \mathrm {C}_{{\textit{pmk}}_{y}}= & {} \frac{d_{y}-\left| y(T_{1}+\Delta _{1},..,T_{n}+\Delta _{n})-m_{y} \right| }{3\left\{ \sum \nolimits _{i=1}^n {\left\{ {\left( \frac{\partial f}{\partial x_{i}}\right) }^{2}\left[ \left( \frac{d_{i}-\left| T_{i}+\Delta _{i}-m_{i} \right| }{3C_{{\textit{pmk}}_{i}}} \right) ^{2}-\Delta _{i}^{2} \right] \right\} +{(y(T_{1}+\Delta _{1},..,T_{n}+\Delta _{n})-y(T_{1},..,T_{n}))}^{2}} \right\} ^{1 / 2}}\qquad \qquad \qquad \qquad \quad \end{aligned}$$
(12)

As the first objective function, the process capability function should be maximization as;

$$\begin{aligned} {{\textit{max}}~f}_{1}=\frac{d_{y}-\left| y(T_{1}+\Delta _{1},..,T_{n}+\Delta _{n})-m_{y} \right| }{3\left\{ \sum \nolimits _{i=1}^n {\left\{ {\left( \frac{\partial f}{\partial x_{i}}\right) }^{2}\left[ \left( \frac{d_{i}-\left| T_{i}+\Delta _{i}-m_{i} \right| }{3C_{{\textit{pmk}}_{i}}} \right) ^{2}-\Delta _{i}^{2} \right] \right\} +{(y(T_{1}+\Delta _{1},..,T_{n}+\Delta _{n})-y(T_{1},..,T_{n}))}^{2}} \right\} ^{1 / 2}} \end{aligned}$$
(13)

where \(C_{{\textit{pmk}}_{i}}\) and \(\Delta _{i}\) are individual process capabilities and statistical tolerances (shift deviations of the process) as the design variables in the optimal design problem can be considered.

2.3 Formulating the manufacturing cost function in terms of individual process indices

Optimal process tolerance design is usually a trade-off between functional specifications and the overall manufacturing cost to allocate proper tolerances to the individual components. In order to reach this aim, it is necessary to use a proper cost-tolerance relationship. The cost-tolerance relationship is a mathematical function that is empirically formulated based on the experimental observations for optimal tolerance allocation that relates the manufacturing cost to the tolerances. Manufacturing of products with tighter tolerances leads to costly machining process with the low speeds, the low feeds, and time-consuming processes. Several cost-tolerance functions have been proposed in the literature [6]. One of the popular and efficient models is the reciprocal power function model. In general form, it can be expressed as;

$$\begin{aligned} C=A+\frac{B}{t^{k}} \end{aligned}$$
(14)

where the constant coefficient A represents fixed costs that may include material, tooling, setup cost, and other operations. The coefficient B describes the manufacturing cost of an individual component dimension to a specified tolerance and includes the charge rate of the machine. Manufacturing of products with tighter tolerances leads to low speeds and low feeds, high quality of products, more time and higher costs. t indicates the manufacturing tolerance. The exponent k indicates the sensitivity of the process cost of design variable to tolerance levels.

To include the manufacturing cost function into the formulation of the optimal design of process tolerances, the manufacturing cost function can be described in terms of the individual process capabilities and shift deviations. In order to reach to this aim, individual tolerances (t) can be described in terms the standard deviation of the effective variables based on the 3-Sigma concept at \(99.74\%\) confidence level (i.e. \({t}_{i}=3\sigma _{i}\)). Therefore, based on the Eq. 14, the manufacturing cost can be rewritten in terms of \(C_{\textit{pmk}}\) and \(\Delta \) as follows;

$$\begin{aligned} MC=A+\frac{B}{\left\{ 3\left( \left( \frac{d-\left| \mu -m \right| }{3C_{\textit{pmk}}} \right) ^{2}-\Delta ^{2} \right) ^{1 / 2} \right\} ^{k}} \end{aligned}$$
(15)

Therefore, the total manufacturing cost function objective of all components of the assembly can be formulated as follows;

$$\begin{aligned} {{\textit{min}}~f}_{2}=\sum \limits _{i=1}^n {\left\{ A_{i}+\frac{B_{i}}{\left\{ 3\left( \left( \frac{d_{i}-\left| T_{i}+\Delta _{i}-m_{i} \right| }{3C_{{\textit{pmk}}_{i}}} \right) ^{2}-\Delta _{i}^{2} \right) \right\} ^{k_{i}}} \right\} } \end{aligned}$$
(16)

2.4 Formulating the optimal tolerance allocation as a multi-criteria optimization problem

The proposed formulation in standard form, the process capability function and the overall manufacturing cost as objective functions should be simultaneously optimized. The requirements of individual process capability indices at the acceptable level of process capability (\(C_{p_{i}}^{*}\)) are considered as the design constraints. Since \(C_{{\textit{pmk}}_{i}}\) and \(\Delta _{i}\) which are main specifications of the process, can be considered as the design variables to find the optimal tolerance design of the manufacturing processes. Consequently, the optimal tolerance design of the manufacturing processes can be expressed as follows;

$$\begin{aligned}&{{\textit{max}}~f}_{1}=\frac{d_{y}-\left| y(T_{1}+\Delta _{1},..,T_{n}+\Delta _{n})-m_{y} \right| }{3\left\{ \sum \nolimits _{i=1}^n {\left\{ {\left( \frac{\partial f}{\partial x_{i}}\right) }^{2}\left[ \left( \frac{d_{i}-\left| T_{i}+\Delta _{i}-m_{i} \right| }{3C_{{\textit{pmk}}_{i}}} \right) ^{2}-\Delta _{i}^{2} \right] \right\} +{(y(T_{1}+\Delta _{1},..,T_{n}+\Delta _{n})-y(T_{1},..,T_{n}))}^{2}} \right\} ^{1 / 2}}\qquad \qquad \qquad \quad \nonumber \\&{\textit{min}}~f_{2}=\sum \limits _{i=1}^n \left\{ A_{i}+\frac{B_{i}}{\left\{ 3\left( \left( \frac{d_{i}-\left| T_{i}+\Delta _{i}-m_{i} \right| }{3C_{{\textit{pmk}}_{i}}} \right) ^{2}-\Delta _{i}^{2} \right) \right\} ^{k_{i}}} \right\} \nonumber \\&{\textit{subject to}}\nonumber \\&C_{{\textit{pmk}}_{i}}^{*}\le C_{{\textit{pmk}}_{i}};\qquad i=1,..,n \end{aligned}$$
(17)

2.5 Solving the multi-criteria optimization problem by the NSGA II method

The NSGA-II is an evolutionary-based algorithm to solve the multi-criteria optimization problem, which has been introduced by Deb et al. [30]. The NSGA II is based on the standard genetic algorithm operators such as the reproduction, the crossover, and the mutation. The NSGA II has been developed based on the selection operator through conjoining the populations and to reach the best solutions with respect to the maximum fitness and the uniform spread on the feasible region. For comparing and selecting the solutions in vector space of objectives, the domination concept is used. In comparing the solutions, the solution that is non-dominated by other solutions can be a candidate solution on the Pareto front. In order to reach the solutions with the uniform spread on the Pareto front, solutions that have the higher crowding distance are preferred.

In this study, in order to solve the multi-criteria optimization problem (Eq. 16), the NSGA II method is utilized.

2.6 Automated decision making for selecting the best tolerances from the optimal Pareto front

One of the important challenges in the optimal tolerance design with multi-criteria is the selection of the best tolerances from the optimal Pareto solutions. The TOPSIS, as a Multiple Criteria Decision Making (MCDM) method, is an effective way to select optimal solutions. TOPSIS method was first presented by Hwang and Yoon for solving MCDM problems [31, 32]. According to TOPSIS technique, the selected optimal solution has the shortest Euclidian distance from the Ideal solution and the farthest from the Nadir solution. A modified TOPSIS method based on the weighted Euclidean distances can be used [33]. One of the difficult tasks of designers for the tolerance design with multi-criteria in using the TOPSIS method is determining the objective weights. To overcome this problem, Shannon‘s entropy-based TOPSIS can be used in the proposed algorithm for automated decision making.

The steps of selecting the optimal solution based on through an enhanced Shannon‘s entropy-based TOPSIS algorithm can be carried out as follows;

  1. 1.

    Constructing an evaluation matrix consisting of m alternatives as rows and n criteria as columns of the evaluation matrix;

    $$\begin{aligned} A={[a_{ij}]}_{m{\times }n} \end{aligned}$$
    (18)
  2. 2.

    Normalizing the evaluation matrix (A) to form the matrix R as follows:

    $$\begin{aligned} R={[r_{ij}]}_{m{\times }n} \end{aligned}$$
    (19)

    where \(\mathrm {r}_{\mathrm {ij}}\) can be computed by;

    $$\begin{aligned} r_{ij}=\frac{a_{ij}}{{\sqrt{\sum _{k=1}^m a_{kj}^{2}}}} \end{aligned}$$
    (20)
  3. 3.

    Since the importance of criteria in the selection process may be not equal, the weighted normalized decision matrix should be computed by allocating the proper weights of the criteria. In general, determining the objective weights is one of the main challenges in using multi-criteria decision making. The entropy-based weighting method is utilized to overcome this problem. Accordingly, the decision matrix should be normalized for each objective \(f_{j}(j=1,2,\ldots ,n\)) to obtain the projection value of each criterion \(p_{\mathrm {ij}}\).

    $$\begin{aligned} p_{ij}=\frac{r_{ij}}{\sum \nolimits _{i=1}^m r_{ij} } \end{aligned}$$
    (21)

    Subsequently, the entropy values    \(e_{j}\) can be obtained as follows;

    $$\begin{aligned} en_{j}=-{(ln(m))}^{-1}\sum \limits _{j=1}^n {p_{ij}\ln p_{ij}} \end{aligned}$$
    (22)

    The divergence degree of each criterion \(f_{\mathrm {j}}\) (\(j=1,2,\ldots ,n\)) can be obtained as below;

    $$\begin{aligned} {d_{j}=1-en}_{j} \end{aligned}$$
    (23)

    The higher value of \(d_{\mathrm {j}}\) means the criterion \(c_{j}\) is more important for selection. Therefore, the weights of criteria can be determined by;

    $$\begin{aligned} w_{j}=\frac{d_{j}}{\sum \nolimits _{k=1}^n d_{k} } \end{aligned}$$
    (24)

    Consequently, the normalized evaluation matrix can be rewritten in the weighted form;

    $$\begin{aligned} U={[u_{ij}]}_{m\times n}={[w_{i}r_{ij}]}_{m\times n} \end{aligned}$$
    (25)
  4. 4.

    Determining the Ideal solution (\(\mathrm {A}^{*})\) and the Nadir solution (\(\mathrm {A}^{-}\));

    $$\begin{aligned} A^{*}= & {} \left\{ u_{1}^{*} ,u_{2}^{*} ,\ldots ,u_{n}^{*} \right\} \nonumber \\ A^{{-}}= & {} \left\{ u_{{1}}^{{-}} ,u_{{2}}^{{-}} ,\ldots ,u_{n}^{-} \right\} \end{aligned}$$
    (26)
  5. 5.

    Computing the distance of each candidate from the ideal and nadir solutions;

    $$\begin{aligned} d_{i}^{*}= & {} \left\{ \sum \nolimits _{j=1}^n {(u_{ij}-u_{j}^{*})}^{2} \right\} ^{1 /2}\nonumber \\ d_{i}^{-}= & {} \left\{ \sum \nolimits _{j=1}^n {(u_{ij}-u_{j}^{-})}^{2} \right\} ^{1/2} \end{aligned}$$
    (27)
  6. 6.

    Calculating the relative distance of each candidate of the best solution to the ideal solution as follow;

    $$\begin{aligned} C_{i}^{*}=\frac{d_{i}^{-}}{d_{i}^{-}+d_{i}^{*}} \end{aligned}$$
    (28)

To select the optimal tolerance, the candidates from the obtained Pareto fronts can be sorted based on the relative distances to the ideal solution. Consequently, a high value of \(C_{i}^{*}\) means the relative distance is closer to the ideal solution and it is equivalent to a better rank. The candidate with the highest relative distance value is the best optimal solution.

3 Case study: a windmill transmission

In this section, to demonstrate the application of the presented method, the optimal process tolerance design of a windmill transmission as a case study from the literature [34] is carried out. The results of the proposed method are compared to the obtained results from the conventional method is presented in Ref [34].

The schematic of the single stage planetary gear transmission of the windmill is shown in Fig. 4. For the optimal process tolerance design of the windmill transmission assembly, the following steps can be carried out;

Step 1: Extracting the design function from the CAD model

The windmill transmission consists of a drive and output housing, a drive and output shaft, a universal ring gear, three planets, a planet holder, and a sun (see Fig. 4). The features and tolerance types of each component and the corresponding processed dimensions based on the design and customer’s requirements are presented in Table 1. According to the virtual model of the windmill transmission in Fig. 4, the distance between centerlines of the drive and output shafts as the assembly function(y) in terms of the processed dimensions (\(x_{i}\)) can be expressed as

$$\begin{aligned} y= & {} 0.321{(x}_{1}+x_{2}+x_{3}-x_{4}-x_{5}+x_{6}-x_{7}+x_{8}+x_{9}+x_{12})\nonumber \\&-\,0.440\left( x_{10}+x_{11} \right) \end{aligned}$$
(29)
Table 1 The features and tolerance types of components based on the design and customer’s requirements
Full size table
Fig. 4
figure 4

2D schematic of the single stage planetary gear transmission and the effective dimensional variables

Full size image

Step 2: Formulating the process capability function in terms of individual process indices

According to Eq. 13, the process capability function in terms of individual process indices can be written as follows:

$$\begin{aligned} \mathrm {f}_{1}=\frac{d_{y}-\left| y(T_{1}+\Delta _{1},..,T_{12}+\Delta _{12})-m_{y} \right| }{3\left\{ \sum _{i=1}^{12} {\left\{ {\left( \frac{\partial f}{\partial x_{i}}\right) }^{2}\left[ \left( \frac{d_{i}-\left| T_{i}+\Delta _{i}-m_{i} \right| }{3C_{{\textit{pmk}}_{i}}} \right) ^{2}-\Delta _{i}^{2} \right] \right\} +{(y(T_{1}+\Delta _{1},..,T_{12}+\Delta _{12}) -y(T_{1},..,T_{12}))}^{2}} \right\} ^{1 / 2}} \end{aligned}$$
(30)

where \(m_{i}=({{\textit{LSL}}}_{i}+{{\textit{USL}}}_{i})/2\) is the mid-point between the lower and the upper specification limits and \(d_{i}=({{\textit{USL}}}_{i}-{{\textit{LSL}}}_{i})/2\) is the half specification width, and \({\textit{LSL}}_{i}\) and \({\textit{USL}}_{i}\) are the lower and upper specification limits and \(\frac{\partial f}{\partial x}\) is the sensitivity coefficient of the design variable i. The target values, the mid-point and the half specification width between the lower and the upper specification limits and sensitivity coefficients of the design variables are listed in Table 2. The lower and the upper specification limits of the functional variable (y) based on the design requirements are − 0.25 and \(+\) 0.25, respectively. Accordingly, \(d_{y}\) and \(m_{y}\) are 0.25 mm and 0, respectively.

Table 2 Values of parameters and specification limits of processed dimensions (design variables)
Full size table

In this work, for formulating the product quality based on the process capability function, the normality assumption which is well supported central limit theorem, is utilized to model the distribution of the product’s variations.

It is worth to note that the proposed statistical model can be developed to include the random variables with non-normal distributions and can be improved by up-dating based on the new experimental observations or data. The Bayesian up-dating model as a powerful model can be used for up-dating the statistical distributions which be used to describe the individual process capability indices, the corresponding tolerances, and the respective manufacturing cost. In general form, Bayesian up-dating model can be expressed as follows [35]:

$$\begin{aligned}&{\textit{Posterior distribution}} \propto {\textit{Likelihood function}} \\&\quad \times {\textit{Prior distribution}} \end{aligned}$$

Therefore, the posterior distribution is estimated based on the likelihood function and the prior distribution which can be known or assumed about the parameter before the data are collected or analysed. Therefore, according to this concept, the Bayesian—tolerance model can be first developed based on a specific assumption about the likelihood function and the prior distribution in the design stage. Then, based on the collected experimental data, the Bayesian—tolerance model can be improved by the Bayesian updating procedure for accurately estimating the process capability and the respective manufacturing cost based on the new experimental observations or data.

Step 3: Formulating manufacturing cost function in terms of individual process indices

In this study, according to Eq. 16, the overall manufacturing cost can be estimated as follows:

$$\begin{aligned} \mathrm {f}_{2}= & {} A_{1}+\frac{B_{1}}{\left\{ 3\left( \left( \frac{d_{1}-\left| T_{1}+\Delta _{1}-m_{1} \right| }{3C_{{\textit{pmk}}_{1}}} \right) ^{2}-\Delta _{1}^{2} \right) \right\} ^{n_{1}}}\nonumber \\&+\,A_{2}+\frac{B_{2}}{\left\{ 3\left( \left( \frac{d_{2}-\left| T_{2}+\Delta _{2}-m_{2} \right| }{3C_{{\textit{pmk}}_{2}}} \right) ^{2}-\Delta _{2}^{2} \right) \right\} ^{n_{2}}}\nonumber \\&+\,A_{3}+\frac{B_{3}}{\left\{ 3\left( \left( \frac{d_{3}-\left| T_{3}+\Delta _{3}-m_{3} \right| }{3C_{{\textit{pmk}}_{3}}} \right) ^{2}-\Delta _{3}^{2} \right) \right\} ^{n_{3}}}\nonumber \\&+\,A_{4}+\frac{B_{4}}{\left\{ 3\left( \left( \frac{d_{4}-\left| T_{4}+\Delta _{4}-m_{4} \right| }{3C_{{\textit{pmk}}_{4}}} \right) ^{2}-\Delta _{4}^{2} \right) \right\} ^{n_{4}}}\nonumber \\&+\,A_{5}+\frac{B_{5}}{\left\{ 3\left( \left( \frac{d_{5}-\left| T_{5}+\Delta _{5}-m_{5} \right| }{3C_{{\textit{pmk}}_{5}}} \right) ^{2}-\Delta _{5}^{2} \right) \right\} ^{n_{5}}}+A_{2}\nonumber \\&+\,\frac{B_{6}}{\left\{ 3\left( \left( \frac{d_{6}-\left| T_{6}+\Delta _{6}-m_{6} \right| }{3C_{{\textit{pmk}}_{6}}} \right) ^{2}-\Delta _{6}^{2} \right) \right\} ^{n_{6}}}\nonumber \\&+\,A_{7}+\frac{B_{7}}{\left\{ 3\left( \left( \frac{d_{7}-\left| T_{7}+\Delta _{7}-m_{7} \right| }{3C_{{\textit{pmk}}_{7}}} \right) ^{2}-\Delta _{7}^{2} \right) \right\} ^{n_{7}}}\nonumber \\&+\,A_{8}+\frac{B_{8}}{\left\{ 3\left( \left( \frac{d_{8}-\left| T_{8}+\Delta _{8}-m_{8} \right| }{3C_{{\textit{pmk}}_{8}}} \right) ^{2}-\Delta _{8}^{2} \right) \right\} ^{n_{8}}}\nonumber \\&+\,A_{9}+\frac{B_{9}}{\left\{ 3\left( \left( \frac{d_{9}-\left| T_{9}+\Delta _{9}-m_{9} \right| }{3C_{{\textit{pmk}}_{9}}} \right) ^{2}-\Delta _{9}^{2} \right) \right\} ^{n_{9}}}\nonumber \\&+\,A_{10}+\frac{B_{10}}{\left\{ 3\left( \left( \frac{d_{10}-\left| T_{10}+\Delta _{10}-m_{10} \right| }{3C_{{\textit{pmk}}_{10}}} \right) ^{2}-\Delta _{10}^{2} \right) \right\} ^{n_{10}}}\nonumber \\&+\,A_{11}+\frac{B_{11}}{\left\{ 3\left( \left( \frac{d_{11}-\left| T_{11}+\Delta _{11}-m_{11} \right| }{3C_{{\textit{pmk}}_{11}}} \right) ^{2}-\Delta _{11}^{2} \right) \right\} ^{n_{11}}}\nonumber \\&+\,A_{12}+\frac{B_{12}}{\left\{ 3\left( \left( \frac{d_{12}-\left| T_{12}+\Delta _{12}-m_{12} \right| }{3C_{{\textit{pmk}}_{12}}} \right) ^{2}-\Delta _{12}^{2} \right) \right\} ^{n_{12}}}\nonumber \\ \end{aligned}$$
(31)

The values of constants A, B, and n of the manufacturing cost function based on the experimental observations for the processed variables are reported in Table 3.

Table 3 The values of constants of the manufacturing cost based on the experimental observations
Full size table

Step 6: Formulating the optimal tolerance allocation as a multi-criteria optimization problem

According to Eq. 16, the optimal process tolerance design of the wind mill transmission can be formulated as constrained bi-objective optimization problem as follows

$$\begin{aligned} \max \mathrm {f}_{1}= & {} \frac{d_{y}-\left| y(T_{1}+\Delta _{1},..,T_{12}+\Delta _{12})-m_{y} \right| }{3\left\{ \sum \nolimits _{i=1}^{12} {\left\{ \alpha _{i}^{2}{\left( \frac{\partial f}{\partial x_{i}}\right) }^{2}\left[ \left( \frac{d_{i}-\left| T_{i}+\Delta _{i}-m_{i} \right| }{3C_{{\textit{pmk}}_{i}}} \right) ^{2}-\Delta _{i}^{2} \right] \right\} +{(y(T_{1}+\Delta _{1},..,T_{12} +\Delta _{12})-y(T_{1},..,T_{12}))}^{2}} \right\} ^{1 / 2}}\nonumber \\ \min \mathrm {f}_{2}= & {} {A}_{1}+\frac{B_{1}}{\left\{ 3\left( \left( \frac{d_{1}-\left| T_{1}+\Delta _{1}-m_{1} \right| }{3C_{{\textit{pmk}}_{1}}} \right) ^{2}-\Delta _{1}^{2} \right) \right\} ^{n_{1}}}+A_{2}+\frac{B_{2}}{\left\{ 3\left( \left( \frac{d_{2}-\left| T_{2}+\Delta _{2}-m_{2} \right| }{3C_{{\textit{pmk}}_{2}}} \right) ^{2}-\Delta _{2}^{2} \right) \right\} ^{n_{2}}}\nonumber \\&+\,A_{3}+\frac{B_{3}}{\left\{ 3\left( \left( \frac{d_{3}-\left| T_{3}+\Delta _{3}-m_{3} \right| }{3C_{{\textit{pmk}}_{3}}} \right) ^{2}-\Delta _{3}^{2} \right) \right\} ^{n_{3}}}+A_{4}+\frac{B_{4}}{\left\{ 3\left( \left( \frac{d_{4}-\left| T_{4}+\Delta _{4}-m_{4} \right| }{3C_{{\textit{pmk}}_{4}}} \right) ^{2}-\Delta _{4}^{2} \right) \right\} ^{n_{4}}}\nonumber \\&+\,A_{5}+\frac{B_{5}}{\left\{ 3\left( \left( \frac{d_{5}-\left| T_{5}+\Delta _{5}-m_{5} \right| }{3C_{{\textit{pmk}}_{5}}} \right) ^{2}-\Delta _{5}^{2} \right) \right\} ^{n_{5}}}+A_{2}+\frac{B_{6}}{\left\{ 3\left( \left( \frac{d_{6}-\left| T_{6}+\Delta _{6}-m_{6} \right| }{3C_{{\textit{pmk}}_{6}}} \right) ^{2}-\Delta _{6}^{2} \right) \right\} ^{n_{6}}}\nonumber \\&+\,A_{7}+\frac{B_{7}}{\left\{ 3\left( \left( \frac{d_{7}-\left| T_{7}+\Delta _{7}-m_{7} \right| }{3C_{{\textit{pmk}}_{7}}} \right) ^{2}-\Delta _{7}^{2} \right) \right\} ^{n_{7}}}+A_{8}+\frac{B_{8}}{\left\{ 3\left( \left( \frac{d_{8}-\left| T_{8}+\Delta _{8}-m_{8} \right| }{3C_{{\textit{pmk}}_{8}}} \right) ^{2}-\Delta _{8}^{2} \right) \right\} ^{n_{8}}}\nonumber \\&+\,A_{9}+\frac{B_{9}}{\left\{ 3\left( \left( \frac{d_{9}-\left| T_{9}+\Delta _{9}-m_{9} \right| }{3C_{{\textit{pmk}}_{9}}} \right) ^{2}-\Delta _{9}^{2} \right) \right\} ^{n_{9}}}+A_{10}+\frac{B_{10}}{\left\{ 3\left( \left( \frac{d_{10}-\left| T_{10}+\Delta _{10}-m_{10} \right| }{3C_{{\textit{pmk}}_{10}}} \right) ^{2}-\Delta _{10}^{2} \right) \right\} ^{n_{10}}}\nonumber \\&+\,A_{11}+\frac{B_{11}}{\left\{ 3\left( \left( \frac{d_{11}-\left| T_{11}+\Delta _{11}-m_{11} \right| }{3C_{{\textit{pmk}}_{11}}} \right) ^{2}-\Delta _{11}^{2} \right) \right\} ^{n_{11}}}+A_{12}+\frac{B_{12}}{\left\{ 3\left( \left( \frac{d_{12}-\left| T_{12}+\Delta _{12}-m_{12} \right| }{3C_{{\textit{pmk}}_{12}}} \right) ^{2}-\Delta _{12}^{2} \right) \right\} ^{n_{12}}}\nonumber \\ \hbox {Subject to}&\nonumber \\ C_{{{\textit{pmk}}}_{i}}^{*}\ge & {} 1 (\hbox {as minimum level of process capability})\nonumber \\&i=1,\ldots ,12 \end{aligned}$$
(32)

Step 7: Solving the multi-criteria optimization problem by the NSGA II method

For solving the obtained multi-objective optimization formulation, the NSAGA II is used. The obtained optimal normalized Pareto front of two objective functions is shown in Fig. 5.

Fig. 5
figure 5

The obtained normalized Pareto front of the process capability of functional variable (y) and the manufacturing cost from NSGA II

Full size image

Step 8: Automated decision making for selecting the best tolerances from the optimal Pareto front

In this step, the optimal tolerances can be determined from the obtained Pareto front through the computer-aided decision making based on Shannon‘s Entropy-based TOPSIS method, without the need to the weighting of the criteria. In order to find the best optimal solution, 20 candidates from optimal Preto front are considered according to Fig. 6. Subsequently, the candidates from the optimal Pareto fronts can be sorted based on the relative distances to the ideal solution.

Fig. 6
figure 6

20 candidates on the obtained normalized Pareto front of the process capability of Y and the manufacturing cost

Full size image

According to the proposed method, the computed relative distances of optimal solutions (\(\mathrm {C}_{\mathrm {i}}^{*})\) through Shannon‘s entropy-based TOPSIS are presented as the bar chart in Fig. 7. According to the obtained results in Fig. 7, \(\hbox {S}_{7}\) is selected as the best optimal solution with \(\mathrm {C}^{*}=73.21\%\) as the highest relative distances that means this optimal solution is the closest to the ideal solution.

Fig. 7
figure 7

The bar chart of sorting optimal solutions from the obtained Pareto front with respect to the relative distances

Full size image

Accordingly, the best optimal solution consists the optimal specifications such as the mean value of variables (\(\mu \)), the standard deviation of variables (\(\sigma \)), the shift deviations \((\Delta )\), the individual process capability indices \((C_{\textit{pmk}})\), the tolerances of processes \((\mathrm {t}_{\mathrm {x}}^{*})\), associated with the solution S4, optimal process tolerances and specifications are reported in Table 4. These obtained optimal results from the automated decision-making approach can be used for optimal process planning in the production design.

Table 4 The obtained optimal process tolerances and specifications from the automated decision making approac
Full size table

For visualization of optimal results, the virtual model of the windmill gearbox assembly can be adapted to the obtained optimal solution in the CAD software environment (see Fig. 8).

Fig. 8
figure 8

The virtual model of the gearbox assembly under the optimal results in the CAD software

Full size image

Based on the obtained results, the functional variable has the mean value, mean, and standard deviation values of the functional variable (y) are 0.0045, 0.007 and 0.0408, respectively. As a skewed normal distribution can be written as \(y=0.0052\pm 0.0408~{\hbox {mm}}\) (Fig. 8). The tolerance of the functional variable (Y) at the obtained optimal solution is presented in the normal distribution in Fig. 9. According to Fig., the \(99.74\% \) confidence interval (based on the 3-Sigma concept) of the process tolerance of the functional variable is \([-\,0.1172, 0.1276]\). In other words, under the optimal process specifications, the obtained confidence interval contains \(99.74\% \) of the true value of the functional variable (y) which may be occurred in the assembly procedure. The optimal results and specifications such as the mean, the standard deviation, the mean shift value, the process capability and the process tolerance of functional variable (y) are reported in Table 5. According these results, the process to produce the functional variable is capable \(({{\varvec{C}}}_{{{\varvec{pmk}}}_{{{\varvec{y}}}}}^{*} =1.58>1)\).

Based on the obtained optimal results (Figs. 8, 9, Table 5), through an interactive manner, the designer/user can be re-evaluated the selected optimal results which are obtained by the computer-aided decision-making procedure from the Pareto front before finalizing the process tolerance design and the process planning procedures.

Fig. 9
figure 9

The normal distribution of the functional variable (y) at the obtained optimal solution

Full size image
Table 5 The optimal results and specifications of functional variable (y)
Full size table
Table 6 Comparing the optimal process tolerances from proposed and conventional method
Full size table
Table 7 Comparing the computational results from the proposed and conventional method
Full size table

For verification of the proposed method, the case study is considered by a conventional method. Comparing the optimal tolerances from proposed and conventional results from Ref. [31] are presented in Table 6. Comparing results from the proposed and conventional methods in Table 7 shows that the relative improvement optimal value of the manufacturing cost is 20.3%. On the other hand, the estimating the functional process capability by the conventional method not applicable. Based on the obtained results, the proposed method as an efficient method can simultaneously optimize the functional process capability and the manufacturing cost of the product under the optimal process tolerances at the design stage.

4 Conclusion

The product designers, manufacturing engineers and process planers usually attempt to allocate the optimal tolerances of manufacturing processes to reach the product with high quality and the minimum cost. The optimal tolerance allocation as a multi-disciplinary process is always a time consuming and difficult procedure in the practice, especially for complex products. The proposed computer-aided tolerancing approach as aninteractive CAD—based tool can be useful in the design stage to help the product designers, manufacturing engineers, and process planers for optimal tolerance design of manufacturing process. According to the proposed method, the optimal tolerance design procedure has been developed as a multi-objective optimization problem where the process capability function and the overall manufacturing cost are simultaneously optimized. In the real industrial problems, the process capability function and the overall manufacturing cost can be formulated through the CAD model of the product based on the design/manufacturing/assembly requirements and the experimental data of manufacturing cost, respectively. In order to reach these practical models, the CAD model of the components and the assembly, the design requirements, manufacturing and assembly restrictions, the custome’s needs, the production process specifications, the experimental data of manufacturing cost are required. The optimal Pareto front of the proposed multi-objective optimization problem can be obtained using NSAGA II. In order to the automated selecting the best optimal solution from the Pareto front without the need to determine the criteria weightings, an improved Shanno’s Entropy TOPSIS methodology was adoptedto rank all optimal solutions from the best to the worst. The obtained optimal solution can presents the optimal specifications of the process such as the mean value of variables (\(\mu \)), the standard deviation of variables (\(\sigma \)), the shift deviations \((\Delta )\), the individual process capability indices \((C_{\textit{pmk}})\), the process tolerances (\(\mathrm {t}_{\mathrm {x}}^{*})\), which can be used for the optimal process planning in the production design. To illustrate the application of the presented method, optimal process tolerance design of a windmill transmission assembly was considered as a case study. The results of the proposed tolerance design method were compared to the obtained results from the conventional method. The computational results show that the proposed method leads to a lower manufacturing cost than the obtained results of the conventional method. Since the proposed algorithm can be simply automated for use within CAD/CAM software, it can be utilized as an interactive tool in the design for the manufacturing process of products. Based on the proposed method, determining the optimal process tolerances of the virtual model in the design stage to reach a real production with higher quality at the lower cost can be an efficient strategy for success in the competitive environment of manufacturing firms and industrial centers.