1 Introduction

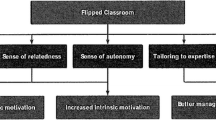
Just as there are many implementations of Flipped Classrooms (FCs) as there are teachers using the method, there are different definition of what FC as a teaching and learning framework entails. We distill some common defining characteristics from the work of Bergmann and Sams (2012), who define FC as a pedagogical system that off-loads the direct instruction to a set of videos for the students to prepare with out-of-class. In-class time is then free for exploring topics in greater depth and with increased interaction. Thus flipping the paradigm of where direct instruction and application occurs.

FCs are usually associated with ICT (Information and Communication Technology) enabled distribution of videos outside of the classroom prior to in-class work. However, one might as well consider this a priori content delivery through other media like written text. This is the well-known pedagogic advice most students get from their lecturers, at least in tertiary education, namely to prepare before lessons. As such, this part of the ‘flip’ can be regarded as old as academic activity itself (Wan 2015). The other part of the ‘flip’, active learning associated with in-class sessions, might be considered a more recent advance associated with student-centered pedagogical shifts (Laursen and Rasmussen 2019; Stephan 2014). The use of multimedia to introduce students to content prior to in-class activities were first introduced in the literature by Lage, Platt, and Treglia (2000) as the inverted classroom and by Baker (2000) as the classroom flip. As such, the FC framework is a new field of pedagogy, and it is associated with the pedagogical approach of blended learning (Bliuc, Goodyear, and Ellis 2007; Hadjerrouit 2008).

There are a growing number of research studies examining the efficacy of FCs, due in part to its growing popularity in the field of mathematics (Borba et al. 2016; Love, Hodge, Grandgenett and Swift 2014). Prior research on FCs is generally encouraging. For example, research indicates that students show improved academic success (Baepler, Walker, and Driessen 2014; Love et al. 2014) or at worst the FCs appear to have negligible effects on student achievement (Bagley 2019; Ziegelmeier and Topaz 2015). In addition, research suggests that FCs are fairly consistent in positively impacting students’ attitudes towards the learning experience (Arnold-Garza 2014) and increasing confidence in their abilities (Baepler et al. 2014).

Most of the current literature to date has documented the specifics of the FC videos (e.g., length of the videos, publication software, etc.) at the loss of detailing other aspects of the learning experience (e.g., classroom activities, design principles, assessment techniques). The two most common factors attributed to the positive experiences of students are the increased social engagement in the classroom and the flexibility allowed by having online didactic videos (Jaster 2017; Love et al. 2014). Yet current research tends to treat these factors (social engagement and flexibility of online environments) as disjoint components, largely due to the fact that they are often designed in isolation from one another. The aim of this paper is to unite the classroom experience and online videos through the use of design heuristics or principles that are complementary to FCs.

Few studies to date have incorporated theoretical frameworks to document how features of FCs align with theoretical constructs of learning. For instance, Baepler and colleagues (2014) documented in over two pages the physical layout of the classroom environment yet described the actual classroom activities in under two sentences as “small groups” and “clicker questions.” De Araujo, Otten and Birisci (2017) provide one of the first case studies leveraging curricular frameworks to document how videos serve as digital curricular resources and not merely as representations of instruction. De Aruajo and colleagues call on future research studies to move beyond the traditional nature of curricular videos and capitalize on new technologies to introduce material so that it might align with more innovative or reform-based teaching. Pepin, Choppin, Ruthven, and Sinclair (2017) in their review of digital curricular resources suggest that teacher design capacity and interaction with digital technologies “might provoke shifts in the perceived authority either of the teacher or the mathematics” (p. 658). Additionally, educators around the world are increasingly faced with the need to support linguistically diverse and multilingual classrooms as global mobility and distance learning increases (Morgan, Craig, Schuette, and Wagner 2014). In this study we take up this call for developing innovative digital curricular resources aligned with reform-based teaching while also addressing issues of equity and access for historically marginalized populations in linguistically diverse classrooms.

We address this opportunity to contribute to the literature by detailing a design-based research approach (Cobb 2000) of a FC teaching experiment that leveraged the instructional design theory of Realistic Mathematics Education (RME) and Culturally Responsive Pedagogy (CRP). Specifically, we draw on the principle of guided reinvention from RME (Gravemeijer and Doorman 1999) and principles of CRP (Aguirre 2009) to develop the curriculum material with the aim of broadening participation and fostering deep engagement in undergraduate mathematics using a FC approach. In order to provide structure and coherence for analysis we use a curricular framework (Stein, Remillard, and Smith 2007) to demonstrate how our instructional and pedagogical theories permeated the curriculum and impacted the student experience. In this paper we address the following research question: How and in what ways do students experience a flipped classroom calculus course designed using Realistic Mathematics Education and Culturally Responsive Pedagogy?

2 Realistic mathematics education and culturally responsive pedagogy

The curricular design leveraged the RME principle of guided reinvention using context problems to promote the reinvention of ideas, which then enables students to make sense of the formal mathematics as the finishing touch of their own creative efforts (Gravemeijer and Doorman 1999). Freudenthal (1991), the founding scholar of RME, was highly critical of traditional mathematics education and opposed what he called the anti-didactical inversion, whereby the historical end results of mathematical work is taken as the starting point for student learning. Through the tenets of RME design, Cobb, Zhao and Visnovska (2008) highlight the need for supporting students, “towards substantial participation in established mathematical practices” (p. 109). As such, the teacher guides the students in becoming familiar with conventional ways of symbolizing and reasoning in mathematics, ways that are “carriers of meanings and are treated as primary vehicles of the enculturation process” (p. 110). In a FC setting, this enculturation initially takes place during out-of-class video watching, then continues through contextualized RME inspired tasks in-class.

CRP is an orientation towards teaching and curricular development that recognizes the importance of including students’ cultural references in all aspects of learning (Ladson-Billings 1994). Characteristics of CRP include reshaping the curriculum to include issues and topics related to students’ background and culture, promoting student-centered instruction that encourages cooperation and collaboration, and embracing culturally mediated instruction that incorporates diverse ways of knowing and understanding (Villegas 1991). CRP provides students equal opportunities to achieve success and requires educators and schools to be active participants in ending oppressive structures.

RME aligns well with CRP and task design. As RME allows for encapsulation of experientially real settings as an informal starting point, there are ample grounds for designers and teachers to connect towards cultural aspects. Gravemeijer (1994) defines students’ mental modelling process as that of going through various levels of activity. As the students consider the initial context of the problem, they are engaged in the situational activity, after which they proceed through referential, general and formal levels of activity. Situational activity refers to acting in a particular task setting that is experientially real for students (Rasmussen and Blumenfeld 2007). Embedding the tasks in a culturally-responsive setting should ease the process of horizontal mathematization during the initial stages of RME, which “involves going from the world of life into that of symbols” (Van den Heuvel-Panhuizen and Drijvers 2014, p. 522). As such, culturally responsive task design have the potential to serve as a powerful mental tool to enable students’ initial structuring of the problem presented. Similarly, Ukpokodu (2011) frames it this way: “Culturally responsive teaching has been defined as an approach to teaching that uses students’ cultural knowledge as a ‘conduit’ to facilitate the teaching–learning process” (p. 48).

3 Curriculum framework

Curriculum, as it is defined broadly, refers to the totality of student experiences related to the content of teaching and learning (Stein et al. 2007). Drawing on the work of Porter and Smithson (2001), we leverage several curriculum constructs to frame the life cycle and fully capture the design, implementation and evaluation of the classroom teaching experiment. A brief definition of each of these constructs is presented followed by subsequent details for how these were implemented within the context of the study.

The written curriculum refers to the documents as part of the formal instruction that shape the content to be covered while teaching. The intended curriculum encompasses the objectives that are a result of the instructional planning. It comprises the goals, student learning outcomes, and activities outlined by school policies, educational standards, textbooks or by teachers. In our study the written curriculum refers to the institutional constraints such as the sequencing of the course within the university as well as the instructional materials developed (e.g., videos, activities). The intended curriculum refers to the student learning goals we developed during the creation of our materials. The enacted curriculum refers to the knowledge and skills actually delivered during instruction, which takes into account a teacher’s prior understanding, beliefs and goals for that particular curriculum content. It encompasses the fidelity for which a teacher uses and implements the formal curriculum. In our study the enacted curriculum refers to the way’s student engaged with the curriculum resources.

There also exists a hidden curriculum which is inferred by students through norms, values, and beliefs conveyed in the classroom and the curriculum content. The hidden curriculum is embedded both within in the messages conveyed through the institutional structures and content standards selected and within the messages and cultural practices of the teacher and students. Although the hidden curriculum is not overt, it does not mean it is unintentional. The hidden curriculum is influenced by issues of power, authority, and agency, often times marginalizing students and relegating them outside the source of knowledge in the mathematics classroom (Shuffelton 2013). Consistent with classroom teaching experiment methodology, this study has a combined role of the curriculum designer, researcher, and teacher, thus the hidden curriculum can be shaped and implemented with high levels of fidelity in a way that can empower student agency.

4 Methodology

As part of this study, we designed and implemented a 2-week classroom teaching experiment (Cobb 2000), which is a type of design-based research (Barab 2005), in a first-year calculus course covering topics in trigonometry and vectors. As illustrated in Fig. 1, the design research cycle in a classroom teaching experiment consists of a cyclical process of ongoing analysis of student reasoning while simultaneously designing tasks and modifying conjectures regarding the possible paths that students’ learning might take (Gravemeijer 1994; Cobb 2000). Both task design and ongoing analysis is necessarily theoretically guided. Our task design work was guided by the instructional design theory of RME and tenets of CRP and was led by the first author in consultation with the other authors. While RME and CRP were a priori driving influences, a more precise articulation of how the corresponding principles and heuristics explicitly map onto the written, intended, and hidden curricula was a retrospective account. This retrospective account (see Sect. 5) took into account drafts and final versions of instructional activities, notes taken by the task designer and by the course instructor, as well as notes from project meetings. The analysis reported here is from the first of four classroom teaching experiment iterations, which took place with 27 first-year computer engineering students enrolled in a first-year course in mathematics at a Norwegian university. We selected a single iteration to allow for a targeted and detailed description of the curriculum and classroom implementation.

Fig. 1
figure 1

The design research cycle

Full size image

The classroom teaching experiments we conducted in Norway address two increasingly important international issues in mathematics education: the growing demand for technologically enhanced mathematics classrooms (e.g., e-learning, FC, online courses) and the need to support linguistically diverse students as a way to broaden participation. As such, the context of this study as a joint collaboration between the researchers from the United States and from Norway provided an ideal setting to address both of these issues. Countries around the world are increasingly looking to make use of technology to offer courses for students with many competing demands and constraints on their time. In addition, all of the students primary (home) language was Norwegian yet were conversationally fluent in English. As such, the Norwegian context provided an ideal context for studying the mechanisms for supporting linguistically diverse mathematical conversations in a technologically enhanced course format.

Most of the students involved in the study were familiar with video tutorials prior to our experiment as supplemental instruction, but none had taken a course in a flipped format prior to our experiment. Although this study took place in the context of Norway, the design and implementation could easily transfer to most introductory university settings. In fact, the use of CRP necessitates addressing local knowledge and context which gives power to this study to provide context for its transferability. Additionally, the mathematical curriculum of the engineering program follows the recommendations set forth by the European Society for Engineering Education (Alpers et al. 2013) further contextualizing this study within the broader efforts of undergraduate mathematics education. The classroom teaching experiment took place during the first 2 weeks of the course and were video recorded and transcribed.

For our analysis of the implemented curriculum (see Sect. 6), we selected one focus group of students (assigned the pseudonyms of Ivan, Eli, and Moritz) who worked together in a small group throughout the entire teaching intervention. The focus group was selected based on their willingness and fluency to communicate using English during small group discussions. Data sources included video recordings of all class sessions, copies of students’ written work, individual debriefing interview with six students, researcher fieldnotes, and records of project meetings and debriefing sessions. Our analysis of this data corpus followed that of thematic analysis as described by Braun and Clarke (2006). Thematic analysis is a qualitative approach that involves “identifying, analyzing and reporting patterns (themes) within data. It minimally organizes and describes the data set in rich detail. However, frequently it goes further than this, and interprets various aspects of the research topic” (Braun and Clarke 2006, p. 79). Following this, we first independently created descriptive accounts of recorded class sessions and then vetted our individual accounts until consensus was reached. Informed by the theories of RME and CRP, we then used these narrative accounts (going back to the original data as needed) to identify emergent themes in the individual debrief interviews related to how students experienced the FC.

In addition, we administered an adaptation of the validated survey instrument known as the Student Assessment of their Learning Gains (SALG) (Seymour, Wiese, Hunter, and Daffinrud 2000) at the conclusion of the teaching experiment. Based on our analysis we illustrate how elements of the design heuristic were included in the written and hidden curriculum and how those considerations were then experienced by the students as part of the enacted components of the curriculum. Finally, we provide recommendations, insights and further areas of research based on the outcomes measured and our professional reflection in this research study.

5 Research context: intended, written and hidden curriculum

5.1 The intended curriculum

As part of the intended curriculum, we created a set of learning goals for the teaching experiment. The learning goals were informed by the United States (US) Common Core State Standards (CCSS) for Mathematics (National Governors Association Center for Best Practices and Council of Chief State School Officers 2010) and the Norwegian Framework Plan for Engineering Education (Rammeplan for ingeniørutdanning 2011). The Norwegian curriculum standards do not mention anything specific about vector analysis, but emphasize communicative skills as an important competency for students, well aligned with RME heuristics (Van den Heuvel-Panhuizen and Drijvers 2014). The US CCSS learning goals include both math content goals (e.g., recognize a vector as having both magnitude and direction) and practice goals (e.g., persevere in problem solving). The CCSS for mathematics are a set of widely adopted college-ready standards designed to ensure that students are prepared to take introductory college courses or enter the workforce. We drew more specifically on the practice standards as outlined in Table 1 for the learning goals we set for the curriculum. These learning goals allowed us to narrow our focus and ensure that our formal curriculum as a whole would address each of these intended curriculum goals.

Table 1 Content and practice goals for the intended curriculum
Full size table

5.2 The written curriculum

The written curriculum was influenced by the institutional constraints imposed by the learning goals of the first-year course at the university. As part of the sequencing of the educational program, students are first enrolled in Mathematics 1 and then take one additional mathematics course in conjunction with computer programming classes and physics. The mathematics department, in communication with their client disciplines, were informed that students were generally lacking a strong background in vector equations and trigonometric functions. Thus, the classroom teaching experiment was aimed at bolstering students’ understandings of these mathematical concepts.

5.2.1 Video resources

In the creation of the videos we were driven by the best practices currently outlined within the FC literature, namely videos should be relatively short (less than 10 min), the pre-lecture videos should be closely tailored to the classroom activities which should utilize active learning strategies, and students must be held accountable for watching the videos prior to attending class (Bagley 2019). In addition, teachers should use a consistent structure or pattern when designing the instructional materials (Ebbeler 2013).

We designed three different types of instructional videos which we refer to as introductory, inquisitive, and illustrative. The sequence of videos for the first teaching experiment is described in turn and a hyperlink for each can be found in Table 2. The introductory videos were the first video students watched that introduced the mathematical topic. They provided an overview of the content, such as basic operations, and then provided connections between the current content and prior mathematical topics. The format for the introductory videos used voice-over PowerPoint slides and static representations to present the mathematical material.

Table 2 Description of video lectures
Full size table

The inquisitive videos posed a single problem, which was discussed at length, giving probing questions and possible solution paths, but without presenting a final solution to the problem. The problem presented in these videos was then discussed in the classroom until students solved the problem. Our intention in creating these videos was to model how a mathematician might think about solving a particular problem through a series of erroneous solution paths. In the design of our videos, we broke with the traditional discursive patterns whereby the teacher gives an expository explanation for the mathematical topic. Instead, the videos show a string of thoughts of the narrator as he attempts to try and solve the mathematical problem but leaves the final solution up to the viewer. This design principle is aligned with both RME and CRP that encourage a variety of ideas, solutions, and representations which have been shown to have the advantage of engaging students in thinking and justifying their answers (Ju and Kwon 2007; Stein et al. 2007).

The illustrative videos were designed to show procedural techniques and operations. The illustrative videos showed from start to finish how to complete a given problem, and often showed a visual representation for the problem task. These videos used a pen-cast style narration with the heavy use of dynamic applications and visual renderings developed in GeoGebra. The problems were drawn from items similar to those in the students’ textbook but were adapted to include contextual references in line with CRP and included such things as leveraging their city as a setting for describing vector motion or modeling data based on local populations.

The setting for this study provided the opportunity to include design elements to support students with varying degrees of fluency in English, a challenge that is faced by many educators in countries throughout the world (Mosqueda and Maldonado 2013). The videos were uploaded to YouTube, which allowed for closed captions and differentiated playback speed. Students were given an accompanying note taking sheet and for each classroom session students watched one introductory video, one inquisitive video, and two illustrative videos.

5.2.2 Classroom activities

Informed by the RME principle of guided reinvention, the classroom activities were designed to leverage experimentally real contexts to promote student mathematization. For instance, as opposed to giving students the formal definition of the span of two vectors and then having them make sense of the mathematical syntax, students started with solving a vector equation in a realistic context and then tried to determine where the linear combination of the vectors would not reach on the plane. The formal definition of span followed naturally students’ informal mathematical activity (Wawro, Rasmussen, Zandieh, Sweeney, and Larson 2012). Additionally, we used activities that required students to create mathematical models; one based on numeric climate changes data, another based on a physical representation of a Ferris wheel. The principle of guided reinvention does not necessarily mean students must reinvent all of the mathematical content, but students must take ownership of the learning process itself and thus regard the information they learn as their own private knowledge (Gravemeijer and Doorman 1999). For this to occur, activities must be designed in a way that promotes student inquiry and engagement into the mathematical content, and social norms within the classroom must promote students to figure things out for themselves and explain their reasoning (Cobb and Yackel 1996). We selected the principle of guided reinvention for this reason in particular, since it necessitates addressing both the out of classroom content and the in-classroom activities, which furthers the aims of our research to unite out of class and in-class activities.

In Table 3, we provide a description of each of the classroom activities for the first classroom session. Although the videos and classroom activities are presented in separate tables, they were designed holistically. Some started with the classroom activity (e.g., the Magic Carpet Ride problem) and then we designed the video, others starting with the video (e.g., A trip to Iceland) followed by tailoring of the classroom activity.

Table 3 Description of classroom activities and intended curriculum goals
Full size table

5.3 The hidden curriculum

As stated earlier, while the hidden curriculum may not be overt, it is becoming more widely recognized and addressed by teachers, school leaders and policy officials (Hidden curriculum 2014). As such, we wanted to be explicit in designing a hidden curriculum that allowed for open access to a broader range of individuals. To accomplish this goal, we drew on elements of CRP (Aguirre et al. 2012; Esmonde and Langer-Osuna 2013) and supports for English language learners (Bresser, Melanese, and Sphar 2012; Gutiérrez 2002).

Our goal in infusing CRP was to have students critically analyze the community they live in and assess how mathematics is used within that realm and their everyday life. We designed the curriculum to include both geographically local examples and culturally salient examples for the students. The geographically local and national problems were based in the context of the town (e.g., using vectors to describe the movement from the local airport to the university) and at a national level (e.g., modeling wolf population zones in Norway, traveling from their local harbor to Iceland). We also wanted students to use mathematics to engage with twenty-first century issues related to their local context, so we designed a curriculum unit around modeling historical temperature data in Norway to make arguments for climate change. The design of the videos was also structured in a way that we, as the creators, would include personal narratives about our lives to humanize the delivery of the content. For example, we included pictures and stories about our identity as it related to the mathematical content (e.g., A trip to the Parthenon showing the trigonometric identities) or connections to the local context and culture of the students.

Since the context of the classroom teaching experiment was set in a Norwegian institution of higher education, all of the students were proficient in Norwegian. Based on individual student interviews and classroom interactions, all of the students were to some level conversationally fluent in English, but they were not native English speakers, and their primary mode of instruction in prior mathematics classes was Norwegian. Given our focus on supporting linguistically diverse conversations, we designed the curriculum to have supports for English language learners. For all of the videos we created a script to provide subtitles in English, and each video made explicit mention to the option of enabling subtitles during viewing. We also reworded the classroom activities to eliminate confusing terminology or technical jargon, which is a recommended principle to support English language learners (Zahner 2012).

6 Results: the enacted curriculum

6.1 Enacted curriculum and students’ classroom experience

The enacted curriculum captures the lived experience of the intended curriculum through the context of the teacher, classroom norms, and what actually transpires in the implementation of the learning experience. The teaching experiment took place in the milieu of a FC designed with RME and CRP, allowing students the opportunity to engage in the mathematics and feel supported with the topics both inside and outside of the formal classroom. Leading up to this in-classroom session, students watched the previously mentioned videos, then in class they engaged with the first activity that connected the inquisitive video problem of traveling to Iceland followed by the two magic carpet ride problems that aimed to have students re-invent notions of span and linear independence. In the following section we present descriptive accounts of our focus group’s work on the introductory task and the magic carpet ride activity along with evidence as it occurs for the group’s engagement with the learning goals of the intended curriculum.

6.1.1 Introductory activity

In the first activity of the class, students were asked to revisit the problem presented in the inquisitive video. The goal of this first activity was to link the learning experience from outside the classroom to the social setting of the classroom, and to assist with subsequent vertical mathematization (which refers to mathematizing ones own mathematical activity) of the second activity. In this classroom session, the problem described a sailing trip from the student’s city to Iceland with a given direction (west), time (24 h), distance (1260 km) and wind speed (south at the current days wind speed). Students were asked to determine the relative speed, bearing speed, express the resultant vector in standard basis and clarify what assumptions were made in solving the problem.

Ivan starts started the group activity by stating that the wind speed today was twice what it was yesterday (referring to the video) so the conversion would be 14.2 km/h. Moritz stated that the total distance was 1260 km and 24 h, so they needed a calculator to solve the problem. As Moritz was calculating the total due south distance, Ivan stated that it should be 343.6 km. The group was surprised that he was able to calculate the distance without a calculator when Ivan stated, “I have the calculation here cause it’s just double the number [from the video], because I actually did my homework.” Eli said that you should not have ruined the surprise by saying it was because of the previous work. Ivan then stated that the relative speed would be the same as the video since it’s the same distance travelled and time period. The group then discussed the constraints of their solution including assuming a flat earth, constant boat speed, no waves and linear distance traveled. The group proceeded to discuss that nothing could change between their city and Iceland, referencing often their own city and the trip that would be taken, grounding themselves within the context of the problem. Eli finished the activity by stating that this was a simple problem that they used a simple solution to solve.

This first activity demonstrates the ways in which the video was a resource for Ivan to build and think through the mathematics before the classroom session. The design of the video using CRP to link the content of the travel to their city seemed salient for the group as they referenced it often in trying to describe the voyage. Additionally, the group stated that this was an easy problem that they solved in a straight forward way, but this grounding in the mathematical experience prepares them for the guided reinvention of the span and linear independence of vectors in the next activity.

6.1.2 Mathematical reinvention task

After this activity, students engaged with the first magic carpet ride activity which sets a context where a person traveling is given two modes of transportations described as a magic carpet that can travel in the (3,1) direction and a hoverboard that can travel in the (1,2) direction, and asked how they would reach Old Man Gauss who lives in a cabin that is 107 miles East and 64 miles North of their home. In the second task, students were asked to determine if there are some locations where Old Man Gauss could hide his cabin such that you cannot reach him using the two modes of transportation.

At the start of the task Ivan led with the mathematical conjecture suggesting that, technically speaking, he [the traveler] should be able to go anywhere. Ivan conveyed a solution to the problem within the context of the traveling language introduced in the videos, by using the language of “go anywhere” to represent the two modes of transportation. Ivan then qualified his mathematical statement saying that it will only hold if we are allowed to use negative numbers. Moritz expanded Ivan’s reasoning from negative numbers to decimals and interpreted the meanings of the solutions (hours) within the context of the problem using the language of “complete hour” and “opposite direction.” Ivan suggested that he is unsure of how to explain his justification but clarified that, “every time you travel this way you go a bit this way.” He elaborated his claim that if you only had the magic carpet you would travel in a line but we can, “reverse with this one to get here.” Eli and Moritz helped construct this claim by adding in that you can “reverse” and go the “opposite direction” with the other form of transportation. Again, we notice that the argument uses language that conveys some contextual meaning of the mathematical operations. For instance, the group members do not just say you have to have negative coefficient for a solution, but it means going in “reverse” and in the “opposite direction.”

After Moritz questioned the group for how they can prove the argument, Ivan suggested, “that X*h + Y*m [h being the hoverboard direction, and m the magic carpet direction] can equal any position, given that X and Y can be negative numbers and decimals.” Given this new algebraic expression, Moritz countered that there are too many unknowns. The group, unable to resolve the algebraic solution for the problem, returned to a graphical solution, first with Ivan suggesting that you can “go here and then you use negative m [magic carpet], and then boom, you go there, and you can move a half a centimeter and do it again.” Moritz elaborated the argument adding the spiraling language, “because you could spiral in on your location, by using tiny increments, so…shouldn’t you get just about anywhere?” Moritz continued to push the group to persist wanting to be able to “prove it” and to “test it”.

The group again switched to algebraic reasoning with Ivan suggesting that while they know that “no matter what number we put in for X and Y we end up with a C, but that doesn’t prove that every C has an X and Y.” Here Ivan was using an algebraic expression to model the variables in the problem and clearly identified an issue with the well-defined nature of the mapping. Moritz agreed with this statement and this was a crucial point in their understanding that span might not be all of R2. After the group struggled to advance the prior argument in the algebraic reasoning, Eli put forth the idea that these two modes of transportation can’t be parallel. Eli drew on the standard basis covered in the videos as being able to “get anywhere with them. So it makes sense that you can also do exactly the same if they are not parallel.” Again there is evidence that Eli is interpreting the context of the problem in relation to the traveling metaphor from the videos by discussing how the standard basis can “get anywhere.” This idea of parallel appears to be very salient to the group, since Ivan and Moritz both repeat in agreement that they cannot be parallel. At this moment one of the instructors comes over to asked them what they have determined. The group shared their visual reasoning that the traveler can get anywhere as long as the vectors are not parallel and then they shared their algebraic expression as a “heavy handed” approach to reasoning. The instructor introduced the language that their algebraic expression is the linear combination of the two modes of transportation, and then led a whole class discussion ascribing formal language to the notion of span and linear independence. The group utilized both graphical and algebraic reasoning to make sense of linear independence and span which was then formalized by the instructor at the end of the session.

6.2 Enacted curriculum and students’ reflections on their experience

Given the iterative nature of classroom teaching experiments, we wanted to further understand how students experienced this FC to inform future implementations. Toward this end, we used the SALG to determine how much each of the class components helped their learnings using a Likert scale from 1 (no help) to 5 (great help). We received a total of 18 student responses. The survey responses were used to help contextualize the debrief interviews with students. As seen in Table 4, the most helpful components, according to the students, were interacting with peers, group work, and watching the video lectures. These elements, taken together, support the notion that students respond positively to a FC experience that combines video lectures and collaborative learning.

Table 4 Student responses from SALG Learning Components
Full size table

Participants reported that the least helpful components were hearing other students explain their work, the pace of the class, and the closed captions on the videos. In follow-up interviews we asked students to elaborate on how effective these components were in helping them throughout the class. Students who commented on the pace said, “It was good, but sometimes I felt like we were moving at a slow pace.” Given that this was familiar material to most students, in the subsequent classroom teaching experiments we structured higher level classroom activities for those who completed the initial task early. Although we were initially discouraged by the low rating for the closed captions, one student who did comment on the closed captions in follow-up interview, saying that he gave that component the highest score because it was “extremely helpful.” Our data also suggest that students who indicated on the survey they were comfortable using English to discuss mathematics in the classroom rated the benefit of the closed captions as less helpful (average 3.1) than students who indicated they were not as comfortable using English to discuss mathematics (average 3.8). This result points to the need to offer differentiated supports to students to allow them equal access to achieve, a principle of CRP.

We also examined how students reported interacting with the inquisitive videos that did not present a completed solution and were designed to link the out of classroom content with the in-classroom. We asked students during the interview and the survey what they thought about these videos, resulting in a wide range of responses. Several students said the videos were frustrating and confusing. Ivan from the focus group said he felt patronized because the correct answer was not displayed and Moritz suggested that when watching videos he would prefer to get the “raw math.” On the other hand some students commented how they enjoyed being able to assess their own knowledge and came prepared to discuss the problems presented in the videos in the classroom. During the interviews Eli shared how he enjoyed the videos because he was left wanting to know the answer and tried to use the internet to resolve his confusion. All of the students in the focus group commented that the videos were relevant and aligned with the activities that were presented in class. Using CRP in our design, we hoped to connect and motivate the material by providing local context. When students were asked about this in the focus group, they commented that it seemed more practical to them and Ivan said he would “get more motivated” to solve the problem. Moritz said the local context was a bonus and Ivan suggested it was “Nifty”. Although the students didn’t regard the context as a compelling factor in their learning experience, it was clearly a positive reaction that helped them engage them with the material.

7 Conclusion

The aim of this paper was to highlight how design theories can be leveraged to create a richer FC model by linking the content presented in the video lectures with the experiences of students inside the classroom. In order to achieve this effort, we drew upon the design principle of guided reinvention from RME and tenants of CRP. Through thematic analysis framed using curriculum we examined the lifecycle of the FC teaching experiment from design to implementation to understand how and in what ways students experienced this flipped classroom calculus course. Our analysis of the enacted curriculum highlights four themes related to how students experience the classroom: FC videos were experientially real experiences that were leveraged in classroom discussions, the ability to shift the mathematical authority through inquisitive videos was not fully realized, the culturally responsive context of the activities were valued but not perceived as critical to the mathematical objectives, and the diverse range of experiences highlight the need for differentiated student supports such as those for English language learners.

The classroom teaching experiment presented here provided the opportunity to critically analyze how FCs can be designed in a way that value the diversity of student experience and move beyond a transferal mode of learning (Baepler et al. 2014). Often times, FCs promote a transfer of knowledge from the video to the student in order for them to demonstrate understanding in the classroom. Our hope was to empower students to critically think about a mathematical problem individually before engaging with the task in a collective environment in-class. RME provided a compatible principle to bridge from videos aimed at providing experientially real tasks to then guide students in the classroom in the reinvention of more cognitively complex tasks. For instance, students in the focus group used the video as referential material to build their understanding of vector as metaphors for travel to develop notions of linear independence and span in the classroom context. Additionally, the connection between the outside video being taken-up in the classroom helped position Ivan as mathematically knowledgeable since he was able to understand how different parameters would impact the solution of the problem in the introductory activity.

Building on De Araujo, Otten and Birisci (2017) and Pepin et al. (2017) we aimed to develop innovative digital resources that would shift the mathematical authority and break the anti-didactical approach often presented in video tutorials. In this vein we implemented the inquisitive video segment which presented a mathematical topic without resolution and instead modeled how a mathematician might reason through solution paths. From the student experience this presented mixed results in their uptake or shift of the mathematical authority. Although the students in the focus group used the inquisitive video as referential material to engage with the classroom activity, two of the members saw them as patronizing and wanted the raw mathematical material presented to them in videos. While the self-reported responses seem to indicate that students might have experienced a conflict based on their reports of confusion and desire for resolution, future research needs to examine the direct role these videos have on the subsequent engagement and mathematical knowledge of the students. The use of these videos is likely to have greater success with university students who have more advanced meta-cognitive skills to intercept and experience dissonance in learning. As such more work is needed to understand the mechanism of digital resources that can shift such authority from the videos to the students. In future iterations of this work, we see a need to create additional innovate curricular videos that challenge the traditional instructor expository of content. For instance, we see promise in dialogue-intensive videos that showcase students mathematical thinking and working (e.g., Lobato, Walters, Walker, and Voigt 2018), which would align with principles of CRP and student-centered instruction.

The tenants of CRP were used to design the materials to including students’ cultural references in all aspects of learning and providing contextually relevant mathematical scenarios (Ladson-Billings 1994). Students were keen to reference such examples during mathematical problem solving. Furthermore, the interviewed focus groups saw their inclusion as a positive experience but not critical to their learning. The use of the videos was is in line with CRP embracing culturally mediated instruction that incorporates diverse ways of knowing and understanding (Villegas 1991) but students didn’t describe it as essential to the mathematical objectives. CRP as a guiding heuristic aligns well with FCs by allowing the teacher/designer to develop videos and activities that can draw on students’ cultural resources both inside and outside the classroom. Often one of the challenges expressed by instructors using CRP in classrooms is a tension between covering the content domain while centering students lived experiences and cultural resources. FCs can help alleviate some of those concerns by providing foresight in the development of lectures that infuses both content coverage based in local contexts, which were seemingly received well by students in this study.

We suggest future research examine the ways in which FCs afford and constrain the experiences of all students in the classroom, but especially those that have historically been marginalized in mathematics. Our initial findings seem to suggest that a FC could be used to promote equitable learning environments especially since they can offer differentiated learning supports, such as guided notes and closed captions for English language learners. Initially, we thought the closed captions were not impactful, but the students who said they benefited the most from these were students who were less comfortable communicating in English. These findings point to the need to analyze classrooms and supports for different students (e.g., women, queer students, students of color), since what is experientially real for some students could be outside the realm of lived experiences for others. The students in our teaching experiment responded positively to the experience in terms of reported learning gains and also exhibited several of the intended learnings goals targeted in the curriculum. In the future we hope to develop even richer FC experiences based on what we have learned here and will continue to make mathematics classrooms a place for all students to understand and engage with rigorous mathematical ideas.