Introduction

Nature has always inspired human technological advancements, and naturally-occurring cellular solids, e.g., honeycombs, wood, marine sponges, and bones, are no exception.1 For thousands of years, their thermal, mechanical, and physical properties have enabled their application in various tools, from thermal insulators to absorption and filtering equipment. This topic was thoroughly discussed in the work published by Gibson and Ashby.2 Based on the topology introduced by the authors, comprising cell connectivity and void space, cellular solids are often classified into two groups: stochastic and periodic. In the context of structural applications, the primary purpose of cellular solids is to provide a robust mechanical response to loading with as little weight as possible.2,3 Conceptually, a periodic cellular solid is defined as a network of interconnected trusses that absorb large amounts of mechanical energy owing to the deformation and collapse of their members under compressive loading.2,4 Under mechanical loading, strut-based cellular solids are characterized by their deformation mechanism: either bending-dominated or stretching-dominated. Stretching-dominated arrangements exhibit better strength-to-weight ratios; however, most arrangements fall into the bending-dominated category.5 This classification relies on Maxwell’s stability criterion, which relates the number of struts, b, to the number of nodes, j:3

$$M=b-3j+6$$
(1)

If M < 0, the structure exhibits one or more degrees of freedom, which is indicative of low stiffness or strength. Stretching-dominated structures exhibit non-negative values of M; thus, tensile and compressive axial forces equilibrate loading such that no bending occurs at the nodes.6

Lattice structures are manufactured in different materials, such as polymers,7 ceramics,8 metals,9 and even composites.10 The desired application and manufacturing process heavily influences material selection. Conventional machining techniques are not well suited to the manufacture of such complex geometries. Hence, cellular solids are manufactured via direct foaming of melt, indirect foaming via precursor,4 or additive manufacturing (AM).6,11,12 Recently, hybrid approaches combining AM and metalcasting have been successfully utilized for the manufacture of lattice structures. One example is the printing of disposable patterns, subsequently prepared for investment casting.13 This study focuses on 3D printed sand molds to produce periodic lattice structures based on the octet-truss unit cell. This method has yielded aluminum A356 alloy parts with identical mechanical properties as those observed in components manufactured using traditional no-bake sand molds.14 Moreover, using sand molds 3D printed via binder jetting achieves equal or better dimensional accuracy than that obtained using green sand molds.15 Previous studies on cast lattice structures attempted to identify a suitable range of materials and the practical limitations of this technique, such as feature size, feeding distance, and mold cleaning. For the specific case of gravity-fed octet-truss lattice structures cast in aluminum A356 alloy, a diameter of 3 mm represents a physical limitation because of the difficulty of de-powdering AM sand molds with smaller cross-sectional dimensions.16,17 Due to the complete design freedom it affords, AM is the logical choice for synthesizing cellular structures; however, the widespread application of direct AM technologies such as laser powder bed fusion (L-PBF) is hindered by defects arising from the high cooling rates. Metal AM components produced via L-PBF suffer from preferred crystallographic orientation, lack of fusion, cracking, and high residual stresses.9,18,19 In contrast, when combined with metalcasting techniques, AM provides foundries with greater versatility by enabling the production of complex geometries while circumventing the challenges associated with direct AM approaches. The mechanical properties of any casting are determined, to a great extent, by the mode of heat transfer or heat removal, and, when proper practices are followed, cast components exhibit consistent mechanical behavior.20

The present work is divided into three sections. First, we used AM sand molds to produce cast lattice structures designed around the octet-truss unit cell and evaluated their performance. The octet-truss unit cell was selected owing to its favorable strength-to-weight ratio and its nearly isotropic behavior.21 Due to their similar chemical compositions, the test specimens used during the first stage were poured in aluminum alloys A356 and F356. The primary difference between these two alloys is the amount of magnesium, which reacts with silicon to form Mg2Si nanoparticles that strengthen this alloy system upon aging. The F356 alloy, containing a lower proportion of Mg, exhibits lower tensile strength and higher ductility compared to the A356 alloy. The mechanical properties of this family of cast aluminum alloys (Al-Si-Mg) are determined by their dendrite arm spacing (DAS),22 as well as the nucleation of the Mg2Si precipitates upon aging to the T6 condition. The size of these particles is in the order of a few nanometers and is often resolved with the aid of transmission electron microscopy.23 During the second stage, we used computational tools to create a finite element (FE) model to reproduce the experimental results to an acceptable agreement. This methodology was then employed for a qualitative assessment of the differences between some bending-dominated truss designs, such as body-centered cubic (BCC), face-center cubic (FCC), and the design known as Kelvin’s cell.24 The performance of the bending-dominated truss designs was compared with that of the stretching-dominated design proposed based on the octet-truss; in our understanding, this design represents the benchmark of strut-based lattice structures. Additionally, a new design consisting of circular trusses swept along circular paths is introduced. All geometries studied in this work were assumed to be moldable using the AM-metalcasting method, and it is hypothesized that some of these designs would require multiple-piece 3D printed cores, primarily for cleaning purposes. Lastly, to understand the contributions of its constituent sets, we once again used specialized software to optimize the FCC and the octahedral sites of the octet-truss unit cell selectively. This optimization study was combined with a parametric assessment of the effect of nodal filleting of the octet-truss lattice structure to produce castings tested under uniaxial compression at low strain rates.

Experimental

Sample Preparation

Lattice Geometrical Parameters

Test specimens were synthesized by creating linear patterns of the octet unit cell—the periodic arrangement comprised 2 × 2 × 3 unit cells oriented along the three cartesian axes. The unit cell was bound to a cube with an interior edge length of 25 mm, and its truss diameter was maintained at 4 mm.

Using the hybrid AM-metalcasting process reported by Snelling et al.,25 a two-piece core mold was printed in silica sand using an ExOne S-Max sand 3D printer. The cope and drag molds were fabricated using traditional patterns and chemically bonded sand (also known as no-bake molding) using a Palmer M50XLD continuous mixer. Further details are provided in Fig. 1.

Fig. 1
figure 1

Schematic of sand molds (left) and finished casting after removal of the gating system (right); dimensions of the unit cell are given in mm.

Full size image

Chemical Composition

In aggregate, eight lattice structures were cast in the aluminum alloys, with half made using A356, and the rest were poured in F356. As mentioned previously, the two alloys exhibit similar chemical compositions, with a slight difference in Mg content. The average weight of the finished cast lattices was 201.6 ± 1.9 g, in contrast to the 211 g predicted from the CAD files, and assuming a density of 2.67 g/cm3.26 This amounted to a difference of ~ 4%, which was partially attributed to the loss of material during surface grinding. Chemical composition was measured using a Bruker Q4 Tasman advanced charge-coupled device spectrometer, and the results are summarized in Table I. The castings were solution heat-treated for 11 h at 540 °C, followed by a 24-h room-temperature aging period, and then artificially aged at 155 °C for 3.5 h following a process known as the T6 temper. As mentioned earlier, the mechanical properties of this alloy family are linked to the DAS, and the nucleation of nano-sized Mg2Si precipitates (supplementary Figure S7 shows a view of the dendritic microstructure prior to heat treatment). All heat treatments were performed in accordance with relevant standards.27,28

Table I Chemical composition of cast aluminum lattice structures (in wt%)
Full size table

Tensile and Impact Testing

Specimens for mechanical testing experiments were machined from bottom-filled cast Y-blocks of the previously mentioned alloys. Despite their relatively simple geometry, the molds for these parts were also additively manufactured to preserve consistency (refer to the online supplementary material, Figures S1 and S2 prompted the re-design of the y-block mold). The tensile tests were performed in accordance with the ASTM standard E8/E8M-16a29 using a universal Instron rig, model 4468. Charpy V-notch testing was conducted by Westmoreland Mechanical Testing and Research, in accordance with the ASTM standard E23-18.30 As presented in Table II, the results indicate that the F356-T6 is significantly more ductile—its average impact energy and lateral expansion are higher by a factor of 200%, and its percent elongation is approximately 131% higher those that of A356-T6 (supplementary Figure S8 provides a graphical comparison of these results). In contrast, the yield strength of the A356-T6 system is 27% higher. For more information regarding the Y-blocks and the rationale behind their design, please see supplementary Figure S3-S6 with the accompanying text.

Table II Tensile and impact properties of A356-T6 and F356-T6 alloys
Full size table

Compression Testing of Cast Lattices

The Instron 4486 universal testing machine was used for compression assessment, and the finished lattice castings were subjected to uniaxial compression loading at a rate of 1 mm per min (see Fig. 2). The process was manually stopped to avoid damage to the equipment once the crosshead displacement reached approximately 15 mm. As expected, the F356-T6 lattices exhibited greater ductility than their A356-T6 counterparts, which was deemed consistent with the results of the tensile and impact tests.

Fig. 2
figure 2

Uniaxial compression testing sequence; (a) undeformed state, (b) state at the end of the test, and (c) normal view of a specimen after testing; the orange circle highlights the location of a broken truss that was later studied using a scanning electron microscope; load–displacement curves comparing the performances of the two alloys; the zoomed-in inset depicts the bedding-in region.

Full size image

On average, the A356-T6 lattice withstood a peak load of 60 kN, and the first truss breakage (hereafter referred to as the first failure) occurred at approximately 6.77 mm, whereas the F356-T6 specimen withstood a maximum of 49 kN at 7.1 mm. Snelling et al. reported a maximum load of 123.2 kN from an aluminum alloy A356-T6 lattice structure designed from a pattern of 2 × 2 × 2 octet-truss unit cells; however, they did not report the truss diameter.25 It is worth noting that the latter specimen did not reach a net-zero load at 15 mm, and it could have withstood even higher displacements leading to potential improvements in internal energy. This topic has been addressed in greater detail in the modeling section of this paper. The load–displacement curves depicted in Fig. 2 compare the performances of the two cast aluminum alloys in lattices of identical dimensions. As discussed by Gibson and Ashby,2 the zoomed inset depicts a seemingly linear region, followed by a plateau before the structures undergo a prolonged densification stage. In the particular case of the octet-truss arrangement, this premature deformation is called bedding-in, and it originates at the nodes as the joints of the octahedral sites bed into the voids of the FCC sites.21 This phenomenon has proven difficult to model using analytical techniques or FE.

Analysis of Fractured Surfaces Using Scanning Electron Microscopy (SEM)

The fractured surfaces of selected samples from the tensile testing test and a broken truss from the lattice compression test (locations indicated in Fig. 2c) were analyzed using an SEM model Quanta 600 with a field-emission gun (FEI) with an accelerating tension of 10 kV and working distance set to 4.2 mm. Two failure modes were observed depending on the type of test (Fig. 3). The tensile specimens failed in a ductile manner as indicated by the presence of micro-voids. In contrast, owing to the difference in loading conditions, the lattice truss failed prematurely, with evidence of dimple fracture. The broken truss studied was obtained from a section of the casting that was not loaded uniaxially. Hence, it buckled before it failed under localized shear. Further insights on this instance are provided in the next section.

Fig. 3
figure 3

SEM images of the fractured surfaces; for clarity, the length of the scale bar in the top row is 1 mm, and that in the bottom row is 100 µm.

Full size image

From a qualitative perspective, all specimens studied using SEM exhibited comparable levels of shrinkage porosity, which verifies that the hybrid AM/metalcasting employed here produces nearly identical properties as those observed in cast components manufactured via traditional techniques.14 Further, this evidence suggests that the mechanical properties of the tensile test specimens are indeed representative of those observed in the cast lattice structures. We intend to conduct a proper quantitative assessment of porosity in a future work.

FE Simulations of Uniaxial Compression Testing

Computational Details

Quasi-static analyses are better suited for implicit time-integration solvers. One key advantage of the implicit solver over explicit time integration is the significant reduction in time steps (supplementary Table S1 provides a brief comparison between the explicit and implicit time-integration frameworks). However, it incurs a higher computational cost because of the need to use an iterative solution algorithm, whose time-to-solution is unknown, to determine convergence or the lack thereof.31 The loading conditions detailed in the experimental section were used, enabling the option of neglecting dynamic phenomena, such as strain rate and temperature dependence. The octet-truss lattice structure was discretized using 8-noded 1-point nodal pressure tetrahedral elements (ELEFROM = 13), and 8-noded hexahedral elements with eight integration points were used (ELEFROM = − 2). The load was defined by applying a prescribed motion along the vertical axis to the platen. A fixed boundary was applied to the bottom face of the lattice structure to constrain its vertical displacement. The final discretized model consisted of 1,151,570 finite elements with an approximate edge length of 0.75 mm, and these parameters were deemed acceptable for maximum load and displacement within a 95% confidence interval and a relative error of 0.08% with respect of a smaller element size of 0.5 mm (please see supplementary Figure S9 for the discretized model). The latter allowed us to account for discretization error with a reasonable time to solution and file size. Further details regarding the convergence studies are provided in the supplementary Table S2.

All contact sets were defined using the mortar automatic contact algorithm: surface-to-surface for the platen-to-lattice interaction and single-surface for the lattice self-contact. Mortar contact is the recommended procedure for implicit time integration.31 The problem was solved using the commercial software, LS-DYNA, R13.0 shared memory parallel with double precision,32 executed on a Cray/AMD EPYC 7702 high-performance computing platform. All simulations reported in this section were solved using 16 cores.

Material Models

The values of engineering strain (εeng) and engineering stress (σeng) of the A356-T6 alloy mentioned in the tensile and impact testing subsection were converted into true strain (εt) and true stress (σt) using the following relationships:33

$${\varepsilon }_{t}=\mathrm{ln}\left(1+{\varepsilon }_{\mathrm{eng}}\right)$$
(2)
$${\sigma }_{t}={\sigma }_{\mathrm{eng}}\left(1+{\varepsilon }_{\mathrm{eng}}\right)$$
(3)

The true strain–stress behavior is usually fitted with a power relationship for materials that undergo necking during the tensile strength test. This step was omitted for the A356-T6 alloy because the tensile test specimens failed, corresponding to the ultimate tensile strength. The plastic region of the true strain–stress curve was then entered into LS-DYNA using the piecewise linear plasticity material model (please see supplementary Figure S11). The mechanical properties of the compression platen were simulated using an identical material formulation and using the typical values for 440C stainless steel tempered at 315 °C (E = 200 GPa, σY = 1900 MPa, ρ = 7.75 g/cm3).34

The failure criteria or failure strain (FS) was determined iteratively, highlighting the importance of access to experimental data for model validation. For clarity, the FS (also known as element erosion) parameter in the piecewise plasticity material model is an ad hoc value, which simply indicates the effective plastic strain value at which any given element will be deleted from the calculation.35 This input is sensitive to mesh size,36 and is not recommended for predictions lacking a source of experimental validation. Figure 4 clearly reveals that the computed load–displacement curve fails to model the bedding-in process. Nonetheless, the calculations for peak load and displacement corresponding to the first truss breakage were observed to lie within 10% of the experimental results. Thus, the FE results exhibited good agreement with the experimental data, with the calculated peak load of 65.3 kN versus the 59.4 kN from the experiment, and, similarly, the prediction for the displacement at the first failure was 6.8 mm against the computed value of 6.2 mm.

Fig. 4
figure 4

Deformation sequence of a lattice structure under compressive loading. The fringe plots are set to effective stress (von Mises), and the scale units are given in MPa. The computed results are in good agreement with the experimental data.

Full size image

The fringe plots of the effective stress presented in Fig. 4 depict a lattice structure’s deformation sequence under uniaxial compression, in which 100% or the final state corresponds to a displacement load of 12.5 mm. During the early stages of deformation (< 25%), the load was roughly uniformly distributed in the trusses of the octet arrangement. At this point, the highest stress values were concentrated at the connection points between the latticed portion and the flat plates. At 50% of the prescribed displacement, the stress concentrations were located at the nodes and the aforementioned connection points. Beyond this stage, the trusses underwent significant buckling until they failed at their weakest sections, which were the lower corners of the outer faces. By the end of the simulation, the displacement of the lattice structure was no longer uniaxial but compound instead. This behavior was also observed during the experiments; hence, the agreement of the FE model is quantitatively correct.

Performance Analysis of Various Truss Arrangements

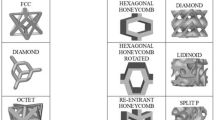
In this subsection, we employ the FE method to assess the performance of other strut-based lattice structures, such as BCC, FCC, and the unit cell derived from Lord Kelvin’s work.24 A new arrangement comprising trusses with circular trajectories is also proposed. These geometries were selected based on their potential for molding with 3D printed sand; in some cases, it is anticipated that multiple-piece cores would be required to perform de-powdering without damaging the molds. The parametric models presented in Fig. 5 were designed similarly to the octet-truss studied earlier in this document. The unit cells were constrained to cubes of 25 mm-long sides, and the trusses were 4 mm in diameter. For the specific case of the circular design, the paths for truss extrusion were described by 25-mm-radius arcs, and all its nodes were located on the faces of the bounding cube.

Fig. 5
figure 5

Truss arrangements analyzed using FEM: (a) Kelvin’s cell, (b) FCC, (c) octet, (d) BBC, and (e) circular truss.

Full size image

Modeling details, such as applied loads, boundary conditions, and material models, were identical to those described in the previous section. Compared to the benchmark of the octet-truss lattice structure's specific internal energy (SIE) (which is the internal energy per unit mass), all other designs exhibited inferior performance. They were also inferior to the octet-truss lattice structure in terms of load-bearing capability, as the octet design withstood a peak load that was approximately 24% higher than the corresponding computed value for the circular truss. The BCC, FCC, and Kelvin’s cell exhibited the lowest masses and the lowest load-bearing capacities; however, no direct correlation between weight and performance was observed (fringe plots of the von Mises stress at 50% loading are shown in supplementary Figure S10).

The computed SIE values (Fig. 6) indicate that the circular truss design proposed in this study outperforms the BCC, FCC, and Kelvin’s cell design; however, it did not exhibit a performance comparable to that of the octet-truss lattice structure. The SIE of Kelvin’s cell and the circular truss decreased after attaining the respective maxima, unlike the other arrangements.

Fig. 6
figure 6

SIE plots. The octet-truss design is the benchmark for comparison.

Full size image

In terms of the calculated results, in conjunction with Maxwell’s criterion for static determinacy, the considered arrangements can be classified into two groups: the octet and circular truss designs are stretching-dominated, whereas the remaining lattices are bending-dominated. As explained by Deshpande et al., since bending at the nodes is eliminated in stretch-dominated cellular solids by design, they exhibit superior strength-to-weight ratios compared to bending-dominated models.5

Selective Optimization of Truss Diameter and Nodal Fillets of the Octet Truss

In this section, we use computational tools to modify the performance of the octet-truss lattice structure. First, we selectively optimize the truss diameter of the unit cell and conduct a parametric assessment of the nodal filleting and its associated weight penalty. These two approaches are then combined to produce a physical component tested under the conditions reported in the Introduction.

Optimization of the Truss Diameters

The octet unit cell was divided into two main components: the FCC sites and the octahedral sites. This approach was adopted for simplicity as it aids the understanding of the individual contribution of each site to the overall performance of this arrangement. It can be generalized to more complex structures if desired; for instance, the diameter of all the trusses could be analyzed independently.

The analysis was conducted using the commercial package, LS-OPT 7.0.0,37 coupled with LS-DYNA, and the following design of experiments (DOE) was used:

  • The diameter of each site was varied between 2 and 5 mm in increments of approximately 0.5 mm, amounting to 49 designs in aggregate.

  • A 2.5 mm displacement load was applied to the upper section of the cell, and the bottom face was constrained against displacements along the vertical axis (Fig. 7).

  • Three responses were selected as the objectives for the DOE: internal energy (IE), reaction force (FR), and mass.

Fig. 7
figure 7

Graphical representation of the octet-truss cell divided into two components; loading and boundary conditions are also indicated.

Full size image

The continuum was discretized into 240 3-dimensional beam elements following the Hughes–Liu formulation. This framework is known for its robustness and simplicity and accounts for transverse shear strains.31,38 A Dell Precision 7920 workstation running Windows 10 was used to solve the DOE.

The computed values of IE and FR are depicted in Fig. 8. An interesting trend is noted for IE, with the higher contributions coinciding with the diameters of the octahedral sites (DOCTA). In contrast, FR exhibits a level of decoupling from the cross-sectional area of the struts. The peak value of FR corresponded to the region where the DOCTA was approximately 3 mm and the diameter of the FCC sites (DFCC) oscillated between 4 and 5 mm.

Fig. 8
figure 8

3-Dimensional graphs of IE (left) and FR (right).

Full size image

All designs with diameters exceeding 4 mm and smaller than 3 mm were eliminated from the analysis following the research of Snelling,17 who, in his thesis, demonstrated that 3D printed sand molds with features smaller than 3 mm in diameter are difficult to de-powder, thus deriving a practical limit.

The individual contribution of each group of struts to the performance of the unit cell during this stage was evaluated, providing important insights. For instance, DOCTA wielded a more direct impact on IE compared to DFCC, the IE corresponding to DOCTA = 5 mm and DFCC = 2 mm was 210, 528.8 N-mm, whereas it was 65, 542.8 N-mm corresponding to DOCTA = 2 mm and DFCC = 5 mm. This was attributed to the response to the loading conditions of the octet unit cell’s component sites as, until the onset of buckling, the octahedral sites were subjected to compressive forces and therefore larger cross-sectional areas were more dominant. On the other hand, load transfer (as represented by FR) was observed to be dependent on a combination of both dimensions. A summary of the computed values is presented in the supplementary Table S3. Subsequently, we focused solely on the design with DFCC = 4 mm and DOCTA = 3 mm, as it exhibited average performances for IE calculation and one of the best FR calculation performances. Thus, it was deemed to exhibit an acceptable compromise with a significant weight reduction at the unit-cell level (approximately 15% with respect to the baseline).

Nodal Filleting

The application of rounded fillets to sharp corners is a well-known design technique to reduce stress amplification, as it typically leads to extended component life under cyclic loading.33,39 Periodic lattice structures generally contain numerous sharp corners at the joints or nodes. Fortunately, this situation can be addressed by adding nodal fillets during the design process, since modern parametric CAD packages include tools created for this purpose. In particular, Latture et al. concluded that nodal filleting of the octet-truss lattice structure improves the bending stiffness of the truss ends, leading to an approximately 20% reduction in buckling stress. However, no significant effect was noted on the axial strain for tensile rupture.40

By nature, cast metals form slightly rounded features at sharp corners. In this section, we discuss the effects of nodal filleting on the performance of cast lattice structures proposed in this work. The fillet radius was varied between 0.5 mm and 1.5 mm in increments of 0.25 mm. The formation of sharp features was observed while incrementing the fillet radius during the design process; these features are speculated to be the result of the constraints imposed by the CAD tool on the fillets of adjacent trusses. Hence, upon reaching a mathematical limit, the fillets expanded along an unconstrained direction to meet the user’s input (see the supplementary Figure S12).

Such sharp features were also noted by Latture et al.;40 however, the text provided no discussion. These artifacts are believed to represent a practical limit regarding the dimensions of nodal fillets. To gain further insights into this phenomenon, we once again relied on the highly non-linear capabilities of the commercial FE package LS-DYNA using the implicit time-integration framework. The discretization and material models used were identical to those described in the computational details subsection.

As anticipated, the load-bearing capabilities of the octet-truss lattice structure increased with the nodal fillet radius. This is illustrated in Fig. 9, in which the applied load is plotted as a function of its resultant displacement. The data are presented until the point of the first predicted failure; the trend in performance appears to be clear up to a radius of 1.25 m. In other words, up to this fillet size, the load and displacement increased with the fillet radius. However, the 1.5-mm model failed at an earlier stage of displacement. Further, the 0.75 mm radius provided the means to classify the performance of these models; below this value, the load–displacement curves exhibited a nearly flat behavior, whereas, when the radius exceeded 0.75 mm, the load just reached a mathematical maximum. The curve representing the 0.75-mm radius achieved a clear peak load, but its first failure occurred a few load steps later.

Fig. 9
figure 9

Effects of nodal filleting; the mechanical response of the structure (right) and its associated weight penalty (left).

Full size image

The performance improvement achieved by adding nodal fillets was accompanied by an inherent weight penalty incurred due to the additional material required to fulfill this operation. For instance, a load-bearing increment of 9% was produced by the 1.0-mm radius at the expense of an additional 3% weight compared to the model with no fillets.

Finally, the computed results from the two previous simulations were used to synthesize additively manufactured sand molds with the following characteristics: DFCC = 4 mm, DOCTA = 3 mm, and nodal fillets of 0.75 mm. The last was selected to account for the mismatch in truss diameters. Four castings were poured in aluminum A356 alloy and two in F356 alloy. After cleaning, all cast lattices were heat treated to the T6 condition under the conditions described in the compression testing subsection. Figure 10 illustrates an example of the structure poured in A356 before and after compression testing.

Fig. 10
figure 10

Experimental load–displacement curves of the A356-T6 octet-truss lattice structures; optimized design of the octet-truss lattice structure; before testing (left) and after testing (right). Unlike the model with a constant truss diameter, the modified version failed at the upper section.

Full size image

During the test, the response of the optimized model to loading and subsequent failure was observed to be different from that of the model with constant truss diameter. The optimized version failed at the upper section of the central row of unit cells. Its displacement followed a vertical trajectory, in contrast to the standard model which failed primarily at the lower corners, with its displacement following compound motion. The most significant improvement achieved using these modifications was the IE enhancement, which was 476 kN mm and 620 kN mm for the standard and optimized models, respectively. From a quantitative perspective, this represents an improvement by 30% in IE with a substantial weight reduction of 12% (the average weight of the optimized model was measured to be 202 g). Similarly, the IE of the optimized model poured in F356 (528 kN mm) was 15% higher than that of the standard version (460 kN mm). It is worth highlighting that the optimized F356 model outperformed the standard A356 in terms of IE by approximately 10%, even though the load-bearing capability of the latter was significantly higher. The load–displacement curves are depicted in Fig. 10. The bedding-in phenomenon was also observed in the optimized model.

Conclusion

Tensile and impact testing of two similar aluminum alloys, A356 and F356, revealed that the more ductile system of the two absorbed more energy. Using these, a hybrid AM/metalcasting technique was utilized to synthesize periodic lattice structures designed around the octet-truss unit cell. Following heat treatment to the T6 condition, the test specimens were subjected to uniaxial loading at low strain rates. The experimental values of IE were observed to be relatively similar, with a net difference of 3% in favor of the structure poured in A356, confirming that ductility plays an essential role in energy absorption. In fact, it is suspected that, if tests were conducted for larger displacements, its role could prove to be dominant.

We developed an FE model based on the experimental results for the A356 cast lattice structure. Subsequently, it was solved using the commercial software, LS-DYNA, under the implicit time-integration framework. Discretization of the continuum was refined until convergence was realized for the applied load and displacement. The failure criteria were determined iteratively using the refined mesh, and good agreement with experimental results was achieved. The model was subsequently employed to study the performance of several strut-based lattice structures: BCC, FCC, Kelvin’s cell, and the octet-truss. Additionally, a new design with circular trusses was introduced. The computed SIE values agreed with Maxwell’s criteria for rigidity, the bending-dominated arrangements (BCC, FCC, and Kelvin’s cell) absorbing significantly less SIE compared to the stretch-dominated designs (octet and circular truss). The circular-truss design introduced in this study failed to match the mechanical performance of the octet truss; however, it represented potential weight reduction of approximately 11%.

The truss diameters of the compounding sites of the octet-truss unit cell were optimized within the constraints of the AM/metalcasting approach. In other words, the cross-sectional dimensions of the octahedral sites were varied independently from the truss diameter of the FCC sites. This task was performed using the optimization package, LS-OPT, in conjunction with LS-DYNA’s FE solver. The results obtained using the full factorial DOE indicated that the octahedral sites exerted the highest impact on the cell’s overall performance in terms of IE. Additionally, LS-DYNA was used to study the effects of nodal filleting on the mechanical response of lattice structures fabricated around the octet unit cell. The load-bearing capacity of the lattice structure increased with the fillet radius until 1.25 mm; beyond this value, additional stress concentrators were inadvertently introduced into the model. Finally, AM molds were designed to incorporate both the truss diameter optimization and nodal filleting. The optimized lattice structures were poured in the aluminum alloys A356 and F356 and heat-treated to the T6 condition. Upon visual observation, it was noted that the optimization tasks altered the failure mode of the lattice structures. The standard model failed, as some of its corner elements broke, leading to subsequent compound displacement. In contrast, the optimized design failed at the upper section of the middle row of unit cells and allowed for more significant deformations. As a result, the optimized models absorbed higher IE with lower FR. Moreover, the optimized F356 component outperformed the A356 version with a constant truss diameter by approximately 10%, proving that ductility exerts a crucial effect on the energy-absorption characteristics of cast lattice structures.