Effects of Applied Pressure on the Atomic Diffusion Coefficient During Spark Plasma Sintering of Crystalline Powders

Abstract

We report on the establishment of a framework to determine the value of the pressure-related atomic diffusion coefficient, D, and its use. Moreover, we clarify the underlying relationships between the as-determined D and the active densification mechanisms during crystalline powder sintering. During spark plasma sintering, the theoretical framework is validated by comparing the densification behaviors of Ti_40.6Zr_9.4Cu_37.5Ni_9.4Sn_3.1 crystalline alloy powders with two types of particle sizes. Our results demonstrate quantitatively that the superimposition of an applied pressure enhances the atomic diffusion to promote densification during crystalline powder sintering.

Introduction

It is well known that powder sintering is a widely used technique of aggregating powder particles into dense compacts by loss of the total interfacial energy of the powder aggregate. During pressureless sintering, the powder shrinkage and densification behavior are generally affected by various physical parameters,1 such as the average particle size (L), surface energy (γ), and viscosity (η). To be more precise, it is affected by the intrinsic driving force γ/L,2 especially during the early densification stage of the neck formation between the powder particles. In terms of pressure-assisted sintering, the applied pressure (P), which acts as an extrinsic driving force, contributes to the powder shrinkage and densification behavior by altering the stacking and geometric structure of the powder particles, shortening the distance between the powder particles and increasing the coordination number, thereby enlarging the contact areas. Based on its unique physicochemical mechanism during the densification stage of the neck formation between powder particles,3 spark plasma sintering (SPS) is a novel consolidation method and is generally used to fabricate fine-grained bulk materials with a novel structure4,5,6,7,8,9 by coupling a thermal-electrical field with an extrinsic mechanical field P.3 Song et al. demonstrated that the applied P has a large influence on the distribution of the temperature field and electrical field, and, consequently, on the densification behavior of the sintered compacts, because the pressure-related effect is similar to hot-pressing, and the individualized contact thermal and electric resistances of powder particles.10 Essentially, as an extrinsic driving force that acts by applying the extrinsic mechanical work to the powder particles, the applied P increases the driving force to promote simultaneous powder shrinkage and densification10 in association with the intrinsic driving force γ/L.2 As classical metallurgy theory shows, the sintering necks and the contact areas increase with the boost of the SPS process during the early stage of powder shrinkage and densification. In terms of physical effects, there is no doubt that atom diffusion plays a crucial role in the early stage of powder shrinkage and densification although complex physicochemical mechanisms occur during SPS.11 However, a pressure-related physical quantity that characterizes the ability of mass transfer has hitherto never been determined during the densification of the crystalline powder particles.

Many studies have reported on the qualitative correlations between the P and the powder shrinkage and densification behavior in SPS.10,12,13,14,15,16 Analytically, Olevsky et al.12 elucidated the influence of the P on the densification mechanism on the basis of the grain-boundary diffusion and power-law creep of the densification-contributing mass transfer. To that effect, Garay et al.15 demonstrated that the applied P promotes the powder shrinkage and accelerates the densification rate. Experimentally, as an additional diffusional driving force, P does not alter the densification mechanism but can increase the densification rate of the powder particles.15 Indisputably, atom diffusion has a key role in the mass transfer and densification behaviors of powder particles during SPS. Hence, it is necessary to establish a quantitative dependence of D on P during SPS.

In this study, we propose a theoretical framework for associating D with P and we demonstrate quantitatively the influence of P on D and thus provide comprehensive insights into the densification mechanisms during SPS of Ti_40.6Zr_9.4Cu_37.5Ni_9.4Sn_3.1 crystalline powders.

Theoretical Methods

Generally speaking, we can estimate the instantaneous relative density, $\rho$ (%), of the sintered compacts through:

$$ \rho = \frac{{H_{0} }}{H}\rho_{0} $$

(1)

where $\rho$ (%) is the relative density when the specimen reaches the height, H (mm), in the die, H₀ (mm) is the initial height of the compacts, and $\rho_{0}$ (%) is the initial relative density. During powder sintering, we can calculate the instantaneous densification rate $\dot{\rho }$ (s⁻¹) by:15

$$ \dot{\rho } = \frac{{{\text{d}}\rho_{i} }}{{{\text{d}}t_{i} }} = \frac{{\rho_{i} - \rho_{i - 1} }}{{t_{i} - t_{i - 1} }} $$

(2)

where the time interval (t_i− t_i−1) is 2 s and $\rho_{i}$ (%) is the instantaneous relative density at time t_i (s).

Generally, viscous flow occurs during the formation and growth of the sintering neck.1 Hence, based on the Frenkel model, the intrinsic driving force, γ/L, induces the shrinkage and densification of the powder during pressureless sintering,2 which can be calculated as follows:16

$$ \frac{\Delta H}{{H_{0} }} = \frac{3\gamma }{4L\eta }t $$

(3)

In the case of pressure-assisted sintering, as an extrinsic driving force, the pressure, P, promotes the shrinkage and densification of the powder particles.2,15,17 In this condition, the contribution of the extrinsic pressure P to the driving force is defined as BP.1,2,17 Correspondingly, we can determine the shrinkage of the powder assembly under the pressure-assisted sintering using the modified equation:

$$ \frac{\Delta H}{{H_{0} }} = \left( {\frac{\gamma }{L}} + {BP} \right)\frac{3t}{4\eta } $$

(4)

where ΔH/H₀ is the shrinkage of the powder assembly, L (m) the average particle size, γ (1 J/m²) the surface energy, P the extrinsically applied pressure, B a constant related to the particle size and powder geometry, t (s) the time, and η (Pa s) the viscosity of the powder material. Accordingly, on the right side of Eq. 4, the first term represents the intrinsic driving force induced by the interfacial energy, γ, and the second term represents the extrinsic driving force caused by the pressure, P.

Generally, viscous flow occurs during the early stage of crystalline powder sintering and generates macroscopic densification shrinkage.1,14,17 Physically, the sintering necks induced by the viscous flow are the result of microscopic atomic diffusion motion.18,19,20 In this regard, we can correlate the coefficient D with the η according to diffusion theory:19,20

$$ \eta = \frac{{kTa^{3} }}{{D\delta^{3} }} $$

(5)

where D (m²/s) is the atom diffusion coefficient, a (m) the average grain size, δ the atom diameter (2.89 Å for Ti), T (K) the absolute temperature, and k (1.38 × 10⁻²³ J/K) the Boltzmann constant.

In pressureless sintering, the diffusion coefficient, D is dependent on the temperature and conforms to the Arrhenius relationship:21

$$ D = D_{0} \exp \left( {\frac{ - Q}{RT}} \right) $$

(6)

where $Q$ (kJ/mol) is the activation energy for the atomic diffusion, R (8.314 J/K/mol) the universal gas constant, and D₀ (m²/s) the pre-exponential factor. In an isochronal experiment, we can determine the relationship between the temperature, T. and time, t, by:

$$ \frac{{{\text{d}}T}}{{{\text{d}}t}} = c $$

(7)

where c (0.5 K/s) is the heating rate. Hence, by differentiating Eq. 4 with reference to T and using Eqs. 5–7, the shrinkage of the powder particles can be defined as:

$$ \frac{{{\text{d}}\left( {\frac{\Delta H}{{H_{0} }}} \right)}}{{{\text{d}}T}} = \left( {\frac{\gamma }{L}} + {BP} \right)\frac{{3\delta^{3} D_{0} \exp \left( {\frac{ - Q}{RT}} \right)}}{{4kca^{3} T}} $$

(8)

By using the logarithm on both sides, Eq. 8 is expressed as:

$$ \ln \left( {T\frac{{{\text{d}}\left( {\frac{\Delta H}{{H_{0} }}} \right)}}{{{\text{d}}T}}} \right) = \ln \left( {\frac{{\left( {\frac{\gamma }{L}} + {BP} \right)3\delta^{3} D_{0} }}{{4kca^{3} }}} \right) - \frac{Q}{RT} $$

(9)

Generally, the γ, L, and D₀ of the powder particles remain constant for a specific composition. Therefore, in our case, a material factor of the powder particles w is defined based on various physical parameters:

$$ w = \frac{{3\delta^{3} D_{0} }}{{4ka^{3} }}\left( {\frac{\gamma }{L}} + {BP} \right) $$

(10)

Hence, at a given pressure, P, we can determine the value of the factors $Q$ and w from the slope and the intercept of the plots of ln(Td(ΔH/H₀)/dT) versus 1/T (Eq. 9), respectively.

On the basis of diffusion theory,15,17 the effect of the extrinsic P on the densification behavior can be qualitatively described as an accelerating densification process by increasing the coefficient D between the powder particles if $Q$ does not change. In other words, the extrinsic P can be considered a potential field to generate a net flux of atoms,15 which influences the diffusion constant of the pre-exponential factor to promote mass transfer:

$$ D^{P} = D_{0}^{P} \exp \left( {\frac{ - Q}{RT}} \right) $$

(11)

where $D_{0}^{P}$ (m²/s) is the corresponding item of the increasing diffusion constant, which results in an additional diffusion flux, $D^{P}$ (m²/s), in combination with the extrinsic P. There is no doubt that the pre-exponential factor, $D_{0}$, in Eq. 6 is closely related to various physical parameters of the powder particles, such as the γ, L, and η. Hence, the $D_{0}^{P}$ resulting from the extrinsic driving force BP is assumed to be dependent on the $D_{0}$ stemming from the intrinsic driving force, γ/L. In our case, this relationship can be rationalized as:

$$ \frac{{\frac{\gamma }{L}}}{{D_{0} }} \cong \frac{BP}{{D_{0}^{P} }} $$

(12)

According to Eqs. 11 and 12, Eq. 10 can also be written as:

$$ w = \frac{{3\delta^{3} D_{0} }}{{4ka^{3} }}\left( {\frac{\gamma }{L} + BP} \right) = \frac{{3\gamma \delta^{3} }}{{4Lka^{3} }}(D_{0} + D_{0}^{P} ) = \frac{{3\gamma \delta^{3} }}{{4Lka^{3} }}D_{0}^{T} $$

(13)

where $D_{0}^{T}$ (m²/s) is the total effective diffusion constant under the condition of the extrinsic P. Furthermore, the total effective diffusion coefficient, $D^{T}$, can be determined by:

$$ D^{T} = D_{0}^{T} \exp \left( {\frac{ - Q}{RT}} \right) $$

(14)

Experimental Procedure

To prove the aforementioned theoretical framework, we selected spherical Ti_40.6Zr_9.4Cu_37.5Ni_9.4Sn_3.1 (at.%) metallic glass powders, which were manufactured via an electrode induction melting gas atomization (EIGA) powder device (AMC-EIGA-50). To ultimately eliminate the deviations induced by the grain size and obtain the crystalline powder particles, the atomized powders were annealed at 1000 K for 40 min in a vacuum-sealed quartz tube, and were then sieved inside a vacuum glove box into two types of particle sizes. Subsequently, the two types of powders were characterized by x-ray diffraction (XRD) (D/MAX-2500/PC, Rigaku, Tokyo, Japan), field emission gun transmission electron microscopy (TEM) (Tecnai G2 F30 FEI, USA), differential scanning calorimetry (DSC) (Netzsch STA 409C, Bavaria, Germany) at 20 K/min, laser scattering particle size distribution analysis (LA-960S; Horiba, Japan), and scanning electron microscopy (SEM) (Philips XL-30 FEG, Amsterdam, Netherlands). Then, the crystalline powders were sintered in the SPS system under the protection of an argon atmosphere (SPS-825; Sumitomo Coal Mining, Japan). To minimize errors in the experiments, the same powder weight of 12 g was used in both cases and the powder was placed into a ϕ15-mm graphite die with sintering pressures of 15 MPa, 30 MPa, 45 MPa, and 60 MPa. The details of the SPS can be found in Refs. 7,8,9. In addition, to derive the values of $D_{0}^{T}$, $Q$, and the resulting $D^{T}$ of the two types of powders, the sintering parameters such as the temperature (T), linear shrinkage (H), and time (t) were recorded every 2 s via software.

Results and Discussion

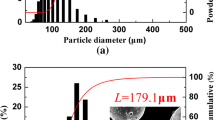
As shown in Fig. 1a and b, the examination of the particle size distribution and the SEM morphology indicates that the two types of powders had spherical particles with size ranges of 25–300 μm and 50–500 μm, which are hereafter called the fine and coarse powders, respectively. The values of the L are approximately 94.7 μm for the fine powder (Fig. 2a) and 179.1 μm for the coarse powder (Fig. 2b). The TEM observations and statistical results of 398 grains (Fig. 1c and d) indicate that the values of the average grain size a are 201 nm for the fine powder (Fig. 2c) and 208 nm for the coarse powder (Fig. 2d). The deviation of less than 3% for the values of a has a negligible influence on the coefficient D^T and the underlying densification mechanism. Furthermore, as depicted in Fig. 3, the XRD patterns and DSC curves of the two types of powders indicate that both powders have identical phase components. These results indicate that the L can be separated from the various physical parameters of the two types of powders, hence providing an approach for investigating the underlying densification-contributing mass transfer (D^T) and thus densification mechanism at various applied pressures.

Fig. 1

SEM morphologies (a, b) and TEM images (c, d) of the fine (a, c) and coarse (b, d) Ti_40.6Zr_9.4Cu_37.5Ni_9.4Sn_3.1 crystalline alloy powders, respectively

Fig. 2

Particle size distributions (a, b) and grain size distributions (c, d) of the fine (a, c) and coarse (b, d) Ti_40.6Zr_9.4Cu_37.5Ni_9.4Sn_3.1 crystalline alloy powders

Fig. 3

XRD patterns (a) and DSC curves (b) of the two types of Ti_40.6Zr_9.4Cu_37.5Ni_9.4Sn_3.1 crystalline alloy powders

To support this inference and on account of Eq. 1, in Fig. 4a and b, we show the plots of the relative density of the two types of powders as a function of the temperature at various value of P. Apparently, all densification curves exhibit the typical S-type curve of the densification process. In addition, the fine powder has a smaller initial density than the coarse powder for the same P, which is ascribed to the larger L of the coarse powder. Peculiarly, the relative density of all the crystalline powders increases with the P at the specific temperature.

Fig. 4

Relative density (a, b) and densification rate (c, d) of the fine (a, c) and coarse (b, d) Ti_40.6Zr_9.4Cu_37.5Ni_9.4Sn_3.1 crystalline alloy powders as a function of temperature at various applied pressures, respectively

To further clarify the densification-related information, according to Eq. 2, Fig. 4c and d shows the instantaneous densification rate of both types of crystalline powders as a function of the temperature at various value of P. We can observe two interesting results. First, at a specific applied pressure, the greater the L, the higher the $\dot{\rho }$ during the early stage of powder densification in the temperature range of about 890–950 K. Second, and more importantly, the $\dot{\rho }$ increases with the P for the two types of crystalline powders at a specific temperature. Rationally, the results may give rise to the different values of $Q$ and w and thus $D^{T}$ for both types of powders.

To verify this inference, Fig. 5a and b shows the plots of ln(Td(ΔH/H₀)/dT) versus 1/T for both crystalline powders at various values of P according to Eqs. 3–9. The values of the derived $Q$ and w are displayed in Table I. It is apparent that the value of $Q$ is almost independent of the P for a particular type of crystalline powder, which conforms to the widely accepted concept that moderate pressure has a negligible effect on the activation energy of atomic diffusion.15 In addition, the value of the intercept w increases with the P for both types of powder, in agreement with Eq. 10. Undoubtedly, this is attributed to the extrinsic P. Subsequently, based on Eq. 13 and the derived w, the $D_{0}^{T}$ is determined (Table I). The lower values of the w and the resulting $D_{0}^{T}$ for the Ti atoms at the specific P for the coarse powder can be rationalized as the comprehensive effects of various physical parameters,14 including the larger L, the smaller γ, and, especially, the BP resulting from the extrinsic P. Finally, the diffusion coefficient, $D^{T}$, of the Ti atom can be determined by the values of $Q$ and $D_{0}^{T}$ using Eq. 14. For example, at a specific pressure of 15 MPa, the coefficient $D^{T}$ of the Ti atom can be expressed as $D_{\text{Fine}}^{T}$= 6.22 × 10⁻¹³exp(− 109.4 kJ·mol⁻¹/RT) m²·s⁻¹ and $D_{\text{Coarse}}^{T}$= 4.46 × 10⁻¹³exp(− 99.6 kJ·mol⁻¹/RT) m²·s⁻¹, respectively. Correspondingly, Fig. 5c and d depict the coefficient $D^{T}$ of the Ti atom dependence on the temperature with various values of P for both types of crystalline powders. The $D^{T}$ increases with the temperature during the early stage of powder densification in the temperature range of about 890–950 K. Importantly, the $D^{T}$ increases with the P at a particular temperature. This definitely proves quantitatively that the extrinsic pressure has a significant impact on the densification-contributing mass transfer $D^{T}$.

Fig. 5

Plots (a, b) of ln(Td(ΔH/H₀)/dT) versus 1/T and Ti atomic diffusion coefficient $D^{T}$ (c) as a function of temperature of Ti_40.6Zr_9.4Cu_37.5Ni_9.4Sn_3.1 crystalline alloy powders at various applied pressures, respectively. (d) The interrelation between Ti atomic diffusion coefficient $D^{T}$ (upper part), densification rate $\dot{\rho }$ (middle part), and relative density ρ (lower part), and difference in relative density (inset) of Ti_40.6Zr_9.4Cu_37.5Ni_9.4Sn_3.1 crystalline fine powders as a function of temperature at 15 MPa and 30 MPa, respectively

Table I The value of the $Q$, the w and the $D_{0}^{T}$ of Ti atom for the two types of Ti_40.6Zr_9.4Cu_37.5Ni_9.4Sn_3.1 crystalline alloy powders at various applied pressures

In the upper part of Fig. 5d, it is observed that the values of the as-determined $D^{T}$ are far greater than the corresponding values of the Ti atoms in α-Ti calculated by a radiotracer method in the same temperature range.22 This may be attributed to the accelerated atomic diffusion ability induced by the high-density pulsed electric current during SPS.23 This result is in agreement with other material system research results. For example, Li et al.24,25 demonstrated the current-enhanced atomic diffusion kinetics and densification kinetics during SPS. Moreover, experiments and modeling have shown that the rapid densification is essentially caused by the current, which accelerates the mass transfer and increases the dislocation mobility. Logically, these results validate the established framework that can be used to derive the value of the coefficient, $D^{T}$. Most importantly and interestingly, we can elucidate the underlying densification mechanism of the two types of powders based on the relationship between the coefficient $D^{T}$ and the $\dot{\rho }$ and thus ρ. Intuitively, the larger the coefficient $D^{T}$ (Fig. 5d, upper part), the higher the $\dot{\rho }$ (Fig. 5d, middle part) and the faster the powder densification (Fig. 5d, lower part). This causes an increasing difference in the ρ at 15 MPa and 30 MPa for the fine powder (inset of Fig. 5d, lower part). A similar result is observed for the coarse powder. In other words, this indicates that the coefficient $D^{T}$ acts as a physical quantity governing the densification mechanism of the powder particles.

In addition, the values of the $D^{T}$ of the coarse powder at a specific applied pressure are always higher than those of the fine powder (Fig. 5c). This may be due to the lower $Q$ for the coarse powder (Table I). For example, Fig. 6a shows the difference in the $D^{T}$ of the Ti atoms and the $\dot{\rho }$ for the two types of powders at 15 MPa as a function of the temperature. Interestingly, the two differences increase with the temperature. Note that the same change trend of the $D^{T}$ and $\dot{\rho }$, i.e., the increased $D^{T}$ accompanied by the increased $\dot{\rho }$ with the temperature during the early stage of powder densification, in the temperature range of about 890–950 K, confirms that the $D^{T}$ may act as a main factor governing the densification mechanism of the powder particles. Similar results can be observed at other pressures. Theoretically, the increase in the $D^{T}$ accompanied by the increase in the L (Fig. 6a) can be explained by local overheating in the contact regions between the powder particles inside the sintering necks. Based on the individualized heating mode during SPS, the overheating can be calculated by:26

$$ \Delta T = \frac{{16I^{3} \rho_{r} \Delta t}}{{\pi^{4} C_{V} \rho_{m}\Phi ^{4} }}\left[ {\frac{{r^{2} }}{{r^{2} - \left( {r - X} \right)^{2} }}} \right]^{2} $$

(15)

where $\Delta T$ is the overheating degree at a distance X from the surface of a powder particle with the radius r, I the current, $\rho_{r}$ isthe material resistivity (1.07 × 10⁻⁶ Ω·cm), $\Delta t$ the pulse time (0.1 s), $C_{V}$ the material heat capacity (25.01 J/K/mol), $\rho_{m}$ the material density (6.65 g/cm³), and $\Phi$ (15 mm) the inner diameter of the die. Therefore, the overheating of the two types of powders can be determined using Eq. 9, and the results are shown in Fig. 6b and c. We observe that the $\Delta T$ decreases with the distance X from the surface of the powder particles, indicating that the overheating only occurs in a very thin surface layer. Specifically, the larger the L, the higher the $\Delta T$. For example, the $\Delta T$ with a distance X of 0.2 μm at 890 K is 375 K and 143 K for the coarse and fine powders, respectively. Therefore, a higher $\Delta T$ for a larger L would generate a stronger degree of thermal softening and localized melting at the contact regions between the powder particles, consequently resulting in a weakening binding force between the atoms,17 decreasing the $Q$ (Table I), and ultimately increasing the $D^{T}$ (Fig. 6a).

Fig. 6

The difference (a) in the $D^{T}$ of Ti atom and the $\dot{\rho }$ for the two types of Ti_40.6Zr_9.4Cu_37.5Ni_9.4Sn_3.1 crystalline alloy powders as a function of temperature at 15 MPa. The overheating $\Delta T$ (b, c) with the distance X from the surface of a powder particle at 890 K (b) and 950 K (c) for the two types of Ti_40.6Zr_9.4Cu_37.5Ni_9.4Sn_3.1 crystalline alloy powders, respectively

Conclusion

A theoretical framework was developed to quantitatively derive the diffusion constant, $D_{0}^{T}$, the activation energy, $Q$, and the resulting $D^{T}$ related to the applied P and provide further insights into the underlying densification mechanism of a Ti_40.6Zr_9.4Cu_37.5Ni_9.4Sn_3.1 crystalline powder during SPS. In the range of 15–60 MPa, the larger the P, the larger the $D^{T}$ and thus the larger the $\dot{\rho }$ for both types of Ti_40.6Zr_9.4Cu_37.5Ni_9.4Sn_3.1 crystalline powder. In addition, the $D^{T}$ is lower for the fine powder than the coarse powder, which is ascribed to the smaller surface, the overheating $\Delta T$, and the larger $Q$. Finally, our results demonstrate quantitatively that the pressure elevates the atomic diffusion flux during crystalline powder sintering.