Envelopes and Offsets of Two Algebraic Plane Curves: Exploration of Their Similarities and Differences

Abstract

Several non equivalent definitions exist for the envelope of a 1-parameter family of plane curves. Another notion, often considered as related to envelopes, is the offset at a given distance of a plane curve. Using the so-called analytic definition, we study and compare the envelope of a 1-parameter family of circles centered on a parabola and an offset of this parabola. Then we perform a similar study for an astroid. This illustrates the non equivalence of the two notions. The work is performed with networking with a Computer Algebra System and a Dynamical Geometry System, bringing them into a certain form of dialog. The obtained curves are sextics, and their discovery as envelopes leads to an automated exploration of Talbot curves. Another output shows these curves within a unifying framework involving a Maltese Cross.

1 Introduction

Dynamic Geometry Systems (DGS) have been developed along the last decades, as a technological tool enabling direct manipulation and visualization of all the objects of plane geometry. These packages offer the possibility of directly modifying features and configurations, either by dragging points with the mouse, or using a slider bar. The adjective ”dynamic” expressed that, once the geometric construction has been performed, the original points may be dragged, either with the mouse or with a slider bar, the changes in the resulting constructs can be analyzed, and results may be conjectured. These systems take an always-growing place in classrooms and labs, for exploration, discovery, experimentation and research; see [4, 5, 7, 8, 31]. We refer to Wu’s work in the 1980’s [37,38,39] and to new algorithms which have been implemented more recently, such as automated proofs and automated discovery. Recio and Vélez say: ”While automatic proving deals with verifying geometric statements, automatic discovery tries to find complementary hypotheses for statements to become true or ... to find the missing hypotheses so that a given conclusion follows from a given incomplete set of hypotheses.”

GeoGebra’s command Locus and LocusEquation for the automated determination of geometric loci are now well documented and widely used; see [1, 4, 29]. A command Envelope exists for the automated determination of envelopes. Kovács reports in [24] that ”animations can be performed quickly enough by using today’s computers with implicit computer algebra use. In the background, without notifying the user on the fact that thousands of symbolic computations are performed, a pure dynamic geometry experience can be relived, making geometry more geometrical than before.” More advanced features are now available as a companion package called GeoGebra discovery (freely downloadable from https://github.com/kovzol/geogebra-discovery). They are described in [30].

The different algorithms have also different requirements. If Locus works when the tracer is either a variable point or a slider (representing a parameter), the current version of Envelope requests the tracer to be a variable point and not a slider for variations of a real parameter; see [11]. This has an influence on our choices here: in some cases, we can rely on a purely geometric construction, but not always.We use parametric representations (whence the necessity of a slider) and not pure geometric constructions. This has been already the case for the study of a Maltese Cross as an envelope in [15].

The basic curves of our study are real algebraic curves. At first,we use a trigonometric parametrization of the astroid, and not a rational one. The reason is that the animations are easier to understand, the mobile point moving more regularly with the trigonometric parametrization than with a rational one. Nevertheless, at a certain step, we transform the trigonometric expressions into rational expressions, then the parametric equations are transformed into polynomial equations. These polynomials generate an ideal, and using the Gröbner bases package of a CAS and the computation of an Elimination Ideal , we obtain an implicit equation for the desired envelope. This method has been used extensively in [14, 15, 17, 18]. Hašek translated ”pure” geometric data into polynomials, then used the same methods. For more details, we refer to [13]. A problem still exists: irrelevant components may appear. This issue is discussed, and ways to solve it are described, in [27] and [10].

We study offsets and envelopes (see Def. 1 in Sect. 2) of the astroid $\mathcal {A}$, given by the implicit equation

$$\begin{aligned} |x|^{\frac{2}{3}} +|y|^{\frac{2}{3}} =1. \end{aligned}$$

(1)

Actually $\mathcal {A}$ is a real algebraic curve given by the following equation:

$$\begin{aligned} (x^2+y^2-1)^3+27x^2+y^2=0. \end{aligned}$$

(2)

It is displayed in Fig. 1.

Fig. 1

An astroid (color figure online)

The astroid $\mathcal {A}$ has a simple trigonometric parametrization

$$\begin{aligned} {\left\{ \begin{array}{ll} x(t)=\cos ^3 t \\ y(t)= \sin ^3 t \end{array}\right. },\quad t \in [0, 2\pi ]. \end{aligned}$$

(3)

which is valid for the entire astroid, i.e. to every point of $\mathcal {A}$ corresponds a value of the parameter. $\mathcal {A}$ has also rational parametrizations (see [35]). One of them is as follows (explained in [15]):

$$\begin{aligned} {\left\{ \begin{array}{ll} x(t)=\left( \frac{1-t^2}{1+t^2} \right) ^3 \\ y(t)=\left( \frac{2t}{1+t^2} \right) ^3 \end{array}\right. },\quad t \in \mathbb {R} \end{aligned}$$

(4)

In this case, the parametric presentation represents almost all points of $\mathcal {A}$. This is a general situation with rational parametrizations of plane curves. Note that we use one specific parametrization of the unit circle, but there are infinitely many. Anyway, the final result of our study is not changed by a change of the rational parametrization of the unit circle. We invite the interested reader to try. When needed, we switch between representations of the astroid.

In next Section, we explore both the envelope of a family of unit circles centered on $\mathcal {A}$ and the offset at distance 1 of $\mathcal {A}$. The output shows a new construction of the family of Talbot curves. By ”new”, we mean that we did not find it in the literature. Another output is the connection with other curves, namely Maltese Cross and ovals, showing them as members of the same family. In this work, we use both a trigonometric and a rational parametrization also for the algebraic curves under study. The respective merits of both kinds of parametrization for constructing the animations are discussed then; see also [15].

2 Envelopes

In [9], Botana and Recio report on up to four different definitions of an envelope and refer to [6], where a detailed description of the history and divergences concerning the definition of an envelope can be found, as well as a set of bibliographic references on this topic, pointing out the classical book by Bruce and Giblin [12], the most reputed and complete source of information on this subtle topic. They describe also difficulties and the then state-of-the-art of the computation of envelopes with a DGS. Usage of these commands have constraints, related to the underlying algorithms and the kind of input that they request. The envelopes studied in [15] illustrate some of the differences between the definitions.

Kock [23] gives three definitions of an envelope of a 1-parameter family of plane curves:

Definition 1

Let $\mathcal {C}_k$ be a family of real plane curves dependent on a real parameter k.

• 1. Synthetic The envelope $\mathcal {E}$ is the union of the characteristic points $M_k$, where the characteristic point $M_k$ is the limit point of intersections $\mathcal {C}_k \cap \mathcal {C}_{k+h}$ as $h \rightarrow 0$. In other words, the envelope is the set of limit points of intersections of nearby curves $\mathcal {C}_{k}$,

• 2. Impredicative The envelope $\mathcal {E}$ is a curve such that at each of its points, it is tangent to a unique curve from the given family. The locus of points where $\mathcal {E}$ touches $\mathcal {C}_k$ is called the $\mathcal {E}-$characteristic point $M_k$.

• 3. Analytic Suppose that the family of curves $\mathcal {C}_k$ is given by an equation $F(x,y,k)=0$ (where k is a real parameter and F is differentiable with respect to k), then an envelope $\mathcal {E}$ is determined by the solution of the system of equations:

  $$\begin{aligned} {\left\{ \begin{array}{ll} F(x,y,k)=0 \\ \frac{\partial F}{\partial k} F(x,y,k)=0 \end{array}\right. },\quad \end{aligned}$$

  (5)

  i.e., the envelope is the projection onto the (x, y)-plane of the points, in the 3-dimensional (x, y, k)-space, belonging to the surface with equation $F(x, y, t) = 0$ and having tangent plane parallel to the k-axis (or being singular points and, thus, not having tangent plane, properly speaking). See [12], p.102.

Note that the analytic definition 1.3 is the only definition given by Berger [3](sections 9.6.7 and 14.6.1).

Bruce and Giblin [12] (p. 107–108) denote the synthetic envelope by $E_1$, the impredicative by $E_2$ and the analytic by $\mathcal {D}$. Then they prove that $E_1 \subset \mathcal {D}$ and $E_2 \subset \mathcal {D}$.

Kock [23] analyzes the problems raised by each of the three definitions that he mentions. In particular he notes that impredicative definition is hard to apply, as the notion of limit points is not well-defined.

If the existence (and the nature) of an envelope $E_2$ has been conjectured, verification is performed that the conjectured curve is tangent to every curve in the given family. This can be done experimentally using a DGS, e.g. with GeoGebra’s command IsTangent, or algebraically, i.e. solving a system of equations and showing that for any value of the parameter, there is a double solution, which describes a point of tangency. An activity with students, based on the impredicative definition, is described in [17], together with a short proof that $E_2 \subset \mathcal {D}$.

A $4^{\text {th}}$ definition of an envelope can read as follows ([6, 9]:

Definition 2

The envelope is the curve that bounds the planar region described by the points belonging to the curves in the family.

This fits Def. 5.16 of an envelope $E_4$ in [12] (p. 110); there they prove that $E_4 \subset \mathcal {D}$. Difficulties in determining such an envelope are pointed out in [15].

None of the definitions has a condition of uniqueness of an envelope. More than two disjoint curves can meet the requirements of one of the definitions, each one is an envelope, and their union also. This is illustrated in Sect. 4.

We study a 1-parameter family of unit circles centered on an astroid, and show also the difference between Def. 1 and Def. 2. On the one hand, work is based on the solution of System (5), then on plots and animations of curves given by parametric equations, and not on pure geometric constructions). Therefore, when working with GeoGebra, we do not use its automated command Envelope, and rely on analytic-algebraic computations. On the other hand, the physical meaning seems different from what is called an offset, a notion explored in Sect. 3.

The kind of needed computations may show the limits of the usage of a DGS only and incite to joint work using both a DGS and a CAS:

• The DGS allows to explore, to make experiments, but may not be able to give a definitive answer. Of course, this depends on the abilities of a CAS which can be included in the DGS.¹ The usage of the DGS’s Trace On command enables to conjecture the existence of an envelope, and even to preview its shape. Once again, this depends on which definition of an envelope is considered.

• Precise computations are performed using the CAS. They provide a parametric presentation of the envelope, and also may provide an implicit equation.

• Copying these equations back into the DGS, an animation can be programmed, and used by hand, we mean moving the tracer using the mouse.

• A more automatic animation can be programmed using the CAS.

Actually, both the DGS and the CAS may have a Trace ability, but their affordances in the two kinds of software are generally different. The CAS requires the writing of commands for animations, where the parameters are defined. After a first plot is displayed, the animation can be launched, and parameters such as speed, number of frames, may be modified by hand. The plot provided by a DGS is immediately interactive and points can be moved by direct action on the screen. Both CAS and DGS enable to export the animation as an animated GIF. In a previous work [20], we expressed the wish to see in the near future automatization of a dialog between CAS and DGS. The present work is another opportunity to express the same wish.

We used generally the GeoGebra discovery package, whose commands Locus, Envelope etc. are more powerful than their parent command in the Classic 5 version of GeoGebra.They have also useful extensions; see [30].

3 Offsets

We begin with the following informal definition of an offset [2, 12]:

Definition 3

An offset to an irreducible algebraic plane curve $\mathcal {C}$ is a curve ”parallel” to $\mathcal {C}$ at a fixed distance d.

Roughly speaking, a first understanding of this definition may be as follows: consider the family of circles centered on $\mathcal {C}$ with radius d and look for the envelope of this family in the sense of the analytic definition 1.3. We may use GeoGebra’s Envelope command, whose output is both a plot of the envelope and an implicit equation.

Actually, Def. 3 should be rephrased:

Definition 4

Let $\mathcal {C}$ be an irreducible real algebraic plane curve, and let $\mathcal {C}_0 \subset \mathcal {C}$ be the set of regular points P of $\mathcal {C}$ i.e. points where the norm, in the metric affine space $\mathbb {R}^2$, of the normal vector is non-zero. Then, the offset of $\mathcal {C}$, at distance d, is the Zariski closure of the intersection points of the circles of radius d centered at each point $P \in \mathcal {C}_0$ and the normal line to $\mathcal {C}$ at p.

A more formal definition can be found in [33].

We study now offsets of a parabola and of an astroid. Comparison with envelopes of families of circles shows that the two objects may coincide, but not always. We chose $d=2$ for the plot to be clear enough at first glance.

3.1 Offsets of a parabola

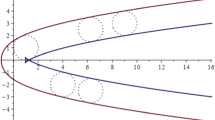
Denote by $\mathcal {P}$ the parabola whose equation is $y=x^2$ and consider the family of circles with radius d centered on $\mathcal {P}$. For every d, an equation of degree 6 is obtained. A GeoGebra applet, for variable d, is available at https://www.geogebra.org/m/vchxdnt4.

As an example, the offset at distance 2 of the parabola $\mathcal {P}$ is displayed in Fig. 2; its has been obtained according to Def. 4. It shows that the offset is the union of two disjoint components.

Fig. 2

Offset at distance 2 of the parabola whose equation is $y=x^2$ (color figure online)

The plot (actually an animation) has been obtained with Maple. The dashed line is the normal to the parabola at the given point. The reader identifies the points of intersection of the normal with the circle as points of tangency with the offset. Here is the code that we used, with general d:

The (general) output provides two parametric presentations:

$$\begin{aligned} {\left\{ \begin{array}{ll} x &{}= t-\frac{2dt}{\sqrt{4t^2+1}} \\ y &{}= t^2 + \frac{d}{\sqrt{4t^2+1}} \end{array}\right. } \end{aligned}$$

(6)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} x &{}= t-\frac{2dt}{\sqrt{4t^2+1}} \\ y &{}= t^2 - \frac{d}{\sqrt{4t^2+1}} \end{array}\right. } \end{aligned}$$

(7)

For $d=2$, Equations (6) define the inner component of the offset (with cusps), and Equations (7) define the outer component of the offset, as shown in Fig. 2.

Algebraic manipulations transform Eq. (6) into polynomial data; two polynomials are obtained:

$$\begin{aligned} P_1(x,y,t)= & {} -4d^2t^2 + 4t^4 - 8t^3x + 4t^2x^2 + t^2 - 2tx + x^2 \\ P_2(x,y,t)= & {} 4t^6 - 8t^4y + t^4 + 4t^2y^2 - 2t^2y - d^2 + y^2 \end{aligned}$$

Let $J=<P_1,P_2>$ be the ideal generated by these polynomials in $\mathbb {R}[x,y,t]$. By elimination of the variable t, an ideal $J_E$ in $\mathbb {R}[x,y]$ is obtained, generated by a single polynomial F(x, y) of degree 12 in x, y. This polynomial is reducible, it has two factors of degree 6:

$$\begin{aligned} F_1(x,y)= & {} 16 d^6 - 48 d^4 x^2 - 16 d^4 y^2 + 48 d^2 x^4 + 32 d^2 x^2 y^2 - 16 x^6 - 16 x^4 y^2 - 32 d^4 y + 24 d^2 x^2 y\\&+ 32 d^2 y^3 + 8 x^4 y + 32 x^2 y^3 - 24 d^4 - 92 d^2 x^2 + 40 d^2 y^2 - 9 x^4 + 32 x^2 y^2 - 16 y^4 + 24 d^2 y \\&+ 18 x^2 y - 24 y^3 + 9 d^2 - 9 y^2\\ F_2(x,y)= & {} 16 d^6 - 48 d^4 x^2 - 16 d^4 y^2 + 48 d^2 x^4 + 32 d^2 x^2 y^2 - 16 x^6 - 16 x^4 y^2 - 32 d^4 y - 8 d^2 x^2 y \\&+ 32 d^2 y^3 + 40 x^4 y + 32 x^2 y^3 + 8 d^4 + 20 d^2 x^2 + 8d^2y^2 - x^4 - 32x^2y^2 - 16y^4 - 8d^2y\\&+ 2x^2y + 8y^3 + d^2 - y^2 \end{aligned}$$

One of them determines the offset (substitute $d=2$ in $F_1(x,y)$ to obtain Fig. 2, both components at once). The $2^{nd}$ factor determines an irrelevant component. A general discussion of this issue is beyond the scope of the present work; we refer to [10, 27]. Applying the same method to Eq. (7) yields the same result.

The code that we used is as follows:

Fig. 3

The offset at distance 1 of the astroid (color figure online)

Remark 1

Applying the analytic definition of an envelope 1.3 , the same curve is obtained. Here $\mathcal {D}$ and the offset at distance 2 are identical. The situation is different for the curves studied in [15]. Section 3.2 and Sect. 4 show also a situation where the two curves, the offset at distance d and the corresponding envelope of circles of radius d, are different; see Fig. 3 sq.

Remark 2

A detailed study of an envelope of unit circles centred on the parabola whose equation is $y=4x^2$ is given as an example in [13] (p. 140 sq.). Work is based on the analytic definition and points out the fact that there is one circle tangent to the envelope at every non singular point, and two circles at singular points. The study contains details on the computation of a Gröbner basis and the meaning of each of the polynomials in this basis. The Elimination Theorem ([13], p. 114) is a central tool. At the end of the study, the authors refer to [12] (Chap. 5) for a more complete treatment of the question.

3.2 Offset of an astroid

Using the DGS, we perform a geometric construction of the offset of the astroid at distance 1: for each point A on the astroid, we plot the unit circle centred at A and the normal to the astroid at A. They intersect at two points, one internal and one external. We denote by B the external point. The offset at unit distance of the astroid is the geometric locus of B when A runs over the entire astroid. The plot generated with GeoGebra’s Locus command is displayed in Fig. 3.

The geometric locus of the point B is the union of four curved triangles, Because of the symmetries of the constructions, the four triangles are isometric and we can analyze the situation in the first quadrant only; things are similar in the 3 other quadrants. Denote by D, E, F the vertices of the curved triangle in the first quadrant, as shown in Fig.  3b. Moving the point A along the arc of astroid in Quadrant I, we discover that the vertices E and F do not correspond to a cusp of the astroid, but when the point A is at the northernmost cusp of $\mathcal {A}$, then the corresponding point C of the offset is at vertex D of the triangle. Actually, here we have a situation of non-uniqueness, as our construction yields two points C, one as vertex of the component of the offset in Quadrant I, and one in Quadrant II.

Looking for an implicit equation for this offset of the astroid requires hard algebraic machinery.

4 Envelope of the family of unit circles centred on the astroid

We consider now the 1-parameter family of unit circles centred on the astroid $\mathcal {A}$ given either by the implicit equation (1) or, equivalently by the parametric presentation (3). The astroid is a very interesting curve, appearing in various ways. In particular, the isoptics of an astroid have been studied in [14].

Recall that parametric plot is generally more accurate than an implicit plot (as explained in [40]), therefore we use mostly the trigonometric parametrization (3) for the curve $\mathcal {A}$. This is true for other issues also; for example, the study of bisoptics of an astroid has been performed in [14], using mostly this parametrization and other formulas derived from it. An implicit plot has some flaws, no matter which software we used (see [40]).

A general equation for the unit circles centered on $\mathcal {A}$ is $F(x,y,t)=0$, where

$$\begin{aligned} F(x,y,t)=(x-\cos ^3 t)^2+(y-\sin ^3 t)^2-1. \end{aligned}$$

(8)

A first trial with GeoGebra provides Fig. 4. For it, we plot a general point on $\mathcal {A}$ and move it along the curve, using GeoGebra’s Move command with the Trace On feature.

Fig. 4

A first trial with GeoGebra (color figure online)

It can be conjectured that an envelope exists, in the sense of Def. 2.

According to the analytic definition 1.3, an envelope $E_2$ of this family of circles, if it exists, is determined by the following system of equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} (x-\cos ^3 t)^2 +(y-\sin ^3 t)^2 -1 =0 \\ (x-\cos ^3 t)^2 \cos ^2 t \sin t +(y-\sin ^3 t)^2 \sin ^2 t \cos t =0 \end{array}\right. } \end{aligned}$$

(9)

The output of Maple’s solve command consisted in a single expression involving the placeholder RootOf, which represents all the roots of an equation in one variable. The allvalues command evaluated the output to more than one value or expression; actually it returned, in an expression sequence, all such values (or expressions) generated by the combinations of different values of the RootOfs². The output contains two different parametric expressions, determining two envelope components:

$$\begin{aligned} {\left\{ \begin{array}{ll} x = \cos ^3 t + \sqrt{\cos ^6 t + \sin ^6 t - 3 \sin ^4 t - 4 \cos ^2 t + 3}\\ y = \frac{1}{\sin t} \left( \cos t \; \left( \cos ^3 t + \sqrt{\cos ^6 t + \sin ^6 t - 3 \sin ^4 t - 4 \cos ^2 t + 3}\right) + 1 - 2 \cos ^2 t \right) \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} {\left\{ \begin{array}{ll} x = \cos ^3 t - \sqrt{\cos ^6 t + \sin ^6 t - 3 \sin ^4 t - 4 \cos ^2 t + 3}\\ y = \frac{1}{\sin t} \left( \cos t \; \left( \cos ^3 t - \sqrt{\cos ^6 t + \sin ^6 t - 3 \sin ^4 t - 4 \cos ^2 t + 3}\right) + 1 - 2 \cos ^2 t \right) \end{array}\right. }. \end{aligned}$$

and, after simplification:

$$\begin{aligned} {\left\{ \begin{array}{ll} x = \cos ^3 t + | \sin t|\\ y = \frac{1}{\sin t} \left( \cos t \; \left( \cos ^3 t + | \sin t| \right) + 1 - 2 \cos ^2 t \right) \end{array}\right. } \end{aligned}$$

(10)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} x = \cos ^3 t - | \sin t|\\ y = \frac{1}{\sin t} \left( \cos t \; \left( \cos ^3 t - | \sin t |\right) + 1 - 2 \cos ^2 t \right) \end{array}\right. } \end{aligned}$$

(11)

Figure 5 has been obtained with the CAS, using these parametric presentations. It displays the given astroid, the two components determined by Equations (10) and (11), and the full envelope.

Fig. 5

The astroid and the full envelope (color figure online)

The interested reader can find an interactive GeoGebra applet and an animated GIF . A screen snapshot of this GeoGebra session is displayed in Fig. 6.

Fig. 6

The tangency points are on the two separate components of the envelope (color figure online)

Figure 7 shows two snapshots of a Maple animation, where the circle moves along the astroid. The envelope is displayed in plain line style. Note that, for each value of the parameter t, the circle is tangent at two different points of the green curve. In this case, also, two components are determined by the parametric presentations, each one being an envelope, and whose union is also considered as an envelope of the family of circles.

Fig. 7

Animation snapshot: Two positions of the circle and the points of tangency with the envelope (color figure online)

Summarizing, we have the following result:

Proposition 1

Each circle of the family is tangent at one point on each component. Actually, each component is an envelope of the family of circles, and their union too.

It can be proven that the astroid $\mathcal {A}$ is tangent to the full envelope that we found at 4 different points.The proof will be easy if we wait until we derive an implicit equation for the envelope.

We take now the GeoGebra applet. Using a strong zoom in and moving the point A along the astroid, we can discover that there is no correspondence between cusps of the astroid and cusps of the envelope. We met this situation already in [15].

The envelope found here is not easy to identify as a classical curve, when only looking at the plot. A further step will be to determine, if possible, an implicit equation for the envelope. The method is similar to what has been done in [14, 16, 17], in two different ways. In order to transform the data into polynomials, we transform the trigonometric parametrization into a rational one. On the one hand, the best known parametrization of the unit circle is the following:

$$\begin{aligned} {\left\{ \begin{array}{ll} x=\cos t \\ y=\sin t \end{array}\right. }. \end{aligned}$$

(12)

On the other hand, consider the line $L_m$ through the point $A(-1,0)$ with slope m. The line $L_m$ intersects the unit circle at A and at a second point, whose coordinates are $\left( \frac{1-m ^2}{1+m ^2}, \frac{2m}{1+m ^2} \right)$. This defines a rational parametrization of the unit circle, valid everywhere but at the point A. It follows that

$$\begin{aligned} \forall t \in \mathbb (R), \; \exists m \in \mathbb {R}, \text {such that} {\left\{ \begin{array}{ll} \cos t = \frac{1-m ^2}{1+m ^2}\\ \sin t = \frac{2m}{1+m ^2} \end{array}\right. } \end{aligned}$$

(13)

We use now this parametrization, replacing back m by t to write the parametric representations with parameter t, according to tradition. Equations (10) can be decomposed into two cases:

• (i) For $t \in [0,\pi ]$, $\sin t \ge 0$, thus we have a first parametrization:

  $$\begin{aligned} {\left\{ \begin{array}{ll} x = \cos ^3 t + \sin t\\ y = \frac{1}{\sin t} \left( \cos t \; \left( \cos ^3 t + \sin t \right) + 1 - 2 \cos ^2 t \right) \end{array}\right. } \end{aligned}$$

  (14)

  The corresponding arc is shown in Fig. 8a.

• (ii) For $t \in [\pi ,2\pi ]$, $\sin t \le 0$, thus we have a second parametrization:

  $$\begin{aligned} {\left\{ \begin{array}{ll} x = \cos ^3 t - \sin t\\ y = \frac{1}{\sin t} \left( \cos t \; \left( \cos ^3 t - \sin t \right) + 1 - 2 \cos ^2 t \right) \end{array}\right. } \end{aligned}$$

  (15)

  The corresponding arc is shown in Fig. 8b. The reader will identify these arcs with parts of Fig. 9.

Fig. 8

Two half arcs of the envelope (color figure online)

We substitute sine and cosine in Equations (14) using equations (13), then multiply both sides by a least common denominator. We obtain the following polynomial equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} (x + 1)t^6 - 2t^5 + (3x - 3)t^4 - 4t^3 + (3x + 3)t^2 - 2t + x - 1 =0 \\ (y + 1)t^6 + (3y + 1)t^4 - 8t^3 + (3y - 1)t^2 + y - 1=0 \end{array}\right. } \end{aligned}$$

(16)

Denote by $P_1(x,y)$ and $Q_1(x,y)$ the polynomials in left hand sides of these equations. These polynomials generate an ideal $J_1$ in the polynomial ring $\mathbb {R}[x,y,t]$. Elimination of the parameter t yields an ideal generated by the following polynomial in two variables:

$$\begin{aligned} F_1(x,y)=x^6 + 3x^4y^2 + 3x^2y^4 + y^6 - 4x^4 - 18x^3y + 19x^2y^2 - 18xy^3 - 4y^4 + 23x^2 - 20xy + 23y^2 - 9. \end{aligned}$$

(17)

The variety $V(F_1)$ is the plane curve displayed in Fig. 9a. By the same way, we derive from Equations (15) another variety $V(F_2)$, where

$$\begin{aligned} F_2(x,y)=x^6 + 3x^4y^2 + 3x^2y^4 + y^6 - 4x^4 + 18x^3y + 19x^2y^2 + 18xy^3 - 4y^4 + 23x^2 + 20xy + 23y^2 - 9. \end{aligned}$$

(18)

This variety is plotted in Fig. 9b. The slight inaccuracy on the sides is a consequence of a general issue with plotting technology discussed in [40].

Fig. 9

Two components of the envelope (color figure online)

The same method starting with Equations (11) yields the same polynomials. There is only one difference. This $2^{nd}$ computation produced an irrelevant factor in the $2^{nd}$ polynomial (i.e., the output is a polynomial of degree 7, with linear factor which is irrelevant to the envelope). This issue and ways to solve it are discussed in [11]. The union $\mathcal {E}=V(F_1) \cup V(F_2)$ is the envelope which has been determined with the parametric presentations (10) and (11).

5 Talbot curves as envelopes

In [15], the computed envelope was quite easy to identify with a reasonable background in plane curves. Here we meet less known curves, namely Talbot curves, and some web search has been necessary in order to identify them [36].

Plane algebraic curves may have numerous constructions and presentations. Talbot curves are rational sextics constructed in various ways from an ellipse. For example, it is the locus of centers of circles tangent to a given ellipse and passing through the center of the ellipse. It can be also constructed as a pedal curve of an ellipse; see [21] and the animations there, and [26] with an interactive applet. Both references give a definition using a trigonometric parametrization. In what follows, the identification of the computed envelope as a Talbot curve is obtained because of the output as a parametric presentation.

Definition 5

A Talbot curve is a plane curve defined by the following parametric presentation:

$$\begin{aligned} {\left\{ \begin{array}{ll} x &{} = (1+ u \sin ^2 t)\; \cos t \\ y &{}= (1 - u - u \cos ^2 t) \; \sin t \end{array}\right. }, \end{aligned}$$

(19)

where u is a real parameter. Note that if $u=1$, these equations define the unit circle centred at the origin. We explore now the curves, using some of the automated abilities of GeoGebra and a slider bar for the parameter u.

We consider now the North-East to South-West component of the envelope $\mathcal {E}$, as displayed in Fig. 9 and denote it by $\mathcal {E}_1$.

• (i) First, plot a Talbot curve using Eq. (19). A slider bar is created. The curve is the dotted curve symmetric about the $x-$axis in Fig.  10a.

• (ii) Rotate the Talbot curve counterclockwise about the origin by an angle of $\pi /4$ (also dotted).

• (iii) Using the slider bar, find a value of u for which the rotated Talbot curve coalesces with $\mathcal {E}_1$.

• (iv) Using the command buttons of GeoGebra, find a suitable homothety transforming this rotate Talbot curve into $\mathcal {E}_1$.

The resulting output is displayed in Fig.  10b.

Fig. 10

Graphical identification of the envelope with a Talbot curve (color figure online)

Of course, the underlying computations are numerical. Working with GeoGebra, a strong zoom out and increasing the decimal precision, better approximation can be obtained, but still depending on the man (hand) and machine (mouse) interaction. With 2 decimal digits and the standard precision we had until now, we obtained $u \simeq 0.67$ and the homothety coefficient is equal to 1.5038; see Fig.  10b. More accurate results will be obtained later in this section.

It is possible to make exact computations. We start with Eq. (19). The given Talbot curve is symmetric about the $x-$axis, and the SW-NE component of the envelope has the first angle bisector of the axes as symmetry axis. We rotate the Talbot counterclockwise by an angle of $\frac{\pi }{4}$, and obtain the following parametrization³:

$$\begin{aligned} {\left\{ \begin{array}{ll} x &{}= \frac{\sqrt{2}}{2} (1+u \sin ^2 t ) \; \cos t + \frac{\sqrt{2}}{2} (1-u-u \cos ^2 t ) \; \sin t\\ y &{} =-\frac{\sqrt{2}}{2}\frac{\sqrt{2}}{2}(1+u \sin ^2 t ) \; \cos t + \frac{\sqrt{2}}{2} (1-u-u \cos ^2 t ) \; \sin t \end{array}\right. }. \end{aligned}$$

(20)

Figure 11 shows the NE-SW component $\mathcal {E}_1$ of the envelope and the rotated Talbot curve(the internal curve).

Fig. 11

The SW-NE component and the rotated Talbot curve (color figure online)

Both have now the same symmetry axis. Our goal is to prove that a suitable homothety transforms the rotated Talbot curve into the given component of the envelope.

• (i) By substitution of $y=x$, we obtain that the $x-$coordinates of the points of intersection of $\mathcal {E}_1$ with the first angle bisector of the axes are the solutions of the polynomial equation $8x^6-25x^4+26x^2-9=0$. There are two double solutions 1 and $-1$ and two simple solutions $3\sqrt{2}/4$ and $-3\sqrt{2}/4$. The corresponding points are easily identified on the figure.

• (ii) The rotated Talbot curve has also two double points and two simple points on the first bisector of the axes. The respective $x-$ coordinates of the double points are $\pm \arcsin \left( \frac{1}{\sqrt{-u}} \right)$.

• (iii) It follows that the double points of the envelope are transformed into the double points of the rotated Talbot curve by an homothety whose center is at the origin and its coefficient is equal to $\frac{1}{\sin ^2 1}$.

• (iv) By substitution into either the implicit equation or into the parametric equations, we verify that the homothetic image of the rotated Talbot curve coalesces with the envelope component $\mathcal {E}_1$.

The same computations yield that the same homothety works for the NW-SE components.

Remark 3

We performed the computations using Maple 2020. Here is part of the code, with some comments.

First, we enter the parametric presentation for Talbot curves. The loop displays the curves for several values of the parameter u in order to have a visual basis for a conjecture which value can fit the envelope which has been computed.

The obtained Talbot curve has to be rotated, for the image to have the same main symmetry axis as $\mathcal {E}_1$. Note that the reverse rotation should be used in order to explore the second component of the envelope. We conjecture that $u=-2$.

Now, we plot the desired component of the envelope, using its implicit equation (we copy it here explicitly; of course, this can be done more elegantly, using previous output).The numpoints=1500 option has been experimentally chosen, to avoid some plot inaccuracy (for similar reasons as those described in [40]):

The substitutions yield actually equivalent polynomial equations, whose solutions are either the $x-$coordinates or the $y-$coordinates of the points of intersection of the angle bisectors of the coordinate axes with the envelope.

What follows checks that the envelope and the homothetic image of the rotated Talbot curve are identical (the code may be modified to apply it for $u=-2$).

6 A unifying framework

We studied the envelope of the family of unit circles centered on the astroid $\mathcal {A}$. This yielded a new construction of Talbot curves. For us, it was a second exploration of this type, after the case of radius 1/2, which provided a new construction of a (rotated) Maltese Cross [15]. Note that in both cases, the envelope which has been determined is different from the offset of the astroid $\mathcal {A}$ at a distance equal to the radius of the circles.

The outputs of both explorations allow the following remark: each component of a Maltese Cross can be considered as a special case of a Talbot curve, for a specific value of the parameter u. Denote by $\mathcal {T}_u$ the Talbot curve with parameter u. It can be shown that:

• $\mathcal {T}_0$ is the unit circle.

• $\mathcal {T}_1$ is a component of a Maltese Cross.

• $\mathcal {T}_2$ is an astroid, namely $\mathcal {A}$ rotated by $\pi / 4$ (either clockwise or counterclockwise) around the origin.

• For $u \rightarrow \infty$, the curve $\mathcal {T}_u$ looks more and more (we do not dare to write ”tends to”) the vertical component of a Maltese Cross. Pay attention that all the curves are bounded, but not in the same bounding box: the minimal and maximal values of the coordinates change with u. See Fig.  13.

Fig. 12

Some special Talbot curves

Fig. 13

Talbot curves for increasing parameter u

Figures 12 and 13 have been obtained with the following Maple code:

Some of these results may seem rather trivial, when considering Def. 5, but this may not be noticed at first glance. We can provide also an animation showing Talbot curves for several values of the parameter u. Note that, for some specific values of the parameter, the corresponding curve is an oval. The exploration of these cases is beyond the scope of the present paper; it will be performed in a subsequent work.

In a 2002 article in the French magazine ”La Recherche”, Jean-Pierre Bourguignon regretted that math educators work with their students in a way too different from the way researchers work. Bourguignon’s concern is met in the papers quoted in Section 1: working in a technology rich environment provides experimental approaches, similar for researchers and their students. Moreover, such an environment enables a revival of classical, and sometimes almost forgotten domains. In the present study we obtained another byproduct: a unifying framework for a family of plane curves, which had been generally viewed as different objects without any connection between them. We have also an opportunity to re-express the wish to see in the near future more advances towards automated networking CAS and DGS. The history of such a wish goes back to the early 2000’s and knew continuous advances, both in programming and in applications (e.g. [20, 25, 30, 31]).

Three years later, Papadopoulos and Dagdilelis wrote in [28] that a ”DGS allows students to generate assumptions that later can be verified or rejected through formal proof”, adding that ”this verification of assumptions takes place much more easily in the DGS environment than in other computational environment or in the more traditional setting of paper and pencil”. We hope that the different sections of our study may be an incentive to develop skills for exploration, discovery, conjecture. An accurate verification may be out of reach from the DGS alone (even when a CAS is implemented in it, like Giac in GeoGebra) , and the derivation of accurate results is obtained by the networking of a DGS and a powerful CAS together, thus answering both the educators’ requirements and Bourguignon’s wish. This networking exists already since the implementation of the Giac CAS into GeoGebra. Other important developments can be found in GeoGebra-discovery.