A Symbolic Dynamic Geometry System Using the Analytical Geometry Method

Abstract

A symbolic geometry system such as Geometry Expressions can generate symbolic measurements in terms of indeterminate inputs from a geometric figure. It has elements of dynamic geometry system and elements of automated theorem prover. Geometry Expressions is based on the analytical geometry method. We describe the method in the style used by expositions of semi-synthetic theorem provers such as the area method. The analytical geometry method differs in that it considers geometry from a traditional Euclidean/Cartesian perspective. To the extent that theorems are proved, they are only proved for figures sufficiently close to the given figure. This clearly has theoretical disadvantages, however they are balanced by the practical advantage that the geometrical model used is familiar to students and engineers. The method decouples constructions from geometrical measurements, and thus admits a broad variety of measurement types and construction types. An algorithm is presented for automatically deriving simple forms for angle expressions and is shown to be equivalent to a class of traditional proofs. A semi-automated proof system comprises the symbolic geometry system, a CAS and the user. The user’s inclusion in the hybrid system is a key pedagogic advantage. A number of examples are presented to illustrate the breadth of applicability of such a system and the user’s role in proof.

1 Introduction

Dynamic geometry software has seen widespread use in high school mathematics education, starting in the mid 80’s with successful commercial packages [7, 10, 13], and latterly with broadly comparable, but free, open-source software [6]. Symbolic computation first became commercially available in the ‘80s, while strongly adopted at the university level, has had more limited uptake in the high school. Automated theorem provers for Euclidean Geometry date back further but have been an area of academic research. Wholly algebraic provers based on Wu’s Method [3, 17] or Groebner Bases [2, 9] give yes/no answers to the correctness of a geometric statement, along with non-degenerate conditions. Semi-synthetic methods, such as the area and full angle methods [4], and the mass point method [18] give human readable proofs, some of which are quite short and worth reading.

Recent work [1] has added theorem proving to dynamic geometry systems. An interesting question is what educational value such capabilities will confer on the user. The pedagogic essence of dynamic geometry lies firmly in the term “dynamic”, in the ability to explore and conjecture. Providing an up or down yes/no answer to whether a conjecture is true seems to cut off exploration rather than promote it. In the words of Botana et al. [1]

This can lead to student responses like ‘So what?’ if the software simply tells you whether a theorem is true or not.

While the proofs generated by the area and full angle methods are sometimes human readable, if the style of proof does not match the way in which a student would work, their value may be limited. These methods in fact came out of work in restructuring middle school mathematics by Zhang [4]. In an environment where students are taught to use the area method by hand, the proofs do indeed correlate with their style of proof, and one would anticipate a significant benefit. An interesting approach to providing students aid in formulating proofs is given in [11]. The geometry system interactively highlights properties of the drawing which may be used by the student in creating their own proof. While not providing proofs on its own, this system would seem to extend the exploratory characteristics of the dynamic geometry system into the theorem proving realm.

A proof by the area method consists of determining that a given geometrical quantity has zero value (or equivalently that two geometrical quantities are equal). The geometric quantity under consideration will involve a number of constrained or semi-constrained points. These are eliminated in reverse order by applying lemmas specific to the construction/quantity combination, leaving a quantity in terms of the free points. The resulting algebraic quantity is then simplified, and the true/false determination based on whether the simplified result is zero or non-zero. The correctness of the algorithm depends on this simplification step being determinative, and this can be guaranteed if the quantity remains rational. This requirement motivates a number of restrictions both on the constructions and on the geometric quantities which may be considered.

The first form of restriction is that the geometry model must be constructible from a prescribed set of constructions. While extensive enough to express many geometric theorems, they are not exhaustive. For example the construction for the intersection between two given circles is not included, just the construction for the other intersection if you already have one [8]. Likewise the general intersection between a line and a circle are not incorporated, just the construction for the second intersection assuming you already have one.

The second form of restriction is in the geometric quantities which may be treated in a proof. For the area method there are four: signed areas, signed ratios of lengths (on the same line or parallel lines), Pythagorean difference, and indeterminates representing real numbers. Pythagorean difference is defined between 3 points A,B,C as:

$$\begin{aligned} P(A,B,C)=|AB|^{2}+|BC|^{2}-|AC|^{2} \end{aligned}$$

Again many theorems may be expressed in these terms. For example, any theorem involving collinearity between three points may use the area of the triangle with the points as vertices. Collinearity corresponds to zero area. Perpendicularity between segments AB and BC corresponds to the Pythagorean difference $P(A,B,C)=0$. Indeed, as area of a triangle corresponds to the outer product of the vectors bounding a triangle and the Pythagorean difference to their inner product, anything which can be expressed in terms of those quantities can be addressed. While square distances can be expressed as Pythagorean differences, distances themselves would require a square root and are thus excluded from consideration.

Another characteristic of the area method is that it does not consider sidedness in its proofs. The proofs hold for different configurations of free points which may in traditional Euclidean geometry require separate proofs. This is powerful in that several different configurations of a theorem may be proved at once. For the student, however, the traditional Euclidean viewpoint may be the more comfortable.

In this paper, we discuss a different approach to combining automated deduction with dynamic geometry. We relax the condition that the algorithm must definitively give a yes or no answer to a specific class of problems. This allows us to consider a broader range of constructions and geometric quantities, but at the cost of sometimes giving an answer which is neither yes nor no. We also make no attempt to prove a result for universal location of inputs, but decide all “sidedness” questions based on the diagram. Our automated deductions apply only in some neighborhood of the diagram as represented in the dynamic geometry system. Again this has the benefit of extending the number of geometric quantities which may be considered, as quantities which do in fact depend on sidedness (such as coordinate location of a point) may be expressed. Such a system can prove theorems, but it can also generate formulas for all the numeric quantities which the user can extract from the dynamic geometry system. It can therefore extend the exploratory aspect which is central to the traditional dynamic geometry system into the symbolic realm.

2 The Analytical Geometry Method

Like the area method, the analytical geometry method has at its core a sequence of constructions. In the area method, a geometric quantity is initially expressed in terms of both dependent and independent points. The dependent points are eliminated from the expression in reverse order of construction, leaving an expression only in terms of the independent points. In the analytical geometry method, a geometric quantity is defined in terms of the coordinates of dependent points (and the coefficients of lines, radii of circles, etc.). To express it in terms of independent quantities, the constraints are effectively run backwards, as in the area technique, but a point is eliminated by an algebraic substitution followed by a simplification step, rather than the application of lemmas which are specific to the geometric quantity. In effect, the geometric eliminations of the area method are replaced by algebraic eliminations. This has the benefit of genericity, but at a cost of losing the capability of generating a geometric proof. As we have abandoned the necessity of guaranteed simplification, our constructions may be of a non-rational character and involve square roots or trigonometric functions.

Fig. 1

Area problem

2.1 The Basic Analytical Geometry Method

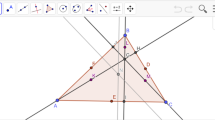
We start with an example which is easily solved using the area method. Given a triangle ABC, point D is placed proportion t along line AB, that is such that $AD/AB=t$. Point E proportion t along BC and point F proportion t along CA. What is the ratio of the area of DEF to the area of ABC?

The construction steps for the model shown in Fig. 1 are these:

• 1. Construct point A at coordinates $(x_{A},y_{A})$

• 2. Construct point B at coordinates $(x_{B},y_{B})$

• 3. Construct point C at coordinates $(x_{C},y_{C})$

• 4. Construct point D proportion t along AB

• 5. Construct point E proportion t along BC

• 6. Construct point F proportion t along CA

The first step of the analytical Geometry Method is to convert the geometric quantity into an analytical quantity involving the coordinates of points A, B, C, D, E, F. Let Q be the ratio of the area of DEF to the area of ABC expressed in terms of the coordinates of the points:

$$\begin{aligned} \begin{array}{l} Q=\dfrac{x_{E}y_{D}-x_{F}y_{D}-x_{D}y_{E}+x_{F}y_{E} +y_{F}x_{D}-y_{F}x_{E}}{x_{B}y_{A}-x_{C}y_{A}-x_{A}y_{B}+x_{C}y_{B} +y_{C}x_{A}-y_{C}x_{B}}\end{array} \end{aligned}$$

We now step backwards through the construction steps, replacing the coordinates of the defined point by expressions involving the coordinates of previously defined points and indeterminates representing real numbers. Each construction has a rule for this. For a point P proportion k along the line segment between U and V, the rule is:

$$\begin{aligned} \begin{array}{c} x_{P}\rightarrow k\cdot x_{V}+(1-k)\cdot x_{U}\\ y_{P}\rightarrow k\cdot y_{V}+(1-k)\cdot y_{U} \end{array} \end{aligned}$$

At the first elimination step, $(x_{F},y_{F})$ are eliminated from expression Q using this rule. At the second elimination step, construction 5 is applied and $(x_{E},y_{E})$ eliminated from Q. At the third elimination step, construction 4 is applied and $(x_{D},y_{D})$ eliminated from Q. Simplification is applied at each stage, however does not achieve much until the final elimination step, when all the dependent variables have been eliminated, and the expression collapses to the following:

$$\begin{aligned} 1-3\cdot t+3\cdot t^{2} \end{aligned}$$

Comparing this sequence with the application of the area method ([4], p. 87) to a similar problem one observes that the intermediate expression swell is considerably greater in the analytical geometry method. For larger problems this is a significant issue, and one towards which a number of modifications of the basic algorithm are addressed. A second point to notice is that the quantity Q is an algebraic expression, rather than a geometric object. The elimination rule is algebraic and can be applied to any such expression. This implies that each construction needs a single elimination rule, rather than a rule for each geometric quantity, as is the case in the area method. In addition, it is clear that Q can be any expression which is defined analytically in terms of the coordinates of the figure’s points, or coefficients of its lines. Elimination rules in the area method depend on clever geometrical lemmas, which lend the method its charm, as well as its efficiency. However the need to match a construction with lemmas for each geometrical quantity limits the potential to add new construction types to the system. In the analytical geometry method, it is clear that for any Dynamic Geometry construction, it is possible to create a corresponding elimination rule which will eliminate the coordinates or coefficients of the point or line introduced.

In summary, the area method has the following characteristics: it can prove theorems universally, it can give human readable proofs and it is efficient. These benefits come at the cost that the method is hard to extend to deal with new constructions or new geometric quantities. Characteristics of the basic analytical geometry method are these: theorems are proved locally and the proof may fail, adding new geometry quantities requires no change to the core algorithm, adding new constructions requires an incremental change to the algorithm, intermediate expression swell can be great.

2.2 A Basic Set of Constructions

We present constructions for an implementation whose geometric elements are points and oriented lines. Oriented lines are represented by the triple (A, B, C), where the underlying line is defined by the equation $A\cdot x+B\cdot y+C=0$, and the orientation is defined by the vector (A, B). Hence the triple $(-A,-B,-C)$ represents the same line as (A, B, C) but with the opposite orientation. In each case we show the elimination step for the point’s coordinates $(x_{P},y_{P})$ or the line’s coefficients $(A_{L},B_{L},C_{L})$. The equation of the line with these coefficients is $A_{L}\cdot x+B_{L}\cdot y+C_{L}=0$. As the geometry is straightforward, we give detailed descriptions only of a sample pair of constructions. The full set is given in Appendix A.

C1 Point given coordinates P is defined to have coordinates(x, y).

C2 Point proportion along a segment Point P is proportion k along the segment $P_{0}P_{1}$.

C3 Point distance from two points If point P is distance $d_{0}$ from point $P_{0}$ and distance $d_{1}$ from point $P_{1}$ and to the left of ordered segment $P_{0}P_{1}$:

$$\begin{aligned}&x_{P}\rightarrow x_{1}+\dfrac{\phi _{3}\left( x_{0}-x_{1}\right) }{2d_{2}^{2}} +\dfrac{\phi _{4}\left( y_{0}-y_{1}\right) }{2d_{2}^{2}}\\&y_{P}\rightarrow y_{1}-\dfrac{\phi _{4}\left( x_{0}-x_{1}\right) }{2d_{2}^{2}} +\dfrac{\phi _{3}\left( y_{0}-y_{1}\right) }{2d_{2}^{2}} \end{aligned}$$

If point P is distance $d_{0}$ from point $P_{0}$ and distance $d_{1}$ from point $P_{1}$ and to the right of ordered segment $P_{0}P_{1}$:

$$\begin{aligned}&x_{P}\rightarrow x_{0}-\dfrac{\phi _{5}\left( x_{0}-x_{1}\right) }{2d_{2}^{2}} -\dfrac{\phi _{4}\left( y_{0}-y_{1}\right) }{2d_{2}^{2}}\\&\begin{array}{c} y_{P}\rightarrow y_{0}+\dfrac{\phi _{4}\left( x_{0}-x_{1}\right) }{2d_{2}^{2}}-\dfrac{\phi _{5}\left( y_{0}-y_{1}\right) }{2d_{2}^{2}}\end{array} \end{aligned}$$

where:

$$\begin{aligned} d_{2}= & {} \sqrt{\left( x_{1}-x_{0}\right) ^{2}+\left( y_{1}-y_{0}\right) ^{2}}\\ \phi _{3}= & {} -d_{0}^{2}+d_{1}^{2}+d_{2}^{2}\\ \phi _{4}= & {} \sqrt{d_{0}+d_{1}+d_{2}}\sqrt{d_{0}+d_{1}-d_{2}}\sqrt{d_{0}-d_{1}+d_{2}}\sqrt{-d_{0}+d_{1}+d_{2}}\\ \phi _{5}= & {} d_{0}^{2}-d_{1}^{2}+d_{2}^{2} \end{aligned}$$

C4 Point distance from two lines Point P is directed distance $d_{0}$ from line $L_{0}$ and directed distance $d_{1}$ from line $L_{1}$.

C5 Point distance from one line and one point We define the 2D wedge product $(x_{0},y_{0})\wedge (x_{1},y_{1})=x_{0}y_{1}-x_{1}y_{0}$

If point P is directed distance $d_{0}$ from line $L_{0}$ and directed distance $d_{1}$ from point $P_{1}$ and $\overrightarrow{P_{0}P}\wedge (A_{0},B_{0})>0$

$$\begin{aligned}&x_{P}\rightarrow x_{0}+B_{0}\cdot d_{3}-\dfrac{A_{0}\cdot \left( d_{2}-d_{0}\right) }{\sqrt{A_{0}^{2}+B_{0}^{2}}}\\&\begin{array}{c} y_{P}\rightarrow y_{0}-A_{0}\cdot d_{3}-\dfrac{B_{0}\cdot \left( d_{2}-d_{0}\right) }{\sqrt{A_{0}^{2}+B_{0}^{2}}}\end{array} \end{aligned}$$

If point P is directed distance $d_{0}$ from line $L_{0}$ and directed distance $d_{1}$ from point $P_{1}$ and $\overrightarrow{P_{0}P}\wedge (A_{0},B_{0})<0$

$$\begin{aligned}&x_{P}\rightarrow x_{0}-B_{0}\cdot d_{3}-\dfrac{A_{0}\cdot \left( d_{2}-d_{0}\right) }{\sqrt{A_{0}^{2}+B_{0}^{2}}}\\&\begin{array}{c} y_{P}\rightarrow y_{0}+A_{0}\cdot d_{3}-\dfrac{B_{0}\cdot \left( d_{2}-d_{0}\right) }{\sqrt{A_{0}^{2}+B_{0}^{2}}}\end{array} \end{aligned}$$

where:

$$\begin{aligned}&d_{2}=\dfrac{C_{0}+A_{0}\cdot x_{0}+B_{0}\cdot y_{0}}{\sqrt{A_{0}^{2}+B_{0}^{2}}}\\&\begin{array}{l} \begin{array}{l} d_{3}=\dfrac{\sqrt{d_{1}^{2} -\left( d_{2}-d_{0}\right) ^{2}}}{\sqrt{A_{0}^{2}+B_{0}^{2}}} \end{array}\end{array} \end{aligned}$$

C6 Line given equation Line L is defined by equation $A\cdot x+B\cdot y+C=0$ and its orientation is aligned with (A, B)

C7 Line distance from two points Line L is directed distance $d_{0}$ from point $P_{0}$ and directed distance $d_{1}$ from point $P_{1}$

C8 Line angle to a line distance from a point Line L is angle $\theta _{0}$ from line $L_{0}$ and directed distance $d_{1}$ from point $P_{1}$

We note that the some of the above constructions have variants dependent on an assessment of sidedness. It is the responsibility of the agent which creates the construction sequence, the dynamic geometry UI for example, to select which variant to insert into the construction sequence. Each of the constructions above fully defines a geometrical object. In a dynamic geometry system, it is common to have geometry which is unconstrained, or partially constrained. For example a point can be located in an arbitrary location, or a point can be placed on a line, or a point can be specified to be at a certain distance from a given point. In such cases, the system can add indeterminates in the process of making the construction. These partial constructions are described below.

C9 Point distance from one point Point P is distance $d_{0}$ from point $P_{0}$

C10 Point distance from one line Point P is directed distance $d_{0}$ from line $L_{0}$

C11 Unconstrained point Point P is unconstrained

C12 Line directed distance from one point Line L is directed distance $d_{0}$ from point $P_{0}$

C13 Line angle to a line Line L is angle $\theta _{0}$ from line $L_{0}$

C14 Unconstrained line Line L is unconstrained

2.3 The elimination algorithm

We define a geometric quantity to be an analytic expression containing the following:

• Coordinates of points in the model.

• Coefficients of lines in the model.

• Indeterminates.

• Numbers.

Given a construction sequence $C_{1},C_{2},\ldots ,C_{n}$ and a geometric quantity Q, the elimination algorithm is the following:

Algorithm 1

• Step 1: for i from n down to 1 do Step 2, 3

• Step 2: apply the elimination corresponding to construction $C_{i}$ to Q

• Step 3: simplify Q

Once the elimination algorithm has run to completion, Q will contain indeterminates which were present in the definition of the constructions and indeterminates introduced by the partial constructions, but no coordinates or coefficients of points or lines. As the eliminations are simply algebraic substitutions, there are few restrictions on what Q can contain. Transcendental functions, functionals such as derivative and integral, indeterminate sums are all possible components. Because of the permissiveness with respect to the form of Q, there are no guarantees on the success of the simplify step. As a theorem prover, the method is at the mercy of a general purpose simplifier dealing with trigonometric functions and square roots. As a formula generator, the simplifier merely makes the difference between the expressions being easy or difficult to read.

The constructions above are simple applications of coordinate geometry. It is a straightforward task to extend the types of geometry object which may be treated, and to add the requisite constructions. For example if one added circles to this system, the following constructions might be added:

• Circle tangent to 3 lines.

• Circle tangent to 2 lines and one circle.

• Circle tangent to 1 line and 2 circles.

• Circle tangent to 3 circles.

2.3.1 Properties of the Method

A number of the constructions have alternate forms, each of which provides a solution which satisfies the constraints. For example in construction C3 for a point given distance to two known points, the form of construction depends on whether the solution point is to the left or right of the directed segment between the given points. In Geometry Expressions, the geometry model which is input to the construction process has geometrical entities (points and lines), constraints between them (distances, angles) and a sketch of the configuration. This sketch is used to determine which solution to choose for a particular construction. For example, when construction C3 is invoked, the sketch locations of the input points and the output point are used to determine whether to use the solution to the left or to the right of the directed segment between the inputs. The effect of this is that the solution is only valid for geometric configurations which maintain this relationship. It would be possible to keep track of the conditions thus imposed on the solution, however the attitude espoused by the software is simply to treat solutions as being valid in some undefined neighborhood of the drawing.

In the above we have presented the analytical geometry method in a way which emphasizes parallels to the area method and to the full angle method. This comparison is reasonable as the method does rely on the existence of a construction sequence. However the fact that the constructions are expressed in terms of Cartesian coordinates invites explicit comparison with algebraic provers, such as those based on Wu’s method or Groebner bases [3, 9].

Algebraic methods convert geometry theorems into a set of polynomial equations representing the hypotheses and another polynomial representing the conclusion. They then triangulate the system of polynomials and use this triangulated system both to show that the conclusion polynomial is implied by the hypotheses and to generate subsidiary conditions. The individual constructions in the analytical geometry method may be expressed as the solution of small sets of polynomial equations. For example C3, the construction of a point given distance between two points can be expressed as the solution of a pair of quadratics, C5 may be expressed as the solution of a linear equation and a quadratic, while C8 can be expressed as the solution of two linear equations and a quadratic for the coefficients of the line. Note that expressing the construction as the solution of a system of equations eliminates the choice of which solution is intended. This would reward consideration of theorems which are true for either choice, and penalize consideration of theorems which depend on the choice. The system of equations corresponding to construction C8 is polynomial in the coefficients of the line, the coordinates of the point and the distance between the point and the line, however it involves the cosine of the angle and is thus polynomial only for specific values of the angle, not for indeterminate angles.

In the pure algebraic methods conclusions should be polynomials. As the analytical geometry method is simply a method of creating a Cartesian representation of the defined geometry, conclusions may take the form of any objective function defined on that geometry. Squared distances are, of course, polynomial, but distances themselves require roots while angles require inverse trigonometrical functions. With the addition of general curves, loci and envelopes to the geometric entities which can be constructed in the system, we add constructions employing derivatives (tangents, envelopes) and objective functions using integrals (arc length, area). For example, Fig. 2 shows a proof of the differential geometry property that a curve is the evolute of its involute. The user has created a parametric curve with equation (f(T), g(T)). He has constructed an arc on that curve and constrained its end points A and B to be at parametric locations 0 and t. He has asked the software to measure the arc-length. As f and g are both generic functions, this arc length is given by the software in terms of an unevaluated integral involving $f'$ and $g'$. The user now constructs a segment BC lying on the tangent to the curve at B and constrains its length to be this arc length subtracted from some putative string length L. Finally, he asks the software for the locus of C as t varies and constructs the tangent to the locus at C. The conclusion sought is that the tangent to the locus is perpendicular to the segment BC. The angle is computed automatically by the software, proving the theorem. Note that the assumption displayed in the solution (that L is longer than the arc length) is automatically added during simplification of absolute values in the Geometry Expressions CAS.

Fig. 2

Proof that a curve is the evolute of its involute

2.4 Performance Enhancements

Even the simple set of eliminations steps in the core algorithm above, if applied directly, suffer from intermediate expression swell. A number of performance enhancements are critical to a practical implementation of the algorithm.

2.4.1 Invariance of Q

Most of the constructions given above are independent of coordinate system. Exceptions are C1 and C6 which explicitly refer a point and line to a coordinate system. If neither of these constructions is present, and if the quantity Q is known to be invariant with respect to rigid body transformations then the model can be translated and rotated without changing Q. If $C_{1}\hbox {is}$ a construction for an unconstrained point, type C11 then we can replace the elimination:

$$\begin{aligned}&x_{P}\rightarrow x_{0}\\&\begin{array}{c} y_{P}\rightarrow y_{0}\end{array} \end{aligned}$$

by the elimination

$$\begin{aligned}&x_{P}\rightarrow 0\\&\begin{array}{c} y_{P}\rightarrow 0\end{array} \end{aligned}$$

This is equivalent to translating the figure by $(-x_{0},-y_{0})$ and should have no impact on a measurement which is invariant under rigid body motion. Now, if $C_{2}$ is of type C8 or C13, then instead of introducing an indeterminate angle $\theta _{0}$, we can introduce the angle 0. This corresponds to applying a rotation of $-\theta _{0}$ to the figure and again should have no effect on a measurement which is invariant under rigid body motion. The complexity of simplification is highly sensitive to the number of variables present. Eliminating three can be valuable. This approach could be carried further if only incidence and parallel constraints are present and if it is determined that Q contains only affine invariants, and if $C_{1},C_{2},C_{3}$ are all of type C11, then the coordinates of these points could be set to (0, 1), (1, 0), (1, 1)

2.4.2 Known Quantities Database

In construction C3 we introduce the distance between the two given points.

$$\begin{aligned} d_{2}=\sqrt{\left( x_{1}-x_{0}\right) ^{2}+\left( y_{1}-y_{0}\right) ^{2}} \end{aligned}$$

In the case where $(x_{1},y_{1})$ was previously constructed at a given distance $d_{1}$ from $(x_{0},y_{0})$, the performance degradation engendered by the round trip to coordinates and back may be avoided by simply remembering that the distance between $(x_{0},y_{0})$ and $(x_{1},y_{1})$ is $d_{1}$. Constructions C3, C4, C5, C7, C8, C9, C10, C12 all use explicit distances between points. These can be added to a known quantities database as a pre-step, and the database can be looked up during elimination to read off the stored value for the distance rather than recomputing it from coordinates. Again looking at construction C3, we see the following quantity:

$$\begin{aligned} \phi _{4}=\sqrt{d_{0}+d_{1}+d_{2}}\sqrt{d_{0}+d_{1}-d_{2}}\sqrt{d_{0}-d_{1}+d_{2}}\sqrt{-d_{0}+d_{1}+d_{2}} \end{aligned}$$

This is four times Heron’s formula for the area of the triangle $PP_{0}P_{1}$. Triangle areas can be added to the database of known geometry and looked up when needed. Finally, the quantities:

$$\begin{aligned} \phi _{3}= & {} -d_{0}^{2}+d_{1}^{2}+d_{2}^{2}\\ \phi _{5}= & {} d_{0}^{2}-d_{1}^{2}+d_{2}^{2} \end{aligned}$$

are Pythagorean differences, as defined in [4, 8]. These are geometric quantities which could also be stored in the database and used as needed.

2.4.3 Exploit Simplified Versions of the Constructions

The constructions above are in general form. However for some special positions of the input geometry, they can have significantly simplified form. As the special forms of some of these constructions are very common, it can be a substantial performance enhancement if the special form is identified and the simplified substitution used, rather than using the general substitution and relying on the brute force simplification step. For example, construction C5 for a point given distance to a line and distance to a point. This construction is significantly simplified if both points lie on the given line.

$$\begin{aligned}&x_{P}\rightarrow x_{0}+\dfrac{B_{0}\cdot d_{1}}{\sqrt{A_{0}^{2}+B_{0}^{2}}}\\&\begin{array}{c} y_{P}\rightarrow y_{0}-\dfrac{A_{0}\cdot d_{1}}{\sqrt{A_{0}^{2}+B_{0}^{2}}}\end{array} \end{aligned}$$

These performance enhancements are essential to the successful deployment of the analytical geometry method. We illustrate the sensitivity of algorithm performance to such seemingly minor enhancements with reference to a study [16] which details the application of the method to 207 examples taken from [4]. With the algorithm implemented at the time of the study, fifteen examples failed to simplify in a reasonable time. A subsequent improvement to the algorithm added a simplified construction for the intersection between a line and a circle in the special case where the other intersection is known. With this enhancement, nine of the fifteen failed examples were fixed.

3 Angle Engine

Fig. 3

P is the reflection of N in L. Q is the reflection of O in M. N and O are parallel. L and M are at angle $\theta$

Expressions for angles can be hard to simplify. Expressed in coordinate terms, the angle quantity involves inverse trig functions. Simplification, in general, will involve reducing an expression involving inverse trigs of trigs. Such simplifications are much simpler if it is possible to stay in an angle domain, and never go to Cartesian coordinates.

There is a class of geometry problems which can be solved in the pure angle domain using a suite of angle theorems such as the following:

• Angles of a triangle add up to $\pi$.

• Exterior angle of a triangle is equal to the sum of the opposite interior angles.

• Alternating angles between parallel lines are equal.

• Angles subtended at the circumference of a circle on the same arc are equal.

• The angle subtended at the center of a circle is twice the angle subtended at the circumference.

• Opposite angles of cyclic quadrilaterals are equal.

In such proofs, it is a legitimate tactic to add an unknown angle, so long as this angle is independent of the given quantities.

3.1 Motivating Example

As an example, consider the angle of intersection of the reflections of a pair of parallel rays in mirrors at angle $\theta$ to each other. In Fig. 3 the mirrors are represented by line segments L and M. Lines N and O are parallel and P is the reflection of N in L, Q is the reflection of O in M. We seek the angle between P and Q.

The reader who attempts to solve this by hand will undoubtedly find himself adding an angle. For example, Fig. 4 illustrates an angle based proof if one adds the angle between M and O. A proof might read as follows, using point labels introduced in Fig. 4:

Fig. 4

In the diagram of Fig. 3, angle DCB is defined to be $\phi$. Other angles in the figure can be readily deduced in terms of $\phi$ and $\theta$

Fig. 5

Directed lines for the diagram of Fig. 4

• 1. Let angle DCE be $\phi$.

• 2. Angle CEA is $\phi$ as it is an alternating angle between parallel lines.

• 3. Angle BCF is $\phi$ as CF is the reflection of CD in CB.

• 4. Angle BAE is $\theta -\phi$ as the external angle of triangle ABE equals the sum of the opposite internal angles.

• 5. Angle BAF is $\theta -\phi$ as AF is the reflection of AE in AB.

• 6. Angle AFC is $2\pi -2\theta$ as the angles of ABCF add up to $2\pi$.

3.2 Traditional Angle Proofs

Before introducing an automated algorithm, we describe the process of traditional angle proofs as a set of rewrite rules.

Figures 3, 4 and 5 refer to the same problem. In Fig. 3, the lines are labeled, but a traditional angle proof would be difficult to describe, as an angle described by the line labels would be ambiguous. The statement let the angle between line L and O be $\phi$ does not state whether the acute angle between the lines is $\phi$ or $\pi -\phi$. The full-angle method avoids this problem by taking the angle to be both. Traditional geometry proofs indicate which angle is intended by labeling points and referring to angles in terms of three points. The statement that angle ABC is $\theta$, specifies both that the angle between lines AB and BC is $\theta$ , but also which sector of their intersection is $\theta$, and which sector is $\pi -\theta$. To facilitate articulation of the traditional proof, Fig. 4 replaces line labels with point labels. An alternative method of dealing with this problem is to make the lines directed. This approach will be described in section 3.2 and is illustrated in Fig. 5.

In our analysis of traditional proofs, we will refer to the angle between line pairs rather than point triples. We will, for the time being, ignore the directionality of the lines.

Given a set of lines $L=\left\{ l_{i}\right\}$ and indeterminates $\varPhi =\left\{ \phi _{j}\right\}$. Let $V_{\varPhi }$ be the vector space over the reals generated by $\varPhi \cup \{1\}$. This is the coefficient space for linear polynomials in $\left\{ \phi _{j}\right\}$. Let the known angles be the set $A\subset L\otimes L$, and the known angle values a(l, m) a mapping from A onto $V_{\varPhi }$. Initially, $(l,m)\in A$ if an explicit angle between line l and line m is given. a(l, m) is set to be $\phi _{i}$. The traditional proof enlarges the set A by the application of theorems. Clearly if $(l,m)\in A$ we can enlarge A by adding angle (m, l), and $a(m,l)=a(l,m)$

Proof steps 2, 4 and 6 are all examples where $(l_{0},l_{1})\in A$ and $(l_{1},l_{2})\in A$ and the theorem application adds $(l_{0},l_{2})$ to A. In each case,

$$\begin{aligned} a(l_{0},l_{2})=n\cdot \pi +s\cdot a(l_{0},l_{1})+t\cdot a(l_{1},l_{2}) \end{aligned}$$

where s and t are 1 or -1 and n is an integer. Their precise values are important in actually performing a proof, but may be ignored for now.

In proof steps 3 and 5, $(l_{1},l_{2})\in A$ and there is a symmetry relationship between $l_{0}$ is symmetric with $l_{1}$ about $l_{2}$. The proof adds $(l_{0},l_{2})$ to A and $a(l_{0},l_{2})=a(l_{1},l_{2})$. We say that angle (l, m) can be proved over $\Psi \subset \Phi$ if a succession of proof steps exist after which $(l,m)\in A$ and $a(l,m)\in V_{\Psi }$. In the example above, the angle (P, Q) can be proved over $\{\theta \}$,while the angle (L, N) can be only proved over $\{\theta ,\phi \}$.

3.3 Directed Lines

Traditional proofs do not consider lines or angles to be directed. However, the precise meaning of an angle symbol is indicated by its location on a diagram, or by referring to it in terms of a point triple. An alternative form of disambiguation is to consider lines and angles as being directed. Under these circumstances, an angle is a rotation between one direction and another.

Given a vector $v=(A,B)$, where A and B are not both zero, we define its direction d(v)

$$\begin{aligned} d(v)={\left\{ \begin{array}{ll} arctan(B/A) &{} A>0\,and\,B>0\\ arctan(B/A)+2\pi &{} A>0\,and\,B<0\\ arctan(B/A)+\pi &{} A<0\\ \frac{\pi }{2} &{} A=0\,and\,B>0\\ \frac{3\pi }{2} &{} A=0\,and\,B<0 \end{array}\right. } \end{aligned}$$

This is the familiar programmer’s function atan2(B, A) shifted to lie between 0 and $2\pi$.

The following clearly holds:

$$\begin{aligned} d(-v)=\pi +d(v)\,mod\,2\pi \end{aligned}$$

We define the angle between $v_{0}$ and $v_{1}$, $a(v_{0},v_{1})$ to be

$$\begin{aligned} a(v_{0},v_{1})=d(v_{1})-d(v_{0})\,mod\,2\pi \end{aligned}$$

The following clearly hold:

$$\begin{aligned} a(v_{1},v_{0})= & {} -a(v_{0},v_{1})\,mod\,2\pi \\ a(v_{0},v_{2})= & {} a(v_{0},v_{1})+a(v_{1,}v_{2})\,mod\,2\pi \\ a(v_{0},-v_{1})= & {} a(-v_{0},v_{1})=\pi +a(v_{0},v_{1})\,mod\,2\pi \end{aligned}$$

3.4 Angle Graph

We note first that the statement P is the reflection of N in L is equivalent to the statement L is the angle bisector of N and P. In the following we will use the angle bisection rather than the symmetry relation.

Given a set of directions V, a bisection relation $b=(u,v,w,n)\in V\otimes V\otimes V\otimes \{0,1,2,3\}$ establishes the following relationship between the vectors.

$$\begin{aligned} d(w)=\frac{d(u)+d(v)+n\cdot \pi }{2}\,mod\,2\pi \end{aligned}$$

Geometrically, n determines which of four possible angle bisection directions are indicated.

Given a set of directions V, a set of angle relations A and a set of bisection relations B, we define an angle graph with two types of vertices:

• 1. A direction node corresponding to each $v\in V$ . Direction nodes are labeled with d the value of the direction.

• 2. A bisector node corresponding to each $b\in B$. Bisector nodes are labeled with n, which is an element of $\{0,1,2,3\}$.

The angle graph contains two types of edges.

• 1. An angle edge between u and v elements of V if $A(u,v)\in A$. The angle edge is directed and labeled with the value of the angle a(e), which may be a constant or an indeterminate.

• 2. A bisector edge between $u\in V$ and $b\in B$ if $b=B(u,v,w)$ or $b=B(v,u,w)$ or $b=B(v,w,u)$ for some v, w. The bisector edge is labeled with a flag which distinguishes between central and peripheral directions of the bisection.

We define three types of elimination step on this graph:

• ES1 vertex of degree 0 is eliminated.

• ES2A A vertex of degree 1 which is the source of a directed angle edge is eliminated along with the edge.

• ES2B A vertex of degree 1 which is the sink of a directed angle edge is eliminated along with the edge.

• ES3A A vertex of degree 1 adjacent to a central bisector edge is eliminated along with the edge and the bisector node and its adjacent edges.

• ES3B A vertex of degree 1 adjacent to a peripheral bisector edge is eliminated along with the edge and the bisector node and its adjacent edges.

We call an angle graph eliminable if there exists a succession of elimination steps (elimination sequence) which leaves us with an empty graph.

Theorem 3.1

An angle graph is eliminable if and only if the graph formed by performing a single elimination step is eliminable.

Proof

The elimination fails if and only if there is a subgraph all of whose direction vertices have degree greater than 1. A single elimination step removes a direction vertex of degree 1, and thus does not change any such subgraph. $\square$

Corollary 3.2

The following algorithm determines if an angle graph is eliminable (by determining an elimination sequence).

• Successively eliminate vertices till you have no eliminable vertices.

• If the graph is empty it is eliminable, otherwise it is not.

Given an elimination step E for an angle graph, the associated construction $C_{E}$ takes as inputs the adjacent direction node or nodes and outputs a value for the new direction.

• ES1:
  $$\begin{aligned} C_{E}()=\phi _{E} \end{aligned}$$
• ES2A:
  $$\begin{aligned} C_{E}(d_{0},\theta _{0})\leftarrow d_{0}-\theta _{0}\,mod\,2\pi \end{aligned}$$
• ES2B:
  $$\begin{aligned} C_{E}(d_{0},\theta _{0})\leftarrow d_{0}+\theta _{0}\,mod\,2\pi \end{aligned}$$
• ES3A:
  $$\begin{aligned} C_{E}(d_{0},d_{1},s)\leftarrow \frac{1}{2}\left( d_{0} +d_{1}+n\cdot \pi \right) \,mod\,2\pi \end{aligned}$$
• ES3B:
  $$\begin{aligned} C_{E}(d_{0},d_{1},s)\leftarrow 2\cdot d_{0}-d_{1}-n\cdot \pi \,mod\,2\pi \end{aligned}$$

Given an elimination sequence

$$\begin{aligned} E_{1},...,E_{n} \end{aligned}$$

we define the associated construction sequence

$$\begin{aligned} C(E_{n}),...,C(E_{1}) \end{aligned}$$

3.5 Angle algorithm

Given an eliminable angle graph, $G={V,A,B}$, and an ordered pair (u, v) of elements of V, we propose the following algorithm to attempt to determine the angle (u, v) as a linear combination of input angle values.

Algorithm 2

• 1. Find an elimination sequence for G.

• 2. Determine the associated construction sequence.

• 3. Execute the construction sequence.

• 4. Evaluate $a(u,v)=d(v)-d(u)$.

• 5. Simplify a.

• 6. If a contains any indeterminate introduced by the algorithm, fail, otherwise return a.

We notice that the constructions are all linear, hence the directions computed for v will be elements in the vector space spanned by indeterminates $\{\phi _{i}\}$ introduced by the constructions of type ES1 and any indeterminate angles $\{\theta _{j}\}$.

As an example, Fig. 6 is the angle graph for the example of 3.1

One possible elimination sequence would be:

• 1. Eliminate Q using ES3B

• 2. Eliminate M using ES2A

• 3. Eliminate O using ES2B

• 4. Eliminate L using ES3A

• 5. Eliminate N using ES1

• 6. Eliminate P using ES1

The corresponding construction sequence would be:

• 1. $d_{P}=\phi$

• 2. $d_{N}=\psi$

• 3. $d_{L}=\frac{1}{2}(d_{P}+d_{N})=\frac{1}{2}(\phi +\psi )$

• 4. $d_{O}=d_{N}+0=\psi$

• 5. $d_{M}=d_{L}-\theta =\frac{1}{2}(\phi +\psi )-\theta$

• 6. $d_{Q}=2\cdot d_{M}-d_{O}=\phi +\psi +2\theta -\psi =\phi -2\theta$

Subtracting and simplifying the angle, we have

$$\begin{aligned} A(P,Q)=d_{Q}-d_{P}=-2\theta \end{aligned}$$

Fig. 6

Angle graph for the example of 3.1. There are two angles, one of $\theta$ between L and M and one of 0 between N and O, which are parallel. The triangles represent bisection relations between L,N and P and between M,Q and O

3.6 Algorithm Properties

We prove first that the success or failure of the algorithm does not depend on the particular elimination sequence used.

Given an eliminable angle graph (V, B, A) and an elimination sequence $Z={E_{i}}$, let indeterminates ${\theta _{1},...,\theta _{m}}$ be introduced by the constructions corresponding to angle constraints in the model (associated with elimination steps ES2A, ES2B). Let indeterminates ${\phi _{1},...,\phi _{n}}$ be introduced by the constructions corresponding to an unconstrained point (elimination step ES1). When the construction sequence $C(E)={C(E_{j})}$ is executed, we derive a set of directions $\left\{ d_{i}\right\}$, corresponding to the elements of the set $V=\{v_{i}\}$. As the constructions are all linear, each $d_{i}$ is an element of the vector space spanned by ${1,\theta _{1},...,\theta _{m},\phi _{1},...,\phi _{n}}$. As the indeterminates are all independent, the set ${1,\theta _{1},...,\theta _{m},\phi _{1},...,\phi _{n}}$ is a basis for the vector space.

Definition 3.3

Let n be the number of direction nodes in a graph and m the number of angle edges. Let b be the number of bisection nodes. Define the degrees of freedom of the graph to be $d(G)=n-m-b$.

Lemma 3.4

Let $Z_{1}$ and $Z_{2}$ be two elimination sequences for angle graph G. The number of indeterminates introduced by each is the same.

Proof

Elimination steps ES2 and ES3 have no effect on d(G), ES1 reduces it by 1. The number of indeterminates introduced is therefore equal to d(G) for any elimination sequence. $\square$

Lemma 3.5

Let $Z_{1}$ and $Z_{2}$be two elimination sequences for angle graph G. Let $\Phi ={\phi _{1},...,\phi _{n}}$ be the indeterminates added by C and $\Psi ={\psi _{1},...,\psi _{n}}$ be the indeterminates added by $Z_{2}$.

*Let $\delta _{i}(1,\theta _{1},...,\theta _{m},\phi _{1},...,\phi _{n})$ be the direction corresponding to added indeterminate $\psi _{i}$ as computed by construction

*$C(Z_{1})$. ${1,\theta _{1},...,\theta _{m},\delta _{1},...,\delta _{n}}$ form a basis for the space generated by $Z_{1}$.

Proof

${1,\theta _{1},...,\theta _{m},\phi _{1},...,\phi _{n}}$ are linearly independent, hence so are ${1,\theta _{1},...,\theta _{m},\delta _{1},...,\delta _{n}}$. $\square$

Theorem 3.6

Let $Z_{1}$ and $Z_{2}\hbox {be}$ two elimination sequences for angle graph G. Let $\Phi ={\phi _{1},...,\phi _{n}}$ be the indeterminates added by C and $\Psi ={\psi _{1},...,\psi _{n}}$ be the indeterminates added by $Z_{2}$. Let $a_{1}\hbox {be}$ the value of angle (u, v) when constructed by $C(Z_{1})$ and let $a_{2}$ be its value when constructed by $C(Z_{2})$. If $a_{1}$ contains none of the added indeterminates ${\phi _{1},...,\phi _{n}}$ , then $a_{2}$ contains none of the added indeterminates ${\psi _{1},...,\psi _{n}}$.

Proof

By hypothesis, $a_{1}$ is an element of the subspace spanned by $\Theta =\{1,\theta _{1},...,\theta _{m}\}$ of the vector space generated by $Z_{1}$, and $a_{2}$ is an element of the subspace spanned by $\Theta$ of the vector space generated by $Z_{2}$. Expressed in terms of the indeterminates introduced by construction $C(Z_{2})$,

$$\begin{aligned} a_{2}=q_{0}+q_{1}\theta _{1}+...+q_{m}\theta _{m}+r_{1}\psi _{1}+...+r_{n}\psi _{n} \end{aligned}$$

$\square$

Let $\delta _{i}(1,\theta _{1},...,\theta _{m},\phi _{1},...,\phi _{n})$ be the direction corresponding to added indeterminate $\psi _{i}$ as computed by construction $C(Z_{1})$ Then

$$\begin{aligned} a_{1}=q_{0}+q_{1}\theta _{1}+...+q_{m}\theta _{m}+r_{1}\delta _{1}+...+r_{n}\delta _{n} \end{aligned}$$

${1,\theta _{1},...,\theta _{m},\delta _{1},...,\delta _{n}}$ is a new basis for the vector space generated by $Z_{1}$. Let $a_{1}'$ be the projection of $a_{1}$ onto the subspace spanned by ${\delta _{1},...,\delta _{n}},$ then $a_{1}'=0$. An alternative basis for this subspace is ${\phi _{1},...,\phi _{n}}$. As $a_{1}'=0$ in this subspace, the coefficient of each $\phi _{i}$is zero.

Theorem 3.7

Given an eliminable angle graph V, B, A , let Z be an elimination sequence for the graph. Given an angle (u, v) whose value a(u, v) can be proved from A using a traditional proof whose steps can be reduced to the application of bisection relations in B angle relations in A. Let ${A_{i}}$ be the angle relations added by the traditional proof. Let ${a_{i}}$ be the values of these angles computed using C(Z). If $|{A_{i}}|=d(G)-1$ and ${a_{i}}$ are linearly independent, then a(u, v) will not involve any of the indeterminates introduced by C(Z).

Proof

Let $\{\chi _{1},..,\chi _{n}\}\hbox {be}$ indeterminates introduced into the traditional proof to represent the values of introduced angles $\left\{ (u_{1},v_{1}),...,(u_{n},v_{n})\right\} .$ If (u, v) is provable, then (u, v) is in the vector space with basis ${1,\theta _{1},...,\theta _{m},\chi _{1},..,\chi _{n}}$. Expressed in terms of these indeterminates let the angle between u and v be: $\square$

$$\begin{aligned} a(u,v)=a_{1}\theta _{1}+...+a_{n}\theta _{n}+r_{1}\chi _{1}+...+r_{n}\chi _{n} \end{aligned}$$

As it is provable over $\{\theta _{1},...,\theta _{m}\}$ it is in the subspace generated by ${1,\theta _{1},...,\theta _{m}}$. Let the indeterminate set introduced by Z be ${\phi _{1},...,\phi _{n}}$. Angle values are differences of direction, and hence are invariant under rotation. Thus we can set $\phi _{1}=0$ and express the introduced angles in terms of ${\phi _{2},...,\phi _{n}}$. Let $\beta _{i}(\theta _{1},...,\theta _{m},\phi _{2},...,\phi _{n})$ be the angle value generated by construction C(Z) for angle $(u_{i},v_{i})$. Then

$$\begin{aligned} a(u,v)=a_{1}\theta _{1}+...+a_{n}\theta _{n}+r_{1}\beta _{1}+...+r_{n}\beta _{n-1} \end{aligned}$$

${1,\theta _{1},...,\theta _{m}, \beta _{1},...,\beta _{n-1}}$ is a new basis for the vector space generated by Z. Let $a(u,v)'$ be the projection of a(u, v) onto the subspace spanned by ${\beta _{1},...,\beta _{n-1}},$ then $a(u,v)'=0$. An alternative basis for this subspace is ${\phi _{2},...,\phi _{n}}$. As $a(u,v)'=0$ in this subspace, the coefficient of each $\phi _{i}\hbox {is}$ zero.

3.7 Additional Angle Proof Types

The algorithm as described above corresponds to a subset of the by-hand methods used in angle derivation. In this section we expand it to cover the circle angle theorems and the derivation of angles in an isosceles triangle. Circle angle theorems include these:

• 1. The angle subtended at the circumference by an arc is half the angle at the center.

• 2. The opposite angles of a cyclic quadrilateral are supplementary.

• 3. Angles subtended at the circumference by a chord, on the same side of the chord are equal.

Fig. 7

A circle angle theorem equivalence reduced to isosceles triangle theorem

The isosceles triangle theorem states that if the angle at the apex of an equilateral triangle is $\theta$, then the angles at the base are $\frac{1}{2}(\pi -\theta )$. We first note that the base of an isosceles triangle is parallel to the external angle bisector of the other sides. Hence considered from an angle perspective, the relationship that three directions form the sides of an isosceles triangle is equivalent to the relationship that one direction is an angle bisector of the other two. The first angle theorem, above, may be reduced to the isosceles triangle theorem by adding the line joining the point on the circumference to the center, and isosceles relationships between the circle chords and the radial lines to their end points. Figure 7 illustrates this. The second and third circle angle theorems may readily be reduced to the first. An enhanced algorithm which deals with circle angle theorems is the following.

Algorithm 3

• 1. Identify explicit isosceles triangles and add corresponding bisector relationships corresponding to the triangles.

• 2. For each chord of a circle, do 3 and 4.

• 3. Add the radial lines between the end points and the center of the circle, if they are not present.

• 4. Add bisector relationships between the radial lines and the chord.

• 5. Run Algorithm 2.

The angle engine is tightly integrated in Geometry Expressions, when an angle quantity is measured, the angle algorithm is first run to see if it is derivable directly from given angles. If the algorithm does not run successfully then the Cartesian coordinates of the model are computed using the analytical geometry method and the angle measurement made from these. Such expressions typically involve trigonometrical functions and their inverses. The incorporation of the angle engine means that a class of simple theorems typical of high school geometry may be solved without the introduction (and tendentious simplification) of trigonometrical functions. The class of problems which the angle engine solves is shown above to be any theorem which may be proved by hand using sequential application of a specific set of angle theorems, which includes theorems relating angles between a transcept and parallel lines, theorems relating angles on a chord at the center and circumference of a circle, angles in isosceles triangles. This set is non-negligible in size and over-represented in high school geometry.

Fig. 8

Automated proof of Archimedes angle trisection construction along with an indication of how automated proofs of many angles in the figure can scaffold a student’s development of a traditional proof

We illustrate its use with the proof of Archimedes angle trisection construction (Fig. 8). To prove the theorem using the software, the user draws the figure, adds constraints of congruence between segments AC and CO, and specifies the angle CAO to be $\theta$. Measuring DOB yields $3\theta$, which is the required result. Beyond machine proof, if one is interested in using Geometry Expressions to help in learning how to prove theorems by hand, one can ask the software to compute all the angles in the Fig. 9. The particular values of these angles can then provide help in discovering a chain of inferences between hypothesis and conclusion. This is a variant of the proof helper approach taken by OK Geometry [11].

Fig. 9

Automated generation of angles in a figure can help a user develop a traditional proof

4 Performance

In order to compare the performance of the approach to that of the area method, the first 207 theorems from [4] were chosen as a substantial representative sample set, which is not “cherry picked”. The results are detailed in [16] and summarized here.

We present two examples from this study, which uses the example numbering from [4]. Example 6.52 requires us to prove that the sum of squares of the medians of a triangle is equal to 3/4 of the sum of squares of the sides of the original triangle. Figure 10 shows the Geometry Expressions model of this problem along with its solution. To create the model, the user draws a triangle ABC, then constructs side midpoints D, E, F and medians AD, BE and CF in a style similar to dynamic geometry systems. The user then specifies symbolic ’constraints’ defining the length of BC to be A, the length of AC to be B and the length of AB to be c. These constraints, in effect parameterize the model, and, as the user is able to ask for distances and angles to be measured from the drawing, defines in what terms these measurements will be expressed. If three lengths, as here, are constrained, then measurements will be returned in terms of those lengths. In this example, the user requests lengths CF, AD and BE by selecting the segments and pressing the symbolic length measurement button in the user interface. Geometry Expressions automatically generates formulas for the measurements. The user then creates an expression for the sum of squares of these quantities. Geometry Expressions evaluates and simplifies this expression, yielding the result.

Fig. 10

Theorem 6.52 of [4] states that the sum of squares of the medians of a triangle is equal to 3/4 of the sum of squares of the sides of the original triangle

In Fig. 11, we see a model for this problem where the user has, somewhat abstrusely, constrained the triangle in terms of two sides and the included angle. The specific measurements are now given in terms of these quantities but the two sums of squares may still be compared by inspection. This artificial example highlights (in reverse) a first strategy for making progress when a direct proof fails, that is to reparameterize the model, hoping to make the algebra more tractable. A second strategy is to apply a more capable CAS to the problem. These strategies only need to be deployed, however, on a small number of the examples tested. The dependence of performance on parametrization of the model may certainly be regarded as a weakness in the method, however it should be pointed out that the corresponding problem formulations for the area method [4] are themselves carefully thought out. In [4] theorem 6.163, for example,concerns a triangle, its incircle and various distances. A natural formulation would have as inputs the vertices of the triangle. With this formulation, Geometry Expressions fails to prove the result. However in [4], two vertices and the incenter are used as the independent quantities. With the same formulation, Geometry Expressions is able to complete the proof.

Fig. 11

Changing the constraints in Fig. 10 changes the evaluated expressions and changes the algebra required for simplification

Example 6.24 is Desargue’s Theorem, which may be stated as follows. Given two triangles ABC, $A_{1}B_{1}C_{1}$, if the three lines $AA_{1},\,BB_{1},\,CC_{1}$ meet in a point S, define P,Q, and R to be the intersections of BC and $B_{1}C_{1}$, CA and $C_{1}A_{1}$, AB and $A_{1}B_{1}$ respectively. Then P, Q, R are collinear.

Figure 12 shows a Geometry Expressions model used in this proof. The user draws a triangles ABC and $A_{1}B_{1}C_{1}$ and a point S. He constrains the coordinates of S to be (0, 0) and points A, B, C to be $(x_{0},y_{0})$, $(x_{1},y_{1})$, $(x_{2},y_{2})$. He draws the segments $SA_{1}$, $SB_{1}$, $SC_{1}$, and constrains A, B and C respectively to be incident to these segments. He now constructs point P at the intersection of BC and $B_{1}C_{1}$, Q at the intersection of AC and $A_{1}C_{1}$, and R at the intersection of AB and $A_{1}B_{1}$. He asks Geometry Expressions to measure the area of the triangle PQR. Geometry Expressions responds with a symbolic value of 0. This proves that the points are collinear.

Of the 207 examples tested in [16], 196 are solved in under 2 minutes on a modern PC by Geometry Expressions, using an initial formulation. In the majority of cases the timing was effectively instantaneous, or a small number of seconds. Five examples failed on the initial formulation, but succeeded on a second formulation of the model (sensitivity to formulation is illustrated in Figs. 10 and 11). In 3 cases, the internal Geometry Expressions CAS was unable to simplify the result, but Maple was able to complete the simplification. In 2 cases, the initial formulation failed, but succeeded after supplying a simple intermediate result. In 1 case neither Geometry Expressions’ CAS nor Maple were able to simplify the result of any obvious parametrization.

Fig. 12

Desargue’s Theorem states that points P, Q, R are collinear. An automated proof in Geometry Expressions consists of confirming that the symbolic area of triangle PQR is zero

5 Examples

The key advantage of the analytical geometry method is its genericity. We illustrate its breadth of applicability by presenting a number of examples using Geometry Expressions [14]. Geometry Expressions has at its core an implementation of the analytical geometry method. It has a constraint based user interface layer based on graph algorithms [15] which converts the constraint model into a construction sequence. The UI does not permit models which are over-constrained, or which are unsequenceable.

The basic user interface of Geometry Expressions allows users to create points, line segments, infinite lines, vectors, conics, functions, curves, regular polygons, general curve arcs, piecewise linear curve approximations, polygons and curvilinear polygons. Functions and curves may be determinate (with a specific formula), or indeterminate. Regular polygons and piecewise linear curve approximations may have determinate or indeterminate numbers of sides. Curvilinear polygons consist of a sequence of arcs and lines. Interacting with the geometric entities are constructions, constraints and measurements. Constructions include those found in typical dynamic geometry system: midpoint, perpendicular bisector, angle bisector, parallel line, perpendicular line, tangent. In addition they include transforms: rotation, reflection, translation, dilation. Further constructions include a locus construction and an envelope construction. these constructions take a point (locus) or line or circle (envelope) along with a parameter to vary, and generate a curve. Some constraints are structural, providing a convenient and expressive alternative to constructions in specifying the model. Other constraints are quantitative, giving an avenue to provide a parametrization of the model and to allow entry of symbols which will appear in the formulas generated by the system. Structural constraints include incidence, tangency, parallellism, perpendicularity, congruence. Quantitative constraints include radius, distance, angle, direction, slope, coordinates, vector coefficients, implicit equation, proportion along a line segment or arc, parametric location on a curve. Measurements which may be made from a model include distance, length or arc length, radius, angle, direction, slope, coordinates, vector coefficients, area, perimeter, parametric equations or implicit equation.

Basic capabilities of the Geometry Expressions CAS are mandated by these features and measurements. Tangents call for differentiation, as do envelope curves. Arc lengths and curvilinear polygon areas call for integration. Areas involving polygonal arc approximations call for indefinite sums. Implicit equations of loci, envelopes and parametric curves calls for variable elimination. In addition a simplification engine performs rational simplification, along with trig and root simplification. The software does not, by design, provide direct user access to the algebra system, rather it provides a wide range of options to export expressions to external algebra systems for further analysis. The interface between geometry system and CAS provides a place for the user in the process, and our examples will illustrate how this creates an environment which recaptures some of the dynamism of Dynamic Geometry, but in the symbolic realm.

5.1 Napoleon’s Theorem

Fig. 13

Napoleon’s Theorem

Given triangle ABC, draw equilateral triangles externally on each side. The triangle whose vertices are the centroids of these equilateral triangles is itself equilateral.

In Fig. 13, the lengths of triangle ABC have been constrained to be a, b, c. Equilateral triangles are defined using congruence constraints, and centroids M,N,O found by intersecting medians (not shown). Side lengths of the triangle MNO are computed by the software and may be verified equal by inspection. A point to note is that these side lengths are given in terms of a, b, c, but are particularly straightforward if expressed in terms of the area of triangle ABC and the sum of squares of its sides. Explicitly, we see by inspection of the formulas in Fig. 13 that the square of the side length of MNO can be expressed

$$\begin{aligned} MN^{2}=\frac{S}{6}+\frac{2A}{\sqrt{3}} \end{aligned}$$

where A is the area of ABC, and S the sum of squares of its sides.

Of course we could have asked the system for the ratio MN/NO, or for the difference $MN-NO$ and acquired the values 1 or 0 respectively. Observing the actual value can sometimes lead to additional insights and discoveries. For example, a student might examine the triangle formed by the apexes of the equilateral triangles and ask if the sum of squares of its side lengths can also be represented as a linear combination of S and A. They could examine the area of the new triangle and ask the same question. Alternatively, the student could examine the distance between the apex of an equilateral triangle and the opposite side of the original triangle.

$$\begin{aligned} DA=\dfrac{\sqrt{2}\sqrt{a^{2}+b^{2}+c^{2}+\sqrt{3}\sqrt{a+b+c}\sqrt{a+b-c}\sqrt{a-b+c}\sqrt{-a+b+c}}}{2} \end{aligned}$$

He could observe the symmetry of the algebraic figure and infer that EB and FC will have the same length. He could observe that this expression is similar to the side length of the Napoleon triangle. Perhaps he would be motivated to find a geometric argument which brings out this similarity.

5.2 Simpson’s Line

Fig. 14

Area of the Pedal Triangle, and the circle whose equation is obtained by setting this expression to be zero

In this example, we take a standard theorem, and ask the question: how could it be discovered by a student exploring with an SDGS? Again our emphasis is on the human part of the process, as this is the part inhabited by the student.

Given a triangle ABC and a point P, construct the pedal triangle DEF by projecting P onto the three sides of the triangle. What is the locus of P for which points $DE\hbox {F}$ are collinear?

Figure 14 shows a direct computation of the area of the pedal triangle of the $\hbox {point}P=(x,y)$. In constructing the figure, the user has elected to enter coordinates for the triangle’s vertices and for the pedal point P. This is a natural approach where the question is asking for a locus, whose equation will be expressed in coordinate terms. The user has positioned the triangle with one vertex at the origin and one side along the x axis. This is a straightforward strategy to ease the complexity of the expected locus equation. Geometry Expressions generates an expression for the area of the pedal triangle. Collinearity is equivalent to this area being zero. At this point, we imagine our user (perhaps with pedagogic prompting) examining the form of the expression and appreciating that an equation setting this expression to zero is in fact the equation of a circle. The required locus is thus established by inspection of the area to be a circle, the question is which circle. The user can then draw a circle in arbitrary location and set its equation as required, using copy and paste to facilitate transcribing the left hand side from the area measurement. With this equation set, the circle appears to be the circumcircle of ABC. This can be attested numerically by dragging the points and confirmed exactly by comparing symbolic distances between the circle’s center and A, B and C.

Fig. 15

Regiomontanus Problem is to maximize the angle CBD. A formula for this angle is generated by Geometry Expressions. This is then copied into Maple, and differentiation and the solve command are used to find the value of x which yields a maximal angle

5.3 Regiomontanus’ Problem

The natural mode of operation of Geometry Expressions being one of formula generation, rather than verification, makes it a convenient tool for theorem discovery. The ability to export these formulas to a CAS opens the way for a wider selection of geometry problems to be solved in a semi-automated fashion.

We call this ’computer aided geometrical deduction’, and the rules of our game are the following. Geometry should be resolved automatically in Geometry Expressions. However, expressions may be copied from Geometry Expressions into an algebra system, and generic algebra operations executed (without further reference to geometry). Algebra operations could include differentiate, solve, simplify, limit. Algebraic solutions may be pasted back into Geometry Expressions to determine whether they are solutions of the underlying geometric problem. This approach can be applied to a broad assortment of geometry problems. In particular, the ability to differentiate and solve allows for semi-automated direct solution of geometrical optimization problems.

For example, Regiomontanus’ problem [5] asks for the place on the earth’s surface where a vertically suspended bar appears the longest. This is in effect asking us to maximize the angle subtended by the bar onto the surface of the earth. Figure 15 illustrates the usage of Geometry Expressions and Maple to solve this problem. The user creates a circle AB and a line segment CD suspended above it. He constrains A to lie on CD extended. He then specifies the length of the segment, its distance from the center of the circle and the radius of the circle. Finally, he constrains the angle between AB and CD to be x. He then draws line segments BC and BD and asks Geometry Expressions to compute the angle between them. He copies this angle into Maple where he differentiates and solves with respect to x. He copies the solution from Maple into Geometry Expressions, pasting it into the angle constraint formerly occupied by x. The solution of course is displayed for specific values of the model parameters (L, h, r in Fig. 15). However, the dynamic geometry features of Geometry Expressions may be used to vary the values of these parameters and watch how the solution evolves. Particularly illuminating is to observe the relationship between the circumcircle of BCD in Fig. 16 and the circle representing the earth’s surface. Varying L and h, it appears that these circles remain tangential at the solution. A machine proof of this is obtained in Fig. 16 by evaluating the symbolic distance between the center of the circumcircle E and AB. The circumcircle is the locus of points at which CD subtends an angle equal to angle CBD. Consideration of this fact may motivate the user to construct a purely geometric proof of the result.

Fig. 16

The circumcircle of the solution point of Regiomontanus’ Problem and the two ends of the vertical bar is tangential to the surface of the earth

Note that in this example, the algebra operations are essentially rote. The fact that Geometry Expressions does not give the user direct access to these routine algebra operations is a matter of design. The system is designed to be an adjunct to an algebra system, communicating via the clipboard. Hence these purely algebraic operations are delegated to the CAS. From an educational perspective there is value to this separation of domain model (Geometry Expressions) from abstracted mathematical model (CAS). While the clipboard may seem a cumbersome communication method when viewed from the perspective of an automated theorem prover, it is a natural one for interactive use both within a CAS and between CAS and domain model. It is a particularly powerful method of communication when copying a result from the CAS back into Geometry Expressions, as the destination for the mathematics may conveniently be specified. Geometry Expressions supports copying of mathematics in the native formats for Derive, Maple, Mathematica, Maxima, MuPad, TI-nSpire and Matlab, along with MathML and Tex.

Fig. 17

Bezier curve defined by its control polygon and de Casteljeu’s algorithm

5.4 Bezier Approximation of a Circular Arc

In Figs. 17, 18, and 19 we solve an area problem posed to the author by a mechanical engineer who was looking for the best cubic spline approximation to a circular arc of arbitrary angle. (He wanted this because his machine tool accepted Bezier control points, but not circular arcs.)

The problem can be stated as follows: Given a circle center O and points B and C on the circumference of the circle, find control points for a Bezier spline S with the following properties:

• 1. S is tangent to the circle at B and C.

• 2. S is symmetric about the angle bisector of CAB.

• 3. The area of the curvilinear polygon bounded by AC, AB and the spline curve BC is the same as the area of the circular sector CAB.

Fig. 18

Area of the curvilinear polygon defined by the Bezier curve and the two radii is computed automatically

To model this, the user first creates a Bezier Spline curve. By de Casteljau’s algorithm [12] he can build the curve using line segments and constraints specifying a point’s proportion along a line segment. First a control polygon CDEB is drawn (Fig. 17) and points F, G, H proportion t along CD, DE, EB respectively. Points I,J are constructed proportion t along FG and GH, then point K proportion t along IJ. The locus of point K as t varies from 0 to 1 is constructed. This is the Bezier curve. The next step for the user is to create the curved polygon whose edges are the Bezier curve and the two radii. As the Bezier Spline is tangential to its control polygon, property 1 above is ensured by constraining lines CD and EB to be tangential to the circle. To ensure property 2 holds, the lengths of CD and EB are constrained to be congruent. The model is parametrized by constraining CD to be length a.. A formula for the area under the curve is computed by Geometry Expressions (Fig. 18). This is then copied into an algebra system and equated to $r^2\theta /2$, the area of the circular sector with angle $\theta$. The CASgenerates two solutions to this equation for a. Copying and pasting these back into Geometry Expressions allows the user to examine the solutions visually. One solution yields a spline curve with a loop. The area is equivalent to the circular sector only after subtracting the area in the loop, and thus a poor solution to the original problem. The other solution is the one pictured in Fig. 19, which closely approximates the circular arc.

Fig. 19

Solutions for a which yield the required area are pasted into the Bezier model

5.5 Pappus Chain

Fig. 20

Radii of circles in a Pappus Chain

Given two externally tangent circles of radius r and s, and a circle of radius $r+s$ externally tangent to both, we investigate the radii of the circles in the Pappus chain whose first element is the circle tangent to these three circles, and whose subsequent members are tangent to the previous member, the circle of radius s and the external circle.

Figure 20 shows a model with the first two circles in the chain. To create this figure in Geometry Expressions, the user first draws the given three circles in an approximately correct location (so that the smaller circles are indeed inside the larger, but not inside each other). He then sets their radii to be r, s and $r+s$. He proceeds to add tangency constraints between the circles. To add a circle to the Pappus chain, he simply draws it in an approximately correct location then adds tangency constraints between the new circle, and the preceding circle in the chain, the outer circle, and the circle of radius s. The radius of the new circle is presented on request by the software. At this point it might boldly be conjectured that the radius for the nth circle is

$$\begin{aligned} \dfrac{r\cdot s\cdot (r+s)}{n^{2}\cdot r^{2}+r\cdot s+s^{2}} \end{aligned}$$

To prove this conjecture by induction, we can create a circle tangent to the outer circle and the circle of radius s, and which has the radius:

$$\begin{aligned} \dfrac{r\cdot s\cdot (r+s)}{(n-1)^{2}\cdot r^{2}+r\cdot s+s^{2}} \end{aligned}$$

This represents the generic $n-1$ element of the series. We now create a the next circle in line and show that its radius is the desired (Fig. 21)

$$\begin{aligned} \dfrac{r\cdot s\cdot (r+s)}{n^{2}\cdot r^{2}+r\cdot s+s^{2}} \end{aligned}$$

completing the proof.

For the user to create this inductive proof from the model of Fig. 20 is quite straightforward. First, he copies the expression for the circle radius $z_{1}$. He then deletes the tangency between the second circle in the chain and its predecessor as well as its measured radius. He now creates a radius constraint and pastes in the copied expression, changing 4 to $n^{2}$.

Fig. 21

An inductive proof of the generic radius in the Pappus Chain

This example illustrates exactly the sort of inductive hypothesis formation which is the strength of dynamic geometry systems, but carried over to the symbolic domain. With the symbolic system, however, we can readily transition from inductive hypothesis to proof by induction.

Fig. 22

Catacaustic curve for generic function y=f(x). Its parametric equations are generated by Geometry Expressions

5.6 Catacaustic is the Focus Locus

In addition to indeterminate variables, Geometry Expression will accept indeterminate functions. Generic derivatives and integrals are used in computation of tangents, arc lengths and areas. Differential geometry theorems may thus be expressed and solved. An example problem follows.

Given a function $y=f(x)$, we define the catacaustic of a family of lines to be the envelope of the reflection of those lines in the tangent to the function. Show that the catacaustic of a family of lines parallel to the y-axis is the same as the locus of the focus of the family of parabolas defined by the 2nd order Taylor Series approximation to the function.

Both derived curves can be readily defined geometrically in terms of the generic function $y=f(x)$ (Fig. 22). Note that the function has some specific “witness” form, which is in fact controllable by the user. This enables a specific derived curve to be displayed. However, the parametric equation for the new curve are computed in terms of the generic function f and its first and second derivatives $f'$ and $f''$. In Fig. 22, the user has created a line parallel to the axis passing through a point at location $x=t$ on the generic function $y=f(x)$. He has constructed the reflection of this line in the tangent to the curve at point t and has invoked the construction for the envelope of the reflected line as t varies. Geometry Expressions has automatically computed the parametric equations of this curve.

In Fig. 23, the user has drawn a parabola with vertex B and focus C, and specified its implicit equation to be:

$$\begin{aligned} y=f(t)+(x-t)f'(t)+\frac{(x-t)^{2}}{2}f''(t) \end{aligned}$$

The parabola is thus the second order Taylor approximation of $y=f(x)$ at $x=t$. He has then constructed the locus of its focus C as t varies. Geometry Expressions has computed the parametric equations of this curve, inspection of the parametric equations (and a little light algebra) confirms that the two curves are the same.

Fig. 23

The locus of the focus of the parabola whose equation is the 2nd order Taylor approximation of a generic curve. Geometry Expressions has computed the parametric equations of the locus

6 Conclusion

We have presented the analytical geometry method in a parallel style to presentations of semi-synthetic automated theorem proving methods such as the area method, the full angle method and the mass point method [4, 8, 18]. We hope this helps clarify the relative strengths and weaknesses of the method in the the specific area of automated theorem proving. We have illustrated the breadth of applicability of a symbolic dynamic geometry system built on the analytical geometry method in providing a general purpose tool which allows the student dynamically to explore the relationship between geometric and algebraic models.

As an automated theorem prover, the analytic geometry method differs by generating symbolic statements which are true only in some neighborhood of the specific geometry presented in the diagram. This neighborhood could be made specific with inequalities generated by the constructions. However, in practice, these can get in the way of clarity. There is a strong tradition in geometry, going back to Euclid, where the diagram has a role which is more important than merely labeling points. Implicit sidedness constraints are embedded in the figure. There is another tradition dating back to Euclid of stating a theorem in all generality, but proving only the illustrated case, leaving the rest to the reader. The analytical geometry method lies firmly in these traditions. We would also point out that this is the model of geometry which is most familiar to high school students, and most useful to engineers.

In presenting an extensive set of examples, we have emphasized the genericity of the analytical geometry method. We have also attempted to illustrate the ways in which a user is involved in the proving process, putting the dynamic into the combination of dynamic geometry and automated theorem proving.

Appendix A

We present constructions for an implementation whose geometric elements are points and oriented lines. Oriented lines are represented by the triple (A, B, C), where the underlying line is defined by the equation $A\cdot x+B\cdot y+C=0$, and the orientation is defined by the vector (A, B). Hence the triple $(-A,-B,-C)$ represents the same line as (A, B, C) but with the opposite orientation. In each case we show the elimination step for the point’s coordinates $(x_{P},y_{P})$ or the line’s coefficients $(A_{L},B_{L},C_{L})$. The equation of the line with these coefficients is $A_{L}\cdot x+B_{L}\cdot y+C_{L}=0$.

C1 Point given coordinates P is defined to have coordinates (x,y).

$$\begin{aligned}&x_{P}\rightarrow x\\&\begin{array}{c} y_{P}\rightarrow y\end{array} \end{aligned}$$

C2 Point proportion along a segment Point P is proportion k along the segment $P_{0}P_{1}$.

$$\begin{aligned}&x_{P}\rightarrow k\cdot x_{1}+(1-k)\cdot x_{0}\\&\begin{array}{c} y_{P}\rightarrow k\cdot y_{1}+(1-k)\cdot y_{0}\end{array} \end{aligned}$$

C3 Point distance from two points If point P is distance $d_{0}$ from point $P_{0}$ and distance $d_{1}$ from point $P_{1}$ and to the left of ordered segment $P_{0}P_{1}$:

$$\begin{aligned}&x_{P}\rightarrow x_{1}+\dfrac{d_{3}\left( x_{0}-x_{1}\right) }{2d_{2}^{2}} +\dfrac{d_{4}\left( y_{0}-y_{1}\right) }{2d_{2}^{2}}\\&y_{P}\rightarrow y_{1} -\dfrac{d_{4}\left( x_{0}-x_{1}\right) }{2d_{2}^{2}}+\dfrac{d_{3} \left( y_{0}-y_{1}\right) }{2d_{2}^{2}} \end{aligned}$$

If point P is distance $d_{0}$ from point $P_{0}$ and distance $d_{1}$ from point $P_{1}$ and to the right of ordered segment $P_{0}P_{1}$:

$$\begin{aligned}&x_{P}\rightarrow x_{0}-\dfrac{d_{5}\left( x_{0}-x_{1}\right) }{2d_{2}^{2}}-\dfrac{d_{4}\left( y_{0}-y_{1}\right) }{2d_{2}^{2}}\\&\begin{array}{c} y_{P}\rightarrow y_{0}+\dfrac{d_{4}\left( x_{0}-x_{1}\right) }{2d_{2}^{2}}-\dfrac{d_{5}\left( y_{0}-y_{1}\right) }{2d_{2}^{2}}\end{array} \end{aligned}$$

where:

$$\begin{aligned} d_{2}= & {} \sqrt{\left( x_{1}-x_{0}\right) ^{2}+\left( y_{1}-y_{0}\right) ^{2}}\\ d_{3}= & {} -d_{0}^{2}+d_{1}^{2}+d_{2}^{2}\\ d_{4}= & {} \sqrt{d_{0}+d_{1}+d_{2}}\sqrt{d_{0}+d_{1}-d_{2}}\sqrt{d_{0}-d_{1}+d_{2}}\sqrt{-d_{0}+d_{1}+d_{2}}\\ d_{5}= & {} d_{0}^{2}-d_{1}^{2}+d_{2}^{2} \end{aligned}$$

C4 Point distance from two lines Point P is directed distance $d_{0}$ from line $L_{0}$ and directed distance $d_{1}$ from line $L_{1}$.

$$\begin{aligned}&x_{P}\rightarrow \dfrac{-B_{1}\left( C_{0}-d_{0} \sqrt{A_{0}^{2}+B_{0}^{2}}\right) +B_{0}\left( C_{1}-d_{1}\sqrt{A_{1}^{2}+B_{1}^{2}}\right) }{A_{0}B_{1}-A_{1}B_{0}}\\&\begin{array}{c} y_{P}\rightarrow \dfrac{A_{1}\left( C_{0}-d_{0}\sqrt{A_{0}^{2}+B_{0}^{2}}\right) -A_{0}\left( C_{1}-d_{1}\sqrt{A_{1}^{2}+B_{1}^{2}}\right) }{A_{0}B_{1}-A_{1}B_{0}}\end{array} \end{aligned}$$

C5 Point distance from one line and one point We define the 2D wedge product $(x_{0},y_{0})\wedge (x_{1},y_{1})=x_{0}y_{1}-x_{1}y_{0}$

If point P is directed distance $d_{0}$ from line $L_{0}$ and directed distance $d_{1}$ from point $P_{1}$ and s $\overrightarrow{P_{0}P}\wedge (A_{0},B_{0})>0$

$$\begin{aligned}&x_{P}\rightarrow x_{0}+B_{0}\cdot d_{3}-\dfrac{A_{0}\cdot \left( d_{2}-d_{0}\right) }{\sqrt{A_{0}^{2}+B_{0}^{2}}}\\&\begin{array}{c} y_{P}\rightarrow y_{0}-A_{0}\cdot d_{3}-\dfrac{B_{0}\cdot \left( d_{2}-d_{0}\right) }{\sqrt{A_{0}^{2}+B_{0}^{2}}}\end{array} \end{aligned}$$

If point P is directed distance $d_{0}$ from line $L_{0}$ and directed distance $d_{1}$ from point $P_{1}$ and $\overrightarrow{P_{0}P}\wedge (A_{0},B_{0})>0$

$$\begin{aligned}&x_{P}\rightarrow x_{0}-B_{0}\cdot d_{3}-\dfrac{A_{0}\cdot \left( d_{2}-d_{0}\right) }{\sqrt{A_{0}^{2}+B_{0}^{2}}}\\&\begin{array}{c} y_{P}\rightarrow y_{0}+A_{0}\cdot d_{3}-\dfrac{B_{0}\cdot \left( d_{2}-d_{0}\right) }{\sqrt{A_{0}^{2}+B_{0}^{2}}}\end{array} \end{aligned}$$

where:

$$\begin{aligned}&d_{2}=\dfrac{C_{0}+A_{0}\cdot x_{0}+B_{0}\cdot y_{0}}{\sqrt{A_{0}^{2}+B_{0}^{2}}}\\&\begin{array}{l} \begin{array}{l} d_{3}=\dfrac{\sqrt{d_{1}^{2}-\left( d_{2}-d_{0}\right) ^{2}}}{\sqrt{A_{0}^{2}+B_{0}^{2}}}\end{array}\end{array} \end{aligned}$$

C6 Line given equation If line L is defined by equation $A\cdot x+B\cdot y+C=0$ and its orientation is aligned with (A,B)

$$\begin{aligned} \begin{array}{c} A_{L}\rightarrow A\\ B_{L}\rightarrow B\\ C_{L}\rightarrow C \end{array} \end{aligned}$$

If line L is defined by equation $A\cdot x+B\cdot y+C=0$ and its orientation is not aligned with (A,B)

$$\begin{aligned} \begin{array}{c} A_{L}\rightarrow -A\\ B_{L}\rightarrow -B\\ C_{L}\rightarrow -C \end{array} \end{aligned}$$

C7 Line distance from two points Line L is directed distance $d_{0}$ from point $P_{0}$ and directed distance $d_{1}$ from point $P_{1}$

$$\begin{aligned}&A_{L}\rightarrow \phi _{0}\\&B_{L}\rightarrow \phi _{1}\\&C_{L}\rightarrow \phi _{2} \end{aligned}$$

where:

$$\begin{aligned} d_{2}= & {} \left( x_{1}-x_{0}\right) ^{2}+\left( y_{1}-y_{0}\right) ^{2}\\ \phi _{0}= & {} \dfrac{\left( d_{1}-d_{0}\right) \left( x_{1}-x_{0}\right) }{d_{2}}+\dfrac{\left( y_{0}-y_{1}\right) \sqrt{d_{2}-\left( d_{0}-d_{1}\right) ^{2}}}{d_{2}}\\ \phi _{1}= & {} \dfrac{\left( d_{0}-d_{1}\right) \left( y_{0}-y_{1}\right) }{d_{2}}+\dfrac{\left( x_{1}-x_{0}\right) \sqrt{d_{2}-\left( d_{0}-d_{1}\right) ^{2}}}{d_{2}}\\ \phi _{2}= & {} d_{1}-x_{1}\cdot \phi _{0}-y_{1}\cdot \phi _{1} \end{aligned}$$

C8 Line angle to a line distance from a point Line L is angle $\theta _{0}$ from line $L_{0}$ and directed distance $d_{1}$ from point $P_{1}$

$$\begin{aligned}&A_{L}\rightarrow A_{0}cos\theta _{0}-B_{0}sin\theta _{0}\\&B_{L}\rightarrow A_{0}sin\theta _{0}+B_{0}cos\theta _{0}\\&\begin{array}{c} C_{L}\rightarrow d_{1}\sqrt{A_{0}^{2}+B_{0}^{2}}+B_{0}\left( x_{1}sin\theta _{0}-y_{1}cos\theta _{0}\right) -A_{0}\left( x_{1}cos\theta _{0}+y_{1}\cdot sin\theta _{0}\right) \end{array} \end{aligned}$$

We note that the some of the above constructions have variants dependent on an assessment of sidedness. It is the responsibility of the agent which creates the construction sequence, the dynamic geometry UI for example, to select which variant to insert into the construction sequence. Each of the constructions above fully defines a geometrical object. In a dynamic geometry system, it is common to have geometry which is unconstrained, or partially constrained. For example a point can be located in an arbitrary location, or a point can be placed on a line, or a point can be specified to be at a certain distance from a given point. In such cases, the system can add indeterminates in the process of making the construction. These partial constructions are specified below.

C9 Point distance from one point Point P is distance $d_{0}$ from point $P_{0}$

$$\begin{aligned} \begin{array}{c} x_{P}\rightarrow x_{0}+d_{0}cos\left( \theta _{0}\right) \\ y_{P}\rightarrow y_{0}+d_{0}sin\left( \theta _{0}\right) \end{array} \end{aligned}$$

where $\theta _{0}$ is an indeterminate introduced by the construction.

C10 Point distance from one line Point P is directed distance $d_{0}$ from line $L_{0}$

$$\begin{aligned} \begin{array}{c} x_{P}\rightarrow \dfrac{B_{0}d_{1}-A_{0}\left( C_{0}-d_{0}\sqrt{A_{0}^{2}+B_{0}^{2}}\right) }{A_{0}^{2}+B_{0}^{2}}\\ y_{P}\rightarrow \dfrac{-A_{0}d_{1}-B_{0}\left( C_{0}-d_{0}\sqrt{A_{0}^{2}+B_{0}^{2}}\right) }{A_{0}^{2}+B_{0}^{2}} \end{array} \end{aligned}$$

where $d_{1}$ is an indeterminate introduced by the construction.

C11 Unconstrained point Point P is unconstrained

$$\begin{aligned} \begin{array}{l} x_{P}\rightarrow x_{0}\\ y_{P}\rightarrow y_{0} \end{array} \end{aligned}$$

where $x_{0},y_{0}$ are indeterminates introduced by the construction.

C12 Line directed distance from one point Line L is directed distance $d_{0}$ from point $P_{0}$

$$\begin{aligned} \begin{array}{l} A_{L}\rightarrow cos\left( \theta _{0}\right) \\ B_{L}\rightarrow sin\left( \theta _{0}\right) \\ C_{L}\rightarrow d_{0}-x_{0}cos\left( \theta _{0}\right) -y_{0}sin\left( \theta _{0}\right) \end{array} \end{aligned}$$

where $\theta _{0}$ is an indeterminate introduced by the construction.

C13 Line angle to a line Line L is angle $\theta _{0}$ from line $L_{0}$

$$\begin{aligned} \begin{array}{c} A_{L}\rightarrow A_{0}cos\left( \theta _{0}\right) -B_{0}sin\left( \theta _{0}\right) \\ B_{L}\rightarrow A_{0}sin\left( \theta _{0}\right) +B_{0}cos\left( \theta _{0}\right) \\ C_{L}\rightarrow d_{0} \end{array} \end{aligned}$$

where $d_{0}$ is an indeterminate introduced by the construction.

C14 Unconstrained line Line L is unconstrained

$$\begin{aligned} \begin{array}{c} A_{L}\rightarrow A_{0}\\ B_{L}\rightarrow B_{0}\\ C_{L}\rightarrow C_{0} \end{array} \end{aligned}$$

where $A_{0},B_{0},C_{0}$ are indeterminates introduced by the construction.