1 Introduction

STAR-RIS allows to transmit data to two users \(U_\textrm{t}\) and \(U_\textrm{r}\) [1,2,3,4,5]. The phases shifts of STAR-RIS are optimized to maximize the SINR at \(U_\textrm{t}\) and \(U_\textrm{r}\) [6,7,8]. STAR-RIS is a good candidate for 6 G communications due to its large throughput and performance enhancement with an increase of number of reflectors N. STAR-RIS for non-orthogonal multiple access (NOMA) was studied in [1,2,3,4,5,6,7,8,9]. The rate of NOMA using STAR-RIS was analyzed in [1]. A comparison of orthogonal multiple access (OMA) and NOMA was presented in [2, 3]. STAR-RIS with federated learning was given in [4]. Channel estimation for STAR-RIS was investigated in [5]. Signal enhancement for STAR-RIS was studied in [6]. Weighted sum rate optimization was discussed in [7]. The security of STAR-RIS was investigated in [8]. Full-duplex communications using STAR-RIS were suggested in [9]. STAR-RIS using multiple antennas was studied in [10, 11]. Sum rate maximization and resource optimization were suggested in [12]. STAR-RIS for unmanned aerial vehicle (UAV) was studied in [13, 14]. Performance analysis of wireless communications using STAR-RIS was suggested in [15]. STAR-RIS with correlated antennas was presented in [16]. The outage probability of STAR-RIS was derived in [17, 18]. The coverage probability of STAR-RIS was derived in [19]. The performance of the network was optimized in [20]. The security of uplink NOMA was studied in [21]. The design of STAR-RIS was discussed in [24,25,26,27,28,29]. The capacity of STAR-RIS with fixed power was derived in [22, 23]. Power allocation was investigated in [24]. The design of NOMA using STAR-RIS was suggested in [25, 26]. Phase design of STAR-RIS was optimized in [27] so that the SINR is maximized at the two studied users. A network with multiple cells was studied in [28]. The security and two-way relaying were studied in [29, 30]. Device-to-device (D2D) communications using STAR-RIS were proposed in [30].

In CRN, primary and secondary users share the same channel. CRN allows larger data rates than non CRN as the throughput is equal to the sum of primary and secondary throughput. In interweave CRN, spectrum sensing is performed to detect a vacant band left unused by primary users. Therefore, secondary users transmit only when primary users are idle and the band is available. In underlay CRN, secondary users transmit over the same channel as primary users and adapt their power to minimize the interference at primary users. In this paper, we evaluate and optimize the throughput of underlay CRN where the secondary source harvests energy from RF signals and adapts its power to control the interference at primary destination. STAR-RIS is between the secondary source and two users \(U_\textrm{t}\) and \(U_\textrm{r}\) so that the signal to interference plus noise ratio (SINR) is maximized. STAR-RIS offers a diversity equal to the number of its elements N and allows a significant throughput enhancement. Therefore, STAR-RIS is a good candidate for 6 G wireless communications.

STAR-RIS with power adaptation was not studied in [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. Therefore, STAR-RIS was not yet proposed for underlay CRN where the secondary source adapts its power to minimize the interference at primary destination. In fact, the transmit power is fixed in [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30] and cannot be used in underlay CRN. In this paper, it is assumed that \(S_\textrm{S}\) harvests power from the node A signal. The harvested power is used to broadcast data to two secondary users \(U_\textrm{t}\) and \(U_\textrm{r}\). \(S_\textrm{S}\) controls the level of interference at \(P_\textrm{D}\) using power adaptation.

  • We evaluate the throughput of STAR-RIS when \(S_\textrm{S}\) harvests power from node A signal. We also consider that \(S_\textrm{S}\) use power adaptation to control the level of interference at \(P_\textrm{D}\).

  • There are two main contributions in this paper. First, we study STAR-RIS for underlay CRN where the secondary source has an adaptive transmit power while the power is fixed in [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. Second, the secondary source does not have a battery that should be recharged as assumed in [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. The secondary source harvests energy from node A RF signal to be able to transmit data to \(U_\textrm{t}\) and \(U_\textrm{r}\) using STAR-RIS.

  • We optimize the throughput by adjusting the harvesting duration.

Next section describes the harvested power. Section 3 computes the throughput of STAR-RIS. Section 4 describes the theoretical and simulation results. Section 5 concludes the article.

2 Energy harvesting

The harvested energy is [30]

$$\begin{aligned} E=P_A\alpha F \varepsilon \mu _0 |h|^2, \end{aligned}$$
(1)

where F and \(0<\alpha F<F\) are frame and harvesting durations, \(P_A\) is the power of node A, \(0<\varepsilon <1\) is the efficiency of the energy conversion, and \(\sqrt{\mu _0} h\) is channel from A to \(S_\textrm{S}\).

Fig. 1
figure 1

STAR-RIS for CRN

Full size image

The available transmit symbol energy is

$$\begin{aligned} E_{s,\text {available}}=\frac{E}{(1-\alpha )\frac{F}{T_s}}=\beta |h|^2, \end{aligned}$$
(2)

where \(T_s\) is the symbol period,

$$\begin{aligned} \beta =\frac{\mu _0E_A\varepsilon \alpha }{1-\alpha } \end{aligned}$$
(3)

where \(E_A=P_AT_s\)

We deduce the symbol energy as

$$\begin{aligned} E_s=\min \left( \frac{T}{|h_{S_\textrm{S}P_\textrm{D}}|^2},E_{s,\text {available}}\right) \end{aligned}$$
(4)

where \(h_{XY}\) is the channel from X to Y and T is the interference threshold. The generated interference at \(P_\textrm{D}\) is less than T: \(E_s |h_{S_\textrm{S}P_\textrm{D}}|^2\le T\). \(E_s\) and T are in Joules, F and \(T_s\) are in seconds, and all other parameters do not have units.

The cumulative distribution function (CDF) of \(E_s\) is

$$\begin{aligned} F_{E_s}(x)=1-P \left( \min \left( \frac{T}{|h_{S_\textrm{S}P_\textrm{D}}|^2},E_{s,\text {available}}\right) >x\right) \end{aligned}$$
(5)

We deduce

$$\begin{aligned} F_{E_s}(x)= & {} 1-P \left( \frac{T}{|h_{S_\textrm{S}P_\textrm{D}}|^2}>x\right) P(E_{s,\text {available}}>x)\nonumber \\= & {} 1-\left[ 1-e^{\frac{-T}{x\rho _{S_\textrm{S}P_\textrm{D}}}}\right] e^{-\frac{x}{\beta }} \end{aligned}$$
(6)

where \(\rho _{S_\textrm{S}P_\textrm{D}}=E(|h_{S_\textrm{S}P_\textrm{D}}|^2)\).

3 STAR-RIS system model

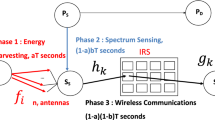
In Fig. 1, the source \(S_\textrm{S}\) harvests power from node A RF signal to broadcast data to two users \(U_\textrm{t}\) and \(U_\textrm{r}\). A STAR-RISS with N elements is between the source \(S_\textrm{S}\) and \(U_\textrm{t}\), \(U_\textrm{r}\). We assume a line-of-sight (LOS) propagation between the secondary source and STAR-RIS and from STAR-RIS to \(U_\textrm{t}\) and \(U_\textrm{r}\) as considered in [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. The transmission and reflection coefficients are \(\eta _n^te^{j\theta _n^t}\) and \(\eta _n^re^{j\theta _n^r}\) where \(0<\theta _n^r,\theta _n^t<1\) and \(0<\eta _n^r<1\), \(0<\eta _n^t<1\) such that \((\eta _n^r)^2+(\eta _n^t)^2=1\). \(U_\textrm{r}\) and \(U_\textrm{t}\) are located, respectively, in the space of reflection and transmission of STAR-RIS. The channel between the source \(S_\textrm{S}\) and STAR-RIS is denoted by \(h_n=|h_n|e^{j\phi _{h_n}}\) while the channel between nth element of STAR-RIS and user \(U_q\) for \(q=t,r\) is \(g_n^q=|g_n^q|e^{j\phi _{g_n^q}}\).

The signal at \(U_q\) \(q=r,t\) is

$$\begin{aligned} y_q&=\sqrt{E_s\zeta _q}\sum _{n=1}^Ng_n^q \eta _n^qe^{j\theta _n^q}h_nx_q\nonumber \\&\quad +\sqrt{E_s\zeta _{q'}}\sum _{n=1}^Ng_n^{q} \eta _n^{q}e^{j\theta _n^{q}}h_nx_{q'}+n_q; \end{aligned}$$
(7)

where \(q'=r\) when \(q=t\) and \(q'=t\) when \(q=r\), \(\zeta _q\) and \(\zeta _{q'}\) are power allocation coefficient for \(U_q\) and \(U_{q'}\) where \(\zeta _q+\zeta _{q'}=1\). \(x_q\) (resp. \(x_{q'}\)) is the symbol of \(U_q\) (resp. \(U_{q'}\)). The broadcasted signal by \(S_\textrm{S}\) is equal to \(\sqrt{E_s}[\sqrt{\zeta _r}x_r+\sqrt{\zeta _t}x_t]\). \(n_q\) is Gaussian, zero mean with variance \(N_0\).

The SNR at \(U_q\) is expressed as

$$\begin{aligned} \gamma _q=\frac{E_s\zeta _q|\sum _{n=1}^N|g_n^q||h_n| \eta _n^q exp(j[\theta _n^q+\phi _{h_n}+\phi _{g_n^q}])|^2}{N_0 +E_s\zeta _{q'}|\sum _{n=1}^N|g_n^{q}||h_n|\eta _n^{q} exp(j[\theta _n^{q}+\phi _{h_n}+\phi _{g_n^{q}}])|^2} \end{aligned}$$
(8)
Fig. 2
figure 2

Throughput for interference threshold \(T=1\) and number of STAR-RIS elements \(N=8,16,32,64,128,256\)

Full size image
Fig. 3
figure 3

Throughput for interference threshold \(T=1,10\) and number of STAR-RIS elements \(N=8\)

Full size image
Fig. 4
figure 4

Throughput for number of STAR-RIS elements \(N=8\), interference threshold \(T=1\), optimal harvesting duration \(\alpha \) and \(\alpha =0.5\)

Full size image
Fig. 5
figure 5

Throughput for number of STAR-RIS elements \(N=16\), interference threshold \(T=1\), optimal harvesting duration \(\alpha \) and \(\alpha =0.5\)

Full size image
Fig. 6
figure 6

Throughput for number of STAR-RIS elements \(N=32\), interference threshold \(T=1\), optimal harvesting duration \(\alpha \) and \(\alpha =0.5\)

Full size image
Fig. 7
figure 7

Throughput versus harvesting duration \(\alpha \) for number of STAR-RIS elements \(N=8\) and interference threshold \(T=1\)

Full size image

The optimal STAR-RIS phase shifts are chosen so that all reflections have a zero phase \(\theta _n^q+\phi _{h_n}+\phi _{g_n^q}=0\) [1]. Therefore, we have

$$\begin{aligned} \theta _n^q=-\phi _{h_n}-\phi _{g_n^q}. \end{aligned}$$
(9)

Using (9), the optimal SINR at \(U_q\) is equal to

$$\begin{aligned} \gamma _q=\frac{E_s\zeta _q A_q^2}{E_s\zeta _{q'} A_{q}^2+N_0} \end{aligned}$$
(10)

where

$$\begin{aligned} A_q=\sum _{n=1}^N|g_n^q||h_n|\eta _n^{q} \end{aligned}$$
(11)

\(A_q\) is Gaussian with mean

$$\begin{aligned} m_{A^q}=\sum _{n=1}^N\eta _n^q\frac{\pi }{4} \frac{1}{d_{\text {STAR-RIS},U_q}^{\text {ple}/2}d_{S_\textrm{S},\text {STAR-RIS}}^{\text {ple}/2}} \end{aligned}$$
(12)

and variance

$$\begin{aligned} \sigma _{A_q}^2=\sum _{n=1}^N(\eta _n^q)^2 \left[ 1-\frac{\pi ^2}{16}\right] \frac{1}{d_{\text {STAR-RIS},U_q}^{\text {ple}}d_{S_\textrm{S},\text {STAR-RIS}}^{\text {ple}}} \end{aligned}$$
(13)

where ple is the path loss exponent and \(d_{XY}\) is the distance from X to Y.

Let \(X_q=A_q^2\) and \(Y_q=E_sA_q^2=E_sX_q\), the CDF of SINR \(\gamma _q\) is deduced from that of \(Y_q\) as

$$\begin{aligned} F_{\gamma _q}(x)=F_{Y_q} \left( \frac{N_0x}{\zeta _q-\zeta _{q'}x}\right) . \end{aligned}$$
(14)

where \(F_{Y_q}(x)\) is provided in (18).

We have

$$\begin{aligned} Y_q=E_sX_q \end{aligned}$$
(15)

where

$$\begin{aligned} X_q=A_q^2, \end{aligned}$$
(16)

The CDF of \(X_q\) is

$$\begin{aligned}&F_{X_q}(x)=P\left( -\sqrt{x}\le A_q\le \sqrt{x}\right) \nonumber \\&\quad \simeq 0.5erfc\left( \frac{-\sqrt{x}-m_{A_q}}{\sqrt{2} \sigma _{A_q}}\right) -0.5erfc \left( \frac{\sqrt{x}-m_{A_q}}{\sqrt{2}\sigma _{A_q}}\right) \end{aligned}$$
(17)

By derivation, the probability density function (PDF) of \(X_q\) is

$$\begin{aligned} p_{X_q}(x)&\simeq \sqrt{\frac{1}{8\pi \sigma _{A_q}^2x}} e^{-\frac{\left[ \sqrt{x}+m_{A_q}\right] ^2}{2\sigma _{A_q}^2}}\nonumber \\&\quad +\sqrt{\frac{1}{8\pi \sigma _{A_q}^2x}} e^{-\frac{\left[ \sqrt{x}-m_{A_q}\right] ^2}{2\sigma _{A_q}^2}}. \end{aligned}$$
(18)

The CDF of \(Y_q\) is evaluated as

$$\begin{aligned} F_{Y_q}(y)=\int _0^{+\infty }F_{E_s} \left( \frac{y}{x}\right) p_{X_q}(x)\textrm{d}x, \end{aligned}$$
(19)

The packet error probability (PEP) is deduced from the CDF of the SINR \(\gamma _q\), \(F_{\gamma _q}(x)\), using the waterfall threshold \(w_0\): [31]

$$\begin{aligned} \text {PEP}_q<F_{\gamma _q}(w_0), \end{aligned}$$
(20)

In this paper, we use the upper bound (20) to evaluate the \(\text {PEP}_q\) at \(U_q\). \(w_0\) is defined as [31]

$$\begin{aligned} w_0=\int _0^{+\infty }[1-\text {SEP}(z)]^{PL}\textrm{d}z, \end{aligned}$$
(21)

SEP is the symbol error probability [32]

$$\begin{aligned} \text {SEP}(z)=2\left( 1-\frac{1}{\sqrt{Q}}\right) erfc\left( \sqrt{\frac{3z}{Q-1}}\right) \end{aligned}$$
(22)

PL and Q are packet and constellation size.

The throughput is

$$\begin{aligned} \text {Thr}_q(\alpha )=(1-\alpha )[1-\text {PEP}_q(\alpha )], \end{aligned}$$
(23)

In Eq. (23), \(0<\alpha <1\) gives the harvesting duration \(\alpha F\) where F is the frame duration in seconds. The throughput is maximized as

$$\begin{aligned} Thr_q^{\max }=\underset{0<\alpha <1}{\max }Thr_q(\alpha ). \end{aligned}$$
(24)

4 Results

We plotted the throughput for \(\varepsilon =0.5\), \(d_{S_\textrm{S},\text {STAR-RIS}}=1\), \(d_{\text {STAR-RIS},U_\textrm{t}}=1\), \(d_{\text {STAR-RIS},U_\textrm{r}}=1.5\), PL = 500, ple = 3. The other parameters are \(\zeta _q=0.8=1-\zeta _{q'}\) \(\eta _n^t=\eta _n^{r}=\frac{1}{\sqrt{2}}\).

Figure 2 shows the throughput for CRN with adaptive power for \(T=1\), \(\alpha =0.5\), \(T=1\) and \(N=8,16,32,64,128,256\). When STAR-RIS is used, the SINR at users \(U_\textrm{t}\) and \(U_\textrm{r}\) is maximized by a wise optimization of STAR-RIS phases. STAR-RIS offers a diversity equal to the number of its elements N. Therefore, when the number of STAR-RIS elements N is doubled, we get 15 dB diversity gain.

Figure 3 depicts the throughput for \(T=10,1\), \(N=8\), and \(\alpha =0.5\). We observe the throughput improves for \(T=10\) as \(S_\textrm{S}\) can increase its power. The numerical results are close to the simulation results and confirms that our derivations are correct.

Figures 4, 5, and 6 depict the throughput for \(N=8,16,32\), \(T=1\). The obtained throughput for optimal \(\alpha \) is better than \(\alpha =0.5\) since harvesting duration optimization offers an important increase in throughput.

Figure 7 depicts the throughput versus \(\alpha \) for \(N=8\) and \(T=1\). Throughput is concave and can be maximized.

5 Conclusion

In this article, we proposed the use of STAR-RIS for underlay cognitive radio networks. We studied the throughput of STAR-RIS with energy harvesting. Power adaptation is used by the secondary source to control the level of interference at \(P_\textrm{D}\). The secondary source transmits data to two users \(U_\textrm{t}\) and \(U_\textrm{r}\). We obtained 15 dB gain when the number of reflectors is doubled. The obtained results can be applied for underlay cognitive radio networks. As a perspective, we can study STAR-RIS with multipath propagation.