Visual object tracking with online sample selection via lasso regularization

Abstract

In the past years, discriminative methods are popular in visual tracking. The main idea of the discriminative method is to learn a classifier to distinguish the target from the background. The key step is the update of the classifier. Usually, the tracked results are chosen as the positive samples to update the classifier, which results in the failure of the updating of the classifier when the tracked results are not accurate. After that the tracker will drift away from the target. Additionally, a large number of training samples would hinder the online updating of the classifier without an appropriate sample selection strategy. To address the drift problem, we propose a score function to predict the optimal candidate directly instead of learning a classifier. Furthermore, to solve the problem of a large number of training samples, we design a sparsity-constrained sample selection strategy to choose some representative support samples from the large number of training samples on the updating stage. To evaluate the effectiveness and robustness of the proposed method, we implement experiments on the object tracking benchmark and 12 challenging sequences. The experiment results demonstrate that our approach achieves promising performance.

1 Introduction

Visual object tracking is an important computer vision problem in real applications, such as surveillance, human computer interaction, vehicle navigation. Several approaches have been proposed in the past years, which can be classified into generative methods [15, 19, 23, 24] and discriminative methods [3, 6, 10, 13, 16, 18, 31]. Generative methods focus on modeling the appearance of the object which might be varied in a different frame. Discriminative methods cast object tracking as a classification problem that distinguishes the tracked target from the background.

Fig. 1

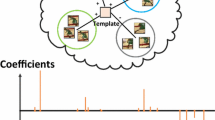
Illustration of the proposed method. Searching stage using the score function to calculate every candidate’s score and choosing the maximum one as the optimal candidate. Updating stage extracting a set of training samples using polar grid sampling around the currently tracked target; appending these samples into the old representative sample set to form a support sample set; exploiting $\ell _{1}$-regularized least squares to obtain some representative samples and updating the target template. The green and red bounding box denote the positive sample and negative sample, respectively

Discriminative methods become more popular in the computer vision, i.e., face recognition [12, 20, 21, 29], object tracking [2, 8, 30], mainly because they do not need to construct a complex appearance model. Some representative discriminative methods have received much attention in recent years. For instances, Kalal et al. [13] proposed a novel tracking framework (TLD) that decomposes the long-term tracking task into tracking, learning and detection. Zhu et al. [31] presented a collaborative correlation tracker (CCT) to deal with the scale variation and the drift problem. Gao and Ling et al. [4] proposed a new transfer learning-based visual tracker to alleviate drift using gaussian processes regression (TGPR). Danelljan et al. [3] proposed a novel approach (DSST) by learning discriminative correlation filters based on a scale pyramid representation in the tracking-by-detection framework. Henriques et al. [10] presented a high-speed kernelized correlation filter (KCF) by using a circulant matrix. All of these methods achieved satisfied performance on the OTB [28] and received much attention from the researchers in recent years.

Generally, discriminative method trains a classifier to identify the object, which heavily depends on the selection of the positive and negative training samples. Most existing discriminative methods regard the currently tracked target as the positive sample and select samples from the neighborhood around the currently tracked target as the negative samples to update the classifier. The classifier will be updated with a sub-optimal positive sample when the currently tracked target is not accurate. After that the tracker would drift in a long time. Additionally, a large number of training samples will hinder the classifier to be updated online in real time. Therefore, it is necessary to design a sample selection strategy for the classifier updating.

Different from the most existing discriminative methods, in this paper, we propose a score function instead of learning a classifier to predict the optimal candidate directly. As shown in step 1 of Fig. 1, we use the similarity of between the candidate which is generated from particle filter and the target template set as our score function and exploit the inner product to measure the similarity. Because our approach does not to update the classifier with a sub-optimal positive sample, thus, it can avoid the drift problem. To address the problem of a large number of training samples, we propose an online sample selection strategy based on $\ell _{1}$-regularized least squares, as shown in step 2 of Fig. 1. We construct a training sample set and calculate the ground truth of it. Then, we minimize the errors of the score function and ground truth to choose some representative support samples for the update of the target template set.

The main contributions of this paper are summarized as follows:

• A simple score function is proposed to predict the optimal candidate directly instead of learning a classifier, which can address the drift problem.

• A sparsity-constrained sample selection method is proposed, through which the representative support samples are chosen to construct the templates.

The rest of this paper is organized as follows. We briefly review the related works in Sect. 2 and describe the proposed approach in Sect. 3. Then, we show the experimental details and results in Sect. 4 and conclude this work in Sect. 5.

2 Related works

In this section, we review the particle filter framework for tracking firstly, because our approach is based on this framework. Then, we briefly introduce sparse representation model for tracking, because the sparse constraint is applied on our approach to solve the tracking problem.

2.1 Particle filter framework

Particle filter [22] is Bayesian sequential importance sampling technique. It provides a general framework for estimating and propagating the posterior probability density function of state variables. During the last years, a large number of popular trackers [1, 5, 7, 11, 19] based on this framework are proposed. Our approach also uses the particle filter as motion model (see the candidates from particle filter of Fig. 1).

Given $t-1$ observed patches $\mathbf {I}_{1:t-1} =\{\mathbf {I}_{1},\mathbf {I}_{2}, \ldots , \mathbf {I}_{t-1}\}$ from the first frame to the $t-1$ frame. Let $\mathbf {b}_{t}=[x,y,w,h]\in \mathbb {R}^{4}$ be the state variables in $t^\mathrm{th}$ frame, where (x, y) are the coordinates of the center point of bounding box and w, h are the width and height of the bounding box, respectively. The state variables $\mathbf {b}_{t}$ can be formulated by the following predicting distribution:

$$\begin{aligned} p(\mathbf {b}_{t}|\mathbf {I}_{1:t-1})=\int p(\mathbf {b}_{t}|\mathbf {b}_{t-1}) p(\mathbf {b}_{t-1}|\mathbf {I}_{1:t-1}) d\mathbf {b}_{t-1}. \end{aligned}$$

(1)

Given the observed patch $\mathbf {I}_{t}$ in frame t, the state variables $\mathbf {b}_{t}$ can be updated by the following formulation:

$$\begin{aligned} p(\mathbf {b}_{t}|\mathbf {I}_{1:t})=\frac{p(\mathbf {I}_{t}|\mathbf {b}_{t}) p(\mathbf {b}_{t}|\mathbf {I}_{1:t-1})}{p(\mathbf {I}_{t}|\mathbf {I}_{1:t-1})}, \end{aligned}$$

(2)

where $p(\mathbf {I}_{t}|\mathbf {b}_{t})$ denotes the observation model.

The observation model $p(\mathbf {I}_{t}|\mathbf {b}_{t})$ represents the similarity between a target candidate and the target template. For an observed patch $\mathbf {I}_{t}$, we use $\mathbf {x}_{t}$ to represent the features extracted from $\mathbf {I}_{t}$. We introduce a score function of $\mathbf {x}_{t}$ to approximate $p(\mathbf {I}_{t}|\mathbf {b}_{t})$:

$$\begin{aligned} p(\mathbf {I}_{t}|\mathbf {b}_{t})\varpropto F(\mathbf {x}_{t}). \end{aligned}$$

(3)

This function is defined as a simple inner product between the candidate and the target template (see Sect. 3.1). The optimal candidate state is the one with the biggest score value.

2.2 Sparse representation-based tracking

Sparse representation has been applied to visual tracking [1, 7, 11, 17, 19, 25, 27] to find the target with the minimum reconstruction error from the target template subspace. These methods can be classified as two categories: holistic sparse representation [1, 19, 25, 26] and local sparse representation [7, 11, 17]. In the first class, Mei et al. [19] cast the tracking problem as finding a sparse approximation in a template subspace. They adopt the holistic representation of the object as the appearance model and, then, track the object by solving the $\ell _{1}$ minimization problem ($\ell _{1}$ tracker). To address the bottleneck of the computational cost of the $\ell _{1}$ tracker, Bao et al. [1] proposed a new $\ell _{1}$ norm-related minimization model based on the accelerated proximal gradient approach ($\ell _{1}$-APG) which can run in real time. This category of methods can handle the partial occlusion and slight deformation effectively.

In contrast to the holistic sparse representation, the local sparse representation encodes the each local patch of a target sparsely with an over-complete dictionary and, then, aggregate the corresponding sparse codes. For instances, Jia et al. [11] proposed a structural local sparse appearance model which exploits both partial information and spatial information of the target based on a novel alignment-pooling method. Liu et al. [17] also presented a robust tracking algorithm using a local sparse appearance model, which used a static sparse dictionary and a dynamically online-updated basis distribution to model the target appearance. Because the local sparse representation can exploit the structural information of the object, it can better deal with the occlusion and deformation. However, it is more complicated and has the higher computational expense. In this paper, we impose a sparse constraint on the score function and we apply holistic sparse representation to solve the tracking problem.

3 Proposed approach

In this section, we give the details of the proposed approach which includes four parts primarily. Specifically, we present the score function in Sect. 3.1 and propose the online sample selection in Sect. 3.2. Then, we give the template updating strategy in Sect. 3.3. Finally, the whole algorithm is summarized in Sect. 3.4.

3.1 Score function

The aim of score function is to predict which candidate is the optimal one. Given a target template set $\mathbf {H}=\{ \mathbf {h}_{1}, \mathbf {h}_{2}, \ldots , \mathbf {h}_{n}\}\in \mathbb {R}^{d\times n}$ and a target candidate $\mathbf {x}$ in the tth frame, where $\mathbf {x}\in \mathbb {R}^{d}$ is the HOG feature vector extracting from the target candidate . We use a simple inner product to measure the similarity between the candidate and the target template as a part of the score function:

$$\begin{aligned} f_{i}(\mathbf {x})=\langle \mathbf {x},\mathbf {h}_{i}\rangle , \end{aligned}$$

(4)

where $\mathbf {x}$ and $\mathbf {h}_i$ are normalized, i.e., $\Vert \mathbf {x}\Vert _2=1, \Vert \mathbf {h}_{i}\Vert _2=1$. For a candidate $\mathbf {x}$, the larger the value of score function $f(\mathbf {x})$ is, the higher the similarity between the candidate and the target template has. However, we explore the target template set $\mathbf {H}$ which is made up of several templates, rather than a single target template. Therefore, the average score of the similarity between the candidate and each target template in $\mathbf {H}$ is adopted as the final score function $F(\mathbf {x})$.

$$\begin{aligned} F(\mathbf {x})=\frac{1}{n}\sum _{i=1}^{n}f_{i}(\mathbf {x}). \end{aligned}$$

(5)

Fig. 2

Illustration of the observation. The bounding box with green line denotes the positive sample in the training sample set and the other are negatives

For the given target template $\mathbf {h}_{i}$ in the tth frame, let $\mathbf {A}_{i}=[\mathbf {x}_{i}^{1},\mathbf {x}_{i}^{2},\ldots ,\mathbf {x}_{i}^{m}]\in \mathbb {R}^{d\times m}$ be the corresponding training sample set which consists of the support sample set $\mathbf {A}_{t-1}$ and updating sample set $\mathbf {X}_{t}$, where $\mathbf {x}_{i}^{j}, j=1,2,\ldots , m$ indicates the jth training sample of the $\mathbf {A}_{i}$, $\mathbf {A}_{t-1}$ is the old support sample set in the $(t-1)$th frame and $\mathbf {X}_{t}$ is updating sample set which is sampled from the currently tracked target in the tth frame. As we know, each template can be linearly represented by the training sample set, i.e.,

$$\begin{aligned} \mathbf {h}_{i}=\mathbf {A}_{i}{\varvec{\omega }}_{i}, \end{aligned}$$

(6)

where ${\varvec{\omega }}_{i}$ is the coefficient vector of the $\mathbf {A}_{i}$.

In a real application, the appearance of the object target is very similar to the certain adjacent frames. Therefore, the target template of these object targets can be sparsely represented by a few positive and negative support samples in these adjacent frames, as shown in Fig. 2. Based on this fact, for a target template, just a few representative support samples are needed to represent it. Therefore, we impose a sparsity constraint on the coefficient vector ${\varvec{\omega }}_{i}$ and reformulate Eq. (6) below:

$$\begin{aligned} \mathbf {h}_{i}\varpropto \mathbf {A}_{i}{\varvec{\omega }}_{i} \quad s.t.\quad \Vert {\varvec{\omega }}_{i}\Vert _{0}\le \alpha , \end{aligned}$$

(7)

where $\alpha$ is a threshold value.

Then, substituting Eq. (7) into Eq. (4), we obtain the following score function:

$$\begin{aligned} \begin{aligned} f_{i}(\mathbf {x})&=\langle \mathbf {x},\mathbf {A}_{i}{\varvec{\omega }}_{i} \rangle \\&=\sum ^{m}_{j=1}\omega _{i}^{j}\langle \mathbf {x}, \mathbf {x}^{j}_{i}\rangle \quad \quad s.t.\quad \Vert {\varvec{\omega }}_{i}\Vert _{0}\le \alpha , \end{aligned} \end{aligned}$$

(8)

where ${\varvec{\omega }}_{i}=[\omega _{i}^{1},\omega _{i}^{2},\ldots ,\omega ^{m}_{i}]^{\mathrm{T}}\in \mathbb {R}^{m}$ ($\omega _{i}^{j}, j=1,2, \ldots , m$) denotes the coefficient of jth inner product.

3.2 Online sample selection via $\ell _{1}$-regularized least squares

Given a target in the tth frame, we exploit the polar grid sampling to obtain an updating sample set $\mathbf {X}_t=[\mathbf {x}_{1},\mathbf {x}_{2}, \ldots , \mathbf {x}_{k}]\in \mathbb {R}^{d\times k}$, where $\mathbf {x}_{r}\in \mathbf {R}^{d}, r=1, 2, \ldots , k$ denotes the rth training sample of $\mathbf {X}_t$. For each training sample $\mathbf {x}_{r}$, we define a function to calculate its ground truth,

$$\begin{aligned} g(\mathbf {x}_{r})=\frac{\hbox {overlap}(b,\hbox {box}(\mathbf {x}_{r}))}{b}, \end{aligned}$$

(9)

where $g(\mathbf {x}_{r})$ is normalized 0 to 1, b represents the bounding box area of the currently tracked target, $\hbox {box}(\mathbf {x}_{r})$ indicates the bounding box area of the training sample $\mathbf {x}_{r}$, and $\hbox {overlap}(,)$ calculates the overlap area of the two bounding boxes. Therefore, for the training sample set $\mathbf {X}_t$, we can obtain its ground truth $\mathbf {y}$ using Eq. (9), where $\mathbf {y}=[y_{1},y_{2}, \ldots , y_{k}]^{\mathrm{T}}=[g(\mathbf {x}_{1}), g(\mathbf {x}_{2}) , \ldots , g(\mathbf {x}_{k})]^{T}\in \mathbb {R}^{k}$.

For the old support sample set $\mathbf {A}_{t-1}=[\mathbf {x}_{1},\mathbf {x}_{2}, \ldots , \mathbf {x}_{u}]\in \mathbb {R}^{d\times u}$ in the $(t-1)$th frame, we also can get its corresponding ground truth $\mathbf {s}=[s_{1},s_{2}, \ldots , s_{u}]^{\mathrm{T}}\in \mathbb {R}^{m}$ using Eq. (9). Combining the old support sample set $\mathbf {A}_{t-1}$ and updating sample set $\mathbf {X}_t$, we get the training sample set $\mathbf {A}_{i}=[\mathbf {A}_{t-1},\mathbf {X}_t]\in \mathbb {R}^{d\times (k+u)}$ and the associated ground truth $\mathbf {q}=[\mathbf {y},\mathbf {s}]\in \mathbb {R}^{(k+u)}$, we call the training sample set $\mathbf {A}_{i}\in \mathbb {R}^{d\times m}$ is the candidate support sample set , where $m=k+u$.

Suppose that the candidate support sample in $\mathbf {A}_{i}$ is normalized. we get coefficient ${\varvec{\omega }}_{i}$ in the tth frame by minimizing following objective function:

$$\begin{aligned} \min _{{\varvec{\omega }}_{i}}\sum ^{m}_{\ell =1}\left( q_{\ell }-\sum _{j=1}^{m} \omega _{i}^{j}\langle \mathbf {x},\mathbf {x}_{i}^{j}\rangle \right) ^{2} +\lambda \Vert {\varvec{\omega }}_{i}\Vert _{1}, \end{aligned}$$

(10)

where $q_{\ell }\in \mathbb {R}$ denotes the $\ell$th ground truth of the $\mathbf {q}$ and $\lambda$ is regularization parameter. Utilizing matrix notation, Eq. (10) can be reformulated as following:

$$\begin{aligned} \min _{{\varvec{\omega }}_{i}} \left\| \mathbf {q}-(\mathbf {A}_{i}^{T}\mathbf {A}_{i}{\varvec{\omega }}_{i}) \right\| ^{2}_{2}+\lambda \Vert {\varvec{\omega }}_{i}\Vert _{1}, \end{aligned}$$

(11)

Let $\mathbf {D}=\mathbf {A}_{i}^{T}\mathbf {A}_{i}$, then Eq. (11) can be simplified as below:

$$\begin{aligned} \min _{{\varvec{\omega }}_{i}} \left\| \mathbf {q}-\mathbf {D} {\varvec{\omega }}_{i} \right\| ^{2}_{2}+\lambda \Vert {\varvec{\omega }}_{i}\Vert _{1}. \end{aligned}$$

(12)

Equation (12) can be solved by $\ell _{1}$-regularized least squares [14]. Then, we choose the corresponding samples which the coefficient are greater than the predefined threshold $\sigma$ as new support samples. The new support sample set $\mathbf {A}_{t}$ in the tth frame is constituted by all these support samples.

3.3 Template updating

Template updating is a very important step in updating stage of visual tracking. If the template set $\mathbf {H}$ is fixed, the tracker will be failed because the target’s appearance changes dynamically. However, if the template set $\mathbf {H}$ is updated too frequently, the errors would be accumulated and the tracker would drift away from the target.

In our method, we adopt a discriminative strategy to update the template set. For a given target, if its score is greater than the predefined threshold $\theta$, we can obtain the vector of coefficient ${\varvec{\omega }}_{i}$ and new support sample set $\mathbf {A}_{t}$ by solving the problem  (10). Based on the assumption the target template can be represented by the linear combination of some representative support samples, the template $\mathbf {h}_{i}$ can be updated by Eq. (6). If the template number in the template set $\mathbf {H}$ is below the given threshold $\eta$, we put this new template $\mathbf {h}_{i}$ into the template set $\mathbf {H}$. Otherwise, this new template will be appended into $\mathbf {H}$ and the oldest template will be discarded.

3.4 Algorithm

The proposed method is described in Algorithm 1 and the details of the algorithm implementing will be given in Sect. 4.1. The overall algorithm includes searching stage and updating stage. In searching stage, the optimal candidate is obtained using the score function. In updating stage, some representative samples are chosen by $\ell _{1}$-regularized least squares and the target template set is updated using the selected samples.

4 Experiments

In this section, we first introduce the experimental implementation details in Sect. 4.1. it includes the parameter setting, datasets, comparison tracker and evaluation. Then, we give the experiment results and analyze in Sect. 4.2.

Fig. 3

Comparison with eight state-of-the-art trackers on 50 image sequences of the precision and success plots using one pass evaluation (OPE)

4.1 Experiment details

Parameter setting: All the methods are carried out in MATLAB 2014a on a PC with an Intel 3.7 GHz Dual Core CPU and 8 GB RAM. The image patches are resized to $32\times 32$ pixels during the tracking process. For the HOG feature, the cell size and the number of orientation bins are set to 4 and 9, respectively. In the updating stage, the radius of the polar grid and the number of angular division are set to 5 and 16, respectively. The other mentioned parameters of the paper are listed as follows.

Parameter name	M	k	$\lambda$	$\sigma$	$\theta$	$\eta$
Parameter value	750	81	0.3	0.01	0.32	160

M denotes the number of the candidates generated from the particle filter, which is set to 750. k is the number of the training samples that sampling by the polar grid and is set to 81. $\lambda$ is a regularization parameter which represents the sparsity degree of the coefficient vector ${\varvec{\omega }}_{i}$ and is set to 0.3. $\sigma$ denotes the threshold of the coefficient vector and is set to 0.01. We choose the corresponding samples as representative samples of which the coefficient is greater than the threshold $\sigma$. $\theta$ is a threshold of the score for the update of support sample set and target template, which is set to 0.32. $\eta$ is the maximum number of the template in target template set and is set to 160.

Datasets Our experiments are carried out on the OTB [28] that contains 50 image sequences. These image sequences have 11 attributes (illumination variation, scale variation, occlusion, deformation, motion blur, fast motion, in-plane rotation, out-of-plane rotation, out-of-view, background clutters and low resolution), which represents the challenging aspects of visual tracking. We also choose 12 challenging sequences in these 50 image sequences to qualitatively evaluate our approach. They are Dudek, jogging-1, jogging-2, Suv, FleetFace, Freeman3, Freeman4, Lemining, Sylvester, Tiger2, woman and Walking2.

Comparison tracker In order to examine the performance of the proposed approach, 8-state-of-the-art trackers which have a superior performance on the OTB are chosen to compare with ours. They are CCT [31], DSST [3], TGPR [4], KCF [10], Struck [6], SVM [27], RR [27] and TLD [13].

Evaluation criterion Two criteria are used to evaluate the performance of our approach. One of the widely used criteria is center location error (CLE), which is the average Euclidean distance between the center locations of the tracked targets and the manually labeled ground truths. We use the precision [9] to measure the overall tracking performance, which is defined as the percentage of frames whose estimated location is within the given threshold distance of the ground truth. Usually, this threshold distance is set to 20 pixels.

Table 1 Percentage of successful frames whose center location error (CLE) within the threshold 20 pixels and the percentage of successful frames whose overlap ratio (VOR) passes the threshold 0.5

Fig. 4

Comparison with eight different trackers in center location error (CLE) of frame by frame on 6 challenging sequences

Another evaluation criterion is the Pascal VOC overlap ratio (VOR) [28], which is defined as $S=|r_{t}\cap r_{a}|/|r_{t}\cup r_{a}|$, where $r_{t}$ and $r_{a}$ represent the bounding box of the tracked target and the ground truth, respectively; $\cap$ and $\cup$ represent the intersection and union of two regions, respectively; $|\cdot |$ denotes the number of the pixel in the region. In order to measure the overall performance on a given image sequence, we count the number of successful frames, whose VOR is larger than the given threshold 0.5. The success plot shows the ratios of successful frames at the thresholds varied from 0 to 1. We use the area under the curve (AUC) of each success plot to rank the comparison trackers.

4.2 Experiment results and analyses

Two groups of experiments are carried out to quantitatively and qualitatively evaluate the proposed approach. The first group is performed on OTB [28] which contains 50 image sequences. We use this group experiments to quantitatively evaluate the overall performance of our tracker and to compare with the other 8 state-of-the-art trackers. Another group experiments are carried out on 12 challenging sequences to qualitatively evaluate our tracker mainly.

Quantitative evaluation The overall performance of our tracker and other 8 compared trackers are shown as in Fig. 3. We use one pass evaluation (OPE) for the overall performance, and precision and success rate as an evaluation criterion, as shown in Fig. 3a, b, respectively. Obviously, the overall performance of our tracker outperforms the other 8 state-of-the-art trackers. What is more, we divide 50 image sequences into different groups according to the different attributes of the image sequences (see datasets of Sect. 4.1). Then, we also use precision and success rate to evaluate the performance of the tracker on different attributes. Due to space limitations, ten groups precision and success plots on 10 different attributes are provided in the supplemental material. The results also demonstrate that our tracker is clearly more accurate and robust.

For better illustrate the proposed method is effective. We give the precision and success rate on another 12 challenging sequences more detailedly, as shown in Table 1. From Table 1 we can see clearly that our approach has a better performance on most challenging sequences. For instances, our tracker achieved the precision score with 0.99 on jogging-2 which has fully occlusion challenge with a short time , while the CCT [31], DSST [3], KCF [10] just obtained 0.19, 0.19, 0.16, respectively. Lemming is a challenging sequence which has occlusion and deformation et al. challenges, and our tracker also achieved the highest score 0.93 while the Struck [6], KCF [10] and DSST [3] obtained 0.50, 0.49, 0.43, respectively. The average precision score of our tracker has improved $30\%$ than that of the second best tracker CCT [31]. It is also obviously that our tracker has achieved the best success rate, and it average success rate of the proposed tracker also has improved $30\%$ than the second best tracker CCT [31].

Qualitative evaluation The second group experiments are carried out on 12 challenging sequences to evaluate the proposed approach more intuitive. Due to space constraints, we just give the center location error (CLE) of the frame by frame on 6 challenging sequences, as shown in Fig. 4a–f. More results are provided in the supplemental material. From Fig. 4, we can see clearly that our tracker has the lowest center location error on the most frames of the most challenging sequences. Specifically, just like jogging-1 (Fig. 4b) and jogging-2 (Fig. 4c), the CLE of our tracker is lower than CCT [31], DSST [3] and TGPR [4] when the full occlusion happened. When the appearance changed slight quickly, the CLE of our tracker is also lower than most other trackers, as shown in Fleetface (Fig. 4d), Freeman3 (Fig. 4e) and Freeman4 (Fig. 4f). The other CLE results can also demonstrate that our tracker outperforms the other eight state-of-the-art trackers. For better understanding the proposed approach achieved promising performance, the tracked results of the trackers in some representative frames are listed in the supplemental material. These tracked results also indicated that our tracker is effective and robust.

5 Conclusion

In this paper, we proposed a score function to predict the optimal candidate directly instead of learning a classifier. Exploiting the score function can avoid the drift problem. Moreover, to solve the problem of a large number of training samples, we impose a sparse constraint on the score function and use $\ell _{1}$-regularized least squares to choose some representative support samples. Then, to evaluate the effectiveness and robustness of the proposed approach, we carry out two groups experiments on the OTB [28] and another 12 challenging sequences. Both quantitative and qualitative evaluations are performed to validate our approach, and experimental results demonstrate that the proposed approach achieved promising performance.