Error-dependent step-size control of adaptive normalized least-mean-square filters used for nonlinear acoustic echo cancellation

Abstract

This paper proposes novel acoustic echo cancellation (AEC) approaches based on linear and Volterra structures. The AECs use modified normalized least-mean-square (NLMS) updates to improve the convergence and to maintain the same steady-state misadjustment. In the first case, starting from a new cost function, the resulting variable step size depends on the instant error value and on an estimated error threshold. Secondly, the need of beforehand steady-state error threshold estimation is removed by an automatic step-size control involving the absolute error envelope evolution. The methods are tested for an acoustic enclosure setup modeled using measured linear and quadratic kernels, and their behavior is compared to that of the traditional NLMS and another technique found in the open literature. Also, they are tested for a change in the echo path and for assorted nonlinearity and local signal powers. The comparison is made in terms of the echo-return loss enhancement for WGN and speech as excitation. The simulations show that the proposed adaptations offer increased convergence rates for the same steady-state error.

1 Introduction

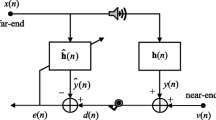
The acoustic echo cancellation (AEC) block scheme is depicted in Fig. 1 [1, 2]. By minimizing the error $e[k]$, that should eventually resemble the local signal $n[k]$ (WGN in the absence of double talk (DT)), the coefficients of the acoustic enclosure $\mathbf{h}[k]$ are replicated using a proper adaptive model $\hat{{\mathbf{h}}}[k]$. $d[k]$ is the microphone signal, $x[k]$ is the far-end signal, and $y[k]$ is $x[k]$ filtered by $\mathbf{h}[k]$.

Fig. 1

Acoustic echo cancellation (AEC) setup

In many cases [3–6], it is assumed that a linear adaptive model is sufficient to replicate the acoustic echo path. However, in real applications, besides the linear components of the echo, one can notice the influence of small and low-cost non-ideal acoustic hardware components, which are important sources of nonlinear distortions [7]. They can cause memoryless nonlinearities like an overdriven amplifier [8] or nonlinearities with memory as a small loudspeaker at high volume [9]. Thus, polynomial structures [10], like the adaptive Wiener [11, 12] and Volterra models [13], can be used as nonlinear AECs.

Other state of the art papers deal with minimizing the trade-off between convergence and final misadjustment [14–16] which here occurs when employing adaptive AECs [17–23]. Thus, the LMS-type algorithm in [17] uses a variable step size for updating the weights and shows an improved convergence over that of similar LMS-based variable step-size algorithms: the variable step-size (VSS) LMS [18], the fixed step-size (FSS) LMS [19] and the gradient adaptive step-size (SGA-GAS) [20].

To overcome the same trade-off, in [21], an adaptive second-order Volterra filter (2VF) is proposed as a proper AEC. Here, optimum time- and tap-variant step sizes are used based on the NLMS (OTTNLMS). It surpasses the 2VF NLMS and the Volterra approach presented in [22]. A modified version of the exponential squared error cost function is proposed in [23] also to improve convergence. The obtained stochastic gradient algorithm, called the exponentiated convex variable step size (ECVSS) shows good convergence rate and tracking abilities in stationary and echo path change situations.

In this work, we present novel exponential step-size control mechanisms applied here, especially on adaptive 2VF. The exponential-type NLMS adaptations are done differently depending on the available information on the local noise. By taking into consideration the evolution of the error, new error-dependent step sizes are developed that lead to an improved convergence compared to the conventional approaches, at the same steady-state misadjustment.

The paper is organized as follows: Sect. 2 gives the signal model of the nonlinear AEC and presents the main features of the proposed updates. The acoustic enclosure model and simulation results are discussed in Sect. 3, while conclusions are drawn in Sect. 4.

2 Proposed structures

2.1 The 2VF NLMS model

In what follows, a 2VF is considered a proper and sufficient approximation model for the input/output characteristics of the acoustic enclosure. The sum of two components form the output of a 2VF $\hat{{y}}_{2\mathrm{VF}} [k]$: a linear one $\hat{{y}}_1 [k]$ and a nonlinear one $\hat{{y}}_2 [k]$ as in [24]:

$$\begin{aligned} \hat{{y}}_{2\mathrm{VF}} [k]=\hat{{y}}_1 [k]+\hat{{y}}_2 [k]. \end{aligned}$$

(1)

The two kernel outputs involve the following vectors:

$$\begin{aligned} \mathbf{x}_1 [k]= & {} (x[k],\,x[k-1],\,\ldots ,\,x[k-M_1 +1])^{T}; \nonumber \\ \hat{{\mathbf{h}}}_1 [k]= & {} (\hat{{h}}_{1,0} [k],\,\hat{{h}}_{1,1} [k],\,\ldots ,\,\hat{{h}}_{1,M_1 -1} [k])^{T}; \nonumber \\ \mathbf{x}_2 [k]= & {} (x^{2}[k],\,x[k]x[k-1],\,\ldots ,\,x[k]x[k-M_2 +1], \nonumber \\&\,x^{2}[k-1],\,x[k-1]x[k-2],\,\ldots ,\,\nonumber \\&x^{2}[k-M_2 +1])^{T}; \nonumber \\ \hat{{\mathbf{h}}}_2 [k]= & {} (\hat{{h}}_{2,0,0} [k],\,\hat{{h}}_{2,0,1} [k],\,\ldots ,\,\hat{{h}}_{2,0,M_2 -1} [k],\,\nonumber \\&\hat{{h}}_{2,1,1} [k],\,\hat{{h}}_{2,1,2} [k],\,\ldots \nonumber \\&\,\ldots ,\,\hat{{h}}_{2,M_2 -1,M_2 -1} [k])^{T}, \end{aligned}$$

(2)

where $x[k]$ is the source signal and $\hat{{h}}_{1,m} [k]$ and $\hat{{h}}_{2,m_1,m_2 } [k]$ represent the linear and quadratic Volterra kernels, while $m=\overline{0,M_1 -1}$, $m_1 =\overline{0,M_2 -1}$, and $m_2 =\overline{m_1,M_2 -1}$. $M_{1}$ and $M_{2}$ are the memory lengths of kernels $\hat{{\mathbf{h}}}_1 [k]$ and $\hat{{\mathbf{h}}}_2 [k]$, respectively. The two components from (1) are evaluated as:

(3)

To update the Volterra kernels, a proper adaptation algorithm is needed to minimize the resulting error:

$$\begin{aligned} e[k]=d[k]-\hat{{y}}_{\mathrm{2VF}} [k]. \end{aligned}$$

(4)

In common AECs, the normalized least-mean-square (NLMS) algorithm [25, 26] is often used because it considers the variation of the input statistics. The update for the linear and quadratic Volterra kernels is:

$$\begin{aligned} \hat{{\mathbf{h}}}_i[k+1]=\hat{{\mathbf{h}}}_i [k]+\frac{\mu _i }{\mathbf{x}_i^T [k]\mathbf{x}_i [k]+\phi }e[k]\mathbf{x}_i [k],\quad i=\{1,2\}, \end{aligned}$$

(5)

where $\phi$ is a positive constant to prevent division by zero. The step-size parameters $\mu _1$ and $\mu _2$ should be chosen in the range (0, 2) for stability. A disadvantage of the NLMS is given by these constant step sizes which affect the convergence and the final misadjustment [8]. Figure 2 illustrates the evolution of the absolute error for a 2VF NLMS AEC and WGN as input. To improve the convergence, we need a larger step size at the beginning of the adaptation for large error samples and, for a lower misadjustment, a smaller step size in the steady-state phase is desired, when almost no adaptation is needed.

Fig. 2

Decreasing envelope of the residual absolute error of a 2VF NLMS for WGN as excitation

If the local noise is known or can be determined from the silences in the signal waveform, the variable step size hinges on an error settlement threshold. Here, it increases or lowers the constant NLMS step size depending on the sign of the difference between the absolute instantaneous error and its global steady-state value. The sign gives information on the adaptation stages: convergence or saturation. The difference needs to be amplified by a variable scaling factor for efficient adaptation. Henceforth, this adaptation will be called the error-dependent step-size control (EDSC). To this approach, a suboptimal error threshold is proposed when no actual misadjustment value is provided.

However, as in most AEC situations $n[k]$ is unknown, an automatic error-dependent step-size control (AEDSC) is proposed with a similar evolution of the step size involving the local samples of the error envelope. In this case, the variable step size grows or stays the same as that of the NLMS according to the phases of the new technique (convergence or saturation). Hints on these phases are provided by the evolution of the absolute error envelope, more precisely, by the difference between its two consecutive values. Having also an exponential conduct, the AEDSC step size is kept in the NLMS stability range of (0, 2). Simultaneously, the necessity of a prior knowledge of the local noise and, implicitly, of the error threshold is removed.

2.2 Error-dependent step-size control (EDSC) adaptation

For this NLMS-type adaptation, the step sizes vary depending on the error decay and also on an error threshold $e_\mathrm{lim}$. The idea of a threshold close to the steady-state error samples is due to the fact that this limit represents the end of the convergence phase, for which a certain step size is proposed. Below this threshold, a different evolution of the step size is developed. Therefore, the following relation is proposed for the error threshold when the local noise can be estimated:

$$\begin{aligned} e_{\lim } =\frac{2}{3}(\max \{\left| {\mathbf{e}_{\mathrm{ss}} [k]} \right| \}-\min \{\left| {\mathbf{e}_{\mathrm{ss}} [k]} \right| \}), \end{aligned}$$

(6)

where the vector $\left| {\mathbf{e}_{\mathrm{ss}} [k]} \right|$ includes the absolute error samples $\left| {e_{\mathrm{ss,}j} [k]} \right|$ found in the steady-state phase $\left| {e_{\mathrm{ss,}j} [k]} \right| \in \left| {\mathbf{e}_{\mathrm{ss}} [k]} \right| ,\,j=\overline{1,M_{\mathrm{ss}} }$, where $M_{\mathrm{ss}} = \hbox {length}(\left| {\mathbf{e}_{\mathrm{ss}} [k]} \right| )$ and $e_{\mathrm{ss,}j} [k]=\mathop {\lim }\limits _{k\rightarrow k_{\mathrm{ss}} } (e_j [k])\cong n_j [k],$ where $n_j [k]\in \mathbf{n}[k].$ The vector $\mathbf{n}[k]$ contains the local signal samples $n_j [k]$. $k_{\mathrm{ss}}$ is the first sample index where the filter reaches steady state. Starting from a proposed cost function

$$\begin{aligned} J[\hat{{\mathbf{h}}}_i [k]]=\frac{\alpha _i [k]\left| {e[k]} \right| -1}{\left\| {\mathbf{x}_i } \right\| ^{2}\alpha _i^2 [k]}e^{\alpha _i [k](\left| {e[k]} \right| -e_{\lim } )},\quad i=\{1,\hbox { 2}\} \end{aligned}$$

(7)

dependent on the error difference $\left| {e[k]} \right| -e_{\lim }$, scaled by $\alpha _i [k]$, a new variable step size is insight for updating the Volterra kernels. Next, the following kernel updates are determined:

$$\begin{aligned} \hat{{\mathbf{h}}}_i[k+1]=\hat{{\mathbf{h}}}_i [k]+\frac{\mu _i e^{\alpha _i [k](\left| {e[k]} \right| -e_{\lim } )}}{\mathbf{x}_i^T [k]\mathbf{x}_i [k]+\phi }e[k]\mathbf{x}_i [k]. \end{aligned}$$

(8)

The general form of the EDSC step size is:

$$\begin{aligned} \mu _{\mathrm{EDSC},i} [k]=\mu _i e^{\alpha _i [k](\left| {e[k]} \right| -e_{\lim } )},\quad i=\{1, 2\}. \end{aligned}$$

(9)

Figure 3 illustrates the characteristics of $\mu _{\mathrm{EDSC},i} [k]$ and $\mu _i$ along the error-dependent exponent. We chose the exponential function due to its behavior toward $e_{\lim }$. Hence, for high absolute errors found especially in convergence, a step size larger than $\mu _i$ will be obtained. When dealing with absolute error samples below $e_\mathrm{lim}$, the exponent of the variable step size becomes negative, which determines $\mu _{\mathrm{EDSC},i} [k]$ to be less than $\mu _i$ in the steady-state phase. Parameter $\alpha _i [k]$ is chosen to enhance the difference between the current absolute error sample and $e_{\lim }$. $\alpha _i [k]$ is computed on small intervals of the absolute error samples in order to keep $\mu _{\mathrm{EDSC},i} [k]$ in the range (0, 2) as $\alpha _i^{f_s } [k]=\frac{\ln (2/\mu _i )}{e_{\max }^{f_s } -e_{\lim } }$, where $e_{\max }^{f_s }$ is the local maximum in the $f_{s}$ error subsequence. If there is no access to the local signal, a suboptimal choice of $e_\mathrm{lim}$ could be:

$$\begin{aligned} \left( {e_{\lim } [k]} \right) _{\mathrm{suboptimal}}= & {} p\left( {\frac{1}{10}\sum _{j=k-9}^k {\left| {e[j]} \right| } } \right) \!,\nonumber \\&k\ge 10,\,0<p<1. \end{aligned}$$

(10)

The optimum $p$ is determined empirically, reaching 0.4 for a well-balanced compromise between convergence and final misadjustment.

Fig. 3

Evolution of the EDSC step-size function

2.3 Automatic error-dependent step-size control (AEDSC) adaptation

However, to fully eliminate the need of either local noise-level estimation or the optimum $p$ for the suboptimal version, in the following, the AEDSC adaptation is proposed. For its implementation, the absolute error envelope $\xi [k]$ is necessary and it is computed using the exponential moving average:

$$\begin{aligned} \xi [k]=\lambda \xi [k-1]+(1-\lambda )\left| {e[k]} \right| ,\quad 0 << \lambda <1. \end{aligned}$$

(11)

For a general outline, in Fig. 4, a three-stage evolution of the error envelope is illustrated. By making use of its decay, the variable AEDSC step size is:

$$\begin{aligned} \mu _{\mathrm{AEDSC}} [k]=\mu e^{\alpha _{\mathrm{AEDSC}} [k](\left| {\xi [k-1]-\xi [k]} \right| )}, \end{aligned}$$

(12)

where

$$\begin{aligned} \alpha _{\mathrm{AEDSC}} [k]\!=\!\frac{\ln (2/\mu )}{\max (\xi [k\!-\!1],\xi [k])\!-\!\lambda \min (\xi [k\!-\!1],\xi [k])}. \end{aligned}$$

(13)

The role of $\alpha _{\mathrm{AEDSC}} [k]$, as in the EDSC case, is to enhance the difference $\left| {\xi [k-1]-\xi [k]} \right|$, while keeping $\mu _{\mathrm{AEDSC}} [k]$ in the NLMS range of stability ($0<\mu _{\mathrm{AEDSC}} [k]<2)$. The degree of enhancement is controlled by $\lambda$. As $\lambda$ is closer to 1, $\mu _{\mathrm{AEDSC}} [k]$ is closer to 2 in convergence. Therefore, using (12), the two AEDSC step sizes for the linear and quadratic kernels are:

$$\begin{aligned} \mu _{\mathrm{AEDSC}}^{(i)} [k]=\lambda \mu _{\mathrm{AEDSC}}^{(i)} [k-1]+(1-\lambda )\mu _{i_{\mathrm{AEDSC}} } [k], \end{aligned}$$

(14)

where

$$\begin{aligned} \mu _{i_{\mathrm{AEDSC}} } [k]=\mu _i e^{\alpha _{_{\mathrm{AEDSC}} }^{(i)} [k](\left| {\xi [k-1]-\xi [k]} \right| )},\quad i=\{1,\hbox { 2}\}, \end{aligned}$$

(15)

$\alpha _{_{\mathrm{AEDSC}} }^{(i)} [k]$ being computed as in (13) using $\mu _1$ and $\mu _2$, respectively. The justification of the AEDSC adaptation emerges from the behavior of $\mu _{\mathrm{AEDSC}} [k]$ on the three stages of the error envelope from Fig. 4:

Fig. 4

A three-stage evolution of the absolute error envelope

(i) Convergence

Therefore, for any $k$ in the convergence stage, the following inequality is true:

$$\begin{aligned} \xi [k-1]>\xi [k], \end{aligned}$$

(16)

resulting in $\max (\xi [k-1],\xi [k])=\xi [k-1]$ and $\min (\xi [k-1],\xi [k])=\xi [k]$. Thus, (12) becomes:

$$\begin{aligned} \mu _{\mathrm{AEDSC}} [k]=\mu e^{\frac{\xi [k-1]-\xi [k]}{\xi [k-1]-\lambda \xi [k]}\ln \frac{2}{\mu }}. \end{aligned}$$

(17)

The requisite to keep the AEDSC faster convergent than the conventional NLMS is $\mu <\mu _{\mathrm{AEDSC}} [k]<2$. This condition leads to:

$$\begin{aligned} 0<\frac{\xi [k-1]-\xi [k]}{\xi [k-1]-\lambda \xi [k]}<1. \end{aligned}$$

(18)

The left-hand side (LHS) of (18) is true because of (16), while the right-hand side (RHS) is valid as $\lambda <1$. Thus, in convergence, the AEDSC step size is larger than the NLMS step size.

(ii) Steady state

When the AEDSC reaches steady state and as $\lambda$ is closer to 1, we can assume that $\xi [k-1]\approx \xi [k]$. Thus, the AEDSC step size becomes $\mu _{\mathrm{AEDSC}} [k]\approx \mu$, meaning that the proposed algorithm behaves as a traditional NLMS in steady state. In this stage, another role for $\lambda$ is to prevent division by 0.

(iii) Error growth in steady state

If a high-valued impulse occurs in the local noise, while the adaptation strategy is in steady state, after the error growth, two consecutive error envelope samples satisfy the condition:

$$\begin{aligned} \xi [k-1]<\xi [k], \end{aligned}$$

(19)

providing $\max (\xi [k-1],\xi [k])=\xi [k]$ and $\min (\xi [k-1],\xi [k])=\xi [k-1]$. Here, the variable AEDSC step size gets:

$$\begin{aligned} \mu _{\mathrm{AEDSC}} [k]=\mu e^{\frac{\xi [k]-\xi [k-1]}{\xi [k]-\lambda \xi [k-1]}\ln \frac{2}{\mu }}. \end{aligned}$$

(20)

As in convergence, the condition for faster adaptation is $\mu <\mu _{\mathrm{AEDSC}} [k]<2$, leading to:

$$\begin{aligned} 0<\frac{\xi [k]-\xi [k-1]}{\xi [k]-\lambda \xi [k-1]}<1. \end{aligned}$$

(21)

The LHS of (21) is true due to (19), and the RHS is correct since $\lambda <1$. From the previous reasoning, a faster convergence is also provided in this scenario by the AEDSC.

3 Simulation results

3.1 The acoustic enclosure model

The proposed AECs are employed for a nonlinear representation of the acoustic enclosure as in [8]:

$$\begin{aligned} d[k]=\underbrace{\mathbf{h}_1^T [k]\mathbf{x}_1 [k]}_{\begin{array}{l} \mathrm{linear } \\ \mathrm{component} \\ \end{array}}+\beta [k]\underbrace{\mathbf{h}_2^T [k]\mathbf{x}_2 [k]}_{\begin{array}{l} \mathrm{nonlinear } \\ \mathrm{component} \\ \end{array}}+\gamma [k]\underbrace{n[k]}_{\begin{array}{l} \mathrm{local } \\ \mathrm{signal} \\ \end{array}}\!,\nonumber \\ \end{aligned}$$

(22)

where $\mathbf{h}_1 [k]$ and $\mathbf{h}_2 [k]$ are the linear and the quadratic kernels from [27]. Here, as we are not dealing with DT, $n[k]\,$ consists only of local noise.

The linear-to-nonlinear ratio (LNLR) and the signal-to-noise ratio (SNR) are controlled with $\beta [k]$ and $\gamma [k]$. The effectiveness of the new techniques is evaluated in terms of echo-return loss enhancement (ERLE):

$$\begin{aligned} \hbox {ERLE}\left[ k \right] =10\log _{10} \frac{\hbox {E}\{d^{2}[k]\}}{\hbox {E}\{e^{2}[k]\}}\hbox { [dB]}, \end{aligned}$$

(23)

where $\hbox {E}\{\cdot \}$ denotes statistical expectation. The lengths of the adaptive linear and quadratic Volterra kernels are identical to those of the acoustic enclosure, meaning 320 and, respectively, $64\,\times \hbox { 64}$ samples. $\phi$ is set 0.1 for input samples in the range $[-1; 1]$.

3.2 Experiments with a sign change in the kernels

3.2.1 WGN as input sequence

An experiment with a sign change in the kernels is performed in Fig. 5 (for linear and nonlinear adaptive structures). WGN is applied as source signal, while as local signal AWGN is used. The following step sizes are selected: $\mu _1 =0.1$ and $\mu _2 =0.05$ for the adaptive 2VF. A linear NLMS with $\mu _{\mathrm{lin}} =0.1$ is also tested. The LNLR and SNR are kept at 10 and 30 dB, respectively. For the EDSC, $e_{\lim }$, computed as in (6), equals 0.03. Also, in the case of the AEDSC, $\lambda =0.998$. The ERLEs are averaged over 3000 samples, using a sliding window. The experiment consists in an echo path change after the steady-state phase of all structures is reached. Therefore, after 50 s a sign change in both Volterra kernels is applied. Before 50 s, the 2VF EDSC and 2VF AEDSC perform better than the 2VF NLMS, gaining better convergence rates, while all three 2VFs settle at 30 dB of discarded echo (when the steady state is reached). After 50 s, all 2VF ERLEs drop due to an excessive error growth because of the change in the echo path. However, they reach the SNR faster than the 2VF NLMS. All 2VFs reach again 30 dB of steady-state ERLE. The 2VF EDSC converges slightly faster than the 2VF AEDSC both at the beginning of the adaptation and after the sign change, yet at the cost of a preliminary fixing of $e_{\lim }$.

Fig. 5

Evolution of the 2VF AEDSC step sizes involved in the linear kernel adaptation (top) and quadratic kernel adaptation (middle); ERLEs of the 2VF EDSC and 2VF AEDSC compared to those of the linear and 2VF NLMS with WGN as input when the echo path has a sign change in the Volterra kernels (bottom)

The developments of $\mu _{\mathrm{AEDSC}}^{(1)} [k]$ and $\mu _{\mathrm{AEDSC}}^{(2)} [k]$ are within the specifications from 2.3, as they gain large values in the convergence phases (smaller than 2 for stability), while settling at $\mu _1$ and $\mu _2$, respectively, in steady state. The rapid decrease right after the pick at the sign change is due to $\lambda$ chosen close to 1.

3.2.2 Speech as input sequence

The experiment with a sign change in the Volterra kernels is reiterated for speech as input, sampled at 8 kHz. Herein, for the 2VF NLMS, $\mu _1 =0.03$ and $\mu _2 =0.015$ are entailed. For the linear NLMS, $\mu _{\mathrm{lin}} =0.03$ is used. The SNR and LNLR are kept the same at 30 dB and 10 dB, respectively. As the error threshold from (6) depends also on the PDF of the input, $e_{\lim }$ in this case is 0.001 for the EDSC. The AEDSC uses the same $\lambda =0.998$. The ERLEs are obtained with a sliding average window of 16,000 samples. Therefore, in Fig. 6 it can be observed that the variable AEDSC step sizes and the ERLEs behave as those in Fig. 5.

Fig. 6

Evolution of the 2VF AEDSC step sizes involved in the linear kernel adaptation (top) and quadratic kernel adaptation (middle); ERLEs of the 2VF EDSC and 2VF AEDSC compared to those of the linear and 2VF NLMS with speech as input when the echo path has a sign change in the Volterra kernels (bottom)

The EDSC and AEDSC adaptations are not DT oriented. Therefore, they may not work properly in DT setups and a DTD may be needed. However, without a DTD and for high EBR values, the DT scenario can be considered related to that from Fig. 6.

3.3 Experiment with variable LNLR and SNR

In Fig. 7, we test the robustness of the 2VF AECs (EDSC, suboptimal EDSC and AEDSC) with respect to varying the LNLR and SNR for WGN as source sequence. The following step sizes $\mu _1 =0.1$ and $\mu _2 =0.05$ are chosen for the 2VFs, while the linear ones use $\mu _{\mathrm{lin}} =0.1$. The ERLEs were averaged over 3000 samples. A discussion on the evolution of the six ERLEs is made on time intervals with constant LNLR and SNR. Therefore, in the first 40 s, the LNLR equals 10 dB while the SNR is kept at 30 dB. In this case, $e_{\lim }$ for the linear EDSC and 2VF EDSC, from (6), are $e_{\lim }^{\mathrm{(lin)}} =0.18$ and $e_{\lim }^{\mathrm{(2VF)}} =0.03$. Also, as in 3.2, $\lambda$ is $0.998$ for the 2VF AEDSC. The proposed 2VFs outperform the conventional 2VF NLMS in convergence, while all approaches reach a final misadjustment of 30 dB of ERLE. While the suboptimal 2VF EDSC converges approximately as the 2VF EDSC, the 2VF AEDSC has a slightly slower convergence. This is because of a better control on $\alpha [k]$ than on $\alpha _{\mathrm{AEDSC}} [k]$ due to prior $e_{\lim }^{\mathrm{(2VF)}}$ estimation.

Fig. 7

Performance comparison of the linear and nonlinear proposed structures with those of the linear and nonlinear NLMS approaches with respect to varying the LNLR and SNR

After 40 s, when all filters are in steady state, the SNR is changed to 60 dB while the LNLR is kept at 10 dB. Therefore, $e_{\lim }^{\mathrm{(2VF)}}$ changes, according to (6), to 0.0006, while $e_{\lim }^{\mathrm{(lin)}}$ remains unchanged. The proposed 2VFs keep their initial convergence hierarchy, reaching the new SNR by gaining a 60 dB steady-state ERLE, faster than the 2VF NLMS.

Moreover, after 80 s, the LNLR is enhanced to 40 dB and the SNR is maintained at 60 dB. Now, $e_{\lim }^{\mathrm{(lin)}}$ is 0.02, according to (6). The change in the LNLR affects the evolution of all involved filters. A faster convergence than the 2VF NLMS, in this case also, is gained by the proposed 2VFs, at the same steady-state value. The two EDSCs (normal and suboptimal) have similar misadjustment recovery, faster than the AEDSC, but with necessary extra hints on the local signal levels.

3.4 Comparison with the normalized ECVSS algorithm

Next, the proposed 2VF technique is compared to a modified NLMS-based version of the update procedure suggested in [23], called the exponentiated convex variable step-size (ECVSS) algorithm. Since in this paper we are dealing with VSS NLMS algorithms, for a fair comparison, a normalized step size is also introduced in the update equations proposed in [23], for the two Volterra kernels:

$$\begin{aligned}&\hat{{\mathbf{h}}}_i [k+1]=\hat{{\mathbf{h}}}_i [k] +\frac{\mu _{i\min } }{\left\| {\mathbf{x}_i } \right\| ^{2}}\min \nonumber \\&\quad \left\{ {\exp [Ae^{2}[k]],\frac{\mu _{\max } }{\mu _{i\min } }} \right\} e[k]\mathbf{x}_i [k],\quad i=\left\{ {1,\hbox { 2}} \right\} , \end{aligned}$$

(24)

where A is a scaling factor, while $\mu _{i \min }$ and $\mu _{\max }$ are the minimum and maximum chosen step sizes. As (24) describes an NLMS-based update, the step sizes should be also kept in the range (0, 2). Therefore, the minimum and maximum step sizes are chosen: $\mu _1 =\mu _{1\min } =0.005$, $\mu _2 =\mu _{2 \min } =0.0025$, and $\mu _{\max } =1$. They were also used for our proposed structures and for the 2VF NLMS. As input sequence, WGN was used. AWGN was also used as local noise. The SNR was set at 30 dB and the LNLR at 10 dB. While the SNR is the same as in Fig. 5, $e_{\lim } =0.03$ remains unchanged. For AEDSC, $\lambda$ remains $0.998$. Figure 8 compares the ERLEs of the proposed nonlinear structures (EDSC, suboptimal EDSC, AEDSC), the normalized ECVSS using $A_1 =40$, $A_2 =60$ and $A_{\mathrm{suboptimal}}$computed as in [23], and that of a NLMS, in terms of convergence and steady-state misadjustment. The modified ECVSS outperforms the 2VF NLMS in convergence for all three values of $A$. However, our proposed structures converge faster than all three versions of the ECVSS, including AEDSC and suboptimal EDSC, and settle to the same final misadjustment. For lower $A$ values, the ECVSS will behave almost like the NLMS, while for larger values of $A$, for the chosen step sizes, the ECVSS will become unstable. The ERLEs were obtained over 6000 averaged samples.

Fig. 8

Convergence and steady state of similar 2VF adaptations (EDSC, suboptimal EDSC, AEDSC, normalized ECVSS, NLMS)

As observed, the selection of the error threshold in EDSC is not critical. Thus, in our conducted simulations, for values of the error threshold less than the optimum $e_{\lim }$, the convergence of EDSC is improved but settles to a slightly lower steady state than with the optimum $e_{\lim }$, computed as in (6). On the other hand, for values of $e_{\lim }$ larger than the optimum $e_{\lim }$, a decrease in the convergence of the EDSC structure is noticed, but it can still be compared to that of the NLMS, while reaching a good final misadjustment.

Regarding computational complexity, the 2VF EDSC and the normalized 2VF ECVSS require almost the same amount of multiplications/divisions/sample. Extra computational effort is needed for the EDSC due to a larger number of comparisons and necessary lookup tables, than for the normalized ECVSS. The AEDSC needs four additional multiplications/ divisions, while reducing the number of comparisons.

4 Conclusions

In this work, a set of step-size control mechanisms was proposed to improve the convergence of the adaptive second-order Volterra filters in acoustic echo cancellation, for setups with linear and nonlinear distortions. Starting from a new cost function, the major element of the first adaptive method is an exponential dependency of the step size on the absolute levels of the error. Together with the constant step size of the NLMS, it forms a varying new step size. The adaptation was done in two ways, depending on the available information on the local noise levels. A comparison between the proposed adaptations, the second-order NLMS Volterra filter and other similar adaptive approach found in the literature was achieved in terms of the power of the residual error for different inputs. The robustness of the proposed models was tested for a change in the acoustic echo path and for different LNLRs and SNRs. The usage of a suboptimal error threshold and an efficient automatic error-dependent step-size control adaptation was proposed when lacking information on the local signal. Simulations prove that the proposed methods present better convergence than the NLMS in all suggested input signal scenarios, without a critical influence on the steady-state error.