1 Introduction

Nowadays, many companies have increased their interest in reducing the inventory costs because this action brings an immediately economic benefit. To reduce the inventory levels and their related cost, many researchers have been building inventory models that determine the right quantity of products to purchase or produce. The basic inventory models are well known as the economic order quantity (EOQ) and the economic production quantity (EPQ). The EOQ inventory model was derived to calculate the optimal order quantity to purchase. On the other hand, the EPQ inventory model was developed to determine the optimal lot size to produce. It is important to mention that both inventory models are based on several unrealistic assumptions. But during last century, some of them are removed and several variants of the EPQ inventory model have been developed under new assumptions. The main topics of this research study are discrete delivery policy, defective items, reworking and pricing. So, only related researches on these topics are reviewed in this section.

The discrete inventory policy has not been investigated in the traditional EPQ inventory model, while it commonly happens in many situations of real life. Therefore, several researchers have been studying this issue widely. For instance, Khan and Sarker (2002) propose an inventory model that determines the optimal batch size for a just-in-time production system with discrete delivery policy. Chiu et al. (2011a) determine replenishment lot size and shipment policy in an EPQ model with delivery and quality assurance issues. Then, Chen et al. (2012) develop a new simple method for the inventory model proposed by Chiu et al. (2011a) to obtain the solution for the decision variables. Chiu et al. (2011b) propose an EPQ inventory model that determines the optimal production quantity and the number of shipments when the manufacturing system produces defective reworkable items. They assume that the rework process does not produce any scraped items. Chiu et al. (2013) present an intra-supply chain system with multiple sales locations and quality assurance and Lin et al. (2013) derive a new solution method for the model proposed by Chiu et al. (2013). Chiu et al. (2012a) focus on the mathematical modeling approach used to determine the replenishment policy for the EPQ inventory model with multiple shipments when rework process is considered. Chiu et al. (2012b) develop an EPQ inventory model with multiple shipments, rework and scrap. They have used a different solution method to obtain the optimal values for lot size and number of shipments instead of the classical optimization technique. Ritha and Martin (2013) study the EPQ inventory model with multiple shipments and packaging. Recently, the optimal number of shipments as a practical issue is studied by Chiu et al. (2011a), Cárdenas-Barrón (2013) and Treviño-Garza et al. (2015) (In press).

In most manufacturing systems, the production of defective items usually happens, but this issue in the traditional EPQ model has not been dealt. Hence, there exist many studies that extend the EPQ inventory model addressing the presence of defective items and rework process. In this direction, Wang (2004) studies the impact of products sold under a free-repair warranty policy and considers the economic production quantity inventory model in the presence of imperfect processes. Other study of interest is work of Jamal et al. (2004). They propose an inventory model that obtains the optimal batch quantity for a production system with two different rework process policies. Later, Cárdenas-Barrón (2007) corrects some errors of the numerical examples presented by Jamal et al. (2004). In a subsequent paper, Cárdenas-Barrón (2008) proposes a simple derivation of the two inventory policies presented by Jamal et al. (2004). In a later paper, Cárdenas-Barrón (2009a) develops an EPQ with rework process and planned backorders. Later, Wee et al. (2013) revisit the work of Cárdenas-Barrón (2009a). They provide an alternative analysis and solution procedure for the work of Cárdenas-Barrón (2009a). Related to this line of research are also the papers by Cárdenas-Barrón (2009b) and Sarker et al. (2008) which deal with the multi-stage production system with rework consideration. Along this line of research, Chen and Khoo (2009) deal with a serial production system with quality loss and rectifying inspection plan to determine optimum process mean and manufacturing quantity. Tsai and Wu (2009) and Shamsi et al. (2009) are other examples of papers that consider reworking process in the EPQ inventory model under different situations. Chung (2011) develops a supply chain management model and presents a solution procedure to find the optimal production quantity with rework process. Roy et al. (2011) build an EOQ inventory model with imperfect quality items which permits shortages and these are partially backordered. On the other hand, Krishnamoorthi and Panayappan (2012) develop an EPQ model with rework of scraped items when return sales are considered. Taleizadeh et al. (2012) derive a multi-product single machine manufacturing model with reworking process. After, Pal et al. (2012) propose an integrated production–inventory model for a supply chain comprised one manufacturer, one supplier and one retailer. Their model considers perfect and imperfect quality items in which the reworking of defective items is done. Later, Pal et al. (2013a) derive an EPQ inventory model to obtain the optimal buffer for a stochastic demand considering preventive maintenance. In a subsequent paper, Pal et al. (2013b) develop a stochastic inventory model that considers two different markets to wholesale the products: (1) for good quality products and (2) for average quality products. This inventory model also assumes that the used products’ recovery rates from clients are random variables and recovery products are placed in storage in two warehouses. Pal et al. (2013c) develop an EPQ inventory model for an imperfect production system which considers that defective items are reworked after the regular production time. Taleizadeh et al. (2013) optimize a joint total cost for an imperfect, multi-product production system with rework subject to budget and service level constraints. Wee and Widyadana (2013) study a deteriorating production inventory model with stochastic preventive maintenance time and rework. Their model considers the first-in first-out (FIFO) rule. After that, Roy et al. (2014) derive an economic production lot size model for a production system that generates defective items. The defective items are accumulated and then reworked. This inventory model also allows shortages and the partial and full backordering situations are compared. Other relevant and related researches are the works of Yu et al. (2013) and Wee et al. (2014).

An interesting and realistic assumption for an inventory model is to include the price; being this sensitive to the demand of products. Pricing is an important issue that one needs to consider it to achieve a better economic benefit. This line of research has been explored by several researchers. For example, Chen and Chen (2007) develop a periodic pricing and replenishment policy for continuously decaying inventory with multivariate demand. Afterwards, Tapiero (2008) considers an inventory system that obtains optimal selling price when both demand and purchasing price are uncertain. Nahapetyan and Pardalos (2008) propose an algorithm to solve the capacitated multi-item dynamic pricing problems. Later, Karakul and Chan (2010) address pricing and procurement of substitutable products when demand has a random behavior. After, Hong and Lee (2013) deal with a single-item inventory system. Their inventory model determines the optimal price, replenishment quantity and dispatch cycle that maximize the total profit. There are many additional researches related to pricing and inventory which are not listed here. But it is interesting to point out that none of them integrate pricing, production and inventory with discrete shipments and rework process issues. So, the novelty of this research paper is to determine the optimal values for the selling price and the production quantity for an inventory system with rework process and discrete shipments. This kind of extension has not been dealt in the context of discrete shipments policy and rework process of defective items; this is the key contribution of this paper and also represents an extension and improvement of Chiu et al. (2011b).

The rest of this paper is organized as follows. Section 2 makes a brief description of the problem and establishes the notation that will be used through the whole paper. Section 3 presents the mathematical formulation of the inventory model. Section 4 describes the solution procedure used to determine jointly the optimal selling price and lot size. Section 5 identifies and explains two special cases. Section 6 illustrates the use of the solution procedure with a numerical example. Finally, Sect. 7 concludes this paper and gives some future research directions.

2 Problem definition

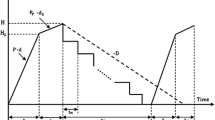
This paper revisits the work of Chiu et al. (2011b) which is described as follows. Consider a situation in which a manufacturing system produces perfect and defective items. The perfect items are ready to cover the customer’s demand. On the other hand, the defective items can be reworked after finishing the regular production process. At the end of the rework process, the manufacturer will deliver \(n \) equal size shipments to the customers during a specific time such that time between two consecutive deliveries during production down time is equal (see Fig. 1). In addition to the mentioned before, it is important to point out that the manufacturing system randomly produces an \(X\) portion of defective items with a production rate \(d\). Consequently, the production rate of defective items \(d\) can be expressed as \(d = pX\). All items manufactured are screened and inspection cost per item is included in the unit manufacturing cost. Furthermore, it is assumed that all defective items are reworkable at the end of the regular production. The reworkable items are recovered at a rate of \(p_{1}\) in each cycle. Nonetheless, during the rework process, a \(\theta _1 \) portion of reworked items fails and becomes scrap. If \(d_{1 }\) represents the production rate of scrap items during the rework process then \(d_{1 }\) is calculated as \(d_{1}= p_{1}\theta _1 \). The behavior of inventory level through time of proposed manufacturing problem is shown in Fig. 1. In the next section, the mathematical inventory model of manufacturing problem is presented.

Fig. 1
figure 1

Inventory level of perfect quality items in the EPQ model with a multi-delivery policy and rework [from Chiu et al. (2011b)]

Full size image

3 Modeling

To formulate the inventory model, the following notation is defined below. Notice that, some symbols are similar as those in Chiu et al. (2011b).

Parameters

\(H_1:\) :

The maximum level of on-hand inventory when regular production process ends (units),

\(H:\) :

The maximum level of on-hand inventory when the rework process ends (units),

\(t_1:\) :

The production uptime for the EPQ inventory model (time units),

\(t_2 :\) :

The time required for reworking of defective items (time units),

\(t_3:\) :

The time required for delivering all perfect finished products (time units),

\(t_n:\) :

The fixed interval of time between each shipment of finished products delivered during production down time \(t_3 \) (time units),

\(n:\) :

The number of shipments of the finished batch to be delivered to customers (a given integer value),

\(T:\) :

The cycle length of production system (time units),

\(Q:\) :

The manufacturing batch size, to be determined for each cycle (time units),

\(I(t):\) :

The on-hand inventory of perfect quality items at time \(t\) (units),

\(a,b:\) :

The constant parameters of price sensitive demand function,

\(S:\) :

The selling price ($/unit),

\(k:\) :

The setup cost($/production run), k1: fixed delivery cost per shipment ($/shipment),

\(h:\) :

The holding cost per unit per unit time ($/unit/time unit),

\(C :\) :

The unit production cost ($/unit),

\(C_R:\) :

The rework cost per unit ($/unit),

\(C_S:\) :

The disposal cost per unit ($/unit),

\(C_T :\) :

The delivery cost per unit ($/unit),

\(\theta _1 :\) :

The portion of scrap items produced during reworking defective items,

\(h_1:\) :

The holding cost of reworked items ($/unit/time unit),

\(X:\) :

The portion of defective items,

\(\lambda :\) :

The annual demand rate (units/time unit),

\(p:\) :

The production rate (units/time unit),

\(d:\) :

The rate of defective production (units/time unit),

\(p_1:\) :

The rework rate of defective items (units/time unit),

\(d_1:\) :

The rate of defective items during the rework process (units/time unit).

Decision variables

\(S:\) :

The selling price ($/unit),

\(Q:\) :

The replenishment lot size (units),

This paper reexamines the research work of  Chiu et al. (2011b) then the development of the inventory model is similar to their derivation until Eq. (8). According to Fig. 1, the following equations can be derived,

$$\begin{aligned} H_1 = ( {p-d})t_1 = ( {p-d})\frac{Q}{p}=(1-X)Q \end{aligned}$$
(1)
$$\begin{aligned} H=H_1 +( {p_1 -d_1 })t_2 =(1-\theta _1 X)Q \end{aligned}$$
(2)
$$\begin{aligned} t_1 =\frac{Q}{p}=\frac{H_1 }{p-d}=\frac{(1-X)Q}{p-d} \end{aligned}$$
(3)
$$\begin{aligned} t_2 =\frac{XQ}{p_1 } \end{aligned}$$
(4)
$$\begin{aligned} t_3 =T-t_1 -t_2 =Q\left( {\frac{( {1-\theta _1 x})}{\lambda }-\frac{1}{p}-\frac{X}{p_1 }}\right) \end{aligned}$$
(5)
$$\begin{aligned} T=t_1 +t_2 +t_3 =\frac{Q( {1-\theta _1 X})}{\lambda } \end{aligned}$$
(6)
$$\begin{aligned} \mathrm{d}t_1 = pXt_1 =XQ \end{aligned}$$
(7)
$$\begin{aligned} \theta _1 \mathrm{d}t_1 =\theta _1 pXt_1 =\theta _1 XQ \end{aligned}$$
(8)

Thus, the profit function for each cycle production is given by

$$\begin{aligned}&CP( {S,Q})\nonumber \\&\quad =SQ-\left[ {\begin{array}{l} CQ+k+C_R \left[ {XQ} \right] +C_S \left[ {X\theta _1 Q} \right] +nk_1 +C_T \left[ {Q(1-\theta _1 X)} \right] +h_1 \frac{p_1 t_2 }{2}t_2 \\ \,+h\left[ {\frac{H_1 +\mathrm{d}t_1 }{2}( {t_1 })+\frac{H_1 +H}{2}( {t_2 })} \right] +h\left( {\frac{n-1}{2n}}\right) Ht_3 \\ \end{array}} \right] \nonumber \\ \end{aligned}$$
(9)

Interested readers may see in Chiu et al. (2011b) the details of the derivation of the second term in the above profit function. Dividing by \(T\), the annual profit function is obtained as follows.

$$\begin{aligned} AP( {S,Q})= & {} \frac{1}{T}CP(S,Q) =\frac{SQ}{T}-\frac{1}{T}\nonumber \\&\times \left[ {\begin{array}{l} CQ+k+C_R \left[ {XQ} \right] +C_S \left[ {X\theta _1 Q} \right] +nk_1 +C_T \left[ {Q(1-\theta _1 X)} \right] \\ +h_1 \frac{p_1 t_2 }{2}t_2 \,+h\left[ {\frac{H_1 +\mathrm{d}t_1 }{2}( {t_1 })+\frac{H_1 +H}{2}( {t_2 })} \right] +h( {\frac{n-1}{2n}})Ht_3 \\ \end{array}} \right] \nonumber \\ \end{aligned}$$
(10)

To incorporate the price in the above inventory model, the demand is considered as a linear function of price and it is expressed as \(\lambda =a-bS\). Substituting, \(\lambda \) with \(a-bS\) and \(E(T)\) with \(\frac{Q( {1-\theta _1 E(X)})}{a-bS}\) then the average annual profit becomes,

$$\begin{aligned} E\left[ {AP( {S,Q})} \right]= & {} \frac{E\left[ {AP(S,Q)} \right] }{E\left[ T \right] }\nonumber \\= & {} \frac{S(a-bS)}{1-\theta _1 E(X)}\nonumber \\&-\left[ {\begin{array}{l} \left( {C+\frac{(k+nk_1 )}{Q}+C_R E(X)+C_S E( X)\theta _1 +\frac{h_1 [E(x)]^2Q}{2p_1 }}\right) \frac{(a-bS)}{( {1-\theta _1 E(X)})} \\ +\frac{hQ(a-bS)}{2p(1-\theta _1 E(X))}+\frac{hQ(a-bS)}{2p_1 (1-\theta _1 E(X))}( {2E( X)-[E(x)]^2-\theta _1 [E(x)]^2}) \\ +hQ\left( {\frac{n-1}{n}}\right) \left( {\frac{( {1-\theta _1 E(X)})}{2}-\frac{(a-bS)}{2p}-\frac{E( X)(a-bS)}{2p_1 }}\right) +C_T (a-bS) \\ \end{array}} \right] \nonumber \\ \end{aligned}$$
(11)

From Calculus, it is well known that \(E\left[ {AP( {S,Q})} \right] \) is concave if and only if the following equations are satisfied,

$$\begin{aligned} \frac{\partial ^2E\left[ {AP( {S,Q})} \right] }{\partial Q^2}<0 \end{aligned}$$
(12)
$$\begin{aligned} \frac{\partial ^2E\left[ {AP( {S,Q})} \right] }{\partial S^2}<0 \end{aligned}$$
(13)
$$\begin{aligned} \left[ {Q S} \right] \left[ {{\begin{array}{ll} {\frac{\partial ^2E\left[ {AP( {S,Q})} \right] }{\partial Q^2}} &{} {\frac{\partial ^2E\left[ {AP( {S,Q})} \right] }{\partial Q\partial S}} \\ {\frac{\partial ^2E\left[ {AP( {S,Q})} \right] }{\partial Q\partial S}} &{} {\frac{\partial ^2E\left[ {AP( {S,Q})} \right] }{\partial S^2}} \\ \end{array} }} \right] \left[ {{\begin{array}{l} Q \\ S \\ \end{array} }} \right] <0 \end{aligned}$$
(14)

Equation (14) can be changed to Eq. (15) as below.

$$\begin{aligned} \left[ {Q^2\frac{\partial ^2E\left[ {AP( {S,Q})} \right] }{\partial Q^2}+2QS\frac{\partial ^2E\left[ {AP( {S,Q})} \right] }{\partial Q\partial S}+S^2\frac{\partial ^2E\left[ {AP( {S,Q})} \right] }{\partial S^2}} \right] <0\qquad \end{aligned}$$
(15)

The elements of Eq. (14) are derived as bellow;

$$\begin{aligned}&\frac{\partial E( {AP( {S,Q})})}{\partial Q}\nonumber \\&\quad =(a-bS)\left( {\begin{array}{l} \frac{k+nk_1 }{Q^2(1-\theta _1 E(X))}-\frac{h}{2p_1 ( {1-\theta _1 E(X)})}( {2E(X)-[E(x)]^2-\theta _1 [E(x)]^2}) \\ -\frac{h_1 [E(x)]^2}{2p_1 ( {1-\theta _1 E(X)})}+\left( {\frac{n-1}{n}}\right) \left( {\frac{h(1-\theta _1 E(X))}{( {a-bS})2}-\frac{h}{2p}-\frac{h E(X)}{2p_1 }}\right) -\frac{h}{2p( {1-\theta _1 E(X)})} \\ \end{array}}\right) \nonumber \\ \end{aligned}$$
(16)
$$\begin{aligned} \frac{\partial E( {AP( {S,Q})})}{\partial S}= & {} \frac{a-2bS}{1-\theta _1 E(X)}\nonumber \\&+\,b\left[ {\begin{array}{l} \left( {C+\frac{( {k+nk_1 })}{Q}+C_R E(X)+C_S E(X)\theta _1 }\right) \frac{1}{1-\theta _1 E(X)}+C_T \\ +\frac{hQ}{2p(1-\theta _1 E(X))}+\frac{hQ( {2E(X)-[E(x)]^2-\theta _1 [E(x)]^2})}{2p_1 ( {1-\theta _1 E(X)})} \\ +\left( {\frac{n-1}{n}}\right) \left( {\frac{-hQ}{2p}-\frac{hQE(X)}{2p_1 }}\right) +\frac{h_1 [E(x)]^2Q}{2p_1 ( {1-\theta _1 E(X)})} \\ \end{array}} \right] \nonumber \\ \end{aligned}$$
(17)

Thus,

$$\begin{aligned} \frac{\partial ^2E[AP( {S,Q})]}{\partial Q^2}=\frac{-2(k+nk_1 )(a-bS)}{Q^3(1-\theta _1 E(X))}<0 \end{aligned}$$
(18)
$$\begin{aligned} \frac{\partial ^2E\left[ {AP( {S,Q})} \right] }{\partial S^2}=\frac{-2b}{1-\theta _1 E(X)}<0 \end{aligned}$$
(19)
$$\begin{aligned} \frac{\partial ^2E\left[ {AP( {S,Q})} \right] }{\partial Q\partial S}= & {} \left( {\begin{array}{l} \frac{-( {k+nk_1 })}{Q^2}+\frac{h}{2p}+\frac{h( {2E(X)-[E(x)]^2-\theta _1 [E(x)]^2})}{2p_1 }+ \\ \left( {\frac{n-1}{n}}\right) \left( {\frac{-h}{2p}-\frac{hE(X)}{2p_1 }}\right) ( {1-\theta _1 E(X)})+\frac{h_1 [E(x)]^2}{2p_1 } \\ \end{array}}\right) \nonumber \\&\times \left( {\frac{b}{( {1-\theta _1 E(X)})}}\right) \end{aligned}$$
(20)

If we show that \(\frac{\partial ^2E\left[ {AP( {S,Q})} \right] }{\partial Q\partial S}<0\), then \(E\left[ {AP( {S,Q})} \right] \) is strictly concave, because both \(\frac{\partial ^2E\left[ {AP( {S,Q})} \right] }{\partial S^2}\) and \(\frac{\partial ^2E\left[ {AP( {S,Q})} \right] }{\partial Q^2}\) are negative. Moreover, \(\frac{\partial ^2E\left[ {AP( {S,Q})} \right] }{\partial Q\partial S}\) is negative only if;

$$\begin{aligned}&Q<Q_\mathrm{{Upper}}\nonumber \\&\quad =\sqrt{\frac{2( {k+nk_1 })}{\frac{h}{p}+\frac{h( {2E(X)-[E(x)]^2-\theta _1 [E(x)]^2})}{p_1 }-\left( {\frac{n-1}{n}}\right) \left( {\frac{h}{p}+\frac{hE(X)}{p_1 }}\right) ( {1-\theta _1 E(X)})+\frac{h_1 [E(x)]^2}{p_1 }}}\nonumber \\ \end{aligned}$$
(21)

Now, setting the first derivative of the objective function with respect to \(Q\), shown in Eq. (16), equal to zero gives:

$$\begin{aligned}&Q^*\nonumber \\&\quad =\sqrt{\!\frac{2(k\!+\!nk_1 )}{\frac{h}{p}\,{+}\,\frac{h}{p_1 }( {2E(X)\!-\![E(x)]^2-\theta _1 [E(x)]^2})+\!\left( {\frac{n-1}{n}}\!\right) \!\left[ {\frac{h(1\!-\!\theta _1 E(X))^2}{(a\!-\!bS)}\!-\!h\left( {\frac{1}{p}+\frac{E(X)}{p_1 }}\!\right) \!\times \! ( {1-\theta _1 E(X)})} \!\right] \!+\!\frac{h_1 [E(x)]^2}{p_1 }}}\nonumber \\ \end{aligned}$$
(22)

It is worth to remark that the lot size \(Q^*\) is strictly less than \(Q_\mathrm{{Upper}}\). Therefore, the objective function is always concave. Then, the optimal value of \(S\) is calculated as follows

$$\begin{aligned}&S^*\nonumber \\&=\frac{a}{b}-\frac{h( {\frac{n-1}{n}})( {1-\theta _1 E(X)})^2Q^{*^2}}{2b(k+nk_1 )-bQ^{*^2}\left[ {\frac{h}{p}+\frac{h_1 [E(x)]^2}{p_1 }+\frac{h\left[ {2E(X)-[E(x)]^2-\theta _1 [E(x)]^2} \!\right] }{p_1 }-h\left( {\frac{n-1}{n}}\!\right) ( {1-\theta _1 E(X)})\left( {\frac{1}{p}\!+\!\frac{E(X)}{p_1 }}\right) } \right] }\nonumber \\ \end{aligned}$$
(23)

In fact, the optimization problem is non-linear and it has two decision variables. From Eqs. (22) and (23), it is easy to see that both decision variables are strictly related. In other words, \(Q\) is a function of \(S\) and \(S\) is a function of \(Q\). To obtain the values for both decision variables, a heuristic algorithm is required and it will be developed in the next section.

4 Solution method

Since \(Q\) is a function of \(S\) and \(S\) is a function of \(Q\) then the following heuristic algorithm is proposed to obtain the solutions to the lot size and selling price.

Heuristic Algorithm

  • Step 1. Set selling price equal to zero and determine the upper level for the replenishment lot size \(Q_\mathrm{{Upper}}\) using Eq. (22).

  • Step 2. Put \(Q=1\), calculate \(S\) and the long-run average profit with Eqs. (23) and (11), respectively.

  • Step 3. Put \(Q=Q+1\), calculate \(S\) and the long-run average profit with Eqs. (23) and (11), respectively.

  • Step 4. If \(Q<Q_\mathrm{{upper}} \) then go to Step 3, otherwise go to Step 5.

  • Step 5. Select the solution with the maximum value of long-run average profit and report the lot size and the selling price (\(Q\) and \(S)\).

5 Special cases

In this section, two special cases are identified and derived. The first one happens when the rework process is perfect, i.e., there is not scrap (\(\theta _1 =0)\). The second one occurs when during regular production there are not defective items (\(X=0)\).

5.1 Rework process is perfect (\(\theta _1 =0\))

If it is assumed that there is no scraped item during the rework process, then during \(t_2 \) the rate of defectives is zero (\(d_1 =0)\). Consequently, Eqs. (11), (21), (22) and (23) reduce to;

$$\begin{aligned} E\left[ {AP( {S,Q})} \right]= & {} \frac{E\left[ {AP(S,Q)} \right] }{E\left[ T \right] }\nonumber \\= & {} \frac{S\lambda }{1-E(X)}-\left[ {\begin{array}{l} \frac{C\lambda }{1-E(X)}+\frac{(k+nk_1 )\lambda }{Q(1-E(X))}+\frac{C_R E(X)\lambda }{1-E(X)}+\frac{C_S E(X)\lambda }{1-E(X)} \\ +C_T \lambda +hQ\left( {\frac{n-1}{n}}\right) \left( {\frac{1-\theta _1 E(X)}{2}-\frac{\lambda }{2p}-\frac{E(X)\lambda }{2p_1 }}\right) \\ \end{array}} \right] \nonumber \\ \end{aligned}$$
(24)
$$\begin{aligned} Q<Q_\mathrm{{Upper}} =\sqrt{\frac{2( {k+nk_1 })}{\frac{h}{p}+\frac{h( {2E(X)-[E(x)]^2})}{p_1 }+\left( {\frac{n-1}{n}}\right) \left( {\frac{-h}{p}-\frac{hE(X)}{p_1 }}\right) +\frac{h_1 [E(x)]^2}{p_1 }}} \end{aligned}$$
(25)
$$\begin{aligned} Q^*=\sqrt{\frac{2(k+nk_1 )}{\frac{h}{p}+\frac{h}{p_1 }( {2E(X)-E^2(X)})+\left( {\frac{n-1}{n}}\right) \left[ {\frac{h}{(a-bS)}-h\left( {\frac{1}{p}+\frac{E(X)}{p_1 }}\right) } \right] +\frac{h_1 E^2(X)}{p_1 }}} \end{aligned}$$
(26)
$$\begin{aligned} S^*= & {} \frac{a}{b}\nonumber \\&-\frac{h\left( {\frac{n-1}{n}}\right) Q^{*2}}{2b(k+nk_1 )-bQ^2\left[ {\frac{h}{p}+\frac{h_1 [E(x)]^2}{p_1 }+\frac{h\left[ {2E(X)-[E(x)]^2} \right] }{p_1 }-h\left( {\frac{n-1}{n}}\right) \left( {\frac{1}{p}+\frac{E(X)}{p_1 }}\right) } \right] }\nonumber \\ \end{aligned}$$
(27)

5.2 Regular production is perfect (\(X=0\))

If it is assumed that all produced items are healthy then \(p\) is used instead of \(p-d\) during the production time \(t_1 \). Obviously, it should be noted in this case there is no rework process. Then, Eqs. (11), (21), (22) and (23) reduce to

$$\begin{aligned} E\left[ {AP( {S,Q})} \right]= & {} \frac{E\left[ {AP(S,Q)} \right] }{E\left[ T \right] }=S\lambda \nonumber \\&-\left[ {C\lambda +\frac{(k+nk_1 )\lambda }{Q}+C_T \lambda +\frac{hQ\lambda }{2p}+hQ\left( {\frac{n-1}{2n}}\right) \left( {1-\frac{\lambda }{p}}\right) } \right] \nonumber \\ \end{aligned}$$
(28)
$$\begin{aligned} Q<Q_\mathrm{{Upper}} =\sqrt{\frac{2( {k+nk_1 })}{\frac{h}{p}-\frac{h}{p}\left( {\frac{n-1}{n}}\right) }} \end{aligned}$$
(29)
$$\begin{aligned} Q^*=\sqrt{\frac{2(k+nk_1 )}{\frac{h}{p}+h\left( {\frac{n-1}{n}}\right) \left[ {\frac{1}{a-bS}-\frac{1}{p}} \right] }} \end{aligned}$$
(30)
$$\begin{aligned} S^*=\frac{a}{b}-\frac{h\left( {\frac{n-1}{n}}\right) Q^2}{2b(k+nk_1 )-\frac{bQ^2h}{np}} \end{aligned}$$
(31)

6 Numerical example

In this section, a numerical example is presented to illustrate the inventory model and its solution through the proposed heuristic algorithm. Suppose that an item can be produced with a rate of 10,000 units per year with price sensitive demand function given by \(\lambda =7000-250\,S\). The random defective rate \(X\) is assumed to follow a uniform distribution between [0, 0.2] during the production uptime. In the next stage, all defective items are reworked at a rate of \(p_1 =1200\), but ten percent of reworkable items is scrap; i.e., \(\theta _1 =0.1\). Other parameters are considered as below.

  • \(K=15{,}000\)$ per production run,

  • \(K_1 =3900\)$ per shipment, a fixed cost,

  • \(h_1 =35\)$ per unit per unit time,

  • \(h=20\)$ per item per unit time,

  • \(C=10\)$ per item,

  • \(C_R =5\)$ per item,

  • \(C_S =2\)$ per item,

  • \(C_T =0.5\)$ per item,

  • \(n=4\) shipments per cycle.

To solve this problem, it is required to apply the proposed heuristic algorithm that was developed in the previous section. Step 1. The upper level for the replenish lot size is \(Q_\mathrm{{upper}} =2441\). Step 2, Step 3 and Step 4 for \(Q=1\) until \(Q=2441\) the selling price \(S\) and the long-run average profit are determined. Step 5, it is obtained that the maximum value of total profit is \(ATP( {S,Q})=24{,}440\) such that the replenishment lot size is \(Q^*=2202\) and the selling price is \(S^*=14.8122\).

7 Conclusion

A continuous inventory policy with a perfect quality production is generally considered in the majority of inventory models to determine optimal lot size. However, normally many manufacturing systems produce some defective items and a discrete delivery is actually applied in practice. In addition, pricing is a critical factor to maximize profits in every organization. Therefore, this paper develops an EPQ inventory model with reworking process, multiple shipment policy and pricing. The proposed EPQ inventory determines the replenishment lot size and the selling price jointly. Also, some special cases are derived and a numerical example is presented. It is worth remarking that this paper improves and complements the research by Chiu et al. (2011b). Finally, further research could be carried out to consider number of shipments as a decision variable, considering shortages with full or partial backordering. Those are some potential future work topics that can be interesting to study.