Introduction

Forests sequester and store large amounts of carbon and play an important role in the carbon cycle (Foley et al. 2005). Above-ground biomass (AGB), which is a crucial indicator of the carbon storage capacity of forest ecosystems (Bonan et al. 1992), is an important parameter for evaluating carbon sinks and analyzing matter and energy flow in forest ecosystems (Alongi et al. 2003). However, many sources of uncertainty can affect forest biomass prediction (Temesgen et al. 2015). One of the challenges confronting scientists is the estimation of uncertainties in forest biomass prediction (Wang et al. 2009).

The traditional method to estimate forest AGB from the individual tree scale to larger scales involves three steps (van Breugel et al. 2011): (1) models are used to predict the AGB of individual trees in forest inventory plots; (2) AGB at the plot level is estimated by summing the AGB of all trees; and (3) Forest AGB at larger spatial scales is estimated by averaging the AGB of all plots. Generally, above-ground biomass of individual trees can be obtained by harvesting trees or by predicting the AGB using models. The first method is costly, time-consuming and destructive and cannot be used at a large scale. In the second method, AGB models are established based on allometric relationships between tree AGB and other variables, such as diameter at breast height (DBH) and height (H). Many countries have established forest inventory systems and have obtained National Forest Inventory (NFI) data at regular intervals. NFI data, in conjunction with AGB models, can be used to predict AGB of trees at the plot level and the data can be used to estimate AGB at larger scales. Therefore, this method has been widely used to estimate the forest above-ground biomass.

Traditional methods to estimate forest biomass have three types of uncertainties (Gertner 1990): uncertainty associated with measurement error, model-related uncertainty, and sampling-related uncertainty. Measurement error occur due to multiple factors, such as recording errors (in reading the tape or recording), tree form, instrument accuracy, measurement methods, measurement skills (McRoberts et al. 1994; Keller et al. 2001; Elzinga et al. 2005; Butt et al. 2013). Errors associated with NFI data and the calibration data set (CDS) can affect biomass estimation. Measurement error in CDS has a greater impact on AGB estimation (Qin et al. 2019).

Model-related uncertainty is associated with the precision of the model predictions that depend on response variables (such as volume, biomass), which are difficult to measure (Petersson et al. 2012). The accuracy of a biomass model is affected by the sample size of the calibration data, the regression methods and the type of model (Sileshi 2014). Model-related uncertainty is attributed to four primary sources: the values of the independent variables, the choice of the allometric model, residual variability, and model parameter estimates (McRoberts and Westfall 2013).

Sampling-related uncertainty occurs with large forest area biomass estimates when inventory data are used over a wide geographic area. Sampling-related uncertainty is affected by the plot size (Mauya et al. 2015), the sample size of the plots (Guo et al. 2016), and heterogeneity of the landscape (Salk et al. 2013). Studies have shown that increasing the sample size and the sample area can reduce the uncertainty caused by sampling variability (Mauya et al. 2015; Guo et al. 2016). Reducing the uncertainty in forest AGB estimation requires an understanding of uncertainty at different levels. Several researchers have predicted the effect of each different uncertainty sources on forest biomass estimation. Qin et al. (2019) quantified the effect of uncertainty due to measurement error and found that the measurement error in the CDS had a larger impact on AGB estimation. Wayson et al. (2015) used a pseudo-data approach to generate the potential distribution of the model parameters and found that this method could generate potential error structures that were used to propagate errors. McRoberts et al. (2014) used Monte Carlo simulation approaches to estimate the model uncertainty caused by residual variability and the model parameters, and found that Monte Carlo simulation approaches worked well in estimating the uncertainty in forest prediction. Fu et al. (2017) used a new method to predict sampling-related and model-related uncertainty; it was found that the model uncertainty was larger than the sampling-related uncertainty. Molto et al. (2013) compared errors associated with model type and the independent variables at the tree and plot levels and observed that the largest source of uncertainty in AGB estimates was the biomass model. McRoberts et al (2016) estimated the uncertainty of six uncertainty sources. These studies indicate that uncertainty in forest AGB estimation has been widely investigated. However, uncertainties in AGB estimation require further in-depth study, particularly in different countries because the results from one country may not be applicable to other countries due to different measurement instruments, input variables, and methods (Berger et al. 2014). Relatively little information is available on NFI data in China. In addition, many biomass models can be used to describe the relationships between single-tree AGB and tree variables. It is necessary to determine which model type has the smallest uncertainty and which uncertainty type contributes the most to the overall error of the models.

In this study, we used Monte Carlo simulation (McRoberts et al. 2014, 2016) and the bootstrap resampling method to estimate uncertainty in AGB estimation using Chinese NFI data. The uncertainties associated with the measurement error of the variables (DBH, H), the residual variability, the variance in the model parameter estimates, and the sampling variability of the NFI data are estimated for five models. The objectives are: (1) to determine which of the four sources of uncertainty has the largest influence on the precision of AGB estimation for the different models; and, (2) to evaluate the performance of these five models for large-area AGB estimation when considering four sources of uncertainty.

Material and methods

Study area

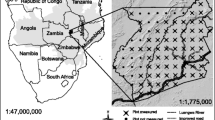
This study was carried out in Longquan County located in eastern of China, southwestern of Zhejiang Province (Fig. 1) and covers an area of 3059 ha. It is located in the subtropical zone with a warm and humid climate. The average annual temperature is 17.6 °C, and annual precipitation is 1645.4 mm. Mountainous and hilly areas dominate the county and cover for more than 97% of the total area. Forest types include coniferous forests, evergreen broad-leaf forests, and deciduous and evergreen broad-leaf mixed forests.

Fig. 1
figure 1

Location of the study area and the sampling plots

Full size image

National forest inventory data

NFI data collected in 2009 was used to estimate the mean AGB per hectare. The data set contained 101 permanent plots (9886 sample trees) systematically distributed using a 4 km × 6 km grid (Fig. 1). The plot size was 28.3 m × 28.3 m (800 m2). In each plot, trees with a DBH ˃ 5 cm were measured. The frequency histogram of the DBH of sample trees at 2 cm intervals is shown in Fig. 2. Because measurements of H are tedious and expensive, the NFI data does not contain information on height. In this study, the height-diameter model developed by Li and Fa (2011) was used to predict the H of Quercus, Cunninghamia lanceolate (Lamb.) Hook and Pinus massoniana Lamb. The calibration data were obtained from the NFI data, which were collected throughout China. Height was divided into nine levels according to different sites, and used the Chapman–Richard function was used to establish the height–diameter model. This method provides more accuracy of height prediction and can be applied throughout China. For the other broad-leaved species, we use the model of height developed by Shen (2002). This model was based on 1356 sample trees and used the Chapman–Richard function. The data set contained more than 10 common subtropical broad-leaved tree species and included a range of possible variations in average stand diameter and average height. Although, our study area was different from that of Shen (2002). But both areas are located in the mid-subtropics and are dominated by mountainous and hilly terrain. This model was used to predict the H of broad-leaved species.

Fig. 2
figure 2

Frequency histogram of each diameter class for the National Forest Inventory data

Full size image

Calibration data

A total of 363 harvested trees were used to develop the AGB model. This dataset was collected from 13 counties across a large geographical area in Zhejiang Province and contained 21 common tree species. In these sites, 363 NFI plots were selected (146 Cunninghamia lanceolate plots, 80 Pinus massoniana plots, 173 broad-leaved tree plots) and one average bole was selected in each plot. According to the average boles, the harvested trees were selected outside the plots. Figure 3 shows the frequency histogram of each diameter class and the relationship between the AGB of harvest trees and DBH.

Fig. 3
figure 3

Frequency histogram of each diameter class and the relationship between DBH and the AGB of harvested trees for the calibration data

Full size image

After sample trees were felled at ground level, the tree species, DBH and H were recorded. The stems were cut at 2-m intervals if the H ≥ 10 m, and cut at 1-m intervals if the H < 10 m. Branches and leaves were divided into four levels: ≤ 1 cm, 1.1–2.0 cm, 2.1–3.0 cm and > 3 cm. One standard branch was selected from each level, and weight of the branch and foliage were determined. Fresh weights of bole, bark, branches, and foliage were measured in the field. The samples of each component were oven-dried until their weight stabilized. The ratio of dry mass to fresh mass was used to predict the biomass of each component, and the total AGB of each harvested tree was estimated by summing all components. As shown in Figs. 2 and 3, the maximum DBH of the CDS is smaller than that of the NFI data. However, only 39 trees in the NFI data are outside of the DBH range of the CDS. Thus, the calibration data are representative the NFI data.

Measurement error data

We performed a double-blind re-measurement of 276 tree samples to estimate the measurement error. The sample size of each species group is determined according to the NFI data, and confirmed that DBH distribution was similar to the DBH distribution of the NFI data. The detailed description of this data set is available in Qin et al. (2019). According to the regulations for continuous NFI in China, the measurement error of H should not exceed 5%. In this study, it was assumed that the measurement error was followed a uniform distribution \(\varepsilon_{{\text{H}}} - \mu ( - 0.05H,0.05H)\); the measurement error was randomly selected from this range. Picard et al. (2015) assumed that the measurement error of DBH followed a uniform distribution due to the lack of measurement error data.

Mean AGB estimation

The calibration data was used to establish individual tree AGB allometric models and were used to predict the individual tree AGB in each plot. The tree-level AGB predictions were aggregated to produce plot-level AGB predictions. Finally, systematic sampling estimators were used with the plot-level AGB predictions to forecast the mean above-ground biomass per unit area. This procedure is referred to as hybrid inference, a term was coined by Corona et al. (2014) to describe the use of a model to predict the response variables of probability samples of auxiliary data. The population parameters (mean, total) were estimated using a probability-based estimator and the probability sample predictions (McRoberts et al. 2016; Ståhl et al. 2016).

Estimation of single-tree above-ground biomass

Many forms of allometric models can be used for developing tree AGB models. In this study, five model types were selected (Wang et al. 2015; Cecep et al. 2018; Martínez-Sánchez et al. 2020):

$$M = \alpha_{1} D^{{\alpha_{2} }} + \varepsilon$$
(1)
$$M = \alpha_{1} + \alpha_{2} D + \alpha_{3} D^{2} + \varepsilon$$
(2)
$$M = \alpha_{1} + \alpha_{2} D + \alpha_{3} D^{2} + \alpha_{4} D^{3} + \varepsilon$$
(3)
$$M = \alpha_{1} D^{{\alpha_{2} }} H^{{\alpha_{3} }} + \varepsilon$$
(4)
$$M = \alpha_{1} (D^{2} H)^{{\alpha_{2} }} + \varepsilon$$
(5)

where D is the DBH (cm), H is H (m); M is the individual tree AGB (kg), \(\alpha_{1}\), \(\alpha_{2}\), \(\alpha_{3}\) and \(\alpha_{4}\) are estimated parameters. The model performances were evaluated with the coefficient of determination (R2).

Uncertainty caused by measurement error

The measurement error is assumed to follow a Gaussian distribution (Chave et al. 2004; Berger et al. 2014; McRoberts and Westfall 2016). We fitted a model to the SD (standard deviation) of measurement error and DBH to simulate the measurement error.

The method consisted of the following steps (Hosmer and Lemeshow 1989; Berger et al. 2014; Qin et al. 2019): (1) All trees were ranked in ascending order with respect to \(\overline{D}\), where \(\overline{D}\) is the mean of two DBH measurement values, and the difference (\(D_{{{\text{Dif}}}}\)) between two measurements for each tree was calculated as: \(D_{{{\text{Dif}}}} = D_{1} - D_{2}\),where D1 and D2 represent the first and second DBH measurement, respectively; (2) After ranking, all trees were divided into n groups according to the new order. Each group contained at least 15 trees to generate a sufficient number of groups. If the last group contained less than 15 trees, the trees in the last group were placed in the previous group; and, (3) for the ith group, the mean DBH (\(\overline{D}_{i}\)) of \(\overline{D}\) and the SD (\(\sigma_{{{\text{Dif}}}}\)) of the differences between the two measurements were calculated. Finally, the relationship between the \(\overline{D}_{i}\) and \(\sigma_{{{\text{Dif}}}}\) was described by a liner model:

$$\sigma_{{{\text{Dif}}}} = a + b\overline{D}_{i}$$
(6)

Based on this model, Monte Carlo simulations were used to predict the effect of the measurement error on AGB estimation. This procedure contained four steps:

Step 1 Using Eq. (6), the SD (\(\sigma_{{{\text{Dij}}}}\)) of the measurement error of DBH for the ith tree in the jth plot was predicted. For each tree in a plot, a measurement error \(\varepsilon_{{{\text{Dij}}}}\) was randomly selected from a Gaussian distribution \(\varepsilon_{{{\text{Dij}}}} \sim N(0,\sigma_{{{\text{Dij}}}} )\). The new DBH for each tree was then calculated by adding \(\varepsilon_{{{\text{Dij}}}}\) to the original DBH.

Step 2 If the individual tree AGB model contained H, the measurement error of H for the ith tree in the jth plot was randomly selected from the uniform distribution \(\varepsilon_{{{\text{Hij}}}} - \mu ( - 0.05H_{i,j} ,0.05H_{i,j} )\), where \(H_{i,j}\) is the original H for the ith tree in the jth plot. The new H (\(H_{i,j}^{^{\prime}}\)) for each tree was then calculated by adding \(\varepsilon_{{{\text{Hij}}}}\) to the original H.

Step 3 For ith tree in the jth plot, the individual tree AGB was predicted using the new DBH and H simulated from step 1 and step 2. The total AGB of the jth plot was predicted by summing all individual tree AGB: \(P_{j} = \sum\nolimits_{i}^{n} {M_{i,j} }\), where n is the number of trees in the jth plot and \(M_{i,j}\) is the AGB of ith tree in the jth plot. The mean AGB per hectare was estimated as:

$$\overline{P} = \frac{1}{m}\sum\limits_{j = 1}^{m} {p_{j} }$$
(7)

where, m is the number of the plot.

Step 4 Steps 1–3 were repeated 2000 times. The mean of AGB per hectare and the variance of the replications were predicted following Rubin (1987):

$$\overline{\mu }_{{{\text{me}}}} = \frac{1}{{n_{{{\text{rep}}}} }}\sum\limits_{k = 1}^{{n_{rep} }} {\overline{p}^{k} }$$
(8)
$$Var(\overline{\mu }_{{{\text{me}}}} ) = \left( {1 + \frac{1}{{n_{{{\text{rep}}}} }}} \right) \times W_{1} + W_{{2}}$$
(9)

where, \(\overline{\mu }_{{{\text{me}}}}\) is the mean AGB over replications, \(W_{1} = \frac{1}{{n_{{{\text{rep}}}} - 1}}\sum\nolimits_{k = 1}^{{n_{rep} }} {(\overline{\mu } - \overline{P}^{k} )^{2} }\) is the between-simulation variance, \(W_{{2}} = \frac{1}{{n_{{{\text{rep}}}} - 1}}Var(\overline{P}^{k} )\) is the mean within-simulation variance,\(\overline{P}^{k}\) is the mean AGB per hectare in the kth replication and \(n_{rep}\) is the number of replications. The replications were continued until \(\mu_{{{\text{me}}}}\) and \(Var(\mu_{{{\text{me}}}} )\) stabilized. The relative uncertainty \(R_{{{\text{me}}}} = \frac{{\sqrt {Var(\overline{\mu }_{{{\text{me}}}} )} }}{{\overline{\mu }_{{{\text{me}}}} }} \times 100{\text{\% }}\) was then used as the index to assess the uncertainty.

Uncertainty caused by residual variability

This was also estimated using Monte-Carlo simulations by adding a random error to each models’ predictions (McRoberts et al. 2014). In this study, we first constructed a model from the standard deviation of the residual and the predicted AGB. The fitting method was the same as fitting models to the SD of the measurement error and DBH. McRoberts and Westfall (2013, 2016) used this method to develop models from the calibration data of tree volume and residual variability. The method had the following steps: (1) \(\varepsilon\), \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M}\) were ranked in ascending order with respect to \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M}\), where \(\varepsilon\) is the residual of each harvested tree, \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M}\) is the model prediction of single tree AGB; (2) All trees in the CDS were divided into n groups after ranking. In this study, 20 trees were placed in a single group. If the last group contained less than 20 trees, the trees in the last group were placed in the previous group; (3) For the ith group, the mean of the \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M}\) and the SD of the \(\varepsilon\) was calculated. The relationships between the SD and the mean of the \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M}\) were then estimated using the liner model:

$$\sigma_{{\upvarepsilon }} = a_{{\upvarepsilon }} + b_{{\upvarepsilon }} \overline{\hat{M}}$$
(10)

where \(\sigma_{{\upvarepsilon }}\) is the SD of the \(\varepsilon\) in each group,\(a_{{\upvarepsilon }}\) and \(b_{{\upvarepsilon }}\) are the model parameters, and \(\overline{\hat{M}}\) is the mean of \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M}\) in each group. Based on this model, a four-step procedure was used to simulate the effect of residual variability on AGB estimation.

Step 1 For the ith sample tree in the jth plot, the tree AGB was predicted using the AGB model established from the CDS.

Step 2 For the ith tree in the jth plot, the SD (\(\sigma_{{\upvarepsilon }}\)) of the residual was predicted by model (10). Based on \(\sigma_{{\upvarepsilon }}\), a random residual (\(\varepsilon_{i,j}\)) of each sample tree was randomly obtained from the Gaussian distribution \(\varepsilon_{i,j} = N(0,\sigma_{{\upvarepsilon {\text{ij}}}} )\),where \(\sigma_{{\upvarepsilon {\text{ij}}}}\) is the SD of the residual of the ith tree within jth plot. Then, the new single-tree AGB value of each element in the NFI data was calculated as \(M_{i,j}^{^{\prime}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M}_{i,j} + \varepsilon_{i,j}\), where \(M_{i,j}^{^{\prime}}\) is the new AGB of ith tree in the jth plot, and \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M}_{i,j}\) is the original predicted value of the single tree AGB.

Step 3 The total AGB of the jth plot was estimated as \(P_{j} = \sum\nolimits_{i}^{n} {M_{i,j}^{^{\prime}} }\), where n is the number of trees in the plot, and \(M_{i,j}^{^{\prime}}\) is the ith individual tree AGB in the jth plot. The mean of all plots was estimated as \(\overline{P} = \frac{1}{m}\sum\nolimits_{j = 1}^{m} {P_{j} }\) where m is the number of the plot.

Step 4 Steps 1–3 were repeated 2000 times.

The relative uncertainty caused by the residual variability was estimated as \(R_{{\text{U(rv)}}} = \frac{{\sqrt {Var(\overline{\mu }_{{{\text{rv}}}} )} }}{{\overline{\mu }_{{{\text{rv}}}} }} \times 100{\text{\% }}\), where \(\overline{\mu }_{{{\text{rv}}}}\) and \(Var(\overline{\mu }_{{{\text{rv}}}} )\) are the mean and variance of the replications, respectively; these were estimated as Eqs. (8) and (9).

Uncertainty caused by the variance of the parameter estimates

Monte-Carlo simulations can be used to simulate the variances of the parameters of the AGB model. This simulates the actual sampling process (if known) of the original data. Wayson et al. (2015) used this method to generate a large pseudo-data of variables and refitted the biomass model. McRoberts et al. (2014) also used this method to simulate the potential distribution of the parameters in the biomass model and predicted the uncertainty caused by the variance of the parameter estimates. In this study, a five-step Monte-Carlo simulation was used to estimate the uncertainty caused by model parameters:

Step 1 The original CDS was grouped into DBH classes at 1-cm intervals. If the sample size in one group was insufficient, then the sample trees were placed in the previous group. Finally, each group contained at least nine sample units.

Step 2 In each group, the AGB, DBH, and H of each harvest tree were randomly resampled until the original class size was achieved. During resampling, AGB, DBH and H were assumed to be a uniform distribution and each variable was randomly selected from the existing range.

Step 3 The new data set generated in Step 2 were used to fit a new single-tree AGB model for each model type and predict the single-tree AGB in each plot.

Step 4 The total AGB of the jth plot was predicted as \(P_{j} = \sum\nolimits_{i}^{n} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{M}_{i,j} }\), where n is the number of trees in the plot, and \(\hat{M}_{i,j}\) is the ith predicted individual tree biomass in the jth plot. The mean AGB of all plots was estimated as: \(\overline{P} = \frac{1}{m}\sum\nolimits_{i}^{m} {P_{j} }\), where m is the number of the plot.

Step 5 Steps 1–4 were repeated 2000 times. The relative uncertainty associated with the parameter estimates was estimated as \(R_{{{\text{par}}}} = \frac{{\sqrt {Var(\overline{\mu }_{{{\text{par}}}} )} }}{{\overline{\mu }_{{{\text{par}}}} }} \times 100{\text{\% }}\), where \(\overline{\mu }_{{{\text{par}}}}\) and \(Var(\overline{\mu }_{{{\text{par}}}} )\) are the mean and variance of the replications; these were estimated using Eqs. (8)–(9).

Uncertainty caused by the sampling variability of the NFI data

In this study, bootstrap resampling was used to estimate the uncertainty associated with the sampling variability of the NFI data. This method assumed that the sample represented the population from which the sample was drawn, and each observation in the sample had an equal probability of being selected from the population (Hinkley 1988). This method can be used to estimated standard errors, confidence intervals, and variances of a survey data (Efron and Tibshirani 1986). In this study, bootstrap sampling was performed using the “bootstrap” package in the R software; the bootstrap times were set to 2000. After 2000 bootstraps times, the mean above-ground biomass and the variance of mean were estimated as:

$$\overline{\mu }_{{{\text{sam}}}} = \frac{{\sum\nolimits_{i}^{n} {\overline{p}^{k}_{{{\text{sam}}}} } }}{n}$$
(11)
$$Var_{{{\text{sam}}}} = \frac{1}{{n_{{}} - 1}}\sum\limits_{k = 1}^{n} {(\overline{\mu }_{{{\text{sam}}}} - \overline{P}_{{{\text{sam}}}}^{k} )^{2} }$$
(12)

where \(\overline{\mu }_{{{\text{sam}}}}\) is the mean AGB after 2000 resampling steps, \(\overline{p}^{k}_{{{\text{sam}}}}\) the mean AGB of kth resampling step, \(Var_{{{\text{sam}}}}\) the variance of the mean AGB after 2000 resampling steps, and n the number of resampling steps. The relative uncertainty associated with the sampling variability of NFI data was estimated \(R_{{{\text{sam}}}} = \frac{{\sqrt {Var(\overline{\mu }_{{{\text{sam}}}} )} }}{{\overline{\mu }_{{{\text{sam}}}} }} \times 100{\text{\% }}\).

Calculation of overall uncertainty

The overall relative uncertainty (\(R_{{\text{T}}}\)) of each model was predicted as:

$$R_{{\text{T}}} = \sqrt {\left( {R_{{{\text{me}}}} } \right)^{2} + \left( {R_{{{\text{rv}}}} } \right)^{2} + \left( {R_{{{\text{par}}}} } \right)^{2} + \left( {R_{{{\text{sam}}}} } \right)^{2} }$$
(13)

We assumed the uncertainty between each other was independent. McRoberts and Westfall (2013) found that this assumption is reasonable for predicting tree volume over large areas. In addition, Berger et al. (2014) used the law of error propagation and a Monte Carlo simulation to estimate the uncertainty associated with measurement error for tree volume estimations; they found that the results of the two methods were similar.

Results

Model fitting

The parameters and R2 of the models are listed in Table 1, and the relationships between the predicted AGB and the AGB of harvested trees are shown in Fig. 4. The fits of all models to the data resulted in large R2 values (R2 > 0.83), and the model that contained DBH and H produced better fitting results than the one with only DBH.

Table 1 Estimated parameters of the models
Full size table
Fig. 4
figure 4

Relationships between the predicted AGB and the AGB of the harvested trees for different models M1–M5 are the biomass models defined in Eqs. (1)–(5)

Full size image

Uncertainty calculation

The model used to predict the standard deviation of the measurement error had the form \(\hat{\sigma }_{{\text{D}}} = 0.0173D + 0.0185\), with an R2 of 0.61 (Qin et al. 2019). Figure 5 shows the mean AGB per hectare and the relative uncertainty for the five models. Both the mean AGB and the relative uncertainty tended to stabilize after 500 simulations. Table 2 shows the sources of uncertainties of the five models. The measurement error had the largest effect on the biomass estimation for model 4 and the smallest for models 1 and model 3. Although the results of the different models were affected to various degrees by the measurement error, the uncertainty related to the measurement error was negligible.

Fig. 5
figure 5

Simulated mean AGB and relative uncertainty associated with the measurement error for the five models M1–M5 described by Eqs. (1)–(5)

Full size image
Table 2 Uncertainties associated with various sources for different models
Full size table

Figure 6 shows the relationships between the standard deviation of the residual and the predicted tree above-ground biomass of each group. The fit of the model describing the relationship between the estimated tree AGB and the SD of the residual was excellent and all models had very large R2 values. Figure 7 shows the mean AGB per hectare and the relative uncertainty of all models for 2000 simulations. Both the mean AGB and the relative uncertainty tended to stabilize after 300 simulations. As shown in Table 2, the residual variability had the largest influence on the biomass estimation for model 1, whereas model 5 was least affected by the residual variability. The uncertainty associated with residual variability was larger than that of the measurement error but did not exceed 1.2%. Therefore, the residual variability also had a slight effect on forest biomass estimation.

Fig. 6
figure 6

Relationships between the estimated tree biomass and the SD of the residual for the 5 selected models M1–M5 described by Eqs. (1)–(5)

Full size image
Fig. 7
figure 7

Simulated mean AGB and relative uncertainty associated with the residual variability of the 5 models M1–M5 described by Eqs. (1)–(5)

Full size image

The uncertainty associated with the variance of the parameter estimates (Table 2; Fig. 8) was larger than that of the measurement error and residual variability and ranged from 3.9% (model 1) to 11.1% (model 2) for the five models.

Fig. 8
figure 8

Simulated mean AGB and relative uncertainty associated with the parameter estimates for 5 models M1–M5 described by Eqs. (1)–(5)

Full size image

Figure 9 shows the frequency histogram of the estimated mean above-ground biomass per unit area for the five models after 2000 bootstraps. Model 2 had the largest sampling uncertainty (10.9%), and model 3 had the smallest sampling uncertainty (9.7%). Sampling variability was the largest source of uncertainty for all models (Table 2). For total uncertainty, model 1 had the smallest uncertainty (11.3%), and model 2 had the largest uncertainty (15.6%) (Table 2).

Fig. 9
figure 9

Frequency histogram of the estimated mean AGB per unit area of the 5 models after 2000 bootstraps; the 5 models were described by Eqs. (1)–(5)

Full size image

Discussion

In recent years, increasing attention has focused on the assessment of uncertainty in forest biomass estimation. Several studies have quantified different types of uncertainty, such as measurement uncertainty, model uncertainty, and sampling uncertainty (Chave et al. 2004; Picard et al. 2015; Shettles et al. 2015). In this study, the uncertainty associated with the measurement error, residual variability, variance of the parameter estimates and sampling variability in NFI data for different models was estimated. The results showed that the sampling variability in the NFI data was the primary source of uncertainty. In addition, the uncertainty caused by the parameter estimates should not be overlooked.

The measurement error may be minimized by training, but is not completely avoidable (Elzinga et al. 2005). In this study, uncertainty associated with the measurement error was negligible, regardless of whether the model contained diameter or diameter and height. This is consistent with that of other studies (Berger et al. 2014; McRoberts and Westfall, 2016). In this study, we assumed that the measurement error were independent, which minimized the total error for a large number of trees, because errors will compensate each other. Dependent errors were not considered, for example, a systematic bias due to faulty material. The uncertainty caused by this source of error needs further examination. In addition, the predicted H was taken as the “true” H. This may produce other uncertaintes, but the referenced studies did not show the distribution of residual and this was not considered.

In this study, the influence of residual variabilities on the results was insignificant. This is consistent with studies by Chen et al. (2015) and Picard et al. (2015). Chave et al. (2004) and Chen et al. (2015) found that the error of single-tree above-ground biomass estimation caused by the residual varibility was more than 30%. This type of uncertainty at a regional scale was much samller than that at tree level. One reason may be that a normal distribution of the residuals was assumed. This residual error at tree level is levelled off when residuals are randomly selested. Trees with positive residuals compensate for trees with negative residuals, resulting in a small variance between simulations. In addition, Chave et al. (2004) and Chen et al. (2015) and found that the uncertainty at the plot level was in negatively correlated with the number of trees in a plot. In this study, the average number of trees in all plots was 99, resulting in relatively low uncertainty at the plot level.

We also found that the model containing diameter at breast height and height resulted in smaller uncertainties associated with residual variability, both at the single tree level (Fig. 5) and at the regional level (Table 2). The inclusion of additional variables in biomass models typically improves model accuracy (Ketterings et al. 2001), which has been confirmed in many studies. Lambert et al. (2005) found that the root mean squared error of tree biomass predictions was reduced by approximately 8% and 25% for hardwood and softwood species, respectively, if height was added to the model. Goodman et al. (2014) found that the addition of crown radius to biomass models further reduced the bias of total above-ground biomass by 11–14%. In addition, additional species traits (e.g., wood density) could be included, especially when a significant species effect on model residuals is found (Ngomanda et al. 2014).

The uncertainty caused by the variance of the model parameter was much larger than that caused by the measurement error and the residual variability. This is consistent with other studies (Breidenbach et al. 2014). Therefore, the greatest potential to improve the accuracy of biomass models is to improve the accuracy of the model parameters. These are affected by the sample size, distribution of the calibration data, and regression methods (Muller-Landau et al. 2006). Increasing the sample size can improve the accuracy of biomass models. Chen et al. (2015) reduced the sample size from 4004 to 400, and to 40, and found that the relative above-ground biomass prediction error increased from 0.7 to 2.5 and 5.7%, respectively. However, single-tree above-ground biomass measurements are difficult to obtained resulting in the limitation of the size of the calibration data set. Jenkins et al. (2004) determined the mean sample size of 2642 biomass models and found that sample sizes for nearly half of the studies did not exceed 20 trees. Therefore, increasing the sample size appears to be a challenge in most studies. In this study, 363 sample trees were used to establish AGB models to predict subtropical forest AGB in China. In addition, different regression methods may also provide widely different estimates of the allometric parameters from the same dataset (Sileshi 2014). This aspect was not covered in this study.

As shown in Table 2, the uncertainty associated with the sampling variability of NFI data was the largest source of uncertainty. This is consistent with Berger et al. (2014) and Breidenbach et al. (2014). One approach to reducing this type of uncertainty is to increase the sample size of the plot or to increase the size of the plot (Peter and Tom 2011). Studies have found that the coefficient of variation of biomass decreased with an increase in size of plot (Chave et al. 2003). However, an increase in the number of plots or plot size may result in different spatial patterns of the biomass. A random plot distribution is more easily achieved for small plots than for a few large plots, whereas the opposite is true for a systematic distribution (Picard et al. 2015). In addition, uncertainty associated with residual variability and plot-model interaction decrease with an increase in the plot size (Picard et al. 2015). Another method to reduce sampling-related uncertainty may be the inclusion of ancillary information for stratification, such as forest characteristics or the forest structure. This method has been proved to be more accurate and efficient than systematic or random sampling (Gharun et al. 2017), especially when remotely sensed data are used (Wallner et al. 2018).

The balance between accuracy and cost is a problem in forest above-ground biomass estimations. One method to improve the precision is to add other variables to the models, but this increases the costs of model development and field inventory. For example, accurate height measurements are time-consuming and expensive, and increase the overall cost of the forest inventory. In this study, we found that model 1 had the least uncertainties, especially when sampling variability was not considered. Our results suggest trade-off between accuracy and cost. However, different models provide different results, as shown in Table 2. One of the problems to address is how to balance the results between different models.

Conclusion

This study estimated four types of uncertainties in five forest above-ground biomass models. The results suggested that the model \(M = \alpha_{1} D^{{\alpha_{2} }}\) was the best to estimate above-ground biomass. This finding can be used to achieve a trade-off between accuracy and cost in biomass estimation. The results also indicate that uncertainty associated with sampling variability in national forest inventory data contributed most to overall uncertainty, followed by the uncertainty associated with the variance of the parameter estimates and the residual variability. Thus, the emphasis is on reducing the sampling-related variability if the objective is the reduction in overall uncertainty of above-ground biomass estimation. If the model-related uncertainty is to be decreased, the focus should be on reducing the uncertainty associated with the variance of the parameter estimates.