A New Perspective on Geometric Thermodynamic Models

Abstract

To estimate the thermodynamic properties of a multi-component system using traditional geometric models, lack of a physical meaning generates many puzzles during choosing a concrete method. In this paper, we introduced a perspective in terms of the molar quantity of the components in the sub-binary of a ternary system affected by the third component and deduced a new model to unify all other traditional geometric models (e.g. Kohler, Muggianu, Toop-Kohler, etc.) into one model. The effects could be represented by so-called contribution coefficients, whose values only depend on the degree of identity between the thermodynamic properties of the third component and those of the selected components in the sub-binary, and which gives the physical meaning for the present model.

1 Introduction

Physicochemical properties of metallic solutions for multicomponent systems are very important for metallurgy and materials science. Nevertheless, due to a huge number of multicomponent systems and difficulties to control the high-temperature conditions in experiments, the thermodynamic properties are practically impossible to be solved completely by experiments, although they are the most reliable methods. So, one has to rely on theoretical calculations. There are two kinds of calculation methods, one is the first-principle calculation method, which is based on quantum mechanics and has a very clear physical picture and a strictly theoretical deduction step. But for practical applications, this method still has a long way to go because the lack of accurate structure information for multicomponent solutions. The other one is an “empirical method” or “phenomenological model”.[1] The “empirical method” doesn’t need much information about the structure but it still can effectively estimate the properties of a multicomponent system, and therefore the “empirical method” has been frequently used in practices, especially in calculating properties in a ternary system in terms of the binary ones.

The “empirical method” refers to a method which decomposes the thermodynamic properties of a multicomponent system into a combination of the corresponding properties for all binary and ternary as well as up interaction terms, and then assigns a proper probability weight for each term.[2,3] In general, the triplet and up interaction terms are always ignored since they are small.[4] As a result, a mathematical expression to estimate the thermodynamic properties of the multicomponent system can be normally expressed as[2,5]:

$$\Delta G^{E} = \sum\limits_{i = 1}^{m} {\sum\limits_{j = i + 1}^{m} {W_{ij} \Delta G_{ij}^{E} } }$$

(1)

where $\Delta G^{E}$ represents the molar property for the multicomponent system, $\Delta G_{ij}^{E}$ is the molar properties for the i-j binary systems, $W_{ij}$ is the probability weights of the i-j binaries in the multicomponent system and can be expressed as[3,5]:

$$W_{ij} = \frac{{x_{i} x_{j} }}{{X_{ij}^{i} X_{ij}^{j} }}$$

(2)

where $x_{i}$ and $x_{j}$ are the molar fractions of the components i and j in the multicomponent system, while the capital $X_{ij}^{i}$ and $X_{ij}^{j}$ are the molar fractions of the components i and j in the selected i-j binary system, respectively, with a relationship of $X_{ij}^{i} + X_{ij}^{j} = 1$.

In a ternary system, the molar compositions of each sub-binary can be obtained from the side of the corresponding binary in the concentration triangle through a certain geometric rule, and therefore the “empirical method” is also called as geometric methods[6] or geometric models.[3] In the past, many geometric models have been suggested in the literature, but the commonly used is only four.[6,7,8,9] Figure 1 lists the graphical illustration of these four geometric models which can be loosely divided into two categories[3,6]: (1) the symmetric models, e.g. the Kohler model[7] of Fig. 1(a) and the Muggianu model[9] of Fig. 1(c); and (2) the asymmetric models, e.g. the Toop-Kohler model[8] of Fig. 1(b) and the Toop-Muggianu model[6] of Fig. 1(d). Different models have different characteristics and applicable systems. For example, the asymmetric models need to determine an asymmetric component before calculating, which makes the treatment of N-component system (N > 3) very complex; while the symmetric model cannot be applicable for the case where the physicochemical properties of constituents are clearly different.[4,10] In addition, the symmetric models have a serious theoretical problem under a limiting condition: when two components of the ternary system are identical, they cannot be correctly reduced to the binary solution model. This problem has been pointed out many times by Chou.[2,5] Furthermore, applying different models (even though belonging to the same category) to a given system would receive different results.[4,10,11] Therefore, in practice, an intractable problem is encountered: which model should be chosen to treat the given system for better results? This problem will be more serious when these models are extended to an N-component system (N > 3).[4]

Fig. 1

Four of most common geometric models

In order to solve these problems, Pelton and Chartrand[4,12] proposed an ingenious method to unite symmetric and asymmetric models into one equation, but, in their method, the choice of the specific geometric model to treat each ternary still depends on artificial preference. Chou[2,5] proposed a general model that can select the composition point of each binary system automatically based on the properties of the ternary system through the introduction of similarity coefficient between two components. Varying the values of the similarity coefficient, Chou’s model[2,5] can be mathematically reduced to many geometric models such as the Muggianu[9]/Toop-Muggianu[6] models. However, Chou’s model[2,5] can’t be mathematically reduced to the Kohler[7]/Toop-Kohler[8] models which have been confirmed in some systems with better predicted results[10,11] than Chou’s model. The Toop-Kohler[8] model also has good applicability in predicting the activity interaction parameters of solutes in a metallic solution[13,14,15] by combining the Miedema model.[16,17] The greatest contribution of Chou’s model[2,5] is to break down the barrier between symmetric and asymmetric models, and it ends the traditional way of constructing new geometric models that by artificially selecting the “sub-binary representative point”. However, same to the other geometric models, Chou’s model[2,5] paid more attention to the choice of the composition point for the sub-binaries and didn’t shed new light on the geometric model itself. To our opinion, giving a new perspective on the geometric model is essential to solve the problem of the choice of the model.

Therefore, the present paper is devoting to describe the geometric model from a new perspective. Before doing that, it’s necessary to review the most used models: the Kohler model,[7] Muggianu model,[9] and Toop model,[8] because of their importance for all geometric models.[3]

2 The Basic Types of the Geometric Models

To illustrate the basic types of geometric models, let’s begin with their mathematical expressions. Here, takes the ternary system 1-2-3 as an example, the mathematical expressions of the molar excess thermodynamic properties $\Delta G_{123}^{E}$ given by the Kohler model,[7] the Muggianu model,[9] the Toop-Kohler model,[8] and the Toop-Muggianu model[6] are expressed as follows.

The Kohler model[7]:

$$\Delta G_{123}^{E} = \sum\limits_{\begin{subarray}{l} i = 1,2,3 \\ j = i + 1 \\ j \le 3 \end{subarray} } {\left( {x_{i} + x_{j} } \right)^{2} \Delta G_{ij}^{E} \left( {\frac{{x_{i} }}{{x_{i} + x_{j} }};\frac{{x_{j} }}{{x_{i} + x_{j} }}} \right)}$$

(3)

The Muggianu model[9]:

$$\Delta G_{123}^{E} = \sum\limits_{\begin{subarray}{l} i = 1,2,3 \\ j = i + 1 \\ j \le 3 \end{subarray} } {\frac{{4x_{i} x_{j} }}{{\left( {1 + x_{i} - x_{j} } \right)\left( {1 + x_{j} - x_{i} } \right)}}\Delta G_{ij}^{E} \left( {\frac{{1 + x_{i} - x_{j} }}{2};\frac{{1 + x_{j} - x_{i} }}{2}} \right)}$$

(4)

The Toop-Kohler[8] and Toop-Muggianu[9] models are asymmetric models in which an asymmetric component is required to be specified before being employed. As shown in Fig. 1(b) and (d), the component 2 is chosen as the asymmetric component, which yield the following mathematical expressions, respectively.

The Toop-Kohler model[8]:

$$\Delta G_{123}^{E} = \frac{{x_{2} }}{{1 - x_{2} }}\Delta G_{12}^{E} (1 - x_{2} ;x_{2} ) + \frac{{x_{2} }}{{1 - x_{2} }}\Delta G_{23}^{E} (x_{2} ;1 - x_{2} ) + \left( {x_{1} + x_{3} } \right)^{2} \Delta G_{13}^{E} \left( {\frac{{x_{1} }}{{x_{1} + x_{3} }};\frac{{x_{3} }}{{x_{1} + x_{3} }}} \right)$$

(5)

The Toop-Muggianu model[6]:

$$\Delta G_{123}^{E} = \frac{{x_{2} }}{{1 - x_{2} }}\Delta G_{12}^{E} (1 - x_{2} ;x_{2} ) + \frac{{x_{2} }}{{1 - x_{2} }}\Delta G_{23}^{E} (x_{2} ;1 - x_{2} ) + \frac{{x_{1} x_{3} }}{{v_{13} v_{31} }}\Delta G_{13}^{E} (v_{13} ;v_{31} )$$

(6)

where $v_{ij} = \frac{{1 + x_{i} - x_{j} }}{2}$.

Comparing Eq 5 and 6, it’s obvious that their difference is the third term on the right of the equation, i.e., the treatment of the sub-binary 1-3. In Eq 5, the treatment of the sub-binary 1-3 is the same as that in the Kohler model (Eq 3). In Eq 6 the treatment of the sub-binary 1-3 is the same as that in the Muggianu model (Eq 4). To distinguish strictly, here, we define the treatment method of the sub-binary 1-2 or 2-3 in Eq 5 or Eq 6 as a Toop type, while the treatment methods of sub-binaries in Eq 3 and 4 as a Kohler type and a Muggianu type, respectively. These three types to the sub-binaries in the ternary system are the basic ones in all traditional geometric models.[3,6,18]

To better present the characterizations of these three types of geometric models, it’s necessary to investigate the general molar fraction of the sub-binary i-j in ternary system i-j-k given by them. (Note: in the ternary system i-j-k, it is always true for the relation of $x_{i} + x_{j} + x_{k} = 1$).

• 1. Toop type

Case 1: j is chosen as an asymmetric component in the ternary i-j-k

$$\left\{ \begin{aligned} & X_{ij}^{i} = 1 - x_{j} = x_{i} + x_{k} \\ & X_{ij}^{j} = x_{j} \\ \end{aligned} \right.$$

(7)

Case 2: i is chosen as an asymmetric component in the ternary i-j-k

$$\left\{ \begin{aligned} & X_{ij}^{i} = x_{i} \\ & X_{ij}^{j} = 1 - x_{i} = x_{j} + x_{k} \\ \end{aligned} \right.$$

(8)

• 2. Kohler type

$$\left\{ \begin{aligned} & X_{ij}^{i} = \frac{{x_{i} }}{{x_{i} + x_{j} }} \\ & X_{ij}^{j} = \frac{{x_{j} }}{{x_{i} + x_{j} }} \\ \end{aligned} \right.$$

(9)

• 3. Muggianu type

$$\left\{ \begin{aligned} X_{ij}^{i} = \frac{{1 + x_{i} - x_{j} }}{2} = x_{i} + \frac{1}{2}x_{k} \hfill \\ X_{ij}^{j} = \frac{{1 + x_{j} - x_{i} }}{2} = x_{j} + \frac{1}{2}x_{k} \hfill \\ \end{aligned} \right.$$

(10)

Figure 2 shows the graphical illustration of these three types. From Fig. 2, the difference of the Toop type, Kohler type, and Muggianu type is the choice of the “sub-binary representative point”. In order to choose a reasonable point, huge efforts have been made by Chou,[2,3,5] who also proposed an interesting model[2,5] that can automatically select the composition point of each sub-binary in a ternary system by introducing the concept of similar coefficient between two components. Later, a specific application guideline for Chou’s model[2,5] was developed by Zhang.[19] Chou’s model[2,5] is expressed as follows.

Fig. 2

Graphical illustration of various methods for selecting the “binary representative point” on a binary side

• 4. Chou’s model

$$\left\{ \begin{aligned} X_{ij}^{i} = x_{i} + \beta_{i(ij)}^{k} x_{k} \hfill \\ X_{ij}^{j} = x_{j} + \beta_{j(ij)}^{k} x_{k} \hfill \\ \end{aligned} \right.$$

(11)

where $\beta_{{i\left( {ij} \right)}}^{k}$ refers to the similar coefficient of the component k to the component i in the i-j binary, and its value only relates to the properties of the given ternary system and satisfies $0 \le \beta_{{i\left( {ij} \right)}}^{k} \le 1$ and $\beta_{{i\left( {ij} \right)}}^{k} + \beta_{{j\left( {ij} \right)}}^{k} = 1$. Obviously, Chou’s model[2,5] can be mathematically reduced to the Toop type (Eq 7 and 8) and Muggianu type (Eq 10) but can’t be reduced to the Kohler type (Eq 9). Because if Chou’s model[2,5] (Eq 11) may reduce to the Kohler type[7] (Eq 9), it would result in the similar coefficients relating to the compositions:

$$\left\{ \begin{aligned} \beta_{i(ij)}^{k} = \frac{{x_{i} }}{{x_{i} + x_{j} }} \hfill \\ \beta_{j(ij)}^{k} = \frac{{x_{j} }}{{x_{i} + x_{j} }} \hfill \\ \end{aligned} \right.$$

(12)

This is contradictory to the fact that the similar coefficient ($\beta_{i(ij)}^{k}$) only relates to the properties of the treated system.[2,5]

3 A New Perspective on the Geometric Model

In the past, how to choose a reasonable model for the treatment of a given system is a prominent problem, and many efforts have been made by previous researchers,[2,4,5,12] but no satisfying one has been reached. The reason is the lack of thinking about the essence behind in geometric models. In the current section, we try to reinterpret the geometric model from a new perspective.

Assuming a ternary system, i-j-k, consisting of $n_{i}$ mole i, $n_{j}$ mole j, and $n_{k}$ mole k, the total mole number is $n_{i} + n_{j} + n_{k} = n$. The mole fractions are generally defined as,

$$x_{i} = \frac{{n_{i} }}{{n_{i} + n_{j} + n_{k} }} = \frac{{n_{i} }}{n}$$

(13)

If let $n_{ij}^{i}$ and $n_{ij}^{j}$ represent the molar quantity of i and j in the sub-binary i-j, respectively, then the molar fractions, $X_{ij}^{i}$ and $X_{ij}^{j}$, are expressed as follows:

$$\left\{ \begin{aligned} X_{ij}^{i} = \frac{{n_{ij}^{i} }}{{n_{ij}^{i} + n_{ij}^{j} }} \hfill \\ X_{ij}^{j} = \frac{{n_{ij}^{j} }}{{n_{ij}^{i} + n_{ij}^{j} }} \hfill \\ \end{aligned} \right.$$

(14)

In the sub-binary system i-j, the $n_{ij}^{i}$ and $n_{ij}^{j}$ are normally different from $n_{i}$ and $n_{j}$, their values are affected by the third component k. But there are two exceptions: one is under “ideal conditions”, that the component k has no effect on component i and component j, in this case, the $n_{ij}^{i}$ and $n_{ij}^{j}$ are equal to $n_{i}$ and $n_{j}$, respectively. In another case, it is a limiting condition that the component k is identical to i or j. When the component k is identical to the component i, it has $n_{ij}^{i} = n_{i} + n_{k}$ and $n_{ij}^{j} = n_{j}$. When the component k is identical to the component j, it has $n_{ij}^{i} = n_{i}$ and $n_{ij}^{j} = n_{j} + n_{k}$. Between these two cases, the component k is neither identical to i nor to j. If employing $\alpha_{{i\left( {ij} \right)}}^{k}$ and $\alpha_{{j\left( {ij} \right)}}^{k}$ to represent the degree of identity between the component k with i and that of the component k with j, respectively, the $n_{ij}^{i}$ and $n_{ij}^{j}$ can be expressed as follows:

$$\left\{ \begin{aligned} n_{ij}^{i} = n_{i} + \alpha_{i(ij)}^{k} n_{k} \hfill \\ n_{ij}^{j} = n_{j} + \alpha_{j(ij)}^{k} n_{k} \hfill \\ \end{aligned} \right.$$

(15)

In Eq 15, the second term of the right side in each sub-equation is aroused by the third component k, which reflects a contribution effect of the component k on the molar quantity of each component of the sub-binary i-j. Therefore, we call these coefficients ($\alpha_{{i\left( {ij} \right)}}^{k}$ and $\alpha_{{j\left( {ij} \right)}}^{k}$) as contribution coefficients, representing the contributions’ size of the component k to the components i and j in the sub-binary i-j, respectively. It is not difficult to know that these coefficients are dimensionless numbers and need to satisfy $\alpha_{{i\left( {ij} \right)}}^{k} + \alpha_{{j\left( {ij} \right)}}^{k} \le 1$ and $0 \le \alpha_{{i\left( {ij} \right)}}^{k} \le 1$.

Then, dividing $n$ (the total molar number) simultaneously on the left and right side of each sub-equation in Eq 15 and marking the results as $\delta_{ij}^{i}$ and $\delta_{ij}^{j}$, we obtain the following equations.

$$\left\{ \begin{aligned} \delta_{ij}^{i} = \frac{{n_{ij}^{i} }}{n} = x_{i} + \alpha_{i(ij)}^{k} x_{k} \hfill \\ \delta_{ij}^{j} = \frac{{n_{ij}^{j} }}{n} = x_{j} + \alpha_{j(ij)}^{k} x_{k} \hfill \\ \end{aligned} \right.$$

(16)

In Eq 14, substituting the $n_{ij}^{i}$ and $n_{ij}^{j}$ with $n\delta_{ij}^{i}$ and $n\delta_{ij}^{j}$, respectively, then it obtains

$$\left\{ \begin{aligned} X_{ij}^{i} = \frac{{\delta_{ij}^{i} }}{{\delta_{ij}^{i} + \delta_{ij}^{j} }} \hfill \\ X_{ij}^{j} = \frac{{\delta_{ij}^{j} }}{{\delta_{ij}^{i} + \delta_{ij}^{j} }} \hfill \\ \end{aligned} \right.$$

(17)

where $\delta_{ij}^{i} = x_{i} + \alpha_{{i\left( {ij} \right)}}^{k} x_{k}$.

In Eq 17, when $\alpha_{{i\left( {ij} \right)}}^{k} = \alpha_{{j\left( {ij} \right)}}^{k} = 0$, $\delta_{ij}^{i}$ and $\delta_{ij}^{j}$ are equal to $x_{i}$ and $x_{j}$, respectively. $X_{ij}^{i}$ and $X_{ij}^{j}$ are then expressed as:

$$\left\{ \begin{aligned} X_{ij}^{i} = \frac{{x_{i} }}{{x_{i} + x_{j} }} \hfill \\ X_{ij}^{j} = \frac{{x_{j} }}{{x_{i} + x_{j} }} \hfill \\ \end{aligned} \right.$$

(18)

Obviously, Eq 18 is equal to the Kohler type (Eq 9). Similarly, it is not difficult to prove that: (1), when $\alpha_{{i\left( {ij} \right)}}^{k} = \alpha_{{j\left( {ij} \right)}}^{k} = 1/2$, the Eq 17 can be reduced correctly to the Muggianu type (Eq 10); (2), when $\alpha_{{i\left( {ij} \right)}}^{k} + \alpha_{{j\left( {ij} \right)}}^{k} = 1$ and $\alpha_{{i\left( {ij} \right)}}^{k} = 1$ or 0, Eq 17 can be reduced correctly to the Toop type (Eq 7 or Eq 8); and (3), if let $\alpha_{{i\left( {ij} \right)}}^{k} + \alpha_{{j\left( {ij} \right)}}^{k} = 1$ and define them as similar coefficients of Chou’s model,[2,5] the Eq 17 will be reduced to Chou’s model (Eq 11). Therefore, it implies that different geometric models can be well-unified into Eq 17 by introducing contribution coefficients.

Similarly, we can extend this perspective to an N-component (N > 3) system, the general compositions of sub-binary i-j are expressed as follows.

$$X_{ij}^{i} = \frac{{\delta_{ij}^{i} }}{{\delta_{ij}^{i} + \delta_{ij}^{j} }}$$

(19)

with

$$\delta_{ij}^{i} = x_{i} + \sum\limits_{k \ne i,j}^{n} {\alpha_{i(ij)}^{k} x_{k} }$$

where the summation is the contributions by all third components k (k = 1,2,3,…, n) to the component i in the selected sub-binary i-j, the $\alpha_{{i\left( {ij} \right)}}^{k}$ is the corresponding contribution coefficient of the component k to the component i.

4 Discussion

Through introducing the perspective that the molar compositions of the selected sub-binary in ternary system are affected by the third component, i.e., the third component arises a contribution effect on the molar quantity of the other two components in the sub-binary and the magnitude of this effect is represented by contribution coefficients, a new model (Eq 17 and/or Eq 19) is deduced. This new model can be mathematically reduced to all geometric models. Consequently, the problem how to choose a geometric model for treating a given ternary system can be transformed into how to deal with the contribution coefficients of the third component to the others in the selected sub-binary systems.

4.1 The Values of the Contribution Coefficients

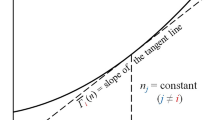
From the perspective of the contribution, in previous models,[3,6,7,8,9,18] the contribution coefficients of the third component to the components of the selected sub-binary are normally set to constants without any reasons. For example, in the Kohler type (Eq 9), the two contribution coefficients are both equal to 0; in the Muggianu type (Eq 10), they are both equal to 1/2; and in the Toop type (Eq 7 and Eq 8), one is 0 and the other one is 1; in Chou’s model (Eq 11), the two contribution coefficients are restricted by their sum of 1.

However, in fact, the values of the contribution coefficients should depend on the degree of identity in the thermodynamic properties of the third component with those of the selected components in the sub-binary. For example, the value of $\alpha_{{i\left( {ij} \right)}}^{k}$ is correlated to the degree of identity in thermodynamic properties between the component k and component i. But to be exact, its value should rely on the degree of identity between the thermodynamic properties of the component k interacting with the component j and those of the component i interacting with j. Because in the selected binary i-j, the part of the component k as a contribution to the component i will interact with the component j just like the component i. If let $\xi_{j}^{k}$ and $\xi_{j}^{i}$ represent the thermodynamic properties of k interacting with j and those of i interacting with j, respectively, then the thermodynamic properties’ identity of the component k with i in the sub-binary i-j is correlated to $- \left| {\xi_{j}^{k} - \xi_{j}^{i} } \right|$, where the $\left| {\xi_{j}^{k} - \xi_{j}^{i} } \right|$ represents the deviation in the thermodynamic properties of k interacting with j from those of the component i interacting with the component j. Here, it needs to emphasize that $\xi_{j}^{k} \ne \xi_{k}^{j}$, which means that this interaction is directional. Considering that the contribution coefficients $\alpha_{{i\left( {ij} \right)}}^{k}$ and $\alpha_{{i\left( {ij} \right)}}^{k}$ need to satisfy the relation of $0 \le \alpha_{{i\left( {ij} \right)}}^{k} + \alpha_{{j\left( {ij} \right)}}^{k} \le 1$ and $0 \le \alpha_{{i\left( {ij} \right)}}^{k} \le 1$, as well as when the component k is identical to the component j(i), the $\alpha_{{i\left( {ij} \right)}}^{k} = 0\left( 1 \right)$, the contribution coefficient $\alpha_{{i\left( {ij} \right)}}^{k}$ can be expressed as follows.

$$\alpha_{i(ij)}^{k} = \frac{{\left| {\xi_{i}^{k} - \xi_{i}^{j} } \right|}}{{\left| {\xi_{i}^{k} - \xi_{i}^{j} } \right| + \left| {\xi_{j}^{k} - \xi_{j}^{i} } \right|}}\exp \left( { - \left| {\xi_{j}^{k} - \xi_{j}^{i} } \right|} \right)$$

(20)

The thermodynamic properties of the component k interacting with j can be represented by the partial molar excess thermodynamic properties of k in the binary system j-k, where the concentration of k is at infinitely dilute, as follows:

$$\xi_{j}^{k} = \frac{1}{RT}\left. {G_{k(jk)}^{E} } \right|_{{x_{k} \to 0}}$$

(21)

where R and T are the gas constant and absolute temperature, respectively; $G_{k(jk)}^{E}$ is the partial molar excess thermodynamic properties of k, the subscript $x_{k} \to 0$ represents the molar fraction of k at infinitely approaching 0.

4.2 The Characterizations of the Present Model

In Eq 20, when $\left| {\xi_{j}^{k} - \xi_{j}^{i} } \right| = 0$, it would result in the $\alpha_{i(ij)}^{k} = 1$ and $\alpha_{j(ij)}^{k} = 0$, in this case, the present model (Eq 17) would be reduced to the Toop type (Eq 7), in which j is chosen as the asymmetric component. When $\left| {\xi_{i}^{k} - \xi_{i}^{j} } \right| = 0$, it would result in another type of Toop model (Eq 8), in which i is chosen as the asymmetric component). That is to say, when the thermodynamic properties of the component k interacting with j(i) are the same to those of i(j) interacting with j(i), the present model would be reduced to the Toop type (Eq 7).

When $\left| {\xi_{j}^{k} - \xi_{j}^{i} } \right| \to \infty$ and $\left| {\xi_{i}^{k} - \xi_{i}^{j} } \right| \to \infty$, it would result in that $\alpha_{i(ij)}^{k} \to 0$ and $\alpha_{j(ij)}^{k} \to 0$, in this case the present model will close to the Kohler type (Eq 9). This implies that when the thermodynamic properties of component k have a large deviation from those of the component i and component j, the present model will be identical to the Kohler type (Eq 9).

Similarly, when $\left| {\xi_{j}^{k} - \xi_{j}^{i} } \right| \approx \left| {\xi_{i}^{k} - \xi_{i}^{j} } \right| \to 0$, but not equal to 0, the present model would approached the Muggianu type (Eq 10).

In addition, any reasonable model should meet the basic requirement[6] that under the limiting conditions the model is able to reduce to its limiting form. That is, if two components in a ternary system are identical, but their concentrations are not, a reasonable model should be able to be mathematically reduced to a binary solution model. The present model meets this requirement. For example, in a ternary i-j-k, if the component i is identical to j but $x_{i} \ne x_{j}$, since, in fact, there are only two components i(j) and k in the system, its thermodynamic properties $\Delta G_{ijk}^{E}$ should be reduced to as follows.

$$\Delta G_{ijk}^{E} = \Delta G_{ik}^{E} \left( {x_{i} + x_{j} ;x_{k} } \right)\quad {\text{or}}\quad \Delta G_{ijk}^{E} = \Delta G_{jk}^{E} \left( {x_{i} + x_{j} ;x_{k} } \right)$$

(22)

According to Eq 1, the $\Delta G_{ijk}^{E}$ is

$$\Delta G_{ijk}^{E} = \frac{{x_{i} x_{j} }}{{X_{ij}^{i} X_{ij}^{J} }}\Delta G_{ij}^{E} \left( {X_{ij}^{i} ;X_{ij}^{i} } \right) + \frac{{x_{i} x_{k} }}{{X_{ik}^{i} X_{ik}^{k} }}\Delta G_{ik}^{E} \left( {X_{ik}^{i} ;X_{ik}^{k} } \right) + \frac{{x_{j} x_{k} }}{{X_{jk}^{j} X_{jk}^{k} }}\Delta G_{jk}^{E} \left( {X_{jk}^{j} ;X_{jk}^{k} } \right)$$

(23)

Because the component i is identical to j, $\Delta G_{ij}^{E} \left( {X_{ij}^{i} ;X_{ij}^{i} } \right) = 0$; and in the sub-binary i-k, $\alpha_{i(ik)}^{j} = 1$ and $\alpha_{k(ik)}^{j} = 0$, and in the sub-binary j-k, $\alpha_{j(jk)}^{i} = 1$ and $\alpha_{k(jk)}^{i} = 0$. Therefore, based on Eq 17 or Eq 19, the $X_{ik}^{i}$, $X_{ik}^{k}$, $X_{jk}^{j}$, and $X_{jk}^{k}$ can be expressed as follows.

$$\left\{ \begin{aligned} & X_{ik}^{i} = \frac{{x_{i} + x_{j} }}{{x_{i} + x_{k} + x_{j} }} = x_{i} + x_{j} \\ & X_{ik}^{k} = 1 - X_{ik}^{i} = x_{k} \\ \end{aligned} \right.\quad {\text{and}}\quad \left\{ \begin{aligned} & X_{jk}^{j} = \frac{{x_{j} + x_{i} }}{{x_{j} + x_{k} + x_{i} }} = x_{j} + x_{i} \\ & X_{jk}^{k} = 1 - X_{jk}^{j} = x_{k} \\ \end{aligned} \right.$$

(24)

By introducing Eq 23, then one obtains

$$\Delta G_{ijk}^{E} = \frac{{x_{i} x_{k} }}{{\left( {x_{i} + x_{j} } \right)x_{k} }}\Delta G_{ik}^{E} \left( {x_{i} + x_{j} ;x_{k} } \right) + \frac{{x_{i} x_{k} }}{{\left( {x_{i} + x_{j} } \right)x_{k} }}\Delta G_{jk}^{E} \left( {x_{i} + x_{j} ;x_{k} } \right)$$

(25)

Because i = j, $\Delta G_{ik}^{E} \left( {x_{i} + x_{j} ;x_{k} } \right) = \Delta G_{jk}^{E} \left( {x_{i} + x_{j} ;x_{k} } \right)$, therefore Eq 25 can be simplified as follows.

$$\Delta G_{ijk}^{E} = \left( {\frac{{x_{i} x_{k} }}{{\left( {x_{i} + x_{j} } \right)x_{k} }} + \frac{{x_{i} x_{k} }}{{\left( {x_{i} + x_{j} } \right)x_{k} }}} \right)\Delta G_{ik}^{E} \left( {x_{i} + x_{j} ;x_{k} } \right) = \Delta G_{ik}^{E} \left( {x_{i} + x_{j} ;x_{k} } \right)$$

(26)

Clearly, the present model can be reasonably reduced to a binary solution model in a limiting condition.

5 Examples of Application

Combining the Miedema model[16] with a geometric model to predict the activity interaction parameters[20] in ternary alloys has proved to be very effective.[13,14,15,21] In this section, the calculation of the activity interaction parameters in iron-based alloys is used as an example for the application of the present model. The calculated results are compared with those calculated with the Muggianu model[9] and available experimental data. The calculation formulas of activity interaction parameters by combining the Miedema model[16] and geometric model are given in Appendix.

In the binary system k-j, the partial molar excess thermodynamic properties of the component k at its infinite dilution have the following relationship with its logarithm of infinite dilution activity coefficient,

$$\left. {\frac{{\partial G_{k(jk)}^{E} }}{{\partial x_{k} }}} \right|_{{x_{k} \to 0}} = RT\ln \gamma_{{k({\text{in }}j )}}^{0}$$

(27)

Therefore, Eq 21 can be rewritten as follows:

$$\xi_{j}^{k} = \ln \gamma_{{k({\text{in }}j)}}^{0}$$

(28)

Similarly,

$$\xi_{j}^{i} = \ln \gamma_{{i({\text{in }}j)}}^{0}$$

(29)

$$\xi_{i}^{k} = \ln \gamma_{{k({\text{in }}i)}}^{0}$$

(30)

$$\xi_{i}^{j} = \ln \gamma_{{j({\text{in }}i)}}^{0}$$

(31)

In the present calculation, the values of $\ln \gamma_{{k({\text{in }}j)}}^{0}$ are estimated by the following equation,[13,15] $\ln \gamma_{{i({\text{in }}j)}}^{0}$, $\ln \gamma_{{k({\text{in }}i)}}^{0}$, and $\ln \gamma_{{j({\text{in }}i)}}^{0}$ can be obtained in the similar way.

$$\ln \gamma_{{k({\text{in }}j)}}^{0} = \frac{ 1}{RT}f_{jk} V_{k}^{2/3} \left\{ {1 + u_{k} \left( {\phi_{k}^{*} - \phi_{j}^{*} } \right)} \right\}$$

(32)

where

$$f_{jk} = \frac{2p}{{\left( {n_{ws}^{1/3} } \right)_{k}^{ - 1} + \left( {n_{ws}^{1/3} } \right)_{j}^{ - 1} }} \times \left[ {9.4\left( {(n_{ws}^{1/3} )_{j} - (n_{ws}^{1/3} )_{k} } \right)^{2} - \left( {\phi_{j}^{*} - \phi_{k}^{*} } \right)^{2} - 0.73r_{jk} } \right]$$

In Eq 32, the parameters $n_{ws}$, $\phi^{*}$, and $V$ are the electronic density (in density unity), the electronegative (in V), and the molar volume (in cm³) of an element, respectively; $p$ and $r$ are parameters related to the constituent; $u$ is a constant depending on the type of metal. The values of all above parameters can be found in the Miedema et al’ article.[16]

So far, the contribution coefficients can be calculated by using Eq 20 and Eq 28–32. Values of the contribution coefficients in some alloy systems are listed in Table 1. From Table 1, it is easy to find that in systems with large differences in properties of the constituents, the contribution coefficients are small (e.g. the Fe-C-Ca alloy system), while in systems with a small difference (e.g. the Fe-Mn-Co alloy system), they are large. It should be emphasized again that the contribution coefficient ($\alpha_{{i\left( {ij} \right)}}^{k}$) in nature weights the degree of identity between the thermodynamic properties of the two components (k and i). We call this parameter as a contribution coefficient ($\alpha_{{i\left( {ij} \right)}}^{k}$), just because the result seems to be a contribution of the third component (k) to the molar compositions of the selected component (i) in the sub-binary (i-j).

Table 1 Values of contribution coefficients in some alloy systems at 1873 K

Figure 3 shows the comparisons of calculated values and experimental data for the activity interaction parameters in the alloy systems of Fe-C-j (Fig. 3a) and Fe-Mn-j (Fig. 3b) at 1873 K, where j is from the fourth periodic element, the calculated values are from the present model and from the Muggianu model,[9] the experimental data are from the recommended values of the Japan Society for the Promotion of Science (JSPS).[22] It can be seen from Fig. 3, the Muggianu model[9] is only applicable to systems with small differences in the properties of the constituents (e.g. Fe-Mn-j, where j is the fourth periodic element), while the present model has good applicability in systems with large or small differences in the properties of the constituents (e.g. Fe-C-j and Fe-Mn-j, where j is the fourth periodic element). This is because the differences of thermodynamic properties between in components are fully considered in the present model.

Fig. 3

Comparisons of model calculated values and experimental data of activity interaction parameters $\varepsilon_{i}^{j}$ ($\varepsilon_{C}^{j}$ in (a) and $\varepsilon_{\text{Mn}}^{j}$ in (b)) in liquid iron at 1873 K. Black squares represent the corresponding values calculated by applying the Muggianu model[9] coupled with the Miedema model[16]; red circles represent the corresponding values calculated by the present model coupled with the Miedema model[16]; blue triangles represent experimental data recommended by the Japan Society for the Promotion of Science[22] (Color figure online)

6 Conclusions

By introducing a new perspective of the molar compositions of the sub-binary in a multi-component system affected by the third component, a general model is deduced. The new model can be mathematically reduced to all other geometric models (Kohler, Muggianu, and Toop-Kohler, etc.).

In the present model, the general compositions of the sub-binary i-j in the multicomponent system i-j-k-… can be expressed as follows.

$$X_{ij}^{i} = \frac{{\delta_{ij}^{i} }}{{\delta_{ij}^{i} + \delta_{ij}^{j} }}$$

with

$$\delta_{ij}^{i} = x_{i} + \sum\limits_{k \ne i,j}^{n} {\alpha_{i(ij)}^{k} x_{k} }$$

where the summation is a contribution term by all third components k to the component i of the selected sub-binary i-j, and the $\alpha_{{i\left( {ij} \right)}}^{k}$ is the corresponding contribution coefficient. The contribution coefficient $\alpha_{{i\left( {ij} \right)}}^{k}$ is a dimensionless parameter and satisfies $0 \le \alpha_{{i\left( {ij} \right)}}^{k} \le 1$ and $\alpha_{{i\left( {ij} \right)}}^{k} + \alpha_{{j\left( {ij} \right)}}^{k} \le 1$. The value of $\alpha_{{i\left( {ij} \right)}}^{k}$ depends on the degree of identity between the thermodynamic properties of the component k and the component i relative to the component j, and its mathematical definition is given in the text (Eq 20).

Appendix: Calculation Formula of Activity Interaction Parameters

In a ternary system i-j-k, where k is the solvent, the activity interaction parameters[20] can be expressed as follows,[13,15] at a certain temperature T.

$$\varepsilon_{i}^{j} = \frac{1}{RT}\left. {\frac{{\partial^{2} G^{E} }}{{\partial x_{i} \partial x_{j} }}} \right|_{{x_{k} \to 1}}$$

(33)

where $\varepsilon_{i}^{j}$ is the first-order activity interaction parameter; $x_{i}$ and $x_{j}$ are the molar fractions of the elements i and j in the solution; $G^{E}$ is the integral molar excess Gibbs free energy of the ternary system, it can be obtained according to the Eq 1 and 2, as follows.

$$\begin{aligned} G^{E} = & \frac{{x_{i} x_{j} }}{{X_{ij}^{i} \left( {1 - X_{ij}^{i} } \right)}}G_{ij}^{E} \left( {X_{ij}^{i} ,1 - X_{ij}^{i} } \right) + \frac{{x_{i} x_{k} }}{{X_{ik}^{i} \left( {1 - X_{ik}^{i} } \right)}}G_{ik}^{E} \left( {X_{ik}^{i} ,1 - X_{ik}^{i} } \right) \\ & \quad + \,\frac{{x_{j} x_{k} }}{{X_{jk}^{j} \left( {1 - X_{jk}^{j} } \right)}}G_{jk}^{E} \left( {X_{jk}^{j} ,1 - X_{jk}^{j} } \right) \\ \end{aligned}$$

(34)

where the capital $X_{ij}^{i}$ is the molar fraction of the component i in the selected sub-binary system i-j, and its value is calculated by the present model as follows.

$$X_{ij}^{i} = \frac{{\delta_{ij}^{i} }}{{\delta_{ij}^{i} + \delta_{ij}^{j} }}$$

(35)

where $\delta_{ij}^{i} = x_{i} + \alpha_{i(ij)}^{k} x_{k}$.

In a dilute metallic solution, the excess entropy is ignorable,[13, 15] then the excess Gibbs free energy can be represented by its mixing enthalpy. For example, in the i-j binary, we obtain

$$G_{ij}^{E} = H_{ij}^{\text{Mix}}$$

(36)

In a binary system i-j, the mixing enthalpy can be obtained by the Miedema model[16] and its mathematical expression in liquid alloys is expressed as follows:

$$\Delta H_{ij}^{\text{Mix}} \left( {X_{ij}^{i} ,X_{ij}^{j} } \right) = f_{ij} \frac{{X_{ij}^{i} X_{ij}^{j} V_{{i{\text{a}}}}^{2/3} V_{{j{\text{a}}}}^{2/3} }}{{X_{ij}^{i} V_{{i{\text{a}}}}^{2/3} + X_{ij}^{j} V_{{j{\text{a}}}}^{2/3} }}$$

(37)

$$\left\{ \begin{aligned} V_{{i{\text{a}}}}^{2/3} = V_{i}^{2/3} \left[ {1 + u_{i} \left( {\phi_{i}^{*} - \phi_{j}^{*} } \right)\frac{{X_{ij}^{j} V_{ja}^{2/3} }}{{X_{ij}^{j} V_{ja}^{2/3} + X_{i} V_{ia}^{2/3} }}} \right] \hfill \\ V_{{j{\text{a}}}}^{2/3} = V_{j}^{2/3} \left[ {1 + u_{j} \left( {\phi_{j}^{*} - \phi_{i}^{*} } \right)\frac{{X_{ij}^{i} V_{ia}^{2/3} }}{{X_{ij}^{j} V_{ja}^{2/3} + X_{ij}^{i} V_{ia}^{2/3} }}} \right] \hfill \\ \end{aligned} \right.$$

(38)

Then, by combining Eq 33–38, we derive a calculation formula for the activity interaction parameters in a dilute metallic solution,

$$\varepsilon_{i}^{j} = \frac{1}{RT}\left( {A_{ij} - A_{ik} - A_{jk} + B_{ik} + B_{jk} } \right)$$

(39)

where

$$\begin{aligned} & A_{ij} = f_{ij} \frac{{V_{i}^{2/3} V_{j}^{2/3} \left( {\alpha_{i(ij)}^{k} + \alpha_{j(ij)}^{k} } \right)\left[ {1 + u_{i} (\phi_{i}^{*} - \phi_{j}^{*} )\frac{{\alpha_{j(ij)}^{k} }}{{\alpha_{i(ij)}^{k} + \alpha_{j(ij)}^{k} }}} \right]\left[ {1 + u_{j} (\phi_{j}^{*} - \phi_{i}^{*} )\frac{{\alpha_{i(ij)}^{k} }}{{\alpha_{i(ij)}^{k} + \alpha_{j(ij)}^{k} }}} \right]}}{{\alpha_{i(ij)}^{k} V_{i}^{2/3} \left[ {1 + u_{i} (\phi_{i}^{*} - \phi_{j}^{*} )\frac{{\alpha_{j(ij)}^{k} }}{{\alpha_{i(ij)}^{k} + \alpha_{j(ij)}^{k} }}} \right] + \alpha_{j(ij)}^{k} V_{j}^{2/3} \left[ {1 + u_{j} (\phi_{j}^{*} - \phi_{i}^{*} )\frac{{\alpha_{i(ij)}^{k} }}{{\alpha_{i(ij)}^{k} + \alpha_{j(ij)}^{k} }}} \right]}} \\ & A_{ik} = f_{ik} V_{i}^{2/3} \left[ {1 + u_{i} \left( {\phi_{i}^{*} - \phi_{k}^{*} } \right)} \right] \\ & A_{jk} = f_{jk} V_{j}^{2/3} \left[ {1 + u_{j} \left( {\phi_{j}^{*} - \phi_{k}^{*} } \right)} \right] \\ & B_{ik} = f_{ik} \alpha_{i(ik)}^{j} \left\{ {1 - \frac{{V_{i}^{2/3} }}{{V_{k}^{2/3} }}\left[ {1 + 2u_{i} \left( {\phi_{i}^{*} - \phi_{k}^{*} } \right)} \right]} \right\}V_{i}^{2/3} \left[ {1 + u_{i} (\phi_{i}^{*} - \phi_{k}^{*} )} \right] \\ & B_{jk} = f_{jk} \alpha_{j(jk)}^{i} \left\{ {1 - \frac{{V_{j}^{2/3} }}{{V_{k}^{2/3} }}\left[ {1 + 2u_{j} \left( {\phi_{j}^{*} - \phi_{k}^{*} } \right)} \right]} \right\}V_{j}^{2/3} \left[ {1 + u_{j} (\phi_{j}^{*} - \phi_{k}^{*} )} \right] \\ \end{aligned}$$

${\text{f}}_{\text{ij}}$, ${\text{f}}_{\text{ik}}$, and ${\text{f}}_{\text{jk}}$ are defined as follows:

$$\begin{aligned} & f_{ij} = \frac{2p}{{\left( {n_{ws}^{1/3} } \right)_{i}^{ - 1} + \left( {n_{ws}^{1/3} } \right)_{j}^{ - 1} }} \times \left[ {9.4\left( {(n_{ws}^{1/3} )_{i} - (n_{ws}^{1/3} )_{j} } \right)^{2} - \left( {\phi_{i}^{*} - \phi_{j}^{*} } \right)^{2} - 0.73r_{ij} } \right] \\ & f_{ik} = \frac{2p}{{\left( {n_{ws}^{1/3} } \right)_{i}^{ - 1} + \left( {n_{ws}^{1/3} } \right)_{k}^{ - 1} }} \times \left[ {9.4\left( {(n_{ws}^{1/3} )_{i} - (n_{ws}^{1/3} )_{k} } \right)^{2} - \left( {\phi_{i}^{*} - \phi_{k}^{*} } \right)^{2} - 0.73r_{ik} } \right] \\ & f_{jk} = \frac{2p}{{\left( {n_{ws}^{1/3} } \right)_{k}^{ - 1} + \left( {n_{ws}^{1/3} } \right)_{j}^{ - 1} }} \times \left[ {9.4\left( {(n_{ws}^{1/3} )_{j} - (n_{ws}^{1/3} )_{k} } \right)^{2} - \left( {\phi_{j}^{*} - \phi_{k}^{*} } \right)^{2} - 0.73r_{jk} } \right] \\ \end{aligned}$$

In Eq 39, the parameters $n_{ws}$, $\phi^{*}$, and $V$ are the electronic density (in density unity), the electronegative (in V), and the molar volume (in cm³) of the element, respectively; $p$ and $r$ are parameters related to the constituents; $u$ is a constant whose value depends on the type of metal. The values of all above parameters can be found in Miedema et al’ article.[16] The contribution coefficient $\alpha_{i(ij)}^{k}$ is calculated by Eq 20.

In Eq 39, if all the contribution coefficients ($\alpha_{i(ij)}^{k}$, $\alpha_{i(ij)}^{k}$,$\alpha_{i(ik)}^{j}$, and $\alpha_{j(jk)}^{i}$) are equal to ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}$, then one obtains the formula of activity interaction parameters which is deduced by coupling the Miedema model[16] with the Muggianu model.[9]