Introduction

Ti belongs to the IV-B group of the periodical table, which crystallizes in a hcp (α) structure at low temperature and translates to a bcc (β) structure at high temperature. Most of (α + β) and β type commercial titanium alloys contain element Sn, because the addition of Sn in titanium alloys has no effect on α to β transformation temperature. β-Ti alloys are widely used as biomedical materials due to the low density, high strength, and low elasticity modulus. In addition, α-Ti alloys also have the widespread use in the industries. Knowledge of diffusion can be very helpful in optimizing material microstructure and understanding some basic processes. Mathematical modeling of various kinetic processes in alloy is necessary in material designs, because simulation can study some important issues. Besides, simulation could estimate the unknown important diffusion data from available data. Combined with thermodynamic parameters, the atomic mobility parameters can be calculated to simulate problems of interest. This work is to assess the atomic mobilities of Ti-Sn alloy by the CALPHAD procedure using the DICTRA software, which based on the available experiment information in the literatures, and the result can provide a useful help for the design of Ti-based alloys.

Literature Review

Some authors have researched the impurity diffusion of Sn in bcc Ti. Murdock et al.[1] studied the self-diffusion coefficients of Ti44 in titanium. Walsöe et al.[2] tested the self-diffusion coefficients of Ti44 in bcc-Ti at the temperature of 1173 to 1853 K by the sectioning method. Gerold and Herzig[3] measured the self-diffusion coefficients of Ti44 in bcc-Ti at 1607, 1681 and 1829 K, using penetration experiments and a section method. Liu et al.[4] assessed it in the Ti-V system. Askill et al.[5] measured the tracer diffusion of Sn113 in bcc-Ti. Seventeen impurity diffusion coefficients at eleven different temperatures from 1226 to 1868 K were tested. According to the Arrhenius equation D = D 0exp(−Q/RT), at the temperature lower than 1473 K the frequency factor D 0 is 3.8 × 10−8 m2/s and activation energy Q is 1.32 × 105 J/mol, while at temperature higher than 1473 K D 0 is 9.5 × 10−4 m2/s and Q is 1.32 × 105 J/mol, where R is the gas content and T is temperature in Kelvin. Iikima et al.[6] tested and analyzed the diffusion of Sn in bcc Ti at the temperature from 1173 to 1823 K using the pure Ti and Ti-1.65 at.%Sn diffusion couples. The diffusion coefficient is expressed as the Koehler and Herzig model,[7] \( D = D_{0} { \exp }\left( { - \frac{Q}{RT}} \right){ \exp }\left( {\frac{{G_{0}^{M} T_{0} }}{{RT^{2} }}} \right) \), where D 0 is the activation energy, Q is the frequency factor and \( G_{0}^{M} \) is free energy for migration of monovacancy. The result of diffusion coefficients of Sn in β-Ti is expressed as D = 6.9 × 10−5 (m2/s)exp{−301(KJ/mol)/RT} × exp{110(MJK/mol)/RT 2}. Araki et al.[8] studied the diffusion coefficients of Sn in bcc-Ti at temperature from 1173 to 1773 K on the pressure of 0.1 Mpa to 2.8 Gpa using the Ti/Ti-4.9 at.%Sn diffusion couples. The interdiffusion coefficient of Sn in bcc-Ti is also expressed as the Koehler and Herzig model. At 0.1 Mpa D is 2.69 × 10−4 (m2/s)exp{−329(KJ/mol)/RT} × exp{126(MJK/mol)/RT 2}. Neumann et al.[9] analyzed the impurity diffusion of Sn in β-Ti on the basis of the assumption that the vacancy-migration enthalpy and the vacancy-formation enthalpy depend on temperature. The diffusion model is expressed as, \( D = D_{0} { \exp }\left( { - \frac{Q}{RT}} \right) \times { \exp }\left( {2\alpha { \ln }\frac{T}{{T_{0} }} - 2\alpha \frac{{T - T_{0} }}{{T_{0} }}} \right) \), where D 0 is the activation energy, Q is the frequency factor, R is gas constant, T 0 is a reference temperature lower than the Debye temperature, and the dimensionless constant α is a measure for the curvature of the Arrhenius plot of D. The fitting α is 7.4, D 0 is 9.8 × 10−6 m2/s and Q is 209.5 kJ/mol. The Neumann model is well agreed with the impurity diffusion of Sn in bcc Ti experiment data, which will be used in the assessed work.

As for the hcp phase in Ti-Sn system, the interdiffusion coefficients have still not been found in reports until now, however, the self-diffusion of hcp-Ti and impurity diffusion of Sn in hcp-Ti can be found in some literatures. Self-diffusion in an extended temperature range in low pure hcp-Ti was measured by Herzig et al.[10] The self-diffusion of Ti of 99.9% (40 at ppm of Fe content) in the range of 776 to 1132 K was measured by Pérez et al.[11] using the intergrated backscatter (IBS) technique. The self-diffusion of high purity hcp-Ti was measured by Köppers et al.[12] Pérez et al.[13] had previously performed measurements of diffusion of Sn in less pure hcp-Ti with the same Backscattering Spectrometry (RBS) technique. The impurity diffusion of Sn in high purity (99.99%) and less purity hcp-Ti (99.9%) was measured by Pérez et al.[14]

Modeling Description

According to the Fick-Onsager law, the diffusion flux J k of specie k is a function of chemical potential gradients in a substitutional solution containing n components. It can be written as

$$ J_{k} = - \sum\limits_{i = 1}^{n} {L_{ki} \frac{{\partial \mu_{i} }}{\partial z}} = \sum\limits_{i = 1}^{n} {L_{ki} \frac{{\partial \mu_{i} }}{{\partial c_{j} }}\frac{{\partial c_{j} }}{\partial z}} $$
(1)

Where L kj is the phenomenological factor; μ i is the chemical potential of specie k; z is the distance. Generally, J k is convenient to be expressed as functions of concentration gradients. When the interdiffusion coefficient \( D_{kj}^{n} \) is introduced, it could be expressed as

$$ J_{k} = - \sum\limits_{j = 1}^{n - 1} {D_{kj}^{n} } \frac{{\partial c_{j} }}{\partial z} $$
(2)

where c j denotes the concentration of the specie j in moles per volume; the summation is made over n − 1 dependent concentration variants of solutes, and the n independent one is treated as solvent; \( D_{kj}^{n} \) in a substitutional solution phase is given as[15,16]

$$ D_{kj}^{n} = \sum\limits_{i}^{n} {\left( {\delta_{ik} - x_{k} } \right)} x_{i} M_{i} \left( {\frac{{\partial \mu_{i} }}{{\partial x_{j} }} - \frac{{\partial \mu_{i} }}{{\partial x_{n} }}} \right) $$
(3)

where \( \delta_{ik} \) is the Kronecker delta, i.e., \( \delta_{ik} \) = 1 when j = k and 0 otherwise. x i is the mole fraction of the element i. M i is the atomic mobility of the element i, which can be expressed as function of an frequency factor \( M_{i}^{0} \) and an activation enthalpy Q i , as given by Eq (4).[17,18]

$$ M_{i} = { \exp }\left( {\frac{{{RT}{\text{ln}}M_{i}^{0} }}{RT}} \right){ \exp }\left( {\frac{ - Q}{RT}} \right)\frac{1}{RT}^{\text{mg}}\Omega = { \exp }\left( {\frac{{{RT}{\text{ln}}M_{i}^{0} - Q_{i} }}{RT}} \right)\frac{1}{RT} $$
(4)

Here R is the gas constant and T is the temperature. \( {}^{\text{mg}}\varOmega \) is the correction factor considering the contribution of ferromagnetic transition to diffusion, which could be neglected as no ferromagnetic transition has been reported in the Ti-Sn system. Introducing the parameter \( \Delta G_{i}^{\varphi } \), it can be expressed as

$$ M_{i} = { \exp }\left( {\frac{{\Delta G_{i}^{\varphi } }}{RT}} \right)\frac{1}{RT} $$
(5)

The expression of \( \Delta G_{i}^{\phi } \) for the Ti-Sn system can be assumed to be a function of composition in the form of Redlich-Kister polynomial suggested by Andersson and Agren.[16] It is expressed as follows.

$$ \Delta G_{i}^{\varphi } = x_{\text{Ti}} \Delta G_{i}^{\text{Ti}} + x_{\text{Sn}} \Delta G_{i}^{\text{Sn}} + x_{\text{Ti}} x_{\text{Sn}} \sum\limits_{j = 0}^{n} {\Delta^{(j)} } G_{i}^{\text{Ti,Sn}} \left( {x_{\text{Ti}} - x_{\text{Sn}} } \right)^{j} $$
(6)

where \( \varphi \) represents the solid solution phase. \( \Delta G_{i}^{\text{Ti}} \). and \( \Delta G_{i}^{\text{Sn}} \) are the value of \( \Delta G_{i}^{\varphi } \). for pure Ti and pure Sn, respectively. \( \Delta^{(j)} G_{i}^{\text{Ti,Sn}} \) is the binary interaction term for diffusion between Ti and Sn.

The tracer diffusion of element i, \( D_{i}^{*} \) is directly related to the mobility \( M_{i} \).by means of Einstein relation.

$$ D_{i}^{*} = {\text{RTM}}_{i} $$
(7)

The interdiffusion coefficient \( \tilde{D} \) can be written as following function to calculate the chemical potential according to Darken’s equation.[19]

$$ \tilde{D} = \left( {x_{\text{Ti}} D_{\text{Sn}}^{*} + x_{\text{Sn}} D_{\text{Ti}}^{*} } \right)\varphi $$
(8)

where \( \varphi \) is thermodynamic factor and it can be expressed as:

$$ \varphi = 1 + \frac{{d{ \ln }\gamma_{\text{Ti}} }}{{d{ \ln }x_{\text{Ti}} }} = \frac{{x_{\text{Ti}} }}{RT}\frac{{\partial \mu_{\text{Ti}} }}{{\partial \mu_{\text{Ti}} }} = \frac{{x_{\text{Ti}} (1 - x_{\text{Ti}} )}}{RT}\frac{{d^{2} G_{\text{m}} }}{{dx_{\text{Ti}}^{2} }} = 1 + \frac{{d{ \ln }\gamma_{\text{Sn}} }}{{d{ \ln }x_{\text{Sn}} }} = \frac{{x_{\text{Sn}} }}{RT}\frac{{\partial \mu_{\text{Sn}} }}{{\partial \mu_{\text{Sn}} }} = \frac{{x_{\text{Sn}} (1 - x_{\text{Sn}} )}}{RT}\frac{{d^{2} G_{\text{m}} }}{{dx_{\text{Sn}}^{2} }} $$
(9)

Here, μ Ti, μ Sn, γ Ti, γ Sn, x Ti, and x Sn are the chemical potential, activity coefficient and mole fraction of Ti and Sn, respectively. G m is the molar Gibbs energy.

Result and Discussion

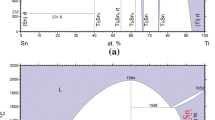
To perform good assessment of the atomic mobilities in bcc and hcp phases in Ti-Sn system, reasonable thermodynamic parameters must be selected to calculate the thermodynamic factor, the accuracy of which has a great influence on the atomic mobilities. Thermodynamic description of bcc and hcp Ti-Sn alloys in this work is obtained from Yin et al.[20] for the good agreement with experiments, phase diagram and thermodynamic properties. The calculated phase diagram of Ti-Sn and the calculated thermodynamic factor of bcc and hcp phase at different temperatures are presented in Fig. 1, 2 and 3, respectively.

Fig. 1
figure 1

The calculated phase diagram of Ti-Sn system from Yin et al.[20]

Full size image
Fig. 2
figure 2

Thermodynamic factor of bcc phase at different temperature

Full size image
Fig. 3
figure 3

Thermodynamic factor of hcp phase at different temperature

Full size image

Self-diffusivities of bcc-Ti and impurity diffusivities of Sn in bcc-Ti were taken from the work of Liu et al.[4] and Neumann et al.,[9] respectively. A good agreement is found between the calculated impurity diffusivities of Sn in bcc-Ti[9] and the experimental data,[5-8] as Fig. 4 shows.

Fig. 4
figure 4

Comparison between calculated impurity diffusion coefficients[9] of Sn in the Ti-Sn system at different temperatures and experimental data[5,6,8]

Full size image

Self-diffusivities of hcp-Ti and impurity diffusivities of Sn in hcp-Ti were from the study of Pérez et al.[14] The calculated results of impurity diffusivities of Sn in hcp-Ti[11,14] compared with the experimental data[13] is listed in Fig. 5, which shows a good agreement. According to the Ti-Sn phase diagram, bcc-Sn and hcp-Sn are the hypothetical phases, the self-diffusivities of which cannot be tested by experiments. Fortunately, the self-diffusivities of bcc-Sn and hcp-Sn can be calculated by the empirical relation suggested by Askill et al.[21] The empirical relation is given as:

$$ Q_{i} = RT_{\text{m}} (K + 1.5\,V) $$
(10)
$$ M_{i}^{0} = 1.04 \times 10^{ - 3} Q_{i} \alpha^{2} $$
(11)

where K is the crystal structure factor, V is the valence, α is the lattice constant and T m is the melting temperature. The melting temperature could be obtained from the SGTE thermodynamic database by Dinsdale et al.[22] and the lattice parameter could be taken from an ab initio calculation.[23] As an approximation, the impurity diffusion coefficient of Ti in bcc-Sn is assumed to have the same value of the self-diffusivity of bcc-Sn, which also applies to the impurity diffusion coefficient of Ti in bcc-Sn.

Fig. 5
figure 5

Comparison of calculated temperature dependence of Sn impurity diffusion coefficients in α-Ti[11,14] with experimental data [13]

Full size image

The optimization of mobility parameters were carried out using the PARRAT module of the DICTRA software package.[24-26] The main operation principle is to minimize the sum of square of the differences between experimental data and calculated values. In the optimization procedure, experimental data on impurity diffusion coefficients, tracer diffusion coefficients, intrinsic diffusion coefficients and interdiffusion coefficients were all used. The mobility parameters for the solution phases bcc(β) and hcp(α) obtained in the work were generalized in Table 1. The mobility parameters of hcp phase have not been calculated completely as no interdiffusion information has been found in literatures, and only boundary mobility parameters about the self-diffusivities and impurity diffusivities of hcp-Ti and hcp-Sn were given.

Table 1 Mobility parameters of bcc and hcp Ti-Sn alloys
Full size table

The calculated interdiffusion coefficients of Sn less than 1.5 at.% in bcc-Ti with the experimental data by Iijima et al.[6] were shown in Fig. 6. As can be seen, the calculated values are in good accordance with experimental data.[6] The interdiffusion coefficients of Sn less than 4.9 at.% at 1223 K was calculated using the mobility parameters by the DICTRA software. The comparison between the calculated results and the experimental data from Araki et al.[8] is given in Fig. 7, as well as the mobility coefficients at the other temperature were also predicted. The calculated results also agree well with the experimental data at 1223 K.[8] To better verify the calculated mobility coefficients, concentration profile of the Ti/Ti-4.9 at.% Sn diffusion couple annealed at 1223 K for 14.4 ks was calculated, which shows a good fit with the calculated results and the experimental data from Araki et al.[8] in Fig. 8. It indicates that the calculated mobility parameters of Sn in bcc-Ti are reasonable.

Fig. 6
figure 6

Comparison between calculated interdiffusion coefficients and experimental data[6] at different temperatures in the Ti-rich Ti-Sn system

Full size image
Fig. 7
figure 7

Comparison of calculated temperature dependence of Sn impurity diffusion coefficients in pure Ti with experimental data[6,8]

Full size image
Fig. 8
figure 8

Calculated concentration profile of the Ti/Ti-4.9 at.%Sn diffusion couple annealed at 1223 K for 14.4 ks with the experimental data from Araki et al.[8]

Full size image

Conclusions

Combined with the thermodynamic parameters of the Ti-Sn system and diffusion mobilities in the literatures, the atomic mobilities of Ti and Sn in bcc Ti-Sn alloys were assessed by the CALPHAD method. The assessed mobility parameters can be successfully used to represent most of experimental data on the bcc Ti-Sn diffusion couples and the concentration profile for the Ti-Sn diffusion couples. In addition, the boundary atomic mobility parameters of hcp Ti-Sn were summarized. The result can enhance the understanding of kinetic behaviors of the Ti-Sn alloys.