Introduction

Nuclear power plants (NPPs) safety is strongly depending on the electrical power system (EPS) reliability during all their operation modes. To satisfy its desired reliability level, the EPS of an NPP follows various design principles, namely: redundancy, diversity, physical separation, single failure criteria and functional independence. It is generally divided on two parts: onsite power supply system and offsite power supply system [1, 2]. The simultaneous occurrence of loss of offsite power (LOOP) and the failure of onsite power supply leads to a Station Blackout (SBO) which has been identified as a major contributor to core damage accident in NPP’s [3,4,5]. The reliability assessment provides the necessary insight of how EPS can contribute to supply the first safety class buses (1E) of an NPP with reasonable continuity and quality. Furthermore, the obtained results would help to identify critical components.

In the literature, many studies of the reliability evaluation of the NPP’s EPS have been performed. The mostly used methods are fault tree analysis (FTA) [6, 7], event tree analysis [8, 9], Monte Carlo simulation [8, 10], state enumeration [9], reliability block diagram [11] and go methodology [12, 13]. However, various works dealing with the reliability assessment of EPS based on FTA method have been performed. In this context, the reliability assessment of auxiliary power supply is demonstrated, and its impact on high-voltage direct current (HVDC) link using FT analysis is presented in [14]. In [15], a dynamic fault tree is proposed considering the sequence-dependent behavior and the priorities of the components, especially when considering a shared facility between EPSs. The unavailability evaluation of diesel generators (DGs) using Fault Tree Analysis method based on ISOGRAPH reliability software is proposed in [16]. In [17], the reliability assessment of an NPP’s connection bus in an interconnected power system using FTA method is performed.

The FTA method is used to model the failure complex systems [18,19,20,21]. Its major aim is to determine the possible combinations of causes that lead to an undesirable top event. The FTA method is based on qualitative and quantitative analysis issues [22,23,24,25].

In this paper, the reliability, importance, sensitivity and uncertainty analyses of an EPS of a French NPP using FTA method developed by RiskSpectrum PSA software is proposed. Furthermore, a detailed reliability model of two standby diesel generators (DGs) is proposed as a function of testing parameters. This allows the analytical unavailability assessment of DGs considering the impact of test caused failures, imperfect testing and effect of failure rate. Also, a reliability goal problem is formulated as an optimization problem aiming to eliminate the aging impact on the DGs reliability by acting on the testing interval (TI) using the genetic algorithms (GAs). For validation purpose, the reliability block diagram (RBD) of the NPP’s EPS is developed and compared with the obtained results.

The paper is organized as follows: Section “NPP’s EPS Description” is devoted to the description of the French NPP’s EPS. Section “Reliability Analysis Methodology” presents the mathematical modeling of fault tree, reliability, importance analysis, sensitivity analysis, uncertainty analysis, extended reliability of DGs and the reliability goal optimization problem. The obtained results, the discussion and the validation of the obtained results are given in Sect. “Results and Discussions.” The gained conclusions are presented in Sect. “Conclusion.”

NPP’s EPS Description

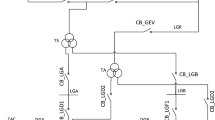
Figure 1 presents the schematic of a French NPP’s EPS, and their related reliability data are presented in Table 1 [26]. Its main task is to provide a reliable electrical power to the first safety class buses (1E) LHA and LHB which supply the essentials components for core cooling and instrumentation and control (I&C).

Fig. 1
figure 1

Schematic of the French NPP’s EPS [26]

Full size image
Table 1 Reliability data [26]
Full size table

The EPS includes repairable components with various failure modes, standby components, redundancies and reconfigurations. It essentially has five electrical sources, two main sources, namely: the transmission network (GRID) and the UNIT and three backup sources including two DGs (DGA and DGB) and a gas turbine (TAC).

In normal operation of the plant, the UNIT operates in regular mode and injects power into the GRID.

Furthermore, a portion of this power is injected to the plant house load via the transformer TS. If the UNIT fails, the GRID can still feed the system through TS.

In case of loss of GRID or an element of its path, the UNIT switches to house load operation mode by reducing its power to feed only the plant itself. It should be noted here that this operation mode is unstable, and therefore its success probability is very low. In case of house load operation failure, the plant can be supplied via the auxiliary transformer TA through the transmission line LGR (on condition that GRID and SUBSTATION are available). Finally, the DGA and DGB and the TAC provide energy to the house load of the plant in case of Loss of Offsite Power (LOOP) event as follows:

  • DGA supplies LHA bus,

  • DGB supplies LHB bus,

  • TAC supplies LHA in case of DGA failure.

For simplicity purpose, the following assumptions are considered in this paper. The direct current (DC) power supply of the circuit breakers is considered 100% reliable, so the low voltage part is not considered. The dynamic behavior of the system is not considered; thus, the FTA method is used to assess the reliability of the system. The success criterion of the system requires that the power supply of one bus LHA or LHB is enough to the system safety.

Reliability Analysis Methodology

Fault Tree Modeling

FTA is a deductive analysis technique that provides a systematic approach to investigate the possible modes of occurrence of an undesired event [18, 19, 27]. It is suitable and efficient for quantitative and qualitative reliability evaluation of the complex and redundant systems based on the combination of the basic events with the Boolean logic gates.

The qualitative analysis of fault tree is based on identification of the MCS. The MCS are defined as the combinations of the smallest number of basic events, which if occur simultaneously, may lead to the top event. In other words, it is the combination of components failures, which may cause the system to fail. The top event probability is calculated based on the MCS probabilities as follows [17]:

$$ Q = \sum\limits_{i = 1}^{n} {MCS_{i} } $$
(1)

where Q is the top event failure probability, MCSi is the MCS number i, and n is the number of MCS.

The probability of an MCS is calculated as follows:

$$ MCS_{i} = \prod\limits_{j = 1}^{m} {B_{j} } $$
(2)

where Bj is the basic event j and m is the number of basic events in the MCSi.

Reliability Models

The reliability models used in this paper are presented below. For more additional information about other models, the reader can refer to [28, 29].

Monitored, Repairable Component’s Reliability Model

This model is applied for components whose failure detection is instant, and the repair starts immediately. The failure process and repair process are assumed to be exponentially distributed. Required parameters are constant failure rate λ and constant repair rate μ. The mean unavailability Q is presented as follows:

$$ Q = \frac{\lambda }{\lambda + \mu } $$
(3)

Fixed Failure Probability Model

This model is calculated from only one parameter, constant unavailability q and does not depend on time of component operation. It is suitable for standby components that experience failure per demand.

$$ Q = q $$
(4)

Importance Analysis

A system is an organized set of components (or subsystems) that are highly integrated to achieve an overall goal. Obviously, some components are more important to system reliability than others, because of their reliability and location in the system. For these reasons, the ranking of components is important for the assessment of system reliability based on the calculation of importance measures. The importance measures may be used to identify the weak points and components that should be improved to improve the system reliability. The measures may also be used to identify components that should be modified or replaced with higher-quality components [30,31,32]. The three importance measures used, in this paper, are Fussell–Vesely (FV), risk reduction worth (RRW) and risk achievement worth (RAW).

Fussell–Vesely Important Measure (FV)

Fussell–Vesely’s (FV) importance measure is defined as the probability that at least one minimal cut set contains component i is failed at time t, given that the system is failed at time t. According to this measure, the importance of a component i in the system depends on the number and the order of the cut-sets where appears. Analytically, FV metric is defined as:

$$ I^{FV} \left( {{\raise0.7ex\hbox{$i$} \!\mathord{\left/ {\vphantom {i t}}\right.\kern-0pt} \!\lower0.7ex\hbox{$t$}}} \right) = \frac{{\sum\limits_{{MCS_{j} :x_{i} \in MCS_{j} }} {p\left( {MCS_{j} } \right)} }}{{1 - h\left( {p\left( t \right)} \right)}} $$
(5)

where \(x_{i}\) represents the failure of component i, \(MCS_{j}\) denotes the minimal cut set, and \(h\left( {p\left( t \right)} \right)\) represent the system reliability with respect to a specified system function.

Risk Reduction Worth (RRW or RDF)

The risk reduction worth (RRW) is a measure of the risk reduction that would be achieved when the unavailability of a component is reduced to zero, i.e., the event certainly does not occur. It is mathematically expressed as:

$$ I^{RRW} \left( {{\raise0.7ex\hbox{$i$} \!\mathord{\left/ {\vphantom {i t}}\right.\kern-0pt} \!\lower0.7ex\hbox{$t$}}} \right) = \frac{{1 - h\left( {p\left( t \right)} \right)}}{{1 - h\left( {1_{i} ,p\left( t \right)} \right)}} $$
(6)

where \(h\left( {1_{i} ,p\left( t \right)} \right)\) denotes the conditional probability that the system is functioning when it is known that component “i” is functioning at time t.

Risk Achievement Worth (RAW)

The risk achievement worth (RRW) is a measure of the risk increase. RAW is the ratio of the (conditional) system unreliability if component “i” is failed with the actual system unreliability. It is mathematically expressed as:

$$ I^{RAW} \left( {{\raise0.7ex\hbox{$i$} \!\mathord{\left/ {\vphantom {i t}}\right.\kern-0pt} \!\lower0.7ex\hbox{$t$}}} \right) = \frac{{1 - h\left( {0_{i} ,p\left( t \right)} \right)}}{{1 - h\left( {p\left( t \right)} \right)}} $$
(7)

where \(h\left( {0_{i} ,p\left( t \right)} \right)\) denotes the (conditional) probability that the system is functioning when component “i” is in a failed state at time t.

Sensitivity Analysis

Sensitivity analysis of the basic events is carried out to find the top event unavailability responses to variations in basic input values of failure rates. The RiskSpectrum PSA software calculates the sensitivity of a basic event as the ratio between high and low sensitivity to assess the sensitivity of a model output to the range of variation of an input [33, 34]. Analytically, sensitivity is defined as [29]:

$$ S = \frac{{Q_{TOP,U} }}{{Q_{TOP,L} }} $$
(8)

\(Q_{TOP,U}\) is the top event unavailability when the basic event is assigned the nominal value multiplied by a sensitivity factor. \(Q_{TOP,L}\) is the top event unavailability when the basic event is assigned the nominal value divided by a sensitivity factor.

Uncertainty Analysis

The evaluation of uncertainty in the top event failure probability is carried out using Monte Carlo simulation. To illustrate this approach, it was considered that the failure rates and failure probabilities on demand have a lognormal distribution. The principle of uncertainty propagation is schematized by Fig. 2.

Fig. 2
figure 2

Propagation of uncertainty (parametric)

Full size image

The density function of the lognormal distribution is presented as follows [35,36,37]:

$$ f\left( y \right) = \frac{1}{{\alpha y\sqrt {2\pi } }}e^{{ - \frac{{\left( {\ln \left( y \right) - \mu } \right)^{2} }}{{2\alpha^{2} }}}} \quad \quad 0 \le y \le \infty $$
(9)

where \(\mu\) and \(\alpha\) are the mean and the variance of \(\ln \left( y \right)\).

The expressions for the characteristics of the variable Y are as follows: Median: \(M = e^{\mu }\), Mean: \(E\left( Y \right) = {\kern 1pt} e^{{\mu + \frac{{\alpha^{2} }}{2}}}\), Error factor: \(EF = e^{1 \cdot 645\alpha } = \frac{M}{{r_{0/05} }} = \frac{{r_{0.95} }}{M}\quad \in \left[ {1, + \infty } \right[\)where \(r_{0.05}\) and \(r_{0.95}\) are, respectively, the 5% and 95% percentiles of the variable.

Extended RiskSpectrum PSA Model of DGs Unavailability

To study the impact of standby DGs parameters on the EPS reliability, the failure on demand of DGs is extended to consider both demand unavailability and standby unavailability. The periodically tested component model of RiskSpectrum PSA software is presented in (10).

$$ Q = 1 - \frac{1}{\lambda TI}\left( {1 - q} \right)\left( {1 - e^{ - \lambda TI} } \right) + \left( {1 - \left( {1 - q} \right)e^{ - \lambda TI} } \right) \times \frac{Tr}{{TI}} $$
(10)

where Q is standby component mean unavailability; TI is the test interval; Tr is mean time to repair; q is failure probability per demand; and λ is failure rate.

Equation 10 is used to model a component failure, which can be detected only during the component test. It is a very limited model which considers few parameters only. Unfortunately, RiskSpectrum PSA software is not able to simulate other effects of test such as imperfection of tests, degradation caused by testing. To overcome this limitation, the detailed standby reliability model of Coleman and Abrams [38, 39] is proposed. The model presents an analytical approach for the most comprehensive expression for the DG unavailability. It is mathematically expressed as:

$$ Q_{DG} = 1 - \frac{{\theta \left( {1 - e^{ - \lambda T} } \right)}}{{\lambda \left( {T + T_{c} } \right)\left\{ {1 + e^{ - \lambda T} \left[ {\beta \left( {1 - \alpha + \alpha P_{c} - P_{c} \theta } \right) - \left( {1 - \theta } \right)} \right]} \right\} + \lambda T_{r} \left[ {1 - \left( {1 - \alpha } \right)\left( {1 - \beta } \right)e^{ - \lambda T} } \right]}} $$
(11)

where QDG is the DG unavailability; λ is component failure rate; β is probability of the failure during a test period; Tc is testing period; α is probability of a false alarm; Pc is probability of failure occurring before actual test of the failure occurs during testing period; θ is probability that a failure will be detected; T is the time between repair times of previous interval to the next testing period which is expressed as follows:

$$ T = TI - \left( {T_{c} + T_{r} } \right) $$
(12)

Therefore, the model presented in (11) considers the imperfect testing, failure due to testing along with differentiating between test time and repair time.

Reliability Goal Optimization Problem

It is well-known that the DG’s reliability is degraded with time because of aging. The aim of this proposed optimization problem is to eliminate the aging impact on DGs reliability. For doing so, the following optimization problem is proposed and solved using GAs toolbox of MATLAB software [40]:

$$ OF = \min \left( {\left| {Q_{DG}^{\lambda \left( t \right)} \left( {TI} \right) - Q_{DG}^{Goal} } \right|} \right) $$
(13)

where OF is the proposed nonlinear objective function, \(Q_{DG}^{\lambda \left( t \right)}\) is the DG unavailability presented in (11) at a specified age t, \(Q_{DG}^{Goal}\) is the unavailability goal of the DGs, TI is the testing interval of DG which is modeled as an integer decision variable of the optimization problem which is limited as follows:

$$ TI_{\min } \le TI \le TI_{\max } $$
(14)

where TImin and TImax are the minimum and the maximum limits of TI, respectively.

The failure rate presented in (11) is updated considering the DG age according to the following linear aging model [41]:

$$ \lambda \left( t \right) = \lambda_{0} + \alpha \times t $$
(15)

where \(\lambda_{0}\) is the constant failure rate of DG, t is the age of DG and \(\alpha\) is the constant aging rate of DG obtained from the aging database TIRGALEX [41].

Results and Discussions

Fault Tree Modeling

Figure 3 shows the main fault tree of the EPS failure developed in RiskSpectrum PSA software. The EPS is modeled with eight Fault trees connected with transfer gates. They have forty-seven basic events, six AND gates and twenty-two OR gates. Figures 3, 4 and 5 present the main fault tree and the fault trees related to failure of buses LHA and LHB, respectively. For the organization purpose, the other fault trees are presented in the annex (see figures from A.1 to A.4 presented in annex A).

Fig. 3
figure 3

Main fault tree of the EPS failure

Full size image
Fig. 4
figure 4

Fault tree of the LHA bus failure

Full size image
Fig. 5
figure 5

Fault tree of the LHB bus failure

Full size image

The top event of the fault tree is chosen as the simultaneous failure of both LHA and LHB buses. This means that the EPS did not assume its role as a support system of the safety systems. The obtained top event failure probability is 1.39E−06 (or frequency of 1.172E−07 f/yr). It requires the occurrence of the two following events: “LHA bus losses power” and “LHB bus losses power” which have a probability of occurrence of 1.58E−05 and 4.47E−05, respectively (see Fig. 3). From the results, the EPS of LHA bus is more reliable than LHB bus. Therefore, the top event is most probably caused by the loss of power in LHB bus with 11% compared with 32% for the loss of power in LHA. This distinction is due to the number of power supply sources connected to each bus, where LHA bus is supplied by three sources, and LHB bus is supplied by two sources. From Fig. 4, the loss of power at LHA bus is mainly due to either the LHA bus is not supplied or circuit breaker LHA1 is shorted. Also, the loss of power at LHA bus requires the simultaneously occurrence of the three following intermediate events: “diesel generator line A fault,” “outage of bus LGD” and “gas turbine line fault.” In the same manner, the intermediate event “LHB bus losses power” occurs if any of the following intermediate events occur: “short circuit fault of circuit breaker LHB1” or “LHB bus loses power supply.” This last intermediate event occurs if the two following events occur simultaneously: “diesel generator line B fault” and “outage of bus LGF.”

Validation of the Fault Tree Results

Since there are no published papers that deal with the same proposed reliability analysis methodology and assumptions, the comparison with published results is not allowed. However, the RBD method is proposed as a tool of comparison and validation of the obtained results. The RBD method has a different principle compared to the fault tree method.

Therefore, the comparison of the results of the two methods is considered as a validation of the proposed method. For doing so, the RBD of the EPS is developed using the Isograph Reliability Workbench 15.0 software [42].

Figure 6 presents the developed RBD of the EPS. The obtained RBD structure is composed of 46 components connected in series and in parallel. This hybrid structure is complex for the resolution [43].

Fig. 6
figure 6

RBD of the NPP’s EPS

Full size image

The failure probability of the EPS and the top ten MCS obtained by FTA and RBD are presented in Table 2.

Table 2 Top ten MCS list for FTA and RBD
Full size table

The comparison of the obtained results shows that the two methods provide almost the same results in terms of EPS failure and MCS probabilities. This means that the proposed reliability modeling and analysis methodology are efficient.

Table 2 shows, also, that no single-order MCS is available, and the most significant MCS contributor to the top event is a fourth-order MCS with a probability of 4.90E−07. These results clearly indicate that the EPS is strongly redundant.

However, the obtained failure frequency of the top event shows that the top event will, averagely, fail once every 974 years for 11 h and 11 min, i.e., the EPS will fail approximately 0.001 times per year.

Table 3 presents the top ten FV, RRW and RAW importance factors obtained by FTA and RBD. The comparison of the results shows that the results are almost the same for the three importance factors. This means that the proposed reliability analysis methodology is able to compute the components importance factors in an efficient manner.

Table 3 Top ten FV, RRW and RAW importance factors
Full size table

The analysis of the FV results presented in Table 3 shows that the main components whose reliability needs to be improved are TAC fails to function, Unit house load fail to function, transmission lines and diesel generators fail to function due to CCF. These results are logic, since these components belong to the first MCS. In addition, they are the most electric sources that feed LHA and LHB buses. From RRW results, the TAC fails during operation has a large value with more than 7.0E+01 which implies that the EPS risk is significantly decreased with TAC reliability improvement. Therefore, it should be given top priority for an overall improvement of the EPS reliability. From RAW results, the transmission lines fail to function due to CCF, grid fails, substation failure and DGs fail to function due to CCF which have the largest values. This implies that the maintenance or the failure of these components contributes to the EPS reliability reduction.

It should be highlighted that the contribution of DGs and transmission lines comes mainly from their corresponding CCF. This implies that the importance of such components is reduced when the CCF probabilities are reduced.

Sensitivity Analysis

Table 4 presents the highest 10 events in terms of sensitivity. The obtained results show that the top event probability is mostly sensitive to the TAC failure in function followed by the failure of transmission lines by CCF and long failure of DGB, respectively.

Table 4 Top ten sensitive components
Full size table

To check the sensibility analysis results, the impact of failure rates increase in TAC and GRID on the EPS unavailability is performed, and the results are presented in Fig. 7. The obtained results show that the top event unavailability increases faster in case of TAC compared with the case of GRID. This is since the TAC is more sensitive than the GRID (see Table 4).

Fig. 7
figure 7

EPS unavailability versus failure rate variation

Full size image

Uncertainty Analysis

The uncertainty analysis is performed by Monte Carlo Simulation method considering 106 samples. The failure rates and probabilities of components are modeled by lognormal distribution considering the appropriate error factors [44]. Figures 8 and 9 present, respectively, the probability density function (PDF) and the cumulative distribution function (CDF) of the top event.

Fig. 8
figure 8

Probability density function (PDF) of top event

Full size image
Fig. 9
figure 9

Cumulative density function (CDF) of top event

Full size image

The obtained results indicate that the top event is distributed according to a lognormal distribution with the following parameters: mean value equals to 1.39E−6, error factor of 3.58, P05 = 5.536E−08, P50 = 4.529E−07 and P95 = 3.598E−06.

Impact of DG Testing Parameters on EPS Unavailability

Figure 10 presents the impact of DG testing parameters on the EPS unavailability. Three case studies are considered:

  • Case 1: perfect testing without failure during test (θ = 1, β = 0)

Fig. 10
figure 10

Effects of test parameters on EPS unavailability

Full size image

In this case, the TI of 15 days gives the minimum unavailability of 1.46E−06.

  • Case 2: perfect testing strategy with test caused failure (θ = 1, β = 1E-2)

The results show that the minimum EPS failure probability is 1.49E−06 for a TI of 14 days.

  • Case 3: imperfect testing with test caused failure (θ = 9E-1, β = 1E-2)

In this case, the EPS reaches its minimum probability of 1.49E−06 for a TI of 20 days.

From the above obtained results, it is shown that the tree cases failure probabilities are very close. However, the reliability of the EPS is more degraded for the cases 2 and 3 followed by case 1.

Reliability Goal Optimization Results

Table 5 presents the GAs results of the reliability goal optimization problem. From this table, the proposed optimization problem is able to maintain the DG reliability at a desired value even after thirty years of operation. It is, also, shown that the optimal value of TI is decreased to compensate the age increase in DG.

Table 5 GAs results of the reliability goal optimization problem
Full size table

Conclusion

Reliability analysis methodology of an electrical power system in a French Nuclear Power Plant (NPP) is performed using fault tree analysis method developed using RiskSpectrum PSA software. The obtained unavailability of electrical power system is 1.39E-6 which is most probably caused by the loss of power in LHB bus with 22% compared with 13% for the loss of power in LHA. The obtained minimal cut set shows that the dominant contribution to the system unavailability has a fourth order with a probability of 4.90E-7 which reflects the strong redundancy of the system. The importance analysis shows that the components with large values of RAW are the best candidates for redundancy application. Also, the large values of RRW imply that the reliability of the respective components must be improved. Furthermore, the sensitivity analysis provides a useful information about the components where the system reliability is very sensitive to their aging or reliability degradation.

The uncertainty results analysis indicates that the top event has a lognormal distribution with the following parameters: error factor of 3.58, mean unavailability of 1.39E−6, 5th percentile is 5.536E−08, and 95th percentile is 3.598E−06.

The proposed tested unavailability model of diesel generators shows its ability to support more detailed analysis considering various testing parameters which cannot be performed using RiskSpectrum PSA tested model.

The proposed reliability goal optimization problem shows a high efficiency to maintain the diesel generators reliability even after thirty years of operation by testing interval optimization using genetic algorithms method.

The obtained results are compared with those given by the reliability block diagram method which show high precision and efficiency.