Testing Device for Rheological Properties of Magnetorheological Fluid at High Shear Rate

Abstract

In order to research the rheological property of MRF at high shear rate, a magnetorheological fluid (MRF) rheological property testing device based on shear mode, is developed. The accurate analytical expressions of MRF rheological parameters in terms of structural dimensions of testing device and shear rate in the parallel plate gap are derived, and the flow state of MRF is considered, which provides the theoretical foundation for testing the rheological property of MRF at high shear rate. The relationship between magnetic indication in the parallel plate gap and excitation electrical current is experimentally obtained. Some elements influencing testing are analyzed and eliminated. The device is used to test the rheological parameters of MRF, and the results show that the yield stress of MRF increases significantly as the magnetic flux density continues to increase, and shear rate has no obvious effect on it. The shear rates in designed device may exceed 3 × 10⁴ s⁻¹, which meets the special demands in MRF testing.

Introduction

In the research field of magnetorheological fluids, magnetorheological brake, clutch and magnetorheological rotating device is one of the most concentrated and rapidly applied fields, which relate to the vehicle brake, clutch and dynamometer. For different applications, the flow rate and shear rate of MRF are very different. For example, in the brake [1], clutch [2, 3], rotary loading system [4, 5], under the action of strong driving torque, the flow rate of MRF is higher and the shear rate can exceed 10⁴ s⁻¹. Compared to the low flow rate and low shear rate conditions, MRF may show different properties under such extreme conditions. The experimental results of literature [1] show that the MRF velocity in the parallel plate gap is very fast when the brake operating at high frequency, which leads to the weakening of the magnetorheological effect, and the controllable braking torque is decreased. The experimental results of literature [4] show that the stability of MRF is reduced when the shear rate is larger than a certain value.

At present, there are many literatures focused on the study of the rheological properties of MRF at low shear rate; however, there is less literature focused on the study of the rheological properties of MRF at high shear rate, and one of the important reasons is lack of corresponding testing device.

According to the working mode of MRF in engineering application, which is divided into flow mode, extrusion mode and shear mode, the flow pattern will become very complex with the change in MRF state [6]. Literature [7] derived the distribution function of the shear stress and shear rate of the MRF in the long pipeline based on the principle of fluid mechanics and the Herschel–Bulkley flow model. The test system due to omitting the driving device, which leading to simplify the structure and effectively reduce the test error, however, it cannot get the high shear rate due to the lack of driving device. Literature [8] designed a slender slit-type test device which has a large range of shear rate, but there are some disadvantages such as complicated structure, add MRF is not convenient, and temperature is not controllable. There are very few testing devices for rheological properties of MRF based on extrusion mode which can be used for reference to the test of the rheological properties of electrorheological fluid from literature [9]. The test methods based on shear mode are divided into the concentric rotary cylinder type and parallel rotary disk type. In terms of concentric rotary cylinder type, Haake RV20 type magnetic rheometer of Germany Haake Company devoted to testing rheological properties of MRF, the maximum shear rate measured by Haake RV20 rheometer in literature [10] was 300 s⁻¹. In terms of parallel rotary disk type, the maximum shear rate measured in literature [11] was 1000 s⁻¹. The rotation radius of the testing device cannot be increased due to the volume limitation of the coil, so the shear rate of MRF in the channel is limited, and the test at the high shear rate cannot be completed. In order to research the rheological property of MRF at high shear rate, a MRF rheological property testing device based on shear mode is developed and the shear rate range of the device is 1000 ~ 3 × 10⁴ s⁻¹.

The Structural Design of the Testing Device for MRF Rheological Property

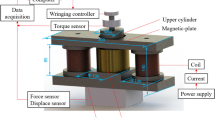
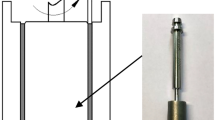
Magnetorheological brake is an important application direction of MRF, in order to close to the practical application, this paper designed a magnetorheological brake which is similar to the structure of the commonly used magnetorheological rotating device to test the shear yield strength of MRF, as shown in Fig. 1. The main parameters of the MRF shear yield strength testing device are as follows: the external radius of the brake disk is $r_{2} = 300\;{\text{mm}}$, the inner radius of the brake disk is $r_{1} = 80\;{\text{mm}}$, the width of the MRF gap is $h = 2\;{\text{mm}}$, the width of the brake disk is $l = 40\;{\text{mm}}$.

Fig. 1

Schematic of MRF testing device

The Testing Principle of Rheological Property of MRF

The Testing Principle of Rheological Properties of MRF Based on Shear Mode

The flow channel of testing device is a parallel plate gap, as shown in Fig. 2. In this section, we analyze the stress state of the MRF micro-unit in the shear channel based on the cylindrical coordinate system $r,\theta ,z$; assume the distribution of MRF flow line speed is as follows:

$$ \left\{ {\begin{array}{*{20}l} {u_{\theta } = r\omega (r)} \hfill \\ {u_{r} = 0} \hfill \\ {u_{z} = 0} \hfill \\ \end{array} } \right. $$

(1)

where $u_{\theta }$, $u_{r}$ and $u_{z}$ are, respectively, the linear velocity of fluid along the direction $r$, $\theta$, $z$, and $r$ is the radius of the micro-ring. $\omega (r)$ is the angular velocity of the MRF at the radius $r$, which is only a function of the radius $r$. A micro-unit is obtained in the MRF; the stress of the micro-unit in the shear channel is shown in Fig. 2 when the MRF flows in the circumferential direction.

Fig. 2

Stress analysis for micro-unit of MRF in the shear channel

The length of the micro-unit along the Z direction is ${\text{d}}z$, all the stress project onto the tangential axis of the unit center, and we obtain the tangent differential equation:

$$ \begin{aligned} & \sigma_{\theta \theta } \cdot {\text{d}}r{\text{d}}z + \left( {\tau_{r\theta } + \frac{{\partial \tau_{r\theta } }}{\partial r}} \right)({\text{d}}r + r){\text{d}}\theta {\text{d}}z + \tau_{\theta r} {\text{d}}r{\text{d}}z\sin \frac{{{\text{d}}\theta }}{2} + \left( {\tau_{\theta r} + \frac{{\partial \tau_{\theta r} }}{\partial \theta }} \right){\text{d}}\theta {\text{d}}r{\text{d}}z\sin \frac{{{\text{d}}\theta }}{2} - \sigma_{\theta \theta } + \frac{{\partial \sigma_{\theta \theta } }}{\partial \theta }{\text{d}}z{\text{d}}r - \tau_{r\theta } r{\text{d}}\theta {\text{d}}z = 0 \\ \quad \\ \end{aligned} $$

(2)

where $\sigma_{\theta \theta }$ is the tangential pressure along the $\theta$ direction, and $\tau_{\theta r}$ and $\tau_{r\theta }$ are the shear stress of the MRF. We regard $\frac{{{\text{d}}\theta }}{2}$ as $\sin \frac{{{\text{d}}\theta }}{2}$ due to ${\text{d}}\theta$ is very small. According to the reciprocal theory of fluid shear stress, and omit second-order differential, Eq 2 can be expressed as:

$$ \frac{{\partial \sigma_{\theta \theta } }}{\partial \theta } + \frac{{\partial \tau_{r\theta } }}{\partial r} + \frac{{2\tau_{r\theta } }}{r} = 0 $$

(3)

We assume the MRF as a continuous flow based on the shear flow of MRF in a concentric cylinder. Due to the thickness of each section in the flow direction is equal, the tangential pressure $\sigma_{\theta \theta }$ along the $\theta$ direction is constant. On both sides at the same time divided by ${\text{d}}r{\text{d}}z{\text{d}}\theta$, in order to simplify the operation symbols, we appoint $\tau_{r\theta } = \tau$ in this paper, and Eq 3 can be expressed as:

$$ \frac{{{\text{d}}\tau }}{{{\text{d}}r}} + \frac{2\tau }{r} = 0 $$

(4)

MRF showed Bingham fluid state in an external magnetic field; the constitutive relation is shown in Eq 5. The material showed fluid state and had a liquid viscosity $\eta$ when the local shear stress is greater than the yield stress $({\kern 1pt} {\kern 1pt} \tau > \tau_{y} )$. The liquid is assumed to be a rigid body when the local shear stress is not greater than the yield stress $({\kern 1pt} {\kern 1pt} \tau < \tau_{y} )$.

$$ \left\{ {\begin{array}{*{20}l} {\tau = \tau_{0}\, \text{sgn} (\dot{\gamma }) + \eta \dot{\gamma }} \hfill & {\tau > \tau_{y} } \hfill \\ {\dot{\gamma }{\kern 1pt} = 0} \hfill & {\tau > \tau_{y} } \hfill \\ \end{array} } \right. $$

(5)

In the channel, the angular velocity of MRF increases with the increase in the radius; shear rate is defined as:

$$ \dot{\gamma }{ = }r\frac{{{\text{d}}\omega (r)}}{{{\text{d}}r}} $$

(6)

where $\dot{\gamma }$ is the shear rate of MRF in the shear channel, $\omega (r)$ is the angular velocity distribution of the MRF in the shear channel, $r$ is the radial coordinate. Equation 6 is integrated into Eq 5, and due to $\text{sgn} \left( {r\frac{{{\text{d}}\omega (r)}}{{{\text{d}}r}}} \right) = 1$, the constitutive equation is as follows:

$$ \tau = \tau_{0} + \eta \left( {r\frac{{{\text{d}}\omega (r)}}{{{\text{d}}r}}} \right) $$

(7)

The general solution of the flow differential Eq 4 is $\tau = C/r^{2}$; then, it is integrated into Eq 5, and the following differential equation is obtained:

$$ \tau_{0} + \eta \cdot r\frac{{{\text{d}}\omega (r)}}{{{\text{d}}r}} = \frac{C}{{r^{2} }} $$

(8)

The solution of the differential equation is

$$ \omega (r) = - \frac{C}{2\eta } \cdot \frac{1}{{r^{2} }} - \frac{{\tau_{0} }}{\eta }\ln r + D $$

(9)

Among them, $C$, $D$ are all undetermined constants, which can be obtained by the boundary conditions.

In combination with the actual situation, the boundary conditions for this equation are:

When $r = r_{1}$, $\frac{{{\text{d}}\omega (r)}}{{{\text{d}}r}} = 0$, $\tau = \tau_{0}$;

When $r = r_{2}$, $\omega (r) = \varOmega$.

The boundary conditions are brought into Eqs 7 and 9:

$$ \left\{ {\begin{array}{*{20}l} {C = r_{1}^{2} \cdot \tau_{0} } \hfill \\ {D = \frac{{r_{1}^{2} \tau_{0} }}{2\eta } \cdot \frac{1}{{r_{2}^{2} }} + \frac{{\tau_{0} }}{\eta } \cdot \ln r_{2} + \varOmega } \hfill \\ \end{array} } \right. $$

(10)

Combining Eqs 9 and 10 gives:

$$ \omega (r) = \frac{{r_{1}^{2} \tau_{0} }}{2\eta }\left( {\frac{1}{{r_{2}^{2} }} - \frac{1}{{r^{2} }}} \right) + \frac{{\tau_{0} }}{\eta }(\ln r_{2} - \ln r) + \varOmega $$

(11)

In the yield stage, the shear yield strength of MRF is independent of the shear strain and is determined only by the shear rate, and the calculation formula of shear stress is:

$$ \tau = \frac{1}{{\pi r^{3} }}\left( {\omega (r)\frac{\partial M}{\partial \omega (r)} + 3M} \right) $$

(12)

where $M$ is the torque of the brake disk.

Combining (11) and (12), the shear yield strength of MRF can be calculated by testing the torque of the brake disk when $r_{1}$, $r_{2}$, $\eta$ and $\tau_{0}$ are known.

Criteria for Judging Fluid Flow

The MRF shear yield strength testing principle is based on the laminar flow model which is only applicable to the analysis of laminar flow. The flow state is likely to develop into turbulent flow when the fluid flows at high speed. Therefore, the determination of the MRF flow state is directly related to the correctness of the application of the mathematical model.

Reynolds number is defined as

$$ {Re} = \frac{{\rho {u_m}h}}{\eta } $$

(13)

where $\rho$ is the density of the liquid, $u_{m}$ is the average velocity of the liquid, $h$ is the width of the parallel plate gap.

Velocity of the maximum diameter of the brake disk is as follows

$$ v = 2\pi r_{2} \cdot n/60 $$

(14)

According to the parallel disk gap, the average velocity of the fluid is half of the velocity of maximum diameter of the brake disk.

$$ u_{m} = \frac{v}{2} $$

(15)

Comprehensive above can be obtained

$$ {Re} = \frac{\rho vh}{2\eta } $$

(16)

The average velocity of the liquid is $39.25\;{\text{m/s}}$ when the brake disk at the maximum speed is $n = 2500\;{\text{r/min}}$. The Reynolds number is about 1962.5 when $\eta = 0.12\;{\text{Pa}}\;{\text{s}}$, $\rho = 3\;{\text{g/cm}}^{ 3}$, still below the critical value of 2300. The mathematical model based on the assumption of laminar flow is established when the average velocity of liquid is $39.25\;{\text{m/s}}$, which can be used to test the shear yield strength.

The Range of Shear Rate Under Zero Field Condition

Under zero field condition, a micro-unit in the channel is analyzed, which can be regarded as a unit between two parallel plates, as shown in Fig. 3.

Fig. 3

Velocity distribution of MRF in the channel

The brake disk rotates with angular velocity $\omega$ can be seen as the velocity $u = \omega \cdot r$ of the micro-level. Since the fluid is adhered to the surface of the plate, the fluid is stationary at $y = 0$ and the fluid is moving along with the flat plate with a velocity $u$ at $y = h$; MRF is in a simple shear flow state. The relationship between the velocity $u$ of any point in the fluid and its longitudinal coordinate value $r$ is:

$$ \dot{\gamma } = \frac{{{\text{d}}u}}{{{\text{d}}r}} = r\frac{{{\text{d}}\omega }}{{{\text{d}}r}} $$

(17)

The property of MRF in the absence of magnetic field is Newton fluid; assuming $\tau_{0} = 0$, the local shear stress can be expressed as:

$$ \tau = \eta_{0} \cdot \dot{\gamma } $$

(18)

The general solution of the flow differential Eq 4 is as follows:

$$ \tau = C/r^{2} $$

(19)

The boundary conditions are as follows:

When $r = r_{1}$, $\omega = 0$;

When $r = r_{2}$, $\omega = \varOmega$.

Combining Eqs 17, 18, and 19 and boundary conditions, the angular velocity equation under zero field is as follows:

$$ \omega = \frac{{r_{1}^{2} \cdot r_{2}^{2} }}{{r_{1}^{2} - r_{2}^{2} }}\left( {\frac{1}{{r^{2} }} - \frac{1}{{r_{1}^{2} }}} \right) \cdot \varOmega $$

(20)

When $\tau_{0} = 0$, the shear rate is as follows:

$$ \dot{\gamma } = r \cdot \frac{{{\text{d}}\omega }}{{{\text{d}}r}} = \frac{2}{{\frac{1}{{r_{1}^{2} }} - \frac{1}{{r_{2}^{2} }}}} \cdot \frac{1}{{r^{2} }} \cdot \varOmega \quad (\tau_{0} = 0) $$

(21)

By formula (21), we can know that the shear rate of MRF under zero field condition is only related to the angular velocity and radius of the fluid, not with the viscosity and other liquid parameters. The maximum shear rate of MRF in the flow channel with the change in fluid angular velocity is shown in Fig. 4.

Fig. 4

Maximum shear rate vs. fluid angular velocity

It can be seen that the maximum shear rate of MRF can reach 3 × 10⁴ s⁻¹ with the rheometer under zero field condition. The maximum shear rate increases with the increase in the shear yield strength, but the increase is limited, and the shear rate under zero field condition is dominant.

Magnetic Flux Density in Flow Channel

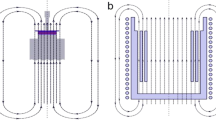
The rheological property of MRF is the relationship between the shear yield strength and the magnetic flux density. Magnetic materials involved with MRF and Q235 steel, the relative permeabilities of these materials are not constant, but with the changes in the magnetic field strength and other magnetic parameters which show the nonlinear. Therefore, it is not easy to estimate the magnetic flux density in the gap of the parallel plate according to the method of the linearization in the past. Finite element simulation is usually adopted in the calculation of the magnetic field, but the simulation result is the magnetic field of the ideal condition, it is difficult to consider the magnetic leakage and magnetic loss caused by the assembly clearance and other factors. In this paper, through the experiment to measure the magnetic flux density in the parallel plate gap, specific methods are as follows: A small hole is reserved on the bottom cover of the device, which is convenient for the probe of the Tesla meter. The magnetic flux density of the parallel plate gap is measured by the Tesla meter when the excitation coil is loaded with different current. Measure the average value of several times, the relationship between the magnetic flux density and the excitation current in the flow channel is obtained by polynomial fitting of the mean value, as shown in Fig. 5.

Fig. 5

Magnetic flux density vs. electrical current

Influence Factors Analysis

The key of MRF shear yield strength testing is to obtain the torque of the brake disk in the flow channel, and the torque is measured directly by the torque sensor in the test bench.

Structure Factor

Effect of structural factors on torque mainly includes two parts: (a) friction torque generated by fluid at the edge of the brake disk and (b) the energy loss caused by the direction change, sudden expansion and sudden contraction of fluid. Although these two parts have theoretical formula or empirical formula, it is necessary to determine the relevant parameter values by experiments, which increases the complexity of the experiment.

Friction Factor

Friction torque with the change in excitation current will change significantly. Although the experiment can be carried out before inputting current, the lubrication characteristics of MRF can be influenced by the current, so that the measured friction torque is not in conformity with the true value.

Temperature Factor

Temperature mainly affects the viscosity and shear yield strength of MRF. The working temperature of MRF will be significantly different for different application objects or environment. Ordinary rheometer finds it difficult to control the working temperature of the MRF, while the rheometer can realize the temperature control by constant temperature box, of course, ignoring temperature rise slightly caused by converting mechanical energy into heat dissipation.

Elimination and Control of Influence Factors

The shear yield strength of MRF is affected by the structural factor, the friction factor and the temperature factor, which should be eliminated or controlled when making the experimental procedure.

In order to eliminate the influence of the structural factors and the friction factors, the width of the parallel plate gap was designed as 2 mm and the width of the brake disk was designed as 40 mm. In order to realize the control of temperature, the temperature sensor is embedded in the device, and the epoxy resin is encapsulated in the conical hole of the end cover which is close to the brake disk. Rheometer is kept warm for 1 h in constant temperature incubator before the test of brake torque. The required brake torque is measured and the temperature monitored immediately after taking out, and the process of thermal insulation and testing is repeated until the test task is completed if the temperature changes. The MRF samples prepared by our research group were tested by using this device; the relationship between the braking torque and the rotational speed of the rotating shaft when the temperature was 50 °C is shown in Fig. 6. The function relation can be obtained by fitting the data:

Fig. 6

Baking torque vs. rotational speed

$$ T = 0.106n + 418.35 $$

(22)

Experimental Results

The Structure of the Test System

MRF rheological properties testing system is composed of the experimental bench, torque sensor, temperature sensor, driving motor, cooling system, signal control and acquisition system, as shown in Fig. 7.

Fig. 7

Photograph of the experimental setup

Apparent Viscosity Test

Viscosity is generally expressed as the relationship with the shear rate, and by the combining formulas (6) and (11), the apparent viscosity of the MRF can be obtained:

$$ \eta { = }\frac{{\tau_{0} }}{{\dot{\gamma }}}\left( {\frac{{r_{1}^{2} }}{{r^{2} }} - 1} \right) $$

(23)

The apparent viscosity changed with the shear rate of MRF when the temperature is 50 °C. It can be seen that the shear thinning of MRF is more obvious when the shear rate is smaller, and the apparent viscosity is basically stable when the shear rate is larger, as shown in Fig. 8.

Fig. 8

Apparent viscosity vs. shear rate

Shear Yield Strength Test

The shear yield stress is a critical point of the solid–liquid properties of MR fluid, which is one of the main performance parameters of MRF. It is the key to test yield stress correctly for mechanism research and application research of MRF. In this paper, the rheological properties of MRF were obtained by several tests with the testing device, and the relationship between the shear stress and the shear rate under different magnetic field strength is shown in Fig. 9. The shear stress increased with the increase in the shear rate when the shear rate was less than 500 s⁻¹. After that, the shear stress increased slowly with the increase in shear rate. At the same time, we can see that the shear stress of MRF increased rapidly with the increase in magnetic field.

Fig. 9

Shear stress vs. shear rate under different magnetic field strength

In addition to the magnetic field, temperature and other factors will affect the shear yield strength of MRF, the time of MRF flows through the flow channel in a week (i.e., dwell time in single cycle) is an important basis for measuring whether the MRF take place the rheological effect under the vertical magnetic field. The calculation formula for the dwell time in single cycle is:

$$ t = \frac{{2\pi r \cdot r_{1} }}{1000 \cdot \omega r \cdot h} = \frac{{2\pi r_{1} }}{1000\omega h} $$

(24)

Literature [12] pointed out that the response time of MRF is 1–2 ms. Only the dwell time of MRF is larger than the response time of the magnetic field, which can ensure the full play of the rheological effect. According to Fig. 10, the larger the width of MRF gap, the smaller the dwell time in single cycle used as the basis for the structural design of the testing device.

Fig. 10

Dwell time in single cycle vs. the width of MRF gap

Literature [8] showed that the shear yield strength of MRF will decrease obviously when the dwell time in single cycle is less than 1 ms, but the shear rate has little effect on the yield strength of the shear. In this paper, the shear yield strength of MRF is expressed as the change in dwell time in single cycle when test temperature is 50 °C, and the magnetic flux density is 0.5T, as shown in Fig. 11. According to Fig. 11, the shear yield strength is about 52 kPa when dwell time in single cycle is long enough. The shear yield strength decreases to 95% when dwell time in single cycle is 1.9 ms, and the shear yield strength decreases to 69.2% when dwell time in single cycle is 0.5 ms. Therefore, in order to make full use of the rheological effect of MRF, dwell time in single cycle should be greater than 2 ms. In addition, attention should be given to the influence of the width of MRF gap on dwell time in single cycle when designing the testing device.

Fig. 11

Yield stress vs. dwell time in single cycle

Conclusion

The accurate analytical expressions of MRF rheological parameters in terms of structural dimensions of testing device and shear rate in the parallel plate gap were derived, which provided the theoretical foundation for designing the testing device.

The flow state of MRF in the parallel plate gap was analyzed. The Reynolds number was less than 2300 when the average flow velocity was 39.25 m/s, and the MRF was in a laminar flow state, which provided a theoretical support for the mathematical model based on the assumption of laminar flow. The testing device of MRF rheological properties was similar to that of the rotating device, and it broadened the thinking of MRF rheological properties testing. Filling the liquid was convenient, which can realize the temperature control based on the temperature sensor.

The maximum shear rate of the testing device for MRF rheological properties was 3 × 10⁴ s⁻¹, which can be used for the experimental study of MRF characteristics under high shear rate and high flow velocity.

The self-made MRF was tested by means of rheological properties testing device. The results showed that the shear thinning of MRF was more obvious when the shear rate was smaller, and it tended to be stable with the increase in shear rate. There was a significant decrease in the shear yield strength when dwell time in single cycle was less than 2 ms. Therefore, under the condition of high flow velocity or impact, the design of MRF rotating device must consider the dwell time in single cycle to ensure the controllability of the rotating torque. The width of the MRF gap affected the dwell time in single cycle, and it should be considered in the design of the device. According to the experimental results, it was known that the more optimal width of the MRF gap is 2 mm in the rotating device.