1 Introduction

In light of the escalating energy crisis, the development of new energy vehicles and reducing dependence on oil and natural gas has gained paramount importance (Ref 1). To enhance the driving range and minimize battery size and costs, original equipment manufacturers (OEMs) are actively exploring novel lightweight designs (Ref 2). Al-Si alloys have emerged as pivotal materials for future lightweight applications, courtesy of their low density, high specific strength and stiffness, and excellent recyclability (Ref 3). However, it is worth noting that Al-Si alloys typically contain some Fe impurities, leading to the formation of the β-AlSiFe (Al9Si2Fe2) phase (Ref 4). This phase exhibits a needle-like morphology and exerts unfavorable effects on alloy properties, especially in terms of ductility. Consequently, the ductility of the β-AlSiFe phase plays a critical role in determining the mechanical properties of Al-Si alloys.

Many studies have been conducted by researchers to enhance the ductility of the β-AlSiFe phase. Among these studies, alloying with other elements has proven to be an effective method for improving the mechanical properties of metals (Ref 5). Specifically, Taylor et al. (Ref 6) demonstrated that the presence of Mn, along with Si, leads to the formation of the cubic Al15(Fe, Mn)3Si2 phase over the hexagonal Al8Fe2Si phase. Chen et al. (Ref 7) observed that the inclusion of Sc introduces primary Al3Sc, enhancing heterogeneous nucleation during the solidification of AlSi10Mg alloy. This results in the formation of an ultrafine network eutectic structure, significantly improving tensile strength (by nearly 23%). Furthermore, Hou et al. (Ref 8) identified that the needle-like δ-Al4FeSi2 phase in the TC-3C alloy can be replaced by the skeletal α-Al (Fe, Mn, Cr) Si phase with the addition of (2Mn + 1Cr). The aforementioned studies suggest that the introduction of additional alloying elements can enhance the ductility of the AlSiFe phase and modify the mechanical properties of Al-Si alloy. However, the specific mechanisms through which these added alloy elements affect the AlSiFe phase remain unclear, and the optimal selection of alloy elements remains a challenge.

According to Knipling (Ref 9), the development of cast aluminum alloys for high-temperature applications necessitates satisfying specific criteria by the alloying elements. Specifically, these elements must be capable of forming thermally stable strengthening phases, have limited solubility in the Al matrix, exhibit low diffusivity within the Al matrix, and maintain the alloy's ability for conventional solidification. Research has highlighted that among alloying elements, transition metals capable of forming thermally stable and coarsening-resistant precipitates offer potential advantages when dealing with Al-Si alloys (Ref 10). Based on this theory, scientific researchers conducted a series of attempts. For instance, Shaha et al. (Ref 11) argued that intermetallic precipitates incorporating Zr, Ti, and V enhance the fatigue life of the Al-Si-Cu-Mg cast alloy. Additionally, they observed a positive effect on alloy strength due to micro-additions of transition metals (Ref 12). However, proposing a simpler design strategy to reduce modification costs is still a focus of scientific researchers.

With advancements in the first-principles methods and computational resources, theoretical modeling provides new opportunities for the rational design of alloying elements. For instance, Han et al. (Ref 13) employed a first-principles approach to calculate the optimal doping sites for rare-earth elements in Mg2Si, revealing that La exhibits the most favorable modification effect on Mg2Si. Kumar et al. (Ref 14) examined the effect of Cr doping on the mechanical properties of the theoretically studied Ni3Al phase and found that Cr-doped Ni3Al outperforms undoped Ni3Al in bulk modulus performance. Based on an integration of the literature reviewed above, we believe that enhancements to the mechanical properties of the AlFeSi phase, achieved through the first-principles calculations, are feasible.

In this study, we utilize a highly accurate first-principles approach to investigate the impact of doping transition metals (M = Cr, Mn, V, Ti, and Zr) on the structural stability and mechanical properties of the β-AlSiFe (Al9Si2Fe2) phase. We assess the structure stability using binding energy and enthalpy of formation. We also evaluate the influence of dopant elements on the modulus of elasticity, Poisson's ratio, and hardness of the AlFeSiM phase. Additionally, we employ uniaxial stretching to assess the tensile properties of the AlSiFeM phase. Specifically, we employ the density of states (DOS) and charge differential to elucidate the mechanism by which dopant elements enhance the mechanical properties of AlSiFe. Simultaneously, we employ the Bader charge to assess the charge transfer surrounding the dopant atoms.

2 Computational Details

2.1 Basic Calculation Parameters

The first-principles calculations were conducted using density functional theory (DFT) implemented in the Vienna ab initio simulation package (VASP) (Ref 15). Electron–ion interactions were described employing the projected augmented wave (PAW) method (Ref 16) with a kinetic energy cutoff of 500 eV. Exchange correlation was modeled using the generalized gradient approximation (GGA) within the Perdew–Burke–Ernzerhof scheme (PBE) (Ref 17). A 7 × 7 × 7 Monkhorst–Pack k-point mesh was utilized to sample the first Brillouin zone (Ref 18), and convergence thresholds for energy and force components were set at 10-6 eV and − 0.01 eV/Å. Notably, Bader charge analysis was conducted using the code developed by Henkelman’s group (Ref 19), and the ElasticPOST code was employed to generate the Poisson ratio in three dimensions.

2.2 Computational Model Building

Figure 1 illustrates the structure of the β-AlSiFe (Al9Si2Fe2) phase, which exhibits C2/C symmetry (space group C2H-6) and a monoclinic lattice. In this representation, cyan atoms correspond to Al, blue atoms represent Fe, and earthy yellow atoms depict Si. The optimized lattice constants are a = 20.752 Å, b = 6.160 Å, and c = 6.157 Å. This structure contains a total of seven Al sites, two Fe sites, and two Si sites. In this study, transition metals (M = Cr, Mn, V, Ti, and Zr) were introduced as substitutions for Al, Fe, and Si sites in each β-AlSiFe model. These modified models were denoted as M-Al-1 to M-Al-7, M-Fe−1, 2, and M-Si-1, 2, respectively.

Fig. 1
figure 1

Schematic diagram of β-AlSiFe phase structure and doping sites

Full size image

2.3 Elastic Constants Calculation

Elastic constants characterize the response of crystals to stress and strain, providing insights into their mechanical properties. In this study, we computed the elastic matrices for the AlSiFeM phase. Subsequently, the bulk elastic modulus (B), shear modulus (G), and Young's modulus (E) were derived from these elastic constants. The bulk modulus, shear modulus, Young's modulus, and Poisson's ratio were determined using the Voigt–Reuss–Hill approximation.

For the monoclinic phase (Ref 20):

$$ B_{V} = \left( {1/9} \right)\left[ {C_{11} + C_{22} + C_{33} + 2\left( {C_{12} + C_{13} + C_{23} } \right)} \right] $$
(1)
$$ G_{V} = (1/15)\left[ {C_{11} + C_{22} + C_{33} + 3\left( {C_{44} + C_{55} + C_{66} } \right) - \left( {C_{12} + C_{13} + C_{23} } \right)} \right] $$
(2)
$$ B_{R} = \Omega \left[ \begin{gathered} a\left( {C_{11} + C_{22} - 2C_{12} } \right) + b\left( {2C_{12} - 2C_{11} - C_{23} } \right) + c\left( {C_{15} - 2C_{25} } \right) \hfill \\ + d\left( {2C_{12} + 2C_{23} - C{}_{13} - 2C_{22} } \right) + 2e\left( {C_{25} - C_{15} } \right) + f \hfill \\ \end{gathered} \right]^{ - 1} $$
(3)
$$ G_{R} = 15\left\{ \begin{gathered} 4\left[ {a\left( {C_{11} + C_{22} + C_{12} } \right) + b\left( {C_{11} - C_{12} - C_{23} } \right) + c\left( {C_{15} + 2C_{25} } \right) + d\left( {C_{22} - C_{12} - C{}_{23} - C_{13} } \right) + e\left( {C_{15} - C_{25} } \right) + f} \right]/\Omega \hfill \\ + 3\left[ {g/\Omega + \left( {C_{44} + C_{66} } \right)/\left( {C_{44} C_{66} - C_{46}^{2} } \right)} \right] \hfill \\ \end{gathered} \right\}^{ - 1} $$
(4)
$$ a = C_{33} C_{55} - C_{35}^{2} $$
(5)
$$ b = C_{23} C_{55} - C_{25} C_{35} $$
(6)
$$ c = C_{13} C_{35} - C_{15} C_{33} $$
(7)
$$ d = C_{13} C_{55} - C_{15} C_{35} $$
(8)
$$ e = C_{13} C_{25} - C_{15} C_{23} $$
(9)
$$ f = C_{11} \left( {C_{22} C_{55} - C_{25}^{2} } \right) - C_{12} \left( {C_{12} C_{55} - C_{15} C_{25} } \right) + C_{15} \left( {C_{12} C_{25} - C_{15} C_{22} } \right) + C_{25} \left( {C_{23} C_{35} - C_{25} C_{33} } \right) $$
(10)
$$ g = C_{11} C_{22} C_{33} - C_{11} C_{23}^{2} - C_{22} C_{13}^{2} - C_{33} C_{12}^{2} + 2C_{12} C_{13} C_{23} $$
(11)
$$ \begin{gathered} \Omega = 2\left[ {C_{15} C_{25} \left( {C_{33} C_{12} - C_{13} C_{23} } \right) + C_{15} C_{35} \left( {C_{22} C_{13} - C_{12} C_{23} } \right) + C_{25} C_{35} \left( {C_{11} C_{23} - C_{12} C_{13} } \right)} \right] \hfill \\ \;\;\;\;\;\; - \left[ {C_{15}^{2} \left( {C_{22} C_{33} - C_{23}^{2} } \right) + C_{25}^{2} \left( {C_{11} C_{33} - C_{13}^{2} } \right) + C_{35}^{2} \left( {C_{11} C_{22} - C_{12}^{2} } \right)} \right] + gC_{55} \hfill \\ \end{gathered} $$
(12)

For triclinic phase (Ref 21):

$$ B_{V} = \frac{1}{9}\left[ {\left( {C_{11} + C_{22} + C_{33} } \right) + 2\left( {C_{12} + C_{23} + C_{13} } \right)} \right] $$
(13)
$$ 1/B_{R} = \left( {S_{11} + S_{22} + S_{33} } \right) + 2\left( {S_{12} + S_{23} + S_{13} } \right) $$
(14)
$$ G_{V} = \frac{1}{15}\left[ {\left( {C_{11} + C_{22} + C_{33} } \right) - \left( {C_{12} + C_{23} + C_{13} } \right) + 3\left( {C_{44} + C_{55} + C_{66} } \right)} \right] $$
(15)
$$ 15/G_{R} = 4\left( {S_{11} + S_{22} + S_{33} } \right) - 4\left( {S_{12} + S_{23} + S_{13} } \right) + 3\left( {S_{44} + S_{55} + S_{66} } \right) $$
(16)
$$ B = \left( {B_{R} + B_{V} } \right)/2 $$
(17)
$$ G = \left( {G_{V} + G_{R} } \right)/2 $$
(18)
$$ E = \frac{9BG}{{3B + G}} $$
(19)
$$ \nu { = }\frac{{{3}B - 2G}}{6B + 2G} $$
(20)

here \(C_{ij}\) is stiffness tensor, and \(S_{ij}\) is the compliance tensor.

3 Results and Discussion

3.1 Structure and Stability

To assess the structural stability following element doping, we examined the binding energy and enthalpy of formation for the AlSiFeM phase, with the formula given as follows (Ref 22):

$$ \Delta H = E_{{{\text{toi}}}} - \frac{{\left( {N_{A} E_{{{\text{solid}}}}^{A} + N_{B} E_{{{\text{solid}}}}^{B} + N_{C} E_{{{\text{solid}}}}^{C} } \right)}}{{N_{A} + N_{B} + N_{C} }} $$
(21)
$$ E_{{{\text{coh}}}} = E_{{{\text{toi}}}} - \frac{{\left( {N_{A} E_{{{\text{atom}}}}^{A} + N_{B} E_{{{\text{atom}}}}^{B} + N_{C} E_{{{\text{atom}}}}^{C} } \right)}}{{N_{A} + N_{B} + N_{C} }} $$
(22)

The formula, \(E_{{{\text{toi}}}}\), represents the total energy per atom for the AlSiFeM phase at the equilibrium lattice constant. N and \(E_{{{\text{solid}}}}\) denote the number of atoms of a specific element and the ground-state energy of an atom in the solid state, respectively. \(E_{{{\text{atom}}}}\) represents the ground-state energy of a single atom of a specific element in its free state. Figure 2 displays the hotmap illustrating binding energy and enthalpy of formation after the introduction of transition metals. In this representation, a blue color in the hotmap corresponds to higher energy values, while a redder color indicates lower energy values. The intensity of color in the hotmap suggests that transition metal atoms are prone to substituting Al sites (Al-4 and Al-6) in order to create a stable phase.

Fig. 2
figure 2

Analysis of formation enthalpy and binding energy of AlSiFeM phase after doping elements (a) hotmap of formation enthalpy and (b) hotmap of binding energy

Full size image

To further evaluate the optimal doping sites and stability of various dopant atoms, the results are presented in Table 1. A more negative binding energy compared to pure AlSiFe suggests higher stabilization of the AlSiFeM compound. Additionally, a more negative enthalpy of formation than that of pure AlSiFe indicates the spontaneous formation of the structure. Notably, Ti-Al-4 (− 0.309 eV) and Zr-Al-6 (− 0.305 eV) exhibit lower enthalpies of formation than pure AlSiFe (− 0.304 eV), suggesting a preference for their generation over pure AlSiFe. Moreover, the binding energy results reveal that all AlSiFeM phases are significantly more stable than AlSiFe. It is worth mentioning that substituting Al for M induces a transition from monoclinic to triclinic crystal systems, reducing crystal symmetry and increasing lattice structure disorder. Additionally, the oblique crystal system typically possesses more slip systems, facilitating easier crystal slip under stress and enhancing material plastic deformation capability.

Table 1 AlSiFeM doping structure and stability performance analysis
Full size table

3.2 Mechanical Properties

Following the crystal mechanical stability criterion (Ref 23), it is established that all AlSiFeM phases exhibit mechanical stability, the compliance tensor of triclinic phases has been provided in the supplementary materials (Tables S1-S5). The calculation results for the elastic constants and mechanical properties of the AlSiFeM phase are presented in Table 2.

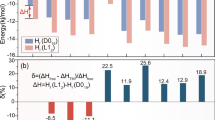
Table 2 Analysis of mechanical properties of AlSiFeM phase
Full size table

Figure 3(a) illustrates the changes in volume modulus, shear modulus, and Young's modulus of the AlSiFe phase following the introduction of different transition metals. Upon the incorporation of transition metals into AlSiFe, there is a gradual decrease in the volume modulus, shear modulus, and Young's modulus. Achieving good toughness necessitates a low shear modulus (G) and a high bulk modulus (B). The Zr-Al-6 site is the one that meets these criteria, with bulk modulus, shear modulus, and Young's modulus values of 88.493 GPa, 62.623 GPa, and 152.011 GPa, respectively. This indicates a substantial improvement in the brittleness of the AlSiFe phase as a result of Zr doping.

Fig. 3
figure 3

Effect of doping elements on elastic modulus of AlSiFe phase (a) elastic modulus and (b) Pugh’s ratio

Full size image

Pugh (Ref 24) proposed that a material is considered ductile if the ratio of bulk modulus to shear modulus (B/G) is greater than 1.75, as indicated in Fig. 3(b). While the B/G ratio for all AlSiFeM phases was below 1.75, suggesting that all phases are brittle, the Zr-Al-6 phase (with a B/G ratio of 1.413) exhibited superior results compared to the pure AlSiFe phase (with a B/G ratio of 1.352).

To further compare the variations in Poisson's ratio resulting from the doping of transition metals in the AlSiFe phase, as depicted in Fig. 4, a higher Poisson's ratio suggests greater transverse contraction during stretching, possibly indicating increased flexibility. Figure 4(a) and (d) exhibits good symmetry, indicating strong resistance to deformation. Notably, the Ti-Al-4 phase demonstrates the highest symmetry, suggesting the smallest Poisson's ratio. The Poisson's ratios for pure AlSiFe and its alloy counterparts, including Cr-Al-4, Mn-Al-3, V-Al-4, Ti-Al-4, and Zr-Al-6, are 0.203, 0.211, 0.191, 0.199, 0.134, and 0.214, respectively. All values fall below 0.25, indicating the brittleness of these materials, in line with the B/G ratio results. Notably, the addition of Zr significantly alters the Poisson's ratio in specific orientations, potentially enhancing plasticity. Furthermore, the higher Poisson's ratio observed for Zr-Al-6 suggests an improvement in toughness compared to other AlSiFeM phases.

Fig. 4
figure 4

Effect of doping elements on Poisson's ratio of AlSiFe phase (a) pure AlSiFe; (b) Cr-Al-4; (c) Mn-Al-3; (d) V-Al-4; (e) Ti-Al-4; and (f) Zr-Al-6

Full size image

Furthermore, in accordance with the empirical model introduced by Chen et al. (Ref 25) for Vicker's hardness (HV), this study calculated the theoretical hardness of the AlSiFeM phase. The evaluation formula is as follows:

$$ H_{v} \, = \,2\left( {K^{2} G} \right)^{0.585} - 3 $$
(23)

In this context, K and G represent the Pugh’s ratio (K = G/B) and shear modulus, respectively. Utilizing this formula, we computed the theoretical hardness of the AlSiFeM phase in this study, as illustrated in Fig. 5. The results indicate that after the doping of transition metals, the hardness of Cr-Al-4 and Zr-Al-6 decreases. With Zr doping, the theoretical hardness reaches a minimum value of 11.618 GPa. This observation highlights a significant reduction in the hardness of Zr-Al-6, which is consistent with the trends in elastic modulus values.

Fig. 5
figure 5

Effect of doping elements on expansion of AlSiFe phase

Full size image

The maximum stress (σmax) was regarded as the theoretical tensile strength (Ref 26). The σmax for Zr-Al-6 was 151.258 GPa, which was lower than that of the pure AlSiFe phase (181.562 GPa), indicating a reduction in maximum stress due to Zr doping. It is important to highlight that the strain of Zr-Al-6 increased by 40% in comparison with the pure AlSiFe phase. This finding aligns with the elastic modulus calculations, indicating an improvement in fracture resistance of the AlSiFe phase due to Zr doping, particularly evident in the Zr-Al-6 phase showing superior crack resistance (Fig. 6).

Fig. 6
figure 6

Effect of doping elements on stress and strain characteristics of AlSiFe

Full size image

3.3 Electronic Characteristics Analysis

To analyze the internal mechanism of the impact of Zr addition on the mechanical properties of the AlSiFe phase, we conducted electronic density of states calculations for AlSiFeM, as illustrated in Fig. 7. The total density of states for AlSiFe remains consistent before and after the introduction of transition metal doping. Electronic states are observed at the Fermi level, confirming the metallic nature of the AlSiFeM alloy, as shown in the results. Notably, the addition of Zr does not result in significant orbital hybridization, leading to a weak pseudogap effect (Ref 27). This effect is the primary reason for the decrease in hardness and the increase in toughness.

Fig. 7
figure 7

Effect of doping elements on electronic properties of AlSiFe phase

Full size image

To better understand the interactions of transition metals with AlSiFe phase, we studied the differences in the charge density (\(\Delta \rho\)) of AlSiFeM:

$$ \Delta \rho = \rho_{{{\text{all}}}} - \rho_{{{\text{atom}}}} $$
(24)

where \(\rho_{{{\text{all}}}}\) and \(\rho_{{{\text{atom}}}}\) are the charge densities and isolated atom of the after-transition metals doping. The green region in Fig. 8 indicates an increase in electron density, and the red region indicates a decrease in it. The redistribution of electrons is clear in the around of transition metal atoms. It is notable that there is no significant charge accumulation around the Zr atom (dark red area), and the electrons are evenly distributed, suggesting that the bond strength with specific surrounding atoms has not notably increased. Additionally, Bader charge analysis reveals that Zr transferred 1.102 |e| to Al, Si, or Fe atoms, contributing to the enhancement of toughness in the AlSiFe phase through the combined effects of the above two factors.

Fig. 8
figure 8

Analysis of charge difference and charge transfer in AlSiFe after doped elements

Full size image

4 Conclusion

We conducted the first-principles calculations to investigate the impact of transition metal (M) doping, including Cr, Mn, V, Ti, and Zr, on the structural stability and mechanical properties of the β-AlSiFe phase. The results indicate that Ti-Al-4 (− 0.309 eV) and Zr-Al-6 (− 0.305 eV) have a lower enthalpy of formation compared to pure AlSiFe (− 0.304 eV), suggesting a propensity for the preferential formation than that of pure AlSiFe. In terms of mechanical properties, the Zr-Al-6 phase (1.413) exhibits improved toughness compared to the pure AlSiFe phase (1.352). Importantly, Zr doping enhances the fracture behavior of the tensile test, resulting in a remarkable 40% increase in strain compared to the pure AlSiFe phase. It is worth noting that Zr incorporation minimally impacts orbital hybridization, thus contributing to the enhancement in toughness. This study offers valuable insights into augmenting the ductility of the β-AlSiFe phase and elevating the overall mechanical properties of Al-Si alloys.