1 Introduction

In the last century, fossil fuel burning has been the main driver of industrial development, which has led to severe environmental problems. The emission of greenhouse gases, such as CO2 and NO2 creates air pollution, directly leading to acid rain and global warming, among many other problems (Ref 1,2,3). Hence, reducing the emission of harmful gases is an urgent issue. Tremendous efforts are being devoted to this initiative in terms of energy, materials, and financial resources. However, this problem is very challenging to solve, and new ideas are required. In the automotive industry, for example, lowering the bodyweight of a motor vehicle can reduce greenhouse gas emission effectively, where an overall weight reduction by 10% would translate into a 6 to 8% increase in efficiency. On the other hand, a reduction in weight by 1% would reduce fuel consumption for 100 kilometers (Ref 4). In this regard, some studies dealing with the reduction in weight of motor vehicle bodies have been carried out via structural design and reduction in material mass. Another method to reduce weight involves designing new materials with high strength. Note that the tensile strength and plasticity cannot be increased at the same time. In other words, the increase in tensile strength will decrease the plasticity of the materials. Hence, designing novel materials without size limitation and relatively small weight is highly desirable. Low-density materials can meet these requirements, which might be suitable for the formation of functional alloys.

Among related materials, Fe-Mn-Al-C series of low-density multi-principal-element high-strength alloys have attracted increasing attention due to their excellent strength and plasticity (Ref 5, 6). To reduce the density of alloys, light-weight elements are often added. Al with a density of 2.7 g/cm3 is the most suitable light-weight element added to alloys. However, the addition of Al as a ferrite stabilizing element can easily form FeAl intermetallic compounds, leading to reduced plasticity and toughness of the alloys. To limit the influence of intermetallic compounds on the properties of the material, austenite stabilizing elements Mn (ρ = 7.47 g/cm3) and C (ρ = 1.8 g/cm3) can be used to enlarge the austenite phase zone. Some studies have reported that the addition of 1 wt.% Al, Mn, and C reduced the alloy density by 0.1 g/cm3, 0.0085 g/cm3, and 0.41 g/cm3, respectively. Hence, the incorporation of low-density elements can effectively reduce the density of alloys (Ref 4, 5, 7, 8).

Various ways to control the mechanical properties of low-density alloys have so far been investigated. For instance, Moon et al. (Ref 9) studied low-density Fe-30Mn-10.5Al-11C-χMo (χ = 0 − 5%) austenite alloy and observed a decrease in yield strength (YS) as Mo content rose to 3 wt.%. In addition, the great enhancements in YS were recorded at Mo contents exceeding 4 wt.%. Wang et al. (Ref 10) investigated high strength low-density alloys via the addition of microalloying elements. They found that the addition of Ti led to an increase in precipitated carbides, thereby improving the YS and ultimate tensile strength. Yang et al. (Ref 11) explored the hot deformation behavior of low-density alloys consisting of Fe, Mn, Al, and C. They found that increasing the deformation temperature and rate led to a gradually enhanced recrystallization degree. On the other hand, cold deformation also effectively strengthens the mechanical properties of low-density alloys. Cold-rolling and annealing are necessary steps for changing the microstructure, grain size, and mechanical properties of low-density alloys (Ref 12,13,14,15,16). However, the relationship among cold deformation, strengthening mechanism, and microstructure in Ti-containing low-density high-strength alloys has not yet been studied.

In the present study, the effects of cold deformation and annealing conditions on microstructures and mechanical properties of low-density Fe-30Mn-10Al-1.57C-2.3Cr-0.3Si-0.6Ti alloy (denoted as low-density high-strength alloy) were studied. To this end, cold deformed low-density alloys deformed by 30% were annealed at different temperatures for 1 h. The results revealed that the mechanical properties of low-density alloys can be optimized by combining cold deformation and annealing treatment.

2 Experimental

2.1 Samples Preparation

The ingot based on Fe-30Mn-10Al-1.57C-2.3Cr-1Si-0.6Ti alloy (50 Kg) was prepared in a vacuum induction melting furnace under high-purity argon protection. The nominal and actual compositions of the as-prepared alloys are listed in Table 1. The as-prepared specimens were referred to as low-density high-strength alloys. The actual chemical compositions of the specimens were obtained through chemical analysis. The elemental contents of Mn and Fe were measured via the perchloric acid oxidation trivalent manganese titrimetric method, and those of Al, Si, Cr, and Ti were analyzed by inductively coupled plasma (ICP) emission spectrometry. The contents of C and S were obtained by carbon sulfur analysis. The ingot was annealed at 1200 °C for 12 h at a rate of 10 °C/min for homogenization, and then cooled to room temperature in a muffle furnace. After the homogenization process, the ingot was forged into a cuboid at 1100 °C followed by cooling to room temperature in the furnace, denoted as furnace cooling (FC). Next, the forged specimens were cut into pieces with dimensions of 10 × 10 × 20 mm via wire electrical discharge machining (WEDM), and then hot-rolled at 950 °C to yield 5 mm total thickness, equivalent to a reduction of 75%. To prevent specimens from cracking, the rolling process followed two steps. The resulting rolled specimens were then placed in a 950 °C muffle furnace for 5 min followed by cooling to room temperature with water. Afterward, the specimens were placed in a muffle furnace at 950 °C for 2 h and then quenched to room temperature in water for solution treatment. The obtained specimens were again placed in a muffle furnace at 350 °C for 6 h followed by cooling to room temperature in air to complete the artificial aging treatment. The obtained specimens were next cold-rolled to 3.5 mm with thickness reduction corresponding to 30%. The specimens were then annealed at 200, 250, 300, 350, 400, 450, 500, and 550 °C for 1 h, followed by cooling to room temperature in water and air to yield specimens denoted as WQ and AQ, respectively. A schematic illustration of thermo-mechanical treatment showing the deformation stage, solution treatment stage, and aging treatment stage is provided in Fig. 1. To study the effects and regular patterns of temperature and cooling method, alloys annealed at 300, 450, and 550 °C were selected and referred to as NA (not annealed), 300 AQ, 300 WQ, 450 AQ, 450 WQ, 550 AQ, and 550 WQ, respectively.

Table 1 Chemical compositions of high Mn/Al low-density alloys (wt.%)
Full size table
Fig. 1
figure 1

Schematic illustration of the cold-rolling and annealing process

Full size image

2.2 Characterization

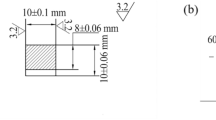
The uniaxial tensile test (ASTM: E8/E8M-16a) was carried out at room temperature using an Instron 5982 universal testing machine, and the strain was measured using a dynamic extensometer (Instron 2620-601) at an initial strain rate of 5 × 10−4 s−1. To ensure the repeatability of data, three identical dog-bone-shaped tensile specimens were prepared from the rolled sheet by wire cutting along the rolling direction. The gauge length was set to 21 mm, and the cross-sectional area was 3.00 × 2.00 mm2. The dimensions of tensile specimens are illustrated in Fig. 9(a).

The phase composition of each sample was analyzed by x-ray diffraction (XRD) with Cu Kα radiation (D/max − 2500/PC, ASTM: D5380-93(2014)), in the 2θ range of 30 to 100°, scan step of 0.02°, and counting time of 2 s. The peak position and full width at half maximum (FWHM) were analyzed by commercial MDI JADE 6.0 software (Materials Data Inc., Liverpool, CA). The microstructures were viewed by optical microscopy (OM, Axiovert 200 MAT), scanning electron microscopy (SEM, ZEISS Gemini 300), and electron backscatter diffraction (EBSD, ZEISS Gemini 300). For optical observation, the longitudinal direction of each specimen was prepared following the standard metallographic surface method. Metallographic and SEM samples were polished using 150 # − 4000 # waterproof abrasive papers followed by machine polishing. The microstructure was revealed by etching with 10% nitric acid and alcohol mixture at room temperature. The EBSD data were analyzed by AztecCrystal software at scan step size of 0.17 μm and grid size of 657 × 493.

The equilibrium phase diagram and fractions of the equilibrium phase of low-density alloys were calculated by TCFE module in Thermo-Calc 4.0 software. To this end, the type and content of elements were first set, and then the valid data were automatically extracted from the database, creating an equilibrium phase diagram. The calculation results can be found in previous research results (Ref 17).

The microstructural details of the alloys were studied by transmission electron microscopy/scanning transmission electron microscopy (TEM/STEM, Talos F200x). The specimens were thinned down to 20 μm and then electrochemically polished by twin-jet. The electrochemical polishing was carried out using a solution of 10% perchloric acid and 90% ethanol at 29 V and − 20 °C. The specimens were first cut from the alloy plates by WEDM and then ground using an abrasive paper (5000 #), followed by polishing with a diamond paste to yield a surface finish of 0.05 μm.

The density of each alloy was measured by the Archimedes method. First, three specimens were cut from the cold-rolled piece, weighed in air to record mass M1, and then weighed again in deionized water to record M2. Then, the density (\(\rho\)) of each specimen was calculated by Eq 1:

$$\rho = \frac{{M_{1} }}{{M_{1} - M_{2} }}$$
(1)

where \(M_{1} - M_{2}\) denotes the volume of the specimen.

The average density of each sample was determined from three independently measured density values.

3 Results

3.1 Crystal Phase Analysis

The phase compositions of low-density alloys cold-rolled and annealed under different conditions were analyzed by XRD. The results of NA, 300 AQ, 300 WQ, 450 AQ, 450 WQ, 550 AQ, and 550 WQ are presented in Fig. 2. The XRD patterns of cold-rolled NA specimens are marked by a black line, those of AQ specimens by a dotted line, and those of WQ specimens by a solid line. The cold-rolled low-density alloys consisted of austenite, ferrite, and TiC carbides. As annealing temperature increased, the ferrite peak intensity of AQ specimens rose, indicating enhancement in (110) content and volume of ferrite. Also, as annealing temperature increased, the ferrite peak intensity of WQ decreased while ferrite peak showed a sudden rise at 550 °C, indicating the presence of ferrite phases of (110), (200), (211), and (220). The cold-rolled specimens annealed at 550 °C exhibited the highest ferrite phase peaks.

Fig. 2
figure 2

XRD patterns of cold-rolled specimens under different annealing conditions

Full size image

The phase diagram of phase composition of low-density alloys was obtained by Thermo-Calc 4.0 software. Phase composition of high Al/Mn content low-density alloys can be found in the previous research paper (Ref 10). In the phase diagram, the phase of the alloy can be altered following L → L + BCC. As temperature decreased, FCC phase formed. A further drop in temperature led to the formation of BCC phase and carbides.

3.2 Microstructural Evolution

The microstructures of NA, 300 AQ, 450 AQ, and 550 AQ specimens cold deformed and annealed under different conditions are shown in Fig. 3 (green dotted frame). The microstructures of the specimens consisted of an austenite matrix containing some strip-shaped small particles distributed along the rolling direction with some carbides. The specimens hot-rolled at 950 °C showed a dual-phase zone, indicating that no α → γ phase transformation occurred during the entire process. The ferrite phase confirmed the presence of δ-ferrite formed from the liquid during the hot-rolling process. As the annealing temperature rose, the number of strip-shaped particles decreased. The compositions of different phases were confirmed by EDS. As shown in Fig. 3, the sharp-cornered particles in the quadrilateral were associated with TiC carbides. Also, the matrix and particles distributed in the rolling direction indicated two different phases with the same compositions of Fe, Mn, Al, and C elements. The strip-shaped particles may be ferrite crushed during the cold-rolling process. The microstructural details of NA, 300 WQ, 450 WQ, and 550 WQ are illustrated in Fig. 4 (pink dotted frame). The red color arrows indicate ferrite phase, blue color arrows are austenite, and yellow color arrows represent TiC carbide. As shown in Fig. 5, the influence of annealing temperature on material structure was further investigated by analyzing the κ-carbides in samples annealed at different temperatures. The results indicated that with the increase in annealing temperature, the size of the κ-carbides increased slightly. As shown in Fig. 6, the increase in annealing temperature led to a decline in the volume of ferrite. To further observe the nanoprecipitates, higher magnification SEM was used, and the data are depicted in Fig. 4. The nanoprecipitation of specimens annealed at different conditions was visible with numerous tiny precipitates. Furthermore, some TiC carbides were observed on the austenite matrix depicted as white balls. The nanoprecipitates were uniformly distributed on the austenite matrix as irregular flocs. The volume fraction was counted by Image-Pro Plus (IPP) software, and the statistical results are presented in Fig. 6(b). The green and pink lines indicate AQ and WQ specimens, respectively. At an annealing temperature of 550 °C, the volume fraction of nanoprecipitates in AQ and WQ specimens decreased from 33.11 to 13.66% and 1.73%, respectively. Before annealing at temperature of 450 °C, the decrease rate of the nanoprecipitates volume fraction of WQ specimens was lower than that of AQ.

Fig. 3
figure 3

Microstructures of AQ specimens (framed by green dashed frame) annealed at: (a) NA (b) 300, (c) 450, and (d) 550 °C, as well as WQ specimens (framed by green dashed frame) annealed at: (a) NA, (b) 300, (c) 450, and (d) 550 °C

Full size image
Fig. 4
figure 4

Nanoprecipitate microstructures of AQ specimens (framed by green dashed frame) annealed at: (a) NA, (b) 300, (c) 450, and (d) 550 °C, as well as WQ specimens (framed by green dashed frame) annealed at: (a) NA, (b) 300, (c) 450, and (d) 550 °C

Full size image
Fig. 5
figure 5

(a) TEM images of κ-carbides annealed at 300 °C, (b) TEM images of κ-carbides annealed at 450 °C, (c) TEM images of κ-carbides annealed at 550 °C

Full size image
Fig. 6
figure 6

(a) Average grain sizes of cold-rolled alloys under different annealing conditions. (b) Volume fraction of nanoprecipitates under different annealing conditions

Full size image

The microstructures of low-density alloys after cold deformation were further studied by EBSD. The typical inverse pole figure (IPF) maps, phase distribution (PD) maps, and Kernel average misorientation (KAM) distribution of cold-rolled WQ and AQ specimens are shown in Fig. 7(a), (b), (c), and (d) corresponding to specimens under different annealed conditions. In IPF images, the increase in annealing temperature indicated a rise in grain size. Phase distribution maps were also obtained to characterize the phases of the specimens, where blue color corresponds to austenite, red color to ferrite, and yellow color to TiC carbides. The results suggested a decline in volume fraction of ferrite phase with increase in annealing temperature. The volume fraction of ferrite was larger in specimens without annealing. The average grain size counted by EBSD maps, and the statistical results are exhibited in Fig. 6(a). As annealing temperature increased, the grain size of both cold-rolled and annealed specimens increased. Furthermore, the grain size of AQ specimens was larger than that of WQ specimens. The grain size of WQ specimens increased from 1.15 to 3.68 μm, and that of AQ specimens rose from 4.29 to 10.23 μm.

Fig. 7
figure 7

Inverse pole figure (IPF) maps, phase distribution (PD) maps, and kernel average misorientation (KAM) distribution of cold-rolled AQ and WQ specimens: (a) NA, (b) annealed at 300 °C, (c) annealed at 450 °C, and (d) annealed at 550 °C

Full size image

Further details on microstructure after cold-rolling were obtained by TEM analysis and the data are summarized in Fig. 8(a), (b), and (c). Cold-rolled alloys consisted of austenite matrix (indicated by red arrow) and ferrite (indicated by blue arrow), as shown in Fig. 8(a). Numerous dislocation pile-ups marked by yellow arrows were also seen due to cold deformation. In the diffraction pattern of ferrite (Fig. 8a), ferrite clearly existed, consistent with the XRD results. In Fig. 8(b), the red line indicated the deformation twins and yellow arrows revealed dislocation pile-up around the twins. Moreover, SADP confirmed the existence of deformation twins. The contrast between twins and matrix can clearly be observed, indicating the presence of high-density dislocations. In Fig. 8(c), the tiny grain sizes were associated with κ-carbides evenly distributed on the austenite matrix. SADP also showed the existence of κ-carbides. To further determine the precipitate, STEM-EDS maps of TiC carbides and κ-carbides were obtained, and the data are given in Fig. 8(d) and (e). In the STEM-EDS maps, all the alloying elements including Fe, Mn, Al, C, and Ti were observed, indicated by different colors.

Fig. 8
figure 8

(a) Bright-field TEM images of cold-rolled specimen and SADP characterization of ferrite. (b) Details of microstructure and SADP characterization of deformation twins. (c) Bright-field TEM image and SADP characterization of κ-carbides. (d) STEM-EDS maps of TiC carbides, including Fe, Mn, Al, C, and Ti. (e) STEM-EDS maps of κ-carbides, including Fe, Mn, Al, C, and Ti

Full size image

3.3 Mechanical Properties and Mechanism

The influence of annealing conditions on the mechanical properties and mechanism of cold-rolled low-density Fe-30Mn-10Al-1.57C-2.3Cr-0.3Si-0.6Ti alloys were studied by room temperature uniaxial tensile testing. The engineering stress-strain curves, true stress-true strain curves, and strain hardening rates of AQ and WQ specimens are shown in Fig. 9. Among the cold-rolled low-density alloys, the NA specimen exhibited the highest YS and lowest total elongation (Table 2, Fig. 9(a), (b), (d), and (e)). The YS of the NA specimen reached 1400.11 MPa, ultimate tensile strength (UTS) reached 1567.77 MPa, and total elongation (TE) was 6.65%. After annealing, the total elongation increased. A further rise in annealing temperature led to a decline in YS and UTS. Herein, the work hardening behavior was better reflected in Fig. 9(c) and (f). The strain hardening rate (Θ) as a function of true strain can be calculated according to Eq 2:

$$\Theta = \frac{d\sigma }{{d\varepsilon }}$$
(2)
Fig. 9
figure 9

(a), (b), and (c) Engineering stress-strain curve, true stress-true strain curves, and strain hardening rate of AQ specimens, respectively. (d), (e), and (f) Engineering stress-strain curve, true stress-true strain curves, and strain hardening rate of WQ specimens, respectively.

Full size image
Table 2 Tensile properties of cold-rolled low-density alloys under different annealing conditions
Full size table

The unannealed specimens exhibited the highest work hardening rates. Furthermore, the increase in annealing temperature led to a decline in the work hardening rate. As seen from the average YS, UTS, and TE data (Table 2), annealed specimens at 450 °C exhibited optimal mechanical properties.

3.4 Alloy Density

The density of cold-rolled alloy measured by the Archimedes’ principle was estimated to be ρ = 6.48 g/cm3.

4 Discussion

4.1 Phase Analysis

As seen from phase compositions of cold-rolled low-density alloy annealed under different conditions (Fig. 2), the low-density alloy consisted of austenite matrix, ferrite, and TiC carbides. These data confirmed the formation of FCC structure with a lattice constant (a) of 0.432 nm. The phase composition of cold-rolled specimens annealed under different conditions showed decreased peak intensities of ferrite in AQ specimens as annealing temperature rose. This indicated diminished ferrite contents, confirming the SEM data that will be discussed later. Thus, cold-rolled specimens were made of duplex alloys containing austenite matrix with some ferrites. The XRD patterns also showed the same regular patterns with decreased ferrite volume fraction as annealing temperature increased.

4.2 Microstructural Evolution

In SEM images of cold-rolled specimens under different annealing conditions (NA, 300 AQ, 300 WQ, 450 AQ, 450 WQ, 550 AQ, and 550 WQ) (Fig. 3a, b, c and d), the microstructure was clearly distinguished. Regardless of annealing conditions, all AQ specimens consisted of austenite matrix, fine ferrite particles with a band-like distribution, and some macroscopic square-angle TiC carbides. The WQ specimens also consisted of austenite matrix, ferrite particles, and TiC carbides. High numbers of fine particles were also distributed on the austenite matrix during cold-rolling of low-density alloys. EDS results showed that fine particles related to ferrite were crushed into fragments during the cold-rolling process. The statistical analysis of grain size revealed an increase in grain size under AQ and WQ conditions (Fig. 6a). Furthermore, the variation in grain size of AQ specimens was larger than that of WQ specimens since elevated annealing temperatures induced greater interfacial force for the growth of grain size. The enlarged SEM photos revealed large numbers of fine particles after cold-rolling of specimens under AQ conditions, and these fine particles were distributed linearly along the rolling direction. The EDS maps demonstrated that the fine particles were ferrite crushed into pieces during the cold-rolling process. The WQ specimens displayed similar phenomena. At increased SEM magnification, tiny precipitates appeared on the austenite matrix and were further studied by EDS to explore the second phase. Accordingly, AQ specimens indicated compositions and proportions consistent with κ-carbides, (Fe, Mn)3AlC, with lattice content (a) of 0.385 nm and L′l2 ordered crystal structure termed E21 resembling that of perovskite oxides (Ref 18). The EDS compositions are summarized in Table 3. The counting of carbides volume fraction revealed that annealing temperature and cooling method influenced their distribution and volume fraction. As shown in Fig. 6(b), the increase in annealing temperature led to a decrease in the volume fraction of κ-carbides because of annealing temperature on precipitation of κ-carbides (Ref 19). In addition, κ-carbides showed effective strengthening of low-density alloys.

Table 3 Composition of κ-carbides of WQ specimens
Full size table

The EBSD diagrams of (IPF + GB), PD, and KAM maps under different annealing conditions of low-density alloys are given in Fig. 7. For IPF, the increase in annealing temperature led to enhanced grain size of cold-rolled specimens. Moreover, the ferrite distribution decreased, and NA sample showed the greatest number of ferrites mainly due to the rise in annealing temperature. Also, the austenite nucleation continued growing and austenite expanded towards the ferrite phase, thereby enhancing the volume fraction of austenite, and reducing ferrite content (Ref 20). The EBSD-KAM maps of cold-rolled low-density alloys annealed under different conditions were used to explain the local misorientation of micro grain and significant lattice distortion by point-to-point measurement with lattice orientation inside of the grain. In Fig. 6, the green color indicated high KAM values related to lattice defects, while the blue color represented areas of low KAM for the stress-free region (Ref 21, 22). The higher KAM values showed regions of high distortion or dislocation. The KAM images of AQ specimens displayed a decline in green areas and an increase in blue areas as a function of annealing temperature. Hence, the dislocation density and distortion decreased with the annealing temperature. The same conclusions were drawn for WQ specimens.

Further details about the microstructure after cold-rolling and annealing under different conditions were obtained by TEM analysis. Fig. 8(a) shows the bright-field TEM images of cold-rolled specimen and SADP characterization of ferrite with a zone of [001]. The dislocations were piled up in the grains, leading to increased YS. As shown in Fig. 8(b), the microstructure and SADP characterization of annealing twins revealed dislocations pile-up around the twins’ boundaries, which leads to an increase in YS. In Fig. 8(c), the bright-field TEM image and SADP characterization of κ-carbides identified the presence of carbides with a zone of [011]. The STEM-EDS maps of TiC and κ-carbides in Fig. 8(d) and (e) revealed the existence of Fe, Mn, Al, C, and Ti.

4.3 Mechanical Properties and Mechanism

The effects of different annealing conditions on the mechanical properties and mechanism of cold-rolled low-density alloys were investigated by uniaxial tensile testing at room temperature. The distribution of engineering strain-stress curves, true strain-stress curves, and strain hardening rates of AQ specimens are depicted in Fig. 9(a), (b), and (c), respectively, while the corresponding data of WQ specimens are illustrated in Fig. 9(d), (e), and (f), respectively. To ensure reproducible results, three specimens were tested under each condition. To further display the tensile strengths, the average YS (σ0.2%), engineering UTS (Rm), and elongation to failure (ε) were obtained and the data are displayed in Table 2. As the annealing temperature rose, the YS decreased while TE increased for both AQ and WQ specimens. The best comprehensive mechanical properties of the specimens were obtained at an annealing temperature of 450 °C regardless of the cooling method. The true stress-strain curves presented in Fig. 9(b) and (e) revealed nearly linear strain hardening from the yield point to the failure point. The work hardening rates of cold-rolled specimens AQ and WQ are given in Fig. 9(c) and (f), respectively. Despite fluctuations at the early deformation stage, the work hardening rate remained at a high level, inconsistent with both multistage strains hardening behavior and serrated flow work hardening (Ref 11, 23, 24). The work hardening rate of cold-rolled specimens can be divided into three stages: i) a rapid decreasing stage, ii) a continuous hardening stage with a relatively stable value, and iii) a rapid reduction stage. For this kind of cold-rolled low-density alloy, the NA specimen exhibited the highest work hardening rate at the same true strain. Furthermore, the increase in annealing temperature led to a decline in the work hardening rate regardless of the cooling method. The first stage may be associated with dislocation glide, a precursor to any deformation mechanism, and the second stage may result from mechanical twinning. The mechanical twins contained high levels of sessile dislocation and acted as strong barriers to dislocation gliding, resulting in high strain hardening capacities (Ref 25, 26).

For low-density alloys, several strengthening mechanisms are required to achieve high strength. Note that the strength of the alloy did not result from a single strengthening method but multiple combined ones (Ref 10, 27). Such mechanisms often include dislocation strengthening (Ref 9, 28), fine-grain boundary strengthening (Ref 29), second-phase partial strengthening (Ref 30, 31), and solid solution strengthening (Ref 32).

In general, the YS (\(\sigma\)) can be calculated by the following Eq 3:

$$\sigma = \sigma_{{{\text{gs}}}} + \sigma_{{{\text{dis}}}} + \sigma_{{{\text{ppt}}}} + \sigma_{{{\text{ss}}}}$$
(3)

where \(\sigma\) refers to YS of the alloy, \(\sigma_{{{\text{gs}}}}\) denotes the YS induced by fine-grain boundary strengthening mechanism, \(\sigma_{{{\text{dis}}}}\) represents YS generated by dislocation strengthening mechanism, \(\sigma_{{{\text{ppt}}}}\) refers to YS induced by the second-phase precipitation, and \(\sigma_{{{\text{ss}}}}\) denotes YS caused by solution treatment.

Here, each strengthening mechanism is discussed separately.

As mentioned above, the grain size significantly affected YS since fine grain size induced many grain boundaries. In turn, the grain boundaries prevented the movement of dislocations, leading to accumulated dislocations in the grain boundaries, thereby increasing YS. YS can be calculated by the Hall-Petch equation (Ref 33, 34). Hence, a decrease in grain size would raise the YS of the alloy. Accordingly, \(\sigma_{{{\text{gs}}}}\) can be expressed by Eq 4:

$$\sigma_{{{\text{gs}}}} = \frac{k}{\sqrt d }$$
(4)

where \(\sigma_{{{\text{gs}}}}\) refers to YS contributed by fine grain size. k = 14.55 MPa mm1/2 denotes a material constant known as Hall-Petch coefficient (Ref 35, 36).

The Hall-Petch coefficient is mainly used to characterize the contribution of grain boundaries to YS. The grain sizes of specimens annealed at 300-550 °C and WQ at room temperature were estimated to be 2.52, 1.15, 2.38, and 3.68 μm. The corresponding grain sizes of AQ specimens were 2.25, 4.29, 5.75, and 10.23 μm. The grain size statistical results of specimens annealed under different conditions are displayed in Fig. 6(a). The contributions of fine grain size strengthening to YS were estimated to be 289.84, 429.06, 298.25, and 239.85 MPa for WQ specimens. The corresponding values for AQ specimens were 289.84, 222.14, 191.88, and 143.86 MPa, respectively.

As mentioned above, the dislocation mechanism can also improve the strength. In this work, the contribution of dislocation strengthening mechanism to YS can be calculated by the Taylor hardening law shown by Eq 5 (Ref 9):

$$\sigma_{{{\text{dis}}}} = M\alpha Gb\sqrt {\rho_{D} }$$
(5)

where M = 2.9 is the Taylor factor (Ref 37). \(\rho_{D}\) refers to dislocation of specimens with dislocation density estimated from XRD analysis. α = 0.23 denotes the interaction strength between dislocations (Ref 38). b = 0.254 nm represents the Burgers vector (Ref 39). G = 67.3 GPa refers to low-density alloy.

To evaluate the torsional stress and torsional strain, the shear moduli of low-density alloys were obtained by torsion testing. The relationship between torsional stress and torsional strain can be described by the Nadai formula (Ref 40):

$$\tau_{{{\text{max}}}} = \frac{1}{{2\pi r^{3} }}\left[ {3T + \theta \left( {\frac{dT}{{d\theta }}} \right)} \right]$$
(6)

where \(\tau_{{{\text{max}}}}\) denotes the torsional stress on the specimen surface, r refers to the section radius of specimens, T is torque, and \(\theta\) denotes the relative torsion angle.

Furthermore, the shear modulus can be calculated according to Eq 7:

$$G = \frac{{32\Delta TL_{0} }}{{\pi \Delta \varphi r^{4} }}$$
(7)

where \(\Delta T\) indicates the torque increment, \(\Delta \varphi\) is the torsion angle increment, and \(L_{0}\) = 100 refers to the gauge length of the specimens.

The contributions of dislocation strengthening mechanism to YS for WQ specimens were 857.21, 642.56, 587.99, and 503.67 MPa. By comparison, the corresponding values for AQ specimens were 857.21, 598.27, 563.74, and 490.83 MPa.

In metal materials, second-phase strengthening is an important strengthening mechanism, which makes an important contribution to the YS of steel. According to the type and strength of the second-phase, the strengthening mechanism can be expressed as Orowan bypassing mechanism, dislocation looping mechanism and shearing mechanism by cutting through κ-carbides. As κ-carbides are easily shearing by gliding dislocations, the strengthening mechanism of second-phase is shearing mechanism (Ref 41,42,43,44).

In the shearing mechanism of low-density steel, coherency strengthening (\(\sigma_{{{\text{ppt}}}}\)), modulus mismatch strengthening (\({\Delta }\sigma_{{{\text{MS}}}}\)), and order strengthening (\({\Delta }\sigma_{{{\text{OS}}}}\)) affect the YS. Therefore, the contribution of each strengthening mechanism can be calculated by the following equations (Ref 41).

$$\sigma_{{{\text{ppt}}}} = M\alpha_{\varepsilon } \left( {G_{{\varepsilon_{c} }} } \right)^{\frac{3}{2}} \left( {\frac{rf}{{0.5Gb}}} \right)^{\frac{1}{2}}$$
(8)

where \(\alpha_{\varepsilon }\) = 2.6 for FCC metals, ε is the constrained lattice parameter misfit, and the unique constrained effective misfit strain \(\varepsilon_{c}\) is (Ref 45):

$$\varepsilon_{c} = \frac{1}{3} \frac{{\left( {1 + v} \right)}}{{\left( {1 - v} \right)}} \frac{{\varepsilon_{{{\text{eff}}}} }}{{\left( {1 + \frac{4G}{{3B_{c} }}} \right)}}$$
(9)

where \(B_{C}\) is the bulk modulus of the precipitates, considered to be 187 GPa for κ-carbides, and \(\varepsilon_{{{\text{eff}}}}\) is:

$$\varepsilon_{{{\text{eff}}}} = \frac{\sqrt 2 }{3}\left[ {\left( {\varepsilon_{11} - \varepsilon_{22} } \right)^{2} + \left( {\varepsilon_{22} - \varepsilon_{33} } \right)^{2} + \left( {\varepsilon_{33} - \varepsilon_{11} } \right)^{2} } \right]^{{{1}/{2}}}$$
(10)

where,

$$\varepsilon_{11} = \frac{{a_{p} }}{{a_{m} }} - 1,\;\varepsilon_{22} = \frac{{\sqrt 3 a_{p} }}{{\sqrt 2 a_{m} }} - 1,\;\varepsilon_{33} = \frac{{c_{p} }}{{\sqrt 2 a_{m} }} - 1$$
(11)

Here, \(a_{m}\) = 0.357 nm is the lattice parameter of the austenite matrix; \(a_{p} = 0.432\) nm; and \(c_{p} = 0.258{ }\) nm is the lattice parameter of the κ-carbides precipitates.

$${\Delta }\sigma_{{{\text{MS}}}} = M0.0055\left( {{\Delta }G} \right)^{\frac{3}{2}} \left( \frac{2f}{G} \right)^{\frac{1}{2}} \left( \frac{r}{b} \right)^{{\frac{3m}{2} - 1}}$$
(12)
$${\Delta }\sigma_{{{\text{OS}}}} = M0.81\frac{{\gamma_{{{\text{apb}}}} }}{2b}\left( {\frac{3\pi f}{8}} \right)^{\frac{1}{2}}$$
(13)

where M = 3.06 for FCC polycrystalline matrix, the shear modulus G = 67.3 GPa (Ref 44, 46), magnitude of the Burgers vector b = 0.286 mm for FCC matrix, m = 0.85; \({\Delta }G\) is the modulus mismatch between the matrix and the precipitates; and the shear modulus of the precipitates is taken to be that of κ-carbides, 93 GPa (Ref 47); therefore, \({\Delta }G =\) 93-67.3 = 25.7 GPa. \(\varepsilon_{c}\) is the constrained lattice parameter misfit; f is the volume fraction of the precipitates; and \(\gamma_{{{\text{apb}}}}\) corresponds to the antiphase boundary free-energy of the precipitate phase (the value of \(\gamma_{{{\text{apb}}}}\) is missing). Hence, the value of \({\Delta }\sigma_{{{\text{OS}}}}\) is not calculated because it does not affect the discussion on the secondary particle strengthening mechanism. Furthermore, with the increase in rolling temperature, the \({\Delta }\sigma_{cs}\) values reached 305.86, 287.28, 249.16, and 104.66 MPa for WQ specimens. By comparison, those of AQ specimens were 305.86, 232.25, 188.42, and 333.91 MPa, respectively.

In addition, the solid solution strengthening mechanism can also be used to evaluate the strength of materials. For current low-density alloys, the solid solution strengthening mechanism can be calculated by Eq 14 (Ref 48, 49):

$$\alpha = 3.578 + 0.033X_{C} + 0.00095X_{{{\text{Mn}}}} + 0.0056X_{{{\text{Al}}}} + 0.0006X_{{{\text{Cr}}}}$$
(14)

where \(\alpha\) = 3.7212 is an austenite lattice parameter (Å). \(X_{C}\), \(X_{{{\text{Mn}}}}\), \(X_{{{\text{Al}}}}\), and \(X_{{{\text{Cr}}}}\) are the concentrations of C, Mn, Al, and Cr (wt.%), respectively.

The solid solution strengthening mechanism also depends on the composition of Fe-Mn-Al-Si-C high manganese alloy, which can be described according to Eq 15 (Ref 50, 51):

$$\sigma_{{{\text{SS}}}} = 279X_{C} - 1.5X_{{{\text{Mn}}}} + 49.6X_{{{\text{Si}}}} + 20.5X_{{{\text{Al}}}}$$
(15)

where \(X_{C}\), \(X_{{{\text{Mn}}}}\), \(X_{{{\text{Al}}}}\), and \(X_{{{\text{Si}}}}\) are the concentrations of C, Mn, Al, and Si, respectively.

In this study, these factors did not affect the strengthening mechanism of the alloys at various annealing temperatures and cooling conditions. Hence, the effect of the solid solution strengthening mechanism can be ignored.

For specimens annealed under different conditions, the mechanical properties changed considerably due to recrystallization. At annealing temperatures of 300, 450, and 550 °C, the YS of specimens displayed a decreasing tendency as the temperature rose (Fig. 9). This may be related to the cold-rolling process, during which primary austenite grains were broken, leading to a sudden drop in grain size of cold-rolled specimens. Moreover, the cold deformation led to the formation of large numbers of mechanical twins and dislocations (Fig. 8b), as well as plenty of broken grain boundaries. In addition, twins blocked the movement of the dislocations to induce dislocations piling up around the grain boundaries and mechanical boundaries. As annealing temperatures increased, the crystal grain recovered. Upon annealing, recrystallization of heavily deformed samples started to occur earlier. The high driving force for nucleation generated many small grains, resulting in dislocations movement and increased plasticity.

5 Conclusions

The effects of annealing conditions on the microstructure and mechanical properties of cold-rolled low-density high-strength Fe-30Mn-10Al-1.57C-2.3Cr-0.3Si − 0.6Ti alloys were clarified. The change trends of microstructure and strengthening mechanism of the alloys were identified. The following conclusions can be drawn:

  1. (1)

    The cold-rolled and annealed specimens under different conditions exhibited σ0.2% = 1400.11 MPa and TE of 6.65%. During annealing, the increase in annealing temperature decreased the YS of low-density alloys while enhancing TE. The specimen annealed at 450 °C followed by cooling to room temperature in air exhibited the best comprehensive mechanical properties with σ0.2% = 1270.28 MPa, Rm = 1318.67 MPa, and ε = 19.47%, while YS decreased by 9.28% and TE increased by 192.78%.

  2. (2)

    The annealing conditions affected the grain size and κ-carbides volume fraction of cold-rolled specimens. As the annealing temperature rose, the grain size increased from 2.52 μm to 3.68 μm under WQ conditions, and to 10.23 μm under AQ conditions. Furthermore, the volume fraction of κ-carbides decreased from 33.11% to 13.66% under AQ conditions, and to 1.73% under WQ conditions. The density of the alloys was estimated to be 6.58 g/cm3, a value 15.6% lower than that of pure Fe (7.8 g/cm3).

  3. (3)

    The precipitation of tiny carbides prevented the movement of dislocations, as well as dislocations piling up around the twins and carbides boundaries. Hence, the dislocation strengthening mechanism and second phase strengthening mechanism were identified for the alloys. The large number of grain boundaries induced by tiny grain sizes also contributed to the strengthening mechanism of low-density alloys. Therefore, the overall strengthening mechanism of the alloys resulted from the combined and synergistic effect of multiple strengthening mechanisms.