Introduction

Ghosh and Hecker (Ref 6) and Ghosh (Ref 7) noted many years ago that after the development of a diffuse instability, the strain-rate sensitivity is extremely important in determining the amount of strain a metal sheet can sustain. For a tensile test, it is commonly assumed that the diffuse instability occurs at a strain equal to the Hollomon work-hardening exponent: \(\varepsilon = n\). This is known as the Considère criterion. Ghosh and Hecker observed that at the deformation instability there is a strain-rate increase, which for a positive strain-rate sensitive material produces a stress increase that is sufficient to postpone necking until a value of at least \(\varepsilon = 2n\). This leads to post-diffuse-instability deformation that can be “quasi stable in nature, it is practically ‘uniform’ and useful.” Ghosh (Ref 7). To verify this phenomenon experimentally, Ghosh and Hecker studied a variety of metals with different strain-rate sensitivities: low-carbon, aluminum-killed, drawing-quality steel, m = 0.012; dispersion hardened Zn-Ti alloy, m = 0.052; AA2036-T4 aluminum (solution treated and aged), m = − 0.0048; and annealed 70:30 brass, m = zero, among others. For this steel, Ghosh (Ref 7) subsequently reported that nearly 40% of total tensile elongation occurred after the diffuse instability. For the dispersion hardened Zn alloy, post-uniform deformation was nearly 90%. The 70:30 brass and AA2036-T4 aluminum showed “small post uniform extension because m is either zero (brass) or slightly negative (− 0.005 for 2036-T4) … aluminum.” Ghosh and Hecker (Ref 6).

The current norm ISO 12004-2:2008 (Ref 10) for measuring the forming-limit diagram (FLD) does not explicitly recognize or take advantage of Ghosh and Hecker’s observation. Rather, the norm specifies the use of a Bragard et al. (Ref 2)-based technique for obtaining the limit strains from an FLD sample tested to failure. According to Bragard, the data lying within the instability are discounted and the remaining points fitted. The fitted points have thus only experienced strains outside of the necking instability. In the standardized FLD experiment, either a semispherical punch, Nakazima et al. (Ref 19), or blunt-nosed punch, Marciniak and Kuczynski (Ref 15), is permitted. These two punch geometries can result in very different fitted profiles. The Nakazima geometry is characterized by significant strain gradients, and the fitted profile can extend up into the region of discounted data, forming a dome. On the other hand, the Marciniak and Kuczynski (MK) experiment is planar with only slight gradients. Thus, even though the data are fitted with an inverse polynomial, the fitted limit strains conform closely to strains outside of the necked region. This would make the standardized FLD measurement conservative.

In the past, FLD strains were measured using etched or deposited circle-grid patterns. These patterns have only millimeter length-scale resolution, which makes the measurement of strains within the necking instability impossible. Such lack of resolution does not prevent measurement of strains outside of the necking instability, leading to the Bragard-type fitting approach.

Today, much higher-resolution strain measurements, limited only by camera and speckle pattern resolution, are possible through the digital-image correlation (DIC) technique. As discussed by Brunet et al. (Ref 3), Vacher et al. (Ref 29) and Sutton et al. (Ref 27), one can obtain displacements and then strains by applying a random pattern of fine black spots over a white background. Successive digital images are recorded of this speckle pattern, as deformation of the test piece occurs. Expansions, contractions and distortions of the pattern then give specimen displacements and subsequently strains. These data are obtained in either two or three dimensions with commercial or open-source software. Commercial software, e.g., GOM (Ref 8), will typically function in either two or three dimensions, while the open-source code Ncorr operates in two dimensions, Blaber et al. (Ref 1). Through a succession of images, it is now possible to not only resolve the strains within a necking instability but to obtain the time history of strains leading up to the necking instability. A number of authors have proposed techniques for obtaining temporal-based limit strains from DIC data and compared these results to those generated for the same specimens with the classic Bragard-type analysis.

Merklein et al. (Ref 17) were some of the first to propose that the limit strain could be obtained by studying the entire temporal evolution or strain history of the Nakazima-specimen geometry. They proposed taking the second derivative of the strain/time history—strain acceleration—across the entire deformation field. In the zone where the neck will form, this history is first linear with respect to time, but then it exhibits a rapid rise, as the instability initiates. They used a correlation-coefficient method to identify the point in time at which a plastic-flow localization develops. The correlation-coefficient value indicates the degree of linearity or randomness of the relationship between two variables. By analyzing experimental data, Merklein et al. (Ref 17) showed a peak in the correlation-coefficient/time history coincident with the development of the necking instability. The peak is associated with a rapid rise in the strain acceleration/time curve. The strains calculated from the image corresponding to this peak are the limit strains. Using this technique, they measured the FLD for two steels, HX260 and HXT600X, and an aluminum alloy, AA6016. They found exceptional agreement between their correlation-coefficient technique and the standard cross-sectional—Bragard—method described in the ISO norm (Ref 10). The only deviation was for the HXT600X steel. In this case, the statistical technique gave higher limit strains in biaxial tension, particularly in balanced-biaxial deformation, by slightly more than 10%.

Hotz et al. (Ref 9) expanded on the idea proposed by Merklein et al. (Ref 17). They also calculated the strain-acceleration data where the neck develops and added a linear function to it. Then, rather than summing all the data up to the point where the correlation coefficient is calculated, as done by Merklein et al., they passed a band of a finite number of points through the data. The correlation coefficient is calculated using just those data within the band, for the point at the center of the band. Thus, this gliding analysis will first take a value of one, driven by the linear function. At the point of maximum curvature in the strain acceleration plus linear function/time curve, the gliding correlation coefficient dips into a valley. As the acceleration enters the necking-instability phase, it rapidly increases the augmented acceleration/time curve becoming linear again. Thus, the gliding correlation coefficient returns toward one. The strains at the time of maximum curvature are taken as the limit strains.

The current authors (Roatta et al. (Ref 21)) showed that experimental noise needs to be present for the criterion of Merklein et al. to work, but at the same time, the predicted limit strain obtained will vary with the amount of noise present. The position of maximum curvature in Hotz et al.’s summed strain-acceleration curve varies only slightly with experimental noise. However, if excessive noise is present, it can be difficult to identify the minimum in the gliding correlation coefficient. In order to compensate for these drawbacks, Roatta et al. proposed combining the approaches of Merklein et al. and Hotz et al. (M-H) by using a smoothing polynomial to obtain a correspondence in the techniques’ results. A unique limit strain was obtained from this correspondence and uncertainties with respect to experimental noise eliminated. These authors’ preliminary results for a cold-rolled steel sheet compared limit strains calculated with their technique—using only necking-zone deformations—to limit strains from the ISO Bragard-type analysis. They found close agreement between results in balanced-biaxial deformation but a divergence in limit strains in plane-strain and uniaxial tension. For the latter two strain states, the Bragard-type limit strains were between 25 and 40% lower.

Martínez-Donaire et al. (Ref 16) examined the strain rates of a profile of points traversing an instability for an AA7075-O aluminum alloy. They observed two very different behaviors depending on the position of a particular point. The strain rate increased continuously for a point that lay within the zone that would develop into the necking instability. However, for a point outside this zone, the strain rate first increased but then decreased with time. They were able to identify a singular point on the profile whose strain-rate, time-history curve increased but then decreased to exactly zero. This point was on the shoulder of the instability and the time step at which its strain rate was a maximum defined the limit strain. These authors also found close agreement between their new technique and results from the ISO norm (Ref 10). In the case of this comparison, they used the Nakazima (Ref 19) semispherical punch geometry.

Wang et al. (Ref 31) used DIC data to study surface topography, surface-height differences or the first derivative of surface-height differences and they sought to identify the point, image, that gives the first indication of a necking instability. This image, at the point of instability initiation, rather than the final image before fracture—as specified in the ISO norm—would be used to calculate the limit strains. They used the Marciniak and Kuczynski (Ref 15) sample geometry for their FLD measurements on an Al-Mg-Si alloy, and found good agreement between their DIC-based technique and the ISO norm, using the final image taken before fracture. Vysochinskiy et al. (Ref 30) also based their temporal limit-strain analysis, for AA6016 aluminum, on the sheet thickness and the thickness reductions that occur as the necking instability initiates. They compared their thickness-controlled results from Nakazima (Ref 19) and Marciniak and Kuczynski (Ref 15) experiments to the Merklein et al. (Ref 17) statistical analysis and standard ISO sectional technique (Ref 10), finding the ISO analysis to be the least conservative and the Merklein method the most. This was for experiments near uniaxial tension and in biaxial deformation when the major strain was parallel to the rolling direction.

Contrarily, Min et al. (Ref 18) reported the ISO method to be the most conservative for their limit-strain measurements based on a fitted surface-curvature technique. They also examined what limit strains resulted from applying the proposed techniques of Martínez-Donaire et al. (Ref 16), Wang et al. (Ref 31) and Hotz (Ref 9). This investigation focused on DP600, MP980 and AA6022-T4 metal sheets.

Researchers have thus proposed a number of temporal-based techniques that include necking instability strains and have studied a variety of materials. However, no one has systematical compared forming-limit strains calculated from only deformation within the necking instability to the ISO-norm limit strains for a suite of materials based on material strain-rate sensitivity. Because, as shown by Ghosh and Hecker (Ref 6) and Ghosh (Ref 7), the material’s strain-rate sensitivity controls the extent of deformation that occurs after formation of the diffuse instability, one would expect the relationship between necking-based and Bragard-type FLD strains to vary depending on the material strain-rate sensitivity. The object of this work was to test that hypothesis.

Experimental Materials and Techniques

Following the example of Ghosh and Hecker, for FLD measurements, we selected three materials with very different strain-rate sensitivities: a cold-rolled steel; a zinc alloy, Zn20; and AA6061-T4 aluminum. In its standard form, the strain-rate sensitivity is defined as:

$$ \frac{{\sigma_{2} }}{{\sigma_{1} }} = \left( {\frac{{\dot{\varepsilon }_{2} }}{{\dot{\varepsilon }_{1} }}} \right)^{m} ,\quad m = \frac{{\ln \left( {\sigma_{2} /\sigma_{1} } \right)}}{{\ln \left( {\dot{\varepsilon }_{2} /\dot{\varepsilon }_{1} } \right)}}. $$
(1)

Where for our steel m = 0.015. In the case of the Zn-Cu-Ti zinc alloy (designated by the manufacturer as Zn20) m = 0.075 and finally, for the AA6061-T4 m = zero. The standard engineering properties for these materials are listed in Table 1.

Table 1 Material mechanical properties
Full size table

We measured the forming-limit curves for our materials using a miniature Marciniak and Kuczynski (MK) specimen geometry and testing device discussed by Leonard et al. (Ref 14). The key to this experiment is an intermediate anneal of the MK carrier blank to prevent tearing at the edge of the central hole. The entire deformation history was recorded in digital images that were analyzed with the two-dimensional, digital-image correlation program Ncorr.

The resulting strain fields were finally subject to both a Bragard-type treatment in the spirit of the ISO norm and our temporal, smoothed Merklein–Hotz (M–H) correlation-coefficient calculation. In this manner, two sets of forming-limit data were generated for each material, one from strains outside of the necking instability and one from those within.

Material Properties

The cold-rolled steel used in this study is typical of that used to fabricate standard formed-sheet products. The sheet was 0.9 mm thick, thin enough to avoid through-thickness stress gradients and bending effects. The steel had a grain size of between 15 and 50 µm. The grains were slightly pancaked in the rolling plane and elongated in the rolling direction. Table 1 shows that the sheet was nearly isotropic in plane with equivalent yield, hardening, and ultimate tensile strengths at 0°, 45° and 90°, as well as equal total elongations, between 35 and 38%. These properties are typical of those found in data bases for cold-rolled steels. It should be noted that this steel’s yield strength, 200 MPa, is slightly lower than that of typical drawing-quality sheet. The R-values or Lankford coefficients were 1.75, 1.30 and 2.05 at 0°, 45° and 90° to the rolling direction, respectively. These values were taken at 15% strain and are again typical of a cold-rolled steel. As previously noted and given in Table 1, this steel is mildly positive strain-rate sensitive with an exponent m = 0.015. Values of K = 610 and n = 0.256 gave a satisfactory fit to the Hollomon hardening law at 90° to the rolling direction. Roatta et al. (Ref 21) gave additional properties and characteristics of this steel.

A commercial AA6061-T4 sheet 1.0 mm thick was studied. This sheet was also nearly isotropic in plane with respect to yield and ultimate tensile strength, total elongation and Lankford coefficient. The 0.2% offset yield strength of the AA6061-T4 was 140 MPa, significantly below that of the steel. However, its Hollomon work-hardening exponent, n = 0.250, was nearly equivalent to the steel’s. As is characteristic of other aluminum alloys, this material’s Lankford coefficients, R-values, were less than one, R = 0.65, 0.68 and 0.6 at 0°, 45° and 90° to the rolling direction, respectively. The R-values were measured at an engineering strain of 0.15. Most significantly, the AA6061-T4 had zero strain-rate sensitivity.

Finally, a Zn-Cu-Ti sheet—Zn20—was selected as a material with a strongly positive strain-rate sensitivity, m = 0.075. The alloying additions resulted in numerous intermetallic particles aligned in the rolling direction. As shown in Fig. 1, these stringers, documented by Schlosser (Ref 23), are a dominant feature of the material’s microstructure. The sheet was 0.8 mm thick and distinctly anisotropic, due to unidirectional rolling and its hexagonal crystal structure. The yield strengths were 144, 160 and 182 MPa at 0°, 45° and 90° to the rolling direction, respectively. The Zn20 exhibited substantial elongations at 0° and 45°, 0.55 and 0.42, but relatively little elongation at 90°, 0.26. This reduction in the elongation at 90° is caused by the presence of the aligned particles. It had little to no work hardening, n = 0.0146. This low value could be a consequence of the continuous dynamic recrystallization that was observed, even at room temperature, for this alloy (Ref 13). The work-hardening measurement was at 90° with respect to the rolling direction.

Fig. 1
figure 1

An optical micrograph of the Zn20 showing the intermetallic particles aligned with the rolling direction typical of this material’s microstructure. The micrograph is in the sheet plane and the rolling direction is indicated (Ref 23)

Full size image

The engineering tensile behaviors of these three metals are plotted together in Fig. 2. In the case of the steel and zinc, we are showing properties at 90° to the rolling direction. For AA6061-T4, the orientation is 0°. For the steel and aluminum, these orientations were selected to be consistent with that that the ISO norm specifies for the FLD determination. In the case of the zinc, Schlosser et al. (Ref 22) showed that the 90° orientation FLD is significantly below that at 0° and thus the most critical.

Fig. 2
figure 2

Engineering stress/strain curves for steel, aluminum and zinc. The location of the peak load for each material is shown as the vertical line cutting the stress/strain curve

Full size image

As Ghosh (Ref 7) discussed, the amount of tensile deformation that occurs after the peak load indicates a material’s ability to shift deformation away from the developing necking instability. In Fig. 2, it is clear that the amount of post-peak-load deformation is very different for each of the three materials. In the case of the AA6061-T4, the amount of post-peak-load deformation is negligible. This indicates that once a necking instability begins the deformation will concentrate there and the material will rapidly fail. For zinc, it is exactly the opposite. Nearly all of the deformation in zinc occurs after the maximum load, and thus, the deformation that occurs after the diffuse instability forms is extensive. The case for steel is intermediate.

Experimental Techniques

Leonard et al. (Ref 14) designed a miniature MK testing device that uses an 80-mm-diameter specimen blank stretched through a 45-mm aperture by a 40-mm diameter x 5-mm shoulder-radius punch. This test fixture is mounted in an Instron universal testing machine so that the experiment can be halted at an intermediate strain and the steel MK carrier blank given a recrystallization heat treatment, 850°C for 30 minutes. It should be noted that the carrier blanks for all experiments were laser cut from the same cold-rolled steel that is described above and was used for the steel FLD measurements. A camera assembly is an integral part of the equipment. The camera records high-resolution images at a rate of one per second and it is attached to the loading punch, such that the camera descends with the punch during testing. Thus, a fixed distance—focus and magnification—is maintained between the camera and specimen surface during testing.

A balanced-biaxial strain state results from the full 80 mm disk. Side cutouts afford intermediate strain paths between balanced-biaxial deformation and nearly uniaxial tension. We used specimens with both an hourglass and parallel-sided geometry. The hourglass geometry had a maximum specimen width of 54 mm, which is 9 mm greater than the die aperture. A specimen 10-mm wide with parallel sides gave nearly pure uniaxial tension. We found a strain state near plane strain for the 45-mm wide hourglass-shaped sample. These specimen geometries are shown in Fig. 3.

Fig. 3
figure 3

Specimen geometries used in the MK forming-limit experiments

Full size image

For all experiments the interface surfaces between the specimens and carrier blanks were sand blasted to maximize friction and the punch/carrier blank surface lubricated with a Molykote 321-R® spray lubricant.

Digital-Image Correlation

Slow drying, 30 min. before applying a second coat, aerosol paints created the random speckle pattern of fine dots for digital-image correlation. Due to the paints’ slow drying characteristic, they remained viscous throughout the experiment, allowing them to attain the very high strains within the necking instability.

High-resolution images were recorded with a commercial photographic camera, Nikon D3300, which had a 4500 × 3000 pixel CCD. This camera allowed us to photograph the developing instability with greater resolution than would be afforded with a high-speed video camera. An AF-S DX Micro NIKKOR 85-mm equivalent lens permitted the camera to be focused over the short distances associated with this experiment and filled the CCD recording frame with the ~30-mm-diameter planar specimen surface.

Blaber et al. (Ref 1) created the open-source, 2-D, digital-image correlation program Ncorr, which was used to calculate the strain-field histories for our MK forming-limit experiments. Ncorr operates within the MATLAB platform and has an intuitive graphic user interface. We selected Ncorr parameters to precisely resolve strains within the actual deformation instability: subset radius = 50 pixels (for the AA6061-T4 30 pixels); subset spacing = 2 pixels; Diff. Norm Cut Off = 10−6; and Number of Iterations Cut Off = 50. A digital-image correlation program measures displacement and then performs a differentiation using a finite number of data points to obtain the strains at a central point. If the region specified contains too many points, fidelity at the instability is lost, while taking too few points might result in excessive noise and numeric artifacts. We used a radius of 5 points, 81 data points in total, for the Ncorr strain calculation. Roatta et al. (Ref 21) showed that a strain radius of five points was sufficient to resolve the strains within the necking instability, without creating excessive noise.

Limit-Strain Calculations

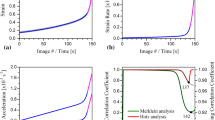
Limit strains were calculated using the classic Bragard-type technique discussed in the ISO norm (Ref 10). In this case, a region centered on the instability was discounted, based on the maximums of the second spatial derivative of the strain perpendicular to the instability. Inverse polynomials were fitted to the remaining data on either side of the instability. The polynomials’ maximum values determined the limit strains. An example of this calculation is shown in Fig. 4, for an AA6061-T4 sample that was 54 mm wide with the hourglass shape. One can clearly see in Fig. 4 that the strain gradients were minimal, for the MK specimen. This was the case for all three materials studied. Figure 4 shows the zone of the developed instability that was excluded from the calculation and the maximums/minimums in the second spatial derivative that determined the borders of the excluded data. These excluded data are those that were used for the smoothed correlation-coefficient calculation.

Fig. 4
figure 4

The principal-strain profiles used in the Bragard-type analysis. Minimal gradients are present in the strain fields. The second spatial-derivative profile is also shown. It determines the border of points excluded from the calculation. These data are for a 54 mm wide, hourglass shaped, AA6061-T4 specimen

Full size image

We also calculated a forming limit with those points within the necking instability, using the smoothed correlation-coefficient technique discussed by Roatta et al. (Ref 21). This technique smoothed the strain/time data to obtain a correspondence between the correlation-coefficients of Merklein et al. (Ref 17) and Hotz et al. (Ref 9). The Merklein technique identifies a deviation from linearity in the second derivative of strain with respect to time or image number, strain acceleration, in the necking zone. The point of deviation appears as a peak in the correlation coefficient/time data. The Hotz technique first adds a linear function to the strain–acceleration data and then passes a band of points through the summed data. The correlation coefficient for the point at the center of the band, called the gliding correlation coefficient, is calculated with only those points within the band. In this manner, the Hotz technique looks for a maximum of curvature in the supplemented strain-acceleration/time curve. This maximum is identified by a valley in the gliding correlation coefficient/time curve. These two techniques are independent and by smoothing the original strain/time data, before calculating the derivatives, they can be brought into coincidence, to give a unique limit-strain result. Figure 5(a) and (b) illustrates the application of Roatta et al.’s (Ref 21) technique for the AA6061-T4, 54 mm wide, hourglass sample. This is the same sample used to illustrate the Bragard calculation in Fig. 4. In the example shown, the strain/time data were smoothed with nine points and a band seven points wide was passed through the supplemented strain-acceleration data to calculate the gliding correlation coefficient. For this sample case, the strains from image 104 were taken to calculate the limit strains.

Fig. 5
figure 5

(a) and (b). The strain acceleration curves used in the smoothed correlation-coefficient calculations are shown in (a). It can be seen that the Hotz et al. (Ref 9) type analysis identifies the maximum curvature, while that of Merklein et al. (Ref 17) seeks a deviation from linearity. Smoothing was applied to the strain/time (image number) data for this 54-mm wide, AA6061-T4 sample to obtain a correspondence in the two types of correlation coefficients. (b) The dashed box to the right indicates the correspondence between smoothed correlation coefficients

Full size image

Experimental Results

Figures 6, 7 and 8 show the measured FLDs for Zn20, cold-rolled steel and AA6061-T4 aluminum, respectively. There are two sets of FLD data in each diagram: the Bragard-type FLD, green symbols, and that measured using the smoothed M-H technique, black symbols. Each symbol type designates a particular sample geometry, and each green and black pair of points is an individual experiment. Two lines indicating the forming limits are drawn in Figs. 6, 7 and 8 based on the experimental data. The dashed lines show the forming limits characterized by the Bragard-type analysis, while the solid lines indicate the limit curves derived from the Merklein–Hotz experiment. As is standard for forming-limit curves, strains below these lines are considered safe, while strains above would indicate sheet failure.

Fig. 6
figure 6

Forming-limit diagram for the Zn20 material. The widths of particular MK specimens are indicated

Full size image
Fig. 7
figure 7

Forming-limit diagram for the cold-rolled steel. The widths of particular MK specimens are indicated

Full size image
Fig. 8
figure 8

Forming-limit diagram for the AA6061-T4 aluminum. The widths of particular MK specimens are indicated

Full size image

In addition, we have listed particular specimen widths on the FLD diagram. In these cases, the specimens had an hourglass geometry.

Zn20

In Fig. 6, one can see that the temporal technique gives a much higher FLD than the classic Bragard measurement. Thus, there is a distinct difference between an FLD determined from uniform deformations and that from the deformation within the necking instability. This is consistent for all strain paths, from uniaxial tension to balanced-biaxial deformation. The limit-strain curves have the classic form with a minimum near or slightly to the right-hand side of plane strain, \(\varepsilon_{11} \sim{ }0.25\), Bragard, and \(\varepsilon_{11} \sim{ }0.33\), M-H analysis. In the case of uniaxial tension, \(\varepsilon_{11} \sim{ }0.45\), Bragard, and \(\varepsilon_{11} \sim{ }0.52\), M-H, smoothed temporal technique and for balanced-biaxial deformation \(\varepsilon_{11} \sim{ }0.42\), Bragard, and \(\varepsilon_{11} \sim{ }0.55\), smoothed temporal M-H analysis. As noted above, we have not just plotted the actual experimental measurements, but have estimated forming-limit curves from the data. The limit-strain numbers given above are from the upper reaches of the Bragard-type data and those for the temporal analyses the lower bound of the data. It should be noted that there is a great deal of scatter in the experimental results, possibly due to the large number of intermetallic stringers in the material’s microstructure. The 54 mm sample gave a strain state close to balanced-biaxial deformation while the 45 mm sample resulted in strains just to the right of plane strain. Strain states from intermediate sample widths were spaced evenly over the FLD between these geometries.

Cold-Rolled Steel

Figure 7 shows the measured FLD for the cold-rolled steel. For the steel, the temporal and Bragard techniques give equivalent results in balanced-biaxial deformation, considering the upper ceiling for the Bragard calculation and the lower data limits for the smoothed temporal analysis, \(\varepsilon_{11} \sim{ }0.48\). However, as one moves toward plane strain, results from the two techniques begin to diverge. In plane strain, the M-H, temporal limit strain, \(\varepsilon_{11} \sim{ }0.50\) is nearly 25% greater than the Bragard type, \(\varepsilon_{11} \sim{ }0.40\). This trend continues through to uniaxial tension where the difference is about 40%: \(\varepsilon_{11} \sim{ }0.90\) temporal; and \(\varepsilon_{11} \sim{ }0.65\) Bragard. For this steel, the limit-strain measurements were consistent between experiments with much less experimental scatter than what was observed in the case of the Zn20. There was also a distinct shift in the strain paths taken by the different sample geometries away from balanced-biaxial deformation. For example, the 45-mm wide specimen strains now lie to the tension side of plane strain, while in the case of the Zn20 they were to the biaxial side of plane strain. This tendency was the same for the 50- and 52-mm wide sample geometries.

AA6061-T4 Aluminum

The forming-limit diagram for the AA6061-T4 aluminum is shown in Fig. 8. The limit strains are not only much lower for this material, in comparison to the cold-rolled steel and Zn20, but now we see almost no difference in results between the M-H, smoothed temporal and Bragard-type analyses. The major limit strains are approximately 0.33, 0.18 and 0.26 in uniaxial tension, plane strain and balanced-biaxial deformation, respectively. In comparison with both the Zn20 and steel, the strain paths have again moved to the left-hand side of the FLD. In the case of the Zn20, the 54-mm wide hourglass specimen took nearly a balanced-biaxial path. For the AA6061-T4, this specimen geometry gave strains closer to plane strain than balanced-biaxial deformation. It is as though there are deformations, the region between data from the 80 mm balanced-biaxial and 54-mm wide specimens, that are nearly unattainable. As with the cold-rolled steel, the limit strains from the aluminum experiments are consistent and there is minimal experimental scatter.

Discussion

The measured FLDs and the relationship between the smoothed temporal, M-H and Bragard-type analyses depended strongly on the strain-rate sensitivity of the material investigated.

The strain-rate insensitive, m = zero, AA6061-T4 is the simplest case studied. As soon as a diffuse instability forms, deformation concentrates in the necking instability and the material fails. Thus, the smoothed temporal, correlation-coefficient analysis, which measures the forming limit from strains within the necking instability, predicted the same limit strains as the Bragard-type analysis which excludes the necking-zone data. In the case of the AA6061-T4, little appears to be gained from the temporal analysis over what is documented in the ISO norm (Ref 10). The exception might be in the case of a zero or negative strain-rate sensitive material that exhibits roping or multiple necks. This is a condition that invalidates the Bragard measurement. The temporal correlation-coefficient analysis looks within the necking instability and thus does not see other pending instabilities.

In the case of the moderately strain-rate sensitive, cold-rolled steel, there appear to be advantages to be gained from the correlation-coefficient analysis. Uniaxial and plane-strain states appear capable of supporting more deformation within the necking instability than afforded by the limits of the Bragard-type analysis. This is consistent with the tensile analyses of Ghosh and Hecker (Ref 6) and Ghosh (Ref 7). We can now put a quantitative number on the maximum deformation that this steel can sustain. In essence the M–H, temporal and Bragard analyses give an engineer an upper and lower bound forming-limit curve. The tensile and plane-strain steel limit specimens developed a line of zero extension. There was a clear necked region to experience the additional deformation provided by the positive strain-rate sensitivity. In balanced-biaxial deformation, Roatta et al. (Ref 21) found that this steel doesn’t develop a line of zero extension, rather failure occurs from an island of high deformation. It is possible this lack of a clearly defined necking instability produces the coincidence of the temporal correlation coefficient and Bragard-type analyses, as seen in balanced-biaxial deformation in Fig. 7.

Although there was much more scatter in the forming-limit strain measurements, the very positive strain-rate sensitive Zn20 behaved similarly to the steel in uniaxial tension and plane strain. In these strain states, the temporal correlation-coefficient analysis gave much higher limit strains than the standard Bragard approach. This was also the case in balanced-biaxial deformation. In fact, the entire Zn20 FLD derived from the temporal measurements within the necking instability was elevated. There is a notable difference in the deformation fields between the Zn20 and cold-rolled steel in balanced-biaxial deformation. The Zn20 alloy sheet developed a line of zero extension. We believe that this is due to the intermetallic stringers present within the material, which are shown in Fig. 1. They are in essence MK defects. Figure 9 shows the major strain field—\(\varepsilon_{xx}\)—in balanced-biaxial deformation, for the Zn20 specimen immediately before fracture. A necking instability is clearly present. The enhanced M-H limit strains could be the result of the presence of this instability and/or the Zn20’s very high, positive strain-rate sensitivity, m = 0.075.

Fig. 9
figure 9

Major strain field in a Zn20 specimen tested in balanced-biaxial deformation. A line of zero extension, necking instability, is present.

Full size image

These metals’ different strain-rate sensitivities explain their forming-limit behaviors and the relationship between FLD measurements inside and outside of the necking instability. However, the strain-rate sensitivities cannot explain the shifts in strain paths among the three different metals for the same sample geometries. To explain these differences, one must look at the materials’ yield/flow loci. Measuring the loci for each of these materials was beyond the scope of this work. However, Charca Ramos et al. (Ref 4), Serenelli et al. (Ref 26) and Schwindt et al. (Ref 25) showed that accurate material yield/flow loci can be obtained through crystal-plasticity simulations.

From the initial textures of these three metals and the stress/strain and Lankford coefficient data given in Table 1, the VPSC—ViscoPlastic Self-Consistent—model was calibrated and run using the parameters given in Table 2. Briefly, this model is based on the viscoplastic behavior of single crystals and uses an SC—Self-Consistent—homogenization scheme for the transition to the polycrystal, allowing each grain to deform differently, according to its directional properties and the strength of the interaction between the grain and its surroundings. The VPSC formulation found in Ref 12 was extended in great detail by Lebensohn et al. (Ref 11). In the cases of cold-rolled steel and AA6061-T4, we followed previous VPSC simulations that are discussed in Refs. 26 and 5, respectively. Continuous dynamic recrystallization occurs during the formability experiments with the present Zn20 alloy sheet, even at room temperature. We mimic this fragmentation (subgrain rotation) process by an ad-hoc empirically model described in Ref 20.

Table 2 Uniaxial tension best-fit hardening parameters for the Zn20, cold-rolled steel and AA6061-T4 shee
Full size table

It is well known that the yield surface is useful in order to understand the forming-limit behavior. The yield potential of the material was calculated by imposing different plastic strain-rate tensors in the plane-stress subspace, \(\sigma_{11}\), \(\sigma_{22}\) (Ref 26). The resulting yield/flow loci are plotted in Fig. 10(a)–(c), for the Zn20, cold-rolled steel and AA6061-T4 aluminum, respectively. Both the initial yield loci, based on the materials’ initial textures, and the subsequent flow loci are plotted. The initial textures were allowed to evolve, which when combined with the hardening laws discussed above produced an expansion and distortion of the initial yield loci. The final flow loci are at deformations consistent with the limit strains plotted in the FLDs, Figs. 6, 7 and 8. The relationships between these loci and the materials’ rolling and transverse directions are noted.

Fig. 10
figure 10

(a)–(c) Simulated yield/flow loci for the Zn20, cold-rolled steel and AA6061-T4, based on the VPSC model. The relationship between the yield/flow loci and the material orientations are indicated by the notations RD, rolling direction, and TD, transverse direction.

Full size image

The loci have different shapes for each material. For the AA6061-T4 there is an extended region of plane strain—either \(\sigma_{11}\) or \(\sigma_{22}\) are nearly constant—and a rounded nose in balanced-biaxial tension. The balanced-biaxial stresses \(\sigma_{11}\) and \(\sigma_{22}\) are approximately equal to the uniaxial stresses, which are nearly equivalent in and at 90° to the rolling direction. In fact, the yield/flow loci are practically symmetric about balanced-biaxial tension. The yield/flow loci for the Zn20 are different from those of the aluminum and are distinctly asymmetric. This asymmetry leads to a rounded nose at a loading angle of about 35°. The yield/flow stresses in balanced-biaxial tension are slightly less than those observed in uniaxial tension, particularly at 90° to the rolling direction. Cold-rolled steel is an intermediate case. The loci are symmetric, as was the case for the aluminum alloy, but the balanced-biaxial yield/flow stresses are significantly greater than those in uniaxial tension. This is different than for either the Zn20 or AA6061-T4.

It is well known that the normals to yield loci tangents define the directions of the plastic strain-increment vectors, and hence the strain paths followed by the MK forming-limit experiments. As in Serenelli et al. (Ref 26), for the yield/flow loci shown in Fig. 10(a)–(c), the directions of the plastic-strain increments are plotted in Fig. 11(a)–(c), as a function of loading direction. To understand this plot, it is important to first recognize that the strain-increment direction is plotted with the same sense as the minimum principal strain in the FLDs. Secondly, it must be noted that uniaxial tension is defined by the loading direction, while plane strain and balanced-biaxial deformation are defined by the strain-increment direction. Thus, the baseline loading direction of 0° is pure uniaxial tension and a strain increment direction, d, of ~ − 27° is isotropic behavior, R = 1. The strain increment for steel is greater than 27°, R > 1 and that for the AA6061-T4 and Zn20 less than 27° or R < 1. These numbers are consistent with the measurements given in Table 1. A strain-increment direction of 0° on the yield/flow locus gives plane-strain deformation on the FLD plot. This state is indicated with vertical lines in Fig. 11(a)–(c). To the left of these lines are strain increments tending toward uniaxial tension on the FLD and to the right biaxial deformation. A strain-increment direction of 45° is pure balanced-biaxial deformation, also indicated by vertical lines. This strain increment is reached by all of the materials. In the case of the steel and aluminum, because of the symmetry of the yield/flow locus, a loading direction of 45° resulted approximately in the 45° strain increment. For the Zn20, a loading direction of only 30° and 41° produces the balanced-biaxial deformation response for the initial yield and final flow loci, respectively. The AA6061-T4 situation is very different from the Zn20. The material deformation would tend toward the uniaxial tension side of the FLD until a loading angle of about 12° is reached, which results in an approach to plane-strain deformation. The aluminum continues to deform in plane strain for an extended period until the loading angle approaches ~32°. Deformation then becomes biaxial in nature and reaches balanced-biaxial deformation as the loading direction nears 45°. This extended region of plane-strain deformation is demarcated by the horizontal lines in Fig. 11(c).

Fig. 11
figure 11

(a)–(c) Directions of the strain increment vectors associated with the yield/flow loci shown in Fig. 10. The orientation of the strain-increment directions coincides with the orientation of the minimum principal strain in the FLD diagrams.

Full size image

For the Zn20 sheet, the strain increment direction changes nearly linearly, while crossing the balanced-biaxial strain increment direction. This linearity and dominance of biaxial strain increments is reflected in the FLD data. There is a smooth transition in strain-increment direction between plane-strain and balanced-biaxial deformation as the MK sample widths change. Different sample widths, producing different loading directions, always resulted in different strain-increment directions. Because the loading/strain-increment line passed balanced-biaxial deformation, it was possible to steadily approach balanced-biaxial deformation with progressively increasing specimen widths of 50, 52 and 54 mm. Strain states over the entire FLD were attained.

In the case of the AA6061-T4, the direction of strain increment changes rapidly from uniaxial tension to a plane strain, 0°, approaching plane strain for a loading angle of 12°. Significantly, as the loading direction increases from 12° to nearly 32°, the strain-increment direction remains near or at plane strain. This is reflected in the FLD where specimen widths of 45, 48 and 52 mm exhibit a maximum principal strain of between 0.15 and 0.23 while the minor principal strain never exceeds 0.05. Three specimens with very different loading directions all return nearly a plane-strain deformation increment. For the Zn20, the 54 mm wide specimen gave approximately balanced-biaxial deformation; yet, in the case of the AA6061-T4 aluminum, this specimen width returned a minor principal strain of only 0.06 for a major principal strain of 0.25. In other words, we found a limit-strain measurement much closer to plane strain than balanced-biaxial deformation. It appears that there is only a small range of sample geometries, if any, that will deform over a loading path between 32°—still near plane strain—and balanced-biaxial tension, 45°.

The drawing-quality steel was intermediate. While steel’s strain-path directional changes are not as smooth as is the case for the Zn20, we were still able to attain all the desired strain states with the MK specimen geometry, and the strain-increment direction never stalled at one particular value, like occurred for the AA6061-T4 in plane strain. The strain states produced by the different specimen geometries were also intermediate between those of the AA6061-T4 and the Zn20.

Conclusions

Based on the Bragard-type and smoothed, M-H, correlation-coefficient FLD results for the Zn20, cold-rolled steel and AA6061-T4 and our yield/flow loci predictions, we can make the following remarks:

  1. 1.

    A material’s strain-rate sensitivity is a key factor in determining how much deformation will occur stably after formation of a diffuse instability. A positive strain-rate sensitivity promotes stable deformation within the necking instability and an enhancement of the deformation possible outside the instability. This was particularly notable in the case of the highly rate-sensitive Zn20. For zero or negative strain-rate sensitive materials, in this case AA6061-T4, the material fails from necking almost as soon as the diffuse instability forms.

  2. 2.

    For the positive strain-rate sensitive metals, there was a distinct difference between the Bragard-type limit strains and those predicted with the temporal analysis from the deformation history within the instability zone. In the case of the Zn20 metal, this characterizes all FLD strain paths. For the cold-rolled steel, the difference occurred in and between uniaxial tension and plane strain, while in balanced-biaxial deformation the temporal analysis predicted the same limit strains as the classic Bragard-type calculation.

  3. 3.

    The Zn20 formed a line of zero extension in balanced-biaxial deformation, possibly due to its intermetallic stringers. The cold-rolled steel gave no indication of a line of zero extension in balanced-biaxial deformation. That a balanced-biaxial deformation MK necking instability formed in the Zn20 possibly produced the higher M-H limit strains, when compared to the Bragard calculations.

  4. 4.

    In the case of the zero strain-rate sensitive AA6061-T4, there was practically no difference between the two analyses, temporal and Bragard. Once an instability began to form, the material failed. No advantages appear to be gained with the correlation-coefficient technique.

  5. 5.

    For positive strain-rate sensitive materials, the Bragard-type analysis could well be excessively conservative, particularly in uniaxial tension and plane strain. Engineers might consider using two FLDs, one from the Bragard type and one from the M-H analysis. Depending on the application of the formed part and the criticality of a successful forming operation, engineers could choose between the two curves.

  6. 6.

    The strain paths that an FLD sample will take depend on the material’s yield/flow loci. For the AA6061-T4 aluminum, there is an extended zone of plane-strain deformation. This is particularly important in the case of the MK sample geometry, which exhibits minimal strain gradients. In essence, there is only a narrow range of loading angles that will give strain states between plane strain and balanced-biaxial deformation. For similar aluminum and other alloys, it would be advantageous to use the Nakazima, semispherical-punch approach. In the case of this punch geometry, friction and strain gradients allow one to obtain strain states close to but not exactly at balanced-biaxial deformation.