Introduction

The presence of stress raisers such as keyways, grooves and fillets necessitates a reliable design of load-bearing engineering components against failure. Highly concentrated stress/strain values at notch roots over asymmetric loading cycles emanate progressive plastic deformation and damage at notch root referred as local ratcheting. This phenomenon is largely influenced by various affecting parameters including materials, operating temperature/environment, component geometry, applied loading levels, steps, sequences and rates (Ref 1). Karry and Dolar (Ref 2) studied cyclic response of brass samples with different notch shapes/sizes. They reported that as notch root radius increased, durability and strength of brass samples were improved. Round bar and flat steel samples made of AISI 1141 were tested at the presence of various notch geometries by Zeng and Fatemi (Ref 3). They reported a noticeable difference between stress distribution at notch root determined through FE analysis and those determined analytically through the Neuber’s rule. Notched nickel-based superalloy samples of DZ125 holding U- and V-shape notches were tested under uniaxial loading cycles at elevated temperatures by Shi et al. (Ref 4). Corresponding number of cycles to failure as well as ratcheting deformation for notched samples was attributed to the notch shape/size and the magnitude of stress concentration factor, Kt. Notch root strain distribution of samples undergoing cyclic loading at elevated temperatures was further studied for Inconel 718 (Ref 5) and nickel-based superalloy (Ref 6) through several experiments. Measured values of local strains based on these experiments deviated from those analyzed through use of Neuber’s rule and numerical simulation. Plastic deformation and crack initiation at notch root of bainitic steel samples subjected to uniaxial loading cycles were studied by Ahmad et al. (Ref 7). They evaluated strain distribution at notch root through elastic–plastic finite element analysis and found a higher crack growth rate within notch plastic zone as compared with those determined from linear elastic fracture mechanics analysis. Low-cycle fatigue of notched samples made of SS316LN was examined at room temperature and 50 °C (Ref 8). The life decreased in the presence of notch for all strain amplitudes at both the temperatures as compared with those of un-notched samples. Circular and rhombic notches in 316L steel samples made by additive manufacturing technique were investigated by Brenne and Niendorf (Ref 9). They mapped strain deformation at the vicinity of notch roots under quasi-static and cyclic loading through use of digital image correlation method. They attributed number of cycles to failure directly to notch shape and stress concentration factor. Liao et al. (Ref 10) evaluated fatigue life of samples in the presence of notches through different approaches of nominal stress, local stress/strain, critical distance and weighted control. They discussed capability and limitation of methods applied for notched samples. Taylor (Ref 11) employed a mechanistic approach to evaluate critical distance at the notch root vicinity of samples undergoing cyclic loads. He evaluated both sharp and blunt notch shapes/geometry through this method. Zhu et al. (Ref 12) investigated the influence of notch size on critical distance and life of Al 2024-T351-centered hole plate samples undergoing fatigue cycles. A probabilistic framework (Ref 13) was further developed based on a generalized local model to assess multiaxial stress and stress gradient and to mimic fatigue response of large-scale structures from small-scale tested notched samples. The effect of notch shape on damage of test samples undergoing loading cycles was further studied by Jiang et al. (Ref 14). In their studies they evaluated the influence of stress level and ratio R of loading cycles on damage of notched samples. The substantial damage in their investigation was attributed to samples holding U- and V-shaped notches as compared to those samples with C-shaped notches. Elhady (Ref 15) performed FE analysis for notched samples with different circular and U-shaped notches undergoing uniaxial and biaxial loading cycles. Observation of fracture surface revealed that cracking started at the edge of notch root on the outer surface of steel plate samples. Rice et al. (Ref 16) measured local strains and evaluated local ratcheting and stress relaxation over asymmetric stress cycles at the vicinity of various notch shapes of semi-circle, blunt ellipse, and sharp ellipse. Their experimental results supported that plastic shakedown occurred for sharp elliptical notch at higher number of cycles than other notch shapes. Mean stress relaxation at notch roots gradually stabilized during asymmetric loading cycles. Varvani and coworkers (Ref 17) lately examined local ratcheting response of 1045 steel samples with different notch shapes and sizes measured at various distances from the root as asymmetric loading cycles proceeded. In their studies, local strains at notch roots were measured through use of strain gauges mounted at the vicinity of notch edge.

The current study examines ratcheting response of notched SS316 plate samples with various notch shapes. Cyclic tests were conducted under LHH and HLL loading sequences for Y-ellipse, circular and X-ellipse notch shapes. Strain gauges were mounted at the vicinity of notch root at a distance of about 0.5 mm from edge of notch to the edge of strain gauge circuit. Nominal asymmetric stress cycles were applied to plate samples with a frequency of 0.5 Hz under load-controlled condition. Local ratcheting response of SS316 samples was further evaluated by means of the A–V and CH hardening rules coupled with Neuber’s rule. Predicted ratcheting curves through the developed frameworks of A–V and CH were compared with measured local ratcheting values for various circular and elliptical notch shapes over different loading sequences. Simulated results of local ratcheting through the application of ABAQUS software were also compared with those of measured and predicted results by means of kinematic hardening frameworks.

Formulation and Modeling

To assess ratcheting response of materials, cyclic plasticity and related constitutive equations were employed. Constitutive equations were constructed on the basis of elastic–plastic behavior, materials yield criterion, flow rule and kinematic hardening rule. The present study employs classic elastic Hookean theory and plastic deformation theory to define contour of elastic–plastic deformation by yield surface based on von Mises criterion. The flow rule controls plastic strain over the loading process as coupled kinematic hardening model moves yield surface in deviatoric stress state. The present study employs two kinematic hardening models of Ahmadzadeh–Varvani (Ref 18) and Chaboche (Ref 19) models to evaluate ratcheting progress in the presence of asymmetric loading cycles. Local strains at the vicinity of notch root calculated through Neuber’s rule (Ref 20) were coupled with the A–V and CH kinematic hardening models.

The Chaboche (CH) Kinematic Hardening Model

The Chaboche kinematic hardening rule was first introduced by Armstrong–Frederick (A-F) (Ref 21). The CH model (Ref 19)-integrated backstress increments consist of linear and nonlinear terms as:

$$\mathrm{d}\overline{\alpha }=\sum_{i=1}^{M}\mathrm{d}{\overline{\alpha }}_{i}, \mathrm{d}{\overline{\alpha }}_{i}=\frac{2}{3}{C}_{i}\mathrm{d}{\overline{\varepsilon }}_{P}-{\gamma }_{i}^{^{\prime}}{\overline{\alpha }}_{i}\mathrm{d}p$$
(1)

Terms \(C\) i and \({\overline{\varepsilon }}_{P}\) in the first term of Eq 1, respectively, correspond to material-dependent coefficient and plastic strain increment. Term \(\mathrm{d}p\) is the equivalent plastic strain increment defined as:

$$\mathrm{d}p=\sqrt{\frac{2}{3}\mathrm{d}{\overline{\varepsilon }}_{P}.\mathrm{d}{\overline{\varepsilon }}_{P}}$$
(2)

Three different sets of \({C}_{1-3}\) and \({\gamma }_{1-3}^{^{\prime}}\) were considered to reach appropriate sets of coefficients based on measured stress/strain hysteresis loop of SS316 tested under a strain-controlled condition at strain amplitude limits of ± 1.5% (Ref 22). These coefficients were calibrated to achieve a close agreement between the measured strain-controlled hysteresis loop and that predicted through the CH model. Figure 1 presents the choice of coefficients \({C}_{1-3}\) and \({\gamma }_{1-3}^{^{\prime}}\) to achieve agreements between measured hysteresis loop and that obtained by means of the CH model. These coefficients were found as \({C}_{1-3}=\mathrm{55,35}, {\text{and}}\; 1 GPa\) and \({\gamma }_{1-3}^{^{\prime}}=500, 148,{\text{and}}\; 1\) in Fig. 1(c). Figure 1(a) and (b) shows how variation of coefficients C2 and \({\gamma }_{2}^{^{\prime}}\) influenced the width and shape of predicted loops as compared with experimental data.

Fig. 1.
figure 1

Coefficients \({C}_{1-3}\) and \({\gamma }_{1-3}^{^{\prime}}\) to generate stabilized hysteresis loop through use of measured hysteresis loop obtained under a strain-controlled test at ± 1.5%: (a) \({C}_{1-3}\)=55,20,1 GPa, and \({\gamma }_{1-3}^{^{\prime}}\)=500,300,1.0, (b) \({C}_{1-3}\)=98,35,1 GPa, and \({\gamma }_{1-3}^{^{\prime}}\)=300,148,1.0, and (c) \({C}_{1-3}\)=55,35,1 GPa and \({\gamma }_{1-3}^{^{\prime}}\)=500,148,1.0

Full size image

The Ahmadzadeh–Varvani (A–V) Kinematic Hardening Rule

The A-V kinematic hardening model is developed based on the A-F model through adapting an internal variable \(\overline{b}\) to control backstress progress and as yield surface is translated in the deviatoric stress space. The model implies new coefficients to control shape and width of generated hysteresis loops and ratcheting rate over loading cycles. The A–V model is formulated as (Ref 18, 23):

$$\mathrm{d}\overline{\alpha }=Cd{\overline{\varepsilon }}_{p}-{\gamma }_{1}\left(\overline{\alpha }-\delta \overline{b}\right)\mathrm{d}p$$
(3a)
$$\mathrm{d}\overline{b}={\gamma }_{2}\left(\overline{\alpha }-\overline{b}\right)\mathrm{d}p$$
(3b)

where \(C, {\gamma }_{1}, {\gamma }_{2}\) are material-dependent coefficients. Coefficients \(C\) and \({\gamma }_{1}\) are determined to coincide with shape and size of measured stress/strain hysteresis loops. The proper choice of these coefficients insures the consistency condition and enables ratcheting progress over loading cycles through open hysteresis loops. Term \(\left(\overline{\alpha }-\delta \overline{b}\right)\) in Eq 3 calibrates backstress evolution over loading cycles analogous to trend of \(\sum_{i=1}^{M}\mathrm{d}{\overline{\alpha }}_{i}\) in the CH model. Coefficient δ is to prevent this term in the dynamic recovery to drop to zero or less. Variable δ is defined as \(\delta ={(\alpha/k)}^{m}\). Constant k is the ratio of coefficients \(C\) and \({\gamma }_{1}\) as k = \(C/\gamma_{1},\) and exponent \(m\) is a material constant. Coefficient \({\gamma }_{2}\) is defined to curve fit measured ratcheting data with those predicted through the A–V model over asymmetric stress cycles. Figure 2 presents hysteresis loops for a typical sample of SS316 tested under stress-controlled condition at 76 ± 242 MPa. In Fig. 2(c) coefficients \(C=70\mathrm{ GPa}\) and \({\gamma }_{1}=100\) resulted in consistency condition at which measured and generated hysteresis loops closely agreed. Deviation from these values changed different loops in width and size as compared with experimental data in Fig. 2(a) and (b). Figure 2(d) and (e) presents measured ratcheting data and those predicted at various \({\gamma }_{2}\) and m, respectively. For steel sample tested at 76 ± 242 MPa, experimental ratcheting data closely agreed with the predicted curve for coefficients \({\gamma }_{2}\)= 20 and m = 0.1. More details on how to determine these coefficients are given in references (Ref 22, 23).

Fig. 2.
figure 2

Coefficients of the A–V model determined through use of experimental stress/strain hysteresis loops and measured ratcheting data from a steel sample tested at 76 ± 242 MPa. (a–c) coefficients C and 1 and (d, e) coefficient 2 and exponent m

Full size image

The Frameworks of CH and A–V Coupled with Neuber’s Rule

Local stresses and strains at the vicinity of notch roots were calculated through use of Neuber’s rule (Ref 20). Nominal applied stress and strain ranges (\(\Delta S\) and \(\Delta e)\) are related to local stress and strain ranges (\(\Delta \sigma\) and \(\Delta \varepsilon )\) through use of Neuber’s hyperbolic equation as:

$$\Delta \sigma .\Delta \varepsilon ={K}_{t}^{2}.\Delta S.\Delta e$$
(4)

where \({K}_{t}\) is the stress concentration factor.

Hardening models of CH (Eq 1) and A–V (Eq 3) were coupled to Neuber’s rule (Eq 4) through plastic strain increment \({d\overline{\varepsilon }}_{p}\). This enabled a relation between backstress and plastic strain components over loading and unloading paths. Backstress components over loading 0→A, unloading A→B and reloading B→C paths are, respectively, defined through \({\alpha }_{AL}=\frac{2}{3}({\sigma }_{AL}-{\sigma }_{y})\), \({\alpha }_{BL}=\frac{2}{3}({\sigma }_{BL}+{\sigma }_{y})\) and \({\alpha }_{CL}=\frac{2}{3}({\sigma }_{CL}-{\sigma }_{y})\) (Ref 25). Points A, B and C are turning points over loading cycles. The subscript L stands for local stress and strain components. At a given local plastic strain, backstress at a turning point is coupled with the hardening rule resulting in local stress to be calculated. Local stresses generated at the vicinity of notch root relax out as plastic strain is accumulated over loading cycles. The A–V and CH hardening rules were employed to govern ratcheting strain over loading cycles, while Neuber’s hyperbolic equation controlled local stress relaxation at notch root. Figure 3 presents an algorithm developed through MATLAB program (Ref 26) to analyze local stress and strain and corresponding ratcheting as nominal asymmetric stress cycles are applied. The coupled framework of A–V and CH controlled ratcheting progress at notch root over unloading and reloading paths. Detailed formulations of the A–V and CH hardening rules coupled with Neuber’s rule are presented in references (Ref 24, 27).

Fig. 3.
figure 3

An algorithm to evaluate ratcheting at notch root of SS316 by means of CH and A–V kinematic hardening models coupled with Neuber’s rule

Full size image

Experimental Procedure

Material, Sample Geometry and Tests

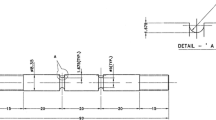
Stainless steel 316 samples were laser-cut to prepare notched plate samples and to examine local ratcheting response of materials at various loading steps and sequences. SS316 samples were tested under monotonic tensile loading at room temperature. The modulus of elasticity, yield strength and ultimate tensile strength for SS316 alloy were found, respectively, E = 218 GPa, σy=306 MPa and σult= 510 MPa. The notched plate samples of SS316 were prepared at 100 \(\times\) 50 \(\times\) 3mm. Notch shapes of circular and elliptical were cut in the center of plates. Vertical–elliptical notch (Y-ellipse) possessed dimensions d1, d2= 5.12 mm, while X-ellipse notches were cut with d1= 12 mm and d2= 5 mm in size. Circular notches of d = 12 mm in diameter were laser-cut in the middle of plates. Strain gauges were mounted at the distance of approximately 0.5 mm from notch root to the edge of gauge circuit, and cyclic tests were conducted with a loading frequency of 0.5 Hz under stress-controlled condition using the Zwick/Roell HB 100 servo-hydraulic machine. Figure 4 presents testing machine and test samples schematically. Data collection was done through a data acquisition system. Experimental data were acquisitioned in volts and then were converted to percentage.

Fig. 4.
figure 4

Schematic presentation of (a) testing machine, (b–d) different notch shapes on plate samples with mounted strain gauge at the vicinity of notch root

Full size image

Table 1 presents cyclic tests conducted on different notch shapes and at various loading steps and sequences. Ratcheting tests were conducted under stress steps and at different mean stresses, while stress amplitude was kept constant over loading steps/sequences. Each loading step/level experienced 100 consecutive asymmetric stress cycles.

Table 1 Ratcheting tests and loading conditions for SS316L samples with different notch shapes
Full size table

Local Ratcheting Measurements

Nominal stress cycles were applied to notched plate samples of SS316 with different notch shapes. Tests were conducted on samples with HLL and LHH loading sequences over consecutive stress steps of 110 ± 50 → 90 ± 50 → 70 ± 50 MPa and 70 ± 50 → 90 ± 50 → 110 ± 50 MPa, respectively. Each loading step contained 100 cycles. Strain gauges were mounted at about a distance of 0.5 mm from notch edge to the grid edge of gauge circuit. This enabled to measure local strain at the vicinity of notch roots. Local ratcheting was determined from the average of measured local maximum and minimum strains at root of various notch shapes. Figure 5 presents local ratcheting data measured from notch root of steel samples with different notch shapes tested at various LHH and HLL loading histories. In this figure ratcheting data measured for X-ellipse positioned, respectively, above ratcheting data collected at the root of circular notch and Y-ellipse over LHH and HLL loading sequences. The magnitude of ratcheting data for X-ellipse was found as large as 60% of those data for Y-ellipse notch under LHH loading sequence as shown in Fig. 5a. In Fig. 5b as the stress level decreased the magnitude of ratcheting shifted down. Over HLL loading sequence, tested samples showed a small drop in ratcheting over the last loading step due to higher stress levels over the first and second steps.

Fig. 5.
figure 5

Experimental data of local ratcheting at different notch shapes of Y-ellipse (d1, d2 = 5,12 mm), circular (d = 12 mm) and X-ellipse (d1, d2 = 12,5 mm) for (a) LHH tests and (b) HLL tests

Full size image

Finite Element Analysis

Local ratcheting of notched SS316 plate samples was simulated through use of ABAQUS software version 6.14 (Ref 28). Rigid bodies were defined at both ends of the notched plate and played the role of the upper and lower jaws of the testing machine. The lower rigid body was fixed, while the upper reference point was mobile only along the loading direction. Testing frequency of 0.5 Hz was applied in simulation with FE method over LHH and HLL loading histories. Five degrees of freedom with three displacement components and two in-surface rotation in each node were assigned for elements. An elastic-plastic material model based on the Chaboche hardening rule was utilized in the ABAQUS software. Local strains at the vicinity of different notch roots were simulated through use of this nonlinear model. Figure 6 presents surrounding area of different notch shapes partitioned with smaller rectangular elements to attain more accurate results over the simulation process.

Fig. 6.
figure 6

Small meshing elements generated at the surrounding area of notch roots with different shapes: (a) Y-ellipse, (b) circular and (c) X-ellipse

Full size image

Local stress and strain values at the vicinity of notch root were numerically calculated through FE analysis. Stress concentration factor was determined from the ratio of local stress at the vicinity of notch root calculated through finite element analysis and the nominal net stress applied to the notched plate samples. Stress concentration factors for notches with different shapes of Y-ellipse, circular and X-ellipse were found, respectively, 1.85, 2.43 and 4.59.

Figure 7 presents simulated local strains at notch root of various tested samples over unloading and reloading paths at the last stress step. Local strain contour was mapped over the last loading step through FE analysis in sample LHH-S1 with Y-ellipse notch. Turning point A with local strain of 0.1168% dropping to lower strain of 0.079% over A → B unloading path is presented, respectively, in Fig. 7(a1) and (a2). The magnitude of local plastic strain at root of this notch dropped to 0.1165% and 0.066%, respectively, for turning points A and B when the sample S5 tested in HLL sequence in Fig. 7(b1) and (b2). Local strains calculated at the vicinity of circular notch achieved higher values of 0.2% and 0.127% than the simulated values at notch root Y-ellipse as shown in Fig. 7(c1) and (c2) during reloading B → C and unloading A → B paths over the last step of sample LHH-S2. A smaller local strain was calculated at root of circular notch in sample S6 over HLL loading sequence as demonstrated in Fig. 7(d1) and (d2). The strain values at turning points A and B for this notch were, respectively, calculated as of 0.191% and 0.115%. The notch root of X-ellipse presented in Fig. 7(e1) and (e2) achieved a plastic strain as high as 0.273% and 0.142% over peak and valley of LHH loading cycles in sample S4 and reduced in magnitudes to 0.251% and 0.077% as loading sequence of HLL was applied in the notched sample S7 (see Fig. 7(f1) and (f2)). Last column in this figure (Fig. 7(a3)–(f3)) compares the simulated ratcheting strain with measured values. Simulated ratcheting results through FE analysis positioned on or above the measured values for various loading steps and sequences.

Fig. 7.
figure 7

Local strain contours at the end of last loading step over unloading and reloading paths: (a1, a2) Y-ellipse notch over LHH sequence, (b1, b2) Y-ellipse notch over HLL sequence, (c1, c2) circular notch over LHH sequence, (d1, d2) circular notch over HLL sequence, (e1, e2) X-ellipse notch over LHH sequence, (f1, f2) X-ellipse notch over HLL sequence and (a3–f3) simulated ratcheting strains vs measured values

Full size image

Predicted Ratcheting Results and Discussion

Algorithm developed in Fig. 3 was employed to predict local ratcheting at notch root of various steel samples under step loading conditions. The coupled frameworks of A–V and CH models enabled to assess local ratcheting of plate samples undergoing various loading steps/sequences. The Neuber’s hyperbolic trend relaxed out stress over loading cycles, while plastic strain at notch root was progressively accumulated. Figure 8 presents measured and predicted ratcheting results for various notch shapes as steel samples tested at various LHH and HLL loading sequences. Due to close agreement between ratcheting data obtained from tests LHH-S2 and LHH-S3, average of these data is presented in Fig. 8(c) and it is referred as test samples S2/S3. Similarly average of test data for HLL-S7 and HLL-S8 is presented in Fig. 8(f) representing samples S7/S8. Plastic shakedown occurred after a few stress cycles over each loading step. Ratcheting curves predicted by means of the A–V model (solid line) in this figure closely agreed with measured values in samples S1 and S5 with Y-ellipse notch shape undergoing, respectively, LHH and HLL loading sequences. Predicted local ratcheting curves for the circular notch shape through the A–V framework closely agreed with experimental data over the first and second loading steps of samples S2/S3 and S6 tested with LHH and HLL loading sequences. Over the third loading step, the A–V model underpredicted ratcheting data in test samples LHH-S2/S3 and HLL-S7/S8. Predicted ratcheting curves by means of the CH framework are presented in Fig. 8 by dashed lines. These curves positioned slightly above those predicted by the A–V model in various loading samples tested under LHH sequence. The predicted curves by the CH model deviated from HLL experimental ratcheting data over steps 2 and 3 as compared with those predicted curves through the A–V model. Ratcheting strain data were found greater in magnitudes for samples with X-ellipse notches as compared to those samples with circular and Y-ellipse notch shapes. The higher stress concentration factor in X-ellipse notch promoted ratcheting of samples LHH-S4 and HLL-S7/S8 as compared with circular notched samples and those test samples with Y-ellipse notch shapes.

Fig. 8.
figure 8

Measured experimental data versus predicted and simulated ratcheting curves by means of the coupled framework of A–V and CH and FE analysis for (a) Y-ellipse notch over LHH loading sequence, (b) Y-ellipse notch over HLL loading sequence, (c) circular notch over LHH loading sequence, (d) circular notch over HLL loading sequence, (e) X-ellipse notch over LHH loading sequence and (f) X-ellipse notch over HLL loading sequence

Full size image

Predicted ratcheting curves through the coupled frameworks of A–V and CH involved the Neuber’s rule to relate nominal and local stress and strain components. These frameworks controlled ratcheting progress at notch root in conjunction with Neuber’s rule over loading cycles. The simulated ratcheting data by FE method in Fig. 7 however calculated local strains at points around notch root meshed through smaller rectangular elements. Numerical analysis in contrast showed no link of Chaboche’s model to the Neuber’s formulation to estimate local strain at the vicinity of notch roots. FE method through utilizing Chaboche’s materials model overestimated ratcheting in the absence of Neuber’s hyperbolic equation. Predicted and simulated local ratcheting results were highly influenced by notch shape, size and plastic strain field at the edge of notch. Simulated and predicted ratcheting values at which the CH model acted as governing hardening model resulted in different ratcheting results for samples undergoing HLL loading sequence. The former underpredicted ratcheting over loading steps and the later overestimated ratcheting. This response may be attributed to the involvement of Neuber’s rule coupled with the CH model resulting lower plastic strain at higher applied stress levels.

Figure 9 presents predicted ratcheting curves through the CH and A–V models for SS316 samples with circular notches under LHH and HLL loading sequences. The evolution of backstress by means of the CH model (through (\(\sum_{i=1}^{M}\mathrm{d}{\overline{\alpha }}_{i}\))) and the A–V model (through \(\left(\overline{\alpha }-\delta \overline{b}\right)\)) is also presented in this figure. Overprediction of ratcheting through CH model in Fig. 9 (a1) consistently agreed with trend of backstress over asymmetric stress cycles in LHH loading sequence as shown in Fig. 9 (a2). Backstress curves generated based on the CH and A-V models were steeply relaxed over early loading cycles in step 1 and at the transition of loading steps 1-2 and 2-3, while ratcheting strain showed nearly a plateau after an initial increase in these transitions. The predicted ratcheting curve based on the CH model initially positioned above the curve predicted by the A–V model in the first step of HLL loading history (Fig. 9(b1)). The backstress curve generated by the CH model in Fig. 9(b2) stayed higher than backstress values governed by the A–V model over this loading step. Backstress by the CH model however fell below those determined by the A–V model over loading cycles for descending steps 2 and 3. Higher ratcheting response in the first step of HLL loading sequence, preserved ratcheting drop over subsequent steps. Backstress generated over steps 2 and 3 initially increased right after transitions of steps 1-2 and 2-3 and stabilized shortly after a few number of cycles. This response may be attributed to slight cyclic hardening of materials over loading cycles in steps 2 and 3, while ratcheting strain stayed unchanged shortly few cycles after transition points. The stabilized backstress levels in HLL history clearly depict stress relaxation over descending steps. For LHH loading sequence drop in backstress however took place dominantly over loading cycles within each step (Fig. 9 (a2)). Stress relaxation over each step in LHH sequence in this figure stayed nearly constant as the stress level increased over subsequent ascending steps. This alleviated the decay in backstress, while ratcheting strains increased over loading steps.

Fig. 9
figure 9

Ratcheting and backstress evolution based on the CH and A–V models for (a1–a2) LHH and (b1–b2) HLL loading sequences

Full size image

Local ratcheting response at notch root of steel samples is highly affected by several factors including loading steps, sequences, applied stress levels and rates, notch shape and geometry, and position of strain gauges to measure strain at notch root. Research on local ratcheting at the vicinity of notch roots with different ascending/descending loading steps/sequences is immature in the open literature. To realistically determine local strains at notch root over stress cycles, the Neuber’s rule should be further amended to address the magnitude of applied nominal stresses beyond elastic limit and to accommodate for evolution of plastic zone at notch root over loading steps/sequences. Authors plan for more tests and examination to account for various aspects of ratcheting at stress raisers and to further address technical challenges involved in ratcheting measurements at the vicinity of notch root.

Conclusion

Ratcheting response of notched SS316 steel plates was examined through conducting several ratcheting tests under various loading steps and sequences. Ratcheting data were the lowest in magnitudes for samples with Y-elliptical notch shape. The circular and X-elliptical notches, respectively, possessed intermediate and the highest ratcheting magnitudes at notch roots. Predicted ratcheting results through the CH model and FE method overpredicted ratcheting values in samples tested under LHH histories. The former approach however underestimated ratcheting over loading steps 2 and 3 for HLL samples. Simulated ratcheting curves over HLL resulted in curves positioned above experimental data. The predicted ratcheting through A–V model consistently agreed with experimental data over loading steps 1 and 2 at different loading sequences of LHH and HLL. Over the last step, the A–V model however underpredicted ratcheting for samples S2/S3 and S7/S8. The choice to employ a method of assessment to evaluate local ratcheting of materials at the vicinity of notch roots was found highly dependent on the complexity of approach and related terms, variables and coefficients.