Introduction

The liquefied natural gas (LNG) is mainly composed of the methane and a small number of secondary components, such as the ethane, propane and nitrogen. It is a clean energy source and is widely used as a domestic and industrial fuel because of its rich, versatile and clean combustion characteristics (Ref 1). The 9Ni steel is a grade of steel with a Ni content of 9% weight that was first developed by the USA in the 1940s. The 9Ni steel can be used at temperatures as low as − 196 °C. The 9Ni steel is widely used for the production of the liquefied natural gas (Ref 2, 3). The 9Ni steel is also used as a low-temperature structural material for LNG tankers and pipelines (Ref 4).

In recent years, there have been many studies on the properties of the 9Ni steel, including measurements of the strength, toughness, tensile and compression properties of the 9Ni steel (Ref 5,6,7). Among these studies, there has been considerable attention on researching the low-temperature toughness of the 9Ni steel. Liu (Ref 8) introduced the influence that different heat treatment specifications have on the low-temperature toughness of the 9Ni steel, and then summarized the mechanism behind the low-temperature toughness of 9Ni steel. The heat treatment process has a great influence on the microstructure of the 9Ni steel (Ref 9). The stability of the 9Ni steel depends on the content of the rotating austenite, the tempering temperature (Ref 10, 11) and the tempering holding time (Ref 12). The two-phase quenching (Ref 13) process also has an influence on the content of the rotating austenite.

However, research is limited on the flow stress of the 9Ni steel at high temperatures, the use of the accurate constitutive equation model and the application of processing maps for the 9Ni steel. Zhang et al. (Ref 14) studied the thermal deformation behavior of the 9Ni steel and plotted stress–strain curves for temperatures from 750 to 1100 °C at strain rates of 0.1-10 s−1 and established a mathematical model for predicting deformation resistance, but they did not plot a hot working diagram for 9Ni steel. Zhao et al. (Ref 15) studied the hot deformation behavior and energy dissipation diagram of the 9Ni martensitic stainless steel and plotted stress–strain curves for temperatures from 850 to 1200 °C with strain rates of 0.01-5 s−1. They construct the equation and plot the energy dissipation map. Yang et al. (Ref 16) obtained the thermal deformation of 9Ni steel and found the influence that deformation temperature, strain rate and deformation have on the deformation resistance. By using the Levenberg–Marquardt method to perform multiple linear regression, they obtained the deformation resistance model and verified the superiority of the model.

Constitutive equations and thermal processing maps are the main techniques frequently used by researchers to investigate the deformation mechanisms of steels and describe the ability of materials to work (Ref 17, 18). The constitutive equation is a mathematical model that represents the macroscopic properties of matters as a function of the specific medium and motion conditions studied. The constitutive equation is also known as the rheological equation, which reflects the intrinsic properties of a particular substance. Thermal processing patterns based on the dynamic material model (DMM) are widely used in the study of the hot deformation behavior of various metals and alloys (Ref 19,20,21). The unstable regions of the studied metals and alloys are analyzed to optimize the thermal processing parameters. Constitutive equations and thermal processing diagrams are not only used for steels but are also widely used for various alloys, such as magnesium alloys (Ref 22,23,24,25,26), titanium alloys (Ref 27,28,29,30,31), aluminum alloys (Ref 32,33,34), nickel-based alloys (Ref 35,36,37,38,39,40,41) and Cu-based alloys (Ref 42,43,44,45). Constitutive equations and thermal processing diagrams have also been applied to a variety of composite materials (Ref 46, 47).

In this paper, stress–strain curves of the 9Ni590B steel are calculated by studying the thermal compression of the 9Ni590B steel in the temperature range of 850-1200 °C for the strain rates of 0.001-5 s−1. The constitutive equation model is derived from the stress–strain curve results. From the experimental stress–strain curve data, the power dissipation and instability diagrams are plotted. The power dissipation and instability diagram are also combined to form a thermal processing diagram to determine the optimal processing parameters. Finally, the feasibility of the hot working drawing of the 9Ni590B steel was verified based on the microstructure of the steel.

Experimental Material and Procedures

The 9Ni590B steel was processed into ingots by electroslag remelting. The chemical composition of this material is shown in Table 1.

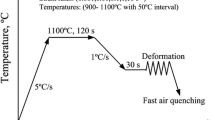
Table 1 Chemical composition of the 9Ni590B steel, wt.%
Full size table

The specimens with dimensions of diameter 10 mm with a height of 15 mm were used. The processing parameters are shown in Fig. 1.

Fig. 1
figure 1

Specimen processing parameters

Full size image

Thermal compression tests were performed using a Gleeble 3180 thermal simulator. A schematic illustration of compression–deformation process is shown in Fig. 2. The temperature was designed from 850 to 1200 °C with an interval of 50 °C; for each temperature, the strain rate was varied from 0.001 to 5 s−1. The final true strain of all specimens was set as 0.7. A crucible foil coated with a graphite lubricant was employed to minimize friction between the specimen and the anvil. After each compression was completed, the specimen was rapidly quenched with water to retain high-temperature microstructure. The deformed specimens were cut perpendicular to the longitudinal compression axis, and the scratches on the specimen surface were sequentially ground on the specimen surface with 250, 400, 1000 and 1500 sandpaper in the same direction at equal intervals. Polish the surface of the specimens without scratches on a mechanical polisher using a 2.5 water-soluble abrasive paste. Then use 7% nitric acid alcohol solution to corrode the specimen surface. Finally, the scanning electron microscope (SEM, Hitachi S-3400 N) was used to observe its microstructure.

Fig. 2
figure 2

Thermal compression–deformation experimental process

Full size image

Results and Discussion

Hot Deformation Flow Curves

Figure 3 and 4 shows the stress–strain curves of the 9Ni590B steel at temperatures from 850 to 1200 °C and strain rates from 0.001 to 5 s−1. This test shows that the true stress–strain curves have a similar shape at all deformation parameters. The flow stress is closely related to the deformation temperature and strain rate. The flow stress increases with the strain rate and decreases with the deformation temperature. The stress–strain curves indicate that in the initial stage of deformation, the flow stress increases sharply due to the work hardening effect caused by dislocations. In the subsequent deformation stages, the slope of the stress–strain curve gradually decreases due to the occurrence of dynamic recrystallization (DRX) during compression.

Fig. 3
figure 3

True stress–strain curves obtained from compression tests at different temperatures: (a) 850 °C, (b) 950 °C, (c) 1000 °C, (d) 1050 °C, (e) 1100 °C, (f) 1200 °C

Full size image
Fig. 4
figure 4

True stress–strain curves obtained from compression tests at different strain rates: (a) 0.001 s−1, (b) 0.01 s−1, (c) 0.1 s−1, (d) 1 s−1, (e) 2 s−1, (f) 5 s−1

Full size image

Generally, a typical flow stress–strain curve is composed of four stages: a work hardening stage, a stable stage, a softening stage and a steady stage. At low strain rates and high deformation temperatures, as shown in Fig. 3(f), 4(a) and (b), the flow stress curves grow rapidly first and then decrease slightly, and finally, the flow stress curves are in the steady stage. This is because during the initial stage of deformation, due to accumulation of dislocations and work hardening caused by entanglement, the softening effect from the dynamic recovery is relatively small, resulting in a rapid increase in the flow stress. As the compression proceeds further, the stress is slightly reduced. During this stage, the temperature is higher, or the strain rate is lower, and the dislocations have enough energy or time to migrate. Thus, many dislocations are eliminated, reducing the strain. The effect of the migration of the high-angle grain boundary is greater than that of strain hardening, resulting in a significant drop in stress. Finally, the strain tends to be stable when the rate of the dislocation formation is equal to the rate of annihilation, and hardening caused by the dislocation entanglement and softening due to dynamic recrystallization tend to balance.

At high strain rates and low temperatures, the flow stress tends to increase, but the rate at which the flow stress increases diminishes. Under these conditions, dynamic hardening plays a major role. This is because at high strain rates or low temperatures, dislocations do not have enough time or energy to migrate, resulting in increased dislocation densities. At the later stages of deformation, dynamic recrystallization (DRX) occurs at the critical strain value, resulting in an increase in the softening effect and a slow increase in the flow stress. We also find that the earlier the peak stress occurs as the deformation temperature increases. This is because at high temperatures, the grain boundary can have a higher mobility; that is, there is enough energy to make the dislocation occur migrate, and dynamic recrystallization occurs earlier, so that the softening effect is enhanced, and the stress is reduced faster, so the peak stress is reached faster.

Establishment of the Constitutive Equation

The constitutive model can predict the flow stresses of deformed materials under different temperatures, strain rates and strain conditions. The Arrhenius equation has been widely used. The constitutive model shows the relationship among the flow stress σ, the strain rate \(\dot{\varepsilon }\) and the deformation temperature T:

$$\dot{\varepsilon } = A_{1} \sigma^{{n_{1} }} \exp \left[ { - \frac{Q}{RT}} \right]\quad (\alpha \sigma < 0.8)$$
(1)
$$\dot{\varepsilon} = A_{2} \exp \left({\beta \sigma} \right)\exp \left[{- \frac{Q}{RT}} \right]\quad (\alpha \sigma > 0.8)$$
(2)
$$\dot{{\dot{\varepsilon} = A\left[{\sinh \left({\alpha \sigma} \right)} \right]^{n} \exp \left({- \frac{Q}{RT}} \right)}} \quad \left({\text{for all}} \right)$$
(3)

where Q is the deformation–activation energy, which is related to the material, n is the stress index, A, A1, A2, α and β are all material-dependent constants, R is the gas constant, T is the absolute deformation temperature and σ is the flow stress, generally taken from the peak stress (Ref 48). The change in α is small, \(\alpha = \beta /n_{1}\). Equation (1) and (2) are obtained by simplifying Eq 3 by Taylor series.

At low stress levels (ασ < 0.8), according to Eq 1, both sides are simultaneously logarithmic and simplified, and the n1 value of 9Ni steel can be obtained:

$$\ln \sigma = \frac{1}{{n_{1} }}\ln \dot{\varepsilon } - \frac{1}{{n_{1} }}\ln A_{1} + \frac{1}{{n_{1} }}\frac{Q}{RT}$$
(4)

At high stress levels (ασ > 0.8), according to Eq 2, both sides take logarithm and simplify at the same time, and the β value of 9Ni steel can be obtained:

$$\sigma = \frac{1}{\beta }\ln \dot{\varepsilon } - \frac{1}{\beta }\ln A_{2} + \frac{1}{\beta }\frac{Q}{RT}$$
(5)

As shown in Fig. 5(a) and (b), by plotting (lnσ − \(\ln \dot{\varepsilon }\)) and (σ − \(\ln \dot{\varepsilon }\)), based on the average of the reciprocal of the slope of the line in the graph, the n1 value for the 9Ni steel is determined to be 7.098, the β value is 0.089, and the value of α is obtained with the following calculation: α = β/n1 = 0.01255.

Fig. 5
figure 5

Plots for the following relationships: (a) lnσ − \(\ln \dot{\varepsilon }\); (b) σ − \(\ln \dot{\varepsilon }\); (c) ln[sinh(ασ)] − 1000/(T + 273); (d) ln[sinh(ασ)] − \(\ln \dot{\varepsilon }\)

Full size image

Taking the logarithm of both sides of Eq 3 gives:

$$\ln [\sinh \left( {\alpha \sigma } \right)] = \frac{1}{n}\ln \dot{\varepsilon } + \frac{Q}{nR}\left( {\frac{1}{T}} \right) - \frac{1}{n}\ln A$$
(6)

If ε is a constant, Eq 6 can be expressed as:

$$Q = R\left[ \frac{{\partial \left( {\ln \dot{\varepsilon }} \right)}}{\partial \ln [\sinh (\alpha \sigma )]}\right]_{T} \left[\frac{\partial \ln [\sinh (\alpha \sigma )]}{{\partial \left( {1/T} \right)}}\right]_{{\dot{\varepsilon }}} = Rnb$$
(7)

By plotting ln[sinh(ασ)] − 1/T and ln[sinh(ασ)] − \(\ln \dot{\varepsilon }\) at different temperatures, and using the average of the reciprocal of the slope of the straight line, b = 7.405 and n = 8.923 for the 9Ni590B steel. By substituting these values of n and b into Eq 7, the dynamic recrystallization deformation–activation energy of the 9Ni steel is calculated to be Q = Rnb = 364.99 kJ/mol.

Z is the Zener–Hollomon parameter (the Z parameter). The Z parameter decreases with an increase in the deformation temperature and decreases with a decrease in the strain rate. The relationship between Z and σ obeys the following relationship:

$$Z = A\left[ {\sinh (\alpha \sigma } \right)]^{n}$$
(8)
$${\text{then:}}\quad \sin (\alpha \sigma ) = (Z/A)^{1/n}$$
(9)

According to the definition of the hyperbolic sine function, the following equation is derived from the above formula:

$$\sigma = \frac{1}{\alpha }\ln \left\{ {\left( {\frac{Z}{A}} \right)^{{\frac{1}{n}}} + \left[ {\left( {\frac{Z}{A}} \right)^{{\frac{2}{n}}} + 1} \right]^{{\frac{1}{2}}} } \right\}$$
(10)

The relationship among the flow stress, deformation temperature and strain rate during plastic deformation of metal materials can be expressed using Eq 11 (Ref 49).

$$Z = \dot{\varepsilon }\exp [Q/\left( {RT} \right)]$$
(11)
$${\text{so:}}\quad Z = \dot{\varepsilon }\exp [364.99/\left( {RT} \right)]$$
(12)

T = (t + 273)/1000

Taking the logarithm of both sides of Eq 8 yields:

$$\ln Z = \ln A + n\ln [\sinh (\alpha \sigma )]$$
(13)

In Fig. 6, the graph of InZ − ln[sinh(ασ)] is shown, and the A value of the 9Ni590B steel can be obtained from the intercept of the straight line on the y-axis in the figure. The A value is calculated as: lnA = 30.56833, A = 1.89 × 1013.

Fig. 6
figure 6

Relationship curve of ln[sinh(ασ)] and InZ for the 9Ni590B steel

Full size image

Substituting the Q, n, α and A values into Eq 3 produces the high-temperature constitutive equation of the 9Ni590B steel for different deformation temperature ranges:

$$\dot{\varepsilon } = 1.89 \times 10^{13} \left[ {\sinh (0.01255\sigma } \right)]^{8.923} \exp [ - 364.99/\left( {RT} \right)]$$
(14)

Substituting the n, α, and A values into Eq 10 gives the flow stress equation of the 9Ni590B steel:

$$\sigma = 79.68\ln \left\{ {\left( {\frac{Z}{{1.89 \times 10^{13} }}} \right)^{0.112} + \left[ {\left( {\frac{Z}{{1.89 \times 10^{13} }}} \right)^{0.224} + 1} \right]^{{\frac{1}{2}}} } \right\}$$
(15)

Processing Map

Thermal processing has a history of more than 50 years. The mathematical models that have been proposed for the thermal deformation behavior of materials include the atomic model, the kinetic model, the dynamic material model and so on. Among these proposed models, Prasad and Seshacharyulu (Ref 50) explained the specific parameters of the dynamic material model (DMM). Not only the DMM method is in the category of medium mechanics, but it also combines the microstructures of materials to describe the characteristics of the thermal deformation behavior of materials. The behavior of thermal deformation can be measured by a simple energy dissipating unit, including the dissipative characteristics, nonlinear characteristics and dynamic characteristics of the material. Subsequently, the heat dissipation map of the material to be processed can be obtained by establishing the power dissipation diagram and the instability diagram.

According to the characteristics and the definition of the dissipative property, the energy, P, obtained by the material per unit time during processing can be calculated by J and G.

$$P = \sigma \dot{\varepsilon } = G + J = \mathop \smallint \limits_{0}^{{\dot{\varepsilon }}} \sigma {\text{d}}\dot{\varepsilon } + \mathop \smallint \limits_{0}^{\sigma } \dot{\varepsilon }{\text{d}}\sigma$$
(16)

where \(G = \mathop \smallint \limits_{0}^{{\dot{\varepsilon }}} \sigma {\text{d}}\dot{\varepsilon }\) represents the power dissipation due to plastic deformation and \(J = \mathop \smallint \limits_{0}^{\sigma } \dot{\varepsilon }{\text{d}}\sigma\) represents the power dissipation caused by the change in the microstructure during material processing.

Under certain temperature and strain conditions, the simple dissipative constitutive equation in the DMM model can be used to describe the relationship between the flow stress and the strain rate of the experimental material.

$$\sigma = K\dot{\varepsilon }^{m}$$
(17)

After taking the logarithm of both sides in Eq 17 and obtaining the partial guide, the following can be obtained:

$$m = \frac{{\partial \left( {\ln \sigma } \right)}}{{\partial \left( {\ln \dot{\varepsilon }} \right)}}\left| {\varepsilon ,T} \right. = \frac{{\dot{\varepsilon }{\text{d}}\sigma }}{{\sigma {\text{d}}\dot{\varepsilon }}} = \frac{{{\text{d}}J}}{{{\text{d}}G}}$$
(18)

where m represents the strain rate sensitivity coefficient of the material.

The thermal deformation process of a material can be characterized by changes in the dissipation efficiency (η):

$$\eta = \frac{2m}{m + 1}$$
(19)

Furthermore, based on the principle of the irreversible thermodynamic extreme, the instability graph is developed, and the unstable parameter (ξ) is used as the criterion for the continuous instability of plastic deformation, which is expressed as follows:

$$\xi \left( {\dot{\varepsilon }} \right) = \frac{{\partial \ln [m/\left( {m + 1} \right)]}}{{\partial \ln \dot{\varepsilon }}} + m < 0$$
(20)

The region where ξ(\(\dot{\varepsilon }\)) < 0 represents a rheological instability region.

In Fig. 7, the number of contour lines represents the power consumption efficiency (η), and the shaded area represents a flow instability (ξ) region. The results in Fig. 7 show that the power dissipation map in the strain range of 0.3-0.6 is similar in the contour shape, and the power consumption efficiency increases with the increased strain. The unstable graph indicates the instantaneous process ability of the material, and the instability map indicates a certain difference from 0.3 to 0.6. As presented in Fig. 7(a), when ε = 0.3, shown in the shaded region, there are two unstable regions, and the left shaded area is relatively large, occupying almost one-third of the entire image, which shows that the hot workability is very low at low temperatures. Figure 3 shows that the stress is constantly increasing at lower temperatures for ε = 0.3, indicating that the dislocation entanglement is more significant during this stage, making this region unsuitable for hot working. When the temperature range is from 1125 to 1200 °C, and the strain rate range is from 0.001 to 0.025 s−1, the power consumption graph shows a relatively high range of values. As exhibited in Fig. 7(b), when ε = 0.4, two unstable regions also appear: The shaded portion on the left is equivalent in size and position to the graph where ε = 0.3, and the shaded region on the right is relatively small and its position is slightly shifted to the left. When the temperature range is from 1130 to 1200 °C and the strain rate ranges from 0.001 to 0.01 s−1, the power consumption graph shows a higher value range, and the processing performance is better in this region.

Fig. 7
figure 7

Thermal processing of the 9Ni590B steel under different strains: (a) 0.3; (b) 0.4; (c) 0.5; (d) 0.6

Full size image

As shown in Fig. 7(c) and (d), when ε = 0.5 and 0.6, the shaded area shrinks significantly, indicating that as the compression progresses, the dislocations begin to migrate, and dynamic recrystallization plays a central role. The power consumption efficiency at the same position is slightly higher than that for ε = 0.3 and ε = 0.4, and the power consumption graph shows the work over a deformation temperature range of 1100-1200 °C and strain rates of 0.001-0.01 s−1. The efficiency is relatively high, nearly exceeding 0.4. As presented in Fig. 3(a) and (b), when the strain rate is above 0.01 s−1, the flow stress curve is constantly increasing, which is in agreement with the shaded areas exhibited in Fig. 7(c) and (d). High power dissipation efficiency indicates that the material consumes more energy for microstructural changes, which may be associated with DRX (Ref 51). The true stress–strain curve in Fig. 4 shows typical DRX characteristics over a temperature range of 1100 to 1200 °C and a strain rate range of 0.001-0.01 s−1.

According to the thermal processing diagram, the optimum processing range of 9Ni590B steel for hot working is a temperature range of 1100-1200 °C and a strain rate range of 0.001-0.01 s−1, and the power consumption efficiency of the 9Ni590B steel can reach 0.4 or more. A stable flow stress and desirable processability can be obtained by simultaneous softening and tissue reconstitution during thermal deformation. Therefore, it is believed that the emergence of DRX is conducive for improving the working performance of the 9Ni590B steel. Therefore, the processing region with a temperature range of 1100-1200 °C and a strain rate range of 0.001-0.01 s−1 is considered a safe working region.

Microstructure and Deformation Mechanism

Figure 8 shows the SEM microstructures at various temperatures for a strain rate of 0.1 s−1. In the subsequent images, the microstructure is slightly coarse, which may be caused by holding at 1200 °C for 3 min before compression, during which time austenite grains grow. When isothermal compression is performed at 850 °C, the microstructure is the elongated martensite, and the grains are coarse and uneven. Isothermal compression may occur at a lower temperature, resulting in the increased dislocation density and grain boundary migration. The lower rate indicates that DRX is insufficient and incomplete in this state. When isothermal compression is carried out at 900 °C, some of the crystal grains are slightly smaller, and the elongated state of the martensite is somewhat improved. The reason may be that nucleation occurs at the grain boundary with a further increase in temperature, resulting in the formation of grains of different sizes. For isothermal compression at 950 °C, some of the grains are significantly smaller, and the grain size is polarized because the dislocation density in the grain boundaries and deformation zones is higher than that inside the grains, thus promoting the edges. The recrystallization nucleation of these parts occurs in the case of grain sizes. The mixed crystal structure formed by partial DRX weakens the mechanical properties of the steel and should be avoided during hot working. The above three temperature parameters (850, 900 and 950 °C) also verify the thermal processing diagram shown in Fig. 7(d). When the strain rate is 0.1 s−1, the above three temperatures (850, 900 and 950 °C) are in the processing instability zone.

Fig. 8
figure 8

Microstructure of the 9Ni590B steel at various temperatures at a strain rate of 0.1 s−1: (a) 850 °C; (b) 900 °C; (c) 950 °C; (d) 1000 °C; (e) 1050 °C; (f) 1100 °C

Full size image

When isothermal compression is performed at 1000 °C, the grain size is significantly smaller, because the activation energy becomes higher as the temperature increases, the grain boundary also has a higher mobility, which facilitates the nucleation of the dynamic recrystallization of grains. The grains become fine at 1050 and 1100 °C, where the size of the crystal grains is not much different from that at 1000 °C, but more uniform, which indicates that the DRX occurring at this temperature is more effective, which is beneficial to the processing of the material under these conditions.

Figure 9 shows a typical structure of the 9Ni590B steel in the stable zone. It is well known that refined grain sizes can promote both the strength and toughness effectively and simultaneously. The microstructure evolution of the stable zone can occur by dynamic recrystallization, dynamic recovery and superplasticity. Figure 9(a) shows an SEM image with a deformation temperature of 1100 °C and a strain rate of 0.001 s−1, and Fig. 9(b) shows an SEM image with a deformation temperature of 1100 °C and a strain rate of 0.01 s−1. The microstructures in these images showed uniform and fine particles, indicating that the complete DRX had occurred. The DRX zone is the first choice for thermal processing because it not only has a stable flow and good processability, but DRX also rebuilds the microstructure. This trend is consistent with the thermal processing diagram shown in Fig. 7(d), and the peak dissipation efficiency is above 0.4 in this zone. These parameters facilitate the processing of the material, and a workpiece with better performance in all aspects is produced. It can also be seen from the image that as the strain rate decreases, the dynamic recrystallized grain size increases.

Fig. 9
figure 9

(a) Microstructure image of 9Ni590B steel at 1100 °C and 0.001 s−1; (b) Microstructure image of 9Ni steel at 1100 °C and 0.01 s−1

Full size image

Conclusions

The hot deformation behavior of the 9Ni590B steel in the temperature range of 850-1200 °C and strain rate range of 0.001-5 s−1 was studied by hot pressing tests. We can draw the following main conclusions from this study:

  1. 1.

    The deformation temperature and strain rate have a significant effect on the flow stress of the 9Ni590B steel. The flow stress increases with the strain rate and decreases with the deformation temperature.

  2. 2.

    The thermal deformation–activation energy of the 9Ni590B steel is calculated to be 364.99 kJ/mol. The constitutive equation for the flow stress can be expressed as: \(\dot{\varepsilon } = 1.89 \times 10^{13} \left[ {\sinh (0.01255\sigma } \right)]^{8.923} \exp [ - 364.99/\left( {RT} \right)]\)

  3. 3.

    According to the hot working diagram, the optimum thermal process parameters of the 9Ni590B steel are with the temperature of 1100-1200 °C and strain rate of 0.001 s−1-0.01 s−1. Its power consumption efficiency can reach 0.4 or more.

  4. 4.

    According to the SEM images at different deformation temperatures and different strain rates, it can be seen that the optimal thermal process parameters are in good agreement with the microstructure of the specimen.