A Method to Estimate Residual Stress in Austenitic Stainless Steel Using a Microindentation Test

Abstract

This study proposed a method to evaluate the residual stress and plastic strain of an austenitic stainless steel using a microindentation test. The austenitic stainless steel SUS316L obeys the Ludwick’s work hardening law and is subjected to in-plane equi-biaxial residual stress. A numerical experiment with the finite element method (FEM) was carried out to simulate an indentation test for SUS316L having various plastic strains (pre-strains) and residual stresses. It was found that the indentation force increased with increasing pre-strain as well as with compressive residual stress. Next, a parametric FEM study by changing both residual stress σ_res and pre-strain ε_pre was conducted to deduce the relationship between the indentation curve and the parameters ε_pre and σ_res (which were employed for the FEM study). This relationship can be expressed by a dimensionless function with simple formulae. Thus, the present method can estimate both ε_pre and σ_res, when a single indentation test is applied to SUS316L.

Introduction

Development of residual stresses is often experienced in engineering steels due to inhomogeneous strain distribution and mechanical constraints. Residual stresses are produced due to many reasons. For instance, residual stress is formed when a material undergoes inhomogeneous plastic deformation due to plastic work (i.e., cold working and sheet forming) and surface treatments/modifications (Ref 1, 2). In particular, tensile residual stress induces environmental-assisted cracking and fatigue crack initiation, resulting in severe damage (Ref 3, 4). Thus, the evaluation of residual stress is very important for industrial steels and structures. For such a case, residual strains caused by local plastic deformation (pre-plastic strain) may be an important issue as it is related to the development of residual stress. In other words, local and inhomogeneous plastic strain induces mechanical constraint, resulting in the development of residual stresses. Therefore, an evaluation of both residual stress and plastic strain may be required to maintain the integrity of a material as well as to design materials and structures. X-ray diffraction is widely used to measure residual stress. This method has been fully developed and is often employed in field inspections. However, a particular crystalline structure (i.e., grain coarsening and crystal texture) may make accurate measurements difficult (Ref 5), and it is not suitable for small material structures. In addition, the x-ray diffraction method cannot evaluate plastic strain (called pre-strain), which is often coupled with the level of residual stress.

Instrumented indentation technique is a convenient process to determine mechanical properties, including Young’s modulus and hardness (Ref 6, 7). Furthermore, elastoplastic properties (i.e., uniaxial stress-strain curve) can be derived from the experimental data of an indentation curve, which represents the relationship between indentation force and penetration depth, and an impression (residual imprint) (Ref 8-10). In these studies, the dimensional function that correlates the parameters of indentation responses (mostly the indentation curve) with the elastoplastic properties of a material is first established through a forward analysis (indentation responses obtained from material properties) using computational approaches (Ref 11-13). The elastoplastic properties can then be identified, when the experimentally obtained indentation responses are assigned to the function (i.e., reverse analysis: material properties identified from indentation responses). Thus, this method may evaluate the plastic strain due to plastic deformation when the estimated stress-strain curve matches with that of the undeformed material (Ref 14). In fact, it is well known that work hardening due to plastic deformation increases the hardness of a material (Ref 6, 15-17). Therefore, the indentation technique is useful for measuring local elastoplastic properties, including the plastic strain.

Several other attempts to evaluate the residual stress based on an indentation test were proposed in previous studies. For example, Suresh and Giannakopoulos (Ref 18) focused on the change of impressions due to residual stress, and their relationship was investigated by an analytical formula. This was based on the findings of Tsui et al. (Ref 19). However, the influence of residual stress on an impression may be relatively small to be measured experimentally. Thus, it is not clear whether the method can be practically applied except when the residual stress is large (near the yield stress). Swadener et al. (Ref 20) proposed a simple approach based on the depth-sensing indentation test. Their method may be useful, when an intermediate indentation force is used since the transition regime between elastic and plastic contact (i.e., elastic-plastic transition) is greatly affected by the residual stress. Xu et al. (Ref 21) proposed a similar idea with a flat punch indenter. Those challenges were reported in a review article (Ref 22). However, in order to apply those methods with a general indentation force, precise depth measurements may be required. In addition, yield strength (plastic properties) should be known prior to the estimation of residual stress. As mentioned previously, simultaneous evaluations of both plastic strain (plastic properties including yield stress) and residual stress are also required through an indentation method, which we understand to still be an open research topic.

Other methods have been proposed in the literature. For example, inverse analysis methods were established to evaluate the residual stress from an indentation curve (Ref 23, 24). These methods can also evaluate other unknown mechanical properties, such as Young’s modulus and yield stress. However, these methods require a great deal of effort and have not found widespread use, since the estimation procedure requires iterative FEM computations (forward analysis) with, for example, an optimization algorithm (Ref 23) and an updating response surface (Ref 24). When a method is required for practical situations, reverse analysis based on a simple framework (without special computational requirements) is more desirable. For instance, Chen et al. proposed a reverse analysis technique based on an indentation curve in order to estimate the elastoplastic property and residual stress (Ref 25, 26). This method is reliable, but there are some issues. For instance, the range of materials application is very limited (i.e., no work hardening), and complex functions are used.

This study proposes a simple method to evaluate both residual stress and plastic strain (plastic properties)¹ using a new indentation method. Since this study is the first step to establish such a simple evaluation framework, we focus only on austenitic stainless steel (SUS316L) having equi-biaxial residual stress. In fact, stainless steel is commercially available, and is widely used in industrial mechanical components and chemical/electronic power plants. In chemical plants, the steel often suffers from mechanical degradation (fatigue and stress corrosion cracking, SCC) due to tensile residual stress. To prevent such issues, compressive residual stresses are usually introduced via a peening technique. This technique may introduce equi-biaxial compressive stress on the material surface. By considering such an engineering background, this study focuses on SUS316L having equi-biaxial residual stress and plastic strain. In other words, it aims to establish reverse analysis with a simple framework to simultaneously evaluate residual stress and plastic strain in SUS316L. In this research, reverse analysis is established via a parametric study using a finite element method (FEM). Our method is subsequently verified by computational and experimental data. Some issues and future challenges are also discussed.

Materials

The material considered in this study is austenitic stainless steel (SUS316L) and its mechanical properties are listed in Table 1. These properties were obtained from a uniaxial tensile test of as-received SUS316L (which is commercially available) (Ref 14). The true stress and true strain curve in the plastic region can be approximated by Ludwick’s law (Ref 14). The constitutive equation in the elastic and plastic region is described as follows:

$$\upsigma = E\upvarepsilon\quad {\text{for}}\quad\upsigma\; \le \;\upsigma_{\text{Y}} \quad {\text{and}}\quad \upsigma =\upsigma_{\text{Y}} + K\upvarepsilon_{\text{p}}^{n} \quad {\text{for}}\quad\upsigma\; \ge \;\upsigma_{\text{Y}} ,$$

(1)

where E is the Young’s modulus, σ_Y is the yield stress, n is the work hardening exponent, and K is the work hardening strength. Note that ε_p is plastic strain. The stress-strain curve of SUS316L is shown in Fig. 1. The curve is expressed by Eq 1 and Table 1.

Table 1 Mechanical properties of austenitic stainless steel (SIS316L) employed in this study

Fig. 1

True stress-strain curve of austenitic stainless steel with various pre-strains

We next considered the plastically deformed steel. This study assumed that when the steel experiences plastic strain due to plastic deformation, the stress-strain data correspond to the curve of the as-received steel by shifting of the applied plastic strain. This example is also shown in Fig. 1, indicating pre-strains of 5, 10, 20, and 30%. In other words, the yield stress of pre-strained steel increased due to work hardening, which was then plotted on the stress-strain curve of as-received steel when it shifted to the value of pre-strain. In fact, this phenomenon was observed, when uniaxial loading was applied to the as-received steel and pre-strained steel (Ref 15, 17). Cyclic plastic deformation along one direction may show a similar trend. However, the increase of yield stress due to work hardening depends on the loading direction. This is well known to be Baushinger effect, and cyclic plastic deformation obeys the kinematic hardening rule. For simplicity, this study assumed that the effect of loading direction of plastic deformation is negligible. In other words, the material obeys the isotropic hardening rule. It was also assumed that the elastic modulus does not change even if the steel undergoes plastic deformation (i.e., the pre-strain is introduced in the steel).

Since this study addresses only SUS316L, the yield stress of pre-strained steel can be expressed by substituting pre-strain into Eq 1. In fact, Fig. 1 shows the stress-strain curves of pre-strained steels having different pre-strain values (5, 10, 20, and 30%) obtained using Eq 1. Therefore, the plastic properties can be expressed by only the parameter of pre-strain ε_pre. The yield stress σ_Y can be obtained from Fig. 1, when the pre-strain value is known.

On the contrary, residual stress is assumed to be introduced equi-biaxially on the specimen surface. The stress component is considered to be both tension and compression. Therefore, this study will evaluate pre-strain (plastic strain) and residual stress of stainless steel.

Numerical Analysis

Model Definition

Figure 2 shows the schematic of an indentation test using a conical sharp indenter. As a typical sharp indenter, the Berkovich indenter is widely used. The indenter has a triangular shape with a diagonal angle of 115°. For the simplicity of computations and to approximate an axisymmetric model, this study used a conical indenter as shown in Fig. 2(a). The half apex angle α is 70.3°, so that the contact area as a function of indentation depth equals between the two (for a Berkovich indenter and conical indenter).

Fig. 2

(a) Schematic of indentation loading and unloading; (b) definition of work volume in the indentation curve; and (c) residual stress state during indentation loading

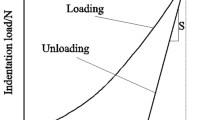
In Fig. 2(a), the indenter penetrates the material surface for a given maximum indentation force F _max, to a certain penetration depth, which is designated by the maximum indentation depth h _max. Note that the indenter penetrates into the region that experiences full plastic deformation. Subsequently, the indenter is withdrawn, such that the maximum force drops to zero. Following this full unloading, a permanent impression (crater) is observed. The residual depth is described by h _r in Fig. 2(a). Such a loading and unloading cycle is shown in Fig. 2(b), where the material locally deforms elastically and plastically during the loading, and then recovers elastically during the unloading. In this figure, the area of indentation curve corresponds to a total work volume W ² due to indenter penetration. Contrary to this, the area corresponding to the unloading (as shown by the blue shaded area, W _u) indicates the work of elastic recovery (unloading work). Here, the recovery depth h _e can be obtained by h _max − h _r. Consequently, the total work, $W = \int_{0}^{{h_{\hbox{max} } }} {Fdh}$ and the unloading work, $W_{\text{u}} = - \int_{{h_{\hbox{max} } }}^{{h_{\text{r}} }} {\begin{array}{*{20}c} {} \\ \end{array} Fdh}$ can be obtained.

Figure 2(c) shows the schematic of in-plane residual stress σ_res which is introduced in the material. This study focuses on the equi-biaxial residual stress with both compression and tension.

Finite Element Method

The axi-symmetric model of the two-dimensional (2D) FEM was created to compute the response of the indentation test, as shown in Fig. 3. The model comprises about 20,000 four-node elements, wherein fine meshes were created around the contact region, and a mesh converge test was carried out. The conical indenter whose half apex angle is 70.3° was employed for the 2D model using the Berkovich indenter (as mentioned above). In the FEM model, the indenter is assumed a rigid body. The indenter penetrates up to 10 μm into the material and is withdrawn until completely unloaded.

Fig. 3

Axi-symmetric two-dimensional FEM model for Berkovich indentation

Computations were carried out using a commercially available software, Marc (Ref 27). Coulomb’s law of friction was assumed, and a coefficient of friction of ν = 0.15 was used, which is often regarded as a minor influence in indentation analysis (Ref 13, 28). In addition, the Poisson’s ratio was set to 0.3 for all computations. As shown in Table 1, Young’s modulus E was set to 195 GPa. Referring to Eq 1, this study employed various plastic properties, which can be expressed by the plastic strain (pre-strain, ε_pre) as described in Fig. 1. As shown in this figure, the yield stress σ_Y increases with an increase in pre-strain, indicating that σ_Y is uniquely dependent on pre-strain ε_pre. Thus, the yield stress present is described by σ_Y(εpre) hereafter. The pre-strain ε_pre values employed were 0, 5, 10, 20, 30, 40, 60, and 100%³. A pre-strain ε_pre of 0% corresponds to the as-received virgin material as shown in Table 1. This study conducted an elastoplastic analysis with the von Mises yield criterion.

In order to introduce the in-plane residual stress, a mechanical loading (edge loading) was applied to the material from the side surface as shown in Fig. 3. Since the model size was relatively large with a depth of 8.4 mm and a radius of 20.4 mm, the effect of boundary conditions due to edge loading on the indentation response could be ignored. Therefore, the residual stress was uniformly introduced to the material. This study introduced various residual stresses σ_res in the material before indenter penetration (indentation loading). Note that σ_res normalized by σ_Y(εpre) (σ_res/σ_Y(εpre)) was used for the assigned parameter in the parametric FEM study. The value of σ_res/σ_Y(εpre) varied among −0.75, −0.25, 0, +0.25, and +0.75. Thus, the eight total pre-strain values and the five total σ_res/σ_Y(εpre) values gave rise to 40 total computations during the course of this study.

Representative Computational Results

To verify our FEM model, a preliminary computation for the as-received steel was carried out. The computed indentation curve is shown in Fig. 4. This was compared to the experimental data, and as can be seen, both curves show good agreement with each other.

Fig. 4

Indentation curves of the as-received SUS316L determined by the FEM computation (circles) and experiment (solid line)

This study next investigated the effect of pre-strain and residual stress on the indentation curve. Figure 5 shows the indentation curves, indicating the dependence of pre-strain (Fig. 5a) and that of residual stress (σ_res/σ_Y(εpre), in Fig. 5b). In Fig. 5(a), the result of no residual stress shows that the indentation force increases as ε_pre increases (owing largely to the higher yielding level). In Fig. 5(b), it is found that the indentation force increases with compressive residual stress. On the other hand, the indentation force decreases with increase in tensile residual stress. A similar trend was observed in a previous study (Ref 26). It is thus concluded that both pre-strain and residual stress affect the indentation curve. These characteristics assist in establishing the dimensionless function for reverse analysis, which will be discussed in the next section.

Fig. 5

Effect of pre-strain (a) and residual stress (b) on the indentation curves

Estimation Method

Dimensionless Analysis

As mentioned above, there are many previous studies on the estimation of elastoplastic properties based on a dimensionless function (Ref 8, 12, 13, 29). Such a simple function may be useful for reverse analysis. Similarly, this study conducted a dimensionless analysis to develop the estimation method of both ε_pre and σ_res. In other words, the dimensionless function, which correlates the indentation curve with the parameters to be identified (ε_pre and σ_res), was established through the parametric FEM study. Since there are two parameters identified (ε_pre and σ_res), two independent parameters are required in an indentation curve. As shown in Fig. 2(b), the total work W and the elastic work W _u were investigated in this study, as these two parameters are independent.

The total work volume W in the indentation curve depends on the elastoplastic properties, mechanical preparation conditions (ε_pre, σ_res), and indentation testing conditions (the maximum depth h _max and indenter tip angle α). It can be expressed as follows:

$$W = f_{ 1} (E^{*} ,\upsigma_{\text{res}} ,\upvarepsilon_{\text{pre}} \;\upsigma_{\text{Y}} ,n,K,h_{ \hbox{max} } ,\upalpha).$$

(2)

As explained above, the plastic property (σ_Y, n, K) is dependent on the pre-strain ε_pre, and can be determined uniquely given ε_pre (see Fig. 1 for the fixed material investigated in the present paper). In addition, the indenter angle α is fixed and can be removed from the current function. Thus, Eq 2 can be simplified using σ_Y(εpre) as follows:

$$W = f_{ 1} (E^{*} ,\upsigma_{\text{res}} ,\;\upsigma_{{{\text{Y(}}\upvarepsilon{\text{pre)}}}} ,\;h_{ \hbox{max} } ).$$

(3)

In this study, σ_Y(εpre) and h _max were varied to investigate their coupled effects, and the dimensionless function with Π theory was used to obtain the following dimensionless function:

$$\frac{W}{{\upsigma_{{{\text{Y}}(\epsilon {\text{pre}})}} h_{\hbox{max} }^{3} }} = \varPi \left( {\frac{{E^{*} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }},\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}} \right).$$

(4)

Similarly, the dimensionless function of elastic work W _u (indentation unloading curve) can be obtained as follows:

$$\frac{{W_{\text{u}} }}{{\upsigma_{{{\text{Y}}(\epsilon {\text{pre}})}} h_{\text{e}}^{3} }} = \varPi \left( {\frac{{E^{*} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }},\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}} \right).$$

(5)

Here, the yield stress σ_Y(εpre) is related to pre-strain ε_pre via Eq 1 (see Fig. 1). In both Eq 4 and 5, E* is the reduced Young’s modulus, which can be expressed by $\frac{1}{{E^{*} }} = \left( {\frac{{1 - \nu_{\text{s}}^{2} }}{{E_{\text{s}} }} + \frac{{1 - \nu_{\text{i}}^{2} }}{{E_{\text{i}} }}} \right)$. Note that the subscripts “s” and “i” denote “specimen” and “indenter”, respectively.

The data of the parametric FEM study on the 40 cases spanning the material parameter space were introduced into Eq 4, and the results are shown in Fig. 6. The values of $\frac{W}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} h_{\hbox{max} }^{3} }}$ increase in $\frac{{E^{*} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ monotonically. In addition, it is strongly dependent on $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y(}}\upvarepsilon {\text{pre}})}} }}$. As shown by the solid lines, the data of $\frac{W}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} h_{\hbox{max} }^{3} }}$ were separately approximated by a polynomial function for each $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$value. The detail approximated function is expressed as follows:

Fig. 6

Relationship between $\frac{W}{{\upsigma_{{Y(\upvarepsilon {\text{pre}})}} h_{\hbox{max} }^{3} }}$ and $\frac{{E^{*} }}{{\upsigma_{{Y(\upvarepsilon {\text{pre}})}} }}$ at each $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{Y(\upvarepsilon {\text{pre}})}} }}$

$$\frac{W}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} h_{\hbox{max} }^{3} }} = A_{1} \left[ {\ln \left( {\frac{{E^{*} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}} \right)} \right]^{3} + A_{2} \left[ {\ln \left( {\frac{{E^{*} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}} \right)} \right]^{2} + A_{3} \left[ {\ln \left( {\frac{{E^{*} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}} \right)} \right] + A_{4}.$$

(6)

The coefficients A ₁-A ₄ are dependent on $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$, and these, along with the correlation factor R, are shown in Table 2. When these coefficients are interpolated as a function of $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$, Eq 6 at a given $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ can be deduced. This interpolation of the coefficients A ₁-A ₄ with $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ is shown in Fig. 12 in the appendix. Therefore, by substituting the values of W and h _max into Eq 6, the relationship between $\frac{{E^{*} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ and $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ can be deduced uniquely.

Table 2 Coefficient of Eq 6 with respect to σ_res/σ_Y(εpre)

For the unloading, the function $\frac{{W{\text{u}}}}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} h_{\text{e}}^{3} }}$ can be deduced by using the parametric FEM data in Eq 5. Figure 7 shows the function of Eq 5, indicating that $\frac{{W{\text{u}}}}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} h_{\text{e}}^{3} }}$ is strongly dependent on $\frac{{E^{*} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$. As shown in the enlarged figure, $\frac{{W{\text{u}}}}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} h_{\text{e}}^{3} }}$ is slightly dependent on the value of $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$. For each $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ value, the data of $\frac{{W{\text{u}}}}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} h_{\text{e}}^{3} }}$ are approximated by the following polynomial function:

Fig. 7

Relationship between $\frac{{W_{\text{u}} }}{{\upsigma_{{Y(\upvarepsilon {\text{pre}})}} h_{\text{e}}^{3} }}$ and $\frac{{E^{*} }}{{\upsigma_{{Y(\upvarepsilon {\text{pre}})}} }}$ at each $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{Y(\upvarepsilon {\text{pre}})}} }}$

$$\frac{{W{\text{u}}}}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} h_{e}^{3} }} = B_{1} \left[ {\ln \left( {\frac{{E^{*} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}} \right)} \right]^{3} + B_{2} \left[ {\ln \left( {\frac{{E^{*} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}} \right)} \right]^{2} + B_{3} \left[ {\ln \left( {\frac{{E^{*} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}} \right)} \right] + B_{4}.$$

(7)

The coefficients B ₁-B ₄ are dependent on $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$, which are shown in Table 3. Similar to Eq 6, by interpolating these coefficients with $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$, the value of Eq 7 at a given $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ can be deduced. This interpolation of the coefficients B ₁-B ₄ with $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ is also shown in Fig. 13 in the appendix. Therefore, by introducing the values of W _u and h _e into Eq 7, the relationship between $\frac{{E^{*} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ and $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ can be deduced uniquely. In conclusion, two independent relationships between $\frac{{E^{*} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ and $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ can be obtained from Eq 6 and 7.

Table 3 Coefficient of Eq 7 with respect to σ_res/σ_Y(εpre)

Reverse Analysis Procedure

This section explains the estimation process of our method. An indentation test with a Berkovich indenter was carried out once (referred to as a single indentation test). As shown in Fig. 2(b), we first obtained the indentation responses of the loading curve (W, h _max) and the unloading curve (W _u, h _e). The loading data (W, h _max) were introduced into Eq 6 and then a relationship between $\frac{{E^{*} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ and $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ was obtained. Subsequently, the unloading data (W _u, h _e) were substituted into Eq 7, yielding another relationship between $\frac{{E^{*} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ and $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$. The reduced modulus E* is known prior. Thus, two independent relationships between $\frac{{E^{*} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ and $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ provide the yield stress σ_Y(εpre) (which further leads to the pre-strain) and residual stress σ_res.

Here, we illustrate the reverse analysis process via an example. The example uses an austenitic stainless steel, SUS316L, having a pre-strain of 20% and a residual stress of 161 MPa. The corresponding yield stress is calculated to be 645 MPa from Eq 1, and then the residual stress normalized by yield stress $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ is calculated to be approximately 0.25. The indentation curve yields the data (W, h _max) from the loading curve and (W _u, h _e) from the unloading curve. These data are introduced to the Eq 6 and 7, yielding two relationships between $\frac{{E^{*} }}{{\upsigma_{\text{Y}} }}$ and $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$. Figure 8 shows the relationship between $\frac{{E^{*} }}{{\upsigma_{{Y(\upvarepsilon {\text{pre}})}} }}$ and $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ derived from Eq 6 and 7. Their relationships have different slopes. They intersect at the point of $\frac{{E^{*} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ = 334 and $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ = 0.23. This is the estimated solution for σ_Y(εpre) = 642 MPa (which corresponds to ε_pre of 19.8%) and σ_res = 148 MPa. As mentioned above, the input value is σ_Y(εpre) = 645 MPa and σ_res = 161 MPa, which are close to our estimation. This emphasizes that our method is very simple, since it uses only two dimensionless functions, and yields reliable estimations. The estimation accuracy and robustness of our method will be investigated in the next section.

Fig. 8

Identification of the estimated solution as being the intersection of the two curves (from Eq 6 and 7)

Method Validation

Numerical Experiment

The method presented was applied to the numerical experiment in order to investigate its estimation accuracy and robustness. As mentioned above, a parametric FEM study was carried out to establish the dimensionless function, and those data were employed to estimate the residual stress and pre-strain. Furthermore, two additional sets (ε_pre = 0.15, $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ = 0.5 and ε_pre = 0.5 $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ = −0.4) were also investigated to verify the method. Note that these two material cases were not included in the FEM parametric study (to establish the dimensionless function of Eq 6 and 7). For all cases, we extracted the loading (W, h _max) and unloading data (W _u, h _e) from the computational indentation curve, and then estimated the values of ε_pre and σ_res.

The estimated values of (ε_pre, $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$) by the method are shown in Fig. 9. The squares indicate the input values (solutions), and the circles denote the estimates. All calculated results agree with the input data, with an error of less than about 20%, which is similar to that of a previously developed estimation method of elastoplastic properties with reverse analysis (Ref 10, 11, 14, 30). This indicates that the present algorithm is fairly reliable and has satisfactory accuracy. Note that the reverse analysis of Fig. 9 can uniquely estimate the input data, indicating that there is no uniqueness issue for the present input cases.

Fig. 9

Comparison of the estimated result by reverse analysis with input values

Another concern for experimental estimations is the perturbation of indentation response. When we experimentally conduct an indentation test in a laboratory, uncertainties in the experimental indentation responses are usually inevitable due to several factors related to the material and indentation measurement equipment. A number of previous studies have investigated the robustness of the method, which is a key issue for accuracy. In other words, it is important to investigate the sensitivity of the determined properties to variations in the input data, and to clarify how scatter in the input data affects these properties. In this study, we conducted a sensitivity analysis for four representative materials (Table 4). For the indentation curve (i.e., indentation work volume and depth), the perturbations were set to 2%, since previous studies have used this value for sensitivity analyses (Ref 26). These perturbation cases (#0, #1. #2) are shown in Table 5.

Table 4 Representative materials for sensitivity analysis

Table 5 Case study for sensitivity analysis of representative materials

The deviations (errors in the estimated values compared to the input values) in the absolute values are shown in Fig. 10(a) and (b) for the pre-strain ε_pre and the residual stress σ_res, respectively. Values of ε_pre (Fig. 10a) show good agreement and robustness for all perturbation cases. On the contrary, values of σ_res show large errors for the perturbation cases. This is because the dependency of σ_res on the indentation curve is smaller than that of ε_pre as shown in Fig. 5. Thus, the estimation of σ_res may be more sensitive on measurement error. Several previous studies on sensitivity analyses reported that their methods induced 50 % error maximum (Ref 26). This indicates that the present method may relatively underperform in the presence of perturbations due to potential experimental errors, but these error cases (Table 5) may represent extreme examples. The actual experimental situation is addressed in the next section.

Fig. 10

Sensitivity study of the representative materials; (a) pre-strain ε_pre, and (b) residual stress σ_res

Experimental Investigation

Experimental Setup

This study used micro indentation equipment (Dynamic Ultra-micro Hardness Tester DUH-501, Shimadzu corp.). A Berkovich indenter was also employed. The loading rate was set to 28 mN/s. The maximum indentation force was set to 1962 mN.

The specimen utilized was austenitic stainless steel, which is commercially available SUS316L. This study prepared several SUS316L steels having different pre-strain and residual stress values. For a pre-strained steel, we used cold-rolled (CR) SUS316L, which is commercially available. The rolling ratio was with 5, 10, and 20% strain. These steels were designated as Mat. 1, 2, 3, and 4. Note that Mat. 1 was the as-received (AR) virgin SUS316L. Their properties are shown in Table 6. We also conducted a uniaxial tensile test to obtain the stress-strain curves of cold-rolled steels (Mat. 2-4). By comparing the curve with that of the as-received steel, the values of pre-strain ε_pre were obtained (see Table 6).

Table 6 Experimental verification of cold-rolled and shot-peened SUS316L, showing the comparison of between the estimations (σ_res and ε_pre) from the present indentation method and those of experimental data (obtained from x-ray diffraction and uniaxial tensile test)

Meanwhile, a residual stress was introduced via shot peening (SP), which utilized a zirconia ball that had a diameter of 0.6 mm. During peening, the shot pressure was set to 0.45 MPa. After peening, we mechanically polished the peening surface to obtain a smooth surface (where indentation test was applicable). The residual stress of the polished surface was measured based on the sin²ψ method using the x-ray diffraction system PSPC-MSF-3M (Rigaku Corporation). We used the x-ray diffraction method to measure the x-ray diffraction. The x-ray source was Cr-Kα, which operated at 35 kV and 8 mA. The diffractive plane was (220) γ-Fe, and the reference diffractive angle 2θ was approximately 130°. The stress factor for the x-ray diffraction was −624.68 MPa/°. Three different points on the surface were selected for the measurement. For each point, the measurements were conducted from the orthogonal axis of two directions. The averaged datum for one direction was σ_res = −507 ± 165 MPa, and that for other direction was −392 ± 104 MPa. Although this result shows a relatively large scatter (due to a mechanically polished condition), the stresses along two orthogonal axes were the same, indicating that the specimen surface experienced in-plane equi-biaxial compressive residual stresses⁴. Therefore, the averaged σ_res was −450 ± 138 MPa.

Experimental Results

Figure 11 shows the indentation curves of sheets that underwent cold rolling and shot peening (as shown in Table 6). Each test was carried out more than ten times, and the curves represent the averaged values. In Fig. 11, the indentation depth became shallower with the increase in the cold-rolled ratio. In addition, the shot peening steel was found to be the hardest material. By using our approach, the pre-strain ε_pre and residual stress σ_res were estimated as shown in Table 6. The virgin steel and cold-rolled steel (Mat. 1-4) show a good estimation of ε_pre. However, the residual stress of cold-rolled steel was not investigated, and the stress on the surface may be very small since the distribution of Vickers hardness in the transverse section is almost constant⁵. Therefore, we described σ_res of zero as in Table 6, indicating that the estimation of σ_res also showed good agreement. Finally, the shot peening steel (Mat. 5) was investigated. The estimation of σ_res was −494 MPa, which agrees well with the measurement data (−450 MPa). The ε_pre was estimated to be 0.444, suggesting that a large plastic strain was introduced. Although this value is not known for the actual property, it was validated as follows. It is reported that the Vickers hardness of present peening steel archives HV = 400 (Ref 31), which is quite larger than that of the as-received steel (HV = 150). Using the Tabor relationship (Ref 6), the corresponding yield stress (plastic flow stress) was approximately 1.3 GPa, which favorably compares with 0.9 GPa (when the ε_pre = 0.444 was substituted into Eq 1). Thus, our present method can apply to SUS316L having pre-strain and residual stress.

Fig. 11

Indentation curves of SUS316L with cold rolling process and shot peening treatment

As mentioned in the Introduction, most previous studies for measuring the residual stress require a reference sample with a stress-free state, and investigated how the indentation response was changed by residual stress (Ref 22). However, the present study does not require a stress-free sample as reference, and it can estimate both residual stress and yield stress (with respect to pre-strain) simultaneously. It is also emphasized that our method follows a very simple framework, since it only needs two dimensionless functions with simple polynomial equations. Although the present method is applicable to only an austenitic stainless steel that obeys the Ludwick’s work hardening law and involves in-plane equi-biaxial residual stress, it may also be applicable to any other material using a similar concept. Such work will be addressed in the future.

Conclusion

This study proposed a new indentation method to simultaneously evaluate the residual stress and plastic strain of an austenitic stainless steel. This method focuses on an austenitic stainless steel, SUS316L, which obeys the Ludwick’s work hardening law and involves in-plane equi-biaxial residual stress. Note that the framework is applicable to any material with little modification. A Berkovich indenter penetrates the steel until it undergoes full plastic deformation, and then the indentation curve, which represents the relationship between indentation force and penetration depth, is obtained. The parameter from the curve is used for a reverse analysis in order to estimate residual stress and plastic strain.

Comprehensive numerical experiments with FEM were first carried out in order to simulate a Berkovich indentation test for SUS316L having various plastic strain (pre-strain) and residual stress values. It was found that the indentation force increases with the increase in the pre-strain as well as compressive residual stress. Next, to establish the reverse analysis, the parametric FEM study by changing the residual stress σ_res and pre-strain ε_pre was conducted, such that we deduced the relationship between the indentation curve and the parameters ε_pre and σ_res for the dimensionless function. In particular, the indentation total work W from the loading curve and elastic work W _u from the unloading curve were employed as the parameter for the proposed reverse analysis. In fact, this relationship can be expressed by only two dimensionless functions with relatively simple formulae. Thus, by substituting the indentation curve (indentation work of W and W _u) into the functions, the present method could estimate both ε_pre and σ_res readily.

The robustness of our method was verified by error estimation against input perturbations using numerical studies. In parallel, laboratory experiments were conducted in order to estimate the plastic strain and residual stress based on the proposed framework. Microindentation tests were conducted for several SUS316L steels, which were as-received steel, pre-strained steel (cold-rolled steel), and peening steel with residual stress. It was revealed that the proposed indentation technique could reasonably and quantitatively evaluate both pre-strain and residual stress. Since the indentation method can evaluate local mechanical properties, our method may be useful for a complex material system, such as welded steel, plastic worked steel, pipe, and mechanical component/structures of SUS316L.

Appendix

This section describes the coefficient of Eq 6 and 7 as shown in Fig. 12 and 13. For all figures, the data are approximated by a quadratic function as indicated by the dotted line. Note that at the boundary of $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ = 0, we separately approximated data by the function of Eq A1. The quadratic function is given as follows:

Fig. 12

Coefficients of Eq 6 with respect to $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{Y(\upvarepsilon {\text{pre}})}} }}$

Fig. 13

Coefficients of Eq 7 with respect to $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{Y(\upvarepsilon {\text{pre}})}} }}$

$$A_{i} \;{\text{or}}\;B_{i} = a\left( {\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}} \right)^{2} + b\left( {\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}} \right) + c\quad (i = 1 - 4)$$

(A1)

This function involves three coefficients, namely a, b, and c, and are listed in Table 7. At the boundary of $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ = 0, these are different for all A _i and B _i (i = 1-4). By using Table 7 and Eq A1, the coefficients of A _i and B _i (i = 1-4) can be obtained for any $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ value. Thus, the dimensionless functions of Eq 6 and 7 for any $\frac{{\upsigma_{\text{res}} }}{{\upsigma_{{{\text{Y}}(\upvarepsilon {\text{pre}})}} }}$ value can be established.

Table 7 Coefficient of Eq. A1