First-Principles Study on the Structural, Elastic and Thermodynamic Properties of Binary Pd-Sn Compounds

Abstract

The structural, mechanical, thermodynamic and electronic properties of Pd-Sn compounds including PdSn₄, PdSn₃, PdSn₂, PdSn, Pd₂Sn and Pd₃Sn have been investigated by first-principles calculation. Results show that all of the Pd-Sn compounds considered here are thermodynamically and mechanically stable, ductile, elastic anisotropic and have low micro-hardness. Among them, Pd₂Sn is the most stable phase due to the lowest formation energy; PdSn exhibits the strongest anisotropy of the bulk modulus and shear modulus; Pd₃Sn shows the isotropy of bulk modulus according to the percentage bulk modulus calculation. Debye temperature and minimum thermal conductivity have approximately the same variation trend with the percentage of Pd where Pd₃Sn (or PdSn₄) has the highest (or lowest) Debye temperature and minimum thermal conductivity. The electronic density of states shows a strong hybridization of Pd-d with Sn-p electrons near the Fermi level, which has an important impact on the reliability of crystal. The three-dimensional (3D) charge density difference map shows ionic properties for these compounds, and the ionicity increases with Pd concentration according to the Bader charge analysis.

Introduction

In recent years, surface treatment technology, for example, the formation of surface-finish Au/Pd/Ni(P) through electroless deposition of a submicron Pd film on a Ni(P) pad, has become increasingly popular in the electronics industry.^1,2 During the heat treatment process, the sandwiched Pd layer not only can improve the wettability but also can serve as an effective diffusion barrier layer^3,4 to prevent the Ni(P) film from galvanic hyper-corrosion.^5,6 Different types of Pd film can be produced by formic acid and alkaline hypophosphite-based solutions. Using formic acid electrolyte, a high-purity polycrystalline Pd film can be formed. By exposure to alkaline hypophosphite conditions, amorphous Pd accompanied by 2–5 wt.% P dissolution can be obtained.⁷ As is well known, Cu-based conductors are widely used as an interconnection with a Sn-based solder. However, the Cu-Sn compounds formed between the solder and conductor are brittle and possess high electrical resistivity, which deteriorates the electrical and mechanical properties of interconnection. To suppress the growth of Cu-Sn compounds, monolayer Ni or a heterojunction consisting of Au (or Pd) and a Ni layer is plated on the Cu-based conductor to form a sandwiched Au/Ni/Cu (or Pd/Ni/Cu) conductor structure.^8,9 As a result, the reactive diffusion occurs at the interface between Sn-based solder and Au (or Pd) during soldering. According to the literature, intermetallic compounds (IMCs) of PdSn₄ and PdSn₃ are formed through the room-temperature interaction between Pd and Sn.¹⁰ Ni solid solution IMCs such as (Pd, Ni)Sn₄, (Pd, Ni)Sn₃ and (Pd, Ni)Sn₂ appear in (Pd-Ni)/Sn diffusion couple at 200°C.¹¹ A thinner intermetallic layer benefits the connection between the solder and substrate. However, the rapid and excessive growth of the compounds will have a deleterious effect on the mechanical reliability of solder joints due to their brittleness.

With the miniaturization of modern solder joints, the intermetallic layer will be proportionately thick. To some extent, the strength and reliability of solder joints are determined by the properties of intermetallics such as elastic, ductile or brittle transition, the thermal expansion and heat transfer coefficient. Based on the binary Pd-Sn phase diagram reported by Hultgren et al.,¹² several compounds can exist, including Pd₃Sn, Pd₂Sn, PdSn, PdSn₂, PdSn₃ and PdSn₄. The compound Pd₂Sn exists at a low temperature but can decompose into Pd₃Sn at a high temperature of 1193 K. The crystal structures of binary Pd-Sn compounds have been measured in experiment. For example, the compound Pd₃Sn, which belongs to the Pm $\overline{3 }$ m space group, has the cubic structure of Cu₃Au prototype with lattice parameters of a = b = c = 3.976 Å.^13,14 The compound PdSn, which belongs to the space group Pbnm, has an orthorhombic structure of FeAs type with lattice parameters of a = 6.126, b = 3.901, c = 6.480 Å.¹⁵ Massalski assessed the Sn-rich corner of Pd-Sn ternary phase diagram and found four compounds (i.e., PdSn at 810°C, PdSn₂ at 600°C, PdSn₃ at 345°C and PdSn₄ at 230°C) in peritectic reactions.¹⁶

As mentioned above, Pd-Sn compounds have been reported in numerous studies. It is well known that the elastic and thermodynamic properties are important factors affecting the reliability of intermetallics appearing at the interconnected interfaces in the microelectronics industry. However, to date, no systematic research has been reported on the essential physical characteristics such as the bulk modulus, shear modulus, Young’s modulus, thermodynamic and electronic properties for the binary Pd-Sn compounds. In view of this, further research is necessary. In our previous research, the physical properties of ternary compounds of (Pd, Ni)Sn₄ were successfully predicted.¹⁷ To enrich the database of physical characteristics of Pd-Sn systems, comprehensive investigations are carried out in this work to detect the intrinsic properties including the structural, elastic, thermodynamic and electronic characteristics. The related findings are helpful to uncover the structural stability and mechanical properties of these intermetallics.

Calculation Details

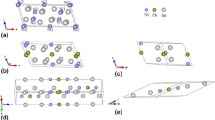
Herein, we performed a first-principles calculation for the Pd-Sn-based intermetallics including PdSn₄, PdSn₃, PdSn₂, PdSn, Pd₂Sn and Pd₃Sn. The original structures used for geometry optimization, which are shown in Fig. 1, are derived from the inorganic crystal structure database (ICSD).^18,19,20,21 The ground state lattice parameters are determined through the Vienna Ab initio Simulation Package (VASP) code.²² The generalized gradient approximation (GGA) of Perdew-Burke-Ernzerhof (PBE) was treated as the exchange correlation function. The Monkhorst–Pack k-point meshes were used to evaluate Brillouin-zone integrations and electronic occupancies were determined according to the Methfessel–Paxton technique with 0.1 eV smearing. The convergence threshold of total energy was set to less than 1 × 10⁻⁵ eV/atom. The valence electron configurations are treated with 5s²5p² for Sn and 4d¹⁰ for Pd. During the structure optimization, full degrees of internal atomic coordinates are allowed to relax. After that, a static total energy calculation is performed to obtain the total energy of the crystal system.

Fig. 1

Crystal structures of binary Pd-Sn compounds (a) PdSn₄, (b) PdSn₃, (c) PdSn₂, (d) PdSn, (e) Pd₂Sn and (f) Pd₃Sn (tin atoms are large and gray, palladium atoms are small and navy) (Color figure online).

Results and Discussion

Structure and Phase Stability

In calculation, all of the models are based on the experimental lattice constants obtained from the ICSD. The crystal structures and space groups of the considered binary Pd-Sn phases are displayed in Table I. For convenient comparison, we listed the lattice parameters of those available in literature together with the results in this work. It is found that the geometric optimized lattice constants are all larger than the experimental results since the GGA method often overestimates the lattice parameters. In addition, the derived values of this calculation have very small errors compared to the experimental data, with the greatest deviation being less than 2%, indicating the reasonability of the computational method.

Table I The structural properties (including lattice constants (Å) and formation energy $\Delta H$ ($\mathrm{kJ}/\mathrm{mol}\bullet \mathrm{atoms}$)) for Pb–Sn IMCs in the present work and other references

To detect the stability of the binary Pd-Sn compounds, formation energy $\Delta H$ is calculated based on the following equation.¹⁷

$$ \Delta H = [E_{{Pd_{x} Sn_{y} }} - (xE_{Pd} + yE_{Sn} )]/(x + y) $$

(1)

Here, $E_{{Pd_{x} Sn_{y} }}$ is the total energy of $Pd_{x} Sn_{y}$ at the relaxed state, $E_{Pd}$ and $E_{Sn}$ are the per-atom energies of Pd with a face-centered cubic structure and $\beta$-Sn with a tetragonal structure in solid state, x and y is the number of Pd and Sn in the unit cell of $Pd_{x} Sn_{y}$, respectively. It is well known that a more negative formation energy is often accompanied by a better thermodynamically stable structure of the crystal system. The calculated formation energy along with the available literature values are listed in Table I. Guadagno and Bryant el al. employed solution calorimetry to derive the formation energies of solid Pd-Sn alloys at 273 K and 320 K, respectively.^23,24 Using the direct synthesis calorimetry, Meschel derived the formation energy of Pd₃Sn at room temperature.²⁵ The electromotive force method was used by Schaller to obtain the thermodynamic activity and Gibbs free energy of formation Pd₃Sn at a high temperature of 1173 K.²⁶ In the present work, the calculation is performed at zero temperature and zero pressure so as to predict the ground state properties of these compounds. It should be noted that the formation energy of −26.35 kJ/mol·atom for PdSn₄ by the first-principles calculation was reported in our previous work.¹⁷ This value is very close to Bryant’s finding of −27.8 kJ/mol·atom through Sn solution calorimetry by the absolute deviation of 1.45 kJ/mol·atom.²⁴ Comparing our first-principles results of formation energy for PdSn₂ and PdSn with that of Guadagno, we found absolute errors of 2.46 kJ/mol·atom and 5.83 kJ/mol·atom, respectively. The small difference validates our calculation scheme. To visualize the variation trend, the relationship between the formation energy and the percentage composition of Pd is depicted in Fig. 2. All of the formation energies are negative, meaning that the structures of these Pd-Sn compounds are thermodynamically stable. Among them, Pd₂Sn is the most thermodynamically stable structure due to the most negative formation energy of −55.12 kJ/mol·atom. The stability of PdSn and Pd₃Sn is slightly lower than Pd₂Sn on account of the corresponding formation energy of −54.47 kJ/mol·atom and −51.32 kJ/mol·atom, respectively. As for PdSn₄, the structure has relatively inferior stability owing to its higher formation energy than others. In fact, PdSn₄ commonly appears and is always accompanied by a high growth rate between the Sn-Ag-Cu solder with Pd surface finish on the Ni/P pad.¹¹ In view of this, we can reasonably assume that the considered Pd-Sn compounds in this work is easy to be formed between the solder and pad.

Fig. 2

Variation in formation energy (unit: kJ/mol·atom) with the percentage of Pd atoms in Pd-Sn compounds.

Elastic Property

Elastic constants are important factors owing to their close connection to the material’s mechanical stability, stiffness, anisotropy, ductility or brittleness. To detect the elastic constants of Pd-Sn compounds, a stress–strain method is used to calculate the elastic stiffness of the relevant phases.^27,28 A strain δ of less than 2% with a step of 0.005 was imposed on the optimized equilibrium crystals to determine the total energy change. The second-order elastic constants are derived through a polynomial fit of strain energy for specific deformation.²⁹ There are nine independent elastic constants in an orthorhombic crystal structure, which are C₁₁, C₂₂, C₃₃, C₄₄, C₅₅, C₆₆, C₁₂, C₁₃, C₂₃, while six are in the tetragonal crystal lattice, namely C₁₁, C₃₃, C₄₄, C₆₆, C₁₂, C₁₃, and three are in the cubic crystal lattice, namely C₁₁, C₄₄, C₁₂. The calculated elastic constants are displayed in Table II.

Table II Calculated elastic stiffness (C_ij) of the Pd-Sn IMCs (unit in GPa)

For orthorhombic crystal, the elastic constants should meet the mechanical stability criteria as follows:³⁰

$$ \begin{aligned} & C_{ii} > 0(i = 1 - 6);\,C_{11} + C_{22} > 2C_{12} ;\,C_{22} + C_{33} > 2C_{23} ; \\ & C_{11} + C_{33} > 2C_{13} ;\,C_{11} + C_{22} + C_{33} + 2C_{12} + 2C_{13} + 2C_{23} > 0 \\ \end{aligned} $$

(2)

For tetragonal crystal, the mechanical stability criteria are given by the expressions:

$$ \begin{aligned} & C_{ii} > 0(i = 1,3,4,6);\,C_{11} - C_{12} > 0; \\ & C_{11} + C_{33} - 2C_{13} > 0;\,2(C_{11} + C_{12} ) + C_{33} + 4C_{13} > 0 \\ \end{aligned} $$

(3)

For cubic crystal, the mechanical stability restrictions are given by the formula:

$$ C_{ii} > 0(i = 1,4);\,C_{11} > \left| {C_{12} } \right|;\,C_{11} + 2C_{12} > 0. $$

(4)

Based on the single-crystal elastic constants listed in Table II, all of the crystal structures satisfy the above criteria, which indicates that the binary Pd-Sn compounds considered in the present work are mechanically stable.

According to the single-crystal elastic constants, the polycrystalline elastic modulus such as the bulk modulus (K), shear modulus (G) and Young’s modulus (E), which are often used to evaluate the material mechanical properties, can be derived through the Voigt-Reuss-Hill approximation.^30,31 The bulk modulus K reflects the materials resistance to volume change under pressure. The shear modulus G gives an index of material resistance to plastic deformation such as shear strain. Young’s modulus E, which is defined as the ratio of tensile stress to the corresponding tensile strain, can provide information on the stiffness characteristics in solid. Generally speaking, a large Young’s modulus often means high stiffness. The calculated results on the polycrystalline elastic modulus are tabulated in Table III, and their variation with the concentration of Pd is displayed in Fig. 3a. It is found that Pd₃Sn has the largest values of bulk modulus, shear modulus and Young’s modulus of 153. GPa, 53.1 GPa and 142.8 GPa, respectively, while PdSn₄ has the lowest bulk modulus, shear modulus and Young’s modulus of 55.8 GPa, 21.3 GPa and 56.7 GPa, respectively. Therefore, it can be confirmed that Pd₃Sn is not easily compressed and sheared and is a hard material among Pd-Sn compounds. According to Fig. 3a, we can see that the bulk modulus obviously increases with the concentration of Pd. But the shear modulus and Young’s modulus no longer increase beyond a concentration of 25% (PdSn₃) and 66.7% (Pd₃Sn). Therefore, the shear modulus and Young’s modulus follow the same increase order of PdSn₄, PdSn₂, PdSn₃, Pd₂Sn, PdSn and Pd₃Sn.

Table III The bulk modulus K, shear modulus G, Young’s modulus E and microhardness H of Pd-Sn IMCs (units in GPa)

Fig. 3

(a) The variation in the elastic modulus with the percentage of Pd atoms (unit: GPa), (b) the variation in Poisson’s ratio and K/G with the percentage of Pd atoms in Pd-Sn compounds (dimensionless).

Poisson’s ratio ν and K/G are often used to estimate the ductile or brittle properties of material. According to Poisson’s ratio, a value of higher than 0.26 is associated with ductility and a value lower than 0.26 is accompanied by brittleness.^32,33 For K/G, dividing ductility from brittleness is 1.75. For example, if K/G is higher than 1.75, the material is ductile; otherwise it is brittle. Poisson’s ratio can also be used to estimate the stability of a crystal against shear deformation. Material with a higher Poisson’s ratio always expresses a better plasticity. The calculated Poisson’s ratio and K/G are listed in Table IV. Both Poisson’s ratio and K/G are higher than 0.26 and 1.75, which means the Pd-Sn compounds involved in present work are ductile and plastic. The ductility increases in the order of PdSn₄, PdSn₃, Pd₃Sn, PdSn, PdSn₂, Pd₂Sn. The variation tendency of Poisson’s ratio and K/G with Pd percentage are depicted in Fig. 3b. It can be found that the degree of ductility almost increases with Pd concentration, except for PdSn and Pd₃Sn due to their relatively lower Poisson ratio and K/G. In view of this, it can be deduced that Pd-Sn compounds formed on the surface between the solder and pad can serve as a good connection in the field of electronics packaging.

Table IV The results of Poisson’s ratio v, ratio of K/G, anisotropic factor, A₁, A₂, A₃, universal anisotropy index A_U, bulk anisotropic index A_K and shear anisotropic index A_G (dimensionless) for the Pd-Sn IMCs

The microhardness parameter H, which is another important factor used to detect the polycrystalline stiffness, can be deduced from Poisson’s ratio and Young’s modulus based on the following equation.³¹

$$ H = \frac{(1 - 2\nu )E}{{6(1 + \nu )}} $$

(5)

Generally speaking, a higher Young’s modulus often accompanies a higher microhardness. The results of hardness are presented in Table III. It can be seen that, overall, the values of hardness are lower than 6 GPa, meaning the lower stiffness of the materials. Among them, Pd₃Sn has the highest microhardness value while PdSn₄ has the lowest one, which is agreement with their Young’s modulus.

Anisotropic Property

During the connection of solder with substrate, failure is often appeared at the interface due to the appearance of microcracks, holes and lattice distortion. The root cause is the crystalline anisotropic property. For example, crystals demonstrate different mechanical and thermodynamic properties in different directions. Research on the elastic anisotropy is beneficial to understand the mechanical durability of material. To quantitatively describe the elastic anisotropy, the anisotropic factors estimated from the elastic constants are used.³⁴ For orthorhombic crystal systems, there are three elastic anisotropic parameters:

$$ A_{1} = \frac{{4C_{44} }}{{C_{11} + C_{33} - 2C_{13} }},\;A_{2} = \frac{{4C_{55} }}{{C_{22} + C_{33} - 2C_{23} }},\;A_{3} = \frac{{4C_{66} }}{{C_{11} + C_{22} - 2C_{12} }} $$

(6)

For tetragonal crystal, two anisotropic factors are used:

$$ A_{1} = \frac{{2C_{66} }}{{C_{11} - C_{12} }},\;A_{2} = \frac{{2C_{44} }}{{C_{11} - C_{12} }}, $$

(7)

For cubic crystal, only one is used:

$$ A_{1} = \frac{{2C_{44} }}{{C_{11} - C_{12} }} $$

(8)

If the value A_i (i = 1, 2, 3) is equal to 1, the crystal will show isotropic characteristics. Any value smaller or larger than 1 indicates anisotropy of crystal. The calculated anisotropic parameters are tabulated in Table IV. It can be seen that the Pd-Sn crystalline systems are all anisotropic.

Ranganathan et al. introduced a concept of universal elastic anisotropy index A_U, which is a measurement of the elastic anisotropy of the crystal with the following expression.³⁵

$$ A_{U} = \frac{{K_{V} }}{{K_{R} }} + 5\frac{{G_{V} }}{{G_{R} }} - 6 $$

(9)

Here, K_V, K_R and G_V, G_R denote the bulk modulus and shear modulus according to the Voigt and Reuss scheme, respectively. A zero value of A_U indicates isotropic properties, and otherwise, anisotropic. The greater the value of A_U, the greater the mechanical anisotropy. The results of A_U displayed in Table IV show that PdSn has the highest mechanical anisotropy, while Pd₃Sn has the lowest universal mechanical anisotropy.

To visualize the anisotropic properties of these binary Pd-Sn compounds, the three-dimensional (3D) representations of elastic modulus with the crystallographic directions are depicted based on the single-crystal elastic constants in Fig. 4. The derivation of formulas and calculation method for the orientation-dependent elastic modulus is discussed in detail in reference,³⁶ and hence it needs no further elaboration. In short, the 3D surface is spherical for an isotropic crystal, and anything other than a sphere indicates an anisotropic crystal. Obviously, the surfaces of the elastic moduli exhibit remarkable anisotropy for all of the Pd-Sn compounds. Among them, the shape of PdSn in Fig. 4d presents a dumbbell-shaped surface, suggesting the greatest anisotropy. This finding is in good agreement with the calculation from the universal elastic anisotropy index A_U.

Fig. 4

Direction dependence of elastic modulus for Pd-Sn compounds: (a) PdSn₄, (b) PdSn₃, (c) PdSn₂, (d) PdSn, (e) Pd₂Sn, (f) Pd₃Sn (unit: GPa).

The percent elastic anisotropy factor such as A_K and A_G is another measurement of elastic anisotropy, which can be used to investigate the degree of elastic anisotropy in compression and shear modes.³⁷ Here, A_K and A_G are calculated through the following expressions.

$$ A_{k} = \frac{{K_{V} - K_{R} }}{{K_{V} + K_{R} }},\;A_{G} = \frac{{G_{V} - G_{R} }}{{G_{V} + G_{R} }} $$

(10)

A zero value of A_K and A_G always indicates isotropy, and any deviations indicate anisotropy. According to the results listed in Table IV, PdSn exhibits the strongest anisotropy of bulk modulus and shear modulus, with A_K of 13.45% and A_G of 29.34%. In contrast, Pd₃Sn shows isotropy of bulk modulus with a value of 0% and the lowest anisotropy of shear modulus with a value of 3.77%, in line with the previous conclusion from A_U. The variation in the anisotropic factors A_U, A_K and A_G with the concentration of Pd is shown in Fig. 5. It is easy to see that the variation tendency of the percentage elastic anisotropy A_G is in good agreement with the trend of A_U, following the decreasing sequence of PdSn, PdSn₃, PdSn₂, PdSn₄, Pd₂Sn and Pd₃Sn.

Fig. 5

The variation in universal anisotropy index A_U, bulk anisotropic index A_K and shear anisotropic index A_G (dimensionless) with the percentage of Pd atoms in Pd-Sn compounds.

Heat Transfer Property

Intermetallics formed at the interface between a solder and substrate are critical for achieving a good connection. For a comprehensive understanding of the physical properties of the considered compounds, the heat transfer property is discussed in detail in present work. The Debye temperature is important for predicting the thermal conductivity. It has been empirically established that a higher Debye temperature generally indicates better thermal conductivity. The Debye temperature can be deduced from the elastic wave velocity through the following equation.³²

$$ \theta_{D} = \frac{h}{{k_{B} }}\left( {\frac{{3nN_{A} \rho }}{4\pi M}} \right)^{\frac{1}{3}} v_{m} $$

(11)

Here, h is Planck’s constant, ${k}_{B}$ is Boltzmann’s constant, ${N}_{A}$ is Avogadro’s constant, $\rho$ is the density of the material, M is the molar mass, and n is the total number of atoms contained in the compound. The factor v_m is the averaged elastic wave velocity which is related to the transverse elastic wave velocity ${v}_{t}$ and the longitudinal wave velocity ${v}_{l}$.

$$ v_{m} = \left[ {\frac{1}{3}\left( {\frac{2}{{v_{t}^{3} }} + \frac{1}{{v_{l}^{3} }}} \right)} \right]^{{ - \frac{1}{3}}} $$

(12)

$$ v_{t} = \left( {\frac{G}{\rho }} \right)^{\frac{1}{2}} $$

(13)

$$ v_{l} = \left( {\frac{3K + 4G}{{3\rho }}} \right)^{\frac{1}{2}} $$

(14)

The calculated Debye temperature ${\theta }_{\mathrm{D}}$ together with the results of the density $\rho$, transverse elastic wave velocity v_t, longitudinal elastic wave velocity v_l and average wave velocity v_m are all listed in Table V. It can be seen that Pd₃Sn has the highest Debye temperature, while PdSn₄ has the lowest. Pd₂Sn has a Debye temperature lower than PdSn, but higher than PdSn₃ and PdSn₂ in sequence.

Table V The density $\rho$ (in kg/m³), transverse elastic wave velocity v_t, longitudinal elastic wave velocity v_l, average elastic wave velocity v_m (in m/s), Debye temperature ${\theta }_{D}$ (in K) and minimum thermal conductivity k_min^a of Clarke’s model and k_min^b of Cahill’s model ( in W/m K) for the Pd-Sn IMCs

Since the material’s heat transfer ability will decrease with increasing temperature at high temperature,³⁸ it is meaningful to explore the minimum thermal conductivity at high temperature to evaluate the material’s application under extreme conditions. To quantitatively clarify the lower limit of thermal conductivity at high temperature, Clarke’s model³⁸ and Cahill’s model^39,40 are used through the following expressions in sequence

$$ k_{\min }^{a} = 0.87k_{B} M_{a}^{{ - \frac{2}{3}}} E^{\frac{1}{2}} \rho^{\frac{1}{6}} $$

(15)

$$ k_{\min }^{b} = \frac{{k_{B} }}{2.48}n\prime^{\frac{2}{3}} (2v_{t} + v_{l} ) $$

(16)

Here, $k_{B}$ and $\rho$ have the same meaning as in Eq. 11. The average mass ${\mathrm{M}}_{\mathrm{a}}$ per atom can be obtained from ${M}_{a}=\frac{M}{n{N}_{A}}$ where $n$ and $M$ are those in Eq. 11. The parameter E stands for the Young’s modulus. In Eq. 16, $n^{\prime }$ is the number of atoms per unit volume, which can be derived from $n^{\prime } = \frac{\rho }{{M_{a} }}$, $v_{t}$ and ${v}_{l}$ are the transverse and longitudinal elastic wave velocities, respectively. The calculated values of $k_{\min }^{a}$ from Clarke’s model and $k_{\min }^{b}$ from Cahill’s model are also displayed in Table V. Since the contribution from the optical phonon cannot be considered, Clarke’s model often gives a lower estimate for the thermal conductivity than Cahill’s model.⁴⁰ Researchers have suggested that the lowest thermal conductivity from Cahill’s model is more accurate than Clarke’s model due to its atomic number density and phonon spectrum.⁴⁰ It is found that the values of $k_{\min }^{a}$ and $k_{\min }^{b}$ roughly increase with Pd concentration except for Pd₂Sn due to its slightly lower value of $k_{\min }^{a}$ than that for PdSn. For convenience, the variation in Debye temperature and $k_{\min }$ with the concentration of Pd is plotted in Fig. 6. It can be seen that the decreasing trend of $k_{\min }$ is roughly the same as that of Debye temperature. Through comparison, the values of $k_{\min }^{a}$ rank in decreasing order of Pd₃Sn, PdSn, Pd₂Sn, PdSn₂, PdSn₃ and PdSn₄. Debye temperature ${\theta }_{D}$ decreases in the order of Pd₃Sn, PdSn, Pd₂Sn, PdSn₃, PdSn₂ and PdSn₄. The slight difference in PdSn₃ and PdSn₂ is caused by the anisotropy of crystals, which can be reflected from the 3D surface map as in Fig. 4 and the universal elastic anisotropy index A_U. To be specific, the 3D shape of PdSn₃ in Fig. 4b presents many convex regions, while that of PdSn₂ in Fig. 4c shows a sunken area, which means that the anisotropic degree of PdSn₃ is higher than PdSn₂. Furthermore, PdSn₃ has a higher value of universal elastic anisotropy index A_U of 2.6987, while PdSn₂ has a lower A_U of 1.7975 (see Table IV). Among the Pd-Sn compounds considered, Pd₃Sn has the highest values of Debye temperature and $k_{\min }$, while PdSn₄ has the lowest values. From this point of view, our finding is fairly consistent with the literature, in which higher Debye temperature is often accompanied by higher minimum thermal conductivity.⁴¹ Thus, the intrinsic thermal properties of the Pd-Sn compound are obtained, which can provide a useful reference for the surface treatment process of solder with pad.

Fig. 6

The variation in Debye temperature ${\theta }_{D}$ (in K) and minimum thermal conductivity k_min (in W/m K, k_min^a of Clarke’s model and k_min^b of Cahill’s model) with the percentage of Pd atoms in Pd-Sn compounds.

Electronic Structure

To illustrate the chemical bonding character for the Pd-Sn compounds, the total density of states (TDOS) and partial density of states (PDOS) are considered, which are depicted in Fig. 7. The six IMCs are all metallic due to a non-zero density of states at the Fermi-level. Through the TDOS, we can see that the contribution to the TDOS at the lower energy range from about −10.8 eV to −5.4 eV for PdSn₄, −11.3 eV to –5.6 eV for PdSn₃, −10.8 eV to −5.8 eV for PdSn₂, −10.9 eV to −6.9 eV for PdSn, is dominated mainly by the Sn-s states together with some Pd-d and Sn-p states. For Pd₂Sn and Pd₃Sn, the low-lying states from −10.6 to −7.7 eV and −9.9 eV to −7.8 eV are driven mainly by Sn-s sates and some Pd-d states, and the Sn-p electrons made scarcely any contribution to the TDOS. Specifically, we focus more on the states near the Fermi level because the electrons nearby have more impact on material properties such as reliability. At the higher energy range from about −4.9 eV to −2.7 eV for PdSn₄, −5.5 eV to −2.4 eV for PdSn₃, PdSn₂ and PdSn, −6.0 eV to −1.9 eV for Pd₂Sn and −5.9 eV to 0 eV for Pd₃Sn, most of the Pd-d states dominated with some Sn-p electrons as the main contributors to the TDOS, meaning a hybridization of Pd-d with Sn-p electrons. Above the Fermi level, Sn-p electrons are the main contributors to the TDOS for PdSn₄, PdSn₃, PdSn₂ and PdSn. For Pd₂Sn, both the Sn-p and Pd-d electrons are the main contributors to the TDOS, indicating a strong hybridization of Sn-p with Pd-d electrons, while for Pd₃Sn, Pd-d electrons are the main contributors for the TDOS, which are slightly hybridized with some Sn-p electrons, meaning a relatively weak hybridization of Pd-d and Sn-p electrons. With the increasing concentration of Pd in Pd-Sn compounds such as PdSn, Pd₂Sn and Pd₃Sn, the dominant Pd-d electrons is increasingly obvious in the TDOS near Fermi level. The interactions of Pd-d electrons together with the hybridization of Pd-d with Sn-p electrons form more stable bonds, leading to more stable structures, which is in agreement with the finding that the compounds of PdSn, Pd₂Sn and Pd₃Sn have relatively more stable structures among Pd-Sn compounds from the results of formation energy.

Fig. 7

TDOS and PDOS for binary Pd-Sn compounds: (a) PdSn₄, (b) PdSn₃, (c) PdSn₂, (d) PdSn, (e) Pd₂Sn, (f) Pd₃Sn. (The dashed lines at 0 eV denote the Fermi level E_f).

To further reveal the bonding mechanism of the Pd-Sn compounds, a 3D charge density difference map is given in Fig. 8 where the yellow and red isosurfaces represent the enrichment and dissipation regions of charge density, respectively. A significant depletion of the charge density at the atom sites along with an accumulation of the charge density in the interstitial region can be found, which means ionic bonding of these Pd-Sn compounds. In Fig. 8f, the enrichment region of charge density has a typical annular shape, which means a strong ionic bonding of Pd and Sn.

Fig. 8

Charge density difference for binary Pd-Sn compounds: (a) PdSn₄, (b) PdSn₃, (c) PdSn₂, (d) PdSn, (e) Pd₂Sn, (f) Pd₃Sn (unit: e/ų; a red isosurface represents negative charge density and a yellow isosurface represents positive charge density, with a maximum value of 0.004 e/ų; tin atoms are large and gray, palladium atoms are small and navy) (Color figure online).

To explore the electronegativity in depth and quantify the charge distribution, Bader charge analysis^42,43 is used with the detailed information listed in Table VI. The effective valence charge q can be obtained from the Bader charge minus the formal charge. The positive value of effective valence charge means the received amount of charge while the negative value means the lost amount. We grouped the same type of Bader charges with the overlapped number n for the Pd-Sn compounds. It can be found from Table VI Sn atoms are lost charges while Pd atoms are gained, which means Sn transferred charges to Pd. The number of transferred charges per Sn is 0.194 for PdSn₄, 0.229 for PdSn₃, 0.329 for PdSn₂, 0.545 for PdSn, 0.669 for Pd₂Sn and 0.849 for Pd₃Sn. So the ionicity of these compounds increases with Pd concentration in the sequence PdSn₄ < PdSn₃ < PdSn₂ < PdSn < Pd₂Sn < Pd₃Sn.

Table VI The calculated Bader charges, charge-overlap number n and effective valence charge q of Pd and Sn for the Pd-Sn IMCs (charge units in e)

Conclusions

First-principles calculations were used to investigate the structure, phase stability, mechanical, thermodynamic and electronic properties of the binary Pd-Sn compounds (PdSn₄, PdSn₃, PdSn₂ PdSn, Pd₂Sn and Pd₃Sn). The optimized lattice parameters accord well with the literature findings. Six compounds are all thermodynamically and elastically stable. Among them, Pd₂Sn is the most stable phase mainly due to a strong hybridization of Pd-d with Sn-p electrons near the Fermi level according to the PDOS. The polycrystalline elastic modulus and anisotropic characters are derived. Pd₃Sn has the largest values of bulk modulus, shear modulus and Young’s modulus while PdSn₄ has the lowest values. The shear modulus and Young’s modulus follow the increasing order of PdSn₄, PdSn₂, PdSn₃, Pd₂Sn, PdSn and Pd₃Sn. The microhardness parameters show that they are all low-stiffness materials. The Pd-Sn compounds are all ductile and anisotropic. Ductility increases with Pd concentration. Among the six compounds, PdSn exhibits the strongest anisotropy of the bulk modulus and shear modulus, while Pd₃Sn shows an isotropy of bulk modulus according to the percentage bulk modulus calculation. The heat transfer property is predicted using the Debye temperature and Clarke’s model and Cahill’s model. The minimum thermal conductivity of $k_{\min }^{a}$ and $k_{\min }^{b}$ roughly increases with Pd concentration, with a value of $k_{\min }^{a}$ lower than $k_{\min }^{b}$. The Debye temperature decreases in the order of Pd₃Sn, PdSn, Pd₂Sn, PdSn₃, PdSn₂ and PdSn₄, and $k_{\min }^{a}$ decreases in the order of Pd₃Sn, PdSn, Pd₂Sn, PdSn₂, PdSn₃ and PdSn₄. The slight difference in order of ${\theta }_{D}$ and $k_{\min }^{a}$ between PdSn₃ and PdSn₂ is discussed based on the anisotropic property. All of the compounds performed ionic bonding from the charge density difference map, and the ionicity increased with Pd concentration according to the Bader charge analysis.

The mechanical and thermal properties are calculated in this work. The results cannot be compared due to the absence of any reported data. Therefore, these results can be used as a prediction and good reference for the future application of the material.