Introduction

The pressure distribution in the molten metal delivery system of a commercial steel continuous caster is important for several reasons: (1) it governs the flow rate and its sensitivity to changes in casting conditions, and (2) the minimum pressure may cause air aspiration and accompanying quality problems.[1,2] The flow is driven by gravity according to the pressure drop between the liquid surface level in the tundish and the liquid surface level in the mold.[1,2] A flow-control device, consisting of either a sliding gate or a stopper-rod, decreases the local cross-sectional area to restrict the flow, which causes a large local pressure drop. This is continuously adjusted during casting to maintain the desired flow rate and casting speed.

In a stopper-rod system, molten steel from the tundish flows through the thin gap between the stopper-rod and the tundish floor, down through the Upper Tundish Nozzle (UTN), into the Submerged Entry Nozzle (SEN), and finally exits the nozzle ports into the mold cavity. Just beneath the minimum gap near the stopper-rod tip, the pressure drops below atmospheric pressure. This tends to aspirate gas leakage into the nozzle through any porous refractory, cracks, or joints in the refractory components.[1,2,3] In some systems, argon gas is supplied to the region in order to aspirate argon instead of air if any leakage occurs.[4,5,6] If air aspiration from the atmosphere occurs, then the nitrogen will dissolve and the oxygen will react with other dissolved alloy elements in the molten steel to form inclusions. The inclusions may adhere to the nozzle walls as clogging, decreasing the local cross-sectional area. Furthermore, inclusions and clog material may agglomerate and become entrapped in the final steel as internal defects, which lower product quality.[7,8] In addition to lower productivity and inclusion defects, by changing the internal geometry of the flow path inside the liquid delivery system, clogging also causes instability in the turbulent flow, leading to variations in flow rate, mold flow problems such as surface level fluctuations, and finally slivers and other serious defects in the steel product.[9,10,11]

Clogging may occur at different places in the nozzle according to its formation mechanism.[1,3,7] The most susceptible places are near joints and/or cracks, where re-oxidation inclusion products form. Clogging buildup may also occur at the entrance to the UTN or at the top of the nozzle port outlets, where there may be flow separation that allows upstream inclusions to attach to the walls.[1,2,3,8] Uniform clogging buildup around the perimeter of the nozzle is common if the superheat drops and a combination of clogging and frozen steel skulls can form, especially in the lower SEN.[7] Further details on clogging mechanisms and their accompanying defects are discussed elsewhere.[1,2,12,13]

Different practices have been implemented in commercial casters aiming to alleviate clogging problems.[13] One option is to modify the nozzle geometry to lessen recirculation and inclusion attachment to the nozzle walls,[7,8] to improve joint sealing,[14] using oversized nozzle bores and ports[15,16] to accommodate longer times of casting while clogging before a nozzle change, and varying nozzle diameter,[17,18] or insulating around the nozzle exterior to lessen skulling-type clogs.[17] A second option is to liquefy the inclusions, if they are alumina-based, by calcium treatment,[19,20,21,22,23] or using a different nozzle material or coating, such as calcia,[24,25,26] or boron nitride[27,28,29] to lessen inclusion adherence to the nozzle walls. Finally, the most common practice is to add argon into the system through stopper-rod tip, UTN, or other places inside the nozzle. Argon acts to less clogging via several different mechanisms, which are discussed elsewhere.[1,2,7]

Several different models have been applied in the previous work to predict the pressure distribution and flow rate in slide-gate or stopper-rod molten metal delivery systems as a function of system geometry and casting conditions. Previous work on slide-gate systems is reviewed elsewhere.[1,2,12] Computational methods for models of stopper-rod systems include computational fluid dynamics (CFD) models,[30,31,32,33,34,35,36] the Bernoulli energy balance approach,[5,6,33,37] and neural networks (machine learning).[38] The results indicate that the combined effects of stopper-rod opening, casting speed, nozzle geometry, argon gas injection rate, tundish height, and submergence depth all determine the gauge pressure distribution in the system. Bai et al.[1] used a 3D multiphase CFD model to calculate how the injection of argon gas can alleviate the problem of negative gauge pressure and quantified how much argon is needed for different nozzle diameters and casting conditions. For most conditions, the required argon is unfeasibly high to completely avoid negative gauge pressure.

A one-dimensional (1D) analytical Bernoulli energy balance approach to model pressure and flow rate has been introduced by several researchers[5,6,33,37] to calculate flow in stopper-rod systems as a function of vertical stopper opening distance. For example, Liu’s Bernoulli-type model[33] revealed the classic pressure distribution. This model used a clogging factor to implement the effect of clogging and quantified how much the stopper-rod had to open to accommodate increasing clogging, in order to maintain the flow rate (and casting speed). Another such Bernoulli-type model, by Javurek et al.,[5,6] calculated pressure at various points in stopper-rod flow systems with a single-tip radius using different empirical loss coefficients for single-phase and multiphase flow. Another 1D Bernoulli-type model by Eck[37] for single-tip radius stopper-rod systems with single-phase flow featured a simple Graphic User Interface (GUI) for input data. The calculated pressure distributions predicted similar trends.

The present work introduces a general, flexible, computationally efficient modeling package for calculating Pressure distribution and Flow rate within Stopper-Rod flow delivery systems: PFSR. Like PFSG,[12] the new PFSR software package features a user-friendly GUI with an inverse-modeling solver which includes the effects of argon gas injection with locally varying gas volume expansion, non-circular stopper-rod tip shape, and clogging that may vary with location in the nozzle. The new model is verified with three-dimensional CFD simulations and validated with measurements in both water models and commercial steel casters. To overcome issues with excessive negative gauge pressure predicted with conventional models in steel casters, methodologies are introduced to include the effects of cavitation and non-primed flow.

PFSR Model Description

PFSR employs the Bernoulli energy balance approach to calculate gauge pressure distribution and flow rate in stopper-rod flow-control systems in continuous casting of steel slabs. The program features a MATLAB[39]-based GUI and several steel plants are using this offline model to understand and improve their operations. The modeled metal delivery system starts from the top surface of the molten steel inside tundish, through the stopper-rod gap region, the upper tundish nozzle (UTN), submerged entry nozzle (SEN), and ends at the top surface level in the mold. In addition to the geometry, model inputs include the casting conditions such as the stopper-rod opening, tundish height, flow rate, slab thickness/width, argon gas injection rate, and possible clogging. The model equations, which are solved using MATLAB, are described in the next section.

Pressure-Energy Model Equations

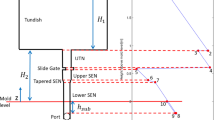
A one-dimensional system of pressure-energy balance equations for continuous casting systems with stopper-rod flow control is solved using PFSR. These Bernoulli-type equations consider kinetic energy, potential energy, and turbulent dissipation pressure/energy losses.[2,12] Similar to the approach used for slide-gate systems, PFSG,[12] general analytical expressions are obtained for the pressure/energy loss between 10 selected points distributed vertically down the flow system (pictured in Figure 1), such that the gauge pressure is calculated at each point by

$${P}_{i}={P}_{i+1}+{\rho }_{m}g{h}_{i+1}-{\rho }_{m}g{h}_{i}+ \frac{1}{2}{\rho }_{m}{{V}_{i+1}}^{2}- \frac{1}{2}\rho {{V}_{i}}^{2}+ \sum {\Delta P}_{L},$$
(1)

where \({P}_{i}\) is gauge pressure of point \(i\) [Pa], \({\rho }_{m}\) is mixture fluid density between point \(i\) and \(i+1\) [kg/m3], \({V}_{i}\) is velocity at point \(i\) [m/s], \({h}_{i}\) is the height of point \(i\) [m], and \(g\) is gravitational acceleration [9.81 m/s2]. Fluid velocities at each point are calculated from the system flow rate, based on the effective local cross-sectional area, as described in the next Section B. Boundary conditions of 0 gauge pressure are applied at the top surface levels of the tundish and mold. The pressure-energy loss terms, \(\sum {\Delta P}_{L}\), [Pa] are explained in Section C below, and depend on the geometric details and flow phenomena between each pair of points. The molten steel velocity at the tundish top surface, \({V}_{1}\), and at top surface in the mold, \({V}_{10}\), are considered to be negligible.[2,12]

Fig. 1
figure 1

Example pressure distribution for all 10 points in stopper-rod metal delivery system (System 1 conditions)

Full size image

Applying Eq. [1] to the pressure drops between the ten points in the flow system shown in Figure 1 gives the following ten equations:

$${\text{Point }1 \; (\text{tundish level}) P}_{1}={P}_{2}-{\rho }_{L}g{h}_{1-2}$$
(2)
$$\text{Point }2 \; (\text{bottom of tundish}) {P}_{2}={P}_{3}+ \frac{1}{2}{\rho }_{m }{{V}_{3}}^{2}+{\Delta P}_{L,cont}+ {\Delta P}_{L,tun}+ {\Delta P}_{L,two}+ {\Delta P}_{L,stopper}$$
(3)
$$\text{Point }3 \; (\text{minimum gap}) {P}_{3}={P}_{4}- \frac{1}{2}{\rho }_{m}{{V}_{3}}^{2}+\frac{1}{2}{\rho }_{m}{{V}_{4}}^{2}+ {\Delta P}_{L,exp}$$
(4)
$${\text{Point }4 \; (\text{UTN entry}) P}_{4}={P}_{5}- {\rho }_{m}g{h}_{4-5}- \frac{1}{2}{\rho }_{m}{{V}_{4}}^{2}+\frac{1}{2}{\rho }_{m}{{V}_{5}}^{2}+ {\Delta P}_{Lf,4-5}+ {\Delta P}_{L,UTN}$$
(5)
$$\text{Point }5 \; (\text{upper SEN entry}) {P}_{5}={P}_{6}- {\rho }_{m}g{h}_{5-6}- \frac{1}{2}{\rho }_{m}{{V}_{5}}^{2}+\frac{1}{2}{\rho }_{m}{{V}_{6}}^{2}+ {\Delta P}_{Lf,5-6}+ {\Delta P}_{L,USEN}$$
(6)
$$\text{Point }6 \; (\text{middle SEN entry}) {P}_{6}={P}_{7}- {\rho }_{m}g{h}_{6-7}- \frac{1}{2}{\rho }_{m}{{V}_{6}}^{2}+ \frac{1}{2}{\rho }_{m}{{V}_{7}}^{2}+ {\Delta P}_{Lf,6-7}+ \Delta {P}_{L,tap}$$
(7)
$$\text{Point }7 \; \left(\text{lower SEN entry}\right){P}_{7}={P}_{8}- {\rho }_{m}g{h}_{7-8}- \frac{1}{2}{\rho }_{m}{{V}_{7}}^{2}+ \frac{1}{2}{\rho }_{m}{{V}_{8}}^{2}+ {\Delta P}_{Lf,7-8}+ {\Delta P}_{L,lSEN}$$
(8)
$$\text{Point }8 \; (\text{lower SEN exit},\text{ same height as point }9) {P}_{8}={P}_{9}- \frac{1}{2}{\rho }_{m}{{V}_{8}}^{2}+ \frac{1}{2}{\rho }_{m}{{V}_{9}}^{2}+ {\Delta P}_{L,port}+ {\Delta P}_{L,tee}+ {\Delta P}_{C,port}$$
(9)
$$\text{Point }9 \; (\text{top of port outlet}) {P}_{9}={\rho }_{L}g{h}_{sub}$$
(10)
$$\text{Point }10 \; (\text{mold level}) {P}_{10}=0$$
(11)

Velocity and Area Calculations

Velocity at each point in the PFSR model, \({V}_{i}\), [m/s] is calculated from the system flow rate as follows:

$${V}_{i}=\frac{Q_{L}}{{A}_{eff,i}},$$
(12)

where \({Q}_{L}\) is the liquid (water or steel) flow rate [m3/s], and \({A}_{eff,i}\) is the effective area of the local horizontal cross section [m2].

Effective area calculations

At any given point, \(i\), in the flow system, \({A}_{eff,i}\) is the effective area of the local cross section of the nozzle [m2]. With no gas injection, this effective area matches the physical cross-sectional area according to the nozzle geometry, \({A}_{i}\) [m2]. However, if argon gas or air is injected, then the effective area occupied by the liquid flow will be smaller:

$${A}_{eff,i}={A}_{i}*(1-{\alpha }_{i}).$$
(13)

The local gas volume fraction, \({\alpha }_{i}\), is calculated as follows, assuming steady state (no gas accumulation) and negligible slip between gas and liquid phases:

$${\alpha }_{i}=\frac{{Q}_{gas,i}}{Q_{L} + {Q}_{gas,i}},$$
(14)

where \({Q}_{gas,i}\) [m3/s] is the flow rate of the “hot” argon gas between the points \(i\) and \(i+1\) (i.e., at the local molten steel pressure and temperature, \({T}_{hot}\)= 1823K) and is calculated as follows:

$${Q}_{gas,i}={Q}_{supply,i}*\frac{{P}_{atm} }{{P}_{atm}+\left(\frac{{P}_{i}+{P}_{i+1}}{2}\right)}* \frac{{T}_{hot}}{{T}_{\infty }},$$
(15)

where \({Q}_{supply,i}\) [SLPM] is the standard flow rate of the “cold” injected argon gas (i.e., at standard absolute pressure \({P}_{atm}\) = 101 kPa and standard temperature \({T}_{\infty }\) = 298 K), which is multiplied by \(\frac{0.001 }{60}\) to convert to m3/s , \({P}_{i}\) is the gauge pressure at point \(i\) [Pa], \({P}_{i+1}\) is the downstream gauge pressure at point \(i+1\) [Pa], which is divided by 1000 to convert to kPa, and \({T}_{hot}\) is the molten steel temperature [K].

The local gas fraction can also be used to calculate the mixture density between the points \(i\) and \(i+1\):

$${\rho }_{m}={\rho }_{L}*(1-{\alpha }_{i}),$$
(16)

where \({\rho }_{L}\) is liquid density [kg/m3].

The cross section of the UTN is considered to be circular, so can be calculated as follows:

$${A}_{i}=\frac{\pi }{4} {{D}_{x}}^{2},$$
(17)

where \({D}_{i}\) is the diameter at that location, \(i\), down the nozzle [m]. At other vertical locations down the nozzle system, the local cross section is based on \({D}_{i}= {D}_{h,i}\), the equivalent hydraulic diameter [m], for more generality, based on the local area and perimeter as follows:

$${D}_{h,i}=\frac{{4A}_{i}}{{p}_{i}},$$
(18)

where \({p}_{i}\) is the perimeter at that location, \(i\) [m]. Also,[12] for a nozzle with bifurcated ports, if the area of each port exceeds half of the lower SEN area, it is set down to only half of the SEN area, because the jet exiting that port cannot expand fast enough to change its area significantly, so the rest of the area, in the upper port, typically has negligible net outward flow.[1,2]

It is important to note that the area of the narrow gap, \({A}_{gap}\), formed between the stopper-rod and the tundish floor radius in [m2] (which is in a shape of a conical frustum[40]), greatly affects both pressure and flow rate calculations in PFSR and is explained in Appendix 1.

Pressure Losses

The pressure loss terms, \(\sum {\Delta P}_{L}\) in Eq. [1], between each pair of points in the PFSR model system in Figure 1, are defined in the following sections.

Tundish liquid level to tundish floor (points 1 to 2)

The simple linear equation for hydrostatic pressure that relates these two points has no undefined pressure loss terms, because velocity at the tundish floor, \({V}_{2}\), is negligible. The top surface of the tundish, \({P}_{1}\), is at atmospheric pressure, which comprises the first boundary condition of the system. Similarly, point 10 at the liquid level in the mold is the final boundary condition fixed at 1 atm.

Gap contraction region (points 2 to 3)

While passing from the tundish floor, point 2, to the minimum gap, point 3, the hydrostatic pressure increase is negligible, but the flow experiences 4 different pressure losses. First, the very large contraction in area from the tundish floor to the UTN inlet causes: \(\Delta {P}_{L,tun}\), [Pa], which is discussed elsewhere.[12]

Second and further down to the UTN is the pressure loss, \(\Delta {P}_{L,cont}\), [Pa], due to contraction of area from \({A}_{UTNr}\) (upper UTN surface area [m2]) to \({A}_{UTNa}\) (UTN inlet surface area [m2]):[41]

$${\Delta P}_{L,cont}= \frac{1}{2}{\rho }_{L}{\left({V}_{UTNa}\right)}^{2}\left(0.42\left(1-\frac{{A}_{UTNa}}{{n*A}_{UTNr}}\right)\right),$$
(19)

where \({V}_{UTNa}\) , \({V}_{4},\) is fluid velocity at UTN entry [m/s], and \(n\) is the number of tundish nozzles (strands) where flow exits the tundish bottom.

Thirdly, \(\Delta {P}_{L,two}\), [Pa], accounts for the pressure drop due to possible argon gas injection, discussed elsewhere.[12]

Finally, the most important pressure drop is caused by the contraction in area from the UTN entry, \({A}_{UTNa}\), to the minimum gap, \({A}_{gap}\):

$${\Delta P}_{L,stopper}= \frac{1}{2}\chi {\rho }_{m}{\left({V}_{3}\right)}^{2},$$
(20)

where \(\chi \) is the effective fraction of the nozzle diameter with recirculating flow and is defined as[42]

$$\chi = {\left(\frac{1}{\nu }-1\right)}^{2}$$
(21)

and \(\nu \) is Weisbach contraction coefficient:[42]

$$\nu =0.63+0.37{\left(\frac{{A}_{gap}}{{A}_{UTNa}}\right)}^{3},$$
(22)

where \({V}_{3}\) is the fluid velocity in the minimum gap (point 3) [m/s]. It is important to note that if the stopper-rod position is high enough that \({A}_{gap}>{A}_{UTNa}\), then the pressure loss caused by the stopper-rod becomes negligible, and only the first 3 pressure losses are present in this region.

Gap expansion region (points 3 to 4)

The expansion region from points 3 to 4 is shown in Figure A3. Again, the hydrostatic pressure drop is negligible, so the pressure drop in this region, \({\Delta P}_{L,exp}\), [Pa], is the expansion component of the diffuser expression,[43] and is calculated from

$${\Delta P}_{L,exp}= \frac{1}{2}\kappa {\rho }_{m}{V}_{3}^{2}{\left(1-\frac{{A}_{gap}}{{A}_{UTNa}}\right)}^{2},$$
(23)

where \(\kappa \) is the diffuser pressure loss constant which is chosen as 0.35.[43] It is very important to note that in case \({A}_{gap}>{A}_{UTNa}\), not only does \({\Delta P}_{L,stopper}\) become zero, but also \({\Delta P}_{L,exp}\) is equal to zero (since \({V}_{3}= {V}_{UTNa}\)). In this case, there is no pressure loss between point 3 and 4, leading to \({P}_{3}= {P}_{4}\).

UTN region (points 4 to 5)

Between points 4 and 5 inside the UTN, there are two pressure losses: \({\Delta P}_{Lf,4-5}\), [Pa], due to wall friction, and \({\Delta P}_{L,UTN}\), [Pa], due to UTN wall tapering. The wall friction loss, \({\Delta P}_{Lf,3-4}\), is defined as

$${\Delta P}_{Lf,4-5}= \frac{1}{8}{\rho }_{m} {f}_{UTN}\left[{{(V}_{UTNa})}^{2}{L}_{UTN}\frac{\left({D}_{UTNa}+{D}_{UTNb}\right)\left({{D}_{UTNa}}^{2}+{{D}_{UTNb}}^{2}\right)}{{{D}_{UTNb}}^{4}}\right],$$
(24)

where \({f}_{UTN}\) is the friction factor[12] in the UTN region, \({L}_{UTN}\) the UTN length [m], \({D}_{UTNa}\) and \({D}_{UTNb}\) are the UTN diameters at entry and exit [m], \({V}_{UTNa}\) is the corresponding flow velocities at UTN entry [m/s]. A derivation for this equation for tapered pipes is provided elsewhere.[12]

The UTN wall tapering term, \({\Delta P}_{L,UTN}\), [Pa], is due to gradual contraction or expansion if the UTN is tapered and is defined[12] as follows:

If \({{\varvec{D}}}_{{\varvec{U}}{\varvec{T}}{\varvec{N}}{\varvec{a}}}<{{\varvec{D}}}_{{\varvec{U}}{\varvec{T}}{\varvec{N}}{\varvec{b}}}\) (gradual expansion)

$$\left\{\begin{array}{l}{\Delta P}_{L,UTN}= \frac{1}{4}{\rho }_{m}{{V}_{UTNa}}^{2}\left(2.6sin\left(\frac{\theta }{2}\right)\right){\left(1-\frac{{A}_{UTN}a}{{A}_{UTNb}}\right)}^{2} \theta <{45}^{0} \\ {\Delta P}_{L,UTN}= \frac{1}{4}{\rho }_{m}{{V}_{UTNa}}^{2}{\left(1-\frac{{A}_{UTNa}}{{A}_{UTNb}}\right)}^{2} {45}^{0}<\theta <{90}^{0}\end{array}\right.$$
(25)

If \({{\varvec{D}}}_{{\varvec{U}}{\varvec{T}}{\varvec{N}}{\varvec{a}}}\ge {{\varvec{D}}}_{{\varvec{U}}{\varvec{T}}{\varvec{N}}{\varvec{b}}}\) (gradual contraction)

$$\left\{\begin{array}{l}{\Delta P}_{L,UTN}= \frac{1}{4}{\rho }_{m}{{V}_{UTNb}}^{2}\left(1.6sin\left(\frac{\theta }{2}\right)\right)\left(1-\frac{{A}_{UTNb}}{{A}_{UTNa}}\right) \theta <{45}^{0} \\ {\Delta P}_{L,UTN}= \frac{1}{4}{\rho }_{m}{{V}_{UTNb}}^{2}\sqrt{sin\left(\frac{\theta }{2}\right)}\left(1-\frac{{A}_{UTNb}}{{A}_{UTNa}}\right) {45}^{0}<\theta <{90}^{0}\end{array}\right.,$$
(26)

where \(\theta =2*arctan\left|\frac{{D}_{UTNa}-{D}_{UTNb}}{2{L}_{UTN}}\right|\), \({V}_{UTNb}\), (or \({V}_{5}\), ) is the velocity at UTN exit [m/s] and \({A}_{UTNa}\) and \({A}_{UTNb}\) are the section areas at UTN entry and exit [m2]. Also, note that according to Figure 2, \({V}_{UTNb}= {V}_{USENa}\) (velocity at upper SEN entry [m/s]).

Fig. 2
figure 2

PFSR V.2.1 user interface showing input data for System 2 conditions

Full size image

Upper SEN region (points 5 to 6)

In the potentially tapered region between points 5 and 6, two pressure loss terms are considered. The first term, \({\Delta P}_{Lf,5-6}\), the wall friction pressure loss [Pa], is similar to Eq. [24] with appropriate changes for the velocity, replacing \({V}_{UTNa}\) with \({V}_{USENa}\), \({V}_{5}\). Additionally, \({L}_{UTN}\) is replaced with \({V}_{USEN}\) (upper SEN length [m]). Finally, \({D}_{UTNa}\) and \({D}_{UTNb}\) are replaced with \({D}_{USENa}\) and \({D}_{USENb}\) (upper SEN exit diameter [m]), respectively.

The second term, \({\Delta P}_{L,USEN}\), is pressure loss due to gradual contraction or expansion in the upper SEN region [Pa]. For gradual expansion, the expression is the same as Eq. [25], with appropriate changes for the velocity, replacing \({V}_{UTNa}\) with \({V}_{USENa}\). Also \({A}_{UTNa}\) is replaced with \({V}_{USENa}\) (upper SEN entry area [m2]), and \({V}_{UTNb}\) is replaced with \({V}_{USENb}\) (upper SEN exit area [m2]). For gradual contraction, the expression is the same as Eq. [26] replacing \({V}_{UTNb}\) with \({V}_{USENb}\) (or \({V}_{6}\)), replacing \({A}_{UTNa}\) with \({A}_{USENa}\) , and replacing \({V}_{UTNb}\) with \({V}_{USENb}\).

Middle SEN (points 6 to 7)

The middle portion of the SEN is often tapered, so again has two pressure loss terms. Firstly, \({\Delta P}_{Lf,6-7}\) is the wall friction between points 6 and 7 [Pa], similar to Eq. [24] with appropriate changes for the velocity, replacing \({V}_{UTNa}\) with \({V}_{USENb}\) [m/s]. For the middle, potentially tapered portion of the SEN length, \({L}_{UTN}\) is replaced with \({L}_{tSEN}\) [m]. For the upper SEN exit diameter, \({D}_{UTNa}\) is replaced with \({D}_{USENb}\). For the middle SEN entry diameter, \({D}_{UTNB}\) [m] is replaced with \({D}_{SENa}\) [m], as middle SEN exit diameter. Finally, for the wall friction factor, \({f}_{UTN}\) is replaced with \({f}_{SEN}\).

Secondly, \(\Delta {P}_{L,tap}\) is a pressure loss term due to gradual contraction or expansion, if this middle portion of the SEN is tapered, \(\Delta {P}_{L,tap}\), [Pa]. This is the same as Eq. [25] or Eq. [26] with appropriate changes in a middle SEN velocity, either replacing \({V}_{UTNa}\) with the entry velocity \({V}_{USENb}\) for gradual expansion, or \({V}_{UTNb}\) with the exit velocity \({V}_{SENa}\), \({V}_{7}\), for gradual contraction. For both cases, \({A}_{UTNa}\) is replaced with middle SEN entry area \({A}_{USENb}\) , and \({A}_{UTNb}\) is replaced with middle SEN exit area, \({A}_{SENa}\) , [m2].

Lower SEN to port region (points 7 to 8)

Similar to the middle SEN region, there are two pressure loss terms in the lower SEN between points 7 and 8. The first term is due to wall friction, \(\Delta {P}_{Lf,7-8}\), [Pa], and is similar to Eq. [24], with appropriate changes for the velocity, replacing \({V}_{UTNa}\) with the lower SEN entry velocity \({V}_{SENa}\) [m/s]. For the potentially tapered lower SEN length, \({L}_{UTN}\) is replaced with \({A}_{SEN}\) [m]. For the SEN entry diameter, \({D}_{UTNa}\) is replaced with \({A}_{SENa}\). For the SEN exit diameter, \({D}_{UTNb}\) is replaced with \({D}_{SENb}\). Finally, for the wall friction factor, \({f}_{UTN}\) is replaced with \({f}_{SEN}\).

The second pressure loss term is the pressure loss due to the possible taper of the lower SEN region, \({\Delta P}_{L,lSEN}\), [Pa], which is the same as Eq. [25] or Eq. [26] with appropriate changes in velocity, replacing \({V}_{UTNb}\) with the exit velocity of the lower SEN, \({V}_{SENb}\) (or \({V}_{8}\)), for gradual contraction, and replacing \({V}_{UTNa}\) with \({V}_{SENa}\), [m/s] for gradual expansion. Finally, for both cases (gradual expansion and/or contraction), \({A}_{UTNa}\) is replaced with lower SEN entry area, \({A}_{SENa}\) [m2], and \({V}_{UTNb}\) is replaced with the exit area, \({V}_{SENb}\).

Port region (points 8 to 9)

In the port region, between points 8 and 9, there are three pressure loss terms: \({\Delta P}_{L,port}, {\Delta P}_{L,tee},\) and \({\Delta P}_{C,port}\). The first pressure loss, \({\Delta P}_{L,port}\), is due to sudden contraction between the lower SEN and the port [Pa], and is defined as[2]

$$\left\{\begin{array}{cc}{\Delta P}_{L,port}= \frac{1}{2}{\rho }_{m}{{V}_{SENb}}^{2}{\left(\frac{{A}_{SEN}}{2{A}_{port}}-1\right)}^{2}& {A}_{SENb}>2{A}_{port}\\ \Delta {P}_{L,port}= 0& {A}_{SENb}\le 2{A}_{port}\end{array}\right.,$$
(27)

where \({A}_{port}\) is port cross-sectional area [m2].

The second pressure drop, \({\Delta P}_{L,tee}\), is due to the change of flow direction[12] [Pa], and is defined as

$${\Delta P}_{L,tee}= \frac{1}{2}{\rho }_{m}K{{V}_{SENb}}^{2},$$
(28)

where \(K\) is the port loss constant, which defaults to 0.2,[12] but can be changed in the Settings menu.

The third pressure loss in the port region, \({\Delta P}_{C,port}\), [Pa] is due to clogging:

$${\Delta P}_{C,port}= \frac{1}{2}{\rho }_{m}{C}_{port}{{V}_{port}}^{2},$$
(29)

where \({V}_{port}\), (or \({V}_{9}\)), is fluid velocity through the port [m/s], and \({C}_{port}\) is the port clogging constant, which can be input (in the Settings menu) or left blank (to default to 1). Further implementation of clogging is discussed in the next section.

Incorporation of Clogging

As shown in Figure 2, possible clogging can be defined at several different places. In the port region, a clogging coefficient is considered, as implemented in the previous section.[12] Elsewhere, (tundish floor opening, UTN, upper SEN, middle SEN, and lower SEN), clogging is specified by a reduction in the diameter of that nozzle portion. Similarly, erosion, such as caused by Ca-treated steel in an alumina nozzle is specified by an appropriate increase in diameter. These methodologies to account for clogging in the stopper-rod flow delivery system are similar to those used in PFSG and are discussed elsewhere.[12]

Solution Procedure

For a given set of geometrical inputs and casting conditions, the 10 fully coupled pressure-energy equations, Eq. [1] defined in the previous section, are solved simultaneously using the implicit solver, FSOLVE, in MATLAB,[39] for exactly one missing user-selected casting condition input. This solver minimizes the error in the total energy balance, which is quantified by the difference between gauge pressure calculated at point 2 (tundish bottom) and the hydrostatic pressure calculated at the tundish bottom (Eq. [2]), which happens to be the largest magnitude pressure in the stopper-rod system (Eq. [12]). The associated error, \({F}_{1}\), is defined then as

$${F}_{1} ={P}_{2}- {\rho }_{L}g{h}_{1-2}.$$
(30)

This means that FSOLVE solves an inverse problem for the value of the user-defined unknown (casting conditions, geometrical input, stopper-rod pressure loss constant, or clogging) in order to ensure the pressure at point 1 is as close as possible to zero gauge pressure. After convergence, this solution error is very small, on the order of 10−12 kJ/m3 (10−10 pct). The entire model runs in less than 10 s on a personal computer and the energy balance error lies within 10−3 kJ/m3. It is important to note that in case all inputs (geometrical and casting conditions) are given by the user, no iteration with FSOLVE is needed then the model simply and very quickly only outputs the error associated with the energy balance.

PFSR Inputs and Outputs

Three different sets of data are input to the PFSR model: (1) nozzle geometry (dimensions), (2) casting conditions and (3) temperature, fluid density, and/or clogging size parameters (if different with the Default values). Input data for studies on four systems where plant and/or water model measurements were available are given in Table I.

Table I Nozzle Dimensions and Plant/Water Model Casting Conditions Studied in this Work
Full size table

An example of the PFSR user interface, with input data conditions for System 2, is shown in Figure 2.

Argon gas flow rate is input to PFSR at standard temperature and (absolute) pressure conditions, \({P}_{atm}\) = 101 kPa and \({T}_{amb}\) = 298 K. This gas is assumed to heat up to the molten steel temperature of 1823 K at the time of injection, which is reasonable from previous work.[12] The dynamic viscosity of the fluid is set at 0.001 and 0.0063 Pa.s for water and molten steel, respectively.

The first output of PFSR is a pressure distribution plot, such as shown in Figure 3(a). This plot shows the gauge pressure at the 10 different points in the system, arranged vertically. The second output is a plot of system flow rate as a function of stopper-rod opening, which is the vertical distance moved above the closed position, \({h}_{sro}\) = 0, (Figure 3(b)). It is important to note that in a water model, which has a slightly flexible plastic floor, the critical height is determined by starting with a fully closed position with no flow, and gradually raising the stopper until the first indication of flow is observed. This height is then declared as the zero reference position (hsro=0). The method (and definition) is the same in a steel caster, but uncertainty arises instead from clogging, erosion, and/or thermal expansion. In either case, an error in zero position would result in a fixed offset, independent of the actual stopper opening. PFSR also outputs the total energy balance error (kJ/m3) in the calculation.

Fig. 3
figure 3

Results for System 2 (PFSR V.2.1) (a) pressure distribution, (b) flow rate for different definitions of gate opening

Full size image

The ability to conduct parametric studies is an important feature of PFSR. This is typically done to investigate the effect of changing a casting condition or geometrical input. Given complete geometry data and all other casting conditions, if a single casting condition (or a clogging size parameter and/or stopper-rod pressure loss constant, given in Figure 2) is unknown, PFSR calculates its value. This “inverse model” feature, also included in PFSG,[12] enables realistic, industry-relevant parametric studies. Before that, the model should be calibrated for a given plant/water model, which is relatively easy to accomplish.

PFSR V.1.0 using FSOLVE, inverse-capability of parametric study, generated the two graphs and output file of useful information. It also included the Settings menu to customize clogging at different places inside the nozzle, absolute roughness in UTN and SEN, pressure loss constant at stopper-rod region and port, fluid density (in case the water model is required to be analyzed), number of nozzles exiting the tundish bottom, and the transition Reynolds number for turbulence. PFSR V.2.1 has variable argon gas flow rate inside the UTN and SEN according to the local pressures when solving Eq. [14]. This enabled incorporating the mixture density, which is highly coupled. The value of any one of 6 missing casting conditions (Main window) or any one of 6 missing Clogging values or the stopper-rod Pressure Drop Constant (Settings Menu) may be left blank (unknown), shown in Figure 2, and solved by PFSR.

Model Verification and Validation

To verify and validate PFSR V.2.1, pressure distribution predictions of the model are compared with CFD simulations and available data from four different sets of plant measurements and water model experiments. The system geometries and flow conditions of the different data sets are given in Table I.

CFD Model

A three-dimensional (3D) finite-volume CFD model was employed to calculate velocity and pressure fields in several stopper-rod nozzle flow systems during continuous casting, for both water model and real steel caster cases. The Eulerian domain includes a portion of the tundish floor, the stopper-rod, UTN, and SEN nozzle interiors. The following continuity and momentum equations were solved with a Reynolds-Averaged Navier–Stokes (RANS) standard k-ε model for steady flow.

$$\frac{\partial }{\partial {x}_{i}}\left(\rho {u}_{i}\right)=0$$
(31)
$$\frac{\partial }{\partial t}\left(\rho {u}_{i}\right)+\frac{\partial }{\partial {x}_{j}}\left(\rho {u}_{i}{u}_{j}\right)=-\frac{\partial {p}^{*}}{\partial {x}_{i}}+\frac{\partial }{\partial {x}_{j}}\left[\left(\mu +{\mu }_{t}\right)\left(\frac{\partial {u}_{i}}{\partial {x}_{j}}+\frac{\partial {u}_{j}}{\partial {x}_{i}}\right)\right],$$
(32)

where \(\rho \) is fluid density [kg/m3], \({u}_{i}\) is velocity in the 3 coordinate directions [m/s]. \({p}^{*}\) is modified pressure (\({p}^{*}=p+\frac{2}{3}\rho {k}_{r}\)) [Pa], \(p\) is gauge static pressure [Pa], \({k}_{r}\) is an unknown residual kinetic energy [m2/s2], \(\mu \) is dynamic viscosity of the fluid [Pa.s], and \({\mu }_{t}\) is turbulent viscosity [Pa.s]. The details on the calculations of turbulent viscosity, turbulent kinetic energy, \(k\), turbulent dissipation rate, \(\varepsilon \) are similar to those used in previous work.[12] For boundary conditions, inlet area at the top of the UTN (tundish bottom) is a constant-velocity inlet. The nozzle port outlets were assigned as pressure outlets, according to the hydrostatic pressure head at the submergence depth. The refractory walls were assigned standard wall functions, with roughness of 0 (smooth) for the water model. The initial condition, finite-volume cell type and size, solver, and convergence criteria are similar to those used in the previous work[12] and the models are solved using Ansys Fluent.[44] Predictions from this CFD model are compared with PFSR model calculations, as well as water model and plant model measurements when available. Predictions of PFSR are also compared with a similar \(k-\omega \) CFD model by Liu[45] for both water model and plant measurements with System 3.

Verification and Validation of PFSR with Water Model 1 Data

The new PFSR V.2.1 model is first verified with CFD simulations and validated with measurements on a 0.5-scale water model of the Plant 1 caster for the conditions and geometry of System 1 given in Table I. These dimensions and casting conditions are all inputs to the model, except for the tundish height, which is output. Gauge pressure distributions predicted by PFSR with the 2.8 mm stopper-rod opening are compared with 3D CFD simulation profiles in Figure 4. Agreement is reasonable, although there are some differences near the stopper tip, likely due to the flow recirculation there. The chosen flow path from the CFD model through this region experiences more pressure variations than the simple 1D flow path of PFSR V.2.1.

Fig. 4
figure 4

Pressure distribution verification of PFSR with CFD simulation for System 1 conditions at 2.8 mm stopper opening

Full size image

To validate the PFSR V.2.1 model, its predictions are compared with measurements for the System 1 water model of the liquid levels in the tundish and mold for the given system geometry. Casting conditions were the same as given in Table I System 1, except for having a vertical stopper opening of 3.0 mm and tundish height of 272 mm. The results, shown in Figure 5, match very well with the water model data.

Fig. 5
figure 5

Pressure distribution validation of PFSR with measurements for System 1 water model conditions, with 3.0 mm stopper opening

Full size image

Validation of PFSR with Water Model 2 Data

Next, PFSR V.2.1 model predictions are compared with measurements using the 0.6-scale water model of a continuous slab caster with a stopper-rod control system housed at the Colorado School of Mines for conditions in Table I for System 2. These dimensions and casting conditions are all inputs to the model, except for the stopper-rod opening, which is output. As shown in Figure 6, the predicted pressure distribution matches fairly well with the water model pressure measurements. More specifically, the predictions match almost exactly in the SEN. Agreement was not as close in the UTN, where turbulent recirculating flow was observed. The stopper-rod opening calculated by PFSR was 13 mm, which compares with the measured opening of 14 mm.

Fig. 6
figure 6

Pressure distribution validation of PFSR with Colorado School of Mines Water Model for System 2 casting conditions

Full size image

Verification of PFSR with Water Model 3 and Plant 3 Data

Finally, PFSR V.2.1 predictions are verified and validated by both water model and plant measurements[45] for System 3 conditions. Water model 3 is a full 1:1 scale model of the Plant 3 geometry and all of the casting conditions are the same, given in Table I. These dimensions and casting conditions are all inputs to the model, except for the casting speed, which is output (calculated as 0.768 m/min). The stopper-rod opening was 5 mm. Figure 7 compares the pressure distribution calculated with PFSR with that of the 3D CFD model with Fluent from Liu,[45] using the \(k-\omega \) shear-stress transport (\(k-\omega \) SST) turbulence model. The PFSR predictions match fairly well with the CFD simulations. In addition, Figure 7 shows that PRSR matches better with the water model measurements[45] than do the CFD simulation results.[45]

Fig. 7
figure 7

Pressure distribution verification[45] and validation of PFSR with CFD simulation and water model measurements for system 3 conditions

Full size image

Pressure predictions from PFSR V.2.1 and the CFD model are next compared in Figure 8 for the System 3 casting conditions in steel Plant 3. These dimensions and casting conditions are all inputs to the model, except for the casting speed, which is output (calculated as 0.768 m/min). For this case, the stopper-rod opening was fixed to 5 mm again, to match the Liu CFD simulation.[45] The PFSR model predictions match fairly well with the CFD simulations. In addition, the water model measurements are scaled to estimate pressure in the steel caster by multiplying by the steel/water density ratio of 7. Again, the two simulations match reasonably with each other and with the scaled measurements, which again verifies PFSR V.2.1.

Fig. 8
figure 8

Pressure distribution verification of PFSR with CFD simulation[45] for system 3 plant conditions (10 mm stopper opening)

Full size image

Note that in both PFSR V.2.1 and the CFD models, the minimum pressure, which occurs in the narrow gap, is more negative than the gauge pressure of − 101.325 kPa for a perfect vacuum. This means that the predicted absolute pressure is negative. Negative absolute pressures (tension) can be achieved in liquids only under highly controlled circumstances.[46] In the feeding system of a continuous caster, however, it is likely that turbulent flow, the many inclusions, and the rough refractory walls will cause gas species dissolved in the liquid steel to nucleate bubbles and “cavitate” at pressures close to their thermodynamic equilibria, similar to regular degassing operations in secondary steelmaking. Molten iron itself could evaporate and cavitate as well, but owing to its very low absolute vapor pressure (4 Pa), and the relatively high level of dissolved gases present in steel alloys (e.g., 40 ppm) which thus cavitate first, iron evaporation is unlikely. If degassing and cavitation of dissolved gas occurs, then both the CFD and PFSR2.1 models are incorrect in their description of the flow in the stopper-rod gap area.

Finally, the PFSR and CFD model predictions[45] of the flow rate variation with stopper-rod opening are compared in Figure 9 with the water model 3 measurements (with mass flow rate scaled 7-fold) and with actual measurements in the plant 3 steel caster. All casting conditions were input according to Table I, except for casting speed, which was calculated (output) by varying the stopper-rod openings from 0 mm to 17 mm. As expected, the PFSR predictions match well with those of the CFD simulation and with the scaled water model 3 measurements. However, the real steel plant measurements disagree with all three of these sets of data. Even the full-scale water model measurements disagree with the plant 3 measurements. Specifically, a given flow rate in the plant requires a significantly greater stopper opening than measured in the water model, or calculated with the CFD and PFSR models, with all other conditions the same. Clogging could not be an explanation, because the plant measurements involved only calcium-treated steel grades.[45]

Fig. 9
figure 9

Flow rate comparison of PFSR with CFD simulation of steel plan 3, water model 3 (where volumetric water flow is converted to equivalent steel mass flow), and plant 3 measurements.[45]

Full size image

Furthermore, the minimum gauge pressures predicted by PFSR are less than − 101.325 kPa (and therefore conspicuously low) for the entire range of stopper-rod movement from 1 to 17 mm. These findings agree exactly with the previous work by Lui et al.[45] These results confirm that other phenomena must be included into the model in order to capture the flow and pressure behavior in the real steel plant for these conditions.

Other Phenomena in Stopper-Rod Flow

Although PFSR V.2.1 has been verified with CFD simulations (both water model and steel plant) and validated with water model experimental data, its minimum pressure prediction is conspicuously low, (\(P\) < − 101.325 kPa, meaning negative absolute pressure), for steel caster plant 3. As discussed in the previous section, CFD simulations and water model measurements have the same problem. This serious problem arises because there are physical phenomena left out of these models. This section introduces two new phenomena into the model system to overcome this problem: 1) cavitation and 2) non-primed flow/waterfall behavior. Each of these phenomena will be introduced, followed by introduction of a new methodology to implement them into PFSR.

Cavitation

The first phenomenon that would increase the minimum pressure to prevent negative absolute pressure is gas “cavitation.” As the local pressure decreases to become very low, dissolved gases in a liquid will exceed their solubility limits[37,46] to nucleate bubbles in the lowest pressure regions of a flow system.[37] This may also be called “degassing.” In molten steel, dissolved gases, such as nitrogen, hydrogen, and carbon monoxide, may form gas bubbles near the stopper-rod (point 3 in Figure A3) if their solubility limits are exceeded. In a water model, easy sealing of the joints makes it difficult to have gas aspiration and/or leakage. In a real caster, however, the refractory system is often susceptible to leakage, (of either air or argon gas) which may cause re-oxidation defects, and may supply the gas source for non-primed flow, and perhaps alleviate the low pressure needed for cavitation. This likely occurs in the lowest pressure regions, such as the lower portion of the narrow gap between the stopper-rod and the tundish floor. Here, the turbulent flow, inclusions in the steel, and the rough refractory walls likely cause gas bubble nucleation, as previously mentioned. These evolved gas bubbles then may expand in these low-pressure regions, to take up space, causing the stopper-rod opening to increase, (such as observed in Figure 9). Such cavitated bubbles are likely to re-dissolve lower inside the UTN or SEN, where the pressure increases. This re-dissolution step often occurs as a sudden collapse, which may cause erosion of adjacent surfaces,[46] but this erosion behavior was not investigated here.

Solubility of gases in liquid steel

The solubility of gasses such as nitrogen or hydrogen in molten steel is governed by Sieverts' law[47]:

$$k= \frac{{C}_{g}^{2}}{{P}_{g}},$$
(33)

where \({C}_{g}\) is the concentration of gas atoms dissolved in the molten metal, and \({P}_{g}\) is the absolute partial pressure of that gas inside the bubble in equilibrium with the dissolved gas in the adjacent liquid solution. The equilibrium constant for the reaction from dissolved gas to nucleated gas bubble, \(k\), depends on temperature and activation energy according to the classic Arrhenius relation:[48]

$$k= A exp\left(-\frac{{E}_{a}}{RT}\right),$$
(34)

where \(A\) is a fitted constant, \({E}_{a}\) is the activation energy [J/mol], \(R\) is the universal gas constant [8.314 J/mol-K],[49] and \(T\) the absolute temperature [K]. Combining Eq. [33] into Eq. [34] and rearranging, gives

$${\mathit{log}}_{10}{C}_{g} = \frac{{A}^{\prime}}{T}+B+ \frac{1}{2}{\mathit{log}}_{10}\left(\frac{{P}_{g} }{{P}_{atm}}\right),$$
(35)

where \( A^{\prime} \) and \(B\) are empirical constants for a given gas dissolved in a given medium, and \({P}_{g}\) is the absolute partial pressure in the gas bubbles.[50,51,52] For the case of nitrogen gas dissolved in molten steel, Eq. [35] becomes[50]

$${\mathit{log}}_{10}{C}_{N} = 4.0-\frac{255.6}{T}-1.26+ \frac{1}{2}{\mathit{log}}_{10}\left(\frac{{P}_{{N}_{2}} }{{P}_{atm}}\right),$$
(36)

where \({C}_{N}\) is dissolved concentration of nitrogen atoms [ppm], \({P}_{{N}_{2}}\) is the absolute partial pressure of nitrogen [kPa], \({P}_{atm}\) = 101 kPa, \(T\) is temperature [K], and the constant 4.0 is needed to change units from wt pct to wt ppm.

Similarly, for hydrogen[53]

$${\mathit{log}}_{10}{C}_{H}= 4.0-\frac{1905}{T}-1.591+ \frac{1}{2}{\mathit{log}}_{10}\left(\frac{{P}_{{H}_{2}} }{{P}_{atm}}\right),$$
(37)

where \({C}_{H}\) is dissolved atomic hydrogen concentration [ppm], \({P}_{{H}_{2}}\) is the absolute partial pressure of hydrogen [kPa], \({P}_{atm}\) = 101 kPa, \(T\) is temperature [K], and the constant 4.0 is needed to change units from wt pct to wt ppm. Figure 10 shows how the maximum concentrations of nitrogen and hydrogen that can dissolve in the molten steel varies with the absolute partial pressure of the gases at different temperatures.

Fig. 10
figure 10

Gas solubility variation with absolute pressure in molten steel at different temperatures of (a) nitrogen (b) hydrogen.[50,53]

Full size image

Variation of gas/steel flow rate with pressure at different gas contents

Knowing the solubility equations in the previous section and the local pressure, the fraction of the gas cavitated into bubbles, \({C}_{g,cav}\), can be calculated from the total (original) dissolved gas content of the steel, \({C}_{g,total}\), and the remaining (equilibrium) dissolved gas fraction, \({C}_{g,diss}\), from the mass balance:

$${C}_{g,cav}= {C}_{g,total}-{C}_{g,diss}.$$
(38)

The cavitated gas flow rate, \({C}_{g,cav}\), [ppm] becomes non-zero after being supersaturated, when the pressure drops sufficiently that the total dissolved gas content exceeds the equilibrium content from Eq. [35], so that \({P}_{g,diss}\)[absolute kPa] is equal to \({P}_{g,cav}\) [absolute kPa] (assuming only one supersaturated gas in the system). Note that both of these pressures equate to \({P}_{3}\), after multiplying them by 1000 to convert to [Pa] and subtracting \({P}_{atm}\) to convert to gauge pressure. The above equations also require the neglect of nucleation kinetics, which seems reasonable considering the rough refractory surfaces.

The volumetric flow rate of cavitated gas, \(\dot{{V}_{g}}\), [m3/s], is then calculated from the ideal gas law:[49]

$$\dot{{V}_{g}}= \frac{RT{\dot{m}}_{g}}{{M}_{g}{P}_{g,diss}},$$
(39)

where \({M}_{g}\) is the molar mass of the gas [kg/mol], \(R\) is the universal gas constant [8.314 J/mol-K], T is temperature [K], \({P}_{g,diss}\) is the absolute pressure of the dissolved gas after multiplying by 1000 to convert from kPa to Pa, and \(\dot{{m}_{g}}\) is mass flow rate of the cavitated gas [kg/s], found from:

$${\dot{m}}_{g}= {\dot{m}}_{steel}{C}_{g,cav}$$
(40)

in which

$${\dot{m}}_{steel}= {\rho }_{steel}{\dot{V}}_{steel},$$
(41)

where \({\dot{m}}_{steel}\) is molten steel mass flow rate [kg/s], \({\rho }_{steel}\) molten steel density [kg/m3], and \({\dot{V}}_{steel}\) molten steel volumetric flow rate. Substituting Eq. [41] into Eq. [39] gives:

$$\dot{{V}_{g}}= \frac{RT{\rho }_{steel}{\dot{V}}_{steel}{C}_{g,cav}}{{M}_{g}{P}_{g,diss}}.$$
(42)

Finally, the flow rate ratio, \(r\), of cavitated gas and total flow rate in the system, is:

$$r= \frac{\dot{{V}_{g}}}{\dot{{V}_{g}}+{\dot{V}}_{steel}},$$
(43)

where the volumetric steel flow rate, \({\dot{V}}_{steel}\) [m3/s] is given in Eq. [41]. The flow rate ratios calculated with Eq. [43] for both nitrogen and hydrogen are plotted in Figure 11 as a function of local absolute pressure at 1550 °C, for different initial gas contents.

Fig. 11
figure 11

Cavitated gas fraction variation with absolute pressure at different total gas contents at 1550 °C for (a) nitrogen (b) hydrogen

Full size image

Figure 11 shows that above the critical absolute pressure, the cavitation flow rate is naturally zero for all curves (scenarios) plotted. As an example for 10 ppm nitrogen, the absolute pressure in Figure 11(a) must drop below the small value of 0.06 kPa to allow any cavitation. This figure also suggests that flow rate may become unstable near the critical absolute pressure, owing to the significant increase in gas flow over a very narrow absolute pressure range. In all six scenarios, as soon as the absolute pressure drops below the critical absolute pressure, the flow rate ratio approaches 100 pct, so almost all of the original gap area becomes filled with cavitated gas, nitrogen or hydrogen. This would require the stopper-rod to lift to maintain the liquid steel flow rate, with accompanying unstable flow and quality problems.

Primed vs Non-primed Flow

The second phenomenon considered here that would increase the minimum pressure is “non-primed” flow. Two different types of flow are possible in stopper-rod nozzles with or without argon gas injection.[54,55] The first, illustrated in Figure 12(a), is “primed flow” where any gas in the system, such as injected or introduced via leaks through the refractory walls, generates “bubbly flow,” where there is continuous fluid or fluid/gas mixture phase in the system and no gas pockets. Primed flow is able to sustain pressure drops, according to Eq. [1].

Fig. 12
figure 12

Schematic of (a) Primed and (b) Non-primed Flow in Stopper-rod Systems

Full size image

The second flow type is “non-primed” flow, or slug flow, which involves large gas pockets. When argon gas is injected through the stopper tip, the non-primed flow that occurs is called “annular” flow, where molten steel enters the upper UTN through the annular-shaped gap and then flows down along the nozzle walls, while argon gas tends to fill the center of the nozzle cross section.[55] As shown in Figure 12(b), large gas pockets form beneath the stopper top in the central region of the nozzle, which move chaotically with the turbulent flow. Non-primed or annular flow tends to be very unstable and periodic,[55] which likely leads to subsequent problems in mold flow and surface quality problems. Other gas sources include argon injection at other locations, leakage through joints or cracks in the refractory, or even degassing of dissolved elements such as H2, N2, or CO in the molten steel due to the very low pressure in the gap, via cavitation.[46] Non-primed flow can occur along the entire length of the nozzle, depending on the flow conditions. It is most common in local portions of the nozzle, especially near the stopper-rod, where pressure is lowest. It typically transitions to continuous bubbly flow part way down the nozzle, often at a sharp interface, which may wander around. Non-primed flow cannot sustain a pressure change over any significant vertical distance, as it contains a continuous gas phase which quickly flows to alter its shape and maintain a roughly constant pressure within the non-primed volume. This behavior is now implemented into the PFSR model as a new phenomenon.

Cavitation/Non-primed Flow Methodology

To incorporate the cavitation and non-primed flow phenomena described in the previous section, a new version of the model, PFSR V.3.0, is introduced. Gauge pressure predictions below − 101,325 Pa at point 3 are corrected in this version by introducing cavitation, non-primed flow, or both.

First, to introduce cavitation, Eq. [36] is rearranged and applied to calculate the equilibrium critical absolute partial pressure of the given gas (e.g., nitrogen) at the given initial dissolved gas content in the steel, \({P}_{{N}_{2}}\):

$${P}_{{N}_{2}}= {{P}_{atm}\left(\frac{{C}_{N,total}}{{10}^{\left(4 -1.26 - \frac{255.6}{T}\right)}}\right)}^{2},$$
(44)

where \(T\) is always the molten steel temperature of 1823 K and \({C}_{N,total}\) is the total dissolved content of nitrogen in molten steel before cavitation [ppm].

Next, a small amount of cavitation is introduced by setting the minimum gauge pressure in the system (at point 3) to slightly below the critical pressure, (as an initial guess). The new equilibrium gas pressure, also called the cavitated gas pressure or \({P}_{cav}\) [Pa], is then given as a gauge pressure and is calculated from

$${P}_{cav} =\left( {P}_{{N}_{2}}-p-{P}_{atm} \right),$$
(45)

where \({P}_{cav}\) is the cavitation pressure [Pa gauge], \(p\) [absolute kPa] is the small pressure difference (increase) from the actual pressure where cavitated gas is evolved, to the critical pressure where the gas is all dissolved at equilibrium, \({P}_{{N}_{2}}\)[absolute kPa], and \({P}_{atm}\) is the atmospheric pressure [kPa]. Finally, all terms on the right-hand side are multiplied by 1000 to convert to [Pa].

The nitrogen that remains dissolved in the molten steel at the new \({P}_{3}\) gauge pressure, \({P}_{cav}\), is calculated using Eq. [36] replacing \({C}_{N}\) with \({C}_{N,diss}\), the remaining dissolved nitrogen content, and also replacing \({P}_{{N}_{2}}\) with \({P}_{cav}\), (after converting to kPa, and to absolute pressure by adding \({P}_{atm}\) ).

Now the cavitated amount of gas can be calculated using Eq. [38]. Then the cavitated gas flow rate, \(\dot{{V}_{{N}_{2}}}\), and the flow rate ratio, \(r\), are determined using Eqs. [42] and [43]). The minimum gauge pressure [Pa] in the system, found in the gap, \({P}_{3}\), is always physically reasonable, at \({P}_{cav}\). The cavitated gas flow takes up some of the minimum gap area, which requires the stopper-rod to lift up in order to increase the gap area and maintain the molten steel flow rate.

Next, to implement the possibility of the non-primed flow situation shown in Figure 12(b), the governing Bernoulli equations of PFSR V.2.1 (Eqs. [2 through 12]) are modified for the 10 points shown in Figure 13. These changes include:

  1. 1)

    liquid density is used everywhere except in the gap, where Eqs. [3] and [4] are used, in which due to cavitation, even without argon gas injection, there is a mixture density (Eq. 16),

  2. 2)

    at point 4, the flow expands to reach its maximum cross-sectional area, with velocity decreased to \({V}_{4}\), which is a new unknown.

  3. 3)

    the gauge pressure at point 4 is set equal to the gauge pressure at point 5 instead of using Eq. [5]. This is because pressure inside the gas pocket can quickly equilibrate to remain relatively constant, owing to the continuous gas phase in this region.

  4. 4)

    the velocity at point 5, \({V}_{5}\), is readily calculated from \({V}_{4}\), by setting the gauge pressure at points 4 and 5 equal in Bernoulli Eq. [5], leading to

    $${V}_{5}= \sqrt{{V}_{4}^{2}+2g{h}_{air}}$$
    (46)
Fig. 13
figure 13

Schematic of flow and pressure points in the waterfall methodology

Full size image

in which \({h}_{air}\) is the gas pocket height [m]. The gas source for the gas pocket is leakage in the current systems studied, although bubble coalescence is another mechanism in systems with argon gas injection.

The new cavitation/non-primed flow methodology introduces three new variables into the model system: the cavitation pressure, \({P}_{cav}\), the velocity at point 4, \({V}_{4}\), and the gas pocket height, \({h}_{air}\). Together with the 10 gauge pressures at the 10 points, and the single missing casting condition of the original PFSR 2.1 model (usually the stopper-rod opening), this gives 14 unknowns total in the general system.

The new methodology also introduces a new constraint equation, which ensures that the minimum gauge pressure in the gap at point 3, \({P}_{3}\), is equal to \({P}_{cav}\) of the cavitated gas:

$${F}_{2} ={P}_{4}- \frac{1}{2}{\rho }_{m}{{V}_{3}}^{2}+\frac{1}{2}{\rho }_{m}{{V}_{UTNa}}^{2}+ {\Delta P}_{L,exp}- {P}_{cav},$$
(47)

where \({F}_{2}\) is the error. Recall that the first constraint equation is Eq. [30], which ensures that the pressure at the top surface, liquid level in the tundish, \({P}_{1}\), is zero gauge pressure. Together with the 10 pressure equations, (one for each of the 10 points, Eqs. [2] through [11]), the two constraint equations, \({F}_{1}\) and \({F}_{2}\) = 0 gives 12 equations total.

Having 14 unknowns and 12 equations means that to find a unique solution, two extra degrees of freedom must be specified. Specifically, any two from the following list of choices can be input: the missing casting condition (so that all casting conditions are provided, including stopper-rod opening), air pocket height, velocity at point 4, cavitation gauge pressure, or any other gauge pressure in the system (i.e., pressure at points 2,5-9, such as from a plant measurement).

Next, to start the solution procedure, initial guesses must be provided for \({h}_{air}\), \({V}_{4}\), and \({P}_{cav}\). When appropriate, this is achieved in part by making an initial guess for \(p\) and evaluating Eq. [45]. Finally, the 12 equations are solved simultaneously (for the 10 gauge pressures and 2 remaining unknowns from the list above), using FSOLVE in PFSR V.3.0, which iterates until the errors in satisfying the constraint equations are very close to zero.

Application of Cavitation/Non-primed Flow Model

Having introduced the new cavitation/non-primed flow methodology, PFSR V.3.0 is applied in the next section to investigate stopper flow systems at two real commercial steel plants (3 and 4), which use System 3 and 4, respectively, for conditions given in Table I. For the simulations involving cavitation in both plants, a reasonable total nitrogen concentration in molten steel of 40 ppm is assumed for the initial dissolved concentration of nitrogen, based on the previous literature.[56]

Application to System 3

The new PFSR V.3.0 with cavitation and non-primed flow is applied here to simulate the conditions of System 3 at Plant 3, which was already investigated with PFSR V.2.1 in Section III D. To obtain a unique solution, steel plant measurements of 1) stopper-rod opening and 2) gauge pressure beneath the stopper-rod tip were input to PFSR V.3.0 to provide the necessary values for the two extra degrees of freedom in this model.

First, the flow rate relation with stopper-rod opening distance for System 3 was used to calibrate PFSR V.3.0 to match the measurements, as shown in Figure 14. This provides the first extra equation needed, which was accomplished for 3 different cases of stopper opening and flow rate.

Fig. 14
figure 14

Flow rate—stopper-rod opening relation for calibration of cavitation / non-primed flow methodology—System 3, adding PFSR V.3.0 to Fig. 9

Full size image

Second, the back pressure in the gas line feeding argon (at negligible flow rate) into the upper tundish nozzle was measured in the real caster to be − 67,000 Pa (gauge pressure).[45] Considering the capillary pressure exiting the refractory pores, (\(\Delta P= \frac{2\sigma }{{r}_{pore}}\))[57] for a pore radius of ~100 micron, and argon/molten steel surface tension of 1.157 N/m,[57] this corresponds to an estimated gauge pressure inside the nozzle, \({P}_{4,Meas}\), which was − 79,000 Pa gauge,[45] This pressure likely corresponds to the entire air pocket region, where pressure is relatively uniform. This provides the second extra equation required by PFSR V.3.0. In order to enforce the gauge pressure at point 4 to this value, a new constraint equation is introduced:

$${F}_{3} ={P}_{4}- {P}_{4,Meas},$$
(48)

where \({F}_{3}\) is the error to be minimized (as close as possible to zero). Together with constraint Eqs. [30, 47], and the 10 gauge pressure Eqs. [2 through 11], this gives 13 equations.

Now, having 13 equations and 13 unknowns, these System 3 cases each have a unique solution, which are shown in Figure 15. Cavitation is predicted in all 3 cases. The calculated minimum gauge pressure in the nozzle, the cavitation gauge pressure, is − 100,365, − 100,357, and − 100,353 Pa, for the 3 cases, which are all above absolute vacuum, so the model predictions are now more realistic.

Fig. 15
figure 15

Pressure distribution for different openings using cavitation/non-primed flow methodology (PFSR V.3.0 system 3 conditions)

Full size image

The inset in Figure 15 contains extra columns for the other two results: velocity at point 4 and air pocket height. Note that air pockets are predicted for all cases, as the cavitated gas alone is insufficient to satisfy equilibrium of the system. Air pocket height is predicted to increase (from 223.5 mm to 513.3 mm) as stopper-rod opening increases. Naturally, the velocity at point 4 and the pressure drop per unit length in the lower nozzle both increase as flow rate increases. Thus, the new model can reasonably explain the pressure and flow conditions in this steel caster.

Application to System 4

Next, for System 4 at steel Plant 4, measurements of stopper-rod opening for a given flow rate are available to provide an equation/constraint for only one of the two extra unknowns (giving 12 equations and 13 unknowns). Therefore, there is still one degree of freedom needed for a unique solution. This is handled here by performing a parametric study on one variable: the air pocket height.

First, similar to System 3, PFSR V.3.0 was calibrated to match the plant measurements of stopper-rod opening and flow rate in commercial caster 4 for System 4, as shown in Figure 16. Owing to the extra degree of freedom remaining: each simulated point on this graph represents results for several different air pocket heights.

Fig. 16
figure 16

Steel flow rate–stopper-rod relation for calibration of cavitation/non-primed flow methodology (PFSR V.3.0)—system 4 conditions

Full size image

As an example, for the stopper-rod opening of 1 mm (and 0.28 tonne per minute or 0.28 t/min), the air pocket height is treated as a known parameter to generate unique solutions, while solving for the other unknowns: cavitation gauge pressure, velocity at point 4, and the 10 gauge pressures. Four possible pressure distributions are shown in Figure 17 for this 1 mm stopper-rod opening condition. Note that this very low flow rate is for illustration purposes only.

Fig. 17
figure 17

Pressure distribution comparison of different solutions for [1 mm stopper-rod opening, 0.28 t/min flow rate] using cavitation/ non-primed flow methodology (PFSR V.3.0)—system 4 conditions

Full size image

Figure 17 shows that a wide range of air pockets are possible for this condition. This includes a potential solution with almost no air pocket height (i.e., only cavitation). At the other extreme, the maximum air pocket height possible is 978 mm, which comprises most of the lower nozzle. Note that cavitation is predicted for all cases, with the same cavitated gas flow rate of 6.31 × 10−4 m3/s and minimum gauge pressure in the gap, \({P}_{3}\), of − 100,314 Pa. The velocity at point 4 depends on the assumed air pocket height and ranges from 0.9 to 5.3 m/s.

A second parametric study on air pocket height is shown in Figure 18, for a more typical operational condition of 10 mm stopper-rod opening and 2.8 t/min flow rate. The possible air pocket height in this situation ranges from 410 mm to 1111 mm. For all four cases in this figure, the cavitated gas flow rate is 6.8 × 10−3 m3/s and the minimum gap gauge pressure, \({P}_{3}\), is − 100,315 Pa. The velocity at point 4 varies with air pocket height from 4 to 5.6 m/s. Note that the slope of the pressure plot in the lower SEN increases with increasing velocity at point 4 (decreasing air pocket height), which is due to the increasing flow resistance of the tapered lower SEN, which has a beaver tail shape.

Fig. 18
figure 18

Pressure distribution comparison of different solutions for [10 mm stopper-rod opening, 2.8 t/min flow rate] using PFSR V.3.0—system 4 conditions

Full size image

Other runs of PFSR V.2.1 indicate negative absolute pressures (less than a perfect vacuum) for all tundish heights above 700 mm. Based on all cases for all systems investigated here, it seems that cavitation and/or gas pocket formation occurs in most commercial casters with stopper-rod flow-control systems. The new PFSR V.3.0 application can reveal new insights, such as these, into the real flow behavior and pressure profiles in commercial steel casters. Further work is needed to improve this initial implementation of cavitation and non-primed flow into this pressure-flow rate model.

Conclusions

This work presents a new, standalone, user-friendly MATLAB-based graphical user interface program, Pressure drop and Flow rate in Stopper-Rod systems (PFSR). The new model solves a one-dimensional system of Bernoulli equations for the pressure distribution and flow rate in stopper-rod nozzle systems for argon-molten steel flow systems including argon gas expansion (varies locally with pressure). The PFSR V.2.1 model has been verified with CFD simulations and validated with measurements in water models of continuous casters with stopper-rod metal delivery systems. The maximum error associated with these cases is approximately 8 pct.

To overcome predictions of negative absolute pressure, which occurred in CFD models and PFSR V.2.1 simulations for all of the real steel casters studied, an improved version of PFSR, V.3.0, is introduced, which includes the phenomena of cavitation and non-primed flow. This methodology introduces two more degrees of freedom, so in order to find a solution: two other variables must be fixed. The two variables can be chosen from the list below:

  • Air pocket height

  • Velocity at maximum expansion point after minimum gap area

  • Cavitation pressure (gauge)

  • Any (other) gauge pressure measured (in the plant)

  • Any one extra of the casting conditions: tundish level height, stopper-rod opening height, argon injection rate, and molten steel flow rate, (or casting speed/width/thickness)

Fixing any two of the above choices enables PFSR V.3.0 to find a unique solution. Fixing one variable according to a plant measurement and running parametric studies on the other variable (as needed) to explore the solution space is another reasonable way to apply the current model, as demonstrated here.

For two special stopper-rod flow systems, PFSR V.3.0 is applied to capture the real physics in the steel plant. It is observed that in System 3, a unique solution is possible. However, for System 4, there is still one degree of freedom, so multiple solutions are presented.

Finally, cavitation is shown to be a phenomenon that likely happens in most commercial casters with stopper-rod flow-control systems, along with the possibility of air pocket formation in some portion of the nozzle. The model system PFSR V.3.0 is ready to apply in future work to investigate pressure drops and flow rates in many real continuous casting systems with stopper-rod flow-control systems. Further work is needed when cavitation and/or non-primed flow are present.