Introduction

Macrosegregation in continuous casting blooms is a key problem that has prevented the wider application of high-quality steel.[1] Many researchers[2,3,4,5] have a long-term commitment to reducing macrosegregation. Such investigations help create improved production processes for continuous casting blooms, enabling the manufacture rolled production products free from defects induced by macrosegregation. At present, electromagnetic stirring (EMS)[6] has been shown to be one of the most effective countermeasures to reduce macrosegregation in continuous casting blooms, particularly when a combination of EMS modes is utilized.[7]

In the 1950s, Junghans and Schaaber[8] first successfully applied mold electromagnetic stirring (M-EMS) in a continuous casting process. As important successors in this field, Alberny et al.[9] from Institut de Recherches de la Siderurgie Francais (IRSID) and Compagnie Electromecanique (CEM) carried out many experiments on industrial applications, which provided a solid theoretical foundation for the subsequent development of M-EMS. Since the 1980s, many researchers[10,11,12,13] have made significant contributions to the physical experiments of M-EMS in continuous casting processes. With the enhancement of computing capabilities, numerical simulations have been increasingly widely used to discover the theoretical mechanism and process parameters of M-EMS. Spitzer et al.[14] presented a three-dimensional model to simulate the effects of different stirring parameters on fluid flow. This model was developed by coupling the continuity equation, the Maxwell equations, and the Navier–Stokes equations. Natarajan and El-Kaddah[15] used a three-dimensional EMS model to investigate the electromagnetic and flow phenomena in continuous casting billets and slabs. The authors of the current study[16] developed a 3D mathematical model by coupling the electromagnetic field, fluid flow, heat transfer, and inclusion trajectory to research the influence of EMS on the multiphase flow phenomena in round billet continuous casting molds. The results showed that the solidification structure, various surface/internal defects, central carbon segregation, and porosity were improved by M-EMS. Hou et al.[17] used a cellular automaton-finite element coupling model to simulate the solidification structure evolution during M-EMS. The relationship between the compactness degree of the central equiaxed grain zone with different process parameters was shown. Yang et al.[18] devised a model that coupled the magnetic field, flow field, and temperature field by using a two-stage simulation. They found that increasing the equiaxed crystal ratio substantially improved the carbon macrosegregation index.

However, up to this point, it was found that M-EMS could not significantly improve the macrosegregation in continuous casting blooms. Therefore, researchers subsequently proposed final EMS (F-EMS), which could stir the high-viscosity molten steel at the solidification end with a higher current and frequency than M-EMS. Kunstreich et al.[19] first realized the combination of M-EMS and F-EMS at Rotelec and Kobe Steel. Afterwards, this combination of EMS modes (referred to hereinafter as “combined EMS”) has been widely researched for improving the internal porosity and macrosegregation in continuous casting processes. Based on laboratory experiments and plant trials, many researchers[20,21,22] have investigated combined EMS to improve the internal quality of continuous casting strands. Zhai et al.[23] investigated the influence of combined EMS modes on the solidification structure and macrosegregation in continuous casting blooms through a series of plant trials. Sun et al.[24] used a coupled mathematical model to investigate the influence of different combined EMS modes on macrosegregation, thereby providing a clearer understanding of the corresponding turbulent fluid flow, heat, and solute transport. They found that the fluid flow velocity and solidification time of the steel melt are two important elements to determine the installation position of the final electromagnetic stirrer. The authors of the current study[25] proposed a multiphase solidification model by taking into account the electromagnetic field to investigate the solidification structure and macrosegregation in the continuous casting processes.

Although there has been much experimental and theoretical analysis of the solidification behavior with M-EMS and F-EMS in continuous casting processes, the synergetic effect between M-EMS and F-EMS in the combined EMS process has not been systemically investigated. In the present work, based on the volume-averaged Eulerian approach, a 3D multiphase solidification model coupling the electromagnetic field, flow field, microstructural evolution, and solute transport was established to investigate the macrosegregation in heavy-rail steel blooms with different EMS processes. In this model, by coupling Maxwell’s equations and the hybrid model of the mushy zone into the calculation of the Navier–Stokes equations, an accurate description of solute transport in heavy-rail steel blooms with electromagnetic stirring is realized. By applying an electromagnetic field at different positions of the continuous caster, a numerical simulation of combined EMS is researched, and the synergetic effect between M-EMS and F-EMS in the combined EMS is further revealed. To validate the multiphase solidification model, the magnetic induction intensity, macrostructure, and macrosegregation are verified with Tesla meter measurements, etched macrostructure analysis, and infrared carbon-sulfur analysis.

Numerical Model

Description of the Multiphase Solidification Model

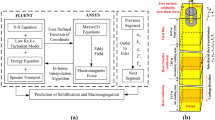
The multiphase solidification model is described in detail in Figure 1. In this model, the macrosegregation in a continuous casting bloom with an electromagnetic field was calculated by solving the mass, momentum, energy, and solute conservation equations.

Fig. 1
figure 1

Description of the multiphase solidification model

Full size image

The modifications to the general conservation equations are as follows. The dynamic dendrite growth model was added to the source term of the mass transfer model to simulate the microstructural evolution in the continuous casting process. By introducing a hybrid model for the mushy zone into the source term of the momentum transfer model, the fluid flow in the mushy zone was simulated. The calculation accuracy of macrosegregation was improved by considering the back-diffusion model in the source term of the solute transfer model.

General Conservation Equations

Basic assumptions of the multiphase model

In the present work, some assumptions have been proposed to simplify the multiphase solidification model.

  1. (1)

    Because the magnetic Reynolds number (0.01) is small,[26] the change in the magnetic field caused by the melt flow is neglected.

  2. (2)

    To address the buoyancy term caused by the temperature difference, the Boussinesq hypothesis[27] is used in the numerical calculation of the natural convection heat transfer.

  3. (3)

    It is assumed that the solidification structure in the continuous casting process consists of columnar, equiaxed, and liquid phases. The interdendritic melt phase of columnar dendrites and solid phase of columnar dendrites constitute the columnar phase. The interdendritic melt phase of equiaxed grains and solid phase of equiaxed grains constitute the equiaxed phase. The phase fraction relationships between each phase are as follows[28]:

    $$ f_{l} + f_{e} + f_{c} = 1 $$
    (1)
    $$ f_{e} = f_{e}^{i} + f_{e}^{s} ,\,f_{c} = f_{c}^{i} + f_{c}^{s} $$
    (2)
    $$ f_{e} c_{e} = f_{e}^{i} c_{e}^{i} + f_{e}^{s} c_{e}^{s} ,\,f_{c} c_{c} = f_{c}^{i} c_{c}^{i} + f_{c}^{s} c_{c}^{s} $$
    (3)

    where the subscripts l, e, and c represent the liquid, equiaxed, and columnar phases, respectively; f and c are the phase fraction and solute concentration of each phase, respectively; \( f_{\text{e}}^{i} \) and \( c_{\text{e}}^{i} \) are the phase fraction and solute concentration of the interdendritic melt phase of the equiaxed phase, respectively; \( f_{\text{e}}^{\text{s}} \) and c se are the phase fraction and solute concentration of the solid phase of the equiaxed phase, respectively; \( f_{\text{c}}^{i} \,{\text{and}}\,c_{\text{c}}^{i} \) are the phase fraction and solute concentration of the interdendritic melt phase of the columnar phase, respectively; and \( f_{\text{e}}^{s} \,{\text{and}}\,c_{\text{e}}^{s} \) are the phase fraction and solute concentration of the solid phase of the equiaxed phase, respectively.

  4. (4)

    On the macroscopic scale, the transport characteristics of other elements (Si, Mn, P, and S) are similar to those of the carbon elements,[29] so the macrosegregation behavior of only the carbon elements is taken into account in this manuscript.

Electromagnetic model

The electromagnetic field produced by the alternating current in the induction coil during EMS is the induction field of the near-field source. Figure 2 shows a geometric model of the mold electromagnetic stirrer and final electromagnetic stirrer. In this work, the winding types of the mold electromagnetic stirrer and final electromagnetic stirrer are different. The design parameters are shown in Table I. The concentrated winding type is used for the mold electromagnetic stirrer, as shown in Figure 2(a). Due to the high viscosity of the molten steel at the solidification end, the Cramer winding type is used for the final electromagnetic stirrer to obtain greater magnetic induction intensity, as shown in Figure 2(b).

Fig. 2
figure 2

Geometric models of the (a) mold electromagnetic stirrer and (b) final electromagnetic stirrer

Full size image
Table I Design Parameters of the Mold Electromagnetic Stirrer and Final Electromagnetic Stirrer
Full size table

The EMS process is simulated by Maxwell’s equations, which are composed of four equations[6]: the Gauss electric field law describing static electricity, the Gauss magnetic field law describing static magnetism, the Faraday law describing magnetoelectricity, and the Ampere–Maxwell law describing electromagnetism. Maxwell’s equations are expressed as follows:

$$ \nabla \cdot \vec{D} = \rho_{\text{elec}} $$
(4)
$$ \nabla \cdot \vec{B} = 0 $$
(5)
$$ \nabla \times \vec{E} = - \frac{{\partial \vec{B}}}{\partial t} $$
(6)
$$ \nabla \times \vec{H} = \vec{J} $$
(7)

Then, the equation for calculating the electromagnetic force is obtained as follows[16]:

$$ \vec{F}_{\text{EMS}} = 0.5 \cdot {\text{Re}} \cdot \left( {\vec{J} \times \vec{B}^{*} } \right) $$
(8)

where \( \vec{D} \) is the electric displacement vector, \( \vec{B} \) is the magnetic induction intensity, \( \vec{E} \) is the electric field intensity, \( \vec{H} \) is the magnetic field intensity, ρelec is the electric charge density, \( \vec{J} \) is the current density, \( \vec{F}_{\text{EMS}} \) is the time averaged electromagnetic volume force in M-EMS or F-EMS, Ra is the real part of the complex number, and \( \vec{B}^{*} \) is the conjugate complex number of \( \vec{B} \).

Mass transfer model

The mass conservation equations are expressed as follows:

$$ \frac{{\partial \left( {\rho_{\text{l}} f_{\text{l}} } \right)}}{\partial t} + \nabla \cdot \left( {f_{\text{l}} \rho_{\text{l}} \vec{v}_{\text{l}} } \right) = - \,S_{\text{le}} - S_{\text{lc}} $$
(9)
$$ \frac{{\partial \left( {\rho_{\text{c}} f_{\text{c}} } \right)}}{\partial t} + \nabla \cdot \left( {f_{\text{c}} \rho_{\text{c}} \vec{v}_{\text{c}} } \right) = S_{\text{lc}} + S_{\text{ce}} $$
(10)
$$ \frac{{\partial \left( {\rho_{\text{e}} f_{\text{e}} } \right)}}{\partial t} + \nabla \cdot \left( {f_{\text{e}} \rho_{\text{e}} \vec{v}_{\text{e}} } \right) = S_{\text{le}} - S_{\text{ec}} $$
(11)
$$ \frac{{\partial \left( {\rho_{\text{c}} f_{\text{c}}^{\text{s}} } \right)}}{\partial t} + \nabla \cdot \left( {f_{\text{c}}^{\text{s}} \rho_{\text{c}} \vec{v}_{\text{c}} } \right) = S_{\text{c}}^{\text{s}} $$
(12)
$$ \frac{{\partial \left( {\rho_{\text{e}} f_{\text{e}}^{\text{s}} } \right)}}{\partial t} + \nabla \cdot \left( {f_{\text{e}}^{\text{s}} \rho_{\text{e}} \vec{v}_{\text{e}} } \right) = S_{\text{e}}^{\text{s}} $$
(13)

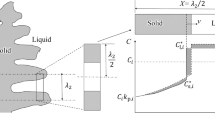
where ρ and \( \vec{v} \) are the densities and the velocity vectors of each phase, respectively. Figure 3 shows a schematic diagram of the growth mechanisms of columnar dendrites and equiaxed grains in the continuous casting process, which are taken into account in the mass transfer source terms: \( S_{\text{le}} ,S_{\text{lc}} ,S_{\text{ce}} ,S_{\text{c}}^{\text{s}} ,{\text{ and}}\,S_{\text{e}}^{\text{s}} \). These source terms are described in the following sections.

Fig. 3
figure 3

Schematic diagram of the growth mechanisms of columnar dendrites and equiaxed grains in the continuous casting process

Full size image

Sle is the mass transfer rate between the liquid and equiaxed phases, which is expressed as follows:

$$ S_{\text{le}} = v^{\prime}_{\text{e}} A^{\prime}_{\text{e}} \rho_{\text{e}} = \left( {I_{\text{s}}^{\text{e}} v_{\text{e}} } \right)\left( {n_{\text{e}} 4\pi R_{\text{e}}^{2} f_{\text{l}} } \right)\rho_{\text{e}} $$
(14)

where \( v^{\prime}_{e} \,{\text{and}}\,v_{e} \) are the average interfacial growth velocity and dendritic tip growth velocity of the equiaxed grains, respectively, which are calculated by the Lipton–Glicksman–Kurz (LGK) model[30]; \( A^{\prime}_{\text{e}} \) is the local interfacial area concentration of unit grains; \( I_{\text{s}}^{\text{e}} \) is the shape factor; ne is the density of the equiaxed grains; and Re is the radius of the equiaxed grains.

Slc is the mass transfer rate between the liquid and columnar phases, which is expressed as follows:

$$ S_{\text{lc}} = v^{\prime}_{\text{c}} A^{\prime}_{\text{c}} \rho_{\text{c}} + i\vec{S}^{\prime}_{\text{c}} = \left( {I_{\text{s}}^{\text{c}} v_{\text{c}}^{ \sec } } \right)\left( {{{2\pi R_{\text{c}} f_{\text{l}} } \mathord{\left/ {\vphantom {{2\pi R_{\text{c}} f_{\text{l}} } {\lambda_{ 1}^{2} }}} \right. \kern-0pt} {\lambda_{ 1}^{2} }}} \right)\rho_{\text{c}} + iv_{\text{c}}^{\text{pri}} n_{\text{c}} \pi R^{\prime}_{\text{c}} \rho_{\text{c}} f_{\text{l}} $$
(15)

where \( v^{\prime}_{c} ,v_{c}^{\text{pri}} ,{\text{ and}}\,v_{c}^{\sec } \) are the average interfacial growth velocity, primary dendritic tip growth velocity, and secondary dendritic tip growth velocity of the columnar dendrites, which are determined by the Kurz–Giovanola–Trivedi (KGT)[31] and LGK models, respectively; \( A^{\prime}_{c} \) is the local interfacial area concentration of unit dendrites; i is the element index, which would be explained in more detail later in this manuscript; \( \vec{S}_{c}^{'} \) is the mass transfer rate of the dendritic tip; \( I_{s}^{c} \) is the shape factor; \( R_{c} \,{\text{and}}\,R^{\prime}_{c} \) are the radii of the dendritic trunk and dendritic tip, respectively; nc is the density of the columnar dendrites; and λ1 is the primary dendritic arm spacing.[25]

Sce is the mass transfer rate between the columnar and equiaxed phases and is neglected in this manuscript. \( S_{c}^{s} \) is the mass transfer rate between the interdendritic melt and solid phase of the equiaxed phase, which is expressed as follows:

$$ S_{e}^{s} = v_{e}^{s} A_{e}^{s} \rho_{e} = \frac{{2D_{l} \left( {c_{l}^{*} - c_{s}^{e} } \right)}}{{\beta \lambda_{2} f_{e}^{s} \left( {c_{l}^{*} - c_{s}^{*} } \right)}} \cdot \frac{{2f_{e}^{s} f_{e} }}{{\lambda_{2} }}\rho_{e} $$
(16)

where \( v_{e}^{s} \) is the interfacial growth velocity between the interdendritic melt phase and solid phase of equiaxed grains; \( A_{e}^{s} \) is the local area concentration of the interfacial surface area; Dl is the diffusion coefficient of the liquid phase; β is a constant; \( c_{l}^{*} \,{\text{and}}\,c_{s}^{*} \) are the equilibrium concentrations of the interdendritic melt phase and solid phase, respectively; and λ2 is the secondary dendritic arm spacing.[32]

\( S_{e}^{s} \) is the mass transfer rate between the interdendritic melt and solid phase of the columnar phase, which is expressed as follows:

$$ S_{c}^{s} = v_{c}^{s} A_{c}^{s} \rho_{c} + i\vec{S}^{\prime}_{c} = \frac{{2D_{l} \left( {c_{l}^{*} - c_{s}^{c} } \right)}}{{\beta \lambda_{2} f_{c}^{s} \left( {c_{l}^{*} - c_{s}^{*} } \right)}} \cdot \frac{{2f_{c}^{s} f_{c} }}{{\lambda_{2} }}\rho_{c} + iv^{\prime}_{c} n_{c} \pi R^{\prime}_{c} \rho_{c} f_{l} $$
(17)

where \( \nu_{c}^{s} \) is the interfacial growth velocity between the interdendritic melt phase and solid phase of the columnar dendrite and \( \nu_{c}^{s} \) is the local area concentration of the interfacial surface area in the columnar dendrite.

Momentum transfer model

The momentum conservation equations are expressed as follows:

$$ \frac{\partial }{\partial t}\left( {f_{l} \rho_{l} \vec{v}_{l} } \right) + \nabla \cdot \left( {f_{l} \rho_{l} \vec{v}_{l} \vec{v}_{l} } \right) = f_{l} \vec{F}_{\text{EMS}} - f_{l} \nabla P + \nabla \cdot \left( {f_{l} \left( {\mu_{l} + \mu_{t,k} } \right)\left( {\nabla \cdot \vec{v}_{l} + \left( {\nabla \cdot \vec{v}_{l} } \right)^{T} } \right)} \right) + \vec{F}_{T}^{l} + \vec{F}_{C}^{l} + \vec{V}_{cl} + \vec{V}_{el} $$
(18)
$$ \frac{\partial }{\partial t}\left( {f_{e} \rho_{e} \vec{v}_{e} } \right) + \nabla \cdot \left( {f_{e} \rho_{e} \vec{v}_{e} \vec{v}_{e} } \right) = f_{e} \vec{F}_{\text{EMS}} - f_{e} \nabla P + \nabla \cdot \left( {f_{e} \left( {\mu_{e} + \mu_{t,k} } \right)\left( {\nabla \cdot \vec{v}_{e} + \left( {\nabla \cdot \vec{v}_{e} } \right)^{T} } \right)} \right) + \vec{F}_{T}^{e} + \vec{F}_{C}^{e} + \vec{F}_{u} + \vec{V}_{le} + \vec{V}_{ce} $$
(19)

where P is the pressure; μ is the viscosity of each phase[33]; μt,k is the turbulent viscosity[28]; \( \vec{F}_{T}^{l} \), \( \vec{F}_{C}^{l} \), \( \vec{F}_{T}^{e} \) and \( \vec{F}_{C}^{e} \) are the source terms related to solute buoyancy and thermal buoyancy in the liquid and equiaxed phases; \( \vec{F}_{u} \) is a matching function related to the fraction of the equiaxed phase in the mushy zone; and \( \vec{V}_{\text{ce}} \) and \( \vec{V}_{\text{el}} \) are the momentum exchange terms between each phase, which can be found in a previous work by the authors of the current study.[25]

In this manuscript, a hybrid model proposed by Ilegbusi[34,35] was introduced into the multiphase solidification model to more accurately describe the fluid flow in the mushy zone. In Eq. [18], \( \vec{V}_{\text{cl}} \) is the momentum exchange term between the columnar and liquid phases, which is described in detail below.

$$ \vec{V}_{\text{cl}} = \left\{ {\begin{array}{ll} {K_{\text{lc}} \left( {\vec{v}_{\text{l}} - \vec{v}_{\text{c}} } \right)} & {f_{\text{l}} \le f_{\text{cri}} } \\ 0 & {f_{\text{l}} > f_{\text{cri}} } \\ \end{array} } \right. $$
(20)

where Klc is the permeability of the mushy zone and fcri is the critical liquid fraction, which varies from 0.70 to 0.91.[36] For heavy-rail steel blooms, fcri is 0.74 in this manuscript, which should be reasonable because the equivalent packing density of perfectly spherical austenite particles with a face-centered cubic structure is 0.74.[34]

If fl is smaller than fcri, the mushy zone is treated as a porous medium. The permeability Klc is calculated with Eq. [21].

$$ K_{lc} = \frac{{f_{l}^{3} }}{{kS_{0}^{2} \left( {1 - f_{l} } \right)^{2} }} $$
(21)

where k is the Kozeny–Carman (KC) constant. Note that k is set to 5 in the standard KC model, which is not suitable for describing the fluid flow in the mushy zone; hence, considering the effect of the dendritic structure on permeability, k is set to 1 in this study.[37] Assuming that the dendritic interface concentration (S0) is equal to the specific surface area of a uniform sphere with a diameter equal to the secondary dendrite arm spacing, S0 is set to 6/λ2. Next, the permeability Klc in Eq. [21] is rewritten as follows:

$$ K_{\text{lc}} = \frac{{\lambda_{2}^{2} \cdot f_{\text{l}}^{3} }}{{36\left( {1 - f_{\text{l}} } \right)^{2} }} $$
(22)

If fl is larger than fcri, the mushy zone is treated as a semi-slurry system, and the liquid viscosity in the mushy zone is written as follows[34]:

$$ \mu_{\text{l}} = m\left| {0.5\left( {\Delta :\Delta } \right)^{0.5} } \right|^{n - 1} $$
(23)

where ∆:∆ is the dyadic product of the deformation tensor rate and m and n are the empirical coefficients, which are defined by the following equations:

$$ m = \exp \left( {9.783f_{s} + 1.435} \right) $$
(24)
$$ n = 0.105 + 0.41f_{s} $$
(25)

Heat transfer model

The energy conservation equations are expressed as follows:

$$ \frac{\partial }{\partial t}\left( {f_{\text{l}} \rho_{\text{l}} H_{\text{l}} } \right) + \nabla \cdot \left( {f_{\text{l}} \rho_{\text{l}} \vec{v}_{\text{l}} H_{\text{l}} } \right) = \nabla \cdot \left( {f_{\text{l}} k^{*} \left( {\nabla \cdot T_{\text{l}} } \right)} \right) - H^{P} \left( {S_{\text{le}} + S_{\text{lc}} } \right) - H^{*} \left( {2T_{\text{l}} - T_{\text{e}} - T_{\text{c}} } \right) $$
(26)
$$ \frac{\partial }{\partial t}\left( {f_{\text{e}} \rho_{\text{e}} H_{\text{e}} } \right) + \nabla \cdot \left( {f_{\text{e}} \rho_{\text{e}} \vec{v}_{\text{e}} H_{\text{e}} } \right) = \nabla \cdot \left( {f_{\text{e}} k^{*} \left( {\nabla \cdot T_{\text{e}} } \right)} \right) + H^{P} S_{\text{le}} + H^{*} \left( {T_{\text{l}} - T_{\text{e}} } \right) $$
(27)
$$ \frac{\partial }{\partial t}\left( {f_{\text{c}} \rho_{\text{c}} H_{\text{c}} } \right) + \nabla \cdot \left( {f_{\text{c}} \rho_{\text{c}} \vec{v}_{\text{c}} H_{\text{c}} } \right) = \nabla \cdot \left( {f_{\text{c}} k^{*} \left( {\nabla \cdot T_{\text{c}} } \right)} \right) + H^{P} S_{\text{lc}} + H^{*} \left( {T_{\text{l}} - T_{\text{c}} } \right) $$
(28)

where H and T are the enthalpies and temperatures of each phase, respectively; k* is the effective thermal conductivity related to the effect of the k–ε mixture turbulence model[38]; H* is the diffusional heat exchange coefficient; and HP is the phase transition enthalpy, which is defined below.

$$ H^{P} = \left\{ {\begin{array}{*{20}c} {H_{l} = h_{l}^{\text{ref}} + \int_{{T_{\text{ref}} }}^{{T_{l} }} {c_{p(l)} } {\text{d}}T + f_{l} L,\quad {\text{solidification}}} \\ {H_{e} = H_{c} = h_{s}^{ref} + \int_{{T_{\text{ref}} }}^{{T_{e} }} {c_{p(s)} } {\text{d}}T + f_{l} L,\quad {\text{remelting}}} \\ \end{array} } \right. $$
(29)

where \( h_{l}^{\text{ref}} {\text{and}}\,h_{s}^{\text{ref}} \) are the reference enthalpies of the liquid and solid (equiaxed or columnar) phases, respectively; Tref is the reference temperature; cp(l) and cp(s) are the specific heats of the liquid and solid phases, respectively; L is the latent heat of fusion; and fl is the liquid fraction related to the effect of the back-diffusion model,[32] which is expressed as follows:

$$ f_{l} = \left\{ \begin{aligned} 1,\quad T \ge T_{l}^{*} \hfill \\ {{\left( {T - T_{s}^{*} } \right)} \mathord{\left/ {\vphantom {{\left( {T - T_{s}^{*} } \right)} {\left( {T_{l}^{*} - T_{s}^{*} } \right),\quad T_{s}^{*} < T < T_{l}^{*} }}} \right. \kern-0pt} {\left( {T_{l}^{*} - T_{s}^{*} } \right),\quad T_{s}^{*} < T < T_{l}^{*} }} \hfill \\ 0,\quad T < T_{s}^{*} \hfill \\ \end{aligned} \right. $$
(30)
$$ T_{l}^{*} = T_{f} + mc_{0} \left( {1 - \left( {1 - \gamma \cdot k} \right)\left( {1 - f_{l} } \right)} \right)^{{{{\left( {k - 1} \right)} \mathord{\left/ {\vphantom {{\left( {k - 1} \right)} {\left( {1 - \gamma k} \right)}}} \right. \kern-0pt} {\left( {1 - \gamma k} \right)}}}} $$
(31)
$$ T_{s}^{*} = T_{f} + \frac{1}{k}mc_{0} \left( {1 - \left( {1 - \gamma \cdot k} \right)\left( {1 - f_{l} } \right)} \right)^{{{{\left( {k - 1} \right)} \mathord{\left/ {\vphantom {{\left( {k - 1} \right)} {\left( {1 - \gamma k} \right)}}} \right. \kern-0pt} {\left( {1 - \gamma k} \right)}}}} $$
(32)

where \( T_{l}^{*} \,{\text{and}}\,T_{s}^{*} \) are the liquidus and solidus temperatures, respectively; Tf is the fusion temperature of pure iron; m is the liquidus slope; c0 is the initial concentration; k is the equilibrium distribution coefficient; and γ is the nondimensional diffusion parameter in the back-diffusion model.

Solute transfer model

The solute conservation equations are expressed as follows:

$$ \frac{{\partial \left( {\rho_{\text{l}} f_{\text{l}} c_{\text{l}} } \right)}}{\partial t} + \nabla \cdot \left( {f_{\text{l}} \rho_{\text{l}} \vec{v}_{\text{l}} c_{\text{l}} } \right) = - C_{\text{le}}^{P} - C_{\text{le}}^{D} - C_{\text{lc}}^{P} - C_{\text{lc}}^{D} $$
(33)
$$ \frac{{\partial \left( {\rho_{\text{e}} f_{\text{e}} c_{\text{e}} } \right)}}{\partial t} + \nabla \cdot \left( {f_{\text{e}} \rho_{\text{e}} \vec{v}_{\text{e}} c_{\text{e}} } \right) = C_{\text{le}}^{P} + C_{\text{le}}^{D} - C_{\text{ec}}^{P} - C_{\text{ec}}^{D} $$
(34)
$$ \frac{{\partial \left( {\rho_{\text{c}} f_{\text{c}} c_{\text{c}} } \right)}}{\partial t} + \nabla \cdot \left( {f_{\text{c}} \rho_{\text{c}} \vec{v}_{\text{c}} c_{\text{c}} } \right) = C_{\text{lc}}^{P} + C_{\text{lc}}^{D} + C_{\text{le}}^{P} + C_{\text{le}}^{D} $$
(35)
$$ \frac{{\partial \left( {\rho_{\text{e}} f_{\text{e}}^{s} c_{\text{e}}^{s} } \right)}}{\partial t} + \nabla \cdot \left( {f_{\text{e}}^{s} \rho_{\text{e}} \vec{v}_{\text{e}} c_{\text{e}}^{s} } \right) = C_{\text{e}}^{sP} + C_{\text{e}}^{sD} $$
(36)
$$ \frac{{\partial \left( {\rho_{\text{c}} f_{\text{c}}^{\text{s}} c_{\text{c}}^{\text{s}} } \right)}}{\partial t} + \nabla \cdot \left( {f_{\text{c}}^{\text{s}} \rho_{\text{c}} \vec{v}_{\text{c}} c_{\text{c}}^{\text{s}} } \right) = C_{\text{c}}^{\text{sP}} + C_{\text{c}}^{\text{sD}} $$
(37)

where \( C_{\text{le}}^{\text{P}} ,\,C_{\text{lc}}^{\text{P}} ,\,C_{\text{ce}}^{\text{P}} ,\,C_{\text{c}}^{\text{sP}} \,{\text{and}}\,C_{\text{e}}^{\text{sP}} \) are the source terms of the solute transfer rate between each phase related to phase transition and \( C_{\text{le}}^{\text{D}} ,\,C_{\text{lc}}^{\text{D}} ,\,C_{\text{ce}}^{\text{D}} ,\,C_{\text{c}}^{\text{sD}} \,{\text{and}}\,C_{\text{e}}^{\text{sD}} \) are the source terms of the solute transfer rate between each phase related to element diffusion. Considering the effect of the back-diffusion model[32,39] on the solute distribution, the above source terms of solute transfer are expressed as follows:

$$ C_{\text{le}}^{\text{P}} + C_{\text{le}}^{\text{D}} = S_{\text{le}} c_{\text{le}}^{*} - S_{\text{h}} \rho_{\text{e}} A^{\prime}_{\text{e}} {{D_{l} \left( {c_{\text{le}}^{*} - c_{\text{l}} } \right)} \mathord{\left/ {\vphantom {{D_{l} \left( {c_{\text{le}}^{*} - c_{\text{l}} } \right)} {l_{\text{l}}^{\text{e}} }}} \right. \kern-0pt} {l_{\text{l}}^{\text{e}} }} - \gamma \rho_{\text{e}} kf_{\text{e}} {{\partial \left( {S_{\text{le}} } \right)} \mathord{\left/ {\vphantom {{\partial \left( {S_{\text{le}} } \right)} {\partial t}}} \right. \kern-0pt} {\partial t}} $$
(38)
$$ C_{\text{lc}}^{\text{P}} + C_{\text{lc}}^{\text{D}} = S_{\text{lc}} c_{\text{lc}}^{*} - S_{\text{h}} \rho_{\text{c}} A^{\prime}_{\text{c}} {{D_{l} \left( {c_{\text{lc}}^{*} - c_{\text{l}} } \right)} \mathord{\left/ {\vphantom {{D_{l} \left( {c_{\text{lc}}^{*} - c_{\text{l}} } \right)} {l_{\text{l}}^{\text{c}} }}} \right. \kern-0pt} {l_{\text{l}}^{\text{c}} }} - \gamma \rho_{\text{c}} kf_{\text{c}} {{\partial \left( {S_{\text{lc}} } \right)} \mathord{\left/ {\vphantom {{\partial \left( {S_{\text{lc}} } \right)} {\partial t}}} \right. \kern-0pt} {\partial t}} $$
(39)
$$ C_{\text{e}}^{\text{sP}} + C_{\text{e}}^{\text{sD}} = S_{\text{e}}^{\text{s}} c_{\text{e}}^{i*} - \gamma \rho_{\text{e}} kf_{\text{e}}^{\text{s}} {{\partial \left( {S_{\text{e}}^{\text{s}} } \right)} \mathord{\left/ {\vphantom {{\partial \left( {S_{\text{e}}^{\text{s}} } \right)} {\partial t}}} \right. \kern-0pt} {\partial t}} $$
(40)
$$ C_{\text{c}}^{\text{sP}} + C_{\text{c}}^{\text{sD}} = S_{\text{c}}^{\text{s}} c_{\text{c}}^{i*} - \gamma \rho_{c} kf_{\text{c}}^{\text{s}} {{\partial \left( {S_{\text{c}}^{\text{s}} } \right)} \mathord{\left/ {\vphantom {{\partial \left( {S_{\text{c}}^{\text{s}} } \right)} {\partial t}}} \right. \kern-0pt} {\partial t}} $$
(41)

where \( c_{\text{le}}^{*} ,\,c_{\text{lc}}^{*} ,\,c_{\text{e}}^{i*} \,{\text{and}}\,c_{\text{c}}^{i*} \) are the equilibrium concentrations at the interface of each phase, lle and llc are the lengths of solute diffusion, and Sh is the Sherwood number, which is described in a previous work by the authors of the current study.[25] In the multiphase solidification model, the segregation degree (cmix/c0) is used to characterize the distribution of the carbon element, as described in Eq. [42].

$$ \frac{{c_{\text{mix}} }}{{c_{0} }} = \frac{{\rho_{\text{l}} f_{\text{l}} c_{\text{l}} + \rho_{\text{e}} f_{\text{e}} c_{\text{e}} + \rho_{\text{c}} f_{\text{c}} c_{\text{c}} }}{{\left( {\rho_{\text{l}} f_{\text{l}} + \rho_{\text{e}} f_{\text{e}} + \rho_{\text{c}} f_{\text{c}} } \right) \cdot c_{0} }} $$
(42)

Dynamic evolution model of the microstructure

According to the concept of cellular automata (CA), the dynamic growth model of columnar dendrites in the continuous casting process is presented. The whole computing region is divided into many volume elements that are later assigned an element index (i). Different element indexes represent different phases (liquid, equiaxed, and columnar phases). As shown in Figure 4, the microstructural evolution in the continuous casting process is described in detail. When the index i is equal to 0, 1, and 2, the corresponding volume elements represent the columnar dendritic trunk, the columnar dendritic tip, and the equiaxed and liquid phases, respectively. Based on the KGT model, the differential form of the columnar dendrite dynamic growth model is obtained as follows:

$$ {\text{d}}l = \left( {a_{1} \Delta T^{2} + a_{2} \Delta T^{3} } \right){\text{d}}t $$
(43)
$$ \Delta T = \Delta T_{t} + \Delta T_{c} + \Delta T_{r} $$
(44)

where l is the growth length of the columnar dendritic tip and a1 and a2 are the fitting coefficients that are found in Hou’s work.[40] In Eq. [44], the effects of heat flow (∆Tt), solute diffusion (∆Tc), and curvature (∆Tr) have been taken into account in the calculation of undercooling (∆T).

Fig. 4
figure 4

Schematic diagram of microstructural evolution in the continuous casting process

Full size image

For the equiaxed phase, the Gaussian kernel density estimation (KDE) model[28] is used to realize the nucleation density estimation.

$$ \frac{\partial }{\partial t}n_{e} + \nabla \cdot \left( {\vec{v}_{e} n_{e} } \right) = \frac{{{\text{d}}\left( {\Delta T} \right)}}{{{\text{d}}t}}\frac{{n_{\hbox{max} } }}{{\sqrt {2\pi } \Delta T_{\sigma } }}e^{{ - \,0.5\left( {\frac{{\Delta T - \Delta T_{N} }}{{\Delta T_{\sigma } }}} \right)^{2} }} $$
(45)

where nmax is the maximum nucleation density of equiaxed grains and ∆TN and ∆Tσ are the average nucleation undercooling and standard deviation, respectively, whose values are referenced from the work of Wu and Ludwig.[41]

Model Geometry, Experimental Parameters, and Solution Strategy

Based on the volume-averaged Eulerian approach, Fluent software (ANSYS, Inc., Canonsburg, PA) is used to realize the coupled calculations of the submodels in the multiphase solidification model and reveal the transfer phenomena of the melt flow, heat transfer, solute transport, grain nucleation, and growth in the continuous casting process. A three-dimensional geometric model with a 320 × 410 mm2 cross section was established, and the number of computational meshes was 3,936,000 with a mesh size of 10 × 10 × 10 mm3. The material properties and process parameters of heavy-rail steel used for this simulation are given in detail in Table II. To increase the calculation efficiency, the entire computational domain was divided into two zones, with the separating interface located 9.5 m from the meniscus, perpendicular to the x direction. At this interface, the data were transferred via Fluent profile files.

Table II Material Properties and Process Parameters Used for the Simulations
Full size table

In this work, the phase-coupled SIMPLE algorithm is adopted to simulate 3D turbulent flow. As shown in Figure 5, the flow chart of the calculation scheme is obtained. In the simulation process, the iterative calculation of the dendritic tip position of the columnar phase is carried out before solving the conservation equations. Then, the calculation process of the source terms and phase transfer rates in each conservation equation is completed. To accelerate the convergence speed, the under-relaxation factors are set to 0.4, and the convergence residuals are set to 10−5.

Fig. 5
figure 5

Flow chart of the calculation scheme

Full size image

In terms of support for modern hardware, a high-performance computer server (Sugon® I620-G20) with two Intel® Xeon® E5-2698 v4 20-core CPUs and 128 Gbit DDR4 memory is used. With this setup, the computation time per case is approximately 400 hours.

Model Validation

To validate the multiphase solidification model, many experiments were carried out in this manuscript, including Tesla meter measurements, etched macrostructure analysis, and infrared carbon-sulfur analysis. Because of the high-frequency effects of the electromagnetic field, the central magnetic induction intensity is a key factor influencing the processing effort of the electromagnetic stirrer. Using a CT-3 Tesla meter, the central magnetic induction intensities with different current intensities were measured. Figure 6(a) shows that the calculated magnetic induction intensities in the center of the mold electromagnetic stirrer with different current intensities (from 400 to 700 A) are 356.88, 431.79, 505.20, and 601.19, and the corresponding measured magnetic induction intensities are 350.00, 420.00, 515.00, and 613.00 Gs, respectively. Figure 6(b) shows that the calculated magnetic induction intensities in the center of the final electromagnetic stirrer with different current intensities (from 200 to 500 A) are 275.12, 419.32, 555.46, and 723.81, and the corresponding measured magnetic induction intensities are 280.00, 426.00, 550.00, and 700.00 Gs, respectively. The experimental results show that the average relative error between the calculated and measured data for magnetic induction intensity is less than or equal to 2.03 pct.

Fig. 6
figure 6

Comparison between the calculated and measured magnetic induction intensities: (a) M-EMS and (b) F-EMS

Full size image

A 320 × 410 × 10 mm3 slice of the continuous casting bloom located on the cross section was used to carry out the etched macrostructure analysis and infrared carbon-sulfur analysis, and 43 5-mm-diameter holes were drilled along the vertical direction of the cross section. Figure 8 compares the simulation results and the etched macrostructure on the cross section of heavy-rail steel blooms. There are bright negative segregation areas (light-colored zones) at the edge and 1/4 position of the continuous casting bloom. The positive segregation areas (deep-colored zones) in the center of the bloom in the simulation results are also in good agreement with those observed in the experimental results. It is shown that there were no obvious differences between the simulated macrosegregation contours and the etched macrostructure. To further explore the accuracy of the multiphase solidification model, the measured and calculated carbon segregation degrees along the vertical direction (y = 0) in the center of the cross section are compared in Figure 9. For the heavy-rail steel blooms, the variation trend of the calculated macrosegregation degree is consistent with that of the measured macrosegregation degree of carbon, which verifies that the multiphase solidification model is correct and reliable (Figure 7).

Fig. 7
figure 7

Schematic diagram of the sampling positions for different experiments

Full size image
Fig. 8
figure 8

Comparison between the (a) calculated macrosegregation and the (b) etched macrostructure on the cross section of heavy-rail steel blooms

Full size image
Fig. 9
figure 9

Measured and calculated carbon segregation along the vertical direction (y = 0) in the center of heavy-rail steel blooms

Full size image
Fig. 10
figure 10

Schematic diagram of the sampling positions along the x and z directions of the bloom

Full size image

Results and Discussion

To enhance the comparability, the sampling positions of the results in Figures 11 through 18 are similar. Figure 10 shows a schematic diagram of the sampling positions in the center of the bloom, which are located along the z direction and at different x positions from the meniscus. This diagram could facilitate the understanding of the results shown in Figures 11 through 18.

Fig. 11
figure 11

Distribution of (a) tangential electromagnetic force and (b) stirring velocity along the z direction of heavy-rail steel blooms in the middle of the mold electromagnetic stirrer

Full size image
Fig. 12
figure 12

Equiaxed grain density in molten steel of heavy-rail steel blooms at the center of the mold outlet with different current intensities

Full size image
Fig. 13
figure 13

(a) Segregation degree of carbon along the z direction of heavy-rail steel blooms at the mold outlet and (b) an enlarged image of local negative macrosegregation at the edge of heavy-rail steel blooms

Full size image
Fig. 14
figure 14

Distribution of (a) tangential electromagnetic force and (b) stirring velocity along the z direction of heavy-rail steel blooms in the middle of the final electromagnetic stirrer

Full size image
Fig. 15
figure 15

Phase fraction of heavy-rail steel blooms along the z direction—10.5 m from the meniscus—with different F-EMS current intensities: (a) columnar phase, (b) equiaxed phase, and (c) liquid phase

Full size image
Fig. 16
figure 16

Schematic diagram of fluid flow, solute transport and equiaxed grain transport with EMS

Full size image
Fig. 17
figure 17

Carbon segregation degree of heavy-rail steel blooms (a) along the z direction—13.0 m from the meniscus—and (b) along the x direction at the solidification end with different F-EMS current intensities

Full size image
Fig. 18
figure 18

Distribution of the sum of the equiaxed and liquid phase fractions 13.0 m from the meniscus: (a) without M-EMS or F-EMS, (b) with M-EMS, (c) with F-EMS, and (d) with M-EMS + F-EMS

Full size image

Effect of M-EMS on Solidification Behavior and Macrosegregation

Based on the multiphase solidification model with M-EMS, the distribution of tangential electromagnetic force and stirring velocity along the z direction of heavy-rail steel blooms in the middle of the mold electromagnetic stirrer are depicted in Figures 11(a) and (b), respectively. The current frequency of M-EMS is 2.4 Hz, and the casting speed is 0.68 m/min.

As shown in Figure 11(a), the maximum tangential electromagnetic force along the z direction of heavy-rail steel blooms increases from 1849.06 to 3648.13 N/m3 as the M-EMS current intensity increases from 300 to 600 A. Under the skin effect of EMS, the tangential electromagnetic force is the largest at the edge of the bloom and gradually weakens towards the bloom center. As the M-EMS current intensity increases, the maximum tangential electromagnetic force along the z direction of the heavy-rail steel blooms obviously increases. As shown in Figure 11(b), the tangential stirring velocity increases linearly from the bloom center. The tangential stirring velocity of molten steel in the middle of the mold electromagnetic stirrer reaches the maximum when it is located 16 mm from the edge of heavy-rail steel blooms. At the edge of the bloom, the tangential stirring velocity decreases to 0 m/s due to the existence of a solidified shell. From the above results, the greater the M-EMS current intensity is, the stronger the stirring effect of molten steel in heavy-rail steel blooms.

Figure 12 shows the equiaxed grain densities in molten steel of heavy-rail steel blooms at the center of the mold outlet with different current intensities. As the M-EMS current intensity increases, the sensible heat of molten steel continuously releases, and the solidification rate increases rapidly. Thus, the equiaxed grain rate in the center of the mold outlet increases significantly, which has a significant effect on improving the centerline macrosegregation. When the M-EMS current intensity is 500 A, the equiaxed grain density in the center of the mold outlet is 5.44 × 108 m−3. When the current intensity is greater than 500 A, the relative increase rate of the equiaxed grain density does not obviously enhance.

Figures 13(a) and (b) show the segregation degree of carbon along the z direction of heavy-rail steel blooms at the mold outlet and an enlarged image of local negative macrosegregation at the edge of heavy-rail steel blooms. With the increase in the current intensity, the long-distance transport of solute-enriched molten steel is accelerated, which causes the formation of negative macrosegregation in front of the solidification interface under the solute washing mechanism. In addition, with the increase in current intensity, the solute washing behavior in front of the solidification interface becomes more intense, which leads to more serious negative macrosegregation at the edge of heavy-rail steel blooms. Therefore, the negative macrosegregation at the edge of the bloom would be worsened by applying M-EMS. According to the calculation results in Figure 12, the M-EMS current intensity should be set to 500 A, which could maximize the equiaxed grain density in the bloom center and control the negative macrosegregation at the edge of the bloom.

Effect of F-EMS on Solidification Behavior and Macrosegregation

Based on the multiphase solidification model with F-EMS, the distribution of the tangential electromagnetic force and stirring velocity along the z direction of heavy-rail steel blooms in the middle of the final electromagnetic stirrer are obtained in Figures 14(a) and (b), respectively. The current frequency of F-EMS is 7.0 Hz, the casting speed is 0.68 m/min, and the final electromagnetic stirrer is located 10.5 m from the meniscus.

When the F-EMS current intensity increases from 250 to 400 A, the maximum tangential electromagnetic force along the z direction of heavy-rail steel blooms increases from 1938.33 to 10,272.72 N/m3, as shown in Figure 14(a). Under the influence of the skin effect, the electromagnetic force decreases linearly along the z direction. As shown in Figure 14(b), the stirring velocity is 0 m/s at the edge of heavy-rail steel blooms because a 47.60 mm solidified shell has been formed. The tangential velocity of molten steel reaches the maximum value 76.92 mm from the edge of heavy-rail steel blooms and decreases gradually towards the bloom center with the skin effect. Similar to M-EMS, in F-EMS, the stirring velocity of molten steel in the bloom increases with increasing current intensity. However, an optimized F-EMS current intensity still exists in industrial applications, which significantly reduces macrosegregation.

Figure 15 shows the results of the phase fraction of heavy-rail steel blooms along the z direction—10.5 m from the meniscus—with different F-EMS current intensities. As shown in Figure 15, as the F-EMS current intensity increases from 250 to 400 A, the distribution range of the columnar phase decreases gradually, the distribution range of the equiaxed phase increases continuously, and the distribution range of the liquid phase in the bloom center decreases constantly. Figure 16 helps further illustrate the information in Figure 15.

Figure 16 shows a schematic diagram of the fluid flow, solute transport and equiaxed grain transport with EMS. With the increase in the F-EMS current intensity, the electromagnetic force continuously accelerates the rotational flow of molten steel, and the columnar dendritic tip located at the front of the solidification interface is constantly broken or remelted by the solute washing mechanism, which reduces the columnar dendrite zone and enlarges the equiaxed grain zone accordingly. In addition, the temperature of the molten steel decreases rapidly with increasing current intensity due to the rotating stirring effect of F-EMS, which leads to an increase in the solidification rate and the formation of more dissociative equiaxed grains. Under the influence of rotational centrifugal force, the dissociative equiaxed grains shift far away from the center of heavy-rail steel blooms and deposit in front of the solidification interface, which enlarges the equiaxed grain zone and reduces the liquid zone.

Figure 17(a) shows the carbon segregation degree of heavy-rail steel blooms along the z direction—13.0 m from the meniscus—with different F-EMS current intensities. As the F-EMS current intensity increases from 250 to 400 A, the positive centerline segregation degree of heavy-rail steel blooms along the z direction—13.0 m from the meniscus—decreases from 1.159 to 1.132. However, the best current intensity for controlling positive centerline segregation is 350 A. When the F-EMS current intensity increases from 250 to 400 A, the negative segregation degree neighboring the bloom center along the z direction—13.0 m from the meniscus—decreases from 0.988 to 0.976. Combined with Figure 15, the rotational flow of molten steel is driven by the electromagnetic force, which results in an increase in the solidification rate and the formation of more solute-poor equiaxed grains. Under the influence of rotational centrifugal force, a large number of solute-poor equiaxed grains deposit in front of the solidification interface to form a local negative segregation zone, which is known as the white band. Therefore, a larger F-EMS current intensity would enhance the solute washing mechanism in front of the solidification interface and exacerbate the negative segregation neighboring the bloom center.

Figure 17(b) shows the carbon segregation degree in the center of heavy-rail steel blooms along the x direction with different F-EMS current intensities. With increasing current intensity, the carbon concentration in the bloom center increases significantly after the molten steel flows into the final electromagnetic stirrer, and the carbon concentration further increases after the molten steel flows out of the final electromagnetic stirrer. The reason is that equiaxed grains deposit in front of the solidification interface under the influence of rotational centrifugal force, which forces the solute-enriched molten steel in front of the solidification interface to transfer to the bloom center and causes the carbon concentration in the bloom center to increase. When the bloom is pulled out of the final electromagnetic stirrer, the carbon concentration in the bloom center would be reduced to a certain extent after reaching its maximum value under the effect of high-temperature diffusion.

However, comparing the carbon concentration with the current intensity of 400 A, the carbon concentration at the bloom center with the current intensity of 350 A is the lowest. These results show that a higher current intensity does not necessarily provide a better control effect on the macrosegregation in the heavy-rail steel blooms at the solidification end. On the one hand, under the influence of F-EMS, the temperature of molten steel in the bloom center decreases rapidly, the solidification rate increases constantly, and the dendritic arm spacing reduces significantly, which effectively controls the macrosegregation in the bloom center. On the other hand, when the F-EMS current intensity is too high, the rotational flow velocity of molten steel increases, which makes the solute-enriched interdendritic melt phase of columnar dendrites flow to the bloom center, thereby increasing the degree of carbon segregation in the bloom center.

Therefore, the positive centerline segregation and the neighboring negative segregation in heavy-rail steel blooms would be well reduced by setting the F-EMS current intensity to 350 A.

Synergetic Effect of M-EMS on F-EMS

To investigate the synergetic effect between M-EMS and F-EMS in the combined EMS (M-EMS and F-EMS) process, comparative experiments of different EMS processes are designed, as shown in Table III. These experiments use the optimal process parameters of M-EMS (a current intensity of 500 A and a current frequency of 2.4 Hz) and F-EMS (a current intensity of 350 A and a current frequency of 7.0 Hz) and a casting speed of 0.68 m/min.

Table III Comparison of the Numerical Experiments with Different EMS Processes
Full size table

Figure 18 shows the distribution of the sum of the equiaxed and liquid phase fractions 13.0 m from the meniscus with different EMS processes. The results show that, compared to without M-EMS or F-EMS, M-EMS provides a slight increase in the equiaxed phase fraction at the edge of the bloom. The distribution of the sum of the equiaxed and liquid phase fraction is approximately the same in Figures 18(a) and (b), which shows that M-EMS has little effect on this distribution. There is no rotating streamline in the bloom center, indicating that the influence of M-EMS has not been exerted on this area (13.0 m from the meniscus). Figures 18(c) and (d) show that F-EMS can effectively promote the rotational flow of the equiaxed and liquid phases in the bloom center. On the basis of increasing the equiaxed grain density by M-EMS, F-EMS could promote the distribution morphology change in the equiaxed and liquid phases under the effect of rotational flow.

Figure 19(a) shows the carbon segregation degree of heavy-rail steel blooms along the z direction—13.0 m from the meniscus—with different EMS processes. When neither M-EMS nor F-EMS are used, the positive centerline segregation degree in this location is the most serious, reaching 1.210. When only M-EMS is used, the positive centerline segregation degree in this location is 1.188. When only F-EMS is used, the positive centerline segregation degree in this location is 1.132. When the combined EMS process (M-EMS + F-EMS) is used, the positive centerline segregation degree in this location is 1.113. The results show that the improvement effect of M-EMS on the positive centerline segregation is limited, the F-EMS effectively reduces the positive centerline segregation, and the combined EMS (M-EMS + F-EMS) further reduces the positive centerline segregation on the basis of F-EMS. In the combined EMS process, there are a large number of solute-poor equiaxed grains in the liquid phase at the bloom center with M-EMS, and they deposit in front of the solidification interface with F-EMS, which makes the negative segregation neighboring the bloom center nearly more severe than that using only F-EMS. After applying the combined EMS process, the carbon segregation ratio of the heavy-rail steel bloom center was still higher than 1.10, and mechanical reduction as an effective method to overcome macrosegregation was subsequently applied.

Fig. 19
figure 19

Carbon segregation degree of heavy-rail steel blooms (a) along the z direction—13.0 m from the meniscus—and (b) along the x direction at the solidification end with different EMS processes

Full size image

Figure 19(b) shows the carbon segregation degree in the center of heavy-rail steel blooms along the x direction with different EMS processes. The M-EMS has little effect on the improvement of the positive centerline segregation, whereas F-EMS is an effective method to reduce positive centerline segregation. Therefore, the application of combined EMS further reduces the positive centerline segregation in heavy-rail steel blooms. It is concluded that the change in solute concentration caused by M-EMS would be inherited by the position of F-EMS, which enhances the metallurgical effects of F-EMS.

Application Results from a Plant

As shown in Figure 20, to further verify the improvement effect of macrosegregation in heavy-rail steel blooms, the solute distribution with different EMS processes was measured by infrared carbon-sulfur analysis. The detailed sampling positions and sizes are shown in Figure 7.

Fig. 20
figure 20

Solute distribution with different EMS processes as measured by infrared carbon-sulfur analysis

Full size image

The positive centerline segregation degrees of heavy-rail steel blooms along the z direction are 1.215 (without M-EMS or F-EMS), 1.195 (with M-EMS), 1.125 (with F-EMS), and 1.105 (with M-EMS + F-EMS). With the gradual implementation of the EMS process, the negative segregation degrees neighboring the bloom center along the z direction constantly deteriorate. The experimental results are in good agreement with the numerical simulation results in Figure 19(a), which verifies that the developed model is accurate and reliable.

Conclusions

Based on the 3D multiphase solidification model, which couples the turbulent fluid flow, heat transfer, microstructural evolution, and solute transport with back diffusion and electromagnetic field, the microstructural evolution and macrosegregation in heavy-rail steel blooms are investigated. The experimental results with different EMS processes are in good agreement with the numerical simulation results, which proves that the multiphase solidification model is accurate and reliable. The main conclusions are summarized as follows:

  1. (1)

    As the M-EMS current intensity increases, the equiaxed grain rate increases significantly, and the increasing trend of the equiaxed grain density is not obvious when the current intensity exceeds 500 A. With the increase in current intensity, the negative macrosegregation at the edge of blooms is more serious under the effect of the solute washing mechanism. Therefore, an M-EMS current intensity of 500 A provides the best macrosegregation control effect.

  2. (2)

    As the F-EMS current intensity increases from 250 to 400 A, the positive centerline segregation degree along the z direction—13.0 m from the meniscus—decreases from 1.159 to 1.132, and the negative segregation degree neighboring the bloom center decreases from 0.988 to 0.976. However, the results show that a higher current intensity does not necessarily provide a better control effect on macrosegregation. When the F-EMS current intensity is set to 350 A, the positive centerline segregation and neighboring negative macrosegregation are effectively reduced.

  3. (3)

    The change in solute concentration caused by M-EMS could be inherited by the position of F-EMS, which enhances the metallurgical effects of F-EMS. The application of combined EMS could further reduce macrosegregation.

After the application of the combined EMS process, the carbon segregation ratio of the heavy-rail steel bloom center is still higher than 1.10; this approach can be combined with mechanical reduction to effectively overcome macrosegregation. Further work will extend the present 3D multiphase solidification model by considering shell deformation, and the solute transport of the mushy zone under EMS and mechanical reduction will be systematically investigated.