Numerical Simulation of Gas and Liquid Two-Phase Flow in the RH Process

Abstract

A mathematical model has been established to simulate the gas–liquid two-phase flow in the RH process. The effects of interphase forces and the bubble-induced turbulence on the fluid flow and motion of gas bubbles were investigated. The interphase forces include the drag force, the virtual mass force, the lift force, and the pressure gradient force, respectively. The prediction results of the liquid velocity and the recirculation rate were compared with the experimental data measured with a Particle Image Velocimetry technique. The results indicated that the drag force and the virtual mass force dominated the gas plume shape in the up-leg snorkel, and significantly influenced the liquid velocity and the distribution of the gas phase. The lift force mainly affected the spreading of gas bubbles in the radial direction of the snorkel. However, the pressure gradient force could be neglected because it had no effect on the liquid velocity and the gas volume fraction. The increase of the bubble-induced turbulence decreased the liquid velocity, and by adjusting the lift force, it widened the shape of the individual gas plumes. To accurately simulate the gas–liquid flow behavior in the RH degasser, these appropriate parameters, such as the drag coefficient, the virtual mass coefficient, the lift coefficient, and the bubble-induced turbulence coefficient, were determined by comparing the predicted results and the measured data.

Introduction

The Ruhrstahl–Heraeus (RH) degasser is widely used for the production of the ultralow-carbon steel. It plays an extremely important role in the refining process for decarburization, deoxidization, desulfurization, temperature control, inclusion removal, and composition homogenization. The above-mentioned operations are closely related to the gas–liquid flow behavior in the RH degasser. Thus, understanding the gas–liquid flow behavior in the RH degasser is of great importance for improving refining efficiency.

Due to the limitations of high temperature, multiphase system, and vacuum conditions, the numerical simulation is considered as an effective way to simulate the fluid flow in the RH degasser. Currently, the modeling approaches mainly involve the quasi-single-phase model,[1,2] the Eulerian–Lagrangian approach,[3] and the Eulerian–Eulerian approach.[4,5,6,7,8] Furthermore, the discrete phase (DPM) and volume of fraction (VOF) models are employed in conjunction to model the multiphase flow in the RH degasser.[9,10,11] The interfacial behavior between the molten steel and the gas phase, and the motion of gas bubbles can be simultaneously tracked and predicted.

Due to the phase interaction, there exists momentum exchange between the molten steel and gas bubbles, which significantly affect the characteristics of circulation and mixing in the RH degasser. Obviously, descriptions of the phase interaction and of momentum exchange between the two phases depend on correct calculation of the interphase forces acting on the gas bubbles. The interphase forces can be divided into the drag force and non-drag forces. The latter include the lift force, the virtual mass force, the pressure gradient force, etc. The effects of interphase forces on the fluid flow and gas phase distribution are extensively investigated in gas-stirred ladles.[12,13,14,15] However, these valuable results obtained in gas-stirred ladles may not be appropriate for gas–liquid two-phase flow in the RH degasser. For the RH system, gas bubbles are injected into the up-leg snorkel horizontally, and they can penetrate the liquid up to a certain depth, and then rise up. Due to the change of movement direction of gas bubbles, the directions of interphase forces are frequently changed. Nevertheless, for gas-stirred ladles gas bubbles enter the liquid from the bottom tuyeres, and then move upwards along the vertical direction. The directions of interphase forces are relatively fixed.

Although some researchers have tried to evaluate the importance of interphase forces acting on the gas bubbles in the RH degasser, the selection of interphase forces in the equation of the bubble motion is still somewhat subjective. The interphase forces considered in the RH simulations are listed in Table I. It can be seen that selections of interphase forces differ in different researchers. Some forces, such as the lift force and the virtual mass force, were neglected before being evaluated. Geng[6] and Zhu et al.[8] pointed out that the absence of the virtual mass force gave rise to the gas-adhering wall effect and resulted in a substantial decline of the recirculation rate. However, Chen et al.[7] reported that the recirculation rate without the virtual mass force was slightly larger than that with the virtual mass force in the water model and actual RH reactor. Similarly, there have not been unified conclusions for the lift force. The different drag coefficient models were also adopted in previous studies. Therefore, the importance of different interphase forces has not yet been known clearly. It is necessary to investigate the effects of the interphase forces on the gas–liquid two-phase flow and set up criteria for selection of these forces in the RH process. In addition, Lou[14] and Duan et al.[15] evaluated the contribution of the bubble-induced turbulence and concluded that the bubble-induced turbulence had significant influence on the liquid turbulence and gas phase distribution in gas-stirred systems. Nevertheless, the effect of the bubble-induced turbulence on the fluid flow in the RH degasser is seldom considered.

Table I Forces Considered in the RH Simulations

In the current study, the gas–liquid flow behavior in the RH degasser is simulated using a mathematical model combining VOF and DPM. The effects of interphase forces and the bubble-induced turbulence on the liquid velocity, gas volume fraction, and recirculation rate are evaluated and discussed in detail. By comparing with the measurements of the water model,[9] the appropriate parameters are summarized for correctly predicting the multiphase flow in the RH degasser.

Mathematical Model

As well known, the liquid phase and the top gas phase in the RH degasser are continuous. The gas bubbles are dispersed in the liquid phase while they become a continuous phase after escaping from the interface between the liquid phase and the top gas phase in the vacuum chamber. Therefore, it can be divided into the liquid–gas phase and the liquid–gas bubbles. For the liquid–gas phase, the VOF model was adopted to track the interface between the liquid phase and the top gas phase. In order to accurately predict the interface tracking, the geo-reconstruct scheme was selected. The evolution of the interface was determined by solving a continuity equation for the volume fraction of each of the secondary phases. An elaborate description of the complete VOF model can be found in previous investigations.[17,18]

For the liquid–gas bubbles, the DPM model was employed to simulate the trajectory of gas bubbles in the liquid phase. The flow of the liquid phase was solved in an Eulerian reference frame, similar to a single-phase calculation. The interactions between the liquid phase and gas bubbles were considered in the form of source terms, including the momentum exchange and the turbulence produced by the bubble motion.

Liquid Flow

The governing equations for the liquid phase can be derived based on the Navier–Stokes equations for single-phase flows. They are expressed as

$$ \frac{\partial }{{\partial t}}\left( {\alpha _{{\text{l}}} \rho _{{\text{l}}} } \right) + \nabla \cdot \left( {\alpha _{{\text{l}}} \rho _{{\text{l}}} \mathop {u_{{\text{l}}} }\limits^{ \to } } \right) = 0 $$

(1)

$$ \frac{\partial }{{\partial t}}\left( {\alpha _{{\text{l}}} \rho _{{\text{l}}} {\text{ }}\overrightarrow {u} _{{\text{l}}} } \right) + \overrightarrow {u} _{{\text{l}}} \cdot\nabla \left( {\alpha _{{\text{l}}} \rho _{{\text{l}}} \overrightarrow {u} _{{\text{l}}} } \right) = - \nabla P + \nabla \cdot\left[ {\alpha _{{\text{l}}} \left( {\mu _{{\text{l}}} + \mu _{{\text{t}}} } \right)} \right]\nabla \overrightarrow {u} _{{\text{l}}} + \overrightarrow {{F_{{\text{b}}} }} , $$

(2)

where α_l is the volume fraction of the liquid phase, ρ_l is the density of the liquid phase (kg/m³), u_l is the velocity of the liquid phase (m/s), P is the pressure (Pa), μ_l is the molecular viscosity of the liquid phase (Pa·s), and μ_t is the turbulent viscosity (Pa·s). F_b is the source term for momentum exchange with bubbles and it is defined by

$$ \overrightarrow {{F_{{\text{b}}} }} = - \alpha _{{\text{l}}} \cdot\sum\limits_{i}^{{N_{{{\text{b,cell}}}} }} {\left( {\vec{F}_{{{\text{D}},i}} + {\text{ }}\vec{F}_{{{\text{VM}},i}} + \vec{F}_{{{\text{L}},i}} + \vec{F}_{{{\text{P}},i}} } \right)} {\text{ }} \cdot {\text{Q}}_{{{\text{b}},i}}^{{\text{s}}} \Delta t, $$

(3)

where N_b,cell is the number of bubbles in the computational cell, $Q_{{{\text{b}},i}}^{s}$ is the flow rate of the injected bubble stream (kg/s), Δt is the time step (s), F_D,i is the drag force, F_VM,i is the virtual mass force, F_L,i is the lift force, and F_P,i is the pressure gradient force, respectively.

The volume fraction of the liquid phase and gas bubbles are calculated by

$$ \alpha_{\text{b}} = \frac{1}{{\Delta V_{\text{cell}} }}\sum\limits_{i}^{{N_{\text{b,cell}} }} {\frac{{Q_{{{\text{b}},i}}^{\text{s}} \cdot \Delta t}}{{\rho_{{{\text{b}},i}} }}} $$

(4)

$$ \alpha_{\text{l}} + \alpha_{\text{b}} = 1, $$

(5)

where α_b is the volume fraction of gas bubbles, ΔV_cell is the computational cell volume (m³), and ρ_b,i is the density of gas bubbles (kg/m³).

The standard k-ɛ model is used to describe the turbulence, and the governing transport equations for turbulent kinetic energy, k, and its dissipation rate, ɛ, are represented as

$$ \alpha _{{\text{l}}} \rho _{{\text{l}}} \left( {\frac{{\partial k}}{{\partial t}} + \overrightarrow {{u_{i} }} \cdot\nabla k} \right) = \nabla \cdot\left[ {\left( {\alpha _{{\text{l}}} \frac{{\mu _{{\text{t}}} }}{{\sigma _{k} }}} \right)\nabla k} \right] + \alpha _{{\text{l}}} G_{k} - \alpha _{{\text{l}}} \rho _{{\text{l}}} \varepsilon + S_{k} $$

(6)

$$ \alpha _{{\text{l}}} \rho _{{\text{l}}} \left( {\frac{{\partial \varepsilon }}{{\partial t}} + \overrightarrow {{u_{i} }} \cdot\nabla \varepsilon } \right) = \nabla \cdot\left[ {\left( {\alpha _{{\text{l}}} \frac{{\mu _{{\text{t}}} }}{{\sigma _{\varepsilon } }}} \right)\nabla \varepsilon } \right] + C_{{1\varepsilon }} \frac{\varepsilon }{k}\cdot\left( {\alpha _{{\text{l}}} G_{k} + S_{k} } \right) - \alpha _{{\text{l}}} C_{{2\varepsilon }} \rho _{{\text{l}}} \frac{{\varepsilon ^{2} }}{k}. $$

(7)

The turbulent viscosity is calculated by

$$ \mu_{\text{t}} = \rho_{\text{l}} C_{\mu } \frac{{k^{2} }}{\varepsilon }, $$

(8)

where the model constants are C_1ɛ = 1.44, C_2ɛ = 1.92, σ_k = 1.0, σ_ɛ = 1.3, and C_μ = 0.09, respectively.[19] S_k is the source term of turbulence caused by the motion of gas bubbles and it is expressed as

$$ S_{k} = \frac{{C_{{sk}} }}{{\Delta V_{{{\text{cell}}}} }}\sum\limits_{i}^{{N_{{{\text{b,cell}}}} }} {\frac{{{\text{3}}\alpha _{{\text{l}}} \mu _{{\text{l}}} C_{{{\text{D}},i}} Re_{i} }}{{4d_{{{\text{b}},i}}^{2} \rho _{{{\text{b}},i}} }}\left| {\overrightarrow {{u_{{\text{l}}} }} - \overrightarrow {{u_{{{\text{b}},i}} }} } \right|^{2} } \cdot Q_{{{\text{b}},i}}^{s} \Delta t, $$

(9)

where d_b,i is the diameter of gas bubbles (m), u_b,i is the velocity of gas bubbles (m/s), C_D,i is the drag coefficient, and Re_i is the Reynolds number of gas bubbles. C_sk is the bubble-induced turbulence coefficient and will be discussed later.

Bubble Tracking

Based on Newton’s second law of motion, the trajectory of gas bubbles is tracked under a Lagrangian reference frame. The discrete random walk model is applied to account for the effect of the turbulent fluctuation on the bubble trajectory. The equation of the bubble motion is described as

$$ \frac{{d\overrightarrow {{u_{{{\text{b}},i}} }} }}{{dt}} = \frac{{\left( {\rho _{{b,i}} - \rho _{l} } \right)}}{{\rho _{{b,i}} }}\cdot\mathop {{\text{ }}g}\limits^{ \to } + \overrightarrow {{F_{{{\text{D}},i}} }} + \overrightarrow {{F_{{{\text{VM}},i}} }} + \overrightarrow {{F_{{{\text{L}},i}} }} + \overrightarrow {{F_{{{\text{P}},i}} }} , $$

(10)

(1) Drag force, F_D,i

The drag force is the most important interphase force and it is proportional to the relative velocity between the liquid phase and gas bubbles.

$$ \overrightarrow {{F_{{{\text{D}},i}} }} = \frac{{3\mu _{{\text{l}}} C_{{{\text{D}},i}} Re_{i} }}{{4\rho _{{{\text{b}},i}} d_{{{\text{b}},i}}^{2} }}\left( {\overrightarrow {{u_{{\text{l}}} }} - \overrightarrow {{u_{{{\text{b}},i}} }} } \right) $$

(11)

$$ Re_{i} = \frac{{\rho _{{\text{l}}} d_{{{\text{b}},i}} \cdot\left| {\overrightarrow {{u_{{\text{l}}} }} - \overrightarrow {{u_{{{\text{b}},i}} }} } \right|}}{{\mu _{{\text{l}}} }}. $$

(12)

The diameter of gas bubbles is assumed to be constant and it is calculated as follows[20]:

$$ d_{b} = 0.35\left( {\frac{{Q^{2} }}{g}} \right)^{0.2}, $$

(13)

where Q is the gas flow rate (m³/s).

In Eq. [11], the magnitude of the drag force is directly influenced by the drag coefficient. Table II indicates six correlations for the drag coefficient, which are commonly adopted in gas-stirred systems. In order to obtain an appropriate drag coefficient, the predicted results of these different drag coefficient models were compared with the measured data.

Table II Six Drag Coefficient Models Used in the Current Study

(2) Virtual mass force, F_VM,i

Due to gas bubbles accelerating relative to the liquid, the velocity of the surrounding liquid will increase. The additional force is called the virtual mass force and it is represented by the following equation.

$$ \overrightarrow {{F_{{{\text{VM}},i}} }} = C_{{{\text{VM}}}} \frac{{\rho _{{\text{l}}} }}{{\rho _{{{\text{b}},i}} }}\frac{d}{{dt}}\left( {\overrightarrow {{u_{{\text{l}}} }} - \overrightarrow {{u_{{{\text{b}},i}} }} } \right), $$

(14)

where C_VM is the virtual mass coefficient, which is different among the literature. Some researchers[7,14] reported that the virtual mass force could be neglected because it has an extremely weak influence on the multiphase flow. Geng[6] and Zhu et al.[8] adopted a value of 0.5 for spherical bubbles, but Méndez et al.[13] suggested a value of 0.04. For deformed bubbles moving near a plane wall, van der Geld and Kuerten[27] indicated that 0.7 is a more reasonable value for the virtual mass coefficient. For the current gas–liquid flow, the virtual mass coefficient was determined by comparing the predicted results with the measured data.

(3) Lift force, F_L,i

When the gas bubble moves in a linear shear flow, there is an unsymmetrical pressure distribution on its external boundary, and the lift force appears. The unsymmetrical pressure distribution is mainly caused by the velocity gradients in the liquid. Pressure is lower in the region of the largest relative velocity. The lift force is defined in terms of the slip velocity and the curl of the liquid velocity.

$$ \overrightarrow {{F_{{{\text{L}},i}} }} = C_{{\text{L}}} \frac{{\rho _{{\text{l}}} }}{{\rho _{{{\text{b}},i}} }}\left( {\overrightarrow {{u_{{\text{l}}} }} - \overrightarrow {{u_{{{\text{b}},i}} }} } \right) \times \nabla \times \overrightarrow {{u_{{\text{l}}} }} , $$

(15)

where C_L is the lift coefficient. Zhang[12] clearly described a better agreement with experimental data when the interphase lift force was taken into account in gas-stirred systems. Drew and Passman[28] found that C_L was 0.5 for an inviscid flow around a sphere and 0.01 for a viscous flow. Pourtousi and Sahu[29] suggested that the lift coefficient C_L for bubbly flow regime with small spherical bubbles was in the range of 0.1 to 0.5. Tomiyama et al.[30] proposed an empirical correlation of C_L as a function of the bubble Reynolds number and a modified Eötvös number in simple shear flows. They reported that the lift coefficient was in the range of 0 < C_L ≤ 0.288 for small bubbles of diameter less than 5.8 mm, whereas for the bubbles of larger diameter (>5.8 mm) the lift coefficient took a negative value. Accordingly, it is necessary to quantitatively analyze the effects of different lift coefficients on the gas–liquid flow behavior.

(4) Pressure gradient force, F_P,i

The pressure gradient force mainly originates from the acceleration of the liquid in the vicinity of gas bubbles. It depends on the velocity of gas bubbles and the acceleration of the liquid. The corresponding expression is as follows:

$$ \overrightarrow {{F_{{{\text{P}},i}} }} = \frac{{\rho _{{\text{l}}} }}{{\rho _{{{\text{b}},i}} }}\overrightarrow {{u_{{{\text{b}},i}} }} \cdot\nabla \overrightarrow {{u_{{\text{l}}} }} . $$

(16)

Computational Procedure and Boundary Conditions

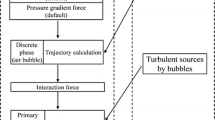
The three-dimensional geometric model and mesh of the RH degasser were created using Gambit version 2.4.6, as shown in Figure 1. By the mesh independence study, the optimum number of mesh cells was approximately 300,000. The system of equations was solved by combining the authors’ user-defined subroutines with a commercial CFD software (Fluent version 17.0). The flow chart of the mathematical models is given in Figure 2. The PISO scheme was used for the pressure–velocity coupling. The convergence criterion for all variables was set to 10⁻⁴. The time step was 0.001 second.

Fig. 1

Geometric model and mesh configuration

Fig. 2

Flow chart of mathematical models

The inlet velocity was calculated according to the total gas flow rate at the nozzle. Non-slip conditions were chosen at the walls. The standard wall function was used to model the turbulence characteristics in the near-wall region. Atmospheric pressure was assumed on the free surface of the ladle. The free surface is allowed to move, considering a manometric pressure in the vacuum chamber of − 4802 Pa. It corresponds with a vacuum degree of 133 Pa in actual operations satisfying the dynamic similarity. The volume fraction of the gas was unity at the top portion of the ladle and the vacuum chamber. The system was assumed to be isothermally at 298 K (25 °C).

Results and Discussion

To verify the accuracy of the developed model, the measurements of velocity fields were performed for a one-fifth-scale water model using a Particle Image Velocimetry (PIV) equipment. The dimensions of the water model and property parameters employed in the simulation are listed in Table III. The details of the measurements of velocity fields are introduced in Reference 9.

Table III Dimensions of Water Model and Parameters Used in the Simulation

The Effect of Drag Force

Figure 3 indicates the velocity fields predicted using different drag coefficient models in two directions as shown in Figure 1, and the results are compared with those measured by PIV. The number of nozzles and gas flow rate are four and 20 L/min, respectively. Figure 3(a) corresponds to the velocity fields in the direction of the flow leaving the down-leg snorkel and Figure 3(b) corresponds to the velocity fields in a radial direction, at a height of 500 mm. It can be observed that the liquid from the down-leg snorkel flows into the ladle at a velocity of 0.23 m/s, and then its velocity gradually decreases as a result of the dissipation of the kinetic energy. At the same time, there are two peaks in velocities in the radial direction of the ladle. The largest peak corresponds to the velocity of the liquid from the down-leg snorkel and the second peak to the liquid ascending to the up-leg snorkel. The results of models A and F agree well with the measured results. When models B, C, D, and E in Table II are adopted in the model, the velocity of the liquid from the down-leg snorkel is decreased by approximately 50 pct. The predicted liquid velocities in the above-mentioned two directions are greatly underestimated.

Fig. 3

Effect of drag coefficient on the velocity distribution (a) along the down-leg and (b) along radial direction at a height of 500 mm

Figure 4 shows the motion of gas bubbles in the up-leg snorkel using models C and F. The color and length of the arrow represent the magnitude of the bubble velocity. For model C, gas bubbles cannot reach the center of the up-leg snorkel and only rise up along the wall. Conversely, when model F proposed by Morsi and Alexander[26] is adopted, the penetration depth of gas bubbles increases and some bubbles reach the center of the up-leg snorkel so that the distribution of gas bubbles is more widely dispersed. It can be also found that the speed of gas bubbles using model F is obviously larger than that using model C.

Fig. 4

Motion of gas bubbles using (a) model C and (b) model F

Figure 5 shows the relationship between the drag coefficient and the Reynolds number of gas bubbles for models A, C, and F. For models A and F, their drag coefficients are almost identical with each other. However, the drag coefficient of model C is constant at about 1.27. Because the drag coefficient of model C as shown in Table II only depends on the Eötvös number Eo, which represents the ratio of buoyancy to surface tension force. At high Reynolds numbers (Re_b~10⁴) such as gas bubbles entering the liquid from the nozzles, the calculated drag forces of models A and F are about a third that of model C. The drag force acts in the opposite direction to the relative motion of gas bubbles, as shown in Figure 6. For model C, the velocity of gas bubbles along the horizontal direction at the nozzles rapidly decreases and they immediately rise up along the wall of the up-leg snorkel, while for models A and F, gas bubbles can penetrate the liquid up to a certain depth, and then rise up. Therefore, the drag coefficient models proposed by Clift et al.[21] or Morsi and Alexander[26] provide accurate predictions of the gas–liquid flow behavior in the RH degasser.

Fig. 5

Relationship between drag coefficient and Re_b for models A, C, and F

Fig. 6

Motion of gas bubbles in the up-leg snorkel for (a) model C and (b) model F

The Effect of Virtual Mass Force

Figures 7 through 9 show the effect of the virtual mass coefficient on the liquid velocity and gas volume fraction, respectively. It clearly indicates that increasing the virtual mass coefficient from 0 to 0.50, the liquid velocity gradually increases, and then decreases for the virtual mass coefficient of 1.0. By taking into account the overall behavior, the predicted values agree well with the measured ones when the virtual mass coefficient of 0.50 is adopted. For other coefficients, the liquid velocities are underpredicted. The virtual mass force is responsible for reasonable prediction of the gas plume shape in the up-leg snorkel, as shown in Figures 8 and 9. Under the conditions of C_VM ≤ 0.10, the motion of gas bubbles is only confined in the vicinity of the wall, which corresponds to an extremely high gas volume fraction. This phenomenon is referred to as the gas-adhering wall effect.[4,5] As the virtual mass coefficient increases, gas bubbles gradually move toward the center of the up-leg snorkel and the gas-adhering wall effect disappears. For the virtual mass coefficient of 1.0, these individual gas plumes in Figure 9 coalesce into a single gas plume. The increase or decrease of the liquid velocity mainly depends on the area of the plume in the up-leg snorkel. By comparison, it can be determined that the area of the plume is largest when the value of C_VM is taken as 0.50. As a result, the liquid velocities in two directions are larger than that of other coefficients.

Fig. 7

Effect of virtual mass coefficient on the velocity distribution (a) along the down-leg and (b) along radial direction at a height of 500 mm

Fig. 8

Comparison of gas volume in the radial direction as a function of virtual mass coefficient, for a gas flow rate of 20 L/min, at a height of 775 mm

Fig. 9

Comparison of the gas volume fraction as a function of virtual mass coefficient for a gas flow rate of 20 L/min, at a height of 775 mm. (a) 0; (b) 0.05; (c) 0.10; (d) 0.25; (e) 0.50; (f) 1.0

Figure 10 shows the motion of gas bubbles in the up-leg snorkel for the virtual mass coefficients of 0 and 1.0. In the case of ignoring the virtual mass force, the motion of gas bubbles is mainly controlled by the drag force. It impedes the horizontal movement of gas bubbles at the nozzles, and they only move upwards along the wall. It should be noted that the virtual mass force acts opposite to the acceleration of gas bubbles, as shown in Figure 10(b). Initially, gas bubbles decelerate in the radial direction and the virtual mass force is a driving force, and then gas bubbles accelerate in the axial direction and it becomes a resisting force. With the increasing virtual mass coefficient, more bubbles can reach the center of the snorkel and they have the opportunity to collide and coalesce. The appropriate virtual mass coefficient is 0.50.

Fig. 10

Motion of gas bubbles in the up-leg snorkel for (a) C_VM = 0; (b) C_VM = 1.0

The Effect of Lift Force

To determine the appropriate lift coefficient, the predicted values for different lift coefficients are compared with the experimental data, as shown in Figure 11. If the lift force is neglected, the liquid velocity discharged from the down-leg snorkel is underestimated, especially along the height ranging from 400 to 600 mm. As the liquid moves to the ladle’s bottom, the model and measured values offer a satisfactory agreement. Figure 12 shows the effect of the lift coefficient on the distribution of gas bubbles for a height of 775 mm. It is clear that the lift coefficient has a significant influence on the distribution of gas bubbles. The lift force is perpendicular to the relative motion of gas bubbles and the liquid. The increase of the lift coefficient facilitates the spreading of gas bubbles in the radial direction of the up-leg snorkel, which is beneficial to enhance the interaction between the liquid and gas bubbles. Thus, the liquid velocity and the recirculation rate increase, as shown in Figures 11(a) and 13. When the lift coefficient takes a value of 0.50 or 1.0, the liquid velocities in two directions are overestimated. Based on the distribution of the liquid velocity and the recirculation rate, the optimum lift coefficient is 0.10 in the current work.

Fig. 11

Effect of lift coefficient on the velocity distribution (a) along the down-leg and (b) along radial direction at a height of 500 mm

Fig. 12

Comparison of distribution of gas bubbles as a function of lift coefficient for a gas flow rate of 20 L/min, at a height of 775 mm. (a) 0; (b) 0.10; (c) 0.25; (d) 0.50; (e) 1.0

Fig. 13

Effect of lift coefficient on the recirculation rate

The Effect of Pressure Gradient Force

Figure 14 shows the effect of the pressure gradient force on the liquid velocities in two directions. It is observed that the results are similar for the cases with and without the pressure gradient force. A similar response is also revealed in the gas volume fraction as shown in Figure 15, indicating that the pressure gradient force has no influence on the fluid flow in the RH degasser. There is a velocity boundary layer near the wall of the up-leg snorkel. The velocity of gas bubbles at the nozzle or near the nozzle is significantly larger than that of the liquid. Outside the boundary layer, the term of $\nabla \overrightarrow {{u_{{_{{\text{l}}} }} }}$ is small. Consequently, the pressure gradient force is obviously smaller than the drag force. It can be neglected in the current equation of the bubble motion.

Fig. 14

Effect of pressure gradient force on the velocity distribution (a) along the down-leg and (b) along radial direction at a height of 500 mm

Fig. 15

Effect of pressure gradient force on the gas volume for a gas flow rate of 20 L/min, at a height of 775 mm

The Effect of Bubble-Induced Turbulence

For a bubble rising in turbulent flow, its energy consists of the pressure energy from the buoyant force, the potential energy, and the kinetic energy. Due to the low density of the gas bubble, the potential and kinetic energies can be negligible in comparison with the pressure energy. Considering the slip between the liquid and the gas bubble, a portion of the pressure energy lost by the bubble is transferred to the liquid turbulence. The rest becomes the liquid kinetic energy. Figure 16 shows the effect of the bubble-induced turbulence coefficient on the liquid velocities in two directions. It can be seen that an increase in the value of C_sk decreases the liquid velocity, thereby lowering the recirculation rate, as shown in Figure 17. Increasing the value of C_sk means that the more energy generated by the bubble rising is transferred to the liquid turbulent kinetic energy and the rest transferred to the liquid kinetic energy is decreased. Hence, the liquid velocity and the recirculation rate decrease. When the value of C_sk is 0.12, the predicted recirculation rate matches well with the measured value.

Fig. 16

Effect of bubble-induced turbulence coefficient on the velocity distribution (a) along the down-leg and (b) along radial direction at a height of 500 mm

Fig. 17

Effect of bubble-induced turbulence coefficient on the recirculation rate

Figures 18 and 19 indicate the effect of the bubble-induced turbulence coefficient on the gas volume fraction. It is found that increasing the value of C_sk gives rise to the expansion of the gas columns but they remain as individual gas plumes. For these given C_sk, the gas penetration depth is almost identical and the maximum gas volume fraction is reported at a depth of approximately 30 mm. Based on the previous analysis, the drag force and the virtual mass force mainly affect the gas penetration depth, while the lift force dominates the spreading of gas bubbles in the radial direction. Therefore, by adjusting the lift force, the bubble-induced turbulence widens the shape of these individual gas plumes.

Fig. 18

Comparison of gas volume in the radial direction as a function of bubble-induced turbulence coefficient, for a gas flow rate of 20 L/min, at a height of 775 mm

Fig. 19

Comparison of the gas volume fraction as a function of bubble-induced turbulence coefficient for a gas flow rate of 20 L/min, at a height of 775 mm. (a) 0; (b) 0.12; (c) 0.30; (d) 0.50; (e) 0.70

Conclusions

A mathematical model combining VOF and DPM was established to investigate the effects of interphase forces and the bubble-induced turbulence on the gas–liquid two-phase flow in the RH degasser. The conclusions were summarized as follows.

• (1) The drag force and the virtual mass force significantly influence the liquid velocity and the distribution of the gas phase, and they dominate the gas plume shape in the up-leg snorkel. By adopting the drag coefficient models proposed by Clift et al. or Morsi and Alexander, the predicted results agree well with the measured data.

• (2) As the virtual mass coefficient increases, gas bubbles gradually move toward the center of the snorkel and coalesce into a single gas plume. The appropriate virtual mass coefficient is 0.50.

• (3) The increase of the lift force is beneficial for the spreading of gas bubbles in the radial direction of the snorkel, thereby increasing the liquid velocity and the recirculation rate. In the current work, the optimum lift coefficient is 0.10.

• (4) The pressure gradient force has no effect on the fluid flow in the RH degasser and it can be neglected in the equation of the bubble motion.

• (5) With the increasing bubble-induced turbulence, the more energy generated by the bubble rising is transferred to the liquid turbulence, and thus decreases the liquid velocity. By adjusting the lift force, the bubble-induced turbulence widens the shape of the individual gas plumes. When the value of C_sk is 0.12, the predicted recirculation rate matches well with the measured value.