Constitutive Modeling for Predicting High-Temperature Flow Behavior in Aluminum 5083+10 Wt Pct SiC_p Composite

Abstract

A constitutive model capable of predicting material flow behavior with high precision is essential for optimizing secondary processing parameters through simulation techniques. In this study, the hot deformation behavior of aluminum 5083+10 wt pct SiC particulate composite was predicted using constitutive equations based on the modified Johnson–Cook (JC), modified Zerilli–Armstrong (ZA), and strain-compensated Arrhenius models. The models were established on the basis of the true stress–strain values obtained from an isothermal hot compression test conducted on the INSTRON 8801 universal tensile testing machine under a temperature range of 473 K to 773 K and strain rate of 0.01 to 10 s⁻¹. The prediction ability of the modified models was compared by calculating the correlation coefficient (R), average absolute relative error, and relative error. All the models could precisely predict the hot flow behavior of the composite. The modified ZA model had the highest accuracy. The JC model required the least number of material constants and had the lowest calculation time, followed by the modified ZA and strain-compensated Arrhenius models.

Introduction

Most commercially used metallic materials undergo at least one of the following bulk deformation processes: rolling, forging, and extrusion. These processes give the materials their final or near-net shapes. Moreover, these deformation processes cause the formation of refined microstructures that result in enhanced mechanical properties.[1,2,3,4] Strain hardening and dynamic softening processes, such as dynamic recovery (DRV) and dynamic recrystallization (DRX), occur during the hot deformation of metallic materials. These phenomena are dependent on process parameters such as temperature, strain rate, and strain and determine the final microstructure and final properties of a material.[5] Numerical methods, such as finite element analysis, involve the use of constitutive equations as input tools to optimize the process parameters in hot forming processes.[6,7,8] The optimization process is strongly dependent on the prediction of the flow stress through constitutive models.[9,10,11] Therefore, a constitutive model with high prediction accuracy is essential in the manufacturing domain.

Over the past few decades, numerous constitutive models have been established and modified to describe the hot deformation behavior of materials under various processing conditions. Among these models, the hyperbolic sine-type Arrhenius model has been widely used. In this model, the internal strain rate is considered to be dependent on the hot activation energy during the hot deformation of a material. Therefore, a temperature-compensated strain rate parameter, known as the Zener–Hollomon parameter Z, is introduced to establish the Arrhenius-type constitutive model.[12,13] The Arrhenius model has been used extensively by researchers for various materials, such as aluminum alloy, magnesium alloy, and steel.[14,15,16,17,18] Material behavior and material constants depend on strain, temperature, and strain rate. Many researchers have proved that strain compensation considerably enhances the flow stress prediction ability of the Arrhenius model.[19,20,21,22,23,24,25]

Due to their simple form and the small number of material constants involved, the Johnson–Cook (JC) model[26,27] and Zerilli–Armstrong (ZA) model[28] are popular in the research community. The original JC model considers that thermal softening, strain rate hardening, and strain hardening as distinct phenomena that do not depend on each other. However, the model considers their cumulative effects, which occur in real conditions.[29] To overcome this insufficiency, a modified JC model that considers all the effects of the aforementioned three factors was proposed.[30] This modification considerably increases the prediction accuracy of the JC model because it reflects the actual conditions during the high-temperature deformation of materials.[31,32,33,34,35,36,37,38,39] In general, the ZA model is preferred over the original JC model because it considers the combined effect of strain rate and temperature.[40,41,42] The primary drawback of this model is that it cannot predict the material flow behavior above a melting temperature (T_m) of 0.6 K and at low strain rates.[43] A modified ZA model was proposed to overcome these drawbacks.[44] This modified model considers the cumulative effect of thermal softening, strain rate hardening, isothermal hardening, temperature, strain rate, and strain, which results in high prediction accuracy of flow stress.[45,46,47,48,49,50,51,52]

In the past few decades, aluminum metal–matrix composites have been used extensively in many industries because the specific strength, rigidity, specific stiffness, and fatigue resistance of the composites are higher than those of other alloys. Aluminum 5083 is a medium-strength wrought alloy of the Al-Mg (5xxx) series and possesses excellent corrosion resistance in seawater and industrial chemical environments. Moreover, it exhibits good formability and retains exceptional strength after welding.[53] Therefore, aluminum 5083 is extensively used in the marine, chemical, and transport industries. Aluminum 5083 is a non-heat-treatable alloy of the aluminum wrought alloy series. This alloy is mainly strengthened by conducting solid solution strengthening and strain hardening through cold working. There exists a considerable scope for enhancing the mechanical properties of aluminum 5083 through composite fabrication, followed by hot metal working. In this study, aluminum 5083 was used as the matrix material for fabricating a composite. Silicon carbide (SiC) particles (10 wt pct) were used as reinforcement materials in the composite to obtain a higher specific strength than the base alloy.[53] Studying the hot deformation behavior of this composite is important for conducting high-temperature processing. To optimize the hot processing parameters of aluminum 5083, composite constitutive modeling with high prediction accuracy is necessary. The objective of this study was to establish the modified JC, modified ZA, and strain-compensated Arrhenius models by using experimental hot compressive true stress–strain data for predicting the high-temperature flow behavior of aluminum 5083. Moreover, a comparative study of the models was performed to determine the best model among them. The accuracy of the models was examined by comparing various statistical parameters, such as correlation coefficient (R), average absolute relative error (AARE), relative error, flow behavior tracking ability, number of material constants involved, and time required for calculating the material constants.

Materials and Experimental Details

Commercially pure aluminum ingots were melted in a furnace with aluminum–manganese (Mn) master alloy (Mn: 10 wt pct) at a temperature of 800 °C. Degassing was performed using argon gas to remove the impurities and dissolved air from the melt. Commercially pure magnesium pieces and chromium powder were also added. Preheated SiC particles (10 wt pct) of size 3 to 18 µm were added into the vortex created by mechanical stirring. While adding the particles, degassing was performed again to create an argon gas environment and remove as much air as possible. The degassing process continued till the end of stirring. After 5 minutes of mixing at a stirrer speed of 480 rpm, the melt was poured into preheated finger shaped molds and allowed to solidify. The cast fingers were homogenized at 793 K for 12 hours and then cooled in still air. The chemical compositions of the matrix alloy were evaluated using optical emission spectroscopy. The homogenized specimen was cut and metallographically polished. The cut and polished specimen was then etched in freshly prepared Keller’s reagent (1 mL HF, 2.5 mL HNO₃, 1.5 mL HCl, and 95 mL H₂O), and its microstructure was examined using field emission scanning electron microscopy. The composites were cut into cylindrical specimens with a diameter of 10 mm and height of 15 mm for compression test in accordance with ASTM E209. An isothermal compression test was performed using the Instron 8801 universal tensile testing machine at intervals of 100 K in the temperature range of 473 K to 773 K and under strain rates of 0.01, 0.1, 1, and 10 s⁻¹. The aforementioned processing range was selected because warm and hot industrial processing is mostly performed in this range. The crosshead and specimen were enclosed in an insulating chamber during the heating and compression test. The samples and cross head were lubricated with graphite powder at both ends to minimize friction. All the specimens were heated inside the closed chamber at a uniform heating rate of 30 K min⁻¹ to the specified temperature. The specimens were soaked for 5 minutes to ensure that they achieved temperature homogeneity. Subsequently, the specimens were subjected to uniaxial compression up to a true strain of 0.5 and then immediately quenched in cold water. The true stress–strain data of hot deformation were recorded in the computer through the Bluehill software. A K-type thermocouple was used to control the heating rate and measure the specimen temperature. In general, the adiabatic heating effect and additional flow softening become significant when the materials are deformed at a strain rate of 10 s⁻¹ or higher. Because aluminum alloys and their composites possess high thermal conductivity, deformation heating at a strain rate of 10 s⁻¹ does not affect the flow behavior. Similar studies on aluminum alloys and composites have neglected the adiabatic heating effect at a strain rate of 10 s⁻¹.[15,35] In this study, no significant flow softening was observed; thus, the effect was neglected. The barreling effect due to friction was very low because a suitable lubrication technique was used.

Results

Chemical Composition and Microstructure

The results of the chemical composition test are presented in Table I. The microstructure of the as-cast composite (Figure 1(a)) indicated the distribution of the angular-type SiC particles in the matrix alloy and the agglomeration of particles in certain places. The average grain size was calculated to be approximately 78 µm by using the imageJ software. The black dots in Figure 1(a) represent the macro porosities that were formed due to insufficient matrix flow around particle clusters or agglomerations. As presented in Figure 1(b), the matrix–particle interface is strong. This finding indicates that effective load transfer occurred from the matrix to the particle during deformation. The calculation results of the composite revealed that the theoretical and real densities were 2.695 and 2.622 gm cm⁻³, respectively. Thus, the relative density and porosity of the composite were 0.973 and 2.7 pct, respectively.

Table I Chemical Compositions of Al-5083 Matrix Alloy in Weight Percent

Fig. 1

(a) FESEM micrograph of the as-cast aluminum 5083+10 pct SiC_p composite, (b) matrix–particle interface of the composite

Flow Stress Behavior

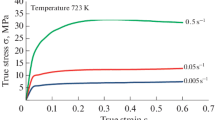
During hot deformation at a relatively low temperature (T_m: 0.5 to 0.6 K), the flow stress of the composite is generally higher than that of the matrix alloy because the strain hardening effect on the composite is higher than that on the matrix alloy due to the pinning effect caused by ceramic particles. At a high temperature, the dislocation density near the particles in the composite is higher than that near the particles in the matrix alloy, which causes higher thermal softening effects in the composite than that in the monolithic alloy. Thus, the difference in the flow stress values of the composite and monolithic alloy is considerably reduced at a relatively high temperature.[54] The true stress–strain results obtained from a high-temperature compression test are displayed in Figures 2(a) through (d). An analysis of the graphs indicates that the flow stress increased rapidly with the strain in the primary stage due to dislocation generation and entanglement. This phenomenon is known as strain hardening.

Fig. 2

True stress–strain curves of aluminum 5083+10 pct SiC composite at various temperatures and at strain rates of (a) 0.01 s⁻¹, (b) 0.1 s⁻¹, (c) 1 s⁻¹, (d) 10 s⁻¹

After the rapid initial increase, a peak stage was attained. The flow stress then almost remained equal to the strain until the final deformation under the following processing conditions: (a) temperature of 473 K to 773 K and strain rate of 0.01 s⁻¹ (Figure 2(a)), (b) temperature of 473 K to 573 K and strain rate of 0.1 to 1 s⁻¹ (Figures 2(b) and (c)), and (c) temperature of 473 K and strain rate of 10 s⁻¹ (Figure 2(d)). The flow stress remained unchanged in the aforementioned conditions because thermal softening began to counteract the strain hardening phenomena in these conditions. At this time, the competition between dislocation generation due to strain hardening and dislocation annihilation and rearrangement due to dynamic softening reached a steady state. Thus, the number of dislocations remained almost constant in the material.[35] The aforementioned characteristic is typical of DRV. After reaching the peak stress, some oscillations followed by the steady state flow behavior was observed under the remaining processing conditions. This observation indicates the occurrence of DRX.[55] Aluminum is a high-stacking-fault-energy material in which thermal softening is mainly predominated by DRV rather than DRX. The rate of nucleation is higher than the rate of grain boundary migration in aluminum because dislocation movement can easily occur through cross slip and climb. The presence of solute Mg and hard ceramic particles (SiC in this study) can considerably influence the thermal softening mechanism of aluminum by hindering the flow of dislocations to a large extent. Therefore, the rate of DRV becomes low and the occurrence of DRX is controlled by the nucleation rate. By contrast, in pure aluminum, DRX is governed by the rate of grain boundary migration. Thus, unlike in pure aluminum, a high temperature and strain rate are required for promoting DRX in aluminum alloys.[56] Previous studies have examined the microstructure of extruded (at 753 K) 5083 monolithic aluminum and 5083 alloy reinforced with SiC particles. The results of these studies indicated less evidence of DRX in aluminum alloys because the microstructure was dynamically recovered completely. However, DRX occurs at a large scale in composite aluminum,[57] which indicates that SiC particles play a more important role than Mg solute atoms in the DRX of Al5083+SiC composite because Mg solute atoms cannot alone promote DRX in Al5083 alloy.[57,58] Therefore, a suitable microstructural study is required to confirm the occurrence of DRX and DRV, which is beyond the scope of this study. At the same strain rate, the peak stress decreases with increase in temperature due to the intensification of thermal activation processes at high temperatures. Moreover, at the same temperature, the peak stress increases with increase in the strain rate because dislocation generation and multiplication occurs at a high rate.[16]

Establishment of Constitutive Models

Modified JC model

The modified JC model can be represented as follows:[30]

$$ \sigma = (A_{1} + B_{1} \varepsilon + B_{2} \varepsilon^{2} )(1 + C_{1} \ln \dot{\varepsilon }^{*} )\exp [(\lambda_{1} + \lambda_{2} \ln \dot{\varepsilon }^{*} )(T - T_{\text{ref}} )], $$

(1)

where σ is the flow stress; ε is the equivalent plastic strain; A₁, B₁, B₂, C₁, λ₁, and λ₂ are material constants; $\dot{\varepsilon }^{*}$ is equal to $\dot{\varepsilon }/\dot{\varepsilon }_{0 }$and is the dimensionless strain rate, where $\dot{\varepsilon }$ is the strain rate and $\dot{\varepsilon }_{0 }$ is the reference strain rate; and T and T_ref are the current absolute temperature and reference temperature in Kelvin, respectively. In this study, the lowest experimental reference temperature (T_ref) and reference strain rate ($\dot{\varepsilon }_{0 } )$ were considered to be 473 K and 0.1 s⁻¹, respectively. The experimental flow stress values obtained in the strain range of 0.1 to 0.5 at intervals of 0.05 were used to establish the modified JC model. At the reference temperature (473 K) and reference strain rate (0.1 s⁻¹), Eq. [1] can be simplified as follows:

$$ \sigma = (A_{1} + B_{1} \varepsilon + B_{2} \varepsilon^{2} ). $$

(2)

By using the experimental true stress–strain data at the reference condition, the relation between ε and σ was obtained (Figure 3). The values of A₁, B₁, and B₂ were obtained by conducting second-order polynomial fitting of the curve (Figure 3). The values of A₁, B₁, and B₂ were 175.281, 305.848, and − 366.37 MPa, respectively.

Fig. 3

Relationship between true strain (ε) and true stress (σ) at the temperature 473 K and strain rate of 0.1 s⁻¹

At the reference temperature (473 K), Eq. [1] can be written as follows:

$$ \sigma = (A_{1} + B_{1} \varepsilon + B_{2} \varepsilon^{2} )(1 + C_{1} \ln \dot{\varepsilon }^{*} ) $$

(3)

By substituting the values of A₁, B₁, B₂, and the experimental flow stress at the reference temperature, the plot between $\ln \dot{\varepsilon }^{*}$ and σ/(A₁ + B₁ε + B₂ε²) was obtained (Figure 4). The average slope of the fitting curve provided the value of C₁ (0.03767).

Fig. 4

Relationship between $\ln \dot{\varepsilon }^{*}$ and σ/(A₁ + B₁ε  + B₂ε²) at temperature of 473 K

To establish the modified JC model, Eq. [1] was simplified by introducing the following relation: $\lambda_{1} + \lambda_{2} \ln \dot{\varepsilon }^{*} = \lambda .$ If the terms in Eq. [1] are rearranged and the natural logarithm is taken on both sides, the following equation is obtained:

$$ \ln [\sigma /\{ (A_{1} + B_{1} \varepsilon + B_{2} \varepsilon^{2} )(1 + C_{1} \ln \dot{\varepsilon }^{*} )\} ] = \lambda [(T - T_{\text{ref}} )]. $$

(4)

All the left-hand side material constants of Eq. [4] were known. Therefore, by substituting the experimental stress values at different temperature, strain, and strain rate conditions, the plots of (T −T_ref) vs${ \ln }[\sigma /\{ (A_{ 1} + B_{ 1} \varepsilon \, + B_{ 2} \varepsilon^{2} )( 1+ C_{ 1} { \ln }\dot{\varepsilon }^{*} )\} ]$ were obtained (Figures 5(a) to (d)).

The average slope of the plots provided the value of λ. Four values of λ were obtained for four different strain rates (Table II). The intercept of the plot between $\ln \dot{\varepsilon }^{*}$ and λ (Figure 6) provided the value of λ₁(−0.00451), and its slope provided the value of λ₂(0.00017). The values of the material constants in the modified JC model are listed in Table III.

Fig. 5

Relationship between T − T_r and ln[σ/{(A₁ + B₁ε + B₂ε²)(1 + C₁$\ln \dot{\varepsilon }^{*}$)}] for strain rates (a) 0.01 s⁻¹, (b) 0.1 s⁻¹, (c) 1 s⁻¹, (d) 10 s⁻¹

Table II Values of λ Under Different Strain Rates

Fig. 6

Relationship between $\ln \dot{\varepsilon }^{*}$ and λ₁ + λ₂$\ln \dot{\varepsilon }^{*}$

Table III Parameters for the Modified Johnson–Cook Model for Predicting High-Temperature Flow Stress of Aluminum 5083+10 Pct SiC_p Composite

Based on the modified JC model, the following constitutive equation was obtained for the Al 5083+10 wt pct SiC_p composite:

$$ \sigma = (175.281 + 305.848\varepsilon - 366.370\varepsilon^{2} )(1 + 0.03767\ln \dot{\varepsilon }^{*} )\exp [( - 0.00451 + 0.00017\ln \dot{\varepsilon }^{*} )(T - T_{\text{ref}} )] $$

(5)

By using Eq. [5], the flow stress of the composite material was predicted by substituting the values of the working temperature, strain rate, and strain.

Modified ZA model

The modified ZA constitutive model for predicting the high-temperature flow stress is as follows:[44]

$$ \sigma = (C_{1} + C_{2} \varepsilon^{n} )\exp [ - (C_{3} + C_{4} \varepsilon )T^{*} + (C_{5} + C_{6} T^{*} )\ln \dot{\varepsilon }^{*} ], $$

(6)

where σ is the flow stress; C₁, C₂, C₃, C₄, C₅, C₆, and n are material constants; ε is the equivalent plastic strain; T^* is equal to T −T_ref, where T and T_ref are the current and reference temperatures, respectively; and $\dot{\varepsilon }^{*}$ is equal to $\dot{\varepsilon }/\dot{\varepsilon }_{0 }$ and is the dimensionless strain rate, where $\dot{\varepsilon }$ and $\dot{\varepsilon }_{0 }$ are the current and reference strain rates, respectively.

The reference temperature and reference strain rate considered in the modified JC model were also used for calculating the material constants of the modified ZA model (T_ref = 473 K and $\dot{\varepsilon }_{0 }$ = 0.1 s⁻¹). The experimental flow stress values obtained in the strain range of 0.1 to 0.5 were employed to establish the ZA model. At the reference strain rate, Eq. [6] is modified as follows:

$$ \sigma = (C_{1} + C_{2} \varepsilon^{n} )\exp [ - (C_{3} + C_{4} \varepsilon ) T^{*} ] $$

(7)

After taking the natural logarithm on both sides of Eq. [7], the following equation is obtained:

$$ { \ln }\sigma = { \ln }(C_{1} + C_{2} \varepsilon^{n} ) - (C_{3} + C_{4} \varepsilon )T^{*} $$

(8)

By substituting the experimental values at $\dot{\varepsilon }_{0 }$ = 0.1 s⁻¹, the relation between T^* and ln σ was obtained (Figure 7). Nine groups of intercepts and slopes were obtained after performing linear fitting of the data points between true strain values of 0.1 to 0.5 at an interval of 0.05.

Fig. 7

Relationship between T^* and lnσ

The intercept and slope can be represented as follows:

$$ I_{1} = \ln (C_{1} + C_{2} \varepsilon^{n} ) $$

(9)

$$ S_{1} = (C_{3} + C_{4} \varepsilon ) $$

(10)

By rearranging the terms in Eq. [9] and taking the natural logarithm on both sides, the following equation is obtained:

$$ \ln (\exp I_{1} - C_{1} ) = \ln C_{2} + n\ln \varepsilon . $$

(11)

The value of C₁ is approximately equal to the yield stress under the reference temperature and reference strain rate. The approximate value of C₁ (130.665 MPa) was obtained from the experimental data at the reference condition. By substituting the value of C₁ in Eq. [11], the relationship between lnε and ln(exp I₁ − C₁) was established (Figure 8). After linear fitting of the data points, the values of n(0.2117) and C₂ (126.716 MPa) were obtained.

Fig. 8

Relationship between lnε and ln (exp I₁ − C₁)

The graph of ε vs S₁ was plotted (Figure 9). After linear fitting, the intercept (C₃) and slope (C₄) were calculated to be 0.00405 and 0.00093, respectively.

Fig. 9

Relationship between true strain (ε) and slope S₁

By taking the natural logarithm of Eq. [6], the following equation is obtained:

$$ \ln \sigma = \ln (C_{1} + C_{2} \varepsilon^{n} ) - (C_{3} + C_{4} \varepsilon )T^{*} + (C_{5} + C_{6} T^{*} )\ln \dot{\varepsilon }^{*} . $$

(12)

The slope of the $\ln \dot{\varepsilon }^{*}$ curve vs the lnσ curve provided the value of (C₅ + C₆T^*). Thus, nine slope values were obtained for nine different strains at each of the four different temperatures. The slope can be expressed as follows:

$$ S_{2} = C_{5} + C_{6} T^{*} . $$

(13)

Therefore, the relationship between T^* and S₂ can be obtained (Figure 10). The values of C₅ and C₆ were obtained from the intercept and slope of the fitting line of the data points, respectively. Nine sets of C₅ and C₆ values were obtained for nine different strains. The values of C₅ and C₆ are listed in Table IV.

Fig. 10

Relationship between T^*and slope S₂

Table IV Nine Group of Values of C₅ and C₆

To determine the most suitable set of C₅ and C₆ values, a standard unbiased statistical parameter, namely the AARE, was used.[1]

$$ {\text{AARE}}({\rm pct}) (\Delta ) = {1 \mathord{\left/ {\vphantom {1 {N\mathop \sum \limits_{i = 0}^{N} \left| {\frac{{E_{i} - P_{i} }}{{E_{i} }}} \right|}}} \right. \kern-0pt} {N\mathop \sum \limits_{i = 0}^{N} \left| {\frac{{E_{i} - P_{i} }}{{E_{i} }}} \right|}} \times 100, $$

(14)

where E_i and P_i are the experimental and predicted data obtained from the equations, respectively, and N is the total number of data involved in the calculation. Optimization was performed by minimizing the AARE value between the experimental and predicted flow stress. The minimum AARE value was achieved at a strain of 0.1, and the corresponding C₅ and C₆ values were 0.03488 and 0.000187, respectively (Figure 11). The material constants of the modified ZA model are presented in Table V.

Fig. 11

Values of AARE percentages derived using different groups of C₅ and C₆ at nine different strains

Table V Parameters for the Modified Zerilli–Armstrong Model for Predicting High-Temperature Flow Stress of Aluminum 5083+10 Pct SiC_p Composite

The constitutive equation based on the modified ZA model can be written as follows:

$$ \sigma = (130.665 + 126.761\varepsilon^{0.2117} )\exp [ - (0.00405 + 0.00093\varepsilon )T^{*} + (0.03488 + 0.00018T^{*} )\ln \dot{\varepsilon }^{*} ] $$

(15)

The flow stress of the composite can be predicted by substituting the values of the process parameters (temperature, strain rate, and strain) in Eq. [15].

Strain-compensated Arrhenius model

The Arrhenius model can predict the flow stress with high accuracy at high-temperature deformation conditions. The flow stress, temperature, and strain rate can be correlated at low and high stress levels with Arrhenius-type equations by using the power law and exponential law, respectively.

$$ \dot{\varepsilon } = A_{1} \sigma^{{n_{1} }} \exp \left( { - Q/RT} \right) $$

(16)

$$ \dot{\varepsilon } = A_{2} \exp (\beta \sigma )\exp ( - Q/RT), $$

(17)

where σ is the flow stress; $\dot{\varepsilon }$ is the strain rate; A₁, A₂, n₁, and β are the material constants; T is the absolute temperature in K; R is the universal gas constant (8.314 J mol⁻¹ K⁻¹); and Q is the activation energy of hot deformation (kJ mol⁻¹).

A hyperbolic sine-type equation is acceptable for the entire stress level range. The hyperbolic sine-type equation is represented as follows:

$$ \dot{\varepsilon } = A\sin [h(\alpha \sigma )]^{n} \exp ( - Q/RT), $$

(18)

where A and n are material constants and α is the stress multiplier that can be expressed as α = β/n₁ MPa⁻¹.

To demonstrate how the deformation behavior was influenced by the combined effect of the temperature and strain rate, a temperature-compensated strain rate parameter, namely the Zener–Hollomon parameter Z, was introduced in the following exponential form:

$$ Z = \dot{\varepsilon }\exp (Q/RT). $$

(19)

By substituting Eq. [19] into Eq. [18], the Zener–Hollomon parameter Z can be expressed as follows:

$$ Z = A[\sinh (\alpha \sigma )]^{n} . $$

(20)

In this study, the solution procedure of the material constants of the Al 5083+10 wt pct SiC_p composite at a strain of 0.1 is elaborated. By applying natural logarithm to both sides of Eqs. [16] and [17], the following equations are obtained:

$$ \ln \dot{\varepsilon } = \ln A_{1} + n_{1} \ln \sigma - (Q/RT) $$

(21)

$$ \ln \dot{\varepsilon } = \ln A_{2} + \beta \sigma {-}(Q/RT). $$

(22)

The experimental flow stress and corresponding strain rate are used in the aforementioned equations. The relationships between ln σ and $\ln \dot{\varepsilon }$ and between σ and $\ln \dot{\varepsilon }$ are displayed in Figures 12(a) and (b), respectively. Linear fitting was performed between the data points. The slopes of the lines in Figures 12(a) and (b) provided the values of n₁ and β at different temperatures, respectively. The average values of n₁ and β were calculated to be 17.5080 and 0.1378, respectively. The average value of the material constant α(α = β/n₁) was 0.0079 MPa⁻¹.

Fig. 12

Relationships between (a) lnσ and $\ln \dot{\varepsilon }^{*}$; (b) σ and $\ln \dot{\varepsilon }$

If the natural logarithm is taken on both sides of Eq. [18], the following equation is obtained:

$$ \ln \dot{\varepsilon } = \ln A + n\ln [\sinh (\alpha \sigma )] - (Q/RT). $$

(23)

For a constant strain rate, differentiating Eq. [26] with respect to 1/T provides the following relation:

$$ Q = R \times n \times \left[ {\frac{{d\{ \ln \sin [h(\alpha \sigma )]\} }}{{d\left( {\frac{1}{T}} \right)}}} \right]_{{\dot{\varepsilon }}} . $$

(24)

The plots of ln[sinh(ασ)] vs ln$\dot{\varepsilon }$ and 1000/T vs ln[sinh(ασ)] are illustrated in Figures 13(a) and (b), respectively. The average slope of these two curves after fitting provided the values of n and $\left[ {\frac{{d\{ \ln \sin [h(\alpha \sigma )]\} }}{{d\left( {\frac{1}{T}} \right)}}} \right]_{{\dot{\varepsilon }}}$ (12.3993 and 1.8401, respectively).

Fig. 13

Relationship between (a) lnsin[h(ασ)]and $\ln \dot{\varepsilon }$, (b) 1000/T and lnsin[h(ασ)]

By using Eq. [24], the average activation energy of the Al5083+10 wt pct SiC_p composite at a strain of 0.1was calculated as follows: Q = 8.314×12.3993×1.8401 = 189.692 kJ mol⁻¹. In a previous study, the average activation energy of the Al5083+2 vol pct TiC composite was calculated to be 185.85 kJ mol⁻¹.[55] In another study, the average activation energy of the Al2014+10 wt pct SiC composite was 168 kJ mol⁻¹.[59] Thus, the activation energy of aluminum composites is considerably higher than the activation energy for self-diffusion in pure aluminum (142 kJ mol⁻¹), which indicates that SiC particles affect the flow behavior to a large extent.

To obtain accurate values of A and n, the natural logarithm is taken on both sides of Eq. [20], and the following equation is obtained:

$$ \ln Z = \ln A + n \ln [\sinh (\alpha \sigma )]. $$

(25)

The values of Z at different temperatures and strain rates were calculated from using Eq. [19] by assuming that Q is equal to189.692 kJ mol⁻¹. Figure 14 illustrates the relationship between ln[sinh(ασ)] and ln Z. The slope and intercept of the linear fitting curve provided accurate value of n and lnA (11.855 and 34.89, respectively). The value of A was 1.42 × 10¹⁵.

Fig. 14

Relationship between lnsin[h(ασ)] and ln Z

Strain compensation

In all the equations of the Arrhenius model (Eqs. [16] to [20]), the effect of strain is neglected. Many researchers have proved that strain has a significant effect on the deformation activation energy and material constants.[15,16,17,18] During hot deformation in a high-strain region, the strain hardening process is either counterbalanced or overpowered by using dynamic softening processes, such as DRV and DRX.[31] Therefore, strain compensation is introduced in the Arrhenius model for predicting flow behavior with a high accuracy.

In this study, the material constants α, n, Q, and A were evaluated under a strain range of 0.1 to 0.5 at strain intervals of 0.05 by using the procedure described previously in the text. Plots of the obtained values are illustrated in Figures 15(a) and (b). The material constants were significantly affected by strain. A fifth-order polynomial equation was employed because it is suitable for determining the influence of strain on the material constants with very good correlation and generalization, as shown by other studies.[33,34,50] The coefficients obtained after fifth-order polynomial fitting of all the curves (Figure 15) are listed in Table VI.

Fig. 15

Variations of materials constants with true strain (ε) (a) α and n; (b) Q and lnA

Table VI Coefficients of Polynomial for α, lnA, n, Q

The material constants under different strains can be derived from the following polynomial equation:

$$ \begin{aligned} \alpha & = \alpha_{0} + \alpha_{1} \varepsilon + \alpha_{2} \varepsilon^{2} + \alpha_{3} \varepsilon^{3} + \alpha_{4} \varepsilon^{4} + \alpha_{5} \varepsilon^{5} \\ n & = n_{0} + n_{1} \varepsilon + n_{2} \varepsilon^{2} + n_{3} \varepsilon^{3} + n_{4} \varepsilon^{4} + n_{5} \varepsilon^{5} \\ Q & = Q_{0} + Q_{1} \varepsilon + Q_{2} \varepsilon^{2} + Q_{3} \varepsilon^{3} + Q_{4} \varepsilon^{4} + Q_{5} \varepsilon^{5} \\ \ln A & = A_{0} + A_{1} \varepsilon + A_{2} \varepsilon^{2} + A_{3} \varepsilon^{3} + A_{4} \varepsilon^{4} + A_{5} \varepsilon^{5} . \\ \end{aligned} $$

(26)

Based on the definition of the hyperbolic law, flow stress can be expressed as a function of the Zener–Hollomon parameter Z as follows:

$$ \sigma = (1/\alpha )\ln \{ (Z/A)^{1/n} + [(Z/A)^{2/n} + 1]^{1/2} \} . $$

(27)

The values of the material constants were determined using polynomial equations (using the values in Table VI) and the corresponding Z parameter values. The material constant values were then used to calculate the flow stress of the composite in various process conditions by using Eq. [27].

Discussion

Constitutive equations were developed for the Al5083+10 wt pct SiC_p composite by using the modified JC, modified ZA, and strain-compensated Arrhenius models. The flow stress of the composite at different strain values, four temperatures, and four strain rates was evaluated using Eqs. [5], [15], and [27] and the data presented in Table VI.

A total of 144 flow stress values were generated for each individual constitutive model under the various processing conditions. The plots of the experimental and predicted flow stress values obtained using the modified JC, modified ZA, and strain-compensated Arrhenius models at different processing conditions are illustrated in Figures 16 through 18, respectively. The graphs indicate that the flow stress values predicted by the three models correlate well with the experimental values for almost all the processing conditions.

Fig. 16

Comparison between experimental and predicted flow stress values by modified Johnson–Cook constitutive equation at various temperatures and at strain rates of (a) 0.01 s⁻¹, (b) 0.1 s⁻¹, (c) 1 s⁻¹, (d) 10 s⁻¹

Fig. 17

Comparison between experimental and predicted flow stress values by modified Zerilli–Armstrong constitutive equation at various temperatures and at strain rates of (a) 0.01 s⁻¹, (b) 0.1 s⁻¹, (c) 1 s⁻¹, (d) 10 s⁻¹

Fig. 18

Comparison between experimental and predicted flow stress values by strain-compensated Arrhenius constitutive equation at different temperatures and at strain rates of (a) 0.01 s⁻¹, (b) 0.1 s⁻¹, (c) 1 s⁻¹, (d) 10 s⁻¹

The accuracies of the three models were verified by comparing their correlation coefficients (R), AAREs, and relative errors.

The correlation coefficient exhibited linearity between the experimental and predicted values.[35,48] The correlation coefficient can be expressed as follows:

$$ R = \frac{{\mathop \sum \nolimits_{i = 1}^{i = N} (E_{i} - \bar{E})(P_{i} - \bar{P})}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{i = N} (E_{i} - \bar{E})^{2} \mathop \sum \nolimits_{i = 1}^{i = N} (P_{i} - \bar{P})^{2} } }}, $$

(28)

where E_i and P_i are the experimental and predicted data, respectively; $\bar{E}$ and $\bar{P}$ are the mean values of the experimental and predicted data, respectively; and N is the total number of data involved in the calculation. Figures 19(a) through (c) display the plots between the experimental and predicted flow stress values. The correlation coefficient values calculated for the modified JC, modified ZA, and strain-compensated Arrhenius model were 0.995, 0.996, and 0.995, respectively. The results indicate that the experimental and predicted values under different processing conditions are very close to the linear fitting line.

Fig. 19

Correlation between experimental and predicted flow stress values obtained from (a) modified JC model, (b) modified ZA model, (c) strain compensated Arrhenius model

The AARE is more precise than the correlation coefficient for determining the accuracy of the models because the AARE is obtained by conducting a term-by-term calculation of the relative error. The expression for obtaining the AARE is presented in Section IIIC2. The AARE value obtained for the modified JC model was 4.296, which is higher than the value obtained for the modified ZA model (3.341). Moreover, the AARE value obtained for the modified ZA model is lower than that obtained for the strain-compensated Arrhenius model (4.621; Figure 20).

Fig. 20

Comparison of average absolute relative error values of three models

The prediction ability of the models was further investigated by calculating the relative error percentage. The relative error can be expressed as follows:

$$ {\text{Relative}}\,\,{\text{error}}\,\,{\text{percentage}} = (E_{i} - P_{i} )/E_{i} \times 100\,{\rm pct}, $$

(29)

where E_i and P_i are the experimental and predicted data, respectively. The relative error percentages of each value in the three models were calculated and plotted (Figures 21(a) to (c)). The numbers above the column in Figure 21 indicate the sample number in a particular relative error range. The relative errors obtained from the modified JC, modified ZA, and strain-compensated Arrhenius models varied from −8.861 to 18.487, −11.845 to 9.356, and −17.457 to 11.967 pct, respectively.

Fig. 21

Results of relative error analysis by means of (a) modified JC model, (b) modified ZA model, and (c) strain compensated Arrhenius model

The high prediction accuracy of the modified ZA model may be due to the fact that it considers physical phenomena, such as the dislocation mobility, with temperature, strain rate, and strain. By contrast, phenomenological models, such as the modified JC and strain-compensated Arrhenius models, do not consider any physical phenomena other than cumulative effect of temperature, strain rate, and strain. As temperature increases, the dislocation mobility increases rapidly through cross slip and climb. The occurrence of thermal softening processes, such as DRV and DRX, solely depends on increase in dislocation mobility. Therefore, in addition to phenomenological parameters, such as temperature, strain rate, and strain, the dislocation movement must also be considered in a constitutive model for the accurate prediction of flow behavior. In the modified ZA model, two coupled effects are considered (Eq. [6]), namely the combined effect of (i) the strain rate and temperature and (ii) the strain and temperature. However, in the modified JC model (Eq. [1]) and strain-compensated Arrhenius model, only the coupled effect of the strain rate and temperature (multiplication term and Z parameter, respectively) is considered. During deformation at a given strain, the dislocation density of composites is generally higher than that of base alloys due to the hindrance of dislocation motion by ceramic particles in composites. The aforementioned condition is favorable for DRX and increased flow softening, which are generally triggered by a high temperature. Therefore, unlike in base alloys, the coupling effect of strain and temperature and the combined effect of the strain rate and temperature are significant in the case of composites. The presence of two significant combined effects may be the reason for the superior prediction ability of the modified ZA model in this study. The modified ZA model was reported to have a higher prediction accuracy than the Arrhenius and JC models for the Al5083+2 pct TiC nanocomposite.[60]

The modified JC model included six material constants, whereas the modified ZA model included seven material constants. The strain-compensated Arrhenius model included almost twice the number of material constants than the ZA and JC models. The JC model required the least calculation time. The calculation time increased for the modified ZA model when the C₅ and C₆ values were optimized by calculating the AARE for different sets of C₅ and C₆ values. In the Arrhenius model, the material constants at every mentioned strain have to be evaluated for the strain-compensation evaluation. Therefore, the Arrhenius model requires considerably higher time for calculation than the other two models. However, the Arrhenius model is necessary for predicting high-temperature flow stress with high accuracy.

Conclusions

A comparative study of the modified JC, modified ZA, and strain-compensated Arrhenius models was performed to determine their ability to predict the high-temperature flow behavior of the Al5083+10 wt pct SiC_p composite in the temperatures ranging from 473 K to 773 K and strain rate from 0.01 to 10 s⁻¹. Based on the results obtained using the three models, the following conclusions can be drawn:

• 1. Constitutive equations based the on modified JC, modified ZA, and strain-compensated Arrhenius models were successfully established. The flow stress values predicted by all the three models were similar to the corresponding experimental values, which implies that these models can represent a high-temperature flow behavior of the aluminum composite with high precision.

• 2. The AARE values of the modified JC, modified ZA, and strain-compensated Arrhenius models were 4.296, 3.341, and 4.621, respectively, which indicate that the predicted values can be useful in numerical analysis. The correlation coefficients of the three models almost had the same value. For the modified JC, modified ZA, and strain-compensated Arrhenius models, 90.97, 95.14, and 82.64 pct of the predicted data were within the relative error percentage range of 0 to ± 10 pct, respectively. The aforementioned results indicate that the modified ZA model is the most suitable for predicting the hot deformation behavior of the aluminum composite in the entire processing domain, followed by the modified JC model.

• 3. The strain-compensated Arrhenius model has the highest number of material constants and requires the highest computation time for evaluating the constants, followed by the modified ZA and modified JC models.