Separating Behavior of Nonmetallic Inclusions in Molten Aluminum Under Super-Gravity Field

Abstract

A new approach to separating nonmetallic inclusions from aluminum melt by super gravity was investigated. To figure out the separating characteristics of inclusions under super-gravity field, the aluminum melt containing MgAl₂O₄ spinel particles was treated with different separating times at 1023 K (750 °C). The significant region with inclusion accumulated appears in the bottom area of the sample obtained by centrifugal separation, and thickness of the region decreases with the increase of the separating time; especially, at the gravity coefficient G = 20, time t = 5 minutes, all inclusions nearly migrate to the bottom of the sample. In addition, the volume fraction, number density, and average size of inclusions gradually increase in the samples along the direction of super gravity, and the distributed gradients of inclusions become sharper with the increase of the separating time. Moreover, the moving velocities of inclusions were theoretical studied for the first time. The moving velocities obtained experimentally agree well with the theoretical ones calculated by Stokes’ law at G ≤ 20, t ≤ 2 minutes. However, there are obvious differences between the experimental and theoretical moving velocities under the conditions of G ≥ 100, t = 2 minutes. It is indicated that Stokes’ law is applicable to the melt with low gravity coefficient in this system.

Introduction

With the rapid growth of automobile manufacturing and aerospace industry, high-quality aluminum alloys are increasingly needed. However, the presence of inclusions within aluminum alloys is considered to have a serious effect on the castability,[1] machinability,[2] and mechanical properties[3,4] of alloys. What is worse, it is almost impossible to avoid the formation of nonmetallic inclusions during the smelting and refining processes of alloys. Therefore, further reducing the level of nonmetallic inclusions in aluminum melt is essential.

Various conventional methods have been proposed for removing inclusions from aluminum melt, such as sedimentation,[5] filtration,[6] bubble floatation,[7] and flux refining.[2] However, due to kinetics and operational limitations,[8] these methods are hardly effective for inclusions removal especially in the case of very fine size and small difference in density between inclusion and metal. For example, the regular gravity sedimentation method is only effective for inclusion larger than 100 μm.[9] Ceramic foam filter is generally effective to remove inclusions larger than 40 μm, but the removal efficiency of inclusions less than 10 μm is only 30 pct.[10] Therefore, as the demand for cleaner metals becomes strict, more efficient methods for inclusion removal are strongly desired.

Higee technology based on super gravity was originally proposed as a process intensification technology in 1979.[11] At present, it has attracted considerable interests from metallurgists because of its advantages of higher efficiency and free-pollution.[12] For example, according to the difference of density between impurities and melt, super gravity can effectively enrich and remove the impurity elements from aluminum alloys, which have been proved to be a potential method for the large-scale purification of metals.[13–15] In addition, enriching the valuable elements from different slags, such as rare-earth-rich slag, by super gravity was investigated, and the recovery ratios of valuable elements were prominent.[16–18] Nevertheless, the study on super-gravity separation of nonmetallic inclusions in the molten metal is seldom reported. In our previous study, the effect of gravity coefficient on inclusion removal in aluminum melt has been investigated by experiments.[19] The results show that inclusions can be effectively separated by super gravity and the separating efficiency increases with increasing of gravity coefficient. However, the moving velocity of inclusions under super-gravity field was not discussed. Therefore, it is necessary to study the movement behavior of inclusions separated by super gravity.

In this work, under a constant super-gravity field, the effect of separating time on inclusions removal in aluminum melt has been investigated. More importantly, moving velocities of inclusions have been calculated based on experimental results and compared to theoretical ones obtained by Stokes’ law. It is expected to provide some theoretical guidance for producing high-clean metal by super gravity.

Experimental

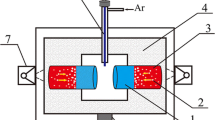
The super-gravity field can be achieved by centrifugal force using a rotating system. A schematic diagram of the experimental apparatus used for the separation of inclusions from Al melt in the super-gravity field is illustrated in Figure 1. It mainly consists of a resistance-heated furnace, a counterweight fixed symmetrically onto the horizontal rotor, and a temperature control system which controls temperature within the observed precision range of ±3 K (±3 °C) with an R type thermocouple. The dashed line represents the furnace and counterweight in stationary status, and they remain horizontal when the centrifugal apparatus is running. The gravity coefficient was calculated as the ratio of super-gravitational acceleration to normal-gravitational acceleration via Eq. [1]

Fig. 1

Schematic diagram of the experimental apparatus in the working state: 1, counterweight; 2, centrifugal axis; 3, resistance coil; 4, metal melt; 5, covering slag; 6, thermocouple

$$ G = \frac{{\sqrt {g^{2} + \left( {r\omega^{2} } \right)^{2} } }}{g} = \frac{{\sqrt {g^{2} + \left( {\frac{{N^{2} \pi^{2} r}}{900}} \right)^{2} } }}{g}, $$

(1)

where, $G$, $\omega$, $N$, $r,$ and $g$ refer to the gravity coefficient, the angular velocity (${\text{rad/s}}$), the rotating speed of the centrifugal (${\text{r/}}\hbox{min}$), the distance from the centrifugal axis to the center of the sample (0.25 m), and the normal-gravitational acceleration (9.8 ${\text{m/s}}^{ 2}$), respectively. When $N = 0$ ${\text{r/}}\hbox{min}$, $G{ = }1$.

A356 alloy was heated to melt in the graphite crucible, and 2 wt pct pure Mg was added into the melt in order to improve the wettability between the melt and nonmetallic inclusion particles. Sequentially 2.5 wt pct SiO₂ (average diameter of 50 μm) was added for simulating nonmetallic inclusions in the aluminum melt, and the molten aluminum was stirred for 10 minutes at a temperature of 903 K (630 °C), and after that, the melt was poured into alloy ingots for experimental materials. Table I represents the chemical composition of the final alloy.

Table I Chemical Composition of the Final Alloy (Mass Percent)

The covering slag for protecting the melt from oxidation during the separation experiments was a mixture of 48 wt pct sodium chloride and 52 wt pct calcium chloride, and both were analytical reagents.

The alloy prepared above (15 g) and the covering slag (5 g) were put into a graphite crucible with the inner diameter of 14 mm as shown in Figure 1 and heated up to a constant temperature of 1023 K (750 °C) to make sure the alloy was entirely melting. Then the centrifugal apparatus was started and adjusted to the specified angular velocity of 267 r/min (G = 20). The centrifugal apparatus was not turned off until the target time, and then the melt was rapidly cooled by water spray. Simultaneously, the parallel experiment was carried out at 1023 K (750 °C) for 5 minutes in normal-gravity field, the sample achieved in this process was named as parallel sample. Each sample was cut into two semicircles along the axial direction, both the semicircles were burnished and polished. One was used for macro-characterization and the other was made into metallographic specimens for microscopic observation. Morphology and chemical composition of inclusions were investigated through a scanning electron microscope-energy dispersive spectroscope (SEM-EDS, MLA250). Optical micrographs were randomly taken along the specific locations (average 20 fields) by an optical microscope (9XB-PC type), and from those, the volume fraction, number, and average size of inclusions were measured using Image-Pro Plus 6.0, and mean values are reported in this paper.

Results and Discussion

Macro-Characterization of the Samples and Separating Efficiency of Inclusions

Figure 2 shows cross section of the samples obtained by super gravity with different separating times. It is seen from Figure 2(a) that the uniform structure presents in the parallel sample without stratification phenomenon under normal-gravity field, while there are significant gray regions with inclusion accumulated at the bottom of the samples under super-gravity field, as illustrated in Figures 2(b) through (d). Moreover, with the increase of separating times, the particle-accumulated region becomes more obvious and the area of particle-accumulated layer decreases.

Fig. 2

Macrographs of the samples obtained by centrifugal treatment with different times: (a) t = 0 min, (b) t = 1 min, (c) t = 2 min, (d) t = 5 min (the microstructure of the areas denoted by A, B, and C are shown in Fig. 6)

To evaluate the separating effect of inclusions by super gravity, the average thickness of particle-accumulated layer ($\delta$) and the separating efficiency of inclusion in the sample ($\eta$) obtained by centrifugal separation were measured. And the separating efficiency is calculated via Eq. [2].[20]

$$ \eta = \left( {1 - \frac{{S_{\text{i}} }}{{{\text{S}}_{\text{t}} }}} \right) \times 100\,{\text{pct}}, $$

(2)

where $S_{\text{i}}$ and $S_{\text{t}}$ are the measured area of the particle-accumulated layer and the total area of the cross section of the sample, respectively.

As illustrated in Figure 3, the separating efficiency of inclusion increases rapidly with the increase of the separating time, while the mean thickness of the particle-accumulated layer sharply decreases with that. However, as the time t is greater than 2 minutes, the separating efficiency increases quite slowly. When the gravity coefficient G = 20, time t = 5 minutes, and the temperature T = 1023 K (750 °C), the separating efficiency of inclusion is up to 83.2 pct. The reason may be that the inclusion concentration becomes higher with the centrifugal separation proceeding, causing the increase of the viscous drag, which leads to more difficult moving for inclusions.

Fig. 3

Average thickness of particle-accumulated layer and separating efficiency with different times. The error bars represent the maximum and minimum values

Micrographs and Quantitative Distributions of Inclusions in the Sample

In order to study the distributions of inclusions in the microstructure of the sample obtained by centrifugal separation, three areas shown in Figure 2(d) were characterized by the metallurgical micrographs. Figure 4 shows the morphology and composition of the inclusion observed by SEM-EDS; the appearance of the inclusion is irregular polygonal. Although Si element was detected, the amount of Si content is quite few. Figure 5 shows SEM-mappings of the inclusion in Figure 4, and it is clearly observed that Si element almost distributes in the metallic matrix. The inclusion is identified to be MgAl₂O₄ spinel particle, and this is because Mg and Al can react with the SiO₂ forming MgAl₂O₄ in this system under high temperature.[21] It also can be seen from Figure 6 that all inclusions nearly aggregate to the bottom of the sample which can hardly find any particles in other areas by centrifugal separation at G = 20, t = 5 minutes. In this system, the density of inclusion (3.60 g/cm³) is larger than that of aluminum melt (2.685 g/cm³);[22] therefore, inclusion particles will move to the bottom of the sample with a specific centrifugal force along the super-gravity direction.

Fig. 4

Inclusion morphology and composition (at. pct) observed by SEM–EDS

Fig. 5

SEM-mappings of the inclusion observed in Fig. 4

Fig. 6

Micrographs of three areas of the sample obtained by super gravity ((a), (b), and (c) refer to A, B, and C marked in Fig. 2(d), respectively)

In order to further characterize the distributions of inclusions at different locations in the sample, the volume fraction and number density of inclusions were measured, as shown in Figures 7 and 8. Compared with the parallel sample, the volume fraction and number density of inclusions sharply increase toward the bottom of samples obtained by centrifugal separation. Moreover, it is also found that the inclusion distributed gradient in the sample becomes steeper with the increase of the separating time. The maximum volume fraction of inclusion at the bottom of the sample reaches 11.3 pct at G = 20, t = 5 minutes. The results show that the gathering effect of inclusions at the bottom of samples becomes better with increasing the separating time.

Fig. 7

Volume fraction of inclusions separated at different distances from top of the sample with different times

Fig. 8

Number density of inclusions at different locations in the sample with different times

Inclusion Size Distributions in Samples Obtained by Super Gravity

It is also known that in a viscous liquid, the velocity of solid particles under a centrifugal force is proportional to the square of the particle diameter [16,22,23] and the separating efficiency of inclusion is strongly affected by the inclusion size. Therefore, it is necessary to determine the inclusion size distributions in the sample obtained by the centrifugal separation. Figure 9 shows the measured size range of inclusions in the melt for centrifugal separating. In this system, inclusion size has a wide range in the sample with the most of inclusions less than 20 μm, and the average diameter of inclusions is calculated to be 7.02 μm. The average inclusion size at different locations is measured and is plotted in Figure 10. It is seen that the average inclusion size is gradually distributed in the sample, and the average inclusion size at the bottom of the sample is greater than that at the upper of the sample. It is noteworthy that the gradient distributions of size are caused by the difference in moving velocity of inclusions with different sizes. Besides, the inclusion size gradient in the sample becomes steeper by increasing the separating time.

Fig. 9

The size range of inclusions in the sample for centrifugal separating

Fig. 10

Average inclusion size distributions in the samples with different times at G = 20, T = 1023 K (750 °C)

Moving Velocity of Inclusions Under Various Gravity Fields

S.G. Shabestari et al. studied the settling velocities of intermetallic particles in liquid aluminum alloys by experiments under normal-gravity field, and the results show that Stokes’ law is applicable to the systems.[24,25] However, the settling velocity of solid particles in the molten metal under super-gravity field has not been studied systematically by experiments. Therefore, in this study, the terminal velocities of the separated inclusions have been calculated from both the experimental data and Stokes’ law for different separating times. In addition, the experimental data for different gravity coefficients from our previous study[19] have also been used for similar calculation. With comparison with these results, the relationship between the experimental and theoretical moving velocity of inclusions is investigated.

Calculation of Moving Velocity Based on the Experimental Results

The moving velocity can be determined by the volumetric flow rate of inclusion particles ($Q$) divided by the effective area ($A_{\text{eff}}$)[24]:

$$ \upsilon = \frac{Q}{{A_{\text{eff}} }}. $$

(3)

The volumetric flow rate of inclusion particles can be written as

$$ Q = \frac{\Delta V}{t}, $$

(4)

where $\Delta V$ is the volume of inclusions which were separated to the bottom of the sample by the centrifugal force, and $t$ is the separating time.

And the effective area ($A_{\text{eff}}$) is the cross-sectional area of inclusions on which the drag force operates along the centrifugal direction and is given by the following equation:

$$ A_{\text{eff}} = \frac{{\pi d_{\text{s}}^{2} A_{\text{avg}} }}{4}, $$

(5)

where $A_{\text{avg}}$ is the average area fraction of inclusions before the centrifugal treatment, here approximately equal to the average area fraction of inclusions in the parallel sample; $d_{\text{s}}$ is the diameter of the sample. For example, at G = 20, separating time of 2 minutes, the experimental moving velocity of inclusions in the melt is calculated as follows.

The difference between volume fraction of inclusions in the particle-accumulated layer of the sample after centrifugal separation and that in the same area of the parallel sample is 5.06 pct (Table II). The volume of the particle-accumulated layer of the sample is 1.08 cm³ (Table II). Hence, the volume of separated inclusions is calculated as

Table II Volume Fraction of Accumulated Inclusions ($\Delta V_{in}$) and Volume of Particle-Accumulated Layer ($V_{ac}$)

$$ \Delta V = 1.08 \times 10^{ - 6} \times 5.06\text{ }{\text{pct}} = 5.46 \times 10^{ - 8} {\text{m}}^{ 3}. $$

And the volumetric flow rate of inclusions is

$$ Q = \frac{\Delta V}{t} = \frac{{5.46 \times 10^{ - 8} }}{2 \times 60} = 4.55 \times 10^{ - 10} {\text{m}}^{ 3} /s. $$

The average area fraction of inclusions in the parallel sample measured by image analysis is 2.07 pct. The effective area is calculated through multiplying the area of cross section of the sample by the average area fraction:

$$ A_{\text{eff}} = 1.54 \times 10^{ - 4} \times 2.07\text{ }{\text{pct}} = 3.19 \times 10^{ - 6} {\text{m}}^{2}. $$

Finally, substituting these values into Eq. [3], the moving velocity of inclusions in the melt at G = 20, t = 2 minutes, T = 1023 K (750 °C) is as follows:

$$ \upsilon = \frac{{4.55 \times 10^{ - 10} }}{{3.19 \times 10^{ - 6} }} = 1.43 \times 10^{ - 4} {\text{m/s}}. $$

Calculation of Moving Velocity Based on Stokes’ Law

It is known that the motion of solid particles in a viscous liquid under a centrifugal force can be determined by Stokes’ law.[26–28] And the terminal velocity attained by a spherical particle moving in the stationary fluid is calculated by the Stokes’ law, which is reached at a very early stage of the centrifugal process.[27, 28] This theoretical moving velocity is given by the following equation:

$$ \upsilon ' = \frac{{\left( {\rho_{\text{p}} - \rho_{\text{L}} } \right)d^{2} Gg}}{18\eta }, $$

(6)

where $\upsilon '$, $\rho_{\text{P}}$, $\rho_{\text{L}}$, $d$, $G$, $g$, and $\eta$ are moving velocity, the density of particle, the density of liquid, particle diameter, the gravity coefficient, gravitational acceleration, and the viscosity of the molten metal, respectively.

The applicable condition of Stokes’ law is that the Reynolds number should be less than 0.2. The Reynolds number is represented as

$$ Re = \frac{{\rho_{\text{L}} \upsilon 'd}}{\eta }. $$

(7)

Substituting the Eq. [6] into Eq. [7], the Reynolds number is expressed as

$$ Re = \frac{{\rho_{\text{L}} \left( {\rho_{\text{P}} - \rho_{\text{L}} } \right)d^{3} Gg}}{{18\eta^{2} }} < 0.2. $$

(8)

And substituting $\rho_{\text{P}} = 3.60 \times 10^{3} {\text{kg/m}}^{3}$, $\rho_{\text{L}} = 2.685 \times 10^{3} {\text{kg/m}}^{ 3}$, $d = 7.02$ μm, $g = 9.81$ m/s², and $\eta = 2.0 \times 10^{ - 3}\;{\text{Pa}}\;{\text{s}}$[22] into Eq. [8],

$$ 1.16 \times 10^{ - 4} \times G < 0.2 $$

Thus, $G < 1724$. It is indicated that when the gravity coefficient is less than 1724, it meets the applicable condition of the Stokes’ law. For example, at G = 20, separating time of 2 minutes, the theoretical moving velocity and the Reynolds number are obtained as follows, respectively:

$$ \upsilon ' = \frac{{(3.60 - 2.685) \times 10^{3} \times (7.02 \times 10^{ - 6} )^{2} \times 9.81 \times 20}}{{18 \times 2.0 \times 10^{ - 3} }} = 2.46 \times 10^{ - 4} {\text{m/s}} $$

$Re = \frac{{(2.685 \times 10^{3}) \times (2.46 \times 10^{-4}) \times (7.02 \times 10^{-6})}}{{2.0 \times 10^{-3}}} = 2.32 \times 10^{-3} < 0.2.$

The similar calculations have also been performed for other experimental results, and the moving velocities obtained from the experiments are compared with those calculated from the Stokes’ law, which are given in Table III. It is evident that there are good agreements between the experimental and theoretical moving velocities at G = 1, t = 5 minutes, G = 20, t = 1 minute, and G = 20, t = 2 minutes, respectively. The small differences between calculated experimental velocity and theoretical velocity may be due to the fact that the inclusions are not truly spherical in the system used here.[25] However, there are obvious differences between the experimental and theoretical moving velocities under the conditions of G ≥ 100, t = 2 minutes. A single inclusion may move at the theoretical moving velocity at the early stage of the separating process when the particle concentration is still low in the lower part of the sample. As the separating process proceeds, the particle concentration becomes higher, leading to the significant increase of the viscous drag. Besides, hindered settling is considered to be arresting when the solid fraction reaches 15 pct or greater.[25,29] In this experiment, for example, the average volume fraction of inclusions reaches 20.20 pct in the particle-accumulated layer of the sample at G = 308, t = 2 minutes. Therefore, the inclusions will move more slowly with the increase of particle concentration, and inclusions can hardly move when they are difficult to overcome the viscous drag.

Table III Moving Velocities of the Inclusion Calculated Based on Experiments and Stokes’ Law (m/s)

Conclusions

The removal of inclusion from aluminum melt with different separating times by super gravity has been investigated. Besides, the relationship between the experimental and theoretical moving velocity is also discussed. The conclusions are summarized as follows:

• 1. Separating nonmetallic inclusions from aluminum melt by super gravity is an effective method. The inclusion-accumulated layer appears in the bottom area of the sample obtained by centrifugal separation.

• 2. The separating efficiency of inclusion increases rapidly with the increase of the separating time. However, when the time t is greater than 2 minutes, the increasing of separating efficiency becomes slow.

• 3. The volume fraction, number density, and the average size are gradually distributed in the samples along the direction of super gravity, and the distributed gradients become steeper with the increase of the separating time.

• 4. Experimental moving velocities are close to the terminal velocities obtained by Stokes’ law when G ≤ 20, t ≤ 5 minutes. However, there are obvious differences between the experimental and theoretical moving velocities under the conditions of G ≥ 100, t  =  2 minutes, due to the fact that the inclusions are not truly spherical and the higher particle concentration causes the greater viscous drag.