1 Introduction

Flow stress is generally determined by compression, tension, and torsion tests of metal specimens using thermomechanical equipment. Among these, the compression test is performed extensively because the pressure direction is similar to that in the industrial manufacturing process of forging or rolling. However, compression generates several uncontrollable effects such as internal–external heat transfer, friction, and heat generation caused by the deformation process. Hence, the axial stresses obtained by the compression tests show considerable errors. An inverse analysis of the axial hot compression test can provide a solution for obtaining a uniaxial flow curve at a uniform temperature T, strain rate \(\dot{\varepsilon }\), and strain \(\varepsilon \). Using a uniaxial flow curve, the dynamic and static kinetics of various alloys have been investigated and quantified. Soltanpour and Yanagimoto[1] reported the kinetics of microstructural evolution by performing an inverse analysis of the hot compression of a Cr–Mo–V steel. They designated the entire acquisition of material data as “material genome.” Ding et al.[2] applied an inverse analysis method to eliminate undesirable effects during the compression experiment and reported the dynamic kinetics of aluminum 5083. Park et al.[3] investigated the flow stresses of 0.2 pct carbon steel at high strain rates of approximately 100 s−1 by analyzing the dynamic response to eliminate noise, such as vibration, in hot compression testing.

From a material viewpoint, different mechanisms of softening occur during the hot deformation of a duplex stainless steel, which consists of two phases, namely, austenite and ferrite. These mechanisms affect the flow stresses of the duplex metal. Duprez et al.[4] investigated the flow stress of a duplex stainless steel during torsional tests and observed that the flow stress is significantly associated with the softening behavior of the phases, which comprises dynamic recrystallization (DRX) and dynamic recovery (DRV). These dissimilar softening behaviors are caused by the difference in the stacking fault energy (SFE) between austenite and ferrite. In general, ferrite, which has a higher SFE, undergoes dominant restoration through DRV, whereas austenite, having a lower SFE, shows dominant restoration by DRX. In austenite, DRX softening is more dominant than DRV softening. This makes the flow behavior of duplex stainless steel complicated. Thus, the mechanism influencing each constituent behavior in duplex stainless steel must be considered. Emami et al.[5] observed the microstructural phenomena occurring during DRV or continuous DRX (cDRX) in the ferrite of SAF 2205 duplex stainless steel. Kumar et al.[6] investigated the flow stress behavior based on the strain rate using the Zener–Hollomon parameter. They reported that the two phases in the Cr–Ni duplex stainless steel exhibited a heterogeneous softening with DRX in austenite and DRV in ferrite, respectively. Cizek[7] found that discontinuous DRX (dDRX) and large-scale subgrain coalescence in austenite as well as cDRX in ferrite are the main factors causing a decrease in the flow stress of 12Cr-10Ni-3Mo duplex stainless steel during high-temperature deformation. Kim et al.[8] developed a method for obtaining decoupled flow stresses between austenite and ferrite in duplex stainless steel based on the dominant dissimilar softening mechanism with DRX in austenite and DRV in ferrite, respectively.

This study aims to investigate the dynamic softening kinetics, regarded as a part of the “material genome” in duplex stainless steel using the inverse analysis with a combination of two decoupled constituent stresses between austenite and ferrite during hot deformation (Table 1).

2 Experiments

2.1 Microstructural Observation Method for Initial and Deformed Specimens

Extruded duplex stainless steel rods of grade SUS329J4L with a diameter of 8 mm and a height of 12 mm were prepared. The chemical composition (wt pct) was 24.79Cr-6.84Ni-2.83Mo-0.69Mn-0.5Si-0.16Co-0.015C-0.14N-0.024P-(bal.)Fe. Microstructural observations were performed using electron backscatter diffraction (EBSD) with a field-emission scanning electron microscope (FE-SEM, JEOL 7100F). The operating condition was set at 13 kV with a TSL orientation imaging microscopy system. The surfaces to be observed were sections cut in the extrusion direction. The surfaces of the cut samples were polished up to 0.04 μm using OP-U non-drying colloidal silica suspensions with no additional additives. The observed area was 150 × 150 μm2 with step sizes of 0.25 μm on the as-received and 0.15 μm on the compressed specimens.

Figure 1 shows the initial microstructures and volume fractions of the extruded rods. The microstructures were analyzed at different points in the extrusion direction sections. The as-received extruded rod exhibited austenite–ferrite structures having elongated grains in the extrusion direction with average volume fractions of 48.5 pct austenite and 51.5 pct ferrite. There is a mixture of partially recrystallized grains and original grains elongated in the deformation direction. The ferrite shows elongated structures with textures in the <001> and <011>//ED and the partially recrystallized austenite shows a relatively random texture.

Fig. 1
figure 1

(a) Phase maps of austenite and ferrite with their respective volume fractions and (b) inverse pole figure (IPF) obtained by EBSD over an area of 150 × 150 μm2 with a step size of 0.25 μm of the as-received specimen

Full size image

To compare the relative chemical partitioning between the austenite and ferrite constituents, FE-SEM with energy-dispersive X-ray spectroscopy (EDS) was conducted at 15 keV. EDS point analysis for Fe, Cr, Ni, Mn, N, C, Mo, Si, Co, and P was performed in the ferrite (dark) and austenite (bright) regions for several hundred seconds. The FE-SEM image of the specimen is presented in Figure 2(a), and the weight percentage of each element is indicated in the box plots of Figure 2(b) to compare the variations in the constituent chemical partitioning of the phases. In the austenite, the weight percentages of Ni, Mn, and N, known as austenite stabilizers, are relatively high. On the contrary, Cr and Mo known as ferrite formers are found in the ferrite phase. The observations are summarized in Table II, and the composition segregations of the austenite stabilizer and ferrite former at each point exhibit the same trends. The partition trends are similar to those reported by Farnoush et al.[9] for 2205 duplex stainless steel, which comprises two constituents: a ferritic phase with 25.9Cr-3.3Ni-2.77Mo-0.4Mn-0.38Si-(bal.)Fe and an austenitic phase with 20Cr-8.78Ni-2.33Mo-2.8Mn-0.26Si-(bal.)Fe.

Fig. 2
figure 2

(a) FE-SEM image of the as-received specimen and (b) variation plots of chemical composition segregation for austenitic stabilizer and ferritic former

Full size image
Table I Nomenclature Used in this Paper
Full size table

2.2 Hot Compression Tests

A high-speed compression testing machine (Thermecmastor Z), depicted in Figure 3(a), was used in the compression experiments. Axial compression was performed to obtain load reduction data at various temperatures, strains, and strain rates. Figure 3(b) shows the time–temperature profile employed in the tests. The specimens were heated using induction coils, and the temperature was regulated by a PID controller through the feedback signal from an R-type thermocouple welded to the surface of the height center of the specimen. Mica sheets were placed between the dies and specimen to reduce friction and heat transfer to the dies. Nitrogen gas, as an inert gas, was used to prevent oxidation on the specimens at elevated temperatures. The specimens were heated at a constant rate of 10 °C/s up to the target temperature, and held therein for 3 minutes to stabilize the temperature distribution in the specimen. Then, the specimens were compressed up to a reduction ratio of 75 pct at temperatures of 1050 °C, 1150 °C, and 1250 °C and strain rates of 0.1, 1, and 10 s−1. Next, the specimens were immediately water-quenched to cool the compressed microstructure. Each experimental condition was repeated twice to ensure reproducibility of the results.

Fig. 3
figure 3

(a) High-speed compression testing machine and (b) experimental condition and temperature profile for compression tests

Full size image

3 Results

3.1 Deformed Microstructures

Duplex stainless steels have two main phases, i.e., ferrite and austenite, which coexist not only at room temperature but also at temperatures above 1000 °C. The flow stresses of these phases are affected by two characteristics of each phase, namely, work hardening and softening, by the combination of their restoration processes with DRX and DRV. Figure 4 shows the results of the EBSD observation after compression for various conditions at temperatures of 1050 °C, 1150 °C, and 1250 °C and strain rates of 0.1, 1, and 10 s−1 with a reduction ratio of 25 pct. In these results, dissimilar microstructural evolutions between the two phases were evident during hot deformation.

Fig. 4
figure 4

IPF maps of compressed specimens at a reduction ratio of 25 pct: (a) fixed strain rate of 0.1 s−1 at temperatures of 1050, 1150, and 1250 °C and (b) fixed temperature of 1150 °C at strain rates of 0.1, 1, and 10 s−1

Full size image

As indicated in Figure 4, restoration occurs during the hot deformation process. The dominant restoration processes of the austenite and ferrite phases in duplex stainless steel are different. In austenite, serrated grain boundaries, severe boundary bulging, and many junctions are observed owing to the occurrence of DRX. Many high-angle grain boundaries (HAGBs) are created in austenite by new grain formation. In contrast, in ferrite, DRX is hardly observed, and DRV is likely the dominant restoration process because of the higher SFE. To obtain the flow stresses and dynamic softening kinetics of duplex stainless steel during hot deformation, the two dominant softening processes, i.e., DRV and DRX, must be considered.

3.2 Results of Compression Tests

The load reduction data obtained from the compression tests are shown in Figure 5. The loads in the experiments decreased as the temperature increased from 1050 °C to 1250 °C and the strain rates decreased from 10 to 0.1 s−1. After a reduction ratio of approximately 50 pct was achieved, the load increased rapidly owing to the effect of increased friction energy between the specimen and dies, which resulted in inhomogeneous barrel deformation on the free surface, and strain hardening. Consequently, a greater load increase occurred toward end of compression stage. The friction barrel effect was inevitable during the experiments.

Fig. 5
figure 5

Reduction loads obtained by hot compression tests at temperatures of 1050 °C, 1150 °C, and 1250 °C and strain rates of 0.1, 1, and 10 s−1

Full size image

In addition, uneven heat distribution in the specimen was inevitable because of the heat dissipation between the specimen and dies and heat generation during the deformation process. Consequently, inhomogeneous distributions of temperature and strain rate had occurred in the specimens, which affected the experimental results. Therefore, inverse analysis must be performed to compensate for the undesirable effects mentioned above and to obtain accurate flow stresses in the uniaxial test.

4 Quantification of Dynamic Softening Kinetics

4.1 Constitutive Flow Stress Model and Procedure for Inverse Analysis

Equations of flow curves to describe the flow stress during hot deformation are available. In this study, Eq. [1] is applied as it includes the critical strain (\({\varepsilon }_{\rm c}\)), strain on peak stress (\({\varepsilon }_{\rm p}\)), and coefficient of steady-state stress (\({\text{F}}_{3}\)) for the flow curve in the austenite phase of duplex stainless steel, which can express the DRX behavior reported by Yanagida et al.[10]

$${\sigma }_{\gamma }=\left\{\begin{array}{ll}F_1{\varepsilon }^{n}& (\varepsilon <{\varepsilon }_{\rm c})\\ F_2{\text{exp}}\left[a{\left(\varepsilon - {\varepsilon }_{\rm p}\right)}^{2}\right]+F_3& (\varepsilon \ge {\varepsilon }_{\rm c})\end{array}\right.$$
(1)

In contrast, in the ferrite phase of duplex stainless steel, a saturated equation without a peak stress is required to represent the dominant DRV behavior. The flow equation of the DRV type may include a saturated stress term when the work hardening and softening are balanced. The saturated stress can be derived from the relationship between dislocation and flow stress, as shown in Eqs. [2, 3] and [4]:

$${\sigma }_{\delta } = {\mathrm{a}}_{\delta }\sqrt{\rho },$$
(2)
$$\frac{\partial \rho }{\partial t}=-{{b}^{{\varvec{D}}}}_{\delta }\rho ,$$
(3)
$${\text{d}}\rho =\frac{\partial \rho }{\partial \varepsilon }{\text{d}}\varepsilon +\frac{\partial \rho }{\partial t}{\text{d}}t,$$
(4)

where \(\rho \) and \({\mathrm{a}}_{\delta }\) are the dislocation density and a material constant, respectively, and \({{b}^{{\varvec{D}}}}_{\delta }\) is the rate of DRV in ferrite. The solution for Eq. [4] can be obtained using the strain and strain rate, as indicated in Eq. [5]. Finally, substituting Eq. [5] into Eq. [2] yields Eq. [6].[11]

$$\uprho =\frac{\mathrm{c}}{{{b}^{{\varvec{D}}}}_{\delta }}\dot{\upvarepsilon }\Big[1-\mathrm{exp}\left(-{{b}^{{\varvec{D}}}}_{\delta }\mathrm{t}\right)\Big]+{\uprho }_{0}\mathrm{exp}\left(-{{b}^{{\varvec{D}}}}_{\delta }\mathrm{t}\right),$$
(5)
$${\sigma }_{\delta }={\mathrm{a}}_{\delta }\{\frac{\mathrm{c}}{{{b}^{{\varvec{D}}}}_{\delta }}\dot{\varepsilon }\Big[1-\mathrm{exp}\left(\frac{-{{b}^{{\varvec{D}}}}_{\delta }}{\dot{\varepsilon }}\varepsilon \right)\Big]+{\uprho }_{0}\mathrm{exp}\left(\frac{-{{b}^{{\varvec{D}}}}_{\delta }}{\dot{\varepsilon }}\varepsilon \right){\}}^\frac{1}{2}.$$
(6)

By considering asymptotic boundary conditions, i.e., when \(\upvarepsilon \) approaches 0 and \(\infty \), the corresponding stress \(\sigma \) is 0 and \({{\sigma }_{\delta }}_{\text{sat}}\), respectively. Subsequently, the DRV-type flow stress equation for the ferrite phase of duplex stainless steel is derived as follows:

$${\sigma }_{\delta }={{\sigma }_{\delta }}_{\text{sat}}\{{1-\mathrm{exp}\left(\frac{-{{b}^{{\varvec{D}}}}_{\delta }}{\dot{\varepsilon }}\varepsilon \right)\}}^{1/2},$$
(7)

where \({{\sigma }_{\delta }}_{\text{sat}}\) = \({\mathrm{a}}_{\delta }{\left(\mathrm{c}/{{b}^{{\varvec{D}}}}_{\delta }\times \dot{\upvarepsilon }\right)}^\frac{1}{2}\).

The rule of mixtures is applied to combine DRX-type Eq. [1] and DRV-type Eq. [7]. It can be expressed as a function of the volume fraction of the constituents and the flow stresses, as follows:[8]

$$\sigma ={\sigma }_{\gamma }\times {Vf}_{\gamma }+{\sigma }_{\updelta }\times {Vf}_{\delta}+{I}_{\gamma /\delta},$$
(8)

where \(\sigma \) is the flow stress of duplex stainless steel; \({\sigma }_{\gamma }\), \({\sigma }_{\delta }\), \({Vf}_{\gamma }\), and \({Vf}_{\delta}\) are the constituent flow stresses and volume fractions of austenite (\(\gamma \)) and ferrite (\(\delta\)) in duplex stainless steel, respectively. A conceptual illustration is presented in Figure 6. The interaction effect (\({I}_{\gamma /\delta}\)) must be included to consider the interactive stresses between the two phases. In this study, we assume that the flow stress exhibits a linear relationship with the volume fractions of the two phases, such that \({I}_{\upgamma /\delta}\) = 0. However, this does not imply the absence of interactions in the grain boundaries of the two phases. Notably, the overall net result of the interactions is negligible due to the balancing of the positive and negative effects, as explained by Ankem et al.[12]

Fig. 6
figure 6

Combination procedure for constituent flow stresses of austenite and ferrite showing each dominant softening effects

Full size image

The flow stress of duplex stainless steel can be derived to include the sensitivity of the strain rate (\(m\)) and temperature (\(A\)) as follows:

$${\sigma }^{*} = \sigma {\dot{\varepsilon }}^{m}\frac{\mathrm{exp}\left(\frac{A}{T}\right)}{\mathrm{exp}\left(\frac{A}{{T}_{0}}\right)},$$
(9)

where \({T}_{0}\) is the reference temperature at the experimental conditions. Using Eq. [9], the sensitivities of temperature and strain rate can be accounted for to consider a much wider range of conditions for hot deformations.

Figure 7 shows the inverse analysis procedure, which involves a comparison of the reduction load data obtained from the tests and thermomechanical finite element method analysis using the flow stresses \(\upsigma \), for the duplex metal, as calculated using Eqs. [1, 7, 8], and [9]. The inverse analysis accounts for the inhomogeneous distribution of temperature induced by induction heating and thermal conduction to the experimental environment, and compensates for the non-uniform deformation of the tested specimen. Thermomechanical computer-aided engineering was performed on each node of the specimen while considering the friction, induction heating, and heat dissipation to the environment from the specimen. For the deformed specimen, the inhomogeneous distributions of temperature, strain, and strain rate were calculated, and those results were subsequently used to determine the coefficients of the flow curves, as described in the previous research.[8] This approach permits to obtain the uniaxial flow stress–strain curves which are expressed by Eqs. [1] and [6]. The inverse analysis was repeated to minimize errors between the experimental data and analyze the load reduction until the optimum values of the independent parameters \({\text{F}}_{1},n,{\varepsilon }_{\rm c},{\text{F}}_{3}\), and \({{b}^{{\varvec{D}}}}_{\delta }\) with the initial sensitivity of strain rate \({m}_{0}\) and temperature A0 were obtained. The values of the dependent parameters \({\text{F}}_{2},a,\) and \({\varepsilon }_{\rm p}\) were calculated based on mathematical continuities of the 1st and 2nd derivatives using the critical strain \({\varepsilon }_{\rm c}\). The stress ratio \(\lambda \), which is associated with \({{\sigma }_{\delta }}_{\text{sat}}\) used in the inverse analysis, is described in the next section.

Fig. 7
figure 7

Inverse analysis procedure for duplex stainless steel of generalized description

Full size image

4.2 Relationship Between Stresses of Austenite and Ferrite

Additional consideration is required to reflect the difference between the constituent flow stresses of austenite and ferrite in duplex stainless steel because only uniaxial experimental curves can be measured in the hot compression test. To calculate the flow stresses of two phases by a single compression test of the duplex stainless steel, an additional boundary condition is required. In this study, \(\uplambda \) is introduced to determine the stress relationship between the two phases.[8] The hot deformation behavior of the duplex stainless steel can be explained by separating each flow stress of the harder austenite and softer ferrite at high temperatures. It is expressed using the rule of mixtures, as presented in Eq. [8]. Because of the dissimilar dominant restorations caused by DRX and DRV in austenite and ferrite, the stress ratio \(\uplambda \) varies depending on the progress of plastic deformation. However, after reaching the saturated or steady-state regime, the two phases converge at the equilibrium state, where the work hardening and softening effects are balanced. In this study, the stress ratio \(\uplambda \) is assumed to be constant for various strains at the equilibrium state. Figure 8 illustrates two methods to calculate the stress ratio \(\uplambda \). The method shown in Figure 8(a) uses an imaginary value of the saturated stress of austenite, whereas that shown in Figure 8(b) employs the actual value of the steady-state stress in the austenite phase.

Fig. 8
figure 8

Conceptual illustration showing the ratio \(\uplambda \) at the equilibrium state based on (a) saturated and (b) steady-state stresses in the austenitic phase

Full size image

To obtain \(\uplambda \), a direct measurement of the constituent stresses between the two phases during hot deformation is required, which is difficult or even impossible. Kim et al.[8] estimated the ratio \(\uplambda \) by changing the chemical composition; subsequently, they simulated the flow stresses of the alloys to determine \(\uplambda \) in the saturated regime of the austenitic and ferritic phases, as presented in Figure 8(a). Because an imaginary value of the saturation stress of austenite was used, the result was difficult to verify. Thus, the ratio \(\uplambda \) was calculated using the steady-state stress of austenite, as shown in Figure 8(b). In this study, we define the ratio \(\uplambda \) using the equilibrium stress \({{\sigma }_{\gamma }}_{\rm ss}\) of the austenitic phase, as expressed in Eq. [10]. Using the steady-state stress of austenite is convenient as it has been published in several reports.

$$\uplambda =\frac{{{\sigma }_{\gamma }}_{\rm ss}}{{{\sigma }_{\delta }}_{\rm sat}}$$
(10)

The value of \(\uplambda \) is determined based on investigated material constants, such as the activation energy of duplex stainless steels from previous studies. The activation energy Q can be calculated to determine the ratio \(\uplambda \) of the steady-state stresses of two constituents using the following.

$$\dot{\varepsilon }\mathrm{exp}\left(\frac{Q}{RT}\right)={A}_{\rm A}\{{\mathrm{sin}h({\alpha }\sigma )\}}^{{n}_{\rm A}},$$
(11)

where \({A}_{\rm A}\), \({n}_{\rm A}\), and \({\alpha }\) are the material constants for duplex stainless steel, Q is the activation energy for hot working (kJ/mol), and R is the universal gas constant (8.314 J/(mol K)).

For strain–stress partitioning, the stresses of multi-component materials can be calculated by two simplifications steps using the isostrain and isostress models. Duplex stainless steel comprises two constituents, namely, austenite and ferrite, which exhibit heterogeneous stress changes. In this study, the isostrain assumption proposed by Taylor et al.[13] was applied to calculate the ratio \(\uplambda \) of the two constituents.

$$\varepsilon ={\varepsilon }_{\gamma }={ \varepsilon }_{\delta }$$
(12)

For each phase, the activation energies can be derived from Eqs. [11] and [12], leading to Eqs. [15] and [16].

$$\mathrm{exp}\left(\frac{{Q}_{\gamma }}{RT}\right)={A}_{\gamma}\{{\mathrm{sin}h({{\alpha }}_{\gamma}{{\sigma }_{\gamma }}_{\rm ss})\}}^{{n}_{A\gamma }}/\dot{\varepsilon }$$
(13)
$$\mathrm{exp}\left(\frac{{Q}_{\delta }}{RT}\right)={A}_{\delta }\{{\mathrm{sin}h({{\alpha }}_{\delta }{{\sigma }_{\delta }}_{\rm sat})\}}^{{n}_{A\delta }}/\dot{\varepsilon }$$
(14)
$$ \frac{{Q_{\gamma } }}{{RT}} = \ln \left[ {A_{\gamma } \frac{{\left\{ {\sinh \left( {\alpha _{\gamma } \sigma _{{\gamma _{{ss}} }} } \right)} \right\}^{{n_{{A\gamma }} }} }}{{\dot{\varepsilon }}}} \right] $$
(15)
$$ \frac{{Q_{\delta } }}{{RT}} = \ln \left[ {A_{\delta } \frac{{\left\{ {\sinh \left( {\alpha _{\delta } \sigma _{{\delta _{{{\text{sat}}}} }} } \right)} \right\}^{{n_{{A\delta }} }} }}{{\dot{\varepsilon }}}} \right] $$
(16)
$$ \frac{{Q_{\gamma } }}{{Q_{\delta } }} = {{\ln \left[ {{{A_{\gamma } \left\{ {\sinh \left( {\alpha _{\gamma } \sigma _{{\gamma _{{ss}} }} } \right)} \right\}^{{n_{{A\gamma }} }} } \mathord{\left/ {\vphantom {{A_{\varUpsilon } \left\{ {\sinh \left( {\alpha _{\varUpsilon } \sigma _{{\gamma _{{ss}} }} } \right)} \right\}^{{n_{{A\gamma }} }} } {\dot{\varepsilon }}}} \right. \kern-\nulldelimiterspace} {\dot{\varepsilon }}}} \right]} \mathord{\left/ {\vphantom {{\ln \left[ {{{A_{\varUpsilon } \left\{ {\sinh \left( {\alpha _{\varUpsilon } \sigma _{{\gamma _{{ss}} }} } \right)} \right\}^{{n_{{A\gamma }} }} } \mathord{\left/ {\vphantom {{A_{\varUpsilon } \left\{ {\sinh \left( {\alpha _{\varUpsilon } \sigma _{{\gamma _{{ss}} }} } \right)} \right\}^{{n_{{A\gamma }} }} } {\dot{\varepsilon }}}} \right. \kern-\nulldelimiterspace} {\dot{\varepsilon }}}} \right]} {\ln \left[ {A_{\delta } \frac{{\left\{ {\sinh \left( {\alpha _{\delta } \sigma _{{\delta _{{sat}} }} } \right)} \right\}^{{n_{{A\delta }} }} }}{{\dot{\varepsilon }}}} \right]}}} \right. \kern-\nulldelimiterspace} {\ln \left[ {A_{\delta } \frac{{\left\{ {\sinh \left( {\alpha _{\delta } \sigma _{{\delta _{{sat}} }} } \right)} \right\}^{{n_{{A\delta }} }} }}{{\dot{\varepsilon }}}} \right]}} $$
(17)

In this study, \(\uplambda \) was determined using the stress relationship between the two phases, as expressed in Eqs. [10] and [17]. The steady-state stress of austenite \({{\sigma }_{\gamma }}_{\rm ss}\) was calculated by assuming the saturated stress of ferrite \({{\sigma }_{\delta }}_{\rm sat}\) as 30 MPa. Subsequently, the activation energy values (\({Q}_{\gamma }=454\) kJ/mol for austenite and \({Q}_{\delta }= 310\) kJ/mol for ferrite) and material parameters (\({A}_{\gamma }=1.44\times {10}^{15},\) \({A}_{\delta }=6.32\times {10}^{12},\) \({\alpha }_{\gamma }=0.0066\), and \({\alpha }_{\delta }=0.0103\)) were selected from the previous study by Farnoush et al.[9] In this research, \(\uplambda \) was assumed as a constant value of 1.89 at strain rates of 0.1, 1, and 10 s−1. This value is consistent with the experimental value of about 2 of the tensile stress ratio for the austenite and the ferrite at temperatures from 1050 °C to 1250 °C.[14]

4.3 Flow Stress of Duplex Stainless Steel and Decoupled Stresses of Each Phase

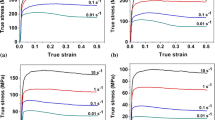
The previous representation for flow stress and activation energy for two phase materials did not encompass the wide strain range \(\varepsilon \) of both work hardening and softening modeling by the combination of DRX and DRV.[15] To obtain accurate flow stresses, an inverse analysis was performed using the results of compression tests. First, an initial set of five independent parameters, i.e., \({\text{F}}_{1},n, {\varepsilon }_{\text{c}}, {\text{F}}_{3}\), and \({{b}^{{\varvec{D}}}}_{\delta}\) (where \({{b}^{{\varvec{D}}}}_{\delta}\) is the recovery rate of ferrite), was selected. The results of flow stress based on the inverse analysis are plotted in Figure 9, and the inverse calculation results of the five parameters are presented in Table III.

Fig. 9
figure 9

Flow stress curves obtained by inverse analysis under various test conditions (blue dotted line: flow stress of duplex phases using generalized parameters; blue line: flow stress of duplex phases calculated by inverse analysis; green dotted line: constituent stress of austenite phase; red line: constituent stress of ferrite phase) (Color figure online)

Full size image
Table II Comparison of Chemical Partitioning on the Two Constituent Phases of Austenite and Ferrite Taken on Ten Different Points Using FE-SEM with EDS (Wt Pct)
Full size table

The steady-state stresses of the two phases are separated by \(\lambda \) (\(\lambda =\) 1.89). It can be inferred that the flow stresses of the harder austenite are higher than those of ferrite. In addition, the restoration process by DRX resulted in a peak stress. The results from EBSD analysis have been used for the calculation of fraction values. However, the analysis was done at room temperature but at the deformation temperature and the repeatability for the volume fractions was not so perfect due to rapid cooling from the deformation temperature. In addition, during the cooling process, phase transformation may occur. In this study, the volume fractions \({Vf}_{\gamma }\) of austenite are 0.61, 0.49, and 0.33 at 1050 °C, 1150 °C, and 1250 °C, respectively, based on a previous study using JMatPro simulation.[8] Because only the two phases of austenite and ferrite coexist at temperatures higher than 1050 °C, the following can be assumed.

$${Vf}_{\gamma } +{Vf}_{\delta}= 1$$
(18)

The five parameters calculated, namely, \({\text{F}}_{1},n, {\varepsilon }_{\rm c}, {\text{F}}_{3}\), and \({{b}^{{\varvec{D}}}}_{\delta }\), which can used to represent flow stress combinations with the austenite stress \({\sigma }_{\gamma }\) and ferrite stress \({\sigma }_{\delta }\), are summarized in Table III. Sensitivities with the strain rate \({m}_{0}\) and temperature \({A}_{0}\) were applied. Initial parameters of \({A}_{0}=11{,}000\) and \({m}_{0}=0.08, 0.11,\) and \(0.16\) at temperatures of 1050 °C, 1150 °C, and 1250 °C were used for the calculation, and \(\uplambda \) was assumed to be a fixed value of 1.89.

4.4 Quantification of Dynamic Softening Kinetics Using Decoupled Equations of Each Phase

The critical strain \({\varepsilon }_{\rm c}\) was calculated using the decoupled results of flow stress to explain the occurrence of DRX in austenite and its initiation at the critical strain \({\varepsilon }_{\rm c}\). The changes in the critical strain of austenite can be obtained by regression method involving the strain rate and temperature, as indicated in Eq. [19]. Because the strain rate and temperature are associated closely with the Zener–Hollomon parameter (\({Z}_{\gamma }\)), the results of \({\varepsilon }_{\rm c}\) agree well with \({Z}_{\gamma }\), as shown in Figure 10. The trend shows that the critical strain for DRX initiation in austenite increases with increasing strain rate and decreasing temperature.

Fig. 10
figure 10

Critical strain in austenite as a function of Zener–Hollomon parameter

Full size image
$$ \bar{\varepsilon }_{{\text{c}}} = 0.00127\left( {\dot{\varepsilon }{\text{exp}}\left( {\frac{{12,760}}{T}} \right)} \right)^{{0.447}} $$
(19)

To calculate the activation energy of each phase, the peak stress \({{\sigma}_{\gamma }}_{\rm p}\) in austenite and the saturated stress \({{\sigma}_{\delta }}_{\rm sat}\) in ferrite are critical. Figure 11 illustrates the relationships between the Zener–Hollomon parameter and each of the \({{\sigma}_{\gamma }}_{\rm p}\) and \({{\sigma}_{\delta }}_{\rm sat}\) of austenite and ferrite, respectively, calculated using the parameters listed in Table III. The calculated logarithm Zener–Hollomon parameter ln(Z) and peak stresses \({{\sigma }^{*}}_{\rm p}\) and \({{\sigma}_{\delta }}_{\rm sat}\) exhibit good linearity.

Fig. 11
figure 11

Relationships of (a) peak stresses in austenite and (b) saturated stresses in ferrite vs. Zener–Hollomon parameter

Full size image

The activation energy (\(Q\)) of hot working for each phase can be obtained using Eqs. [20, 21] and [22]. The activation energies for austenite \({Q}_{\gamma }\) and ferrite \({Q}_{\delta }\) calculated using the decoupled flow stresses were 584.3 and 394.7 kJ/mol, respectively, whereas \({n}_{\gamma}\) and \({n}_{\delta }\) were calculated to be 4.52 and 2.88, respectively.

$$Z=\dot{\varepsilon }\mathrm{exp}\left(\frac{Q}{RT}\right)$$
(20)
$${Z}_{\gamma }={A}_{\gamma}{[\mathrm{sin}h\alpha {{\sigma}_{\gamma}}_{\rm p}]}^{{n}_{\gamma }}$$
(21)
$${Z}_{\delta }={A}_{\delta }{[\mathrm{sin}h\alpha {{\sigma}_{\delta }}_{\rm sat}]}^{{n}_{\delta }}$$
(22)

To calculate the recrystallized volume fraction \({X}_{\rm D}\) by DRX, the approach based on a flow curve used by Yanagida and Yanagimoto[21] can be considered. The authors presented a method to obtain the volume fraction of recrystallized grains as a function of plastic strain. In this study, it was calculated at strain rates of 0.1, 1, and 10 s−1 and a fixed temperature of 1150 °C. The regressed volume fraction of DRX was represented by the general Avrami equation and determined using the rate of DRX \({G}^{\rm D}\) as follows:

$${X}_{\rm D}=1-\mathrm{exp}(-{G}^{\rm D}{\left(\varepsilon -{\overline{\varepsilon }}_{\rm c}\right)}^{P}),$$
(23)

where the material constant \(P\) was assumed to be 2.

Using this method, the regression analysis of the obtained DRX rates \({G}^{\rm D}\) resulted in the following:

$${G}^{\rm D}=262.0{ \dot{\varepsilon }}^{-0.535}\mathrm{exp}\left(\frac{-4927}{T}\right)$$
(24)

The volume fraction of DRX was significantly larger at lower strain rates and higher temperatures. When the strain rate increased or the temperature decreased, DRX barely proceed because of insufficient time and kinetic energy, as shown in Figures 12(a) and (b), respectively.

Fig. 12
figure 12

DRX kinetics at different (a) strain rates and (b) temperatures

Full size image

Based on the EBSD observations of the compressed specimens, the recrystallized average grain sizes were determined to be a function of temperature and strain rate such that

$${d}_{\rm DRX}=3044{ \dot{\varepsilon }}^{-0.0153}\mathrm{exp}\left(\frac{-9762}{T}\right)$$
(25)

The DRX grain size increased with increasing temperature and decreasing strain rate. However, the effect of temperature was greater than that of strain rate, as depicted in Figures 13(a) and (b).

Fig. 13
figure 13

DRX grain size vs. (a) temperature and (b) strain rate

Full size image

4.5 Quantification of Dynamic Softening Kinetics by Using a Unified Equation for Duplex Stainless Steel

The flow stress for duplex stainless steel was calculated using a unified flow equation \({\bar{\sigma }}^{*}\) with the regression results at each condition, as shown in Figure 7. Eqs. [26] and [27] express \({\bar{\sigma }}^{*}\) and \(\bar{\sigma }\), respectively. The flow stress was calculated based on a unified description with a set of material constants as functions of temperature and strain rate, as summarized in Table IV.

Table III Parameters of \(\upsigma \) for Duplex Stainless Steel Calculated by Inverse Analysis
Full size table
$${\bar{\sigma }}^{*} = \bar{\sigma } {\dot{\overline{\varepsilon } }}^{m}\frac{\mathrm{exp}\left(\frac{A}{T}\right)}{\mathrm{exp}\left(\frac{A}{{T}_{0}}\right)}$$
(26)
$$\bar{\sigma }=\left\{\begin{array}{ll}\bar{\text{F}}_{1}{\overline{\varepsilon }}^{\overline{n} }& (\overline{\varepsilon }<{\overline{\varepsilon }}_{\rm c})\\ \bar{\text{F}}_{2}\mathrm{exp}\left[a{\left(\overline{\varepsilon }-{\overline{\varepsilon }}_{\rm p}\right)}^{2}\right]+\bar{\text{F}}_{3}& (\overline{\varepsilon }\ge {\overline{\varepsilon }}_{\rm c})\end{array}\right.$$
(27)

The set of unified parameters for strain rate sensitivity \(m\) and temperature sensitivity \(A\) was obtained based on the iterations shown in Figure 7. The values of strain rate sensitivity \(m\) were regressed using Eq. [28], and the results show that \(m\) increased with temperature, as illustrated in Figure 14.

Fig. 14
figure 14

Regression result of strain rate sensitivity m

Full size image
$$m=0.000117\times T\left(K\right)-0.002573$$
(28)

The calculated Zener–Hollomon parameter ln(Z) and peak stress \({{\bar{\sigma }}^{*}}_{\rm p}\) for duplex stainless steel indicated good agreement, with \({R}^{2}=0.9722\), as shown in Figure 15.

Fig. 15
figure 15

Correlation between \(\text{ln[sin}h(\alpha {{\bar{\sigma }}^{*}}_{\rm p}{)]}\) and \(\mathrm{ln}(Z)\)

Full size image

DRV occurs not only in ferrite, but also in austenite. To obtain the DRV coefficient \({b}^{{\varvec{D}}}\) of duplex stainless steel, Eqs. [29] and [30] were used. The saturated stress \({\sigma }_{\rm Sat}\) was calculated using the method described by Jonas et al.[20] The initial dislocation density was assumed to be \({1\times 10}^{8}\) \({\mathrm{cm}}^{-2}\). As a result of the regression analysis, the value of \({b}^{{\varvec{D}}}\) can be described by Eq. [31].

$${\bar \sigma ^*} = \sqrt {{[{{\bar \sigma }^{*}}_{{\text{Sat}}}]^2} - \left( {{[{{\bar \sigma }^{*}}_{{\text{Sat}}}]^2} - {[{{\bar \sigma }^{*}}_{0}}]^2} \right)\exp \left( { - \frac{{{b^{\varvec{D}}}}}{{\dot{\overline{\varepsilon }}}}\bar \varepsilon } \right)}$$
(29)
$$\mathrm{ln}\left(\frac{{[{{{\bar{\sigma }}^{*}}_{{\rm Sat}}}]^2}-{[ {{\bar{\sigma }}^{*}}_{0}}]^2}{{[{{\bar{\sigma }}^{*}}_{{\rm Sat}}]^2}-{[ {\bar{\sigma }}^{*}]^2}}\right)=-\frac{\overline{\varepsilon }}{\dot{\overline{\varepsilon }}}{b}^{{\varvec{D}}}$$
(30)
$${b}^{{\varvec{D}}}=57{,}581{ \dot{\overline{\varepsilon }}}^{0.427}\mathrm{exp}\left(\frac{-9414}{T}\right)$$
(31)

The activation energy \(Q\) of duplex stainless steel for hot working using the unified flow stress \({\bar{\sigma }}^{*}\) was 552 kJ/mol in this study. This value is close to that obtained by Cabrera et al.[16] for SAF 2205 (569 kJ/mol) and slightly larger than those obtained in other studies, as presented in Table V.

Table IV Values of Unified Parameters of \({\bar{\sigma }}^{*}\) for Duplex Stainless Steel
Full size table
Table V Calculated \({A}_{\rm A}\), \({n}_{A,} \alpha ,\; \mathrm{and} \;Q\) Values for Different Duplex Stainless Steels
Full size table

5 Discussion

During the manufacturing of duplex stainless steel, the two phases (austenite and ferrite) coexist at high temperatures. This results in complicated flow stresses owing to the different softening behaviors of the two phases. Dissimilarity in softening due to different SFEs significantly affects the flow stress during hot deformation processing. Despite the complicated softening dissimilarity in the two phases, the flow curve can be analyzed by inverse analysis using a combination of decoupled different equations for the flow stresses in the two phases. Consequently, the important parameters for dynamic kinetics, i.e., the activation energies (\({Q}_{\gamma }\) and \({Q}_{\delta }\)) of the constituents, can be calculated.

The microstructure shown in Figure 4 suggests that the grain morphology and size as well as the DRX occurrence are affected by the deformation caused by strain, temperature, and strain rate. The changes in the grain morphology, size, and DRX occurrence induced by the deformation due to the strain, temperature, and strain rate are schematically illustrated in Figure 16. The restoration of the dislocations occurred differently by DRX or DRV for austenite and ferrite, respectively. Higher temperatures and lower strain rates increase the mobility of grain boundaries and decrease the speed of dislocation pileup, thus leading to grain growth after DRX.[22] As demonstrated by Emami et al.,[23] the different SFEs of the austenite and ferrite phases in SAF2205 duplex stainless steel are attributed to their dissimilar behaviors. Based on a comparison of their high-temperature microhardness and rate of work hardening, as reported by Kumar et al.,[24] DRV can be said to be the primary restoration mechanism in ferrite, whereas DRX is the dominant one in austenite.

Fig. 16
figure 16

Schematic of the microstructural evolution with strain, time, and temperature during hot working

Full size image

Regarding the changes in DRX fractions caused by the strain and strain rate, it can be concluded that the more frequent the DRX occurrence, the greater is the number of equiaxed grains. DRX was prevalent in austenite, and high-angle grain boundaries (HAGBs) were more created in austenite than in ferrite, as depicted in Figure 17. The HAGBs are indicated by black lines as determined from at least 15° disorientation on the inverse pole figure map. In austenite, a lower strain rate allows sufficient time for activation of DRX. Thus, more HAGBs at a strain rate of 1 s−1 are observed than those at a strain rate of 10 s−1. After completion of DRX, a longer duration and higher temperature resulted in grain boundary migration and coarsening in austenite, resulting in grain growth.

Fig. 17
figure 17

Comparison of DRX fractions at different reduction ratios of 25 and 50 pct, and strain rates of 1 s−1 and 10 s−1 by the IPF map of EBSD

Full size image

In contrast, DRV was prevalent in ferrite. The textures in <001>  and <111> developed strongly in ferrite. This finding is consistent with those reported by Park and Yanagimoto[25] and Park et al.[26]. Therefore, the methods used dissimilar types of flow stresses in the austenite and ferrite phases of duplex stainless steel are agreeable.

6 Conclusions

The dynamic softening kinetics of SUS329J4L duplex stainless steel having composition 24.79Cr-6.84Ni-2.83Mo-0.69Mn-0.5Si-0.16Co-0.015C-0.14N-0.024P-(bal.)Fe (wt pct) were investigated using the proposed inverse analysis and regression methods. The main findings can be summarized as follows:

  1. (1)

    A method for calculating the flow stress using the constituent flow stresses of austenite and ferrite was proposed. The combination of constituent flow stresses was used to calculate the flow stresses of duplex stainless steel by performing an inverse analysis to compensate for the uncontrollable experimental effects.

  2. (2)

    The material parameters for the dynamic softening kinetics of duplex stainless steel were investigated using the flow stresses obtained by inverse analysis and regression methods at temperatures of 1050 °C, 1150 °C, and 1250 °C and strain rates of 0.1, 1, and 10 s−1.

  3. (3)

    Microstructural observation via EBSD showed that the microstructural evolutions occurred heterogeneously, i.e., via DRX and DRV in austenite and ferrite of duplex stainless steel, respectively, indicating that the flow stresses using the combination of different equations of the two phases were reasonable.