Kissinger-Style Kinetic Analysis for Sintering Dilatometry Data

Abstract

The kinetics of densification during sintering are often analyzed by techniques such as the master sintering curve and Wang–Raj analysis to determine activation energies. These methods, while versatile, do not always form a complete picture or isolate individual processes that occur during sintering. This report develops a densification rate peak method for determining activation energies analogous to the traditional Kissinger analysis for chemical reactions. The difference between using the present analysis and the traditional Kissinger analysis is explored and evaluated for a range of theoretical examples. Finally, three previous sintering reports are re-examined with the new analysis: ThO₂-4 pct UO₂, Gd and Bi co-doped ceria, and mechanically alloyed W-Cu. The results obtained using the Kissinger-style analysis are in line with MSC and WR analysis where appropriate, and expand the information obtained from densification rate data beyond that of the original reports in some cases.

1 Introduction

In order to design optimized sintering processes, it is helpful to know the diffusion mechanisms that facilitate sintering and their kinetics. Even in single component materials these are multiple and competitive; neck formation can occur through surface, grain boundary, or volume diffusion,[1,2] while the kinetically dominant sintering mechanism can change depending on the temperature and density.[3,4] As the composition of the material becomes more complex, the number of possible diffusion pathways and reactions proliferate, and the dominant sintering mechanisms become even harder to determine. For these reasons, experimental methods that can assess activation energies for sintering, and by extension speak to the rate-limiting kinetic processes for densification, are essential tools.

One such method is known as the master sintering curve (MSC),[5] which assumes a densification rate of the form

$$ \frac{{{\text{d}}\rho }}{{\rho {\text{d}}t}} = \frac{{\gamma \Omega D_{0} }}{{RTG^{n} }}\Gamma \left( \rho \right)e^{{ - \frac{Q}{\text{RT}}}}, $$

(1)

where $\rho$ is relative density, $\gamma$ is surface energy, ${\Omega}$ is molar volume, $T$ is temperature, $G$ is grain/particle size, $n$ is 3 for volume diffusion or 4 for grain boundary diffusion, $D_{0}$ is the diffusion prefactor (for grain boundary diffusion this is written as $\delta D_{0}$, where ${\delta}$ is the grain boundary thickness), $R$ is the ideal gas constant, and $Q$ is the activation energy of the primary diffusion mechanism.[6] ${\Gamma}\left( {\rho} \right)$ is a non-dimensional term that encapsulates how the current density of the material relates to the current surface area and curvature of the densifying particles, and thus how these effects impact the densification rate. This definition was first proposed by Hansan et al.[6] who modeled densification as a function of pore filling, and can be separated into two components and integrated.[5] The components independent of temperature/time are integrated from the initial density $\rho_{0}$ to the final density $\rho$:

$$ \Phi \left( \rho \right) = \frac{{RG^{n} }}{{\gamma \Omega D_{0} }}\mathop \smallint \limits_{{\rho_{0} }}^{\rho } \rho \Gamma \left( \rho \right){\text{d}}\rho $$

(2)

and those dependent on temperature and time are integrated over time:

$$ \theta \left( {t, T\left( t \right)} \right) = \mathop \smallint \limits_{0}^{t} \frac{1}{T}e^{{ - \frac{Q}{\text{RT}}}} {\text{d}}t. $$

(3)

According to Eq. [1] $\Phi \left( \rho \right) = \theta \left( {t, T\left( t \right)} \right)$, and that equality is exploited to determine the activation energy of sintering. This is achieved by plotting density as a function of $\theta \left( {t, T\left( t \right)} \right)$ for otherwise identical samples sintered at different heating rates, using dilatometry data. The curves from such experiments should all collapse together when the activation energy used in $\theta \left( {t, T\left( t \right)} \right)$ is correct. The degree of collapse among independent experiments at different rates can be evaluated for many different activation energies and the activation energy with the minimum error among the collapsed curves best describes the densification kinetics.[5]

The benefit of the MSC method is that it is independent of geometric factors of the powder, and dilatometry experiments are low cost and easy to perform. This method has therefore been applied to many systems.[7,8,9,10,11,12,13,14,15] However, there is one major assumption that limits the utility of the MSC approach, namely, that it assumes that the entire sintering process is dominated by a single kinetics, characterized by a single activation energy.[5,16] This contradicts the well-known categorization of multiple diffusion mechanisms that compete for dominance and which may each be sampled in a single sintering run. Many reports using MSC are therefore limited to an analysis of an aggregate, average activation energy, or more specifically, to that associated with the majority of the measured densification.

A complementary analysis method proposed by Wang and Raj (WR)[17,18] improves the ability to analyze separate processes using a rearranged form of Eq. [1]:

$$ \ln \left[ {\frac{{{\text{d}}\rho }}{{ {\text{d}}T}}\left( {\frac{{{\text{d}}T}}{{{\text{d}}t}}} \right)T} \right] = \ln \frac{{\gamma \Omega D_{0} }}{{RG^{n} }} + \ln \rho \Gamma \left( \rho \right) - \frac{Q}{RT}. $$

(4)

By taking densification data at different heating rates and separating out individual data points all at the same density, the first two terms on the right-hand side become constants, allowing a plot of $\ln \left[ {\frac{{{\text{d}}\rho }}{{ {\text{d}}T}}\left( {\frac{{{\text{d}}T}}{{{\text{d}}t}}} \right)T} \right]$ vs $\frac{1}{T}$ to obtain the activation energy of sintering at that density. This approach generalizes the MSC analysis to allow the activation energy to be calculated for a variety of different points along the densification curve. Since the WR analysis assumes that the activation energy is a function only of density, it is best applied to small densifications and requires care to ensure constant particle size and limited variations in initial densities.[17,19]

Both MSC and WR analyses assume that sintering mechanisms being analyzed are independent of temperature. However, as noted above, dominant diffusion pathways are expected to change with temperature generally, and many sintering contexts specifically seek to trigger different behaviors at different temperatures. For example, accelerated sintering methods such as activated sintering,[1,20] liquid phase sintering,[21,22] and nanophase separation sintering[11,12,23] all involve changes in chemical configuration and multiple different kinetics that set on as temperature rises. Similarly, in multiphase materials, the formation of different phases may facilitate different sintering mechanisms in different temperature ranges. For these more complex sintering situations, an alternative kinetic analysis is to directly analyze peaks in densification rate, with a traditional Kissinger-style analysis. Peak rate data have been used to analyze sintering based on heat flow measurements from differential scanning calorimetry (DSC) or differential temperature analysis (DTA).[24,25] The heat flow arises from the reduction of surface area during sintering, and peaks at the moment of fastest surface area loss; experiments at higher heating rates see the peak temperature shifting to higher values.[26,27] The traditional Kissinger analysis determines the activation energy associated with the peak from the slope of $\ln \left[ {\frac{{\beta}}{{{{T}}^{2} }}} \right]$ vs $\frac{1}{T}$,[24,25,28,29,30] where T is the peak temperature and $\beta$ is the heating rate.

One aspect of this type of Kissinger analysis is that it is dependent on the magnitude of the surface area of the sample. Samples made from nano-size particles will produce a strong calorimetry signal during the experiment making the analysis easy and fruitful.[26,27,31,32] However, this signal decreases rapidly with particle size,[33] rendering it challenging or not useful for more practical powders of relevance in industrial settings. There is also a concern about conflation of the densification heat signal with that from other structural changes (recovery, recrystallization and grain growth, the formation and decomposing of new phases and intermetallics,[34,35,36] etc.). Alternatively, DSC and DTA experiments can be conducted in parallel with dilatometry measurements to compare crystal growth and the formation of new phases with shrinkage data,[37] as has been conducted for liquid phase sintering to optimize the sintering parameters around the formation of the liquid phase.[38,39,40] While these measurements are useful for defining material processes that occur around various critical temperatures and may facilitate sintering, these processes are not directly the defining mechanism of densification.[41]

The original Kissinger analysis was derived from an expression of reaction rate commonly associated with chemical decomposition,[24] and has been extended to other reaction types as well.[25,29] These reactions are traditionally assessed in energetic terms relevant to calorimetry. It would be desirable to establish an equivalent approach for sintering in terms of densification directly, rather than by inference from the energy of lost surface area or indirect correlations with other material phenomena. It is our purpose in this article to provide the analytical form of the Kissinger analysis for sintering using the combined stage sintering model of Eq. [1] as a basis. The result is a kinetic tool that can be used to identify local mechanistic events during the course of a complex sintering process, and associate characteristic temperatures with activation energies for those events.

2 Analytical

We start with the expression for densification rate presented in Eq. [1], and for simplicity combine all of the terms that are not dependent on either density or temperature into a single constant A:

$$ \frac{{{\text{d}}\rho }}{{{\text{d}}t}} = A\frac{1}{T}\rho \Gamma \left( \rho \right)e^{{ - \frac{Q}{{RT}}}} $$

(5)

Grain size is assumed to be a constant with respect to both density and temperature around a densification rate peak and is therefore included in the constant A. The thermal histories of a material at its densification rate peak would be similar for different heating rates, so one would expect the grain size around the different peaks to vary negligibly.

We note that the combination $\rho {\Gamma}\left( \rho \right)$ contains information about how the instantaneous density affects the rate of densification, and provides a convenient analogy to the original Kissinger model in which the degree of completion of a reaction affects the current reaction rate. The exact relationship between $\Gamma \left( \rho \right)$ and $\rho$ is not specified due to the many factors that contribute to the geometric effects, and which might vary from situation to situation. However, a critical component of the Kissinger approach is that this term must be deceleratory, i.e., locally within some range of density being analyzed, densification must lead to lower densification rates. From a broad perspective, this is certainly a reasonable assumption for densification processes in general, which kinetically asymptote as full density (or limiting density) is approached, i.e., as $\rho \to 1$, $\Gamma \left( \rho \right) \to 0$. Experiments performed by Hansen et al. confirm the deceleratory nature of $\Gamma \left( \rho \right)$ with the term decreasing as a function of density for the sintering of alumina,[6] while work by Seidel and Johnson[42] and Shingu[43] do the same for silver and iron, respectively. These experiments are represented in Figure 1.

Fig. 1

Experimentally obtained Γ values for iron,[43] silver,[42] and alumina[6] reproduced assuming grain boundary diffusion the dominant densification mechanism

One of the main contributing factors of $\Gamma \left( \rho \right)$, the changing surface area during densification, has been modeled as an nth order reaction[44,45,46,47] suggesting that the density components of $\Gamma \left( \rho \right)$ take a form similar to those of reaction type models. In multi-stage sintering processes such as liquid phase sintering or activated sintering, local decelerations of this kind may also be expected when individual processes shut off or complete. We therefore proceed taking Eq. [5] to be deceleratory in nature, which allows us to combine the density terms into one densification model term $f\left( \rho \right)$. If grain size was assumed to be a significant function of density instead of the constant value assumed above, then it would also be encapsulated in the $f\left( \rho \right)$ term instead of in A. This distinction will be shown to not impact the results of this analysis.

For a dilatometry experiment at a constant heating rate $\beta$, the densification rate can be recast as a temperature derivative, giving

$$ \frac{{{\text{d}}\rho }}{{{\text{d}}T}} = \frac{A}{\beta }\left( {\frac{1}{T}} \right)f\left( \rho \right)e^{{ - \frac{Q}{{RT}}}} $$

(6)

This form is now similar to that used by Kissinger for his original analysis based on reaction rate,[24] but it is not exactly the same, with an additional 1/T term here as required by the kinetic model of sintering. This additional temperature dependence remains throughout the following analysis, leading to a different outcome than the traditional Kissinger analysis. Differentiating Eq. [6] and reintroducing Eq. [6] yields

$$ \frac{{{\text{d}}^{2} \rho }}{{{\text{d}}T^{2} }} = \frac{{{\text{d}}\rho }}{{{\text{d}}T}}\left( {\frac{{f^{\prime}\left( \rho \right)}}{f\left( \rho \right)}\frac{{{\text{d}}\rho }}{{{\text{d}}T}} - \frac{1}{T} + \frac{Q}{{RT^{2} }}} \right) = \frac{{{\text{d}}\rho }}{{{\text{d}}T}}\left( {\frac{A}{\beta }\left( {\frac{1}{T}} \right)f^{\prime}\left( \rho \right)e^{{ - \frac{Q}{{RT}}}} - \frac{1}{T} + \frac{Q}{{{{RT}}^{2} }}} \right). $$

(7)

When a peak appears in the densification rate data, the second derivative is zero, and at the peak we have

$$ \frac{Q}{RT} = - \frac{A}{\beta }f^{\prime}\left( \rho \right)e^{{ - \frac{Q}{{RT}}}} + 1. $$

(8)

Rearranging and taking the natural logarithm of both sides gives

$$ \ln \left( {\frac{Q}{{RT}}} \right) = \ln \left( A \right) - \ln \left( \beta \right) + \ln \left( { - \frac{{f^{\prime}\left( \rho \right)}}{{1 - {{{RT}} \mathord{\left/ {\vphantom {{\text{RT}} Q}} \right. \kern-0pt} Q}}}} \right) - \frac{Q}{{RT}}. $$

(9)

Rearranging so that the left-hand side relates only to heating rate and temperature gives

$$ \ln \left( {\frac{\beta }{T}} \right) = \ln \left( {{{AR}}/Q} \right) + \ln \left( { - \frac{{f^{\prime}\left( \rho \right)}}{{1 - {{{RT}} \mathord{\left/ {\vphantom {{{RT}} Q}} \right. \kern-0pt} Q}}}} \right) - \frac{Q}{{RT}}. $$

(10)

Now the leading term on the right-hand side, $\ln \left( {{{AR}}/Q} \right)$, is not a function of temperature, while the second term is small compared to the last, $\frac{Q}{{RT}}$ term. In prior reports on the Kissinger method neglecting the second term has been shown to have a maximum error of < 1.5 pct for the determined activation energy regardless of the exact form of the deceleratory term.[25] More specifically, Elder[25] considered an extensive list of practical models for the deceleratory term, including the nth order reaction model that, as described earlier, can also be used to describe surface area reduction during sintering. This quantitative support for ignoring the term containing $f^{\prime}\left( \rho \right)$ aligns with Kissinger’s original work where these terms were neglected outright. Furthermore, we note that the decision to consider grain size $G$ as either a constant or a function of density would lead, at most, to its inclusion in this negligible term.

Therefore, upon differentiating with respect to 1/T

$$ \frac{{{\text{d}} \ln \left( {{\beta \mathord{\left/ {\vphantom {\beta T}} \right. \kern-0pt} T}} \right)}}{{{\text{d}}\left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T}} \right)}} \approx - \frac{Q}{R}. $$

(11)

The result in Eq. [11], based specifically on densification, differs from the original Kissinger analysis because the $\ln \left[ {\frac{\beta }{{T^{2} }}} \right]$ in the original is replaced with $\ln \left[ {\frac{\beta }{T}} \right]$ here. This difference arises from the form of the densification rate not being a simple Arrhenius expression of T but also contains a function of T outside the exponential. Reports that have extended the Kissinger expression to other functions of time have derived forms similar to ours, albeit in the context of reaction energies rather than densification rates.[25] For sintering dilatometry data the present analysis suggests that slopes taken from plots of $\ln \left[ {\frac{\beta }{T}} \right]$ vs $\frac{1}{T}$ from densification rate peaks should yield the relevant activation energy underlying that peak. We note that the identification of the peak position can be carried out either using a densification rate $\frac{{{\text{d}}\rho }}{{{\text{d}}t}}$ or the temperature differential of a dilatometer curve $\frac{{{\text{d}}\rho }}{{{\text{d}}T}}$; these quantities differ by the heating rate and do not affect the location of the peak in T.

Due to the popularity of the standard Kissinger analysis it may be tempting to use the classical slope of $\ln \left[ {\frac{\beta }{{T^{2} }}} \right]$ vs $\frac{1}{T}$ to determine the activation energy of sintering, and we have identified some studies that do so.[36,51,52] The above analysis suggests that this approach is incorrect, and it is important to understand whether the different forms of analysis (i.e., use of $\ln \left[ {\frac{\beta }{{T^{2} }}} \right]$ vs $\ln \left[ {\frac{{\beta}}{T}} \right]$) produce different results. The absolute error that would be produced on the activation energy Q by using the traditional Kissinger method is given by the difference between the slopes of the two approaches. Dividing that result by the true slope given by Eq. [11] produces an expression for the relative error:

$$ {\text{Relative}}\;{\text{Error}} = \frac{{\left| {{{{\text{d}}\ln \left( {{\beta \mathord{\left/ {\vphantom {\beta T}} \right. \kern-0pt} T}} \right)} \mathord{\left/ {\vphantom {{{\text{d}}\ln \left( {{\beta \mathord{\left/ {\vphantom {\beta T}} \right. \kern-0pt} T}} \right)} {{\text{d}}\left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T}} \right)}}} \right. \kern-0pt} {{\text{d}}\left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T}} \right)}} - {{{\text{d}} \ln \left( {{\beta \mathord{\left/ {\vphantom {\beta {T^{2} }}} \right. \kern-0pt} {T^{2} }}} \right)} \mathord{\left/ {\vphantom {{{\text{d}} \ln \left( {{\beta \mathord{\left/ {\vphantom {\beta {T^{2} }}} \right. \kern-0pt} {T^{2} }}} \right)} {{\text{d}}\left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T}} \right)}}} \right. \kern-0pt} {{\text{d}}\left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T}} \right)}}} \right|}}{{{{{\text{d}}\ln \left( {{\beta \mathord{\left/ {\vphantom {\beta T}} \right. \kern-0pt} T}} \right)} \mathord{\left/ {\vphantom {{{\text{d}}\ln \left( {{\beta \mathord{\left/ {\vphantom {\beta T}} \right. \kern-0pt} T}} \right)} {{\text{d}}\left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T}} \right)}}} \right. \kern-0pt} {{\text{d}}\left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T}} \right)}}}} = \frac{{\left( {{{{\text{d}}\ln \left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T}} \right)} \mathord{\left/ {\vphantom {{{\text{d}}\ln \left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T}} \right)} {{\text{d}}\left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T}} \right)}}} \right. \kern-0pt} {{\text{d}}\left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T}} \right)}}} \right)}}{{\left( {{{{\text{d}}\ln \left( {{\beta \mathord{\left/ {\vphantom {\beta T}} \right. \kern-0pt} T}} \right)} \mathord{\left/ {\vphantom {{{\text{d}}\ln \left( {{\beta \mathord{\left/ {\vphantom {\beta T}} \right. \kern-0pt} T}} \right)} {{\text{d}}\left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T}} \right)}}} \right. \kern-0pt} {{\text{d}}\left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T}} \right)}}} \right)}} = \frac{T}{{\left( {{Q \mathord{\left/ {\vphantom {Q R}} \right. \kern-0pt} R}} \right)}}. $$

(12)

Plotting the percent error caused by using the traditional Kissinger as a function of Q/RT in Figure 2 we see that for low temperature or high activation energy processes, the error can be low. It is encouraging to note that the studies cited above using standard Kissinger analysis are for ceramics where activation energies tend to be high and the resulting error would be small. However, importantly, for high temperature sintering and/or low activation energy processes, the error can be very important, e.g., for Q/RT < 10 the error is greater than 10 pct; this is enough to present significant mismatches between experimentally measured Q values and tabulated diffusion activation energies, for example. Figure 2 also shows some sintering processes and mechanisms and their susceptibility to such errors. Sintering mechanisms with lower activation energies such as grain boundary (GB)[49] diffusion dominated densification, as well as accelerated processing methods such as microwave sintering[49,50] would be misrepresented by a traditional Kissinger analysis. Most importantly for our own research, we see that accelerated sintering methods may be especially susceptible to these errors. Methods like activated sintering, liquid phase sintering, and nanophase separation sintering are of interest for their lowering of activation energies, and are often applied to systems with high sintering temperatures. Some of our future work will address the latter case more explicitly.

Fig. 2

Percent error of using traditional Kissinger analysis (which was derived for chemical reactions) for sintering analysis, determined from Eq. [12], as function of Q/RT. Data showing how much error would be incurred in various sintering systems[7,26,48,49,50] when using the traditional Kissinger analysis

3 Application to Dilatometric Sintering Data

To evaluate the applicability of this analysis to the study of sintering processes, we now revisit some previously published studies in which the activation energy was calculated using one of the other methods described in the Introduction, but where the data are also amenable to a Kissinger-style analysis following Eq. [11]. Since our method is dilatometric, we specifically sought studies in which a high density of dilatometry data points was available at multiple constant heating rates; the data must be dense enough to obtain an acceptable temperature resolution of the rate peaks for the analysis. We avoid studies that present isolated data points (as by interrupted sintering and quenching) or those with a paucity of data making differentiation challenging. The error associated with these calculations arises from two sources: the process of extracting the data and determining peak temperature from it. Based on past reports on material analysis from extracted data, we estimate the error to be conservatively ~ 1 pct.[53] While this approach results in error bars wider than one might expect from a Kissinger-style analysis, we are confident that the error is not underestimated.

3.1 ThO₂-4 pct UO₂

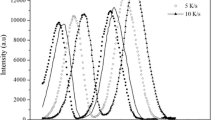
As a first example, we consider a work by Banerjee et al.[54]in which the densification behavior of ThO₂-4 pct UO₂ is characterized. In their first report on this system, the authors provided measurements of the densification rate for different constant heating rates of 2, 5, 10, and 15 °C/min, which are reproduced in Figure 3. For all three runs there is a single dominant peak in densification rate, supporting the authors’ analysis of a single dominant densification mechanism. The authors used a Wang and Raj method (Eq. [4]) at relative densities between 70 and 85 pct to determine the activation energy. The result of the analysis is an activation energy of Q_WR = 350 kJ/mol, which compares very favorably to a later MSC analysis of the same data by Banerjee et al.,[55] which gave Q_MSC = 343 kJ/mol. Based on these analyses, the authors interpreted the sintering of ThO₂-4 pct UO₂ as being controlled by grain boundary diffusion. Performing our Kissinger-style analysis on the primary peak from Figure 3, we obtain a value of Q_K = 349 ± 17 kJ/mol. This agrees very well with the two previously reported analyses, and thus provides a first validation point for a simple system with a single dominant densification rate peak that has been well understood by previous techniques. Note also that this system is one where a classical Kissinger analysis (rather than the current modified version based on Eq. [11]) would provide a Q with little error according to Figure 2 (Q/RT > 30).

Fig. 3

Shown above are the original shrinkage rate data for the sintering of ThO₂-4 pct UO₂ obtained from Banerjee et al.[54] (a) with the first densification rate peaks shown by the black arrows and the second densification rate peak represented by the red arrows, and a Kissinger-style analysis of the two present densification peaks (b) (Color figure online)

Upon closer inspection of the data in Figure 3(a), a smaller peak appears in the 2, 5, and 10 °C/min runs tests at a higher temperature around 1650 K to 1700 K. While no secondary mechanism is discussed in the studies of this system by Banerjee et al., this could indicate a higher temperature mechanism that is only active for a small portion of the densification. Performing our analysis on this peak obtains a Q_K = 561 kJ/mol. For comparison, the volume diffusion of pure ThO₂ is 600 kJ/mol.[56] This hints that perhaps at the highest temperatures of these sintering cycles, the system may cross over into a range where densification may become rate limited by bulk diffusion rather than grain boundary diffusion. This transition is one that is indeed typically expected at high temperatures, and may bear more detailed study. In any event the ability of isolating separate peaks in densification rate and analyzing their kinetics separately provides additional information for this system, to enhance the understanding of its higher temperature/late stage sintering.

3.2 Gadolinium- and Bismuth-Doped Ceria

Guan et al. studied gadolinium-doped ceria with and without the addition of bismuth.[57] The goal of their work was to determine how co-doping with Bi would impact both the sintering and the grain growth of Gd-doped Ceria. With no Bismuth, constant heating rate experiments showed one prominent peak in densification rate between 700 °C and 800 °C as seen in Figure 4(a). Guan et al. used data points from 60 to 68 pct relative density to perform the WR analysis, giving them an activation energy Q_WR = 745 kJ/mol. Using our Kissinger-style analysis as in Figure 4(b), we obtain a very similar activation energy of Q_K = 752 kJ/mol using just the peak positions.

Fig. 4

Shrinkage rate data for sintering of Gd-doped ceria obtained from Guan et al.[57] (a), with the densification rate peaks shown by the black arrows, and Kissinger-style analysis of the densification peaks (b)

Guan et al.’s samples co-doped with both Gd and Bi, on the other hand, showed three separate peaks in densification rate, near 700 °C, 1100 °C, and 1350 °C as seen in Figure 5. Those authors limited their analysis to densities from 70 to 74 pct in order to perform the WR analysis, giving a single sintering activation energy of Q_WR = 419 kJ/mol. By demonstrating a decrease in the sintering activation energy, their analysis demonstrated how the addition of co-dopant Bi leads to much faster sintering kinetics in Gd-doped Ceria.

Fig. 5

Shrinkage rate data for the sintering of Gd and Bi co-doped ceria obtained from Guan et al.[57] (a) with the first densification rate peaks shown by the black arrows, the second densification rate peak represented by the red arrows, and the third densification rate peak represented by the blue arrows, and a Kissinger-style analysis of the two present densification peaks (b) (Color figure online)

With the Kissinger analysis of Eq. [11], we can extend the analysis of sintering kinetics to examine all of the peaks in Figure 5(a). The first densification peak occurs at a similar temperature as the peak seen earlier in Figure 4(a) for Gd-doped ceria without Bi. Performing our Kissinger-style analysis on this peak, we obtain an activation energy Q_K = 715 kJ/mol, which agrees reasonably with that of the Bi-free system (752 kJ/mol, Figure 4). However, when this analysis is conducted on the secondary peak, its activation energy is determined to be Q_K = 418 kJ/mol, matching closely to the authors’ result of Q_WR = 419 kJ/mol. This indicates that the authors obtained the activation energy of the second densification mechanism that takes place, which is reasonable since they specifically targeted a narrow density range of 70 to 74 pct, which happens to coincide with the second peak in Figure 5. The third peak had an apparent activation energy of 390 kJ/mol.

Since the area under the second densification rate curve is the largest, it is clearly the event that results in the most densification and is the most important to sintering, which supports the authors’ use of the WR method on densities from this region. However, this does bring into question the importance of the first and third peak, and their associated mechanisms. In an independent study on a similar system, Gil et al. also noticed distinct regions in the densification curves of Bi and Gd co-doped ceria.[58] At lower temperatures, they established that sintering is dominated by solid-state diffusion processes. However, in the temperature range of ~ 1000 to 1200 °C they suggested that a transient Bi liquid phase forms and promotes more rapid densification. Since the second and third densification rate peaks only occur in the samples with Bi additions it is probable that these peaks and the activation energies associated with them relate to the liquid phase sintering that occurred at higher temperatures. The reason the first peak in the samples with Bi closely matched that of the samples without Bi is that the solid-state sintering region occurs in both systems and is minimally impacted by the addition of Bi. This illustrates the value of a Kissinger-style analysis, to identify processes and rigorously extract activation energies for the different sintering processes of complex materials.

3.3 Mechanically Alloyed W-Cu

Another example worth exploring is the sintering of W-Cu alloys, which are commonly produced using liquid phase sintering due to the low melting temperature of Cu that allows the consolidation of bulk tungsten products at significantly lower temperatures. Traditionally, this is achieved with separate elemental powders of Cu and W mixed together. However, some work, including that of Ryu et al.,[59] has shown that there are benefits to prealloying the W-Cu powders before sintering. Ryu et al. compared the sintering of W-30 wt pct Cu between milled (solutionized) and unmilled powders. In their experiments, the unmilled samples densified due to the rearrangement of the W particles in the liquid Cu phase and not due to a diffusive process; this resulted in densification peaks that do not shift significantly with heating rate because particle rearrangement is not thermally activated. However, for the milled samples, initial densification peaks form before the melting point of copper is reached, as shown in their data replotted in Figure 6. This early densification can be attributed to the phase separation of immiscible Cu, which emerges and covers the surfaces in the milled powders. The authors note that that both the nanocrystalline W crystallites and the larger powder particles are lined with pockets of Cu that facilitates densification through a coupled sintering effect. The early formation of such Cu regions was proposed by the authors to be kinetically governed by the bulk diffusion of Cu,[59,60,61] although they did not extract an activation energy to support this assertion. Later, a second densification peak develops above the melting temperature of Cu (marked by a dashed vertical line in Figure 6(a)), representing melting and particle redistribution in liquid Cu. For heating rates of 1, 3, and 5 °C/min, the two peaks are well separated from each other. For the heating rate of 10 °C/min, the two peaks are close and appear as one peak.

Fig. 6

Shrinkage rate data for the sintering of mechanically alloyed W-Cu from Ryu et al.[59] are replotted including a dashed line representing the melting point of Cu (a) with the densification rate peaks shown by the black arrows, and our analysis of densification peaks (b)

A Kissinger-style analysis can be performed on the densification rate curves in Figure 6(a), giving an activation energy of Q_K = 183 kJ/mol. For comparison, the activation energy of Cu self-diffusion is 184 to 237 kJ/mol,[62,63,64] in excellent agreement with the extracted value. In comparison, the bulk and grain boundary diffusion of W involve activation energies of ~ 650 kJ/mol[64] and ~ 370 kJ/mol,[65] respectively, and the diffusion of W though liquid Cu involves Q = 104 kJ/mol[65]; none of these mechanisms provide a match to the experimentally extracted Q_K value. It is apparent that the self-diffusion of Cu most closely matches the result of our analysis, which quantitatively supports the original interpretation of Ryu et al.[59]

4 Conclusion

Sintering can involve a complicated superposition of mechanisms that make the prediction and optimization of processing difficult. The Johnson model for combined stage sintering forms the basis of experimental dilatometry methods such as the master sintering curve (MSC) and Wang–Raj (WR) analysis, to determine the dominant diffusion mechanisms. While each of these methods has proven extremely useful over the last few decades, they also have limitations, especially for multi-stage sintering processes. Here, we have developed a closely related analysis method based on peaks in the derivative of the densification curve at constant heating rate. Applying a Kissinger-style analysis method to densification rate peaks results in a method of extracting activation as the slope of a of $\ln \left[ {\frac{\beta }{T}} \right]$ vs $\frac{1}{T}$ plot, with $\beta$ the heating rate and T the absolute temperature. We note that this plot is different from classical Kissinger analysis by a factor 1/T, and naïve use of the classical form can produce errors up to 30 pct for low activation energy sintering processes.

This technique was applied to a number of literature studies. In cases where a single mechanism dominates the sintering cycle, such as ThO₂-4 pct UO₂ and Gd-doped ceria, the modified Kissinger analysis agrees quantitatively with other MSC and WR analyses. What is more, in more complicated systems where multiple critical events occur during sintering, the Kissinger-style analysis permits separate analysis of multiple densification peaks, providing more insight on the various processes involved.