Mechanistic Modeling of Strain Hardening in Ni-Based Superalloys

Abstract

This article presents a mechanistic approach for modeling the strain hardening response of polycrystalline Ni-based superalloys such as ME3, RR 1000, Alloy 720 Li, and IN 100. The mechanistic approach considers strain hardening in Ni-based superalloys in two stages: (a) self-hardening of individual {111} slip systems in the low plastic strain regime and (2) latent hardening of multiple {111} slip systems in the high plastic strain regime. Both strain hardening regimes have been modeled on the basis of interactions of superkinks with Kear–Wilsdorf locks and related to pertinent microstructural parameters such as the volume fractions of γ′ precipitates, grain orientation, and dislocation substructure. The mechanistic strain hardening model predicts that the strain hardening exponents in both the low plastic strain (n₁) and the high plastic strain (n₂) regimes increase with increasing values of the sum of the squares of the volume fractions of the primary and secondary γ′ precipitates, the number of {111} and {010} slip systems activated, and the critical height of the superkinks. A comparison of model predictions against experimental strain hardening exponents indicates good agreement between model predictions and experimental data. Implications of the operative strain hardening mechanisms during low-cycle fatigue and high-cycle fatigue are elucidated.

1 Introduction

In recent years, several physics-based yield strength models have been developed for predicting the onset of plastic flow in polycrystalline Ni-based superalloys.[1,2,3,4] These yield strength models consider interactions of dislocations with the microstructure to assess the material’s resistance against plastic deformation. Individual hardening mechanisms such as Hall–Petch hardening, solid solution hardening, and precipitation hardening were treated. For precipitation hardening, shearing of γ′ (Ni₃Al, L1₂ structure) precipitates, cross-slip-induced anomalous hardening, and dislocation bowing around γ′ particles were considered in the development of the yield strength models, since Ni-based superalloys are generally strengthened by ordered γ′ precipitates with the L1₂ crystal structure. Most of these constitutive models treated the onset of yielding only, while one model also considered the strain hardening response beyond yielding. The yield strength models were successful in predicting the variability of yield strength due to microstructural variations in Ni-based superalloys.[1,2]

The Ramberg–Osgood equation[5] is a constitutive model that is commonly used for structural analysis and life prediction applications of gas turbine engine components. According to this model, the total strain is comprised of an elastic strain component and a plastic strain component. The stress, σ, is governed by a power law of the plastic strain, as described by

$$ \sigma = k\varepsilon_{\text{p}}^{n} , $$

(1)

where ε_p is the plastic strain, k is the strength coefficient, and n is the strain hardening exponent. Both k and n are empirical constants which are considered to be independent of plastic strains and are evaluated by fitting to experimental data. By itself, Eq. [1] provides little information on the underlying dislocation mechanisms or microstructural parameters responsible for the strain hardening behavior. However, the influence of microstructure factors on the strength coefficient and the strain hardening exponent can be correlated with the grain size of the γ matrix, and the size and volume fraction of γ′. Such an approach was applied to IN 100[4] and low solvus high refractory (LSHR) Ni-based superalloys.[6] Complex correlations and expressions were observed between these microstructural parameters and yield strength and the strength coefficient, but no clear correlation was obtained for the strain hardening exponent n.[4]

While Eq. [1] is well known and has been shown to be applicable for a variety of engineering alloys and metals, there have been reports that the linear relation between log σ and log ε_p implied by Eq. [1] does not occur over the entire plastic strain range, but occurs in two distinct stages: (1) a lower strain hardening exponent, n_1, in the low plastic strain regime, and (2) a higher strain exponent, n_2, in the higher plastic strain regime. These observations have been made in NIMONIC 80A[7,8] under monotonic[7] and cyclic loading,[8] and in Alloy 720 Li[9,10] and ME3[10] (currently called Rene 104) under tensile deformation. By virtue of the different strain hardening response, Eq. [1] has been applied to NIMONIC[7,8] and Alloy 720 Li[9] in two stages with different values of k and n for the low plastic strain and the high plastic strain regimes.

Recently, a physics-based constitutive model, called MicroROM, was developed by Chan,[10] who extended the yield stress model of Kozar et al.[1] to include the stress–strain response beyond initial yielding. This was accomplished by considering self-hardening of individual slip systems at low plastic strains and latent hardening of multiple interacting slip systems at high plastic strains. The modeling efforts led to the following constitutive equation[10]:

$$ \sigma = k\left( {\varepsilon_{\text{p}} } \right)\left[ {\varepsilon_{\text{p}} } \right]^{{n\left( {\varepsilon_{\text{p}} } \right)}} $$

(2)

which is of the Ramberg–Osgood type formulation, but with k(ε_p) and n(ε_p) being functions of plastic strain. In particular, k(ε_p) was taken to evolve with plastic deformation according to Reference 10

$$ k\left( {\varepsilon_{\text{p}} } \right) = k_{1} + \left( {k_{2} - k_{1} } \right)\left[ {1 - \exp \left( { - \beta \varepsilon_{\text{p}} } \right)} \right] $$

(3)

which is similar to the Voce law.[11,12] In Eq. [3], k₁ and k₂ are the strength coefficients for the low and high plastic strain regimes, respectively, and β is an empirical constant. In accordance with experimental observations, the strain hardening function was taken to be[10]

$$ n\left( {\varepsilon_{\text{p}} } \right) = n_{1} + \left( {n_{2} - n_{1} } \right)\left[ {1 - \exp \left( { - \beta \varepsilon_{\text{p}} } \right)} \right], $$

(4)

where n₁ is the strain hardening exponent at low plastic strains and n₂ is the counterpart in the high plastic strain regime. The earlier work by Chan demonstrated the application of MicroROM (Eqs. [2] through [4]) for predicting the stress–strain response of ME3[10] and Alloy 720 Li[10] and subsequently ATI 718Plus and additively manufactured (AM) 718Plus[13] by using the experimental values of n₁ and n₂ because the physics-based model had not been developed sufficiently robust for predicting the strain hardening exponents. Thus, there is a need to improve the current understanding of the operative strain hardening mechanisms and to develop appropriate models for predicting the strain hardening behaviors of Ni-based superalloys.

It is well known that anomalous hardening in Ni-based superalloys is caused by cross-slip from {111} planes to {010} planes to form a rectilinear sessile screw dislocation configuration that is commonly known as Kear–Wilsdorf (K–W) locks.[14] Two types of K–W locks are possible, including complete K–W locks[14] and incomplete K–W locks.[15,16,17] In a complete K–W lock, the superdislocation is dissociated into two superpartial dislocations connected by an antiphase boundary (APB) fault in the cube cross-slip plane.[14] In an incomplete K–W lock, the APB fault of the sessile dislocations lies in both the cube and the octahedral plane. The dislocations glide on the octahedral plane by series of jumps between these sessile configurations.[15,16,17] Before setting into the rectilinear sessile screw dislocation (K–W) configuration, many of the superdislocation segments contain edge segments or kinks, known as superkinks,[18,19,20] that are mobile in the octahedral plane, even though the screw segments are sessile and locked in the {010} cross-slip plane. Superkinks with various kink heights have been observed during in situ transmission electron microscopy (TEM) studies of plastic deformation in Ni₃Al,[18,21,22] Ni₃Ga,[23,24,25] and Ni₃Si[26] single crystals. The statistics of superkink shape and height, i.e., dislocation substructure, on the plastic deformation of Ni₃Si has been studied and analyzed by Couret et al.[23,24] Recently, Sun[27] proposed the concept of a critical kink height for explaining the low strain-rate sensitivity observed by Ezz and Hirsch[28] in Ni₃Al and Ni-based superalloys. Besides strain rate sensitivity, Ezz and Hirsch[28] also discussed the dislocation mechanisms that influence the yield strength and the work hardening rate of Ni₃(Al, Hf) single crystals. According to these authors, the onset of yielding is facilitated by the propagation of edge and screw dislocations on {111}. In the presence of incomplete K–W locks, slip on {111} occurs by lateral glide of edge character superkinks that bypass sessile screw dislocation segments locked by cross-slip to {010}. In contrast, the work hardening rate is the results of interactions of the superkinks with forest dislocations formed on {111} and {010} planes.[28] Despite these advances in the understanding of dislocation mechanisms in Ni₃Al and other ordered L1₂ compounds, there is still a lack of a constitutive model for predicting the strain hardening response of Ni-based superalloys.

In this investigation, MicroROM[10] was further developed to include a robust mechanistic strain hardening model for predicting the strain hardening behaviors of Ni-based superalloys in both the low plastic strain and the high plastic strain regimes. In Section II, the origin of the existence of the different strain hardening behaviors in the low plastic strain and the high plastic strain regimes are elucidated on the basis of existing literature data. Based on the experimental evidence, strain hardening models are developed for (1) self-hardening of individual {111} slip systems in the low plastic strain regime and (2) latent hardening of multiple interacting {111} slip with {010} cross-slip in the high plastic strain regime. Details of the strain hardening models are presented in Section III. The role of relevant microstructural parameters that influence the strain hardening exponent as a function of plastic strains is identified and compared against experimental data from the literature. In the Section IV, the contributions of various hardening mechanisms in the microplastic, near-yield, and beyond yielding regions of the stress–strain curves of Ni-based superalloys are elucidated and discussed.

2 Origins of Bilinear Strain Hardening Response

One of the Ni-based superalloys that have been shown to exhibit a bilinear strain hardening behavior in a plot of log stress vs log plastic strain is NIMONIC 80A.[7,8] Figure 1(a) illustrates that for both the monotonic and cyclic stress–strain response, NIMONIC 80A shows a bilinear strain hardening behavior with a lower n₁ value in the low plastic strain regime and a higher n₂ value in the higher plastic strain regime. The transition point from n₁ to n₂ varies with the alloys. Solid lines with no data points are presented in Figure 1(a) for the monotonic case because only the fitted results were reported by Lerch and Gerold.[7] This type of bilinear strain hardening behavior has also been observed in Alloy 720 Li[9,10] and ME3.[10] Analyses of the stress–strain curves of several Ni-based superalloys by the present author indicated that the bilinear strain hardening behavior also occurs in RR 1000,[29] IN 100,[4] and LSHR superalloy,[6] and NIMONIC PE16.[30] For RR 1000, the bilinear strain hardening behavior was observed in microstructures with coarse and intermediate-sized γ′, but not in a microstructure with fine γ′ precipitates, as shown in Figure 1(b). The bilinear strain hardening behaviors observed in subsolvus IN 100 and supersolvus LSHR[6] are presented in Figure 1(c). Table I summarizes the Ni-based superalloys that have been found to exhibit the bilinear log σ vs log ε_p behaviors. As tabulated in Table I, these alloys include wrought and powder-metallurgy (PM) Ni-based superalloys with subsolvus and supersolvus microstructures that are characterized by grain sizes ranging from 5 to 60 μm and strengthened by γ′ precipitates with sizes ranging from 0.02 to 1 μm. Based on this information, it is evident that the bilinear strain hardening behaviors are fairly common in γ′-strengthened Ni-based superalloys. The underlying mechanism(s) responsible for the observed bilinear strain hardening response will be elucidated and modeled. Furthermore, the reason for the linear strain hardening behavior observed in RR 1000 with fine γ′ shown in Figure 1(b) will also be identified and compared against the bilinear strain hardening mechanisms observed in RR 1000 with coarse γ′ precipitates.

Fig. 1

Bilinear strain hardening response observed in Ni-based superalloys: (a) NIMONIC 80A[7,8] subjected to cyclic and monotonic loading at 293 K (20 °C), (b) bilinear log stress–log plastic strain in RR 1000[29] with coarse γ′ compared with linear response in RR 1000 with fine γ′ at 293 K (20 °C), and (c) bilinear strain hardening curves of IN 100[4] and LSHR[6] at 298 K (25C). Experimental data are from the literature.[4,6,7,8,29]

Table I A Summary of the Processing Route, Microstructure, Grain Size, and Precipitate Size of Ni-Based Superalloys that Exhibit Bilinear Strain Hardening Behavior

In addition to the bilinear strain hardening curves, Lerch and Gerold[8] also reported the number of {111} slip systems observed in grains of NIMONIC 80A subjected to cyclic loading. These results were utilized to construct the percentage of number of slip systems activated as a function of the imposed plastic strain amplitudes, Δε_p/2. It is noted that NIMONIC 80A is a Ni-based superalloy with a face-centered cubic (fcc) Ni solid solution matrix strengthened with ordered fcc γ′ (Ni₃Al, L1₂ structure) precipitates. Although the fcc matrix material contains 12 octahedral slip systems, only 5 independent slip systems[33] are required to be activated to maintain plastic compatibility among fully plastic grains. The number of independent active slip systems may be reduced to be less than 5 in the microplastic region when some of the grains remain elastic and maintain compatibility by elastic deformation. The number of {111} $\langle 110\rangle$ slip systems activated during cyclic loading in NIMONIC 80A is presented in Figures 2(a) and (b) for γ′ size of 13 and 20 nm, respectively. Figure 2 shows that in the microplastic strain (Δε_p/2 < 0.2 pct) region where the n₁ regime resides, most of the grains exhibit slip on one {111} slip systems followed by grains that remain elastic and exhibit no slip (No = 0) on any slip systems. Only a few percentage of grains exhibit slip on two or three slip systems. In the macroplastic (Δε_p/2 ≥ 0.3 pct) region where the n₂ regime resides, the number of {111} slip systems activated increases with increasing plastic strains above 0.2 pct. In this region, most the grains exhibit slip on one or two slip systems with some grains deform on three slip systems and very few grains remain elastic (zero slip systems). The dominance of single slip in microplastic n₁ regime (Δε_p/2 < 0.2 pct) is compared against the presence of multiple slip on two or three slip systems in the macroplastic n₂ regime (Δε_p/2 ≥ 0.3 pct) in Figures 2(a) and (b) for NIMONIC 80A with γ′ sizes of 13 and 20 nm, respectively.

Fig. 2

Number of {111} slip systems observed during cyclic loading of NIMONIC 80A as a function plastic strain amplitude: (a) γ′ size of 13 nm and (b) γ′ size of 20 nm. Experimental data from Lerch and Gerold[8] were utilized to construct these plots

The number of slip systems activated within a grain is expected to depend on the grain orientation. Birosea[31] studied the deformation behavior of hard and soft grains in RR 1000 using an electron backscatter diffraction (EBSD) technique. This investigator showed that single {111} slip was prevalent in soft grains with the cube texture and high Schmid factor[34] values of 0.42 to 0.5, which corresponded to Taylor factor[35] values of about 2 to 2.38. The Schmid factor[34] is defined as m = cosθcosλ, where θ and λ are the angles between the stress axis and the slip plane normal and the slip direction, respectively. The Schmid factor has a maximum value of 0.5 when the slip system is optimally oriented for slip. The Taylor factor[35] is the inverse of the Schmid factor and it has a minimum value of 2 when the slip system is optimally oriented for slip. Thus, the soft grains are grains that are optimally oriented for single slip on the octahedral slip planes. In contrast, two or more {111} slip systems are prevalent in hard grains with the brass texture, which are not optimally oriented for slip and exhibit low Schmid factors (0.28 to 0.35) and high Taylor factors (3.57 to 4). The difference in the number of active slip systems subsequently led to differences in the development of geometrically necessary dislocations (GND) near grain boundaries and the transmission of slip into neighboring grains. Taken together, the results of Lerch and Gerold[8] and Birosea[31] suggest that the low strain hardening n₁ regime in the microplastic or low plastic strain regime might originates from single {111} slip in soft grains with high Schmid factors (i.e., low Taylor factors). In contrast, the high strain hardening n₂ regime in the fully plastic regime appears to originate from interactions of multiple {111} slip in hard grains with low Schmid factors (i.e., high Taylor factors). These observations are consistent with the previous findings[10] that the low n₁ regime at low plastic strains was the consequence of self-hardening of individual {111} slip systems and the high n₂ regime at high plastic strain was caused by latent hardening of multiple interacting slip systems.

3 Strain Hardening Models

3.1 Identification of Strain Hardening Mechanisms

In the model developed by Kozar et al.,[1] the macroscopic yield stress, $\sigma_{\text{ys}}$($\sigma_{\text{ys}} = {\text{YS}}$), is comprised of six terms arising from contributions of six hardening mechanisms. In particular,

$$ \sigma_{\text{ys}} = \sum\limits_{i = 1}^{i = 6} {\Delta \sigma_{i} } , $$

(5)

where Δσ_i is the yield stress increment contributed by the ith hardening mechanism. The six hardening mechanisms in the model of Kozar et al.[1] include (1) Hall–Petch hardening[36,37] of the γ grains (matrix), (2) solid solution hardening[38] of the γ matrix, (3) Hall–Petch hardening[36,37] of the primary γ′ precipitates, (4) solid solution hardening and anomalous hardening of γ′ precipitates by K–W lock formation,[14] (5) shearing of tertiary γ′ via the weak-pair dislocation coupling mechanism,[39] and (6) shearing of secondary γ′ by the strong-pair dislocation coupling mechanism.[39] The same six hardening mechanisms are considered in other yield strength models in the literatures[2,4,40] and in MicroROM.[10] Since these six hardening mechanisms are discussed extensively in the literature, they are not repeated here in order to reduce the amounts of overlaps with a previous publication.[10] Interested readers are referred to previous publications.[1,2,4,10,40] Some of the yield strength models also include bowing of dislocations[1,41] around γ′ precipitates, but the dislocation bowing mechanism is often not activated because it is preceded by γ′ shearing by weak-pair and strong-pair dislocation coupling mechanisms.

The strain hardening exponent n₁ in the low plastic strain regime encompasses the microplastic region, the yield region, and can go substantially above the yield strength at 0.2 pct plastic strains, as depicted in Figure 1. To identify the pertinent strain hardening mechanisms, it is thus necessary to consider the various hardening mechanisms or obstacles that are overcome by dislocations during plastic deformation in the microplastic region and through the yield region. Upon increasing plastic straining, the obstacles to be overcome by dislocations are expected in the order as follows: (i) solid solution hardening of the γ matrix (S2), (ii) shearing of tertiary γ′ precipitated located in the γ channels by weak-pair dislocation coupling (S5), (iii) shearing of secondary γ′ precipitates by strong-pair dislocation coupling (S6), (iv) solid solution hardening and anomalous hardening of γ′ precipitates due to cross-slip onto the cube plane and K–W lock formation (S4), (v) Hall–Petch hardening of the γ grains (S1), and (vi) Hall–Petch hardening of the primary γ′ grains (S3) in the subsolvus microstructure. The first four hardening mechanisms can be operative on a single {111} slip system within individual γ grains (i.e., the γ matrix), while the two Hall–Petch hardening mechanisms are operative only when one or more {111} slip system approach the boundaries of γ or γ′ grains.

To elucidate a clearer picture of the sequence of the strain hardening process, it is instructive to consider the critical stress for cross-slip from the {111} plane to the {001} plane that is responsible for the onset of anomalous hardening in γ′ and in Ni-based superalloys. In a series of papers, Yoo et al.[42,43] investigated the role of elastic anisotropy plays in the cross-slip of screw dislocations from {111} onto {010}. They showed that there exists a significant tangential interaction force that tends to assist the screw dislocations to cross-slip from the {111} plane to the {010} plane. For anisotropic elastic materials such as Ni₃Al, the critical force for cross-slip from {111} to {010} is given by[44]

$$ F_{\text{cs}} = \gamma_{\text{o}} \left[ {\frac{1}{3}\left( {\frac{{\gamma_{\text{o}} }}{{\gamma_{\text{c}} }}} \right)\left( {\frac{5A - 2}{A + 2}} \right) - 1} \right] $$

(6)

and the corresponding critical stress, σ_cs, for cross-slip is as follows:

$$ \sigma_{\text{cs}} = \frac{{\sqrt 3 \gamma_{\text{o}} }}{b}\left[ {\frac{1}{3}\left( {\frac{{\gamma_{\text{o}} }}{{\gamma_{\text{c}} }}} \right)\left( {\frac{5A - 2}{A + 2}} \right) - 1} \right], $$

(7)

where γ_ο is the APB energy for the {111} plane, γ_c is the APB energy for the {010} plane, b is the magnitude of the Burgers vector, and A is Zener’s elastic anisotropy factor,[45] which is defined as the ratio of 2C₄₄/(C₁₁ − C₁₂), where C₁₁, C₁₂, and C₄₄ are the elastic constants of a cubic crystal.

Once the critical stress for cross-slip is met, the screw dislocation can undergo double cross-slip between octahedral and cube planes, leading to the formation of incomplete or complete K–W locks. These interaction mechanisms provide various means for increasing the number of double kinks or superkinks, thereby enhancing the strain hardening exponent. The critical stresses for the incomplete and complete K–W locks are different, but both are directly related to the APB energy values on the {111} and {001} planes. For incomplete K–W locks, the critical unlocking stress, σ_IK–W, is given by[17]

$$ \sigma_{{{\text{IK}} - {\text{W}}}} = \frac{{\sqrt 3 \gamma_{\text{o}} }}{b}\left[ {1 - \frac{{(1 + 2/A)\gamma_{\text{c}} }}{{\sqrt 3 \gamma_{\text{o}} }}} \right] $$

(8)

and the critical unlocking stress, σ_K–W, is given by[17]

$$ \sigma_{{{\text{K}} - {\text{W}}}} = \frac{{\sqrt 3 \gamma_{\text{o}} }}{b}\left[ {1 - \frac{{\gamma_{\text{c}} }}{{\sqrt 3 \gamma_{\text{o}} }}} \right] $$

(9)

for complete K–W locks. Previous work by Chan[10] has shown that the critical unlocking stress for incomplete K–W locks is on the order of the yield stress for ME3 and Alloy 720 Li. On this basis, it would be insightful to normalize the critical stresses for cross-slip and for unlocking the complete K–W locks by the counterpart for the incomplete K–W locks, leading to

$$ \frac{{\sigma_{\text{cs}} }}{{\sigma_{{{\text{IK}} - {\text{W}}}} }} = \frac{{\frac{1}{3}\left( {\frac{{\gamma_{\text{o}} }}{{\gamma_{\text{c}} }}} \right)\left( {\frac{5A - 2}{A + 2}} \right) - 1}}{{1 - \frac{{\left( {1 + 2/A} \right)\gamma_{\text{c}} }}{{\sqrt 3 \gamma_{\text{o}} }}}} $$

(10)

and

$$ \frac{{\sigma_{{{\text{K}} - {\text{W}}}} }}{{\sigma_{{{\text{IK}} - {\text{W}}}} }} = \frac{{1 - \frac{{\gamma_{\text{c}} }}{{\sqrt 3 \gamma_{\text{o}} }}}}{{1 - \frac{{\left( {1 + 2/A} \right)\gamma_{\text{c}} }}{{\sqrt 3 \gamma_{\text{o}} }}}} $$

(11)

which show that both ratios are function of A, γ_o, and γ_c. For Ni₃Al, A = 3.3, γ_o/γ_c = 1.25. Substituting these values into Eq. [10] leads one to

$$ \frac{{\sigma_{\text{cs}} }}{{\sigma_{{{\text{IK}} - {\text{W}}}} }} = 0.542 $$

(12)

and

$$ \frac{{\sigma_{{{\text{K}} - {\text{W}}}} }}{{\sigma_{{{\text{IK}} - {\text{W}}}} }} = 2.084. $$

(13)

Since $\sigma_{{{\text{IK}} - {\text{W}}}}$ is approximately equal to the yield stress (= 1000 MPa) of ME3 and Alloy 720 Li,[10] the critical stress for cross-slip is about 542 MPa and the critical unlocking stress of complete K–W locks is about 2084 MPa. The n₁ strain hardening regime straddles from the microplastic region, the yield region, and lies slightly (up to 3 to 5 pct plastic strains) beyond the yield region. Based on these considerations, it can be inferred that the relevant strain hardening mechanism(s) must occur at stresses above the critical stress for the onset of cross-slip and slightly below the critical unlocking stress for the incomplete K–W locks. A review of the six hardening mechanisms in the yield stress models in the literature and in MicroROM indicates that anomalous hardening of γ′ precipitates due to cross-slip and K–W lock formation (S4) lies in the stress regime of interest and should be considered in greater details.

3.2 Strain Hardening in the Low Plastic Strain Regime

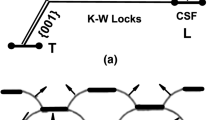
The dislocation structures of Ni₃Al and other similar L1₂-ordered alloys deformed in the yield stress anomaly regime are characterized by long segment of sessile screw dislocations in the K–W configuration with the APB on the {010}, and the segments are connected with one another by short segments of near-edge dislocations on the {111} plane.[15,16,17] These near-edge dislocations, called superkinks,[18,19,20,21] are mobile and can move on the {111} plane. This dislocation structure is considered to be created by a double cross-slip mechanism[46] that results in a double kink configuration.[21] During the double cross-slip process, the screw dislocation segments on {010} are dissociated and separated by an APB fault, while the edge dislocation segments on {111} are dissociated into two Shockley partials separated by complex stacking faults CSF,[21] which can be superlattice intrinsic stacking faults (SISF) or superlattice extrinsic stacking faults (SESF). The stress required to activate the double cross-slip configuration is given by

$$ \sigma = \chi \sigma_{{{\text{IK}} - {\text{W}}}} , $$

(14)

where $0.542 < \chi \le 1$ since the stress must be greater the critical stress for cross-slip and less than the yield stress in order to remain within the low plastic strain hardening regime.

Slip on {111} plane by lateral propagation of an edge superkink on straight, immobile screw dislocations on {010} plane was analyzed by Sun,[27] who investigated the interaction force, energy, and the stability of the superkink as the shape of the superkink changes in height and width. The propagation of a superkink with a critical kink height, $\bar{h},$ is illustrated schematically in Figure 3, which shows sessile screw segments on {001} and a mobile superkink (edge segment) on {111}. The earlier work by Sun[27] showed that an edge superkink can propagate stably or unstably, depending whether or not a critical kink height is exceeded. At or below the critical kink height, the superkink propagates stably in a fixed width and expands laterally until it is exhausted. Above the critical kink height, the superkink is unstable and keeps widening as it propagates. For plastic deformation to continue, the superkink must maintain at a kink height greater than the critical kink height so that unstable superkink propagation can continue. The corresponding strain hardening is therefore related to the increase in the flow stress required to move the edge character dislocation segment in lateral glide on {111} and bypass the sessile screw dislocation segment(s) locked by cross-slip on to {010}. According to Sun,[27] the increase in the flow stress to maintain the superkink at the critical kink height to continue lateral glide is given by

Fig. 3

Modified from Sun.[27]

Formation and propagation of an unstable superkink with a critical kink height, $\bar{h}$.

$$ \sigma_{\text{sk}} = \frac{2M\Delta E}{{\bar{h}b}} $$

(15)

with

$$ \Delta E = \frac{{\mu b^{2} }}{8\pi \sqrt A }\ln \left[ {\left( {\frac{{\gamma_{\text{o}} }}{{\gamma_{{_{\text{C}} }} }}} \right)\sqrt {\frac{3A}{A + 2}} } \right], $$

(16)

where μ is the shear modulus, $\bar{h}$ is the critical kink height, and M is the Taylor factor. The Taylor factor has been added to Eq. [15] to convert shear stress to direct stress. A combination of Eqs. [15] and [16] leads one to

$$ \sigma_{\text{sk}} = \frac{M\mu b}{{40\bar{h}}} $$

(17)

when A = 3.3 and γ_ο/γ_c = 1.2 are substituted into Eq. [16].

Furthermore, previous work by Chan[10] has shown that the strain hardening exponent in the low plastic strain regime is given by

$$ n_{1} = \frac{{\rho_{\text{sk}} }}{{\rho_{\text{f}} }}, $$

(18)

where ρ_sk and ρ_f are the dislocation density of the superkinks and the forest dislocation density, respectively. Since the dislocation density is related to the stress according to

$$ \sigma = \alpha \mu b\sqrt \rho , $$

(19)

where ρ is dislocation density and α is a material constant with a value on the order of 0.3 to 0.5. Applying Eq. [19] through Eqs. [15] and [17] and combining with Eq. [18] lead one to

$$ n_{1} = \left[ {\frac{M\mu b}{{40\bar{h}\chi \sigma_{{{\text{IK}} - {\text{W}}}} }}} \right]^{2} $$

(20)

which can be utilized to predict the strain hardening exponent n₁ in the low plastic strain regime once the critical kink height ($\bar{h}$) and χ values are specified. The TEM results of Couret et al.[23,24] indicated that $\bar{h} \simeq 30b$ and $0.542 < \chi \le 1$ based on Eq. [12]. These values are used to compute n₁ as a function of χ in Figure 4 for M values of 2, 3.06, and 4, which correspond to the Taylor factors of soft grains, average grains, and hard grains, respectively. Figure 4 shows that for M = 2, the n₁ has a value of 0.0631 at the critical stress for cross-slip (χ = 0.54) and it decreases with increasing χ values to give n₁ = 0.0188 at χ = 1.0. The mean value is 0.0346 and the standard deviations are ± 0.0127. The n₁ values are increased with increasing M values from M = 2 to 4, as shown in Figure 4.

Fig. 4

Strain hardening exponent n₁ for the low plastic strain regime for various values of the Taylor factor (M) as a function of stress normalized by the critical stress, σ_IK–W, for unlocking incomplete K–W locks

The possible dependence of n₁ on microstructural parameters such as the volume fractions and sizes of primary, secondary, and tertiary γ′ was previously considered by Chan,[10] who showed that in the low plastic strain regime

$$ n_{1} = \frac{6}{\pi }\left( {\frac{{N_{\text{sk}} }}{{\rho_{\text{f}} }}} \right)\left[ {f_{1} d_{1}^{ - 3} + f_{2} d_{2}^{ - 3} + f_{3} d_{3}^{ - 3} } \right], $$

(21)

where f_i an d_i are the volume fraction and diameter of the ith type of γ′, where i = 1, 2, and 3 for primary, secondary, and tertiary γ′ precipitates, respectively. Equation [21] also corrects a typographical error shown in Eq. [25] of the earlier publication.[10] By defining

$$ N_{\text{if}} = \rho_{\text{f}} d_{i}^{3}, $$

(22)

where N_if is the number of forest dislocations in the ith type γ′ precipitates, Eq. [21] can be rewritten as follows:

$$ n_{1} = \frac{6}{\pi }\left[ {f_{1} \left( {\frac{{N_{{1{\text{sk}}}} }}{{N_{{1{\text{f}}}} }}} \right) + f_{2} \left( {\frac{{N_{{2{\text{sk}}}} }}{{N_{{2{\text{f}}}} }}} \right) + f_{3} \left( {\frac{{N_{{3{\text{sk}}}} }}{{N_{{3{\text{f}}}} }}} \right)} \right] . $$

(23)

when Eq. [22] is substituted into Eq. [21]. Furthermore, Eq. [23] can be simplified to

$$ n_{1} = \frac{6}{\pi }\left[ {f_{1}^{2} \omega_{1} + f_{2}^{2} \omega_{2} + f_{3}^{2} \omega_{3} } \right] $$

(24)

when

$$ \frac{{N_{\text{isk}} }}{{N_{\text{if}} }} = f_{i} \omega_{i} $$

(25)

is invoked where ω_i is the number of superkinks per unit number of forest dislocation in the ith type γ′ precipitates. If the number of superkinks per unit number forest dislocation is taken to be the same for all three types of γ′ precipitates, Eq. [24] can then be reduced to

$$ n_{1} = \frac{6\omega }{\pi }\left[ {f_{1}^{2} + f_{2}^{2} + f_{3}^{2} } \right], $$

(26)

where ω is the average number of superkink per unit number of forest dislocation per γ′ precipitate. Since tertiary γ′ precipitates are expected to be sheared and cut by the weak-pair dislocation coupling mechanism, ω₃ in Εq. [24] may be taken to be zero and Eq. [26] becomes

$$ n_{1} = \frac{6\omega }{\pi }\left[ {f_{1}^{2} + f_{2}^{2} } \right]. $$

(27)

The ω parameter can be evaluated by setting Eq. [26] or Eq. [27] through Eq. [20] using experimental values of n₁, f₁, f₂, and f₃ from the literature.[4,7,8,29] Using this approach, ω was determined to be about 0.1168, which indicates that the number of superkink per unit number of forest dislocation is 0.1168 or there is 1 superkink formed in about 9 γ′ precipitates.

3.3 Strain Hardening in the High Plastic Strain Regime

The high n₂ strain hardening regime commences when multiple {111} slip systems appear to be active with concurrent cross-slip on {010}. Figure 5(a) illustrates schematically the activation of one {111} slip system that exhibits cross-slip of a simple superkink[24] onto to a cube plane and then returns to the original {111} plane again. While the screw dislocation segments are immobile on the cube plane, the edge dislocation segments (superkinks) can move laterally along the slip direction. In addition, a superkink can undergo cross-slip from {111} to {010} and then switches back to slip on a different {111} plane, e.g., $\left( {1\bar{1}1} \right).$ Such a superkink is referred to as a switch-over superkink.[24] The glide process of a switch-over superkink is illustrated schematically in Figure 5(b). The interactions of two switch-over superkinks (upper and lower parts of Figure 5(b)) results in a dislocation configuration shown in Figure 5(c). The same dislocation mechanism configuration is obtained when simple superkinks are activated on two {111} slip systems and cross-slip onto one {010} plane, as shown in Figure 5(c). Cutting of γ′ on two {111} planes can promote the formation of a dislocation network with a pair-coupling structure.[47] The dislocation interaction configuration shown in Figure 5(c) can be extended to the activation of four independent {111} slip systems and cross-slip onto {010} to form K–W locks[14] or Lomer–Cottrell locks[48,49] at the apex of the Thompson’s tetrahedron,[50] where four independent {111} slip systems and one {010} slip system can be activated. The role of superlattice intrinsic stacking fault (SISF) in increasing the strain hardening rate has also been modeled by discrete dislocation dynamics.[51] A total energy-based approach was utilized to model the transition of APB to SISF based on mechanisms proposed in the literature.[52,53,54,55,56] The SISF hinders the propagation of superkinks on {111} as well as cross-slip onto {010} since the dissociated Shockley partials must be constricted and recombined before they can move onto {010}. The computational results show that both SISF on {111} and APB on {010} help contribute to a higher strain hardening exponent. Thus, the propensity of interactions of superkinks on {111} with sessile screw dislocation segments on {010} increases with increasing number of activated {111} slip systems.

Fig. 5

(a) Double {111} cross-slip by a simple superkink to form an APB on a {010} plane operative on one {111} slip system, (b) double {111} cross-slip by a switch-over superkink to form an APB fault on a {010} plane operative on two {111} slip system, and (c) double {111} cross-slip by a switch-over superkink or a simple superkink to form an APB fault on a {010} plane operative on two {111} slip system. Complex stacking faults (CSF) are formed on the {111} planes

For plastic compatibility in a polycrystalline material, the activation of a minimum of five independent slip systems is required in individual grains.[33] To achieve anomalous hardening, cross-slip onto one or more cube planes is required.[14,15,16,17] Thus, the five individual slip systems may include three {111} slip systems with two cross-slip on two {010} planes. Since slip on {010} is quite limited, four {111} slip systems with cross-slip on one {010} planes are also possible. Latent hardening on these multiple {111} slip systems and {010} cross-slip plane would lead to a higher strain hardening exponent n₂, which can be obtained by summing the contributions of individual slip systems,[10] leading to

$$ n_{2} = \frac{{6\omega n_{\text{s}} }}{\pi }\left( {\frac{M}{2}} \right)^{2} \left[ {f_{1}^{2} + f_{2}^{2} + f_{3}^{2} } \right], $$

(28)

where n_s is the number of active slip systems and M is the Taylor factor for the less favorably oriented grains (M ≥ 2). Similarly, Eq. [28] becomes

$$ n_{2} = \frac{{6\omega n_{\text{s}} }}{\pi }\left( {\frac{M}{2}} \right)^{2} \left[ {f_{1}^{2} + f_{2}^{2} } \right] $$

(29)

when the tertiary γ′ precipitates are too small for cross-slip onto {010} plane to occur prior to cutting by the weak-pair dislocation coupling mechanism.

The strain hardening models were evaluated by comparing experimental data of n₁ and n₂ of a number of Ni-based superalloys in Figure 6, which plots the n₁ and n₂ values as a function of the sum of the squares of the volume fractions of primary γ′ (f₁), secondary γ′ (f₂), and tertiary γ′ (f₃). The n₁ line was computed with ω = 0.1168 and one active {111} slip and immobilized cross- slip on {010}, while the n₂ line were computed using n_s values ranging from 2 to 5 with M = 2.366. The n_s number refers to the number of {111} slip systems activated up to three {111} and up to two {010} slip or alternatively, four {111} slip systems with one {010} slip system. Figure 6 shows that the n₁ values correspond to slip on one {111} system. Some of the high n₁ and low n₂ values can be attributed to slip on two {111} plane. Most of the n₂ values corresponds to multiple slip on three or more {111} plane plus cross-slip on {010} planes. In Figure 6(a), the values of n₁ and n₂ are correlated with the volume fractions of primary (f₁) and secondary (f₂) γ′ precipitates. In Figure 6(b), the correlation also includes the volume fraction of tertiary (f₃) γ′ together with those of primary and secondary γ′ precipitates. In all cases, the n₁ and n₂ values increase with increasing values of the sum of the squares of f₁ and f₂, while the volume fraction of tertiary γ′ does not appear to affect either n₁ or n₂. A comparison of n₁ and n₂ with and without the contribution of f₃ indicates that similar, if not the same, correlations with n₁ or n₂ are obtained, as shown in Figures 6(a) and (b). The implication is that the volume fraction of tertiary γ′ (f₃) exerts little or no influence on the strain hardening exponents (n₁ and n₂).

Fig. 6

Strain hardening exponent n₁ (filled symbols) in the low plastic strain regime and the strain hardening exponent n₂ (open symbols) in the high plastic strain regime as a function of the sum of squares the primary (f₁) and secondary (f₂) γ′ precipitates without (a) and (b) with tertiary (f₃) γ′ precipitates for selected Ni-based superalloys. The calculated values of the strain hardening exponents increase with increasing number (n_s) of active slip systems. M = 2 for n_s = 1 and M = 2.366 for n_s ≥ 2. Experimental data are from the literature.[4,7,8,9,10,29]

3.4 Relation of Slip Band Spacing and Strain Hardening

Slip uniformity and strain hardening are often related but an explicit relation between slip band spacing and strain hardening remains elusive. In the studies of NIMONIC 80A, Lerch and Gerold have showed that a Hall–Petch type relation exists between slip band spacing and stress according to the expression given by[8]

$$ \sigma = k_{\text{HP}} \lambda^{ - 1/2} , $$

(30)

where k_HP is a Hall–Petch type constant and λ is slip line or slip band spacing. More uniform slip occurs after multiple slip has occurred and its strain hardening response is characterized by Eq. [2] in the high plastic strain hardening (n₂) regime. In this regime, the stress–strain relation is given by

$$ \sigma = k_{2} \varepsilon_{\text{p}}^{{n_{2} }} $$

(31)

which can be combined with Eq. [30] to obtain

$$ \lambda = \left( {\frac{{k_{\text{HP}} }}{{k_{2} }}} \right)^{2} \varepsilon_{\text{p}}^{{ - 2n_{2} }}. $$

(32)

The Hall–Petch type constant k_HP can be taken to be related to the grain size, D, such that

$$ k_{\text{HP}} = k_{\text{o}} \sqrt D , $$

(33)

where k_o is a constant with a unit of stress (e.g., MPa). Substituting Eq. [33] into Eq. [32] leads one to

$$ \lambda = \left( {\frac{{k_{\text{o}} }}{{k_{2} }}} \right)^{2} D\varepsilon_{\text{p}}^{{ - 2n_{2} }} $$

(34)

which indicates that the slip band spacing decreases with increasing plastic strain according to a power law with an exponent of − 2n₂.

The slip band spacing of NIMONIC 80A subjected to cyclic loading was previously measured as a function of plastic strain range. These experimental results are compared against the slip band spacing model, Eq. [34], using relevant values for the model constants. The values for k₂ and n₂ are available from the stress–strain curves (k₂ = 2378.0 MPa, n₂ = 0.231) while the grain size (D = 60 μm) was measured and reported by Lerch and Gerold.[8] The only unknown was k_o (181.62 MPa), which was determined by invoking the condition that λ = D/2 at a small plastic strain (ε_p = Δε_p/2 = 1e−4). Figure 7 shows a comparison of the model calculation against experimental data of slip band spacing as a function of plastic strain. Figure 7 shows that the n₁ regime lies in the microplastic strain region (Δε_p/2 < 1 × 10⁻⁴) while the n₂ regime resides mostly in the macroplastic region (Δε_p/2 > 1 × 10⁻⁴). The power law relation between slip line spacing and Δε_p/2 is evident in the n₂ regime, as shown in Figure 7(a). Plotting the slip line spacing in a linear scale in Figure 7(b) depicts more clearly the n₁ regime in the microplastic strain range and the existence of an asymptotic limit for the slip line spacing as the plastic strain becomes large. There is good agreement between model calculation and experimental data over the entire range of plastic strains. For comparison, the slip line spacing computed for the microplastic regime using experimental values of k₁ and n₁ (903 MPa and 0.0542) and a k_o value of 360 MPa is also shown in Figure 7. In this regime, the slip line spacing is relatively constant and is on the order of D/2. Near the yield region, the calculated slip band spacing approaches D/2 at ε_p = 1e−4 and decreases rapidly with increasing plastic strains. At larger plastic strains, the slip band spacing appears to approach a lower critical limit, λ*, given by

$$ \lambda^{*} = \frac{\alpha \mu b}{{k_{2} }} = \, 0.286\;\mu {\text{m}} $$

(35)

based on α = 0.3, μ = 8.156 Ε+4 MPa, and b = 2.8E-10 m. The critical limit of dislocation spacing, λ^*, can be the mean free path of statistically-stored dislocations,[57] geometrically necessary dislocations,[57] dislocation tangles[58] or dislocation cell size, depending on the operative dislocation mechanism(s) in the high plastic strain regime. According to Eq. [34], the evolution of slip line spacing is controlled by a power law of the plastic strain and the strain hardening exponent n₂. Thus, Eq. [34] provides an explicit relation between slip uniformity and strain hardening exponent. In contrast, the critical limit of the slip spacing is controlled by strength coefficient k₂ in the constitutive equation for the high plastic strain regime.

Fig. 7

Evolution of slip line spacing as a function of plastic strain amplitude: (a) logarithmic relation between slip band spacing and plastic strain amplitude showing decrease of slip line spacing with increasing plastic strain amplitude, and (b) slip line spacing approaching a critical limit of minimum slip line spacing. Experimental data are from Ref. [8]

4 Discussion

The power law relation shown in Eq. [2] is formulated in the one-dimensional (1D) case for simplicity. It can be generalized to three-dimensional (3D) cases by replacing the uniaxial stress (σ) and plastic strain (ε_p) with the effective stress ($\bar{\sigma }$) and effective plastic strain ($\bar{\varepsilon }_{\text{p}}$). The 3D version of the Ramberg–Osgood equation is available in the literature.[59] Both the Ramberg–Osgood equation and the MicroROM model have been implemented in DARWIN^®,[60] a probabilistic life prediction and risk assessment code, for analyzing the local stress–strain response of individual zones of gas turbine engine components. The local stresses and strains can be utilized in conjunction with relevant life prediction models to predict fatigue crack nucleation lives under variable loads and temperatures. The model constants in the Ramberg–Osgood equation are empirically evaluated from experimental data, but these model constants provide little or no microstructural information. These disadvantages are remediated by the equations in the MicroROM model, which provides the simplicity found in the Ramberg–Osgood equation with detailed information and insight of the influence of microstructural parameters such as the grain size and the sizes and the volume fractions of primary, secondary, and tertiary γ′ precipitates on the constitutive behaviors of Ni-based superalloys. Similarly, MicroROM differs from constitutive models with internal variables and empirically derived models (e.g., References 61, and 62) by providing explicit relations between the strain hardening variables (n₁ and n₂) and microstructural parameters (grain size, volume fractions, and sizes of primary, secondary, and tertiary γ′). Furthermore, MicroROM differs from a number of existing physics-based yield stress models[1,2,3,4,40,63] by providing the yield stresses as well as the entire stress–strain curves for various temperatures ranging from ambient temperature to elevated temperatures beyond the anomalous hardening region (i.e., 298 K to 1033 K (25 °C to 760 °C). Other physically based constitutive models[64,65] in literature, which are intended for predicting hot deformation at elevated temperatures, consider the flow behavior of Ni-based superalloys on the basis of evolution of γ grains during dynamic grain growth and recrystallization without considerations of the flow stress contributions due to the γ′ precipitates.

According to Eq. [5], six hardening mechanisms contribute to the yield strength of Ni-based superalloys. The yield strength of superalloys is on the order of the critical stress, $\sigma_{{{\text{IK}} - {\text{W}}}} ,$ for unlocking incomplete K–W locks, while the critical stress, $\sigma_{\text{cs}} ,$ for the onset of cross-slip from the {111} plane to {010} occurs at about $0.542\sigma_{{{\text{IK}} - {\text{W}}}} ,$ (Eq. [12]). By comparing the various contributors to the yield strength in Eq. [5] against $\sigma_{\text{cs}}$ and $\sigma_{{{\text{IK}} - {\text{W}}}} ,$ it might be possible to discern the sequence of the hardening mechanism(s) that contribute to the strain hardening processes in the microplastic regime. Equation [5] was utilized in a previous investigation[10] to model the yield strength and the stress–strain response of ME3 with the supersolvus and subsolvus microstructures and Alloy 720 Li with the subsolvus microstructure. The earlier investigation[10] showed that MicroROM was able to predict the yield strength (YS) and ultimate tensile strength (UTS) of ME3 and Alloy 720 Li from 298 K to 1033 K (25 °C to 760 °C), including the anomalous increase of yield strength with increasing temperatures in the intermediate temperatures (673 K (400 °C) to 923 K (650 °C)). For example, the anomalous YS behavior of Alloy 720 Li with the subsolvus microstructure can be found in Figure 8 of Reference 10, while the anomalous YS behaviors of subsolvus and supersolvus ME3 can be found in Figures 10 and 11 of Reference 10, respectively. These results were utilized to obtain the various contributors (Si, i = 1 to 6) to the yield strengths of these two Ni-based superalloys in Figures 8 and 9, for ME3 and Alloy 720 Li, respectively. For both alloys, the critical stresses for cross-slip were higher than those for instigating shearing of tertiary γ′ by the weak-pair coupling mechanism (σ_cs > (S1 + S5)). In contrast, the critical stresses for cross-slip were lower than those for instigating shearing of secondary γ′ by the strong-pair coupling mechanism (σ_cs < (S1 + S5 + S6)). Thus, cross-slip onto {010} plane can be operative during {111} slip in secondary γ′, but is unlikely to be activated during {111} slip in tertiary γ′. Once shearing of γ′ by strong-pair coupling mechanism is activated, cross-lip from the {111} plane to {010} can lead to incomplete and/or complete K–W locks and instigate anomalous hardening, even though slip remains within the microplastic regime and occurs mostly on one {111} slip plane. The self-hardening mechanism on the activated {111} plane is caused by the resistance encountered by the superkinks in overcoming the immobile screw segments on {010} during lateral glide on {111}. The consequence is that the strain hardening exponent n₁ is relatively low until multiple {111} slip systems are activated when the critical stress for unlocking incomplete K–W locks and the yield stress are exceeded. At higher plastic strains, latent hardening of multiple {111} planes by cross-slip on multiple {010} planes leads to a higher strain hardening exponent n₂, which magnitude depends on the number of interacting slip systems and crystallographic orientations of the grains (through the Taylor factor), as well as the critical kink height. Thus, the transition from the low strain hardening (n₁) regime to the high strain hardening (n₂) regime is dictated by the evolution from predominantly single slip to multiple slip in individual grains. A single strain hardening regime such as that observed in RR 1000 with fine γ′ precipitates when the transition of single slip to multiple slip occurs over a wide range of plastic strains so that the two hardening regimes overlap and merge as one, as shown in Figure 1(b).

Fig. 8

Yield strength component, Si, normalized by yield strength (YS) compared to normalized critical stress for cross-slip and critical stress for unlocking incomplete K–W locks as a function of temperature for ME3 with the supersolvus microstructure

Fig. 9

Yield strength component, Si, normalized by yield strength (YS) compared to normalized critical stress for cross-slip and critical stress for unlocking incomplete K–W locks as a function of temperature for Alloy 720 Li with the subsolvus microstructure

Figure 10 presents a summary of the strain hardening mechanisms on the basis of the various critical stresses for cross-slip, unlocking incomplete and complete K–W locks, all normalized by the yield stress (YS) as a function of temperature. At stresses below the critical stress for cross-slip, the hardening mechanisms are operative mostly on one {111} plane and include solid solution hardening of the γ matrix, and shearing of tertiary and secondary γ′ without the activation of cross-slip on {010}. At stresses above σ_cs but below σ_ikw, the strain hardening mechanisms include shearing of primary (if present) and secondary γ′, anomalous hardening induced by cross-slip on {010}, and Hall–Petch hardening of the γ matrix and primary γ′. These hardening mechanisms may occur on one or two {111} slip systems. At stresses above the YS, the strain hardening mechanisms are operative on multiple {111} slip systems with cross-slip on {010} to induce anomalous hardening encountered by the interactions of superkinks with the incomplete and complete K–W locks.

Fig. 10

A summary of the operative strain hardening mechanisms at various σ/YS values and temperatures

The variation of the operative hardening mechanisms with stress level has significant implications on the fatigue limits under low-cycle fatigue (LCF) and high-cycle fatigue (HCF) loading. Previous work by Ren and Nicholas[66] on Udimet 720 indicated that the LCF limits of Udimet 720 at a stress ratio, R, of 0.1 was above the yield stress. Prior LCF cycling was found to significantly reduce the subsequent HCF limit by localizing slip on one {111} slip plane. From Figure 10, it is apparent that the operative strain hardening mechanisms above the yield stress during LCF loading are different from those at HCF loading below the YS. At stresses below the yield strength (YS), inelastic strains are not exactly zero since microplastic strains can accumulate below the macroscopic yield stress, which is typically defined at the onset of 0.2 pct plastic strain. For example, Figure 1 shows clearly that plastic strains are not zero but occur at detectable levels below the macroscopic yield stress defined at 0.2 pct plastic strains. The critical stress for the onset of cross-slip is also significantly below the yield stress (about 0.5 of the YS). More importantly, slip below the critical stress for cross-slip can be operative on just one single {111} slip plane, as observed by Ren and Nicholas,[66] while multiple slips on {111} are operative at stresses above the yield strength. Besides differences in the strain hardening mechanisms, the strain hardening exponent (n₁) in the microplastic regime where the HCF limit resides may be significantly lower than the strain hardening exponent (n₂) in the LCF (high plastic strain) regime. A change from LCF loading to HCF loading can result in the activation of {111} slip with {010} cross-slip that subsequently turns into localized slip on a single {111} slip on an individual slip plane when the HCF cyclic stresses are below the critical stress for cross-slip onto {010} so that the operative deformation mechanisms are shearing of primary, secondary, and tertiary γ′ precipitates, which have the propensity to promote fatigue crack nucleation along slip bands, as observed in many Ni-based superalloys including Udimet 720.[66]

One of the significant findings of this investigation is the identification of the role plays by the microstructure in influencing the strain hardening exponents. In particular, the results show that neither n₁ nor n₂ is dependent on the size of the γ′ precipitates. Instead, n₁ and n₂ are proportional to the sum of the squares of volume fractions (f ²₁ + f ²₂ ) of the primary and secondary γ′. Since the volume fraction of tertiary γ′ is generally small, the square of f₃ is usually very small and is negligible when either n₁ or n₂ is considered for a number of Ni-based superalloys. The source of strain hardening in Ni-based superalloys originates from cross-slip from {111} to {010} to form incomplete and complete K–W locks that must be overcome and bypassed by superkinks. Since cross-slip is not operative in tertiary γ′ precipitates due to a higher critical stress for cross-slip as dislocations cut tertiary γ′ via the weak-pair coupling mechanisms, it is reasonable to expect the absence of a contribution of f₃ to either n₁ or n₂, as shown in Figure 6. Even for primary and secondary γ′, the number of superkink per number of forest dislocation per γ′ is about 0.1168, meaning a superkink occurs in about 8.5 γ′ precipitates. There are at least two reasons for such a low number of γ′ precipitates that contain a superkink: (1) not all γ′ precipitates lie on the operative slip planes and are cut by dislocations, and (2) the superkinks in the γ′ precipitates may not exhibit a kink height that is higher than the critical kink height. The ω value of 0.1168 suggests that only one critical superkink (i.e., one with a kink height that exceeds the critical kink height) occurs in about 8.5 γ′ precipitates. In two previous studies, Couret et al.[23,24] measured the kink heights of superkinks in Ni₃Ga at 20, 200, and 400 °C. For 20 °C, they found that the number of superkinks with critical kink height was about 80, while the number of superkinks exhibiting kink height in excess of the critical kink height (i.e., post-critical superkinks) was 16. Thus, the corresponding ratio was 16/80 or 0.2. For 200 °C, the number of critical superkinks was 40, while the number of post-critical superkinks was 4, leading to a ratio of post-critical to critical superkink of 0.1 Similarly, they reported the number of critical superkinks was 55 and the corresponding post-critical superkinks was 10 at 400 °C. The post-critical to critical kink height ratio was thus 0.18. The average post-critical to critical superkink ratio is 0.153, which is on the order of the ω parameter. The implication is that the ω parameter may be related to the post-critical to critical kink height ratio. More precisely, the strain hardening exponent may be influenced by the number of post-critical superkinks in the γ′ since only these superkinks are capable of continuing cross-slip on the {010} planes and instigating anomalous hardening through incomplete and complete K–W lock formation. The critical or subcritical superkinks may continue lateral slip on the {111} plane, but they may eventually stop expanding and provide little or no additional strain hardening. Specifically, it is considered that the ω parameter is related to the number of post-critical superkink by the equation given by

$$ \varpi = c_{{_{1} }} \frac{{N_{\text{sk}}^{\text{p}} }}{{N_{\text{sk}}^{*} }}, $$

(36)

where $N_{\text{sk}}^{\text{p}}$is the number of post-critical superkinks, $N_{\text{sk}}^{*}$is the number of critical superkinks, and c₁ is an empirical constant. Based on the data for Ni₃Ga from Couret et al.,[23,24] the value of c₁ is about 0.763, assuming the results of Ni₃Ga are applicable to Ni₃Al. Comparable results of post-critical superkink height population in Ni₃Al are not available in the literature. Nonetheless, the results on Ni₃Ga indicate that the strain hardening response of Ni₃Al and Ni-based superalloys strengthened by Ni₃Al is strongly influenced by the dislocation substructure, which includes the height, shape, number, and type (simple or switch-over) of superkinks.

The proposed strain hardening models, Eqs. [27] and [29], provide explicit relations between the strain hardening exponents (n₁ and n₂) to the relevant microstructural parameters (f₁, f₂, M, and n_s) as well as the dislocation substructure (ω, $N_{\text{sk}}^{\text{p}} ,$, and $N_{\text{sk}}^{*}$) through Eq. [36]. The volume fractions of primary (f₁) and secondary γ′ (f₂) can easily be measured or predicted using a heat-treatment model (e.g., Reference 13). The Taylor factor M and the number of {111} slip systems activated depend on grain orientation and both are bound within a small range. In particular, M ranges from 2 to 4; n_s ranges from 1 in the low plastic strain regime and 3 to 5 in the high plastic strain regime. In contrast, the ω parameter is more difficult to obtain and requires TEM studies to characterize the dislocation substructure and to identify the number of superkinks per unit number of forest dislocation. Since post-critical superkinks are required to continue slip on one or more {111} planes and cross-slip on {010} planes, one possible approach to obtain the ω parameter is to measure the superkink height distribution using TEM; alternately, the ω parameter may be obtained by fitting Eq. [27] to the strain hardening exponent n₁ for the low plastic strain regime. Furthermore, Eq. [34] provides an explicit relation between strain uniformity and strain hardening exponent that describes how the slip line spacing decreases with increasing plastic strain accumulation without the need to identify the underlying hardening mechanism(s). The slip line spacing can be characterized via optical metallography (OM) or scanning electron metallography (SEM); both are easier to apply than transmission electron microscopy. On the other hand, Eq. [35] provides an estimate of the lower limit of the minimum distance of the underlying dislocation barriers, which can be measured and validated by SEM or TEM.

5 Conclusions

In this investigation, the MicroROM constitutive model has been extended to include a set of mechanism-based strain hardening laws for the low plastic strain and the high plastic strain regimes. The conclusions reached as the results of this investigation are as follows:

• (1) The underlying strain hardening mechanisms in low and high plastic strain regimes can be attributed to cross-slip from {111} plane(s) to {010} plane(s) to form incomplete and complete K–W locks. The difference in the strain exponent values in the two regime has been shown to arise from the number of active {111} slip systems activated during plastic deformation.

• (2) In the low plastic strain regime that includes the microplastic region, the number of {111} activated is mostly one, while three or more {111} slip systems are operative in the high plastic strain regime and their interactions with cross-slip onto the {010} planes lead to latent hardening and a considerably higher strain hardening exponent.

• (3) Besides the number of active {111} slip systems, the strain hardening exponent depends on the crystallographic orientation of the grains through the Taylor factor, the sum of the squares of the volume fractions of the primary and secondary γ′, but not the volume fraction of tertiary γ′.

• (4) The strain hardening exponent is influenced by the number of superkink per unit number of forest dislocation, which, in turn, is related to the ratio of the number of post-critical superkinks to the number of critical superkinks.

• (5) The strain hardening exponents depend not only on microstructural variables, but also on the dislocation substructure such as the height, number, and type of superkinks (simple or switch-over superkinks), as well as the population of post-critical superkinks in the total population of forest dislocations.

• (6) The evolution of slip line spacing is mostly controlled by the strain hardening exponent in the high plastic strain (n₂) regime, while the critical limit of the slip line spacing is controlled by the strength coefficient k₂.