Analysis of Martensitic Transformation Plasticity Under Various Loadings in a Low-Carbon Steel: An Elastoplastic Phase Field Study

Abstract

An elastoplastic phase field model for the martensitic transformation of a Fe-0.22C-1.58Mn-0.81Si (wt pct) alloy was developed, to investigate transformation plasticity in response to uniaxial, biaxial, shear and axial-shear loadings below half the yield strength of austenite. The simulation results clearly demonstrate the preferential orientation of martensite variants as well as plastic behavior during transformation. The data also suggest that the transformation plasticity coefficient is independent of external stress. Preferential orientation can occur under both axial and shear loading conditions, and the equivalent values of transformation plastic strains are roughly the same regardless of the stress components in the combined axial and shear loadings. Similar microstructural evolution and deformation behaviors were identified in response to both uniaxial and biaxial loadings when the uniaxial stress was equal to the difference in applied stresses along both axes during biaxial loading. The Magee mechanism is considered to play a predominant role in martensitic transformation plasticity, although both the Magee and Greenwood-Johnson mechanisms can be identified through simulations. This work demonstrates that the accumulated plastic strain in martensite is primarily inherited from the parent austenite phase, with only a negligible portion due to the yielding of martensite.

1 Introduction

Permanent volume and shape changes can be induced in various materials as a result of solid–solid phase transformations under applied stress, even in the case that the stress is much less than the yield strength of the material. This phenomenon is referred to as transformation plasticity.[1] Several distinct mechanisms have been suggested for this plastic behavior, including the Greenwood-Johnson,[2] migrating interface diffusion[3,4] and Magee mechanisms.[5] It should be noted that these mechanisms are believed to induce transformation plasticity during various transformation processes. The Greenwood-Johnson and migrating interface diffusion mechanisms assume diffusional transformation in conjunction with a volume mismatch-induced internal stress model and atomic diffusion along the migrating phase interface, respectively, while the Magee mechanism is based on martensitic transformation. However, in recent years, some studies have indicated that both the Greenwood-Johnson and Magee mechanisms can occur during martensitic transformation, although it is unclear which mechanism is predominant when an external load is applied.[6,7] The Leblond model is derived from the Greenwood-Johnson mechanism assuming diffusional transformation. This model attempts to predict plasticity during martensitic transformation, and has generated results that agree with experimental data.[8,9,10]

The effect of various loadings on transformation plasticity is an ongoing field of study. Research has shown that the external stress threshold is equal to half the yield stress of the weaker phase, which is considered to be responsible for variations in the relationship between applied stress and transformation plastic strain in different materials.[11] Furthermore, a linear relationship defined by a constant transformation plastic coefficient has been reported in the case that the applied stress is less than the threshold value, for both tensile and compressive loadings.[7,12] In recent years, axial-torsional loadings have been widely studied, and the same linear relationship for equivalent transformation plastic strain associated with an equivalent stress has been established.[13,14] Furthermore, several improved models have been proposed to describe transformation plasticity behaviors under various loadings.[15,16,17,18] However, it should be noted that existing models require improvement, especially with regard to the prediction of the effects of complex loading conditions, such as full or partial unloading, pre-hardening, cyclic loading and butterfly loading.[13,19,20,21,22] In addition, based on thermodynamic theory and micromechanical models, numerical simulations have also been used in attempts to predict transformation plastic behaviors for diffusional and diffusionless transformations. However, only deformation behavior associated with microscopic plastic strain can be provided by most of these simulations, while microstructural features during transformation cannot be described.[12,23,24,25,26,27]

Phase field models are reasonably effective at providing microscopic-scale simulations by predicting microstructural morphologies, and have recently emerged as a versatile tool for describing microstructural evolution during material processing.[28,29,30] Recently, a phase field microelasticity model based on the time-dependent Ginzburg–Landau (TDGL) phase transformation theory integrated with the Khachaturyan–Shatalov (K-S) theory of elastic energy has been proposed. This model permits investigation of microstructural evolution and the corresponding distribution of elastic strain during martensitic transformation.[31,32] Furthermore, the plastic deformation is also involved in the phase field modelling via a TDGL kinetic equation or an crystal plasticity equation used to model plastic flow, referred to as elastoplastic phase field model.[33,34] In this manner, it becomes possible to predict various microstructural or mechanical phenomena occurring during martensitic transformation on both the microscopic and macroscopic scales. These include stress-assisted and strain-induced transformations as well as the preferential orientation of martensite variants and pseudoplasticity in shape memory alloys.[35,36,37,38]

In the present study, an elastoplastic phase field model was employed to investigate transformation plasticity during martensitic transformation in a low carbon steel with various loadings, including uniaxial, biaxial, shear and axial-shear. A phase-dependent exponential hardening equation for yield strength was implemented during this modelling, assuming the complete inheritance of plastic strain on going from austenite to martensite during the simulation. Various interesting transformation plastic behaviors were observed and are discussed herein. These include the preferential orientation of martensite variants under different loadings, the equivalence of transformation plastic strain under biaxial and axial-shear loadings, and the effects of the Greenwood-Johnson and Magee mechanisms on transformation plasticity.

2 Elastoplastic Phase-Field Model

The Allen–Cahn equation was applied to simulate microstructural evolution during martensitic transformation. This equation contains an elastic strain energy term and evolves on a dimensionless temporal scale.[39,40] The equation can be expressed as[33,35,40]:

$$ \frac{{\partial \emptyset_{i} }}{\partial t} = - \mathop \sum \limits_{i = 1}^{i = \upsilon } L\frac{\delta G}{{\delta \phi_{i} }}, $$

(1)

where $\emptyset_{i}$ is an order parameter that tracks the evolution of martensite, $\upsilon$ is the number of martensite variants, it is generally known that three types of body-centered tetragonal (BCT) structure are produced from the face-centered cubic (FCC) following the Bain correspondence during martensitic transformation, suggesting three martensite variants (such that $\upsilon = 2$ for a two-dimensional simulation). $L$ is a mobility factor, $G$ is the total Gibbs energy, and can be described as:

$$ G = \mathop \smallint \limits_{V}^{{}} \left( {g_{ch} + g_{gr} + g_{el} + g_{ap} } \right)dV, $$

(2)

where $g_{ch}$ corresponds to the chemical part of the Gibbs energy density, $g_{gr}$ is the gradient energy density term, $g_{el}$ is the elastic strain energy density and $g_{ap}$ is an additional energy term.

The value of $g_{ch}$ can be determined from a Landau polynomial expansion, written as:

$$ g_{ch} = \frac{1}{{V_{m} }}\left( {\frac{A}{2}\left( {\emptyset_{1}^{2} + \emptyset_{2}^{2} } \right) - \frac{B}{3}\left( {\emptyset_{1}^{3} + \emptyset_{2}^{3} } \right) + \frac{C}{4}\left( {\emptyset_{1}^{2} + \emptyset_{2}^{2} } \right)^{2} } \right) , $$

(3)

where $V_{m}$ is the molar volume and the coefficients A, B, and C are expressed in terms of the Gibbs energy barrier and the driving force:$A = 32\Delta G^{*}$,$B = 3A - 12\Delta G^{{\gamma - \alpha^{\prime}}}$ and $C = 2A - 12\Delta G^{{\gamma - \alpha^{\prime}}}$. The term $\Delta G^{{\gamma - \alpha^{\prime}}}$ is the driving force calculated using the Thermo-Calc software package based on the TCFE8 database,[41] $\Delta G^{*}$ is the Gibbs energy barrier (which can be expressed as $\Delta G^{*} = 3\sqrt 2 \sigma V_{m} /8\delta$[33]), $\sigma$ is the interfacial energy and $\delta$ is the interface thickness. The gradient energy density term, $g_{gr}$, is expressed as:

$$ g_{gr} = \frac{1}{2}\beta \mathop \sum \limits_{i = 1}^{i = \nu } \Vert \nabla \emptyset_{i}^{2}\Vert, $$

(4)

where $\beta$ is the gradient coefficient, obtained from $\beta = 3\sqrt 2 \sigma \delta /4$.[33]

The elastic strain energy density, $g_{el}$, is expressed as:

$$ g_{el} = \frac{1}{2}C_{ijkl} \left( {\varepsilon_{ij} - \varepsilon_{ij}^{tr} - \varepsilon_{ij}^{p} } \right)\left( {\varepsilon_{kl} - \varepsilon_{kl}^{tr} - \varepsilon_{kl}^{p} } \right), $$

(5)

For simplicity, the material has been assumed to be isotropic, which means the elastic modulus tensor, $C_{ijkl}$, is independent of the local orientation and can be written as $C_{ijkl} = C_{ijkl}^{\gamma } + \emptyset_{1} \left( {C_{ijkl}^{{\alpha^{\prime}}} - C_{ijkl}^{\gamma } } \right) + \emptyset_{2} \left( {C_{ijkl}^{{\alpha^{\prime}}} - C_{ijkl}^{\gamma } } \right)$.[42] $\varepsilon_{ij}$ is the local strain (expressed as $\varepsilon_{ij} = 0.5\left( {u_{i,j} + u_{j,i} } \right)$ where $u_{i,j}$ is the derivative of $u_{i}$ with respect to the j-th spatial coordinate) and $\varepsilon_{ij}^{p}$ is the plastic strain. Here, the global and local coordinate systems are considered in polycrystalline material, in which the axes of global coordinate system are parallel to boundaries of simulation domain in two-dimensions, while the local coordinate system is defined in each austenite grain, the rotation angle, $\theta$, between two coordinate systems represents the crystal orientation of specific austenite grain.[32] Therefore, the transformation strain, $\varepsilon_{ij}^{tr}$, within a global coordinate system can be expressed as:

$$ \varepsilon_{ij}^{tr} = \mathop \sum \limits_{x = 1}^{\nu } R_{ik} \left( \theta \right)R_{jl} \left( \theta \right)\varepsilon_{kl}^{00} \left( x \right)\emptyset_{x} , $$

(6)

The term $R_{ij} \left( \theta \right)$ is a rotation matrix in two-dimensions and can be written as[43]:

$$ R_{ij} \left( \theta \right) = \left[ {\begin{array}{ll} {\cos \theta\quad-\sin \theta } \\ {\sin \theta \quad \cos \theta} \\ \end{array}}\right], $$

(7)

and $\varepsilon_{ij}^{00} \left( 1 \right)$ and $\varepsilon_{ij}^{00} \left( 2 \right)$ are the Bain strains that are expressed as:

$$ \varepsilon_{ij}^{00} \left( 1 \right) = \left[ {\begin{array}{*{20}l} {\varepsilon_{1}\quad0} \\ {0 \quad \varepsilon_{3} } \\ \end{array} } \right]\;\varepsilon_{ij}^{00} \left( 2 \right) = \left[ {\begin{array}{*{20}c} {\varepsilon_{3} \quad0} \\ {0 \quad \varepsilon_{1} } \\ \end{array} } \right], $$

(8)

where the transformation-induced eigen strains are given by $\varepsilon_{1} = 0.1$ and $\varepsilon_{3} = - 0.1$.[31]

When an external stress is applied, an additional energy term is introduced that can be expressed as[35]:

$$ g_{ap} = - \sigma_{ij}^{ap} \varepsilon_{ij}^{tr} , $$

(9)

where $\sigma_{ij}^{ap}$ is the external stress.

The plastic strain was evaluated by minimizing the shear strain energy as a TDGL description, as proposed by Guo et al.[44] According to elastoplastic theory, plastic deformation is initiated when the Von-Mises equivalent stress satisfies the following yield criterion[31,32]:

$$ F_{y} = \frac{1}{2}\left\{ {\left( {\sigma_{xx} - \sigma_{yy} } \right)^{2} + \left( {\sigma_{yy} - \sigma_{zz} } \right)^{2} + \left( {\sigma_{zz} - \sigma_{xx} } \right)^{2} } \right\} + 3\left( {\sigma_{xy}^{2} + \sigma_{yz}^{2} + \sigma_{zx}^{2} } \right) - \sigma_{y}^{2} = 0, $$

(10)

where $F_{y}$ is the yield function, $\sigma_{ij}$ is a local stress tensor and $\sigma_{y}$ denotes the yield stress. The last term can be expressed as an exponential hardening equation associated with equivalent plastic strain:

$$ \sigma_{y} = \mathop \sum \limits_{i = 1}^{i = \nu } \emptyset_{i} \left( {\sigma_{{\alpha^{\prime}}} + H_{{\alpha^{\prime}}} *\varepsilon_{eq}^{{pb_{{\alpha^{\prime}}} }} } \right) + \left( {1 - \mathop \sum \limits_{i = 1}^{i = \nu } \emptyset_{i} } \right)\left( {\sigma_{\gamma } + H_{\gamma } *\varepsilon_{eq}^{{pb_{\gamma } }} } \right), $$

(11)

where $\varepsilon_{eq}^{p}$ is the local equivalent plastic strain, $\sigma_{{\alpha^{\prime}}}$ and $\sigma_{\gamma }$ are the initial yield stresses of martensite and austenite excluding the effect of strain hardening, $H_{{\alpha^{\prime}}}$ and $H_{\gamma }$ are the hardening coefficients of martensite and austenite, and $b_{{\alpha^{\prime}}}$ and $b_{\gamma }$ are the hardening exponents of martensite and austenite, respectively. All the phase-dependent hardening parameters were fitted based on mechanical calculations using the JMatPro software package.[45]

The evolution of plastic strain can be expressed as:

$$ \frac{{\partial \varepsilon_{ij}^{p} }}{\partial t} = - K_{ijkl} \frac{{\partial G_{shear} }}{{\partial \varepsilon_{kl}^{p} }}, $$

(12)

where $K_{ijkl}$ is the plastic kinetic coefficient (expressed by $K_{ijkl} = \left( {kC_{ijkl} } \right)^{ - 1}$ with a constant kinetics parameter $k$) and $G_{shear}$ is the shear strain energy density, written as[33,46]:

$$ G_{shear} = \mathop \smallint \limits_{{e_{ij}^{tot} }}^{{e_{ij} }} \sigma_{ij} de_{ij} = c_{ijkl} \left( {\frac{1}{2}e_{ij} e_{kl} + \frac{1}{2}e_{ij}^{tot} e_{kl}^{tot} - e_{ij} e_{kl}^{tot} } \right), $$

(13)

where $e_{ij}$ and $e_{ij}^{tot}$ are the deviatoric local actual strain tensor and deviatoric local permanent strain tensor. These terms are calculated as:

$$ e_{ij} = \varepsilon_{ij} - \frac{1}{3}\varepsilon_{kk} \delta_{ij} $$

(14)

and

$$ e_{ij}^{tot} = \left( {\varepsilon_{ij}^{tr} + \varepsilon_{ij}^{p} } \right) - \frac{1}{3}\left( {\varepsilon_{kk}^{tr} + \varepsilon_{kk}^{p} } \right)\delta_{ij} $$

(15)

where $\delta_{ij}$ is the Kronecker delta.

The macroscopic permanent strain that incorporates average values of the transformation strain, $\varepsilon^{tr}$, and plastic strain, $\varepsilon^{p}$, can be adopted to describe transformation plasticity in response to an external load on the macroscopic scale.[47,48] Because a small permanent strain was present even in the absence of external stress during these simulations (which can be attributed to an error in the simulated system), the transformation plastic strain can be expressed as:

$$ \varepsilon_{ij}^{tp} = \varepsilon_{ij}^{p} + \varepsilon_{ij}^{tr} - \varepsilon_{0ij}^{per} , $$

(16)

where $\varepsilon_{ij}^{tp}$ represents the transformation plastic strain and $\varepsilon_{0ij}^{per}$ is the permanent strain without loading.

3 Simulation Set-Up and Loading Conditions

3.1 Simulation Set-Up

The material investigated in the present study of transformation plasticity was a low-carbon steel with the chemical composition Fe-0.22C-1.58Mn-0.81Si (where the numerals indicate wt pct). The initial microstructure prior to quenching comprised a fully austenitized polycrystalline structure containing 10 austenite grains homogenously distributed in a $2.0 \mu {\text{m}} \times 2.0 \mu {\text{m}}$ simulation domain with random orientations. The isothermal temperature for martensitic transformation was assumed to be 200 °C, which is below the martensite-finish temperature.[49] The simulation domain was discretized using tri-node isoparametric elements containing $129 \times 129$ nodes. A constrained boundary condition was imposed to take into account the effect of the surrounding matrix, and the displacements along the x-axis for the left boundary and the y-axis for the lower boundary were given values of zero, as shown in Figure 1.[38] At the beginning of each simulation, a martensite nucleus was situated at the center of the calculation domain. The parameters used in these simulations are summarized in Table I.

Fig. 1

A diagram showing the polycrystalline structure used during simulations. The white solid lines represent the initial austenite grain boundaries, while the gray dashed line indicates the initial boundaries of the simulated domain

Table I Parameters Used in the Phase Field Simulations

3.2 Loading Conditions

The effects of loading conditions on microstructural evolution and transformation plasticity during martensitic transformation were assessed by simulating uniaxial, biaxial, shear and axial-shear loadings. In each case, the stress was less than half the yield strength of austenite at the temperature applied in the simulation. The dependence of transformation plasticity on the magnitude and directions of the external stress during martensitic transformation was examined under uniaxial loading conditions. Both tensile and compressive loads were applied along the x-axis in these simulations, with values of 25, 50, 75 and 100 MPa, respectively. In the case of biaxial loading, a constant tensile value of 50 MPa was applied along the x-axis, while stresses ranging from −50 to 150 MPa were simultaneously applied along the y-axis. The von Mises equivalent stress level ($\sigma_{eq} = \sqrt {\sigma^{2} + 3\tau^{2} }$) was applied during shear loading simulations,[13] employing shear stress values, $\tau \sqrt 3$, of − 100 and 100 MPa. In addition, axial-shear loading conditions combined with different axial and shear loads were employed in the simulations, with the load applied along an equivalent stress circle, as shown in Figure 2.

Fig. 2

Axial and shear loading conditions applied in the simulations

4 Results

4.1 Martensitic Transformation Without External Loading

Figure 3 shows the simulated microstructural evolution and the corresponding distribution of equivalent plastic strain during martensitic transformation without external loading. As indicated by Figure 3(a), two types of martensite variants were formed due to the different Bain strain tensors in these two-dimensional simulations. The formation of a new martensite variant was triggered by self-nucleation, after which this phase grew into the parent austenite phase in a plate-like shape to minimize the elastic strain energy during the martensitic transformation.[31,33] Plastic behavior accompanying the transformation process was evident, and this can be attributed to the high level of local stress caused by the transformation strain.[50] The distribution of equivalent plastic strain during the martensitic transformation is shown in Figure 3(b), where it can be seen that the plastic strain was primarily accumulated in the vicinity of the initial austenite grain boundaries and junctions between martensite laths.[28] This plastic strain is thought to reduce the elastic strain energy during martensitic transformation, such that the self-nucleation of the martensite variant associated with internal stress will be suppressed compared to the results obtained from simulations using a phase field microelasticity model.[31,50] This phenomenon will also generate a coarse lamellar martensite structure during the transformation. Based on this plastic accommodation, a complete martensitic transformation was achieved after 300 steps, as demonstrated in Figure 3(a).

Fig. 3

(a) Microstructural evolution and (b) the corresponding distribution of equivalent plastic strain during martensitic transformation without external loading. Blue, red and grey in (a) represent austenite and two martensite variants, respectively (Color figure online)

Figure 4 summarizes the changes in the volume fractions of the martensite variants and macroscopic permanent strains during martensitic transformation without an external load. It is apparent that the simulated martensitic transformation without an external load was complete after 300 steps (Figure 4(a)). The two martensite variants were continuously generated at almost the same rate and exhibited typical sigmoidal transformation behavior, with no significant difference in the volume fractions of the two variants.[28,32] These results suggest that preferential orientation of the martensite variant did not occur. Figure 4(b) shows that small macroscopic permanent strains were present along the x-axis and shear directions, although these were expected to be nil when no external stress was applied. This phenomenon can be attributed to the use of an insufficient number of finite element nodes, such that the effect of non-physical factors was not completely offset during simulations. However, these permanent strains are not believed to have had a significant effect in the present study because they were much smaller than the permanent strains predicted under external loads. Furthermore, these small values were used as the initial values when predicting transformation plastic strains along the axial and shear directions, as shown in Eq. [16].

Fig. 4

The evolution over time of (a) martensite variant fractions and (b) macroscopic permanent strains during martensitic transformation without applied stress

4.2 Martensitic Transformation Under Uniaxial Loading

The simulated microstructures obtained from various uniaxial loading conditions are presented in Figure 5. These results confirm significant differences in the volume fractions of the martensite variants, and demonstrate that these differences became more pronounced as the external stress was increased, due to the preferential orientation of the martensite variant. This effect is ascribed to the oriented contribution of the external energy term in the total Gibbs-free energy, which can promote the preferential nucleation and growth of a specific martensite variant in response to external loads in the simulation domain.[35,38] The dependence of this preferential orientation phenomenon on the loading direction was also determined, and different martensite variants were found to be promoted by tensile and compressive stresses, as shown in Figures 5(a) and (b). Figure 5 also summarizes the time required for completion of the system evolution under various uniaxial loads. These data suggest that the martensitic transformation was accelerated under an external load, in agreement with previous studies.[35,53] Figure 5 also confirms the macroscopic deformation behavior of the simulated domain resulting from preferential orientation, and contraction or expansion along the loading direction are predicted based on the migration of free boundaries.

Fig. 5

Simulated microstructures occurring during martensitic transformation under uniaxial loading with (a) compressive and (b) tensile stress

Figure 6 summarizes the variations in the volume fraction of martensite variant 1 and the transformation plastic strain along the x-axis at various uniaxial loads. It can be seen that the formation of martensite variant 1 is promoted by tensile stress and suppressed by compressive stress. These data indicate a near linear relationship between the preferential orientation behavior and the applied uniaxial stress. Furthermore, a similar trend is also evident in the case of the axial transformation plastic strain data in Figure 6, meaning that transformation plastic coefficient that defines transformation plasticity behavior remained constant under uniaxial loads. This observation is in agreement with various reports based on theoretical calculations and experimental results.[10,54]

Fig. 6

The volume fraction of martensite variant 1 (V1) and the transformation plastic strain along the x-axis as functions of the applied uniaxial stress

4.3 Simulated Results Under Biaxial Loading

Biaxial loading containing stresses along both the x- and y-axes was employed to investigate the microstructural evolution and macroscopic deformation behavior during the present simulations. The simulated microstructures are provided in Figure 7, based on applying a constant value of 50 MPa along the x-axis, with various loads ranging from − 50 to 150 MPa along the y-axis. The results in Figure 7(c) confirm that there was no obvious preferential orientation of martensite variants or macroscopic deformation when 50 MPa was applied along the y-axis. This phenomenon is similar to the case without loading (in Figure 3(a)), suggesting a non-orientated contribution of external energy during the simulation. However, a slight contraction along the x-axis accompanied by the preferential orientation of martensite variant 2 was obtained when the applied load along the y-axis was increased to 100 MPa, as shown in Figure 7(b). More significant preferential orientation behaviors appeared as the tensile stress was increased to 150 MPa along the y-axis (Figure 7(a)). Therefore, it is evident that the orientated contribution of the external energy term was enhanced as the load along the y-axis was increased, establishing a correlation between the preferential orientation and the biaxial loads. These results are similar to the simulation outcomes obtained using various uniaxial loads. In contrast, when the external load along the y-axis was changed to a compressive stress (as in Figure 7(d)), expansion occurred along the x-axis accompanied by preferential orientation of martensite variant 1. This phenomenon is also similar to the results obtained with uniaxial loads.

Fig. 7

Simulated microstructures of martensitic transformation under biaxial loadings with a constant value of 50 MPa along the x-axis and values along the y-axis of: (a) 150, (b) 100, (c) 50 and (d) − 50 MPa

The volume fractions of martensite variant 1 and transformation plastic strains along the x-axis under biaxial loading are presented in Figure 8. The martensite variant 1 fraction is seen to have increased with decreases in the external stress applied along the y-axis, which suggests that the preferential orientation of this variant was enhanced as the applied stress along the y-axis decreased (Figure 8(a)). These results also suggest that similar values are predicted for the biaxial and uniaxial cases when the applied stress during uniaxial loading is equal to the difference between the applied stresses along the x- and y-axes during biaxial loading. The same phenomenon can also be observed in the data for axial transformation plastic strain in Figure 8(b). Therefore, biaxial loading is thought to have been equivalent to uniaxial loading in the case that the applied stress during the former was equal to the difference between loads during the latter.

Fig. 8

(a) Volume fractions of martensite V1 and (b) transformation plastic strains along the x-axis under biaxial and uniaxial loading conditions

4.4 Martensitic Transformation Under Shear Loading

The shear stress was also found to significantly affect both the preferential orientation and transformation plastic behaviors during martensitic transformation, as has previously been demonstrated by various other studies.[13,14,35] To quantitatively investigate the effect of applied shear stress on microstructural evolution and deformation behavior during martensitic transformation, simulated microstructures were generated under both positive and negative shear loads, as demonstrated in Figure 9. These results confirm preferential orientation behaviors associated with martensite variants. Different preferential variants are suggested under positive and negative loads, indicating that there was an oriented contribution of the external energy associated with the shear load. Macroscopic deformation can also be observed in Figures 9(a) and (b), although the deformation along the axial direction is less obvious than that which appeared in conjunction with axial loading.

Fig. 9

Simulated microstructures obtained during martensitic transformation under shear loading with (a) $\tau \sqrt 3 = - 100\, {\text{MPa}}$ and (b) $\tau \sqrt 3 = 100\, {\text{MPa}}$

Figure 10 plots the axial and shear transformation plastic strains against the volume fraction of martensite. Axial transformation plastic strain was demonstrated although no axial load was applied, and this result can be attributed to an external permanent strain along the axial direction provided by the preferential orientation of martensite variants. This axial strain was quite small compared to the values obtained from uniaxial loadings (in Figure 6), resulting in minimal deformation behaviors along the x-axis in Figure 9. Conversely, significant transformation plastic strain is apparent along the shear direction in Figure 10, and a positive correlation can also be confirmed as the martensitic transformation progresses. This phenomenon is in good agreement with some experimental results.[13]

Fig. 10

Transformation plastic strains along the x-axis and shear directions as functions of the volume fraction of martensite in response to shear loading

4.5 Martensitic Transformation Under Axial-Shear Loading

To investigate the effect of the multiaxial character of mechanical loading on transformation plasticity, various combinations of axial and shear loads were compared in the present simulations, while maintaining a constant total equivalent external stress of 100 MPa (Figure 2). Figure 11 presents simulated microstructures under partial axial-shear loadings. The preferential orientation of martensite variant 2 is apparent in Figure 11(a). However, a tensile stress that promotes the formation of martensite variant 1 was applied, suggesting that the shear load played the primary role in defining the microstructural evolution. No obvious contraction or expansion along the x-axis are apparent in Figure 11(a), whereas a contracted deformation is revealed in Figure 11(b).

Fig. 11

Simulated microstructures of martensitic transformations under axial-shear loadings of (a) $\sigma _{xx}^{ap} = 70.7\, {\text{MPa}}$, $\tau \sqrt 3$=70.7 ${\text{MPa}}$ and (b) $\sigma _{xx}^{ap} = - 70.7\, {\text{MPa}}$, $\tau \sqrt 3$=70.7 ${\text{MPa}}$

The statistical data regarding the volume fractions of martensite variant 1 and various transformation plastic strains under axial-shear loads are summarized in Figure 12. Here, the preferential orientation of the martensite variant 1 fraction can be observed at various loadings in Figure 12(a). However, there is no clear relationship between preferential orientation and applied load, meaning that axial and shear loads may induce preferential orientation via different processes during martensitic transformation. In addition, as the axial applied stress was decreased, a negative correlation of the axial transformation plastic strain appeared, as shown in Figure 12(b), indicating that the dominant contribution to the axial transformation plastic strain was provided by axial loads. These data also demonstrate that the shear transformation plastic strain increased along with increases in the shear load, as shown in Figure 12(c). These results suggest that the shear load played a major role in providing shear transformation plastic strain under axial-shear loading. Finally, an equivalent transformation plastic strain combined with axial and shear transformation plastic strains was considered, as in Figure 12(d). The results suggest an approximate value of 0.024 under various axial-shear loads. These data illustrate that the equivalent transformation plastic strain levels were identical regardless of the type of mechanical loading, a result that is in good agreement with experimental data.[13,14]

Fig. 12

Statistical data obtained under axial-shear loadings: (a) the volume fraction of martensite V 1, (b) transformation plastic strain values along the x-axis, (c) transformation plastic strain values along the shear direction and (d) equivalent transformation plastic strain values

5 Discussion

5.1 Analysis of Microscopic Plastic Strain During Martensitic Transformation

The simulated microstructure and distribution of related equivalent stress after 200 simulated steps under a uniaxial stress of 50 MPa are depicted in Figures 13(a) and (b). It can be seen that a high level of equivalent stress was produced, such that the yield strengths of both phases could be exceeded. As a result, a plastic strain caused by the yielding of both austenite and martensite was produced, as demonstrated in Figures 13(c) and (d). This result is different from the behavior assumed in the Leblond model, in which the product phase is assumed to remain elastic or its plastic strain rate is assumed to remain much smaller than that of the austenite phase.[10] This aspect of the Leblond model has also been questioned by other researchers, because orientation gradients caused by dislocations in martensite have been previously observed during high resolution point-to-point scans, indicating that plastic strain exists in martensite.[55] Furthermore, Takayuki et al. [12] demonstrated that the plastic behavior in the product phase should not be neglected, and this is considered to make a major contribution to the underestimation at the end of the phase transformation in the case of the Leblond model. The simulated results also confirm that a plastic strain increment is primarily produced in the vicinity of the interface between the martensite and austenite, such that a high degree of stress can be induced to accommodate transformation strain caused by the martensitic transformation.[28] Furthermore, much higher values of plastic strain will be found in the austenite compared to those in the martensite, because the high yield strength of martensite suppresses the occurrence of plastic behavior.

Fig. 13

(a) The simulated microstructural morphology and (b) the corresponding distribution of equivalent stress, (c, d) incremental and (e, f) accumulated equivalent plastic strains produced by (c, e) austenite and (d, f) martensite yielding during martensitic transformation under uniaxial loading along the x-axis with an applied stress of 50 MPa after evolving for 200 calculation steps

Because the data suggest a coherent interface between martensite and austenite, which is thought to favor the transfer of plastic strain from the austenite to the martensite, it is reasonable to assume that plastic strain can be accumulated in the martensite as it is inherited from the austenite while the martensitic transformation progresses.[55,56] Figures 13(e) and (f) show the cumulative equivalent plastic strain produced by austenite and martensite yielding after 200 steps, respectively. Figure 13(e) demonstrates a high accumulated value of plastic strain in the martensite, which is attributed to plastic strain inherited from the austenite. The accumulation of plastic strain in conjunction with the yield of martensite is confirmed by Figure 13(f), although the values are much smaller than those inherited from the austenite.

5.2 Different Mechanisms for Transformation Plasticity During Martensitic Transformation

As noted above, both the Magee and Greenwood-Johnson mechanisms are believed to generate transformation plasticity during martensitic transformation.[6,7] To allow an assessment of the effects of both mechanisms, different microscopic permanent strains along the x-axis associated with microstructural morphologies at a uniaxial stress of 100 MPa are provided in Figure 14. A heterogeneous distribution of the total permanent strain is evident in Figure 14(b), which determines the macroscopic transformation plastic behavior. The total permanent strain can be considered to represent the accumulation of microscopic transformation strain and plastic strain, as shown in Figures 14(c) and (d), respectively. The Magee mechanism involves morphological changes during martensitic transformation associated with preferential orientation, which can be expressed by transformation strain as indicated in Figure 14(c). These data confirm the dependence of the transformation strain on the initial austenite grains, because various values of transformation strain appeared in the initial austenite grains as a result of their random orientations. The particular type of martensite variant also seems to determine the local transformation strain in the initial austenite grains, based on the simulated results in Figures 14(a) and (c), because the Bain strain tensors are used for lattice distortion during martensitic transformation. In contrast, the Greenwood-Johnson mechanism was associated with microscopic plastic strain, as can be seen in Figure 14(d). Here, the degree of plastic strain was much smaller than the transformation strain in the simulated domain, indicating that the Magee mechanism had the greatest effect on martensitic transformation plasticity, in good agreement with prior experimental results.[7]

Fig. 14

(a) The simulated microstructural morphology and the corresponding distribution of microscopic permanent strains along the x-axis: (b) total permanent strain, $\varepsilon_{xx}^{per}$, (c) microscopic transformation strain, $\varepsilon_{xx}^{tr}$, and (d) plastic strain, $\varepsilon_{xx}^{p}$, under a uniaxial stress of 100 MPa

5.3 Effect of Axial and Shear Loads on the Preferential Orientation of Martensite Variants

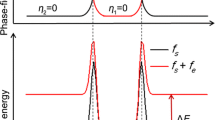
As noted, the formation of martensite variants via different processes may occur in conjunction with axial and shear loads, since there were no regular trends when axial-shear loads were applied (see Figure 12(a)). Therefore, two specific initial austenite grains were selected from Figure 1 to investigate the preferential orientation processes under both axial and shear loading conditions. The partial curve of the Gibbs energy density containing the chemical Gibbs energy density, $g_{ch}$, and an additional energy term, $g_{ap}$, is plotted in Figure 15, in which the Gibbs energy density for the two variants without an additional energy term is represented as a blue-dashed line. Figures 15(a) and (b) show the Gibbs energy density curves for the martensite variants under a tensile stress of 100 MPa in grains G1 and G2, respectively. It can be seen that the external mechanical energy increased the Gibbs energy density of variant 2 and produced a higher transformation energy barrier, $\Delta G^{*}$. This result indicates that the formation of this variant in both grains was suppressed because the evolutionary system always tended to minimize the total energy.[35] In contrast, the Gibbs energy density of variant 1 was reduced compared to the blue-dashed line, meaning that variant 1 was promoted. Therefore, the preferential orientation of martensite variant 1 was suggested by the axial tensile stress in the two grains. However, when a shear stress of 100 MPa was applied, a reduced Gibbs energy density curve appeared for martensite variant 2 in grain G1, as shown in Figure 15(c), whereas a contrary result was obtained for grain G2, as shown in Figure 15(d). Thus, it appears that there were different preferential orientation behaviors for the martensite variants in grains G1 and G2, which can be attributed to the opposite contribution of the external energy term in the total Gibbs-free energy. It is evident that different preferential orientation trends were obtained under axial and shear loads, resulting in a lack of regular relationships between preferential orientations and axial–shear loads.

Fig. 15

Partial Gibbs energy density values $\left( {g_{ch} + g_{ap} } \right)$ for the formation of different martensite variants in two specific prior austenite grains (denoted as G1 and G2 in Fig. 1) under an applied stress of 100 MPa for (a, b) uniaxial tension and (c, d) shear, respectively. The blue-dashed lines represent partial plots of the chemical Gibbs energy density, $g_{ch}$ (Color figure online)

6 Conclusions

To investigate transformation plasticity during martensitic transformation, an elastoplastic phase field model was applied in conjunction with Fe-0.22C-1.58Mn-0.81Si (wt pct) steel under various external loads less than half the yield strength of austenite. Simulated microstructural evolutions were used to characterize the preferential orientation of martensite variants. The analysis of permanent strains containing transformation and plastic strains on the microscopic scale enabled the prediction of transformation plasticity on the macroscopic scale. Some conclusions are as follows.

• (1) The preferential orientation of martensite variants depends on the magnitude and direction of external loads, while the transformation plasticity coefficient is independent of such loads. The different preferential orientation behaviors observed with axial and shear loads can be attributed to different contribution of the external energy term in the total Gibbs-free energy.

• (2) Plastic strain is produced primarily through austenite yielding and can be inherited into martensite as the transformation progresses, while the contribution from martensite yielding is insignificant. The transformation plastic strain generated during martensitic transformation is controlled by both the Magee and Greenwood-Johnson mechanisms, with the Magee mechanism playing a more dominant role.

• (3) Similar microstructure and deformation behaviors during martensitic transformation under biaxial and uniaxial loadings were confirmed, suggesting the equivalence of the two loading conditions. Simulated results also predict an identical level of equivalent transformation plastic strains under various axial-shear loadings when the same equivalent stress is applied.