1 Introduction

The Weibull distribution is widely applied for the modeling and analysis of strength data in the material field, such as brittle materials,[1,2] metals,[3] polymers[4] and dental materials.[5] This distribution is based on a “weakest link theory”, which means that the most serious flaw in the material will control its strength, similar to a chain breaking if the weakest link fails.[6]

For the two-parameter Weibull distribution, when the strength of material is at or below a stress S, the cumulative probability of failure F is

$$\begin{aligned} \displaystyle F = 1- \exp \left[ - \left( \frac{S}{S_{0}} \right) ^{m} \right] , \end{aligned}$$
(1)

where \( S_{0} \) is the scale parameter and m is the Weibull modulus, which is also called the shape parameter. There are different forms of failure, such as flaw and fracture. The Weibull modulus m determines the scattering extent of failure strength. Given a set of stress data such as experimentally measured fracture stresses, numerous methods have been proposed to estimate the parameters \( S_{0} \) and m, including method of moments, maximum likelihood (ML) method, and linear least squares (LLS) method.

The method of moments conforms to the assumption that the mean and variance of the experimental data are equal to those of the Weibull distribution.[7] This method can not obtain a closed-form estimation of Weibull modulus. In addition, the precision of estimation is also poor.[8]

The ML method[7,9] is derived from the likelihood function describing the possibility of the experimental data. The likelihood function is the product of the probability density function (PDF)

$$\begin{aligned} \displaystyle f = \frac{m}{S_{0}} \left( \frac{S}{S_{0}} \right) ^{m-1} exp\left[ -\left( \frac{S}{S_{0}} \right) ^{m} \right] \end{aligned}$$
(2)

over all the experimental data. The values of m and \( S_0 \) that make the likelihood function largest are the ML estimates. The ML method has been claimed to be capable of achieving the highest estimation precision.[6,7] However, this method usually overestimates m,[8,10] which would, in turn, yield overestimates of the reliability at low stresses, i.e. the values of stresses are small, and lead to lower safety in reliability prediction,[6,8,10] as the overestimate of reliability brings misleading judgement making the usage of material insecure. From an engineering perspective, safety must be prioritized over estimation precision. Hence, overestimation and decreased safety are disadvantages in the use of ML method.

Given its straightforwardness and simplicity, LLS is by far the most popular method used to estimate Weibull parameters for stress data. The LLS is especially favored in material science with applications in bulk metallic glass,[11] borosilicate glass,[12] nuclear materials,[13] rock grains,[14] cast aluminum,[15] cement,[16] austenitic steel[17] and asphalt pavements[18] etc. The LLS method is based on the linear form

$$\begin{aligned} \displaystyle Y = mX + b, \end{aligned}$$
(3)

where \( Y = \ln \left[ -\ln (1-F)\right] \), \( X = \ln S \) and \( b = -m \ln S_{0} \). This equation follows by taking the logarithm of Eq. [1] twice. For a set of experimental stresses of size N, after arranging in ascending order as \( s_{1} \le s_{2} \le \cdots \le s_{N} \), the estimation \( {\hat{F}}_{i} \) of cumulative probability F could be determined for any individual specimen stress \( s_{i} \), where \( i = 1, \ldots , N \). Denoting \( y_{i} = \ln \left[ -\ln \left( 1 - {\hat{F}}_{i} \right) \right] \) and \( x_{i} = \ln s_{i} \), the estimations of m and b could be obtained by minimizing the sum of squares of vertical residuals

$$\begin{aligned} \displaystyle r = \sum _{i=1}^{N} \left( y_{i} - mx_{i} - b \right) ^{2}. \end{aligned}$$
(4)

Further, the derivatives of r with respect to m and b are derived as

$$\begin{aligned} \displaystyle \frac{\partial r}{\partial m}= & {} 2 \sum _{i=1}^{n} (-x_{i})( y_{i} - mx_{i} - b), \end{aligned}$$
(5)
$$\begin{aligned} \displaystyle \frac{\partial r}{\partial b}= & {} 2 \sum _{i=1}^{n} -( y_{i} - mx_{i} - b). \end{aligned}$$
(6)

By setting them to zero, the estimations of m and b are determined as

$$\begin{aligned} \displaystyle&{\hat{m}} = \frac{\displaystyle N \sum _{i=1}^{N} x_{i}y_{i} - \sum _{i=1}^{N} y_{i} \sum _{i=1}^{N} x_{i}}{\displaystyle N \sum _{i=1}^{N} x_{i}^{2} - \left( \sum _{i=1}^{N} x_{i} \right) ^{2} }, \end{aligned}$$
(7)
$$\begin{aligned} \displaystyle&{\hat{b}} = \frac{\displaystyle \sum _{i=1}^{N} y_{i} \sum _{i=1}^{N} x_{i}^{2} - \sum _{i=1}^{N} x_{i}y_{i} \sum _{i=1}^{N} x_{i}}{\displaystyle N \sum _{i=1}^{N} x_{i}^{2} - \left( \sum _{i=1}^{N} x_{i} \right) ^{2}}. \end{aligned}$$
(8)

The estimation of \( S_{0} \) can be derived easily from Eqs. [7] to [8] according to \( b = -m \ln S_{0} \) as

$$\begin{aligned} \displaystyle {\hat{S}}_{0} = \exp \left( - \frac{{\hat{b}}}{{\hat{m}}} \right) = \exp \left( \frac{\displaystyle \sum _{i=1}^{N} x_{i}y_{i} \sum _{i=1}^{N} x_{i} - \sum _{i=1}^{N} y_{i} \sum _{i=1}^{N} x_{i}^{2}}{\displaystyle N \sum _{i=1}^{N} x_{i}y_{i} - \sum _{i=1}^{N} y_{i} \sum _{i=1}^{N} x_{i} } \right) . \end{aligned}$$
(9)

The Weibull modulus m is generally regarded as a characteristic material parameter. Researchers have found that estimating \( {\hat{m}} \) using the LLS method is usually biased,[19] whereas the estimation of the scale parameter is approximately unbiased.[6,20]

To improve the precision of estimation \( {\hat{m}} \), several methods have been proposed. One technique was the weighted factor, such as the application of solid catalysts.[8] It is added for each \( s_{i} \) to obtain the estimations of Weibull parameters by minimizing the weighted sum of squares of vertical residuals as

$$\begin{aligned} \displaystyle r_{w} = \sum _{i=1}^{N} w_{i} \left( y_{i} - mx_{i} - b\right) ^{2}. \end{aligned}$$
(10)

Different weighted factors have been presented in References 8 and 20 and it has been stated that the weighted factors together with the probability estimator are sensitive to the accuracy of the estimation.[8] However, it is not clear which weighted factor is best in the view of accuracy.

The second technique was optimal probability estimators for F, such as the application of alumina agglomerates.[6] The common estimators were

$$\begin{aligned} \displaystyle F_{i} = \frac{i}{N+1}, \end{aligned}$$
(11)
$$\begin{aligned} \displaystyle F_{i} = \frac{i-0.3}{N+0.4}, \end{aligned}$$
(12)
$$\begin{aligned} \displaystyle F_{i} = \frac{i-0.5}{N}, \end{aligned}$$
(13)

and

$$\begin{aligned} \displaystyle F_{i} = \frac{i-0.375}{N+0.25}, \end{aligned}$$
(14)

where i is the rank of the ordered stress data \( s_{i}\) and N is the number of data points. Due to the deviation from the true values of F, these estimators lead to the biased estimation of Weibull modulus accordingly.[6] Using the general form of the probability estimator

$$\begin{aligned} \displaystyle F_{i} = \frac{i-\alpha }{N+\beta }, \end{aligned}$$
(15)

many researchers attempted to determine the values of \( \alpha \) and \( \beta \) to obtain unbiased estimations of Weibull parameters using Monte Carlo simulation. Given N, m, and \( S_{0} \), sufficient data sets of simulated stresses are generated. With the varying values of \( \alpha \) and \( \beta \), the estimations of m were computed through Eq. [7] and compared with the true value. The combination of \( \alpha \) and \( \beta \) causing the estimations equal to true values yields unbiased estimation of m and determines the optimal probability estimator[6,10,21,22] in Eq. [15]. However, the optimal probability estimator are related to N as well as the true value of m and extensive computations are required for the determination. It becomes rather inconvenient for the analysis of engineering problems with real data.

The third technique was the correction factor. As the accuracy of \( {\hat{S}}_{0} \) was significantly high, the correction factor was only discussed for m. The idea was that the mean value of bias from the LLS method could be obtained for any N and m to determine the corresponding correction factor. However, only the Monte Carlo simulation was considered in existing literature.[19,23] And numerous simulations are necessary making the application inconvenient.

Accurate and reliable estimates of Weibull parameters are important. For the above three techniques, it is possible to study the correction factor theoretically by analyzing the distribution of \( {\hat{m}} \). Accordingly, the proposed correction factor could produce the unbiased estimation of m. Hence, the theoretical results not only guarantee the validity but also make the application convenient, which would be demonstrated in the following study and illustrative examples.

The rest of this paper is organized as follows. The mathematical analysis of the bias of \( {\hat{m}} \) and the correction factor are presented in Section II. The performance of unbiased estimation after correction is investigated in Section III. In Section IV, several real data examples are discussed. The paper is concluded in Section V.

2 The Proposed Correction Factor

2.1 The Distribution of the Estimates of the Weibull Parameters

Suppose there is a group of experimental stresses of size N from the Weibull distribution with Weibull modulus m and scale parameter \( S_{0} \). When the data are sorted in ascending order as \( s_{1} \le s_{2} \le \cdots \le s_{N} \), the estimation \( F_{i} \) of the cumulative probability F at specimen stress \( s_{i} \) could be given for \( i = 1, \ldots , N \) through Eq. [15] for particular values of \( \alpha \) and \( \beta \). Then the estimations \( {\hat{m}} \) and \( {\hat{S}}_{0} \) could be produced by the Eqs. [7] and [9].

Let \( s_{1}^{1} \le s_{2}^{1} \le \cdots \le s_{N}^{1} \) denote the ordered stresses from the Weibull distribution with both the modulus and scale parameter being one. Through similar procedures, the estimations \( {\hat{m}}^{1} \) and \( {\hat{S}}_{0}^{1} \) can be obtained as

$$\begin{aligned}&\displaystyle {\hat{m}}^{1} = \frac{\displaystyle N \sum _{i=1}^{N} x_{i}^{1}y_{i}^{1} - \sum _{i=1}^{N} y_{i}^{1} \sum _{i=1}^{N} x_{i}^{1}}{\displaystyle N \sum _{i=1}^{N} \left( x_{i}^{1}\right) ^{2} - \left( \sum _{i=1}^{N} x_{i}^{1} \right) ^{2} }, \end{aligned}$$
(16)
$$\begin{aligned}&\displaystyle {\hat{S}}_{0}^{1} = \exp \left[ \frac{\displaystyle \sum _{i=1}^{N} x_{i}^{1}y_{i}^{1} \sum _{i=1}^{N} x_{i}^{1} - \sum _{i=1}^{N} y_{i}^{1} \sum _{i=1}^{N} \left( x_{i}^{1}\right) ^{2}}{\displaystyle N \sum _{i=1}^{N} x_{i}^{1}y_{i}^{1} - \sum _{i=1}^{N} y_{i}^{1} \sum _{i=1}^{N} x_{i}^{1} } \right] , \end{aligned}$$
(17)

where \( y_{i}^{1} = \ln \left[ -\ln \left( 1 - {\hat{F}}_{i}^{1} \right) \right] \), \( x_{i}^{1} = \ln s_{i}^{1} \), and \( {\hat{F}}_{i}^{1} \) is the estimation of the cumulative probability F at specimen stress \( s_{i}^{1} \) for \( i = 1, \ldots , N \) using the same probability estimator in Eq. [15].

Note that the probability estimator in Eq. [15] depends only on N and the rank of experimental data.[24] Although the ordered experimental data \( s_{1} \le s_{2} \le \cdots \le s_{N} \) and \( s_{1}^{1} \le s_{2}^{1} \le \cdots \le s_{N}^{1} \) are from different Weibull distributions, these data share the same size. Hence, \( {\hat{F}}_{i} = {\hat{F}}_{i}^{1} \) for \( i = 1, \ldots , N \) according to the identical probability estimator in Eq. [15]. Furthermore, \( y_{i} = y_{i}^{1} \) for \( i = 1, \ldots , N \). Next, as \( s_{i} \) is from the Weibull distribution with Weibull parameters m and \( S_{0} \), whereas \( s_{i}^{1} \) is from the Weibull distribution with Weibull parameters both being one, \( s_{i} = S_{0} \left( s_{i}^{1} \right) ^{\frac{1}{m}} \) holds in the view of statistics.[24,25] By taking the logarithm, \( s_{i} = S_{0} \left( s_{i}^{1} \right) ^{\frac{1}{m}} \) is equivalent to

$$\begin{aligned} \displaystyle x_{i} = \ln S_{0} + \frac{x_{i}^{1}}{m} \end{aligned}$$
(18)

for \( i = 1, \ldots,\, N \). With the above relationships, the Eq. [7] can be rewritten as

$$\begin{aligned} \displaystyle {\hat{m}} = \frac{\displaystyle N \sum _{i=1}^{N} \left( \ln S_{0} + \frac{x_{i}^{1} }{m} \right) y_{i}^{1} - \sum _{i=1}^{N} y_{i}^{1} \sum _{i=1}^{N} \left( \ln S_{0} + \frac{x_{i}^{1} }{m} \right) }{\displaystyle N \sum _{i=1}^{N} \left( \ln S_{0} + \frac{x_{i}^{1} }{m} \right) ^{2} - \left[ \sum _{i=1}^{N} \left( \ln S_{0} + \frac{x_{i}^{1} }{m} \right) \right] ^{2}}. \end{aligned}$$
(19)

After simplification, we have

$$\begin{aligned} \displaystyle {\hat{m}} = m \frac{\displaystyle N \sum _{i=1}^{N} x_{i}^{1} y_{i}^{1} - \sum _{i=1}^{N} y_{i}^{1} \sum _{i=1}^{N} x_{i}^{1} }{\displaystyle N \sum _{i=1}^{N} \left( x_{i}^{1}\right) ^{2} - \left( \sum _{i=1}^{N} x_{i}^{1} \right) ^{2} }. \end{aligned}$$
(20)

According to the Eq. [16], there is

$$\begin{aligned} \displaystyle {\hat{m}} = m {\hat{m}}^{1}. \end{aligned}$$
(21)

Similarly, by substituting the Eq. [18] into the Eq. [9],

$$\begin{aligned} \displaystyle \ln {\hat{S}}_{0} = \frac{\displaystyle \sum _{i=1}^{N} \left( \ln S_{0} + \frac{x_{i}^{1}}{m} \right) y_{i}^{1} \sum _{i=1}^{N} \left( \ln S_{0} + \frac{x_{i}^{1}}{m} \right) - \sum _{i=1}^{N} y_{i}^{1} \sum _{i=1}^{N} \left( \ln S_{0} + \frac{x_{i}^{1}}{m} \right) ^{2}}{\displaystyle N \sum _{i=1}^{N} \left( \ln S_{0} + \frac{x_{i}^{1}}{m} \right) y_{i}^{1} - \sum _{i=1}^{N} y_{i}^{1} \sum _{i=1}^{N} \left( \ln S_{0} + \frac{x_{i}^{1}}{m} \right) }. \end{aligned}$$
(22)

After some simple calculations, we obtain

$$\begin{aligned} \displaystyle \ln {\hat{S}}_{0}= & {} \displaystyle \ln S_{0} + \frac{1}{m} \frac{\displaystyle \sum _{i=1}^{N} x_{i}^{1}y_{i}^{1} \sum _{i=1}^{N} x_{i}^{1} - \sum _{i=1}^{N} y_{i}^{1} \left( \sum _{i=1}^{N}x_{i}^{1} \right) ^{2}}{\displaystyle N \sum _{i=1}^{N} x_{i}^{1} y_{i}^{1} - \sum _{i=1}^{N} y_{i}^{1} \sum _{i=1}^{N} x_{i}^{1}} \nonumber \\= & {} \displaystyle \ln S_{0} + \frac{{\hat{m}}^{1} \ln {\hat{S}}_{0}^{1}}{{\hat{m}}}. \end{aligned}$$
(23)

Hence, there is

$$\begin{aligned} \displaystyle \left( \frac{{\hat{S}}_{0}}{S_{0}} \right) ^{{\hat{m}}} = \left( {\hat{S}}_{0}^{1} \right) ^{{\hat{m}}^{1}}. \end{aligned}$$
(24)

Based on the Eq. [21], the distribution of \( {\hat{m}}\) is clear. The ratio of \( {\hat{m}} \) to the true value m is clearly independent of m, and the distribution of this ratio is identical to that of \( {\hat{m}}^{1}\). And according to the Eq. [24], the distribution of \( {\hat{S}}_{0} \) is related to \( {\hat{m}} \). In existing literature, these conclusions were observed.[6,7,8,9,21] However, they were concluded from the simulation results rather than mathematical proof.

To validate the theoretical result in Eq. [21], a Monte Carlo simulation is conducted in this study to show the simulation results. The simulation study is based on the simulated stress data. First, to generate the simulated stress data, N random numbers are generated between 0 and 1 using the Mersenne Twister generator.[26] According to

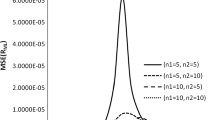
$$\begin{aligned} \displaystyle s = S_{0} \left[ -\ln (1-F) \right] ^{\frac{1}{m}}, \end{aligned}$$
(25)

the simulated stresses data of size N are provided to represent the random data from the Weibull distribution with modulus m and scale parameter \( S_{0} \). After the numbers are sorted as \( s_{1} \le s_{2} \le \cdots \le s_{N}\), we compute \( {\hat{F}}_{i} \) through the Eq. [15] with particular values of \( \alpha \) and \( \beta \). Then, the estimation \( {\hat{m}} \) of m can be obtained by the Eq. [7]. Repeating this process \( 10^6 \) times will obtain estimations \( {\hat{m}} \) of size \( 10^6 \) that can be used to observe the distribution of \( {\hat{m}} \). The distribution of the normalized estimates \( \frac{{\hat{m}}}{m} \) are compared with the estimates \( {\hat{m}}^{1} \) of Weibull modulus \( m = 1 \) to check the Eq. [21]. Without loss of generality, the value of \( S_{0} = 1 \) is consistent in the simulations. Equation (21) is demonstrated from three aspects. The first is to investigate different values of m. We adopt the probability estimator in Eq. [11], \( N = 10 \) and \( m = 1, 3, 5 \). The probability densities of the normalized estimates \( \frac{{\hat{m}}}{m} \) are displayed in Figure 1(a), which shows that \( \frac{{\hat{m}}}{m} \) for different values of m shares the same distribution. This conclusion was also observed in Reference 21. Here, it is further pointed out that this distribution is that of estimation \( {\hat{m}}^{1} \). The second aspect is to observe different values of N. We set the probability estimator in Eq. [11], \( N = 50 \) and \( m = 1, 5 \). Then the probability densities of \( \frac{{\hat{m}}}{m} \) from \( N = 50 \) and \( N = 10 \) are compared in Figure 1(b). The outcome indicates that the probability densities of \( \frac{{\hat{m}}}{m} \) are different under different values of N. The third aspect is to check different probability estimators. We use the probability estimator in Eq. [12], \( N = 10 \) and \( m = 1, 5 \). The probability densities of \( \frac{{\hat{m}}}{m} \) from probability estimators in Eqs. [11] and [12] are presented in Figure 1(c). Clearly, different probability estimators obtain different probability densities of \( \frac{{\hat{m}}}{m} \).

Fig. 1
figure 1

Probability distribution of the normalized \( {\hat{m}} \)

Full size image

The simulation results prove that the distribution of the normalized estimate \( \frac{{\hat{m}}}{m} \) is independent of m and identical to that of \( {\hat{m}}^{1} \). In addition, the distribution of the normalized estimate is associated with the probability estimator and N. These observations could justify the Eq. [21]. By the way, a similar conclusion has been presented in Reference 25 using the ML estimates of Weibull modulus. And it should be stressed that the conclusion in this paper is for the estimates \( {\hat{m}} \) using the LLS method. What’s more, the theoretical result in the Eq. [21] is based on the condition that all the stress data are failure data. If only part stress data are failure data, the identical conclusion still holds by referring to Reference 27.

2.2 The Correction Factor for the Unbiased Estimation of m

Let c denote the proposed correction factor for the unbiased estimation of m, i.e.\( E \left( c{\hat{m}} \right) = m \), where \( E(\cdot ) \) represents the expectation of a random variable. From the Eq. [21],

$$\begin{aligned} \displaystyle E\left( c {\hat{m}} \right) = c E \left( {\hat{m}} \right) = c m E \left( {\hat{m}}^{1} \right) . \end{aligned}$$
(26)

Hence, the correction factor c is

$$\begin{aligned} \displaystyle c = \frac{1}{E\left( {\hat{m}}^{1} \right) }. \end{aligned}$$
(27)

The correction factor in Eq. [27] derived from the Eq. [21] is convincing, given that mathematical proof and simulation results both confirm the Eq. [21]. Moreover, the correction factor only depends on \( {\hat{m}}^{1} \), the estimation of \( m = 1 \). Hence, the correction factor is independent of m, indicating its applicability to any experimental stress data from Weibull distribution with any value of m. Compared with the result in References 19 and 23, the derived correction factor in this study avoids extensive simulation computations by considering different values of m.

2.3 The Computation of Correction Factor

The problem is how to compute the correction factor, i.e., the expectation \( E\left( {\hat{m}}^{1} \right) \). According to the Eq. [16], the estimation of \( {\hat{m}}^{1} \) is only based on N and the probability estimator in Eq. [15]. Developing closed-form expressions for the distribution of \( {\hat{m}}^{1} \) is difficult. However, producing the sample of \( {\hat{m}}^{1} \) is easy through the use of generated simulated stress data from Weibull distribution with both parameters being one. Hence, the expectation \( E\left( {\hat{m}}^{1} \right) \) can be computed by simulation.

The simulated stress data of size N can be generated by the Eq. [25] with \( m = 1 \) and \( S_{0} = 1 \). The estimation \( {\hat{m}}^{1} \) of \( m = 1 \) can be obtained by the Eq. [16]. After repeating this process \( 10^6 \) times, the obtained estimations \( {\hat{m}}^{1} \) of size \( 10^6 \) can be used to observe the distribution of \( {\hat{m}}^{1} \) and determine the value of \( E\left( {\hat{m}}^{1} \right) \). According to this idea, the following procedures are developed to determine the correction factor c for correcting the estimation \( {\hat{m}} \) during the application.

Given \( {\hat{m}} \) obtained from the experimental stress data with size N using the probability estimator in Eq. [15]:

  1. (1)

    Simulate N random stresses using the Eq. [25] with \( m = 1 \) and \( S_{0} = 1 \).

  2. (2)

    Estimate the cumulative probability F with the same values of \( \alpha \) and \( \beta \) for \( {\hat{m}} \).

  3. (3)

    Compute \( {\hat{m}}^{1} \) through the Eq. [16].

  4. (4)

    Repeat steps (1) - (3) \( 10^6 \) times.

The correction factor c can be computed as

$$\begin{aligned} \displaystyle c = \frac{\displaystyle 10^6}{\displaystyle \sum _{i=1}^{10^6} {\hat{m}}^{1}_{i}}. \end{aligned}$$
(28)

\( c{\hat{m}} \) is then the unbiased estimation of m.

2.4 The Correction Factors for the Common Probability Estimators

The four probability estimators in Eqs. [11] through [14] are commonly used in engineering application. Thus, the correction factors for these probability estimators are provided here for illustration. Given that the distribution of \( {\hat{m}}^{1} \) is important for the correction factor, we first present the distributions for the four common probability estimators under particular values of N in Figure 2. Figure 2(a) shows different distributions with different values of N using the probability estimator in Eq. [11]. Figure 2(b) displays different distributions with different probability estimators in Eqs. [11] through [14] under \( N = 10 \). Next, the correction factors for the four common probability estimators are presented in Figure 3. For each estimator, the range of N for the experimental stresses is typically considered as \( 10, 11, 12, \ldots , 100 \). For ease of comparison, during the computation of the correction factor, the simulated stresses from Weibull distribution with \( m = 1 \) are equivalent for each probability estimator.

Fig. 2
figure 2

Probability distribution of \( {\hat{m}}^{1} \)

Full size image
Fig. 3
figure 3

The correction factors for the common probability estimators

Full size image

The following findings can be observed from Figure 3.

  1. 1.

    Almost all the correction factors are larger than one, implying that the estimations \( {\hat{m}} \) of m are usually biased toward lower values than the true value of m. As we know, the lower estimation \( {\hat{m}} \) of m will lead to high safety if the reliability is predicted in material applications such as brittle and dental materials. Hence, the LLS method under the common probability estimators in Eqs. [11] through [14] is safer than ML method for reliability prediction. Though the estimation \( {\hat{m}} \) using the LLS method is safe, the higher precision is in urgent need. And the correction factors in Figure 3 could be used to make the estimation unbiased.

  2. 2.

    All correction factors approach one as N increases, which indicates that the precision of \( {\hat{m}} \) improves as N increases.

  3. 3.

    The correction factors for the probability estimators in Eq. [13] are closest to one for \( N \ge 20 \), while the correction factors for Eq. [11] are the largest. This finding means that among the four probability estimators, the Eq. [11] gives the largest bias, whereas the Eq. [13] gives the least bias. These conclusions match those in References 6, 8, 21 and 23 and thus further rationalize the correction factors in Figure 3.

Figure 3 shows only the correction factors for N in the typical range and four common probability estimators. Given that the computations required to compute the correction factor are not difficult and not extensive, when the sample size N is out of the 10 - 100 range, or the probability estimator is from the Eq. [15] rather than the four common ones, the correction factor can be computed by simply following the procedures.

3 Discussion

During the application, any value of \( \alpha \) and \( \beta \) in the Eq. [15] could be used to produce the estimation \( {\hat{m}} \) of m. Regardless of which combination of \( \alpha \) and \( \beta \) is used, the corresponding correction factor can be computed based on the proposed procedures to correct the estimation \( {\hat{m}} \). The following problem is determining which probability estimator in Eq. [15] is best. In this Section, we will discuss this problem to choose the optimal values of \( \alpha \) and \( \beta \).

3.1 The Coefficient of Variation and Mode of Unbiased Estimation After Correction

The correction factor is proposed based on the expectation of \( {\hat{m}} \). In addition to the mean of \( {\hat{m}} \), the precision of \( {\hat{m}} \) is also often examined by the coefficient of variation (CV) to describe the dispersion of the distribution.[8,21] The definition of CV is

$$\begin{aligned} \displaystyle CV = \frac{\sigma }{\mu }, \end{aligned}$$
(29)

where \( \sigma \) and \( \mu \) are the standard deviation and mean of \( {\hat{m}} \), respectively. A small CV results in high precision. To determine the optimal values of \( \alpha \) and \( \beta \) in terms of CV, the CV of the normalized estimate \( \frac{{\hat{m}}}{m} \) is usually analyzed. Similarly, the CV of the normalized unbiased estimate \( \frac{c {\hat{m}}}{m} \) must be checked. Note that the normalized unbiased estimate \( \frac{c {\hat{m}}}{m} \) is the product of the correction factor c and the normalized estimate \( \frac{{\hat{m}}}{m} \). As c is a constant, the standard deviation and mean of \( \frac{c {\hat{m}}}{m} \) are both identically proportional to those of \( \frac{{\hat{m}}}{m} \). Therefore, the CV of \( \frac{c {\hat{m}}}{m} \) is the same as that of \( \frac{{\hat{m}}}{m} \). Furthermore, the CV of the normalized estimate \( \frac{{\hat{m}}}{m} \) is equal to that of \( {\hat{m}}^{1} \) by Eq. [21]. This outcome indicates that the CV of the normalized unbiased estimate \( \frac{c {\hat{m}}}{m} \) is equivalent to that of \( {\hat{m}}^{1} \).

The mode of \( {\hat{m}} \), the value of \( {\hat{m}} \) with the highest probability of occurrence, is also an important indicator of the bias of \( {\hat{m}} \).[19,23] The normalized mode \( {\hat{m}}_{mode}^{*} \) is the mode of the normalized estimate \( \frac{{\hat{m}}}{m} \). The closer the value of \( {\hat{m}}_{mode}^{*} \) is to unity, the higher the precision is. Usually, the normalized mode is analyzed to determine the optimal values of \( \alpha \) and \( \beta \) in terms of mode. Let \( {\widehat{cm}}_{mode}^{*} \) represent the mode of the normalized unbiased estimate \( \frac{c {\hat{m}}}{m} \). Similarly, \( {\widehat{cm}}_{mode}^{*} \) must be examined. In the view of statistics, \( {\widehat{cm}}_{mode}^{*} \) is the product of c and \( {\hat{m}}_{mode}^{*} \), because \( \frac{c {\hat{m}}}{m} \) is the product of c and \( \frac{{\hat{m}}}{m} \). Furthermore, the normalized mode \( {\hat{m}}_{mode}^{*} \) is equal to that of \( {\hat{m}}^{1} \) by the Eq. [21]. Hence, \( {\widehat{cm}}_{mode}^{*} \) is the product of c and the mode of \( {\hat{m}}^{1} \).

Table I The Simulation Results to Check CV and Mode Based on the Probability Estimator in Eq. [13]
Full size table

To prove the above analysis, a Monte Carlo simulation is conducted considering N in the typical range of \( 10 - 100 \). Without loss of generality, the value of \( S_{0} \) is kept as one. For the CV, by assuming \( m = 3 \), simulated stress data are generated through the Eq. [25]. After the cumulative probabilities are estimated by the Eq. [13], the estimation \( {\hat{m}} \) is calculated through the Eq. [7]. The unbiased estimation \( c {\hat{m}} \) can also be computed using the value of c in Figure 3. After repeating this process \( 10^6 \) times, the CV values of \( \frac{c {\hat{m}}}{m} \) and \( \frac{{\hat{m}}}{m} \) are obtained. Similarly, the CV value of \( {\hat{m}}^{1} \) can be produced for \( m = 1 \). The details to collect \( {\widehat{cm}}_{mode}^{*} \), \( {\hat{m}}_{mode}^{*} \) and the mode of \( {\hat{m}}^{1} \) are similar to those for CV. All the simulation results are tabulated in Table I.

The simulation results in Table I clearly support the above analysis. Therefore, the application of the correction factor has no effect on the CV and changes the mode proportionally. That is, the CV values of \( \frac{c {\hat{m}}}{m} \) and \( \frac{{\hat{m}}}{m} \) are identical, and the mode \( {\widehat{cm}}_{mode}^{*} \) is proportional to \( {\hat{m}}_{mode}^{*} \). Remember that the CV of \( \frac{{\hat{m}}}{m} \) and mode \( {\hat{m}}_{mode}^{*} \) are equal to those of \( {\hat{m}}^{1} \). Therefore, investigating the CV of \( \frac{c{\hat{m}}}{m} \) and mode \( {\widehat{cm}}_{mode}^{*} \) are equivalent to examine the CV of \( {\hat{m}}^{1} \) and the product of c and the mode of \( {\hat{m}}^{1} \), respectively. The advantage of focusing on the CV and mode of \( {\hat{m}}^{1} \) rather than those of \( \frac{c {\hat{m}}}{m} \) is that it can eliminate the huge work by considering various true values of m in the simulation study. In the existing literature,[6,21,22] the true value of m is usually assumed with some particular values, which fail to cover all cases. Meanwhile, the CV and mode of \( {\hat{m}}^{1} \) are associated with the selection of the probability estimator. Investigating the CV and mode of \( {\hat{m}}^{1} \) from different probability estimators will help determine the optimal values of \( \alpha \) and \( \beta \).

3.2 The Optimal Values of \( \alpha \) and \( \beta \)

To determine the optimal values of \( \alpha \) and \( \beta \), a Monte Carlo simulation must be carried out by considering different combinations of \( \alpha \) and \( \beta \). The numerical areas of \( \alpha \) and \( \beta \) in Eq. [15] are \( 0 \le \alpha < 1 \) and \( \beta \ge 0 \), respectively. However, when \( \beta > 1 \), the range of F values can easily be unusual.[21] Hence, the range of \( \beta \) is usually considered as \( 0 \le \beta \le 1 \). When the interval width of 0.05 is considered, 21 values for \( \beta \) and 20 values for \( \alpha \) can be produced. After \( \alpha = 0.999 \) is added by referring to Reference 6 to represent the case of \( \alpha = 1 \), \( 21^{2} \) combinations of \( \alpha \) and \( \beta \) are obtained. Next, simulated stress data of size N with \( m = 1 \) and \( S_{0} = 1 \) are generated. Based on this data set, each combination of \( \alpha \) and \( \beta \) are tried to obtain \( {\hat{m}}^{1} \). The combination of \( \alpha = 0 \) and \( \beta = 0 \) will cause an error when \( i = N \) because \( F_{N} = 1 \) and \( ln(1-F_{N}) \) tends to infinity. In this case, for a consistent computation, the value is adjusted to be \( F_{N} = 0.9999 \). After this process is repeated \( 10^{6} \) times, the CV and mode of \( {\hat{m}}^{1} \) can be computed. The CV of \( {\hat{m}}^{1} \) is just the CV of \( \frac{c {\hat{m}}}{m} \). Let \( {\hat{m}}^{1}_{mode} \) denote the mode of \( {\hat{m}}^{1} \). Then, \( c {\hat{m}}^{1}_{mode} \) is the mode \( {\widehat{cm}}_{mode}^{*} \). And the value of c for the corresponding combination of \( \alpha \) and \( \beta \) is obtained using the proposed procedures. The combination of \( \alpha \) and \( \beta \) yielding the smallest CV and \( c {\hat{m}}^{1}_{mode} \) closest to one is the optimal values of \( \alpha \) and \( \beta \) for this value of N.

From the simulation results by \( 21^{2} \) combinations of \( \alpha \) and \( \beta \), the values of the chosen \( \alpha \) and \( \beta \) must be as large as possible for the lower CV of \( {\hat{m}}^{1} \). This observation is equivalent to that in Reference 21. In this simulation, the lowest CV of \( {\hat{m}}^{1} \) is yielded by the combination of \( \alpha = 0.999 \) and \( \beta = 1 \). Accordingly, the combination of \( \alpha = 0 \) and \( \beta = 0 \) leads to the largest CV. For the mode \( c {\hat{m}}^{1}_{mode} \), all values are less than one, which indicates that a large mode value results in a better estimator probability. The simulation results show that the greatest mode value is from \( \alpha = 0.999 \) and \( \beta = 0 \), whereas the mode value is smallest when \( \alpha = 0 \) and \( \beta = 1 \).

The common probability estimators in Eqs. [11] through [13] are included in the simulation. The CV and mode from the three probability estimators are obtained in the simulation. For the remaining Eq. [14], the CV and mode are computed separately. Furthermore, the values of CV and mode among the four common probability estimators are compared. The comparison among the four common probability estimators reveals that the Eq. [13] leads to the lowest CV and the largest mode, whereas the Eq. [11] yields the greatest CV and the lowest mode. Therefore, the Eq. [13] is best among the four probability estimators, whereas the Eq. [11] is the worst. The maximum and minimum values of CV in the simulation, together with the ones from the Eqs. [13] and [11] are shown in Figure 4. Similarly, the maximum and minimum modes and the ones from the Eq. [13] are displayed in Figure 5.

Fig. 4
figure 4

The CVs from different probability estimators with respect to N

Full size image
Fig. 5
figure 5

The mode from different probability estimators with respect to N

Full size image

The simulation results demonstrate that the probability estimator with \( \alpha = 0.999 \) and \( \beta = 1 \) is optimal in the view of CV, while the one with \( \alpha = 0.999 \) and \( \beta = 0 \) is best in terms of mode. There seems to be no combination of \( \alpha \) and \( \beta \) that makes the CV the lowest and the mode the closest to one simultaneously. As the CV is more significant than the mode in determining the optimal probability estimator, the combination of \( \alpha \) and \( \beta \) leading to the lowest CV should be chosen. A comparison of simulation results reveals that the values of the chosen \( \alpha \) and \( \beta \) should be as large as possible. Hence, the value of \( \beta \) is determined to be \( \beta = 1 \), which corresponds to the suggestion in Reference 21. And the largest value of \( \alpha \) in the simulation is \( \alpha = 0.999 \), representing the case of \( \alpha = 1 \). However, this value is just an assumption in the simulation. To check whether the optimal value of \( \alpha \) is 0.999 when \( \beta = 1 \), a Monte Carlo simulation is carried out again by considering the range \( 0.95 \le \alpha \le 0.9999 \) in increments of \( 10^{-4} \) and \( N = 10, 11, 12, 13, \cdots , 100 \). For each combination of \( \alpha \) and N, the simulation is repeated \( 10^{6} \) times to compute the value of CV. After choosing the least CV from 500 values of \( \alpha \) for a given N, the optimal values of \( \alpha \) are determined and shown in Figure 6.

Fig. 6
figure 6

The optimal values of \( \alpha \) with respect to N

Full size image

To sum up, the probability estimator in Eq. [15] with the values of \( \alpha \) in Figure 6 and \( \beta = 1 \) should be used to estimate F. After the estimation \( {\hat{m}} \) of m is computed by the Eq. [7], the corrected estimation \( c {\hat{m}} \) is the unbiased estimation. Moreover, the CV of this unbiased estimation is least. For convenience of application, the correction factors for the optimal values of \( \alpha \) with respect to N are presented in Figure 7. As shown in Figure 7, under the optimal values of \( \alpha \) and \( \beta = 1 \), the values of correction factor are less than 1, implying that the estimation \( {\hat{m}} \) here is overestimated. In the view of safe reliability prediction, the correction factor is necessary in this case.

Fig. 7
figure 7

The correction factor for the optimal values of \( \alpha \) and \( \beta = 1 \) with respect to N

Full size image

During the application, if the data size N is in the typical range of \( 10 - 100 \), the optimal values of \( \alpha \) and corresponding correction factors could be found directly in Figures 6 and 7, respectively. If the value of N is not in the typical range, the optimal value of \( \alpha \) is still be \( \alpha = 0.9999 \) by observing the Figure 6 clearly. And there is no need to find the optimal value of \( \alpha \) through the Monte Carlo simulation again. But the corresponding correction factor needs to be computed separately. As the proposed procedures are simple, it is not a difficult work.

3.3 Comparison with Previous Research

When \( \beta = 1 \), the optimal values of \( \alpha \) as a function of N in the typical range as well as the values of CV are presented in Reference 21. Between the study in this paper and previous research in Reference 21, the values of \( \beta \) are the same while the optimal values of \( \alpha \) and CV values are different. To demonstrate which one is better, the values of CV in this study and the ones in Reference 21 are compared in Figure 8, which clearly shows that the values of CV suggested in this study are less than the ones in Reference 21. The reason is that in the previous research,[21] the value of \( \alpha \) and \( \beta = 1 \) must first lead to unbiased estimation of m. Then, among these conditional values, the optimal values of \( \alpha \) yielding the lowest CV are determined. The condition will confine the value range of \( \alpha \) for determination. However, in this study, the unbiased estimation of m is obtained by correction. The correction does not change the CV of the previous estimation. Hence, the value range of \( \alpha \) has no restriction and it is possible to obtain the value of \( \alpha \) that produces a lower CV than the previous research. Actually, we indeed find this value. Note that the correction will not change the CV of previous estimation. Therefore, the optimal values of \( \alpha \) in Figure 6 and \( \beta = 1 \) suggested in this study are superior to the ones in previous research, because the value of CV in this study is lower.

Fig. 8
figure 8

The comparison of CV between the suggested values (solid line) and previous research (dashed line) with respect to N

Full size image

4 Illustrative Examples

In this section, the proposed correction factor is applied to several published stress data for illustration and demonstration.

The first dataset concerns the tensile strength of alumina agglomerates used as catalyst supports in the chemical industry.[6] The collected specimens of size 500 are brittle materials that are spherical in shape, with a diameter of 5.1 ± 0.2 mm and a pellet density of 1.382 \( g/cm^{3}. \)[6] With the four probability estimators in Eqs. [11] through [14], the four estimations \( {\hat{m}} \) of m are obtained.[6] Further, the four estimations \( {\hat{m}} \) would be corrected using the proposed correction factor in this paper. Though the correction factors in Figure 3 do not include the case of \( N = 500 \), the correction factors c for the four probability estimators with \( N = 500 \) can be computed by performing the procedures easily. The unbiased estimations \( c {\hat{m}} \) are then obtained. All the results are tabulated in Table II. The ML estimate of 4.43 for m are given in Reference 6 and regarded as the true value of m for this dataset. From Table II, after the correction, all four unbiased estimations of m are closer to the true value than the previous ones. In addition, among the four correction factors corresponding to the Eqs. [11] through [14], the correction factor from the Eq. [13] is closest to 1, thus agreeing with the findings in Figure 3.

Table II The Results from the Analysis of Tensile Strength for Alumina Agglomerate
Full size table

The second dataset is about the shear strength of ball studs according to the resistance welding.[28] For the ball, the surface hardness was HRc 55-65 and the carburization depth was 1.0-2.0 mm. For the stud, the HRc hardness was 33-37 and elongation was 22.4 pct. In the strength test, ten ball studs were welded at different combinations of welding currents, pressure levels and cooling types.[28] Then, the shear stress data of the welded sample were collected to estimate the Weibull modulus.[28] Further, the estimations \( {\hat{m}} \) of Weibull modulus are corrected using the proposed correction factor in this paper. As the probability estimator adopted in Reference 28 is the Eq. [11] and ten data points are used, the corresponding correction factor c for \( {\hat{m}} \) could be found in Figure 3. The unbiased estimations \( c{\hat{m}} \) are then obtained easily. All the results are tabulated in Table III. As the correction correction factor \( c>1 \), the estimations of Weibull modulus are less than the true values. After the correction, the unbiased estimations \( c{\hat{m}} \) are presented.

Table III The Results from the Analysis of Shear Strength for Ball Stud
Full size table

The third dataset is concerning the delamination strength of coated conductor (CC).[29] When an epoxy-impregnated CC coil is cooled, the radial thermal stress is generated. The stress could cause the delamination of CCs and lead to degradation of the coil. Hence, the delamination strength of the CC is important to be evaluated. 122 tested CC specimens were 4-mm-wide and had a 75-m-thick Hastelloy substrate, buffer layers, a 2-m-thick superconducting layer, a silver capped layer as well as a 20-m-thick electroplated copper stabilizer.[29] Then, the collected delamination strength data are analyzed to estimate the Weibull modulus as \( {\hat{m}} = 1.88 \) based on the probability estimator in the Eq. [11].[29] Further, this estimation would be corrected using the proposed correction factor in this paper. Though the correction factors in Figure 3 do not include the case of \( N = 122 \), the correction factor \( c = 1.0452 \) for the probability estimator in Eq. [11] with \( N = 122 \) can be computed by performing the procedures simply. The unbiased estimation \( c {\hat{m}} = 1.9650 \) is then obtained.

The fourth dataset is about the fracture strength of ferritic/martensitic steel.[30] In this experiment, the fracture behavior of Indian Reduced Activation Ferritic/Martensitic Steel (In-RAFMS) was investigated at different combinations of test temperatures and dK/dt, which is the rate of change of opening mode stress intensity factor. Then, the observed data were analyzed to obtain the estimations of Weibull modulus based on the probability estimator in Eq. [11].[30] Further, these estimations are corrected by finding the corresponding correction factors to compute the unbiased estimations of Weibull modulus easily. All the results are tabulated in Table IV.

Table IV The Results from the Analysis of Fracture Strength for Steel
Full size table

5 Conclusions

The LLS method is popularly used to estimate Weibull parameters in material science concerning the stress analysis. However, the estimation \( {\hat{m}} \) of the Weibull modulus m is usually biased using the LLS method, whereas the estimation \( \hat{S_{0}} \) of the Weibull scale parameter \( S_{0} \) is almost unbiased. Hence, the correction factor technique is considered to obtain an unbiased estimation of m in this paper. In the existing literature, the correction factor is determined mainly based on the Monte Carlo simulation requiring extensive computations. And the correction factor in this paper is proposed by deriving the distribution of \( {\hat{m}} \) mathematically. For completeness, a Monte Carlo simulation is also conducted to prove the theoretical results. Moreover, simple procedures are presented to calculate the correction factor without extensive computations. The proposed approach could be extensively used in the materials and metallurgy communities. During the engineering application, the estimation \( {\hat{m}} \) is obtained with the LLS method using the four common probability estimators in Eqs. [11] through [14] typically. And these biased estimations could be corrected using the proposed correction factors in Figure 3 to be unbiased. Besides, if the estimation \( {\hat{m}} \) is computed through other probability estimator in Eq. [15] rather than the four common ones, this estimation could still be adjusted to be unbiased based on the proposed correction factor in Eq. [28]. Hence, the proposed correction factor in this paper is extremely universal to obtain the unbiased estimation of m. The four illustrative examples concerning the alumina agglomerate, ball stud, coated conductor and steel, respectively, also show that the proposed correction factor is feasible and simple for engineering application.

Further, the CV and mode of the unbiased estimation after correction are examined and compared with the existing literature using the simulation results. The examination and comparison lead to the optimal probability estimator in Figure 6 for Eq. [15]. It is recommended that this determined optimal probability estimator should be adopted to obtain the estimation \( {\hat{m}} \) achieving superior CV and mode for engineering purpose. All these demonstrate that the study in this paper is novel, superior and feasible.