Density of Liquid Ni-Ti and a New Optical Method for its Determination

Abstract

Liquid Ni-Ti alloys were processed in a containerless way using the technique of electromagnetic levitation in order to determine their densities. An improved optical method was utilized where, in addition to recording shadowgraph images from the side, a second camera recorded images of the sample from the top. A correction factor for the density was calculated from the top-view images. This method yields measurements insensitive to droplet rotation and static deformation which removes the need to assume axial symmetry. The measured densities are discussed in terms of the molar volume. A negative molar excess volume was obtained, indicating that Ni-Ti is a highly non-ideal system. These measurements were then used to test a recently proposed relationship between the molar excess volume, the excess free energy, and the isothermal compressibility. For the first time, the excess volume of a binary alloy, i.e., Ni-Ti, is adequately predicted by a thermodynamic model.

1 Introduction

Ni-based superalloys maintain stability with respect to their structure, surface, and properties at high temperatures and high stress. They are also resistant to corrosive atmospheres and degradation.[1] For these reasons, they are primarily used in applications where extreme operational conditions are encountered, i.e., in gas turbines, in coal conversion plants, in chemical processing, or in other specialized applications where the conditions require resistant materials.[1]

A typical example is the use of Ni-superalloys in different components of an aircraft turbojet engine.[2] When casting these alloys, Ti plays the role of an important precipitation hardening admixing.[1,2,3] However, due to the large differences in the densities of Ni and Ti, macro-segregation can occur in large-scale casting processes, leading to undesirable inhomogeneities in the casted product.

In order to understand how this problem can be avoided, for instance, by optimization of the cooling process, the density of liquid Ni-Ti needs to be known as function of both, composition and temperature. In addition to this very specific motivation, Ni-Ti and Ni-Ti-Hf are also interesting systems as they became famous as one of the first shape memory alloys.[4,5,6]

Literature containing thermophysical properties of liquid Ti-based alloys is relatively sparse. Ti exhibits a comparatively high melting point of 1941 K (1668 °C) and is chemically highly reactive. Therefore, investigation of Ti-containing liquid alloys with classical container-based methods is nearly impossible. Most existing data were measured using containerless levitation methods.

Electromagnetic levitation[7] has been successfully used to measure density and surface tension of liquid Ti-44-Al-8Nb-1B[8,9] as well as liquid Cu-Ti.[10,11] The density and surface tension of liquid Al-Ti was reported in Reference 12. Thermophysical property data of a number of technical Al-Ti alloys were measured within the IMPRESS project[13] in the solid and liquid state using various experimental methods, among which was also the electromagnetic levitation technique. The latter technique was also applied under microgravity conditions during a parabolic flight campaign. Ozawa[14] investigated the surface tension of liquid steels under the influence of oxygen with electromagnetic levitation. Paradis reported data of liquid Ti measured in an electrostatic levitation furnace.[15] Pottlacher[16] reported thermodynamic and thermophysical property data for Ti in the solid and liquid state using the exploding wire technique. A good overview on these activities is given in.[17] In addition, Mills[18] reviewed thermophysical property data for selected commercial alloys among which are also Ni-based and Ti-based systems. However, data, in particular density data, are not available for Ni-Ti liquid binary alloys, apart from the very recent publication of Zhou[19] who studied the system independently from us using the technique of electrostatic levitation and molecular simulation.

Therefore, the primary goal of the present work is to measure the density of Ni-Ti liquid binary alloys as function of their composition and temperature. Density is a very fundamental property, often needed as an input parameter in order to derive other thermophysical properties from measured raw data. For instance, if the isothermal compressibility is calculated from the sound velocity, the density must be used in the calculation. An error in the density would consequently lead to an error in the derived thermophysical property. Density is also closely related to short-range order in a liquid.[20] It is therefore also interesting to understand which factors determine the density and the molar volume of a specific liquid system. In this context, the excess volume plays a crucial role. Until recently, there was a lack of understanding of what mechanisms cause an excess volume on the atomic scale. Progress was made, however, by theoretical work performed by Horbach[21] and ourselves[20] leading to an idea of a mechanism causing the large negative excess volumes typically observed in Al-based liquid alloys. A simple thermodynamic relationship followed in Reference 22 (see Appendix). It succeeded in describing the empirical relation between the excess volume and the excess free energy observed by Watanabe[23] for this class of systems. This model offers the potential to predict the excess volume of a specific system, only from the knowledge of its excess free energy and isothermal compressibility. It is, hence, the second goal of the present work to show that this is indeed possible, using measurements of the Ni-Ti system.

The final motivation for this study is to improve the conventional measurement technique. Measuring the density in electromagnetic levitation can be challenging, due to sample movements that can make an accurate measurement impossible (i.e., spinning, oscillations). One solution could be to perform the experiment under a strong dc-magnetic field, suppressing all fluid flow in the droplet and minimizing also the droplet motion.[24] This method generally requires extensive experimental modifications and is also not immune to static deformation of the sample. In the present work, we will present a small modification of a “conventional” method (see below) of measuring the density and show that it produces reliable results, regardless of deformation.

2 Experimental

2.1 Electromagnetic Levitation

The experiments were performed in a standard stainless steel high vacuum chamber[18,25] filled with 800 mbar He, Ar, or a mixture of both after prior evacuation to at least 10⁻⁶ mbar. The purity of the gases was 99.9999 vol pct.

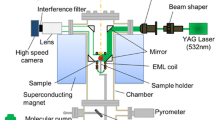
The samples, which had typical diameters of 4 mm, were positioned in the center of a levitation coil. A schematic depiction of the setup is shown in Figure 1.

Fig. 1

Schematic diagram of the optical setup used in present work in order to measure density

The coil generated an inhomogeneous electromagnetic field which induced eddy currents inside the sample, so that the sample could be levitated in a stable position. Due to ohmic losses, the specimen was also heated and eventually melted. In order to adjust to a desired temperature, the droplet was cooled in a laminar flow of the processing gas mixture. The temperature T was measured using a pyrometer focussed at the sample from the side. As the emissivity is generally not well known in these experiments, it was determined from the pyrometer output signal, T_P,L at the known liquidus temperature T_L under the assumption that within the operating wavelength range of the pyrometer, the emissivity of the specimen material did not change with temperature. T could be estimated from the following relation:

$$ \frac{1}{T} - \frac{1}{{T_{\text{P}} }} = \frac{1}{{T_{\text{L}} }} - \frac{1}{{T_{\text{L,P}} }}, $$

(1)

where T_P is the uncorrected pyrometer temperature. The details of this procedure are described in Reference 26.

In the present work, values for T_L were obtained from the phase diagram of Ni-Ti reported in Reference 27. They are also listed in Tables I and II.

Table I Density of Pure Liquid Ni and Ti

Table II Minimum T_min and Maximum T_max Temperature of the Temperature Range Investigated for Each Composition of the Ni-Ti System

Alloy samples were produced from the pure elements (purities 99.999 pct for Ni and 99.99 pct for Ti) after grinding to the required masses. After grinding, the pieces were cleaned with isopropanol in an ultrasound bath and melted together in an arc furnace. Before inserting them into the measurement apparatus, another ultrasound cleaning cycle was performed.

2.2 Conventional Density Determination

Conventionally, the density of a levitated droplet is determined via a measurement of its volume and the known sample mass. In order to measure the volume of the levitated droplet, a technique has become standard during the past 20 years in which shadowgraphs were taken from the levitated sample.[7,15,18,25] The optical setup is identical to that shown in Figure 1, except the 2nd Camera which is not in a conventional setup.

The shadow images are produced by illuminating the sample with an expanded laser beam from one side and recording the images with a digital camera on the other side. The camera is equipped with a polarizer and an interference filter. The latter assures that only light from the laser is detected. The lens and the pinhole act together as optical Fourier filters removing scattered light and reflections. The images are analyzed by an edge detection algorithm which locates the edge curve, R(φ). Here, R and φ are the radius and azimuthal angle with respect to the drop center. In order to eliminate the influence of oscillations, the edge curve is averaged over 1000 frames and fitted with Legendre polynomials of order ≤ 6.

$$ \left\langle {R\left( \varphi \right)} \right\rangle \; = \;\sum\limits_{i\; = \;0}^{6} {a_{i} \varPi {}_{i}\left( {\cos \left( \varphi \right)} \right)}, $$

(2)

with Π_i being the ith Legendre polynomial and a_i the corresponding expansion coefficient. If it can be assumed that the averaged edge curve corresponds to a body which is rotational symmetric with respect to the vertical axis, the volume of this body can be calculated using the following integral:

$$ V_{\text{P}} {}_{{ , {\text{Circle}}}}\; = \;\frac{2}{3}\pi \int\limits_{0}^{\pi } {\left\langle {R\left( \varphi \right)} \right\rangle^{3} \sin \left( \varphi \right)d\varphi } . $$

(3)

In Eq. [3], V_P,Circle is the volume in pixel units. The subscript “Circle” indicates that the cross sections are circular. The pixel volume is related to the real volume of the sample ^SV by a scaling factor q which is determined through a calibration procedure using bearing balls as described in Reference 28. The density is calculated from $\rho \; = \;{}^{S}M/{}^{S}V$, where ^SM is the mass of the sample. In contrast to the molar volume, V, and the molar mass, M, the index “S” indicates here that this not a specific property of the material but rather a property of the sample.

If the condition of axial symmetry is fulfilled, it can be shown that the absolute experimental uncertainty in the density is Δρ /ρ = ± 1 pct.[18,25] The main contributions to this uncertainty originate from the mass loss which must not be larger than 0.1 pct, and the calibration procedure, using the bearings balls. In the present work, this method shall be called the “conventional method” in order to distinguish it from the new advanced method proposed below.

2.3 Axial Symmetry

The “conventional method” has been applied successfully to a large number of systems by several authors, including the authors of this work.[7,8,9,10,12,15,18,19,20,21,22,23] Moreover, it has been used in combination with other levitation techniques, such as electrostatic or aerodynamic levitation.[15,19,29]

It relies, however, on the precondition that the time-averaged sample is symmetric with respect to the vertical axis. If this condition is not fulfilled, Eq. [3] cannot be applied. A violation of this condition might occur if the time-averaged sample shape is permanently deformed. This could occur due to strong rotations, surface oscillations, translational motion, or if it is just statically deformed. The latter might be caused, for example, by rotation around a horizontal axis.

Equation [3] can be rewritten in the following form:

$$ V_{\text{P,Circle}} \; = \;\int\limits_{0}^{\pi } {\left[ {\pi \left\langle {R\left( \varphi \right)} \right\rangle^{2} \sin^{2} \left( \varphi \right)} \right]\frac{2}{3}\frac{{\left\langle {R\left( \varphi \right)} \right\rangle }}{\sin \left( \varphi \right)}d\varphi }, $$

(4)

which implies that the integral sums the volumes of small cylindrical discs with circular cross sections each having a diameter of 2〈R(φ)〉sin(φ), an area of 〈Q_circle(φ)〉 = π[〈R(φ)〉sin(φ)]², and a height of h(φ) = 2/3〈R(φ)〉sin⁻¹(φ)dφ as function of φ.

However, this is based on the assumption of axial symmetry and the real cross sections, 〈Q_real(φ)〉, might deviate from the circular ones. The ratio a_asy(φ) of 〈Q_real(φ)〉 and 〈Q_circle(φ)〉 describes the asymmetry of the real cross section relative to the ideal circular one. In an experiment, the condition of axial symmetry is fulfilled in a strict sense only, if for each angle φ the temporal average of Q_real(φ) equals the one of Q_circle(φ), i.e., if

$$ a_{\text{asy}} (\varphi ) = \frac{{\langle Q_{\text{real}} (\varphi )\rangle }}{{\langle Q_{\text{circle}} (\varphi )\rangle }} = 1. $$

(5)

If the condition of axial symmetry is not fulfilled, Eq. [3] needs to be changed so that it reads

$$ V_{{P,{\text{real}}}} \; = \;\frac{2}{3}\pi \int\limits_{0}^{\pi } {a_{\text{asy}} \left( \varphi \right)\left\langle {R\left( \varphi \right)} \right\rangle^{3} \sin \left( \varphi \right)d\varphi } . $$

(6)

In order to determine the relative error which is encountered in Eq. [3] when Eq. [5] is violated, it is assumed that a_asy is independent of the polar angle φ and that the real cross sections have elliptical shapes with half axes a and b, so that 〈Q_real〉 = π〈ab〉 and 〈Q_circle〉 = π〈b²〉. It is further assumed that a is oriented perpendicular to the planes of the shadowgraph images in the conventional method.

The uncertainty encountered from a violation of Eq. [3] is then given by

$$ \left( {\frac{{\Delta V_{{P,{\text{real}}}} }}{{V_{{P,{\text{real}}}} }}\;} \right)^{2} = \left( {1 - a_{asy} } \right)^{2} \approx \left( {1 - \frac{\langle b\rangle }{\langle a\rangle }} \right)^{2} . $$

(7)

Depending on the choice of 〈a〉 and 〈b〉, the error can vary in Eq. [7]. It is zero in case that axial symmetry is fulfilled, i.e., 〈a〉 = 〈b〉, it reaches 100 pct if 〈b〉  → 0 and can reach ∞ if 〈a〉 approaches zero. Hence, the conventional method can produce wrong results, if the condition of axial symmetry is not fulfilled.

2.4 Density Determination with Two Cameras

There are in principle two ways to deal with situations where the condition of axial symmetry is violated. The problem may be avoided by assuring that the sample is axially symmetric through careful and sometimes tedious adjustment of the coil or by applying strong static magnetic fields suppressing turbulent fluid flow and, hence, pronounced sample rotations.[24] Although this method is very powerful, it is also accompanied with high experimental efforts and sometimes, static deformations of the sample can still not be removed completely.

The second way is the one proposed in the present work. Here, the experimental setup is equipped with a second camera directed at the sample from the top, see Figure 1.

The second camera records independently from the first camera 1000 images from the sample. For each of these images, the edge curve, R^top(ϕ), is obtained where R^top and ϕ are the radius and azimuthal angle with respect to the drop center. The superscript “top” indicates that these coordinates refer to an image recorded by the top-view camera. The cartesian edge-point components X^top(ϕ) and Y^top(ϕ) depend on the azimuthal angle and are fitted for each frame with the following polynomials:

$$ \begin{aligned} X^{\text{top}} (\varphi ) = \sum\nolimits_{i} {a_{\text{i,X}} \sin^{\text{i}} (\varphi ) + b_{\text{i,X}} \cos^{\text{i}} (\varphi )} \hfill \\ Y^{\text{top}} (\varphi ) = \sum\nolimits_{i} {a_{\text{i,Y}} \sin^{\text{i}} (\varphi ) + b_{\text{i,Y}} \cos^{\text{i}} (\varphi )} . \hfill \\ \end{aligned}. $$

(8)

Here, i is an index and a_i,X,b_i,X and a_i,Y,b_i,Y are corresponding coefficients, whereas the suffices X and Y mark the appropriate component.

Using the polynomial form of Eq. [8], it is assured that droplet shapes can be represented, even when they are rotated in the image plane by an arbitrary angle and whether symmetric or non-symmetric with respect to their principal axes. This is demonstrated in Figure 2.

Fig. 2

Image (snapshot) of a deformed Ni₅₀Ti₅₀ droplet recorded with the 2nd camera from the top. The edge curve is approximated by the fitted polynomial (bright solid line). An edge point is represented in cartesian coordinates X^top, Y^top which depend on the parameter ϕ, i.e., on the azimuthal angle. The dark 15 × 15 squares near the edge are those regions where the software investigates the image pixel by pixel in order to identify the edge points

Using Eq. [8], 〈Q_Real〉 and 〈Q_Circle〉 can be obtained as follows:

$$ \begin{aligned} \langle Q_{\text{Real}} \rangle = \frac{1}{2}\langle \int_{ - \pi }^{\pi } {[X^{\text{top}} (\varphi )]^{2} } + [Y^{\text{top}} (\varphi )]^{2} d\varphi \rangle \hfill \\ \langle Q_{\text{Circle}} \rangle = \pi \langle [X_{ \hbox{max} }^{\text{top}} - X_{ \hbox{min} }^{\text{top}} ]^{2} \rangle , \hfill \\ \end{aligned} $$

(9)

where $X_{\hbox{max} }^{\text{top}}$ and $X_{\hbox{min} }^{\text{top}}$ are the maximum and minimum values of X^top(ϕ), respectively (see Figure 2), and X^top is oriented parallel to the horizontal direction in the lateral shadowgraph image. Therefore, Y^top is oriented parallel to the laser beam. In order to determine the asymmetry factor a_asy in Eq. [9], it is assumed that the ratio of 〈Q_Real〉 and 〈Q_Circle〉 does not change along the vertical axis of the droplet, which means that a_asy has to be a constant. This is only a weak condition, as the main contribution to the overall volume origins from the center part of the sample where its cross section is largest. This part also determines the values of 〈Q_Real〉 and 〈Q_Circle〉 determined by the top-view camera. A violation of this assumption would only cause a negligible error to the measured volume.

Hence, a_asy= 〈Q_Real〉/〈Q_Circle〉 and Eq. [6] may be rewritten as:

$$ V_{{P,{\text{real}}}} \; = \;\frac{2}{3}\pi a_{\text{asy}} \int\limits_{0}^{\pi } {\left\langle {R\left( \varphi \right)} \right\rangle^{3} \sin \left( \varphi \right)d\varphi } . $$

(10)

As in the conventional method, the pixel volume V_P,real is related to the real volume of the sample ^SV by a scaling factor q. q is determined in a calibration procedure using bearing balls as described in reference.[28]

The accuracy of this new method mainly depends on the accuracy of the calibration method. As the latter is accurate within ± 1 pct, the error of the density is estimated to be of the same order, i.e., not larger than ± 1 pct, if the mass loss is smaller than approximately 0.5 pct.

3 Results

3.1 Pure Elements

Results for the density of pure elements Ni and Ti are shown in Figures 3 and 4, respectively. These results were obtained by using the “conventional method.” The different symbols in each figure indicate separate samples. The agreement among these individual measurements is within an error of +/− 1 pct. This agrees well with the error of the method estimated above.

Fig. 3

Density of liquid Ni as function of temperature. The data are measured using the conventional technique. Different symbols represent individual measurements on different samples. The solid line corresponds to a fit of Eq. [11] to all data. For comparison, the representations reported by Mills[17] (dashed line) and Kobatake[30] (dotted line) are also shown

Fig. 4

Density of liquid Ti as function of temperature measured using the conventional technique. Different symbols represent individual measurements on different samples. The solid line corresponds to a fit of Eq. [11] to all data. For comparison, the representations reported by Mills[17] (dashed line) and Amore[10] (dotted line) are also shown

In the case of liquid Ni, the density shown in Figure 3 decays from approximately 7.9 g cm⁻³ at 1600 K (1327 °C) down to approximately 7.6 g cm⁻³ at 1950 K (1677 °C). There seems to be a small kink in the data at 1650 K (1377 °C), which is insignificant with respect to the experimental error.

In the case of liquid Ti, Figure 4, the absolute values of the density are approximately 55 pct smaller. The decay of ρ with increasing temperature is also more moderate: At 1930 K (1657 °C), ρ ≈ 4.15 g cm⁻³ and ρ ≈ 4.12 g cm⁻³ at 2150 K (1877 °C). For comparison, selected representative results from literature[10,17,30] are shown in both figures as straight lines. The overall agreement is reasonable.

All measured densities ρ are linear functions of the temperature, T, and the following linear law can be fitted:

$$ \rho \; = \rho_{\text{L}} + \rho_{\text{T}} (T - T_{\text{L}} ). $$

(11)

Here, ρ_L is the density of the liquid at the liquidus temperature T_L. ρ_T= ∂ρ/∂T is the temperature coefficient. The parameters ρ_L and ρ_T obtained from these fits are listed in Table I. The investigated temperature ranges are shown in Table II.

3.2 Alloys

Levitation of liquid Ni-Ti alloys was more challenging than the pure elements. In many cases, strong turbulent flows were induced inside the samples leading to pronounced translational movements and strong rotations of the droplets. In the latter case, the shapes of the samples became distorted so that Eq. [5] was violated.

The hollow symbols in Figure 5 show apparent density values measured on Ni₅₀Ti₅₀ as function of temperature using the “conventional technique.” The values of the obtained apparent density are scattered around a value of 4.5 g cm⁻³. This is comparable with the density of pure Ti. However, the density of Ni₅₀Ti₅₀ should be near the average of the densities of pure liquid Ni and Ti, which corresponds to ≈ 6 g cm⁻³. Values near 4.5 g cm⁻³, as observed with the conventional technique, would correspond to an excess volume of ≈ 3.0 cm³mol⁻¹ which is extraordinarily, if not unphysically, large for liquid transition metals. The densities obtained in this case are far too low. In addition, the curve exhibits very unusual artifacts like kinks, positive and negative slopes, or large scatters. These artifacts do normally not appear in a proper density measurement. The obtained values are therefore severely wrong.

Fig. 5

Example density of a levitated Ni₅₀Ti₅₀ sample. The hollow symbols are evaluated assuming rotational symmetry (a_asy= 1), i.e., by the conventional technique. Obviously, they are far too small. Applying the 2nd camera technique and calculating the sample volume from Eq. [10] yields the true density (solid). The dotted line shows data measured by Zhou.[19]

In fact, this curve was recorded from a sample that rotated rapidly and underwent severe translational oscillatory movements. A snapshot of this sample with the second (top-view) camera is shown in Figure 2. Clearly, its shape deviates from the circular one and it is obvious that Eq. [5], i.e., the condition of axis symmetry, is violated. In this case, the “conventional method” is no longer applicable.

The solid symbols in Figure 5 show the same data but corrected using Eq. [10] where the factor a_asy was determined with a second camera looking at the sample from the top. All artifacts are removed from the data. The points lie on a straight line with a negative slope. Over the investigated temperature interval, the density values range from 6.05 to 5.95 g cm⁻³. This is in the expected range, so we assume these data to be valid. This is also confirmed by the recent work of Zhou.[19] Their results for liquid Ni₅₀Ti₅₀ are shown in Figure 5 by the dotted line. The agreement with our data is excellent and demonstrates convincingly that our new method works reliably.

Figure 6 shows the density ρ of binary liquid alloys vs temperature T. For each composition, the temperature ranges are shown in Table II. With the exception of Ni_83.5Ti_16.5, each measurement covers a temperature range of approximately 300 to 400 K. In the case of Ni_83.5Ti_16.5, the temperature interval was limited due to experimental restrictions to 1517 K (1244 °C) < T < 1558 K (1285 °C), see Table II. This might, in principle, cause a larger uncertainty in the data affecting, in particular, the determination of the temperature coefficient.

Fig. 6

Density of liquid Ni, Ti, and Ni-Ti binary liquid alloys as function of temperature. Different symbols represent individual measurements on different samples per composition. Hollow symbols represent measurements that are carried out by using the conventional technique while solid symbols mark measurements carried out using the 2nd camera method. The lines represent fits of Eq. [11] to the all measurements of one composition. The dashed lines indicate that Eq. [11] is extrapolated outside the actually measured temperature range

For the sake of completeness, this figure also shows the data of the pure elements Ni and Ti. Different symbols correspond to measurements on different samples. The hollow symbols indicate that the corresponding measurement was carried out using the conventional method. This refers to Ni, Ti, Ni_83.5Ti_16.5, and partially to Ni₇₅Ti₂₅. The data of the latter composition demonstrate the good agreement between the results of the conventional method, obtained from a droplet where the condition of axis symmetry, i.e., Eq. [5], was fulfilled, and results from the new method obtained from a droplet where Eq. [5] is violated. This demonstrates the validity of the new method, again.

It was found that for each composition, the density decreased linearly with increasing temperature. Fits to the data of Eq. [11] are shown in Figure 6 by solid or dashed lines. Dashed lines indicate that Eq. [11] was extrapolated outside the temperature range where the sample was actually processed. The obtained values for the fit parameters ρ_L, ρ_T and the parameter T_L are listed for each composition in Table III. The table also specifies whether the measurement was performed using the 2nd camera method or using the conventional method.

Table III Parameters T_L, ρ_L, ρ_T for Each Investigated Sample of the Ni-Ti System. Values printed in bold correspond to the average of the individual measurements

In general, the densities increase with increasing Ni-mole fraction. In order to further study the dependence of ρ on the composition, it is calculated from Eq. [11] for each sample at a temperature of 1673 K (1400 °C). This temperature was chosen, as it overlaps with the investigated temperature intervals of most of the compositions, see Table II. Only in two cases, namely, in the case of pure Ti and in the case of Ni_83.5Ti_16.5, ρ had to be extrapolated by Eq. [11] to a temperature significantly outside the experimentally investigated range. The result of this calculation, i.e., the density at 1673 K (1400 °C) is plotted in Figure 7 vs the Ti mole fraction x_Ti.

Fig. 7

Isothermal density of Ti-Ni at 1673 K (1400 °C) vs Ti mole fraction x_Ti. The symbols represent the experimental data measured by the conventional method (hollow squares) or the 2nd camera technique (solid symbols). The dashed line represents the density of an ideal solution, with the molar volume from Eq. [13], and the solid line represents the density calculated from the excess free energy and the isothermal compressibility, based on the excess volume calculated from Eq. [18]. The recent data of Zhou[19] are shown for comparison (circles)

The hollow squares indicate that the measurement was performed using the conventional technique while solid symbols indicate that the new 2nd camera technique was applied. The good agreement among the two methods was observed again. For comparison, Figure 7 also shows the data of Zhou[19] exhibiting an excellent agreement with our work and supporting once again the new method. At x_Ti= 0 at. pct, the measured densities of pure Ni have a slight scatter around their mean of 7.8 (± 0.03) g cm⁻³. When x_Ti is increased, the density decreases nearly linearly, with only a small convex curvature. At x_Ti= 50 at. pct, ρ equals 6.01 g cm⁻³ and at x_Ti= 100 at. pct, the final value of pure liquid Ti, 4.22 g cm⁻³ (± 0.04) is reached. The numerical values of the isothermal density at 1673 K (1400 °C) are also listed in Table II.

The temperature coefficient ρ_T is plotted vsx_Ti in Figure 8. Again, hollow squares indicate that the conventional method was used while solid symbols indicate that the new method was applied. The scatter of the data is larger in Figure 8 than the scatter of the data for ρ shown in Figure 7. This is expected and has been discussed in previous paper.[18,31,32,33] Moreover, ρ_T increases monotonically with x_Ti from − 7.2 (± 0.7) 10⁻⁴ g cm⁻³K⁻¹ for pure Ni to a value of − 2.85 (± 0.7) 10⁻⁴ g cm⁻³K⁻¹ for pure Ti. The resulting curve is slightly concave. The value of ρ_T corresponding to the composition of Ni_83.5Ti_16.5 might eventually be seen as a freak value due to the reduced temperature range as discussed before. Another freak value is visible for one measurement at x_Ti= 39 at. pct. The reason for the latter is unclear. For comparison, Figure 8 shows the data of Zhou.[19] The agreement is excellent, too.

Fig. 8

Temperature coefficient ρ_T of the density of liquid Ni-Ti alloys vs the Ti mole fraction x_Ti. Hollow squares indicate that the conventional method was used while solid symbols indicate the use of the 2nd camera methods. The dashed line represents Eq. [16]. For comparison, data of Zhou[19] are shown by the circles

4 Discussion

4.1 Concentration Dependence

Due to the significant difference in the atomic masses of Ni and Ti, the observed dependency of the density on composition is dominated by the composition dependence of the molar mass. The packing of atoms, i.e., the packing density is in fact the more relevant parameter as it directly correlates with the structure. As the packing density is directly obtained from the molar volume, V, it shall be discussed in the following.

The isothermal molar volumes of the investigated Ni-Ti samples are calculated from the corresponding densities at 1673 K (1400 °C) and plotted in Figure 9 vsx_Ti together with the data of Zhou.[19] It is shown in this figure that V increases monotonically with x_Ti from a value of 7.6 cm³mol⁻¹ corresponding to pure Ni to approximately 11.4 cm³mol⁻¹, the value for liquid Ti. The experimental data form a curve which is slightly convex. This latter observation can be explained by the fact that, in general, the molar volume of a liquid alloy deviates from the molar volume of an ideal solution, ^idV, i.e., the linear interpolation of the molar volumes of the pure components. The difference is equal to the excess volume ^EV, which can be zero, positive, or negative. Often, the excess volume is small and it may be neglected. In the case of Ni-Ti, the observed convex curvature indicates a non-negligible negative excess volume, ^EV<0. The excess volume ^EV is defined by the following relation:

Fig. 9

Isothermal molar volume of Ti-Ni at 1673 K (1400 °C) vs Ti mole fraction x_Ti. The symbols represent the experimental data measured by the conventional method (hollow squares) or the 2nd camera technique (solid symbols). Data measured by Zhou[19] are shown by the circles. The dashed line represents the molar volume of an ideal solution, i.e., Eq. [13]. The solid line represents Eq. [12], whereas the excess volume is calculated from the excess free energy and the isothermal compressibility via Eq. [18]

$$ V = {}^{\text{id}}V + {}^{\text{E}}V. $$

(12)

In the case of Ni-Ti, the molar volume of the ideal solution is defined as

$$ {}^{\text{id}}V = x_{\text{Ti}} V_{\text{Ti}} + x_{\text{Ni}} V_{\text{Ni}}, $$

(13)

where V_Ti and V_Ni denote the molar volumes of the pure liquid elements Ti and Ni with corresponding mole fractions x_Ti and x_Ni, with x_Ti+x_Ni=1.

Equation [13] is shown in Figure 9 by the dashed line. Here, the molar volumes V_Ti and V_Ni are calculated from the densities of the pure elements. As shown, Eq. [13] overestimates the empirical molar volumes of the alloys by approximately 6 pct.

Significant deviation from ideal mixing is already apparent in Figure 7, where the dashed line shows the density calculated from the ideal molar volume in comparison with the measured data. The densities of the ideal solution deviate from the real ones by a comparable amount, i.e., by roughly 8 pct.

In terms of the ideal volume, Al-based alloys exhibit similar deviations.[12,18,20,22,23,32,34] For instance, the excess volume amounts 3.2, 5.0, 6.0, and 7.7 pct of the ideal volume for Ag-Al,[32] Al-Au,[20] Al-Ti,[12] and Al-Cu,[32] respectively. In the cases of Al-Fe[34] and Al-Ni,[34] these numbers are 14 and 22 pct, respectively, i.e., they are more than twice as large for these latter systems.

The excess volume can be obtained from the measured volume V and the ideal volume, ^idV, calculated from Eq. [13] using Eq. [12]. The result, ^EV as function of x_Ti, is shown in Figure 10.

Fig. 10

Excess volume of Ni-Ti binary liquid alloys at 1673 K (1400 °C) vs the Ti mole fraction x_Ti. The hollow circles represent data of Zhou.[19] The dotted line shows a fit of Eq. [14]. The solid line is calculated (not fitted) by Eq. [18] from the excess free energy ^EG and the isothermal compressibility κ_T. The latter is given by Eq. [20]

The data obtained for ^EV form a curve similar to a parabola with a minimum at x_Ti= 40 at. pct ,where ^EV ≈ − 7 cm³mol⁻¹. Good agreement is also obtained with the data of Zhou.[19]

In the simplest case, ^EV can be expressed as a parabola in concentration.[28] That is

$$ {}^{\text{E}}V = x_{\text{Ti}} x_{\text{Ni}} {}^{0}V, $$

(14)

where ⁰V is an interaction constant which is independent of composition. Eq. [14] is fitted to the data in Figure 10 by adjusting the parameter ⁰V. This is shown in the figure by the dotted line. Obviously, this fit approximates the experimental data with reasonable agreement. However, ⁰V would also slightly depend on x_Ti in reality. Due to the fact that ⁰V is a constant in Eq. [14], the fitting procedure effectively averages over this dependence. Hence, some small deviations become visible in Figure 10. For instance, the fit slightly overestimates the data for x_Ti= 39 at. pct and x_Ti= 16.5 at. pct.

At 1673 K (1400 °C), a value of − 2.17 cm³mol⁻¹ is obtained for ⁰V. This number is comparable to what is observed in other attractively interacting systems like Ag-Al (− 2.68 cm³mol⁻¹),[32] Al-Au (− 2.24 cm³mol⁻¹),[20] Al-Ti (− 2.4 cm³mol⁻¹),[12] Al-Cu (− 3.37 cm³mol⁻¹),[32] and Al-Fe (− 1.7 cm³mol⁻¹).[34] Non-surprisingly, the strongly interacting system Ni-Ti is also strongly interacting with respect to molar volume.

4.2 Temperature Dependence

In general, ⁰V may depend weakly on temperature as follows[12,18,32]:

$$ {}^{0}V(T) = {}^{0}A + {}^{0}BT, $$

(15)

where ⁰A and ⁰B are linear coefficients which can be obtained by fitting Eq. (15) to a plot of ⁰V vs temperature. This procedure yields ⁰A = − 1.915 cm³mol⁻¹ and ⁰B = − 7.14 × 10⁻⁵ cm³mol⁻¹K⁻¹ for liquid Ni-Ti. The latter value indicates that the variation of ⁰V with temperature is, indeed very small and can, in principle, be neglected.

The temperature coefficient ρ_T can be expressed by differentiation of ρ(T) = M/V(T) with respect to temperature, if M is the molar mass and V the molar volume. If, in addition, ^EV and ⁰B are both set equal to zero, the following simple approximation is obtained for ρ_T[32]:

$$ \rho_{\text{T}} = M \times \frac{{\left[ {x_{\text{Ni}} \frac{{M_{\text{Ni}} \rho_{\text{T,Ni}}^{{}} }}{{\rho_{\text{Ni}}^{ 2} }} + x_{\text{Ti}} \frac{{M_{\text{Ti}} \rho_{\text{T,Ti}}^{{}} }}{{\rho_{\text{Ti}}^{ 2} }}} \right]}}{{{}^{\text{id}}V^{2} }}. $$

(16)

In Eq. [16], M_Ni and M_Ti are the molar masses of Ni and Ti, respectively. ρ_T,Ni and ρ_T,_Ti are their respective temperature coefficients of the density. All parameters in Eq. [16] can be derived from the pure element data. Eq. [16] is plotted in Figure 8 as a dashed line. This simplified model is in excellent agreement with the experimental data.

4.3 Relation with Isothermal Compressibility

In general, the molar volume can be derived from the excess free energy ^EG by differentiating the latter with respect to pressure. Therefore, it makes sense to consider the excess free energy of liquid Ni-Ti. A mathematical representation of ^EG as function of temperature and mole fraction is given in Reference 35. For Ni-Ti at T=1673 K (1400 °C), ^EG is negative and exhibits a shape which is similar to the curve of ^EV shown in Figure 10, i.e., a parabola with a horizontally shifted minimum at x_Ti≈ 40 at. pct.

A thermodynamic relation between ^EV and ^EG has recently been proposed by the authors in Reference 22, where the isothermal compressibility κ_T is involved. The relation follows from the definition of κ_T, Vκ_T= − ∂V/∂P. However, the minus sign was neglected in Reference 22, because it was argued that the pressure ∂P corresponds to an internal pressure originating when an alien element is added to the matrix under the assumption that the volume is constant. In reality, however, the volume would increase by ∂V compensating for ∂P so that one may write the following relation:

$$ \kappa_{\text{e}} = \frac{1}{V}\frac{\partial V}{\partial P}, $$

(17)

where κ_e was introduced in Reference 22 as an effective isothermal compressibility. After carrying out the same transformations and simplifications as in Reference 22 (see also Appendix), the following relation between the excess volume and the excess free energy is obtained, where R_m= 8.314 kJ mol⁻¹ is the molar gas constant:

$$ {}^{E}V \approx 2\kappa_{\text{e}} {}^{\text{E}}G\exp \Bigg(\frac{{{}^{\text{E}}G}}{{3R_{\text{m}} T}}\Bigg). $$

(18)

In order to apply Eq. [18], a reasonable estimate for the isothermal compressibility is needed. In our previous publication,[22] we found that Eq. [18] reproduced the experimentally observed excess volumes for a number of systems with ^EV < 0, if a value of κ_e= 3.2 × 10⁻¹¹Pa⁻¹ was used. This value corresponds to the isothermal compressibility of liquid Al and makes it appropriate for the Al alloys considered in Reference 22 as Al-based alloys. However, the data of the present work are underestimated this way with this value.

In general, κ_T can be calculated from the measured ultrasonic sound velocity u_S according to the following relation,[36] where c_p is the specific heat (in Jg⁻¹K⁻¹ units):

$$ \kappa_{\text{T}} = \frac{1}{{\rho u_{\text{S}}^{ 2} }} + \frac{T}{{\rho c_{\text{P}} }}\left( {\frac{{\rho_{\text{T}} }}{{\rho_{\text{L}} }}} \right)^{2} . $$

(19)

Using the parameters listed in Table IV for the pure elements Ni and Ti, one obtains for their respective isothermal compressibilities at 1673 K (1400 °C), values of κ_T,Ni= 1.97 × 10⁻¹¹ Pa⁻¹ and κ_T,Ti=1.26 × 10⁻¹¹ Pa⁻¹. The best agreement of Eq. [18] with the experimental data is obtained if, in the case of Ni-Ti, κ_e is set equal to the weighed average of κ_T,Ni and κ_T,Ti, i.e.,

Table IV Auxiliary Data Needed in Order to Calculate the Isothermal Compressibility Coefficient κ_T for Ni and Ti

$$ \kappa_{e} = x_{\text{Ni}} \kappa_{\text{T,Ni}} + x_{\text{Ti}} \kappa_{\text{T,Ti}}. $$

(20)

This may also be interpreted as the isothermal compressibility of the ideal solution. The result is shown by the solid line in Figure 10. Apart from the value of ^EV at x_Ti= 25 at. pct, the agreement of Eq. [18] with the measured excess volumes is excellent. It should be emphasized that the solid line shown in Figure 10 is not a fit and Eq. [18] does not contain any fit parameters making it adjustable to the data.

Knowing the excess volume from Eq. [18], the molar volume V is obtained from Eq. [12] and plotted in Figure 9, while ρ is calculated via Eq. [12] and shown by the solid line in Figure 7. The agreement with the experimental data is excellent in both figures, though this is a trivial consequence.

Equation [19] appears to be a new inter-property relation establishing a link between quantities including excess free energy, ultra sound velocity, excess volume, and heat capacity. Of particular interest is calculation of the isothermal compressibility. Equation [18] provides a promising new way of determining this property in such cases from the excess volume and vice versa.

We applied Eq. [18] under the following two conditions: first, Eq. [20] is valid, i.e., the isothermal compressibility of Ni-Ti follows an ideal law and the corresponding excess property can be neglected and second that, in addition to translational degrees of freedom, rotational degrees of freedom are also allowed, see Reference 22 and Appendix.

It will be subject to future investigations to determine whether these assumptions are always valid or, if not, under which conditions Eq. [18] can be applied.

5 Summary

Densities of liquid binary Ni-Ti alloys have been determined as function of temperature and composition using the containerless technique of electromagnetic levitation. As the levitated droplets tended to exhibit strong rotations, large translational movements, and strong surface oscillations, the use of the conventional method was seen to be inappropriate. Due to the presence of these movements, it occurred that the samples were no longer symmetric with respect to their vertical axes. Hence, the experimental setup was improved by installing a second camera aimed at the sample from the top. This camera measured the correct cross sections of the distorted droplets. This enabled measurement of accurate densities, even in cases where the condition of axial symmetry was heavily violated.

The measured densities were discussed in terms of the molar volume. A negative deviation of the real molar volume from the ideal one was found, implying the corresponding excess volume was also negative. The non-ideal molar volume confirmed that Ni-Ti is a highly non-ideal system and comparable to a number of Al-based alloys, such as Al-Au, Al-Cu, Al-Fe.

A recently proposed relation between the excess volume, the excess free energy, and the isothermal compressibility was successfully applied to the Ni-Ti measurements of this study. For the first time, the excess volume of a binary metallic alloy was predicted from a thermodynamic relation with only a few assumptions.

Appendix

A detailed discussion of the model, Eq. [18], is given in Reference 22. In the following, it is briefly outlined how Eq. [18] is obtained in Reference 22 from Eq. [17].

Formally, Eq. [17] is the same as the definition of the isothermal compressibility, except that the meaning of the pressure is different and that the minus sign is omitted. It is easily seen by multiplying both sides by V = ^idV +^EV, that Eq. [17] also holds for the excess volume ^EV:

$$ {}^{\text{E}}V \cdot \kappa_{\text{e}} (^{\text{E}} G) = \frac{{\partial {}^{\text{E}}G}}{\partial P} \cdot \kappa_{\text{e}} (^{\text{E}} G) = \frac{{\partial {}^{\text{E}}V}}{\partial P} . $$

(A1)

In Eq. [A1], it is shown that the excess volume can be obtained by differentiation of the excess free energy ^EG. Moreover, κ_e is assumed to be a function of ^EG. To the first degree of approximation, this function would be linear with κ_e,0 and κ_e,1 being the corresponding coefficients:

$$ \kappa_{\text{e}} (^{\text{E}} G) \approx \kappa_{\text{e,0}} + \kappa_{\text{e,1}} {}^{\text{E}}G . $$

(A2)

Combining Eqs. [A1] and [A2] yields:

$$ \kappa_{\text{e,0}} \frac{{\partial {}^{\text{E}}G}}{\partial P} + \kappa_{\text{e,1}} {}^{\text{E}}G\frac{{\partial {}^{\text{E}}G}}{\partial P} \approx \frac{{\partial {}^{\text{E}}V}}{\partial P}. $$

(A3)

The pressure is eliminated by integration of Eq. [A3]:

$$ \left[ {\kappa_{\text{e,0}} {}^{\text{E}}G + \frac{1}{2}\kappa_{\text{e,1}} {}^{\text{E}}G^{2} } \right] \approx {}^{\text{E}}V. $$

(A4)

This expression can be transformed further by expanding the linear approximation into an exponential and letting the ratio of κ_e,0 to κ_e,1 be written as λ/R_mT:

$$ {}^{\text{E}}V \approx 2\kappa_{\text{e,0}} {}^{\text{E}}G\exp (\lambda \frac{{{}^{\text{E}}G}}{{R}_m{T}}). $$

(A5)

In reality, this relation is not necessarily true generally as there are also systems where the signs of ^EV and ^EG are different.[18,21] However, Eq. [A5] may be true for a large number of systems.

Mathematically, Eq. [A5] exhibits a minimum at ^EG = ^EG_min, where ^EG_min is obtained as

$$ {}^{\text{E}}G_{\hbox{min} } = - \frac{{R}_m{T}}{\lambda }. $$

(A6)

However, the internal energy U = 3R_mT is a lower limit for ^EG if it is assumed that in addition to translations also a rotational degree of freedom exists. This holds at least as an approximation, as the excess entropy was neglected. Hence, it follows from Eq. [A6] that

$$ \lambda = \frac{1}{3}. $$

(A7)

Combining Eqs. [A5] and [A7] yields Eq. [18].