1 Introduction

The design of bulk metalworking processes and solid-state-joining operations via finite-element-method (FEM) simulations often requires material data at large strains, high strain rates, and high temperatures. These data comprise flow-stress behavior, failure strains, and quantitative descriptions of microstructure evolution. To meet such needs, the hot torsion test is one of the most useful workability methods because large deformations can be readily imposed without diffuse or localized necking, as in the uniaxial tension test, or free-surface barreling, as in uniaxial compression.[1] Nevertheless, flow localization, typically in the form of non-uniform shear strain along the length of solid round bars or tubes, can develop during hot torsion. The source of the flow non-uniformity can be an axial temperature gradient, which is present prior to or which evolves during twisting, or material flow-softening response in conjunction with a material imperfection such as a small inhomogeneity in cross-sectional area.[2,3] The rate of development of strain concentrations can be exacerbated by deformation heating during high-strain-rate testing, especially for materials with a marked dependence of flow stress on temperature and small strain-rate sensitivity of the flow stress.

Hot-torsion samples are usually heated by one of several techniques, including radiant (within a furnace), induction, and direct-resistance methods. The rate of heating is usually least rapid for radiant and fastest for direct-resistance techniques. Because of its rapid-heating capability, the latter method is also frequently utilized to obtain insight into the effect of transient heating (or cooling) conditions on hot ductility, ultimate tensile strength/fracture stress, etc during tension, compression, or torsion testing.[4,5,6,7,8,9,10] Transient tests are usually one of two types, “on-heating” or “on-cooling” which consist of preheating (and soaking) at a specified temperature, rapid heating or cooling, respectively, to another temperature, followed immediately by deformation. By such means, the effect of the retention of a metastable microstructure on plastic flow can be quantified and related to such industrially-important processes as conventional hot forging (hot metal deformed between low-temperature dies), inertia/linear friction welding (metal concurrently heated and deformed), and fusion welding (metal concurrently cooled and deformed after solidification).

High-temperature mechanical testing based on direct-resistance heating has been performed for over 50 years. Two of the best-known systems for conducting such tests are the Gleeble® (Dynamic Systems, Inc., Poestenkill, NY) and Electro-Thermal Mechanical Testing (ETMT®) system (Instron, Norwood, MA). Despite the attractive features of direct-resistance heating for the simulation of large-strain mechanical behavior and its ever-increasing popularity, relatively little research related to the uniformity of heating by such methods has been performed. Several notable exceptions for the heating of tension or torsion specimens are the efforts reported by Brown et al.,[11] Norris and Wilson,[12] Forrest and Sinfield,[13] Kardoulaki et al.,[14] Peterson,[15] Zhang et al.[16,17] This prior research has suggested that axial temperature gradients for such specimens can be of the order of 200 K to 600 K (200 °C to 600 °C), the lower and higher values typical of samples gripped in so-called hot (uncooled) stainless steel jaws and water-cooled copper jaws, respectively.

The early work of Brown, Norris, and their coworkers[11,12] focused on Gleeble® hot tension testing of solid round bars. Predictions of axial temperature gradients were derived via numerical (finite-difference) solutions of the partial differential equations describing the voltage drop across the specimen, current density, and heat conduction (including a heat-generation term) with appropriate boundary and initial conditions. Similar analyses of the axial temperature and deformation fields developed during the Gleeble® hot torsion test of thick-walled tubes, the Gleeble® hot tension test, and ETMT® heating of thin sheets were performed by Forrest and Sinfield[13] (using the commercial FEM code DEFORM™), Kardoulaki et al.[14] (using ABAQUS™), and Peterson[15] (using the computational fluid dynamics package CFD-ACE+™), respectively. Most recently, Zhang et al.[16,17] applied an FEM technique to quantify the axial and radial temperature gradients that characterize preheating and straining of round bars in the Gleeble® hot tension test. A number of input model parameters (e.g., free surface heat-transfer coefficients) were fit using an inverse-solution technique and thermocouple measurements of temperature at the free surface and radial centerline. Unfortunately, these authors did not discuss the accuracy of the heat transfer coefficients so derived or the possible disruption of the current/temperature field associated with embedding a thermocouple into the bulk of a test sample.

A number of investigators (e.g., Bennett et al.[18]) have also examined the direct-resistance heating of short compression samples and quantified the effect of the die-workpiece interface heat transfer coefficient on temperature gradients.

In a previous effort,[19] the axial temperature gradients developed in Gleeble® hot torsion samples were measured and used to assess the degree of flow localization during torsion and its effect on the reduction of torque-twist data to effective stress–strain. The present work represents a continuation of this earlier effort. Its objectives were threefold: (1) develop a microstructure-signature technique to quantify the radial temperature gradients developed during the direct-resistance heating of round bars, (2) develop and validate a simple analytical model for quantifying the radial temperature gradients, and (3) establish the effect of radial temperature gradients on the interpretation of torque-twist data from the Gleeble® hot torsion test.

2 Material and Procedures

2.1 Material

Because of the availability of highly-pedigreed phase-equilibria data, the powder-metallurgy (PM), γ-γ′ nickel-base superalloy LSHR was chosen to develop a microstructure-signature method to infer local temperature during direct-resistance heating. LSHR (denoting “low-solvus, high refractory”) was developed by NASA for jet-engine-disk applications. It provides an attractive balance of properties at the bore and rim of disks that have been subjected to a graded-microstructure heat treatment in which only the component rim is exposed above the γ′-precipitate solvus temperature to promote local growth of fcc γ grains.[20]

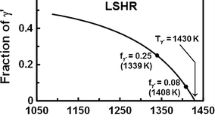
The program material was identical to that used in several previous investigations of the thermomechanical processing of PM superalloys.[19,21,22,23] It consisted of 230-mm-diameter extruded billet produced by Special Metals (Princeton, KY). Although the processing parameters for the billet were proprietary, extrusion of such materials is typically done at a temperature of ~1339 K (1066 °C) and a reduction/ram speed that imparts an effective strain rate of ~1 s−1. The material composition is given in Table I. In the as-received condition, the alloy had a fine, microduplex microstructure of γ grains and primary γ′ precipitates, each of whose average diameter was ~2 μm. There was also a small amount (<5 pct) of fine (≤400 nm) secondary (“cooling”) γ′ and ~0.33 volume percent of carbide/boride particles with an average diameter of 315 nm. The γ′-solvus temperature, T γ′, was 1430 K (1157 °C). The material showed a typical variation of γ′ volume fraction with temperature (Figure 1).[24]

Table I Chemical Composition (Weight Percent) of LSHR Program Material
Full size table
Fig. 1
figure 1

Equilibrium γ′ solvus-approach curve for LSHR: (a) Experimental data points with an analytical fit and (b) replot of the analytical fit in terms of temperature as a function of γ′ fraction for the region of interest in the present work

Full size image

2.2 Experimental Procedures

Two types of direct-resistance heating trials were performed with LSHR torsion samples of a design identical to that used previously.[19] The sample geometry was one recommended by the manufacturer of Gleeble® equipment, i.e., SMT001. It comprised a solid reduced section (measuring 20-mm length × 10 mm diameter), tubular shoulders (each with an outer diameter of 14 mm, inner diameter of 8.33 mm, and length of 70 mm), and a transition from tubular to solid over a short length just outside the reduced section. The outer 20 mm of each shoulder was inserted in a stainless steel “hot jaw”, thus leaving a length of 50 mm that was exposed. The use of the stainless steel jaws and the long length of exposed shoulder minimized the axial temperature gradient in the reduced section to between ~5 K and 15 K (~5 °C and 15 °C).[19] Heating was done under evacuated conditions in a Gleeble® 3800-499 thermal-mechanical test system.

In the first set of experiments, which were designed to establish the microstructure-signature technique, torsion samples were instrumented with three type-K thermocouples spot welded to the surface of the reduced section near the left fillet, at the mid-length, and near the right fillet. Each sample was heated at a rate of 2.75 K/s (2.75 °C/s) and soaked at test temperature (based on the mid-length (control) thermocouple) for 30 minutes to equilibrate the microstructure and then water quenched. The nominal test temperatures were 1308 K or 1377 K (1035 °C or 1104 °C).

Following heat treatment, each sample was sectioned axially and prepared using standard metallographic techniques. The local area fractions of the γ′ precipitates (used to deduce the local soak temperature) were determined via point counting on backscattered-electron (BSE) images taken at 2000× and 5000× in a Sirion scanning electron microscope (FEI, Hillsboro, OR). For each cross section, images were taken at three radial positions (r = 0, +0.8a, −0.8a, in which a denotes the outer radius) and three axial positions (near the left fillet, the mid-length, and near the right fillet), yielding a total of nine discrete locations. At least 2 images (superimposed with ~3000 point-count grid intersections) were each “read” independently by two different individuals for each heat treatment/location. For selected images, the area fraction of γ′ was also determined via hand painting the precipitates and taking the ratio of the number of pixels lying within the γ′ to the total number of pixels in the photograph. The local temperature was deduced by comparison of the measured area fraction of γ′ to the equilibrium solvus approach curve (Figure 1).

The second set of trials, designed to establish the emissivity (e) and thus the surface heat transfer coefficient, was identical in nature to the first, except that the power was turned off at the end of the 30-minute soak. The initial temperatures for these experiments [1330 K and 1403 K (1057 °C and 1130 °C)] were chosen to provide a cooling curve (which was used to establish the value of e) that passed through the respective soak temperatures used for the first set of trials.

2.3 Modeling-and-Simulation Procedures

2.3.1 Thermal model

Local temperatures inferred from the microstructure observations were interpreted in the context of a classical heat-conduction analysis. Because the axial temperature gradient in the reduced section was minimal, the analysis was based on the one-dimensional heat conduction equation (in cylindrical coordinates) for a round bar of infinite length, i.e.,

$$ \frac{{\partial {\text{T}}}}{{\partial {\text{t}}}} = \mathop {\text{k}}\nolimits_{\text{d}} \left\{ {\frac{{\partial^{ 2} {\text{T}}}}{{\partial {\text{r}}^{ 2} }} + ( 1 / {\text{r)}}\left( {\frac{{\partial {\text{T}}}}{{\partial {\text{r}}}}} \right)} \right\} $$
(1a)

Here, T(r, t) denotes the temperature distribution within a cylinder (of outer radius a) as a function of the radial coordinate r and time t, and kd is the thermal diffusivity.

For the steady-state case in which heat is generated uniformly within the body at a specified (constant) rate Ao (in W/m3), the heat conduction equation becomes the following[25]:

$$ \left\{ {\frac{{\partial^{ 2} {\text{T}}}}{{\partial {\text{r}}^{ 2} }} + ( 1 / {\text{r)}}\left( {\frac{{\partial {\text{T}}}}{{\partial {\text{r}}}}} \right)} \right\} + \, \frac{{{\text{A}}_{\text{o}} }}{\text{K}} = 0 , $$
(1b)

in which K denotes the thermal conductivity of the workpiece. Assuming that heat is lost at the surface (r = a) due to radiation, an energy balance for a unit length of the bar yields the relations:

$$ \pi {\text{a}}^{ 2} {\text{A}}_{\text{o}} = 2\pi {\text{aH}}_{\text{r}} ({\text{T}}_{\text{s}} - {\text{T}}_{\text{e}} ) $$
(2a)
$$ {\text{or}},\quad {\text{A}}_{\text{o}} = \, \left( { 2 {\text{H}}_{\text{r}} / {\text{a}}} \right)\left( {{\text{T}}_{\text{s}} - {\text{T}}_{\text{e}} } \right) $$
(2b)

Here, Ts, Te, and Hr represent the surface temperature, the environment (ambient) temperature, and the surface heat-transfer coefficient, respectively. With the surface boundary condition given by Eq. [2b], the radial temperature distribution is similar to that derived originally in Reference 25 for the special case of Te = 0, i.e.,

$$ {\text{T(r)}} - {\text{T}}_{\text{e}} = \frac{{{\text{aA}}_{\text{o}} }}{{ 2 {\text{H}}_{\text{r}} }} + \frac{{{\text{A}}_{\text{o}} ( {\text{a}}^{ 2} - {\text{r}}^{ 2} )}}{{ 4 {\text{K}}}}, $$
(3)

Rearranging Eq. [2b] as:

$$ {\text{T}}_{\text{s}} - {\text{T}}_{\text{e}} = \frac{{{\text{aA}}_{\text{o}} }}{{ 2 {\text{H}}_{\text{r}} }} $$
(4)

and subtracting it from Eq. [3] yields the relation

$$ {\text{T(r)}} - {\text{T}}_{\text{s}} = \frac{{\mathop {\text{A}}\nolimits_{\text{o}} \left( {\mathop {\text{a}}\nolimits^{ 2} - \mathop {\text{r}}\nolimits^{ 2} } \right)}}{{4{\text{K}}}}. $$
(5)

Inserting Eq. [2b] into Eq. [5] and normalizing the radial coordinate by a, the following final expression is obtained:

$$ {\text{T(r)}} - {\text{T}}_{\text{S}} = \frac{{{\text{a(T}}_{\text{s}} - {\text{T}}_{\text{e}} ) {\text{H}}_{\text{r}} }}{{ 2 {\text{K}}}} ( 1- ( {\text{r/a)}}^{ 2} ). $$
(6)

The center-to-surface temperature difference (∆T) is therefore

$$ {\Delta\text{T}} = {\text{T(r}} = 0 )- {\text{T}}_{\text{S}} = \frac{{{\text{a(T}}_{\text{s}} - {\text{T}}_{\text{e}} ) {\text{H}}_{\text{r}} }}{{ 2 {\text{K}}}}. $$
(7)

For the specific case in which the surface heat loss is via radiation per the Stefan–Boltzmann law, the surface heat flux Qr can be expressed alternatively as follows

$$ {\text{Q}}_{\text{r}} = {\text{ H}}_{\text{r}} \left( {{\text{T}}_{\text{s}} {-}{\text{ T}}_{\text{e}} } \right) \, = {\text{e}}\sigma ( {\text{T}}_{\text{s}}^{ 4} - {\text{T}}_{\text{e}}^{ 4} ) $$
(8)

in which e is the emissivity, and σ is the Stefan–Boltzmann constant (5.67 × 10−8 W/m2 K4). Hr is then given as

$$ {\text{H}}_{\text{r}} = {\text{e}}\sigma ( {\text{T}}_{\text{s}}^{ 2} + {\text{T}}_{\text{e}}^{ 2} ) ( {\text{T}}_{\text{s}} + {\text{T}}_{\text{e}} ). $$
(9)

Equation [7] reveals that ΔT is linearly proportional to the bar radius and inversely proportional to the conductivity K. Moreover, the maximum temperature difference (∆Tmax) is that for which the emissivity is equal to unity. Sample calculations based on Eqs. [7] and [9] with e = 1, a = 5 mm, and typical values of K (Figure 2) indicate that ∆Tmax increases rapidly with increasing Ts.

Fig. 2
figure 2

Predictions from Eq. [7] of the maximum steady-state temperature difference between the center and surface of a 10-mm-diameter bar as a function of its surface temperature Ts and thermal conductivity K

Full size image

The heat conduction analysis was also used to provide a simple relation to estimate the emissivity pertinent to the direct-resistance heating of LSHR. Because of the small axial temperature gradient, the instantaneous rate of temperature drop immediately after the electric power is turned off is controlled by the radial temperature gradient at the surface (present just before the power is turned off) per Eqs. [1a] and [5], i.e.,

$$ \frac{{\partial {\text{T}}}}{{\partial {\text{t}}}} ( {\text{r}} = {\text{a)}} = {\text{k}}_{\text{d}} \left( { - \frac{{{\text{A}}_{\text{o}} }}{{ 2 {\text{K}}}} - \frac{{{\text{A}}_{\text{o}} }}{{ 2 {\text{K}}}}} \right) = {\text{k}}_{\text{d}} \left( { - \frac{\text{Ao}}{\text{K}}} \right) = - \frac{{{\text{A}}_{\text{o}} }}{{{\rho\text{c}}}}. $$
(10)

In Eq. [10], the relation between thermal conductivity (K) and thermal diffusivity (kd) has been used, i.e., kd = K/ρc, in which ρ and c denote density and specific heat, respectively. Combining Eqs. [4] and [10] yields the following alternate relation:

$$ \frac{{\partial {\text{T}}}}{{\partial {\text{t}}}} ( {\text{r}} = {\text{a)}} = - \frac{{{\text{A}}_{\text{o}} }}{{{\rho\text{c}}}} = - \frac{{ 2 ( {\text{T}}_{\text{s}} - {\text{T}}_{\text{e}} ) {\text{H}}_{\text{r}} }}{{{\rho\text{ca}}}}, $$
(11a)

in which Hr is given by Eq. [9]. The emissivity can thus be determined from the measured rate of temperature drop and known values of Ts, Te, ρ, c, and a. An approximate relation between the rate of temperate drop and the emissivity can also be obtained from a simple “lumped-parameter” analysis in which the workpiece is assumed to have an infinite conductivity and thus a uniform temperature Tb. In this case, a heat balance yields the following relation:

$$ \frac{{{\text{dT}}{}_{\text{b}}}}{\text{dt}} = \frac{{ 2 ( {\text{T}}_{\text{b}} - {\text{T}}_{\text{e}} ) {\text{H}}_{\text{r}} }}{{{\rho\text{ca}}}} $$
(11b)

in which Hr is again given by Eq. [9], but with Ts replaced by Tb. A comparison of Eqs. [11a] and [11b] reveals nearly-identical relations with the sole exception that Ts is replaced by Tb everywhere it appears.

2.3.2 Torsion simulations

The effect of a radial temperature gradient on torsion testing of round bars was established by a series of numerical simulations for the LSHR program material. Unlike previous work[19] that focused on the effect of axial temperature gradients on flow localization, the present calculations assumed a uniform axial temperature, and the evolution of the local shear stresses across the radial section and the total torque were quantified.

For the present simulations, the cross section of a 10-mm-diameter torsion sample was discretized into a series of ten annuli of equal radial increment. The initial temperature distribution was assumed to be either uniform or vary per Eqs. [6] and [9]. For the cases involving an initial radial temperature gradient, the initial surface metal temperature was assumed to be either 1339 K or 1394 K (1066 °C or 1121 °C), or values that approximate those deduced from the microstructure-signature results. Simulations were performed assuming isothermal conditions for which T(r, t > 0) = T(r, 0) or perfectly-adiabatic conditions in which radial heat conduction was assumed to be negligible. These two cases thus bracketed behaviors typical of very slow or very rapid deformation. As is standard practice for the torsion of solid-round bars, the shear strain and shear strain rate were assumed to vary linearly with radius.

The total torque generated (M) during torsion of LSHR was determined by numerical integration over the radial cross section of the moment of the shear forces using the constitutive equation developed in Reference 19, i.e.,

$$ M = \int\limits_{r = 0}^{r = a} {2\pi \mathop r\nolimits^{2} \tau dr} $$
(12)

in which τ denotes the local shear stress as a function of local shear strain (Γ = rθ/L, in which θ denotes the applied twist, and L the length of the reduced section), shear strain rate (\( \dot{\Gamma } = {\text{r}}\dot{\theta }/{\text{L}} \), in which \( \dot{\theta } \) denotes the applied twisting rate), and temperature. For each simulation, an increment of twist θ was applied to the discretized sample, and the shear strain/strain rate were calculated for each annular slice. In turn, the shear strains and shear strain rates were related to effective strains and strain rates using standard relations. In both the isothermal and adiabatic simulations, the surface effective strain rate was fixed as 1 s−1, and the initial strain-hardening transient in material response (for effective strains between 0 and 0.05) was neglected. The local values of effective strain \( \bar{\varepsilon } \)/strain rate \( \dot{\bar{\varepsilon }} \) and temperature T were used to estimate the effective stress \( \bar{\sigma } \) (and thus \( \tau = \bar{\sigma }/\sqrt 3 \)) using a previously-determined constitutive equation for LSHR[19]:

$$ {\bar{{\sigma }}}^{\text{n}} = {\text{A}}\dot{\bar{\varepsilon }}\exp ({\text{Q}}/{\text{RT}}){\text{h(}}\bar{\varepsilon }/\bar{\varepsilon }_{\text{p}} ). $$
(13)

Here, n is the stress exponent of the strain rate (=4 for LSHR), A is a fitting constant (=exp(−29.73) s), Q is an apparent activation energy for plastic flow/dynamic recrystallization (=591 kJ/mol), R is the gas constant, \( \bar{\varepsilon }_{p} \) is the effective strain corresponding to the peak flow stress (≈0.05), and \( {\text{h(}}\bar{\varepsilon }/\bar{\varepsilon }_{\text{p}} ) \) describes the flow-softening behavior. At \( \bar{\varepsilon } = \bar{\varepsilon }_{\text{p}} \), h = 1 and \( \bar{\sigma } = \bar{\sigma }_{\text{p}} \). The following phenomenological relation was used to fit flow-softening response[19]:

$$ {\text{h}}=(\bar{\varepsilon }/\bar{\varepsilon }_{\text{p}} )^{{{\text{q}} \cdot {\text{n}}}} $$
(14)

in which the coefficient q was a negative number lying between −0.125 (for lower-temperature simulations) and −0.07 (for higher-temperature simulations).

For the adiabatic simulations, the temperature rise dT in each slice for each increment of time dt, was calculated with the aid of the equation[1]:

$$ {\text{dT}} = 0.95(\tau \dot{\Gamma }/\rho {\text{c)dt}} . $$
(15)

in which \( \dot{\Gamma } \) is the local shear strain rate; it was assumed that 95 pct of the deformation work was converted into heat. For tests at high strain rates of the order of 1 s−1 or greater, the adiabatic assumption is a good approximation[26]; c was taken to be the average value over the temperature range of interest.

3 Results and Discussion

The principal results of this investigation consisted of microstructure-signature analysis of the radial temperature gradient in direct-resistance heated LSHR specimens, comparison of such measurements to model predictions, and quantitative assessment of the effect of radial temperature gradients on torsional-flow response.

3.1 Microstructure-Signature Determination of Local Temperatures

Microstructure observations showed a measurable variation with radial position, but little discernible variation with axial position at a given radial location. Hence, the discussion here is restricted to results for the mid-length of the reduced section of the Gleeble® torsion samples. Another reason why results at mid-length position were utilized was because the axial temperature gradient tended to be approximately zero here (due to symmetry considerations), and heat flow was essentially radial as assumed in the model. Furthermore, attention was focused at two principal locations on cross-sectioned samples, r/a = 0 and ±0.8, to avoid the complicating factor of possible alloying element losses at the surface and concomitant changes in phase equilibria.[27]

Figures 3 and 4 summarize typical BSE microstructures for each of the two nominal test temperatures for which the surface thermocouple reading was 1308 K or 1377 K(1035 °C or 1104 °C), respectively. (In such micrographs, the precipitates correspond to the generally smaller (sometimes darker) microstructural features, the larger equiaxed grains are the matrix γ phase, and the sporadic white dots are boride/carbide particles.) The γ′ distributions for the two different nominal temperatures varied considerably. At the lower temperature (Figure 3), the γ′ size distribution was bimodal, comprising coarse (~1.5 to 2.5 μm) primary-γ′ precipitates as well as intragranular/finer (~0.5 to 1 μm) cooling-γ′ precipitates. By contrast, the microstructure was simpler after exposure at the higher temperature at which the finer cooling γ′ had dissolved fully; it consisted of a unimodal distribution of γ′ precipitates each of whose diameter was ~1 to 2 μm.

Fig. 3
figure 3

Backscattered-electron (BSE) images of the microstructures developed at r/a = 0 and 0.8 during heating of an LSHR sample to a nominal temperature (as indicated by a surface thermocouple) of 1308 K (1035 °C)

Full size image
Fig. 4
figure 4

Backscattered-electron (BSE) images of the microstructures developed at r/a = 0 and 0.8 during heating of an LSHR sample to a nominal temperature (as indicated by a surface thermocouple) of 1377 K (1104 °C)

Full size image

Quantitative metallography for the two samples (Tables II and III) revealed a difference in the area/volume fraction of γ′ (f) at the two radial locations; uncertainty in the measurements was estimated to be approximately 0.01 or 0.005 at the lower and higher temperatures, respectively. At each nominal test temperature, the value of f was lower at r/a = 0 and higher at r/a = 0.8, thus indicating a decreasing temperature with increasing radial position. Local temperatures and hence the radial temperature gradient were quantified via reference to the equilibrium γ′-solvus-approach curve (Figure 1), which was fitted by the following analytical expression[24]:

Table II Gamma-Prime Measurements via Point Counting
Full size table
Table III Gamma-Prime Measurements Using Hand Painting
Full size table
$$ {{f}} = - \frac{{ 4 {\text{C*}}\left( { 1- { \exp }\left[ {\frac{{Q}}{{R}}\left( {\frac{{{{T - T}}_{\gamma '} }}{{{{TxT}}_{\gamma '} }}} \right)} \right]} \right)}}{{ 1- 4 {\text{C*exp}}\left[ {\frac{{Q}}{{R}}\left( {\frac{{{{T - T}}_{\gamma '} }}{{{{TxT}}_{\gamma '} }}} \right)} \right]}} $$
(16)

Here, C* denotes the atomic fraction of gamma-prime formers in the alloy (~0.535 for LSHR), and Q is a fitting parameter (=60 kJ/mol). The reader is referred to Reference 28 for more details on the derivation of Eq. [16].

The estimated temperatures at r/a = 0 and ±0.8 are also summarized in Tables II and III. For the sample heated to a nominal temperature of 1308 K (1035 °C), the temperature difference at the two locations was estimated to be 17 K (17 °C) (point-counting results, Table II) or 9 K (9 °C) (hand-painting results, Table III), thus yielding an average difference of 13 K (13 °C). The difference in ∆T estimated by the two techniques can be ascribed to several possible factors:

  1. (i)

    The grid used for point counting. Because the precipitate-size distribution at 1308 K (1035 °C) was bimodal, the use of a grid with uniform spacing could have biased the readings.

  2. (ii)

    Slope of the temperature-vs.-f curve. The (absolute) magnitude of the slope of the temperature-vs.-equilibrium-area-fraction-curve (Figure 1(b)) was relatively high [~500 K (~500 °C) = 5 K (5 °C) per percent volume fraction of γ′] at 1308 K (1035 °C). Hence, a small error in the determination of the area fraction would have a large effect on temperature correlations.

  3. (iii)

    Hand-painting errors. Hand painting is especially difficult in microstructures with a large number of fine precipitates, thus leading to increased uncertainty in area-fraction measurements.

For the higher nominal test temperature, 1377 K (1105 °C), γ′ area fraction measurements at r/a = 0 and 0.8 (Table II) indicated a ∆T of 12 K (12 °C) at the two locations. The presence of a unimodal distribution of precipitates and the lower slope of the temperature-vs.-equilibrium-area-fraction-curve in this temperature regime (Figure 1(b)) suggested a higher reliability for the correlation of area fraction of γ′ and ∆T for such higher-temperature results.

The microstructure signature results also revealed a large difference in temperature between that indicated by a thermocouple spot welded to the surface and that which the metal surface actually experienced. Based on estimates of the metal temperature at r/a = 1, this difference was ~20 K or ~15 K (~20 °C or ~15 °C) at the lower and higher nominal test temperatures, respectively. The lower temperature indicated by the thermocouple in comparison to the actual metal temperature at the surface was likely a result of the fact that one side of it was touching the metal while the other was exposed to the ambient environment.

3.2 Comparison of Measured and Predicted Temperature Gradients

Local temperatures inferred from the microstructure observations were used to validate the heat-conduction analysis described in Section II–C–1. The principal inputs to the model were the thermal conductivity (K) and emissivity (e) of LSHR. Measurements by the Thermophysical Properties Research Laboratory (West Lafayette, IN) indicated that the value of K varied less than 3 pct over the temperature range of interest; hence, an average value of 21.7 W/mK was employed.

As described in Section II–C–1, the emissivity was deduced from the initial cooling transient immediately after the power was turned off during a heating trial. Inserting the definition of Hr into Eq. [11a] and solving for e yields the following expression:

$$ {\text{e}} = \left[ {\frac{{{\rho\text{ca}/{\sigma }}}}{{ 2\left( {{\text{T}}_{\text{s}} - {\text{T}}_{\text{e}} } \right)}}} \right]\left[ {\frac{{\partial {\text{T}}}}{{\partial {\text{t}}}} ( {\text{r}} = {\text{a)}}} \right]\left[ {\left( {{\text{T}}_{\text{s}}^{ 2} + {\text{T}}_{\text{e}}^{ 2} } \right)\left( {{\text{T}}_{\text{s}} + {\text{T}}_{\text{e}} } \right)} \right]^{ - 1} $$
(17)

For LSHR at the temperatures of interest, ρ = 8.0 × 106 g/m3, c = 0.732 Nm/gK, and a = 0.0051 m. Taking Te = 298 K (25 °C), the dependence of e/(∂T/∂t) on the surface temperature Ts per Eq. [17] is shown in Figure 5(a). Measured temperature transients at the onset of cooling for two high-temperature tests (Figures 5(b) and (c)) revealed slopes of −10 and −12.5 K/s at surface temperatures of 1330 K and 1403 K (1057 °C and 1130 °C), respectively. Inserting these values into Eq. [17] led to an emissivity of 0.88 ± 0.01 for such high temperatures. (The cooling curve in Figure 5(c) also shows a retardation after a modest undercooling. This behavior is related to the latent heat associated with nucleation and growth of γ′.)

Fig. 5
figure 5

Application of the surface temperature drop (after the power is turned off) to estimate the emissivity (e) of LSHR specimens: (a) Model predictions of e/∂T/∂t (at r = a) as a function of Ts, and (b, c) surface thermocouple measurements of temperature vs. time for nominal surface temperatures of (b) 1330 K (1057 °C) or (c) 1403 K (1130 °C)

Full size image

Model predictions of the radial temperature profile based on Eq. [6] for surface metal temperatures comparable to those in the experiments showed the expected trends (Figure 6). That is to say, the magnitude of the temperature gradient increased with increasing emissivity at a given temperature or with temperature for a given emissivity. For the emissivity of the LSHR program alloy (0.88), the surface-to-center temperature difference was predicted to be of the order of 20 K (20 °C). Furthermore, the temperature difference at r/a = 0 and 0.8 were predicted to be 12 K or 13.5 K (12 °C or 13.5 °C) for the lower and higher simulation temperatures, respectively. These values showed reasonably-good agreement with the measurements, i.e., 12 K to 13 K (12 °C to 13 °C).

Fig. 6
figure 6

Model predictions of the radial temperature profile in 10-mm diameter LSHR samples as a function of emissivity (e) for a surface temperature Ts of (a) 1339 K (1066 °C) or (b) 1394 K (1121 °C)

Full size image

The benefit of the present analytical-modeling approach for the radial temperature gradient can also be gaged by comparison to predictions from the more-complex numerical (FEM) technique employed by Zhang et al.[16,17] In this earlier effort, the direct-resistance heating of 10-mm diameter bars of an ultrahigh-strength steel was simulated. The surface heat-transfer coefficient was determined using an inverse-solution method based on temperature measurements from mid-length thermocouples attached to the surface and embedded at r = 0; although a large axial temperature gradient was developed due to the use of water-cooled copper jaws in this prior work, the heat flow would be expected to be purely radial at the mid-length location due to symmetry considerations. As shown above for LSHR, a surface thermocouple reading can be substantially lower than the actual metal temperature at this location. Furthermore, thermocouples placed within a resistance-heated body may interrupt the current path and perhaps produce an anomalous reading as well.

The radial temperature distribution from the FEM simulations of Zhang et al.[16,17] for several (surface) temperatures are summarized in Figure 7. These results are compared to those from the present analytical model using the same values of thermal conductivity reported in the earlier work (i.e., 29.7, 30.7, or 32.3 W/mK for temperatures of 1473 K, 1573 K, or 1673 K (1200 °C, 1300 °C, or 1400 °C), respectively) and an assumed emissivity of unity, i.e., the maximum possible value. The comparison revealed that the predictions of Zhang et al.[16,17] at r = 0 were higher by approximately 20, 60, or 115 pct than the analytical predictions. Because the surface-to-center temperature difference is linearly proportional to the emissivity, such differences suggest that physically-unrealistic values of e (i.e., e > 1) were obtained via the inverse solution method.

Fig. 7
figure 7

Comparison of model predictions (from Zhang et al.[16] and the present work) of the radial temperature gradient developed in direct-resistance-heated, 10-mm diameter, ultra-high-strength-steel samples heated to the temperatures indicated

Full size image

3.3 Effect of Radial Temperature Gradient on Torsion Response

Numerical simulations of the round-bar torsion test under the limiting cases of purely-isothermal or adiabatic conditions shed insight into the effect of the radial temperature gradient on interpretation of torque-twist data. For both conditions, the simulations enabled the identification of the temperature of a (hypothetical) uniformly-preheated bar which would give identical mechanical response as a sample with an initial radial temperature gradient.

3.3.1 Nominally-isothermal response

Mechanical behaviors under nominally-isothermal test conditions (i.e., those cases in which there is no heat generation or change in the initial radial temperature profile) were compared for two different nominal torsion temperatures. For the non-uniform radial temperature cases, the surface (metal) temperature Ts was either 1339 K or 1394 K (1066 °C or 1121 °C), and the radial temperature profiles were given by the e = 0.88 results in Figure 6. The temperature of the uniformly-heated bar was chosen in each instance to yield a torque at a surface effective strain of 0.05 which was identical to that developed in the corresponding sample with a radial temperature gradient. (The strain of 0.05 corresponded to the peak stress as noted in Section II–C–2). Furthermore, as described in Eq. [14], the flow softening function h was assumed to depend only on local strain and hence the radial coordinate r (because \( {\bar{{\varepsilon }}} = {\bar{{\varepsilon }}}_{\text{s}} ({\text{r}}/{\text{R}}) \), in which R denotes the outer radius). Similarly, the strain rate varies linearly with r. Hence, for cases in which the temperature is taken to be invariant during torsion, the ratio of the shear stress at a given radius to that at the surface is fixed. Thus, setting the torque for the uniformly-heated and radial-temperature gradient cases to be equivalent at one level of twist forced the torque to be equivalent at all levels of deformation.

The temperature of the uniformly-heated bars which produced the same torque as the samples with a radial temperature gradient were determined by a trial-and-error procedure to be 1345.4 K or 1401.9 K (1076.8 °C or 1131.6 °C) for the lower or higher-temperature simulations, respectively. The radial location of such temperatures within the bars with a radial gradient were r/a = 0.79 in both cases. Although the torque increment associated with a given annular volume element follows a complex dependence on radius, largely due to the complex nature of the constitutive behavior at hot working temperatures, it is not surprising that the temperature which appears to control the magnitude of the torque lies near the outer radius. This conclusion can be rationalized based on the fact that the torque to deform a thin-walled tube varies as r2, thus implying that most of the torque for torsion of a solid bar is generated by the deformation of the outer layers.

3.3.2 Adiabatic response

Numerical simulations assuming adiabatic conditions provided additional useful information regarding the effect of deformation heating on temperature evolution during hot torsion testing. As for the isothermal comparisons in Section III–C–1, simulations for samples with the same uniform or radially-varying initial temperature distributions were analyzed. The specific initial temperature for each uniform-temperature instantiation was again that which produced the same initial torque as the corresponding case with the radial temperature distribution.

Simulation results for two nominal test temperatures are summarized in Figures 8 and 9. For the lower temperature, the predictions revealed an unusual behavior with regard to the evolution of the temperature profile (Figure 8(a)). For the case with an initial radial temperature variation (solid lines), the center-to-surface temperature difference (δT) decreased significantly initially and then increased. Specifically, δT decreased from ~20 K to ~2 K (~20 °C to ~2 °C) after a surface effective strain (\( \bar{\varepsilon }_{\text{s}} \)) of 0.5, and then increased to ~15 K (~15 °C) at \( \bar{\varepsilon }_{\text{s}} = 1 \). Such a trend can be ascribed to the linear increase in strain (and thus plastic work and temperature increase) with radius. By contrast, δT increased monotonically with strain for the simulation with a uniform initial temperature (broken lines in Figure 8(a)). At \( \bar{\varepsilon }_{\text{s}} = 1, \) δT was predicted to be 30 K (30 °C), or a value approximately twice that for the radially-varying initial temperature distribution case at this strain level.

Fig. 8
figure 8

Numerical-simulation predictions of (a) radial temperature profiles and (b) torque-twist curves for LSHR hot torsion tests at a nominal temperature of 1339 K (1066 °C). The results pertain to cases in which the initial radial temperature distribution was non-uniform or uniform

Full size image
Fig. 9
figure 9

Numerical-simulation predictions of (a) radial temperature profiles and (b) torque-twist curves for LSHR hot torsion tests at a nominal temperature of 1394 K (1121 °C). The results pertain to cases in which the initial radial temperature distribution was non-uniform or uniform

Full size image

Despite the difference in the temporal evolution of the temperature distributions, the torque-twist curves for the initially-uniform and radially-varying temperature distributions were remarkably similar, at least to the maximum twist (corresponding to \( \bar{\varepsilon }_{\text{s}} = 1 \)) imposed during the simulations (Figure 8(b)). In fact, the difference in torque at \( \bar{\varepsilon }_{\text{s}} = 1 \) was ~0.5 pct. This behavior can be attributed to the similarity in the temperature (Figure 8(a)), strain, strain rate, and hence shear stress at the outer fibers of the specimens which dominate the overall deformation resistance in torsion.

The temperature transient results for the higher nominal simulation temperature (Figure 9(a)) were similar, and the torque-twist curves were also essentially identical (Figure 9(b)).

4 Summary and Conclusions

The effect of direct-resistance heating on the generation of a radial temperature gradient and its effect on the torque generated during hot torsion testing of round bars was quantified using analytical and numerical models and validated using the nickel-base superalloy LSHR. The following conclusions were drawn from this work:

  1. 1.

    The magnitude of the center-to-surface temperature difference is directly proportional to the bar radius, the emissivity, and (approximately) the surface temperature to the power of four and inversely proportional to the thermal conductivity. For the testing of round bars of LSHR with a radius of 5 mm at hot working temperatures [~1350 K (1077 °C)], the temperature difference is approximately 20 K (20 °C).

  2. 2.

    The microstructure-signature technique can be used to validate temperature-profile predictions. For nickel-base superalloys, temperature estimates based on the local fraction of γ′ precipitates (f) tend to be more accurate in the regime in which small changes in temperature lead to large changes in f, i.e., near the γ′ solvus temperature.

  3. 3.

    The surface (metal) temperature can show large differences relative to that determined by a thermocouple spot welded to the surface. For Type K thermocouples spot welded to LSHR, such differences are approximately 20 K (20 °C).

  4. 4.

    The torque-twist curve (and hence stress–strain curve) deduced from a Gleeble® hot torsion test of an LSHR sample with an initial radial temperature gradient is essentially identical to that for a hypothetical sample preheated to a uniform initial temperature equal to that at a fractional radius of 0.8 in the sample with the radial temperature gradient. This correlation applies to both isothermal and adiabatic test conditions.