1 Introduction

The understanding of the hot deformation behavior together with the constitutive relations describing material flow is a prerequisite for large-scale production in the industry. The constitutive modeling of flow stress is thus important in forming processes because any feasible mathematical simulation needs accurate flow description.[1,2,3] In the past several decades, a number of research groups have paid attention to hot deformation behaviors of microalloyed steels,[4,5,6] carbon manganese steels,[7,8] and stainless steels.[9,10,11]

During hot working, dynamic recovery (DRV) and dynamic recrystallization (DRX) are the restoration phenomena that significantly affect the flow behavior. DRX is an important mechanism for the microstructure control during hot deformation. DRX plays a major role in reducing the flow stress and is a powerful tool for controlling mechanical properties during processing. In the previous research, DRX behavior during hot deformation of metallic materials has been widely investigated. Mirzadeh investigated the constitutive relationships and DRX characteristics of a medium carbon V-Ti microalloyed steel.[12] Lv et al. investigated the DRX behavior of Mg-2.0Zn-0.3Zr alloy by hot compression experiments.[13] Wang et al. evaluated the DRX behavior and microstructural evolution of V-Ti microalloyed forged steel.[14]

However, limited research has focused on the hot deformation characteristics of medium carbon steels, which are widely used in forging due to their superior properties such as high strength and plasticity. The medium carbon steel LZ50 tested in this study is widely used in railway axles. In order to improve the mechanical performance of the products, microstructural evolution of LZ50 steel during hot deformation process should be controlled precisely. However, up to now, microstructural modeling and simulation for LZ50 steel during hot deformation have not been reported. In this paper, the effects of deformation temperature and strain rate on the flow stress and microstructure are experimentally determined, which is followed by a description of the flow behavior under conditions hot compression. Two-stage flow stress model is used to predict its flow stress behavior. Finally, the evolution of DRX microstructure, as well as DRX models of the volume fraction and average grain size is proposed.

2 Experimental Procedure

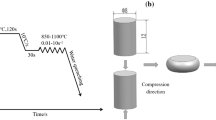
The isothermal compression was conducted using a Gleeble-3500 thermo-mechanical simulator. The cylindrical compression samples, with a height of 15 mm and a diameter of 10 mm, were prepared from an as-received square blank. The A C1 and A C3 temperatures for this steel are 998 K and 1033 K (725 °C and 760 °C), respectively. Microstructure of the as-received material is illustrated in Figure 1. The chemical composition of the studied medium carbon steel is shown in Table I.

Fig. 1
figure 1

Initial microstructure of the LZ50 steel

Full size image
Table I Chemical Composition of the LZ50 Steel (In Wt Pct)
Full size table

Figure 2 illustrates the experimental procedure designed for hot compression. The specimens were heated to 1473 K (1200 °C) at a heating rate of 5 K/s (5 °C/s) and held for 5 min prior to compression so as to obtain a uniform temperature as shown in Figure 2. They were then cooled to the deformation temperatures 1143 K, 1243 K, 1293 K, 1343 K, and 1443 K (i.e., 870 °C, 970 °C, 1020 °C, 1070 °C, and 1170 °C) with the cooling rate of 5 K/s (5 °C/s). All the specimens were kept at the test temperature for 30s before compression. Hot compression experiments were conducted with strain rate of 0.05, 0.1, 0.5, 1, and 3 s−1. Specimens were deformed to a strain rate of 0.8, followed by water quenching immediately. The deformed specimens were sectioned along the longitudinal axis, and then polished and chemically etched with a saturated aqueous picric acid solution to observe the microstructure.

Fig. 2
figure 2

Experimental processes

Full size image

3 Results and Discussion

3.1 True Stress–True Strain Curves

Figure 3 shows the stress–strain curves at different deformation temperatures and strain rates in the isothermal compression of the steel. It can be seen that the flow stress of the experimental steel increased with the increase of strain rate and decrease of deformation temperature. The σ–ε curves displayed both characteristics of DRV and DRX under different deformation conditions. The sample exhibited a typical DRX behavior at higher deformation temperatures and lower strain rates such as temperature 1443 K (1170 °C) and strain rate of 0.05 s−1. However, at the strain rate of 3 s−1 and temperature 1293 K (1020 °C), characteristics of the sample were more close to DRV. It can also be seen that the peak stress increased with the increase of strain rate and decrease of temperature. Increase in deformation temperature was beneficial for the occurrence of DRX. The higher temperature resulted in higher mobility of grain boundaries for the DRX and dislocation annihilations. However, an increase of strain rate enhanced the work hardening effect, and shortened the time of recrystallization which inhibited the occurrence of DRX.

Fig. 3
figure 3

True stress–true strain curves of LZ50 steel at (a) deformation temperature 1293 K (1020 °C) and (b) strain rate 0.05 s−1

Full size image

3.2 Constitutive Analysis

As we known, thermal activation dominates the process of plastic deformation at high temperatures. Generally, the Zener–Hollomon (Z) parameter can be used in hot deformation to characterize the combined effect of deformation temperature and strain rate on DRX as shown in Eq. [1].[15,16]

$$ Z = \dot{\varepsilon }\exp \left(\frac{Q}{RT}\right) = \left\{ \begin{aligned} A_{1} \sigma^{{n_{1} }} \hfill \\ A_{2} \exp (\beta \sigma ) \hfill \\ A[\sinh (\alpha \sigma )]^{n} \hfill \\ \end{aligned} \right. $$
(1)

where Q is the hot deformation activation energy (J/mol); \( \dot{\varepsilon } \) is the strain rate (s−1); T is the absolute temperature (K); R is the universal gas constant (8.3145J mol−1 K−1); σ is the flow stress (MPa); and A 1 , A 2, A, n 1, n, α, and β are the material’s parameters. The power law is suitable for relatively low stresses when ασ < 0.8, the exponential law is preferred for high stresses when ασ > 1.2, and the hyperbolic sine law can be used for a wide range of stresses and gives better approximations between Z-parameter and flow stress. The stress multiplier α can be calculated from α=β/n 1,[1,15,16] with the value of n1 and β obtained from the slope of the lines \( \ln \dot{\varepsilon } - \ln \sigma_{p} \) and \( \ln \dot{\varepsilon } - \sigma_{p} \) plots, respectively.

Figure 4 shows both the experimental data and the regression results of \( \ln \dot{\varepsilon } - \ln \sigma_{p} \) (Figures 4(a) and \( \ln \dot{\varepsilon } - \sigma_{p} \) 4(b)) plots. The mean values of n 1 and β can be calculated from these plots, as 6.38 and 0.0683, respectively, leading to α=0.010709.

Fig. 4
figure 4

Relationship between strain rates and peak stresses (a) ln\( \dot{\varepsilon } \) vs lnσ p and (b) ln\( \dot{\varepsilon } \) vs σ p

Full size image

Taking the natural logarithms of both sides of Eq. [1], Eq. [2] can be obtained as follows:

$$ \ln Z = \ln \dot{\varepsilon } + \frac{Q}{R}\left( {\frac{1}{T}} \right) = \ln A + n\ln [\sinh (\alpha \sigma )] $$
(2)

The partial differentiation of Eq. [2] is as follows:

$$ \frac{1}{n} = \frac{\partial \ln [\sinh (\alpha \sigma )]}{{\partial \ln \dot{\varepsilon }}} $$
(3)

The value of n can be determined by the corresponding slopes of the fitted lines as shown in Figure 5, the plots of \( \ln \dot{\varepsilon } - \ln \left[ {\sinh \left( {\alpha \sigma_{p} } \right)} \right] \). The average value of n is estimated to be 4.4036. It can be seen that the value of n is near 4.5. It has been shown that the climb-controlled intragranular flow of dislocation can be represented by n = 4.5 to 5.[17,18,19] Therefore, it can be concluded that the flow stress of the investigated steels during hot deformation is controlled by dislocation climb.

Fig. 5
figure 5

Relationship between ln \( \dot{\varepsilon } \) and ln[sinh(ασ p)]

Full size image

For the constant \( \dot{\varepsilon } \), Eq. [4] is obtained as follows:

$$ Q = R_{n} \frac{\partial \ln [\sinh (\alpha \sigma )}{\partial (1/T)} $$
(4)

In accordance with the relationship curves of ln[sinh(ασ p)] and 103/T (Figure 6), the average value of Q can be obtained, which is 304.27 KJ/mol.

Fig. 6
figure 6

Relationship between ln[sinh(ασ p)] and 103/T

Full size image

The activation energy Q is an important material parameter serving as an indicator of the deformation difficulty degree in hot deformation.[20] The Q determined for this steel is very close to the value (301.4 KJ/mol), reported in Reference 1. Q is nearly consistent with the lattice self-diffusion activation energy of austenite (270 KJ/mol),[21] indicating that the rate-controlling mechanism of hot deformation is dislocation climb during their intragranular motion. Table II lists the activation energy of several steels. From Table II, it is found that the activation energy of the experimental steel is very close to the previously reported Q values. It can also be seen that alloy content has an important influence on hot deformation activation energy Q.

Table II The Activation Energy of Some Steels Obtained by Compression Testing
Full size table

Generally, the value of Q is affected by the chemical composition of the alloy and increases with the contents of the alloying elements, except for the case of carbon, where Q decreases with the increase of carbon content. The equation below shows Q as a function of the mass percent of microalloyed steels:[21]

$$ \begin{aligned} Q({\text{J}}/{\text{mol}}) = 267000 - 2535.52({\text{C}}{\rm {pct}} ) + 1010({\text{Mn}}{\rm {pct}} ) + 33620.76({\text{Si}}{\rm {pct}} ) \hfill \\ + 35651.28({\text{Mo}}{\rm {pct}} ) + 93680.52({\text{Ti}}{\rm {pct}} )^{0.5919} + 31673.46({\text{V}}{\rm {pct}} ) + 70729.85({\text{Nb}}{\rm {pct}} )^{0.5649} \hfill \\ \end{aligned} $$
(5)

According to Eq. [5], the Q value is estimated to be 276.837 KJ/mol. The calculated Q is very close to the lattice self-diffusion activation energy of austenite (270 KJ/mol), which probably due to the fact that vanadium addition in microalloyed steels has a negligible effect on the activation energy. The calculated Q is lower than our paper, because the effects of elements Ni and Cr on Q are not taken into account in Eq. [5]. As shown in Table II, the Q values are much higher than the self-diffusion activation energy of austenite. Elements such as Nb and Ti in microalloyed steels can increase the activation energy dramatically. In addition, Cr and Ni in steels will result in a strong solution dragging effect, therefore increasing the activation energy significantly. Addition of Ni can act as extra obstacles for dislocation motion, and increase the flow stress level during hot deformation.[4]

According to Eq. [2], the plots of lnZ vs ln[sinh(ασ p)] can be employed to find the relationship between Z and σ p. In accordance with the relationship curves of lnZ − ln[sinh(ασ p)], the average value of parameter A is obtained as 3.5884 × 1011.

When the values of Q, n, A, and α are substituted to the Z-parameter equation, the following equations can be derived as follows:

$$ \sigma_{\text{p}} = 93.3794\sinh^{ - 1} (0.00 2 4Z^{0.2271} ). $$
(6)

3.3 Characteristic Points of the Flow Curves

In order to study DRX, characteristic points including the critical strain (stress) and the peak strain (stress) must be researched. Work hardening rate θ (θ=dσ/dε), defined as the derivative of true stress to true strain, reflects the relationship between the work hardening level and true strain. Representative of θ–ε and θ–σ curves is shown in Figure 7. Characteristic strains were determined from the θ–ε curves as shown in Figure 7(a). The critical stresses (σ c) for initiation of DRX can be obtained from the inflection points in the work hardening rate (θ=dσ/dε) vs flow stress (σ) curves or from the minimums in the –dθ/dσ vs σ curves as shown in Figure 7(b). Other characteristic stresses can also be determined from Figure 7(b).[1]

Fig. 7
figure 7

Relationship between (a) θ and ε with strain rate 0.05 s−1 at 1293 K (1020 °C); and (b) θ and σ at with strain rate 0.5 s−1 at 1343 K (1070 °C)

Full size image

The equation ε p = k ′ Z p can be employed to find the relation between ε p and Z, where k ′ and p are the constants determined by the linear regression equation between lnε p and lnZ, as shown in Figure 8.

Fig. 8
figure 8

Relationship between ln ε p and lnZ

Full size image
$$ \varepsilon_{\text{p}} = 0.0013Z^{0.2105} $$
(7)

In previous reports, ε c has a fixed proportion with ε p. In this paper, relationship between ε c and ε p is plotted, as illustrated in Figure 9. It is clear that ε c and ε p have a linear relationship, following the equation below.

Fig. 9
figure 9

Relationship between ε c and ε p

Full size image
$$ \varepsilon_{\text{c}} = 0.5146\varepsilon_{\text{p}} $$
(8)

It has been reported that the ratio of ε c to ε p is typically between 0.4 and 0.8.[1,25,26] The ratio (0.5146) obtained in Eq. [8] is in reasonable agreement with the values reported in the literature.

3.4 Two-Stage Flow Stress Model and DRX

Two-stage flow stress model is taken to predict flow stress behavior with DRX characteristics of LZ50 steel. The critical strain while dynamic recrystallization occurs is taken as demarcation point.[27]

$$ \sigma_{\text{WH}} = \sigma_{\text{s}} + \left( {\sigma_{0} - \sigma_{\text{s}} } \right)e^{{ - \frac{{k_{2} }}{2}\varepsilon }} (\varepsilon < \varepsilon_{\text{c}} ) $$
(9)
$$ \sigma = \sigma_{\text{WH}} - \left( {\sigma_{\text{s}} - \sigma_{\text{ss}} } \right)\left( {1 - \exp \left( { - k_{\text{d}} \left( {\frac{{\varepsilon - \varepsilon_{\text{c}} }}{{\varepsilon_{\text{p}} }}} \right)^{{n_{\text{d}} }} } \right)} \right)\left( {\varepsilon \ge \varepsilon_{\text{c}} } \right) $$
(10)

Here, σ WH is the flow stress when DRV is the only softening mechanism, σ s is the saturation stress, σ 0 is the initial stress, σ ss is the steady-state stress after DRX has progressed through the material; and k d, n d, k 2 are the constants.

3.4.1 Determination of characteristic parameters

Initial stress is also yield stress which is set as the stress at 0.2 pct plastic deformation. σ 0 can be expressed as function of Z as follows:

$$ \sigma_{0} = a_{1} Z^{{b_{1} }} $$
(11)

Initial stress can be obtained through linear regression as follows:

$$ \sigma_{0} = 1.6465Z^{0.1089} $$
(12)

Steady-state stress σ ss and saturation stress σ s can also be described as a function of Z.[28]

$$ \sinh \left( {\alpha \sigma_{\text{ss}} } \right) = n_{3} Z^{{n_{4} }} $$
(13)
$$ \sinh \left( {\alpha \sigma_{\text{s}} } \right) = n_{5} Z^{{n_{6} }} $$
(14)

where n 3, n 4, n 5, and n 6 are the constants. Ln[sinh(ασ ss)] vs lnZ and ln[sinh(ασ s)] vs lnZ are plotted in Figures 10(a) and 10(b), respectively. By linear regression, steady-state stress σ ss and saturation stress σ s can be obtained as follows:

Fig. 10
figure 10

Relationship between (a) ln[sinh(ασ ss)] and lnZ; and (b) ln[sinh(ασ s)] and lnZ

Full size image
$$ \sigma_{\text{ss}} = 93.3794\sinh^{ - 1} \left( {0.0015Z^{0.2375} } \right) $$
(15)
$$ \sigma_{\text{s}} = 9 3. 3 7 9 4\sinh^{ - 1} \left( { 0. 0 0 5 6 Z^{0.2080} } \right) $$
(16)

With the input of initial stress, saturated stress, as well as ε and σ under different deformation conditions during work hardening stage to Eq. [9], k2 can be calculated as follows:

$$ {\text{k}}_{2} = a_{3} {\text{Z}}^{{b_{3} }} $$
(17)

where a 3, b 3 are constants. Through linear regression between lnk2 and lnZ, the following relationship between k2 and Z is obtained:

$$ {\text{k}}_{2} = 9 4. 3 4 4 0 {\text{Z}}^{ - 0.0627} $$
(18)

3.4.2 Analysis of DRX

As indicated in Figure 11, the initiation of DRX requires that the strain reaches or exceeds the critical strain. With the increase of Z-parameter, the critical strain increases. Onset of DRX will be easy at the high temperatures and low strain rates (low Zener–Hollomon parameter), which is reflected by the low critical strain required for the initiation of DRX. When the strain is less than the critical strain, work hardening is dominant and DRX has not yet been initiated. The dislocation density and distortion energy increase with the increase in deformation strain, and DRX commences. The degree of DRX and grain refinement is enhanced with an increase in deformation capacity. When the deformation strain exceeds the peak strain, stress softening becomes dominant. During steady deformation, with an increase in strain, dynamic equilibrium is reached between work hardening and stress softening, and the DRX will be finished.

Fig. 11
figure 11

Characteristic strains for different Z-parameters

Full size image

As shown in Figure 11, while deformation temperature is 1343 K (1070 °C) and strain rate is 0.5 s−1, Z, ε c, ε p, and ε ss are 4.865E11, 0.1817, 0.2757, and 0.69, respectively. Recrystallization microstructure is strongly related to the deformation conditions of temperature and strain rate (or the value of Z). At moderate Z values, the necklace structure and subsequent evolution of the DRX microstructure are clearly visible. While the strain was less than the critical strain, the straight prior grain boundaries were distorted and developed an irregular shape in the form of serrations, as shown in Figure 12(a). While the strain exceeded the critical strain, deformation stored energy increased which led to the increase of the dislocation density, and the bulges started to be separated from the original boundaries and formed new grains (Figure 12(b)). As the strain further increased, much more new small grains nucleated at the preexisting grain boundaries, as shown in Figure 12(c). Finally, at the strain of 0.8, recrystallized grains replaced all of the original deformed microstructure and appeared nearly equiaxed (Figure 12(d)).

Fig. 12
figure 12

Microstructures of LZ50 steel at different strains [0.5s−1, 1343 K (1070 °C))] (a) 0.163;(b) 0.223;(c) 0.511; and (d) 0.8

Full size image

Taking the dislocation density as the driving force for DRX, a two-dimensional Cellular Automata (CA) method combined with metallurgical principles was developed to investigate the microstructure evolution during hot deformation.[29,30] Flow curves exhibit typical DRX behavior with a single peak stress followed by a gradual fall toward a steady-state stress. While the strain exceeded critical dislocation density, nucleation of DRX began at a critical strain, by the bulging of preexisting grain boundaries, as shown in Figure 13(a), where necklace structure was obvious. Strain-induced boundary migration was the mechanism of onset of DRX. Nucleation occurred mainly along existing grain boundaries. As the strain increased, the growth of grain was stopped by the concurrent deformation with the dislocation density increasing of the new grain. The first layer of the necklace structure formed. With the further increasing of strain, the formation of new DRX grains continued and the second layer of necklace structure formed, as illustrated in Figure 13(b) and 13(c). As shown in Figure 13(d), the new DRX grain eventually replaced all of the original microstructure.

Fig. 13
figure 13

Microstructure evolution of deformation by CA for tested steel at different strains [1343 K (1070 °C), 0.5s−1] (a) 0.3;(b) 0.5;(c) 0.7; and (d) 0.8

Full size image

The relationship between the volume fraction of DRX (X drx) and the stress (strain) can be described by Eq. [19][31]

$$ X_{\text{drx}} = \frac{{\sigma_{\text{WH}} - \sigma }}{{\sigma_{\text{s}} - \sigma_{\text{ss}} }} = 1 - \exp \left( - k_{d} \left(\frac{{\varepsilon - \varepsilon_{\text{c}} }}{{\varepsilon_{\text{p}} }}\right)^{{n_{d} }} \right) $$
(19)

The definitions of all the variables in Eq. [19] are already given for Eq. [10].

In order to determine the values of k d and n d, Eq. [19] can be rewritten in double natural logarithm form as Eq. [20].

$$ \ln \left[ { - \ln \left( {1 - X_{\text{drx}} } \right)} \right] = \ln k_{\text{d}} + n_{\text{d}} \ln \left( {\frac{{\varepsilon - \varepsilon_{\text{c}} }}{{\varepsilon_{\text{p}} }}} \right) $$
(20)

All of the values determined are analyzed by linear regression according to Eq. [20] and shown in Figure 14; the results of n d=2.9389 and, k d=0.8959 are acquired as the average values of n d and kd. The volume fraction model of DRX for the tested steel can be expressed as Eq. [21].

Fig. 14
figure 14

Relationship between ln[−ln(1 − X drx)] and ln[(ε − ε c)/ε p]

Full size image
$$ X_{\text{drx}} = 1 - \exp \left( { - 0.8959\left( {\frac{{\varepsilon - \varepsilon_{\text{c}} }}{{\varepsilon_{\text{p}} }}} \right)^{2.9389} } \right)\left( {\varepsilon \ge \varepsilon_{\text{c}} } \right) $$
(21)

The comparison of the calculated volume fraction of DRX with the experimental results at different processing parameters is shown in Figure 15, indicating a good agreement. Hence, the present model can be used to predict the volume fraction of DRX.

Fig. 15
figure 15

Comparisons between the experimental and the predicted dynamic recrystallized fractions of the LZ50 steel under (a)deformation temperature 1293 K (1020 °C); and (b)strain rate 0.05 s−1

Full size image

3.4.3 Flow stress model

Based on all the above characteristic values and model equations, the flow stress model can be described as follows:

$$ \left\{ {\begin{array}{*{20}c} {\sigma _{{{\text{WH}}}} = \sigma _{{\text{s}}} + (\sigma _{0} - \sigma _{{\text{s}}} )e^{{ - \frac{{k_{2} }}{2}\varepsilon }} } & {(\varepsilon < \varepsilon _{{\text{c}}} )} \\ {\sigma = \sigma _{{{\text{WH}}}} - (\sigma _{{\text{s}}} - \sigma _{{{\text{ss}}}} )\left( {1 - \exp \left( { - 0.8959\left( {\frac{{\varepsilon - \varepsilon _{{\text{c}}} }}{{\varepsilon _{{\text{p}}} }}} \right)^{{2.9389}} } \right)} \right)} & {(\varepsilon \ge \varepsilon _{{\text{c}}} )} \\ \end{array} } \right. $$
(22)

where, \( \sigma _{0} = 1.6465Z^{ 0.1089} \) \( k_{2} = 94.3440Z^{ - 0.0627} \), \( \varepsilon_{\text{p}} = 0.0013Z^{0.2105} \), \( \varepsilon_{\text{c}} = 0.5146\varepsilon_{\text{p}} \), \( \sigma_{\text{ss}} = 93.3794\sinh^{ - 1} \left( {0.0015Z^{0.2375} } \right) \), \( \sigma_{s} = 93.3794\sinh^{ - 1} \left( {0.0056Z^{0.2080} } \right) .\)

Figure 16 shows the comparison of the predicted and experimental flow stress curves at deformation temperature of 1293 K (1020 °C) and the strain rate of 0.05 s−1. It can be seen from Figure 16 that the predicted values are in agreement with the experimental results.

Fig. 16
figure 16

Comparisons between the experimental and the calculated flow stress curves of the LZ50 steel at (a) deformation temperature 1293 K (1020 °C); and (b)strain rate 0.05 s−1

Full size image

3.5 Austenite Grain Size of DRX

Austenite grain size of complete DRX decreases with the decrease of deformation temperature and the increase of strain rate. It is, however, independent of initial grain size and accumulated strain. The relationship between the average grain size of DRX and the Z-parameter can be expressed by as Eq. [23] when the DRX reaches the steady state.[32]

$$ D_{\text{drx}} = CZ^{ - k} $$
(23)

where D drx is the austenite grain size of complete DRX (in μm), and C and k are the material constants. C and k can be obtained from linear regression between ln D drx and lnZ. Therefore, D drx can be expressed as the power law function of Z-parameter as follows:

$$ D_{\text{drx}} = 9.8738 \times 10^{4} Z^{ - 0.2956} $$
(24)

The Zener–Hollomon exponent k=0.2956 is in accordance with those reported in the literature; e.g., 0.22,[33] or 0.27.[34]

The microstructures of the compressed LZ50 steel at different deformation temperatures and a strain rate 0.5 s−1 are shown in Figure 17. It is obvious that both the volume fraction of DRX and austenite grain size increase with the increase of deformation temperature. Deformation stored energy and the nucleation rate for DRX increase with the increase of the deformation temperature. Moreover, the higher the deformation temperature, the faster the grain boundary migration.

Fig. 17
figure 17

Microstructures of tested steel after deformation at different temperatures (\( \dot{\varepsilon } \) = 0.5s−1) (a) 1143 K (870 °C); (b) 1243 K (970 °C); (c) (1293 K (1020 °C); (d) 1343 K (1070 °C); and (e) 1443 K (1170 °C)

Full size image

From Figure 18, the grains of the samples after deformation are refined gradually when the strain rate is varied from 0.05 to 1 s−1. DRX has not completed at the higher strain rate. Some small grains of DRX locate along the grain boundaries of elongated austenite grains. The lower the strain rate, the higher the volume fraction of DRX is observed. Lower strain rate results in a prolonged deformation time for sufficient grain growth. Meanwhile, higher strain rate will increase the work hardening rate.

Fig. 18
figure 18

Microstructures of tested steel after DRX at different deformation strain rates [1293 K (1020 °C)] (a) 0. 05s−1 and (b) 1s−1

Full size image

Calculated grain size and measured grain size are listed in Table III. It can be seen from Table. III that the DRX grain size model can predict the grain size very well.

Table III Comparisons Between the Calculated and Measured Grain Sizes
Full size table

4 Conclusions

The following conclusions can be drawn from this study on the hot deformation of tested steel at deformation temperatures from 1143 Kto 1443 K (870 °C to 1170 °C) and strain rates from 0.05 to 3 s−1:

  1. (1)

    The constitutive models for LZ50 steel were investigated. The deformation activation energy was determined as 304.27 KJ/mol .The activation energy was higher than the self-diffusion activation energy of austenite (270 KJ/mol), which may be due to the fact that the steel contains Cr and Ni, resulting in a strong solution dragging effect. The obtained hyperbolic sine powers were close to 4.5, which signified that the flow stress of the investigated materials during hot deformation was controlled by the dislocation climb step.

  2. (2)

    Flow stress model can be described as follows:

    $$ \left\{ {\begin{array}{*{20}c} {\sigma _{{{\text{WH}}}} = \sigma _{{\text{s}}} + (\sigma _{0} - \sigma _{{\text{s}}} )e^{{ - \frac{{k_{2} }}{2}\varepsilon }} } & {(\varepsilon < \varepsilon _{{\text{c}}} )} \\ {\sigma = \sigma _{{{\text{WH}}}} - (\sigma _{{\text{s}}} - \sigma _{{{\text{ss}}}} )\left( {1 - \exp \left( { - 0.8959\left( {\frac{{\varepsilon - \varepsilon _{{\text{c}}} }}{{\varepsilon _{{\text{p}}} }}} \right)^{{2.9389}} } \right)} \right)} & {(\varepsilon \ge \varepsilon _{{\text{c}}} )} \\ \end{array} } \right. $$

    Here, \( \sigma _{0} = 1.6465Z^{ 0.1089} \) \( k_{2} = 94.3440Z^{ - 0.0627} \), \( \varepsilon_{\text{p}} = 0.0013Z^{0.2105} \), \( \varepsilon_{\text{c}} = 0.5146\varepsilon_{\text{p}} \), \( \sigma_{\text{ss}} = 93.3794\sinh^{ - 1} \left( {0.0015Z^{0.2375} } \right) \), \( \sigma_{\text{s}} = 93.3794\sinh^{ - 1} \left( {0.0056Z^{0.2080} } \right). \)

  3. (3)

    The microstructure evolution of the tested steel during deformation was analyzed. The DRX models of volume fraction and average grain size of the tested steel can be expressed as \( X_{\text{drx}} = 1 - \exp \left( { - 0.8959\left( {\frac{{\varepsilon - \varepsilon_{\text{c}} }}{{\varepsilon_{\text{p}} }}} \right)^{2.9389} } \right) \) and \( D_{\text{drx}} = 9.8738 \times 10^{4} Z^{ - 0.2956} \).