Crystal Plasticity Model Validation Using Combined High-Energy Diffraction Microscopy Data for a Ti-7Al Specimen

Abstract

High-Energy Diffraction Microscopy (HEDM) is a 3-d X-ray characterization method that is uniquely suited to measuring the evolving micro-mechanical state and microstructure of polycrystalline materials during in situ processing. The near-field and far-field configurations provide complementary information; orientation maps computed from the near-field measurements provide grain morphologies, while the high angular resolution of the far-field measurements provides intergranular strain tensors. The ability to measure these data during deformation in situ makes HEDM an ideal tool for validating micro-mechanical deformation models that make their predictions at the scale of individual grains. Crystal Plasticity Finite Element Models (CPFEM) are one such class of micro-mechanical models. While there have been extensive studies validating homogenized CPFEM response at a macroscopic level, a lack of detailed data measured at the level of the microstructure has hindered more stringent model validation efforts. We utilize an HEDM dataset from an alpha-titanium alloy (Ti-7Al), collected at the Advanced Photon Source, Argonne National Laboratory, under in situ tensile deformation. The initial microstructure of the central slab of the gage section, measured via near-field HEDM, is used to inform a CPFEM model. The predicted intergranular stresses for 39 internal grains are then directly compared to data from 4 far-field measurements taken between ~4 and ~80 pct of the macroscopic yield strength. The evolution of the elastic strain state from the CPFEM model and far-field HEDM measurements up to incipient yield are shown to be in good agreement, while residual stress at the individual grain level is found to influence the intergranular stress state even upon loading. Implications for application of such an integrated computational/experimental approach to phenomena such as fatigue are discussed.

1 Introduction

One of the great hopes in the materials community is to better link modeling and design work in order to both develop new engineering materials, as well as to use current or legacy materials in new applications. This shift to an increased reliance on predictive models is often referred to as Integrated Computational Materials Engineering (ICME).[1] Currently, extensive experimental testing regimes are utilized to certify materials for any given application. This empirical approach generates large amounts of data, which is both time consuming and costly. While modeling is used extensively in engineering design, linking materials models that predict properties and performance across the component life cycle from processing to final insertion remains elusive. This is in large part due to a lack of data collected at the relevant length scales. For instance, how can we validate models that predict fatigue initiation or small crack growth when we do not have validated experimental data on the length scale of these phenomena? As a consequence, advanced computational methods are bypassed for large-scale testing programs. This inherently limits the insertion of novel materials or innovative designs due to time and fiscal constraints.

High-Energy Diffraction Microscopy (HEDM) is an experimental technique that utilizes monochromatic synchrotron radiation to non-destructively probe the micro-mechanical state of a material and its microstructure during deformation.[2–11] For the dataset presented and utilized in this work, we combine near-field HEDM (nf-HEDM)[4–7] and far-field HEDM (ff-HEDM) measurements[8–11] which were concurrently collected. The nf-HEDM technique utilizes an area X-ray detector placed close to the specimen (approximately 5 mm) and provides spatially resolved orientation maps from which intragranular misorientation and grain morphology are calculated. This is used to provide the initial microstructure that we utilize to instantiate our modeling effort. The ff-HEDM technique yields data from which centroids and elastic strain tensors can be associated with each grain by means of orientation contrast. These two data streams (nf-HEDM and ff-HEDM) are co-registered into an HEDM dataset that is used to track the deformation at the single-crystal level during in situ mechanical loading. The details of the data collection, including the development of specialized hardware developed specifically for this type of measurement, are outlined in Schuren et al.[2] and more recently in Shade et al.[12] These two data modalities offer a truly unique method for characterizing the evolution of both microstructure and micro-mechanical state of polycrystalline materials during thermomechanical processing in situ. As such, HEDM is a powerful tool to validate micro- and meso-scale models such as Crystal Plasticity Finite Element Models (CPFEM).[13–16]

Many previous studies have attempted to measure quantities to validate CPFEM and other micro-mechanical models. The early instances include work that evaluated crystallographic texture with deformation, while more recent work has focused on sub-granular orientation changes and the development of intragranular deformation and misorientation.[15–27] Those studies are useful in setting a baseline for the current effort, although they either represent a macroscopic approach that homogenizes the model response to compare with experiments, or they examine the surface of a deforming specimen in order to compare grain-level deformations to model predictions. The use of diffraction data can aid in further model validation, particularly where it is focused on utilizing the full three-dimensional data associated with HEDM to instantiate the modeling effort. In particular, studies that utilize this kind of data show good correlation on a grain-by-grain comparison between simulations and experiments.[28–32] However, the widespread use of this type of data is still limited by the near-heroic effort it takes to collect, which directly relates to the relatively sparse amount of data that have been made available to the community.

In this paper, we will present a combined nf-HEDM and ff-HEDM dataset collected during a tensile deformation of a Ti-7Al tensile specimen. The dataset is available and described in detail in Turner et al.,[33,34] and the method of collection is extensively described in References 2 and 12. The material utilized for this work is a single-phase, large grain, titanium alloy. While most engineering materials will have a finer and more complex microstructure, to include differences such as multiple phases, twins, and/or a finer grain size, the current study is meant to produce a baseline for HEDM analysis. The hope is to refine the HEDM techniques, to include the data analytics necessary to fully process these data-rich experiments, and then develop methodologies to deal with more mainstream materials.

Finally, we go beyond the experimental analysis, and utilize the dataset to instantiate a CPFEM simulation using the Arbitrary Lagrangian/Eulerian 3D (ALE3D) finite element code from Lawrence Livermore National Laboratory.[35] We will then compare the strain fields measured experimentally to those predicted through the simulation, highlighting areas of success as well as limitations of our modeling approach.

2 Materials and Experimental Procedures

2.1 Material

The material utilized for this work was a single α-phase titanium alloy (Ti-7Al), with a hexagonal close packed crystal structure. It was cast as an ingot with a diameter of 75 mm, then hot isostatic pressed, and finally extruded into a 30 mm² bar. Subsequently, it was unidirectionally rolled at a temperature of 1228.15 K (955 °C) until it reached a final thickness of 7.5 mm. Finally, the material was recrystallized at 1228.15 K (955 °C) for 24 hours and furnace cooled. This processing route created a single-phase material with an approximate 100 μm grain size.[2,12,36] The particular processing route acted to minimize the macroscopic residual stress in the material. Qualitatively this is evidenced by the fact that at the specimen length scale we were able to machine specimens without the typical distortion associated with bulk residual stresses. As we will show later, however, significant residual stresses still persist at the individual grain level. We fabricated the specimen with the tensile axis normal to the short transverse and rolling directions. Significant plastic and elastic anisotropy exist in this material,[37–39] indicating that heterogeneous deformation develops even under nominally elastic loading conditions. This makes it a perfect material for this study.

2.2 In Situ HEDM Experiments

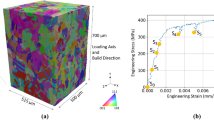
Although a more detailed description of the experiments may be found in Shade et al.,[12] enough detail will be presented here to put the modeling component of this paper into context. Specifically, the dataset was collected during an HEDM experiment at the Advanced Photon Source (APS) at Argonne National Laboratory (ANL) in the 1-ID-E beamline. The experimental methods were described by Schuren et al.,[2] while the unique in situ experimental equipment for combining HEDM measurements with in situ loading is detailed in Shade et al.[12] That paper describes the Rotational and Axial Motion System (RAMS), which concurrently rotates the tensile specimen while at the same time applies axial loading. The specimen is shown in Figure 1(a). The RAMS system was designed to be an insert gripped by an MTS 858 load frame, providing simultaneous and independent rotation of the specimen, while the sample is mechanically loaded through the load frame.

Fig. 1

(a) Schematic of the HEDM tensile specimen, (b) a scanning electron microscopy image of the specimen surface along the gage length, showing two gold fiducial markers placed on the specimen for proper registration, and (c) a reconstruction of the nf-HEDM data recorded from the specimen

The specimen shown in Figure 1(a) had a gage length of 8 mm, with an approximate 1 mm² cross section. Small blocks manufactured from gold foil (30 μm × 30 μm × 50 μm) were attached to the specimen surface to act as fiducial markers. They helped locate the X-ray beam on the specimen, aided in the co-registration of the HEDM data streams in the subsequent data analysis, were used as a means to measure strain along the gage length, and were utilized as a calibration check of the experimental setup.[40] Figure 1(b) shows the surface of the specimen with the gold markers attached.

2.2.1 Initial far-field data collection

We collected ff-HEDM data from a 600 μm tall volume along the gage length (1 mm × 600 μm × 1 mm) before mechanically loading the specimen. This included the whole gage cross section. Figure 1(b) shows the relative location of this ff-HEDM volume. To collect the data, we used a 1.5 mm wide by 600 μm tall “box” X-ray beam, which consequently defined the measurement volume. The RAMS device allows for the ff-HEDM measurements to be collected over the full 360 deg angular range, and diffraction images were taken over 0.25 deg rotation intervals. While the images are collected in a flying mode at 1.25 deg/s, the limited memory buffer of the detector forces a pause to dump the data after 240 images have been collected. This limits the current acquisition speed for a full volume scan to 12 minutes, rather than the 288 seconds achievable with the rotation rate.

The raw ff-HEDM data consist of diffraction images projected onto an area detector placed approximately 1 m behind the specimen. We performed analysis of the diffraction image stacks using the HEXRD program,[11] which is open source and freely available for download on GitHub.[41] This analysis provided the initial grain centroid location (to a resolution of ~20 μm), as well as the grain-average elastic strain tensor within each grain before the deformation. The strain resolution is ~5 × 10⁻⁵.[11,42] HEXRD provides a simple figure of merit for each grain indexed from the ff-HEDM data. This metric—referred to as completeness—is a scalar value in [0, 1], and represents the ratio of observed Bragg reflections to those predicted by the diffraction model in HEXRD. Therefore, a completeness of 1.0 indicates that HEXRD found a signal in the raw data within user-specified tolerances for all expected Bragg reflections for the corresponding grain. While more complex figures of merit can be calculated, completeness has been shown to be a powerful figure of merit to rank the quality of fits for crystallographic orientation, position, and strain. While completeness values <1.0 indicates that not all of the expected diffraction peaks were observed in the experimental data for the corresponding grain, this does not necessarily indicate bad fits. In particular, for small grains specific Bragg reflections with low structure factors may systematically fall below the signal-to-noise threshold and be absent, while the strong reflections fit with very low residual errors. Generally speaking, in the automated analysis grains with completeness values of 70 pct or higher are taken to be valid in a simplistic effort to not systematically bias out small grains. Furthermore, orientations that score below 50 pct completeness for realistic tolerances have been shown to be generally unreliable, noting that the orientation indexing procedure generates initial orientation estimates with completeness values > 0 by construction.

The initial ff-HEDM measurement and corresponding data provide the first look at the structure of the specimen within the 600 μm tall volume. These data can be found in Turner et al.,[33,34] and consist of 605 grains within the volume. Each grain is defined by a centroid location, an average crystallographic orientation, and the initial strain tensor. These strain tensors can be converted to stress tensors using linear elasticity and the single-crystal elastic constants.[33,43–45] At this unloaded state, the strain tensors provide information about the residual stress in the material with intergranular resolution.

2.2.2 Initial near-field data collection

Next, we used the nf-HEDM technique to gather resolved spatial information about the specimen. This technique is more time intensive, and required 24 hours to measure 53 slices, each separated by 4 μm along the tensile axis. For the nf-HEDM experiment, we used a 2-μm-tall line-focused X-ray beam. In this manner, we measured 240 grains in the ~200 μm tall volume along the tensile axis. This nf-HEDM volume was centered within the larger 600 μm tall ff-HEDM volume. Figure 1(b) shows the relative positions of the nf-HEDM and ff-HEDM volumes.

The nf-HEDM raw data also consist of diffraction patterns; however, these are recorded on a much smaller detector situated approximately 5 mm from the specimen. We utilized the IceNine code[7,46] to process the nf-HEDM data, providing the 3D grain morphology and intragranular orientation distribution within the 200 μm tall volume. These measurements have a spatial resolution of approximately 2 μm and an accuracy in crystallographic orientation of ~0.1 deg.[7]

Figure 1(c) shows the reconstruction of the nf-HEDM data after processing through IceNine.[46] The nf-HEDM data largely resemble Electron Back-Scattered Diffraction (EBSD) data, where a single grain comprises multiple data points. In fact, a “3D EBSD” experiment is a good analogy for the nf-HEDM technique, where instead of single pixels on a 2D surface, we have voxels in 3D space for each data point. The same data could be obtained through the combination of serial sectioning and EBSD measurements to make a 3D volume. EBSD data have the advantage of finer spatial resolution (at least in the measurement plane), while nf-HEDM provides the advantage of being a non-destructive technique where the material can be subsequently tested.

The combination of the ff-HEDM and nf-HEDM datasets, collected on the same sample volume (or overlapping sample volumes in this case), provides a powerful non-destructive characterization of the initial material state. This includes the full 3D morphology to include intragranular orientation gradients within the nf-HEDM data, and the grain-average full 3D elastic strain tensor and crystallographic orientation from the ff-HEDM data stream.

It is important to note that during these initial measurements (ff-HEDM and nf-HEDM), the specimen was subjected to an axial load of 23 MPa due to the initial procedure of loading the specimen into the RAMS device. This occurred while tightening the grip in the RAMS that constrain the specimen during testing. Although we desired this to be a truly unloaded state, we will discuss the ramifications in subsequent sections of this paper. The unloaded state, with the 23 MPa applied to the specimen, will be called Load 0.

2.2.3 Tensile experiment

After measuring the initial state of the material with both the ff-HEDM and nf-HEDM techniques, we axially loaded the specimen in displacement control along the y-axis to three axial load levels: Load 1 (180.9 MPa), Load 2 (339.8 MPa), and Load 3 (495.9 MPa). Each of these loading points was nominally below macroscopic yield. This is shown in Figure 2, where the red line is the macroscopic stress-strain curve from the RAMS machine. At each load level, ff-HEDM measurements were conducted. The specimen was initially loaded past these measurement load levels, and then unloaded by approximately 10 pct to minimize changes in the material state due to stress relaxation during the ff-HEDM measurements. This procedure is more critical after fully developed plastic flow has started; however, we chose to utilize it for all loading stages to remain consistent. This follows the methodology first outlined in Dawson et al.[47]

Fig. 2

Loading curve (axial stress vs axial strain) for the tensile specimen, and the subsequent CPFEM simulations

The more time intensive nf-HEDM measurements were not conducted at Load 1, Load 2, or Load 3, due to limits of experimental time and the fact that in the elastic regime we expected little change in the grain morphology or rotation of the crystallographic orientation. However, the ff-HEDM scans provide detailed information on an intergranular basis for how the elastic strain tensor evolves throughout the loading. This in turn reveals how the stress is distributed among the grains, and how loads are redistributed with increasing applied load and deformation. This will be the basis of comparison between the experiments with the CPFEM model described later in this paper.

Upon examining Figure 2, between Load 2 and Load 3 the flow curve deviates from linearity. Admittedly, this is hard to determine with such few points plotted in Figure 2, but it may indicate the onset of plasticity. We used a two-point digital image correlation on the specimen surface to measure macroscopic axial strain levels. This was accomplished by measuring the distance between the two gold fiducial markers on the specimen surface.[40] Before we placed the sample in the grips we made no DIC measurement, and therefore, the strain at Load 0 was assumed as zero despite the 23MPa axial load.

Although we only show the experimental loading curve up to Load 3, after this point the specimen was held at a fixed axial load to conduct a room temperature creep experiment. That portion of the experimental test will be the subject of future work, so the loading curve beyond Load 3 is not presented in order to eliminate confusion in the scope of the current effort.

2.2.4 Combining the data streams

The dataset presented in Turner et al.[33,34] represents processed (through HEXRD for the ff-HEDM data and through IceNine for the nf-HEDM data) and aligned data. However, the act of aligning and co-registering the initial nf-HEDM data with the initial ff-HEDM data was non-trivial. Registering these two datasets is necessary so that we may use the initial combined data stream as the instantiation for the CPFEM model (discussed next), and then use the subsequent ff-HEDM data from Load 1, Load 2, or Load 3 as a comparison point to validate the CPFEM model.

The first step in registering the data is to convert each to a common framework for comparison. In this case, the ff-HEDM has the simplest data structure with a grain centroid and an average orientation for each grain. Therefore, the nf-HEDM data were reduced to this simpler format. This is similar to the manner where EBSD data are averaged across a grain to provide average statistics for each grain. In the initial data reduction using the IceNine software, a critical misorientation was chosen to aggregate spatially similar data points into a single grain. For this study, we used a 0.5 deg misorientation, such that data points measured next to one another within that misorientation tolerance were assigned the same grain ID. In this manner, IceNine provided the data seen in Turner et al.,[33,34] where the nf-HEDM data are already segregated into individual grains.

At this point, it becomes a simple matter to average the spatial location of each nf-HEDM data point within a grain to obtain the analog to the ff-HEDM data. In a similar manner, we also calculated the average orientation of each grain.[48] By taking these two averages, the nf-HEDM data reduce to the same form as the ff-HEDM data. Registering the two datasets is an exercise in keeping one dataset fixed, while the other is moved relative to it (through rigid body rotations and translations), until the error between nf-HEDM and ff-HEDM centroids and grain-average crystallographic orientations was minimized. This then determines the best possible fit between the data streams.

The one subtle caveat to this method is that it requires the use of only the nf-HEDM grains which are fully contained within the nf-HEDM volume. If a given grain is not fully contained within the measurement volume (i.e., it is “sliced” off and not fully represented), then the grain-average centroid and orientation computed from the nf-HEDM data will be skewed with respect to the ff-HEDM values for the same grain. In the nf-HEDM volume, 69 of the 240 grains were fully contained within the volume. We further restricted these grains to those where we had a high confidence in the solution for the ff-HEDM data, by selecting only the matching grains with a ff-HEDM Completeness of 0.9 or higher, thus requiring that at least 90 pct of the expected diffraction peaks were observed. By applying this filter, the set of grains reduced to 39, and we were able to find rigid translations and rotations of the nf-HEDM data such that each grain was paired with a ff-HEDM grain. These 39 matches were done within an average crystallographic misorientation between matching pairs of 0.13 deg, and a 16.3-μm difference in their centroid positions. Considering that the ff-HEDM has a resolution of ~20 μm in the location of the grain centroid, and the orientation resolution for nf-HEDM is ~0.1 deg, we are confident this alignment represents a valid registration of the two data streams.

Figure 3 shows a representation of the ff-HEDM and the nf-HEDM datasets. This figure utilizes the finite element construct as a means to visualize the grains. The formation of these virtual microstructures is discussed in the next section of this paper. In Figure 3(a), the ff-HEDM data were used to fill space in a Voronoi-like method, while Figure 3(b) displays the 39 grains that were interior to the nf-HEDM volume and used to align the two data streams. Future work will also include a secondary method to assess the accuracy of the microstructure reconstructed through the HEDM methods described here. For example, we will do 3D serial sectioning with EBSD on future specimens in order to consider a direct comparison with the nf-HEDM measurements. This would have been impractical with the current specimen because following these initial HEDM measurements it was subsequently utilized in a creep experiment, which permanently changed the microstructure.

Fig. 3

Visualization of the HEDM data where (a) displays the full ff-HEDM dataset, and (b) presents the grains located interior to the nf-HEDM data

3 Modeling Approach

To model the tensile deformation of the HEDM specimen, we employed a CPFEM model and the ALE3D finite element code.[35] The details of the crystal plasticity model, the instantiation of the digital microstructure from the HEDM data, and the incorporation into the ALE3D simulations are outlined below.

3.1 Polycrystal Model

The CPFEM model utilized in this paper is a continuum slip model that approximates plastic flow in crystalline metals through slip on associated slip planes. It consists of a single-crystal anisotropic elastic response and a constitutive model written at the slip-system level. The finite element method assembles the individual finite element response into a single-crystal response, and then the responses at the single-crystal level are assembled into the response of the polycrystalline aggregate. The crystallographic orientations of the individual grains, coupled with the anisotropy in the single-crystal elastic and plastic responses, are the leading source of anisotropy in the macroscopic response. An overview of the constitutive model written at the single-crystal length scale is presented here, but the interested reader is directed to some of the seminal work in the field found in References 17 through 19,21.

The important features of the crystal plasticity model include the elastic approximation, the constitutive model, and the hardening equation. We assume that the crystal elasticity is anisotropic and linear. In the case where we assume small elastic strains, this is expressed below:

$$ \bar{\tau } = L\bar{\varepsilon }^{*} , $$

(1)

where $\bar{\tau }$ is the Kirchhoff stress, L is the elasticity tensor, and $\bar{\varepsilon }^{*}$ represents the elastic strain tensor. The elasticity tensor, L, is written in terms of the single-crystal anisotropic elastic constants (C ₁₁, C ₁₂, C ₁₃, C ₃₃, and C ₄₄) for hexagonal materials.[43–45] The shearing rate on each slip system can be determined from a rate-dependent constitutive formulation. This is found in Eq. [2], and relates the resolved shear stress to the shearing rate:

$$ \dot{\gamma }^{\alpha } = \varPhi (\tau^{\alpha } ,g^{\alpha } ) = \dot{\gamma }_{o} \left| {\frac{{\tau^{\alpha } }}{{g^{\alpha } }}} \right|^{1/m} \text{sgn} (\tau^{\alpha } ), $$

(2)

where $\dot{\gamma }^{\alpha }$denotes the shearing rate on the αth slip system, g ^α and τ ^α are the slip-system strength and resolved shear stress of the αth slip system, respectively, while the rate-sensitivity is expressed as m, and $\dot{\gamma }_{\text{o}}$ is a model parameter. Slip-system strengths are evolved with a Voce-type saturation law[23–26] as follows:

$$ \dot{g}^{\alpha } = \theta (\dot{\gamma },g) = h_{0} \left( {\frac{{g_{\text{so}} - g^{\alpha } }}{{g_{\text{so}} - h_{\text{s}} }}} \right)\dot{\gamma }, $$

(3)

where h _o, g _so, and h _s are material parameters, and $\dot{\gamma }$ is the net slip rate on all slip systems within the crystal.

Since Ti-7Al is a single-phase α-alloy, with a hexagonal structure, we utilize three active slip systems in the model: the Pyramidal where the family of planes and directions are defined as (in Schmid notation) $m = \{ 10\bar{1}1\} ,\;s = \left\langle {11\bar{2}3} \right\rangle$, the Basal with $m = \{ 0001\} ,\;s = \left\langle {11\bar{2}0} \right\rangle$, and the Prismatic with $m = \{ 10\bar{1}0\} ,\;s = \left\langle {11\bar{2}0} \right\rangle$. We also make a simplifying assumption that while the state variable describing the slip-system strength ($g_{\text{bas}}^{\alpha }$) evolves according to a Voce law, the strengths of the slip-system families scale as follows: $g_{\text{bas}}^{\alpha } = 0.897g_{pyris}^{\alpha } = 1.586g_{\text{pyr}}^{\alpha }$. While the Pyramidal slip systems are significantly stronger than the other slip-system families, they remain critical to include in the model as they are the only systems allowing for the extension of the c-axis.[49]

The general form of this model was introduced by Asaro and coworkers.[50–53] However, we do not include latent hardening, as we apply a further simplification to the hardening law in Eq. [3]. In this assumption, we use unique basal slip-system strengths in each crystal $\left( {g^{\alpha } = g_{\text{bas}} } \right)$, enforcing a constraint that the basal slip systems in the crystal have the same strength. We then scale the strengths of the other families. This is sometimes called Taylor hardening,[54] and is an assumption adopted by other researchers when examining large strain deformations.[15–24]

3.2 Finite Element Model

The polycrystal model presented above underlies the mechanical response of each finite element in the model. Collections of spatially correlated elements are assigned as grains, and then their collective response is assembled into the macroscopic response. In this case, a velocity gradient is applied at the macroscopic level. This deformation is then partitioned among individual crystals through decomposition through the finite element method.[17,18] This ensures equilibrium in the finite element weak sense, and satisfies compatibility through the choice of element shape functions. For each finite element, we used an individual crystal orientation, and then an assemblage of elements with the same or similar orientation-defined unique grains. This technique is often to define virtual microstructures for CPFEM simulations.[15,16,20]

To model the HEDM measurement volume of the tensile specimen, we developed a volume representing the 1 mm × 600 μm × 1 mm (x-y-z direction in Figure 3(a)) ff-HEDM diffraction volume. This space was evenly partitioned into 6 million hexahedral elements with 8 nodes (200 × 150 × 200 elements), each utilizing an 8-point quadrature rule. Each element was then assigned a grain ID from either the co-registered 39 grains within the interior of the HEDM volume, or from one of the ff-HEDM grains. Table I contains the relative measurement resolution of the nf-HEDM data compared to the spatial resolution in the finite element mesh. The ff-HEDM measurement resolution was not included in this table as that technique returns only 1-point per grain. Therefore, the number of ff-HEDM measurements is a function of the number of grains, not an experimental parameter to vary in order to change the measurement resolution.

Table I Measurement Resolution for the nf-HEDM and Finite Element Mesh

More descriptively, we used the ff-HEDM and the nf-HEDM to instantiate the model in the following manner. Each of the 39 co-registered grains contained thousands of nf-HEDM measurement points. For each finite element in the volume, we checked if any nf-HEDM measurement points from the 39 co-registered grains were contained within the element volume. If the element had at least one data point from these grains, the element was assigned the grain ID (and the corresponding crystallographic orientation) of that measurement point. If the element contained more than one nf-HEDM data point from the 39 co-registered grains, we assigned the element to the grain ID of the data point closest to the element centroid—this also assigned the crystallographic orientation for the element. Many elements contained several nf-HEDM data points, most often corresponding to a single co-registered grain. The elements near grain boundaries sometimes contained data points from two or more of these grains. In this case, we again selected the grain ID for the element based on which data point was nearest to the element centroid. This creates the volume depicted in Figure 3(b), where the 39 grains in the interior of the nf-HEDM volume are explicitly represented by finite elements. It is important to note that the representation of the co-registered grains (Figure 3b), also contains any gradient in crystallographic orientation measured by the nf-HEDM technique.

To complete the finite element model, we assigned grain IDs to the elements that did not contain data points from the 39 co-registered grains. These grain IDs came from the ff-HEDM data. Here the procedure differs slightly, as most elements did not contain a ff-HEDM data point within their volume. Instead, we chose the grain ID for each unassigned element based on the grain ID of the ff-HEDM data point nearest to that element centroid. This creates a situation akin to a Voronoi representation for the remaining volume, where each ff-HEDM data point is allowed to “grow” into the remaining unassigned elements. Figure 3(a) shows the exterior of the model, and the individual grains look like a Voronoi representation of the microstructure. In this manner, the 39 grains in the center of the diffraction volume are well resolved with the nf-HEDM data (at least to the resolution of the mesh), and the volume of material surrounding those grains is filled from the ff-HEDM data. This allows us a means to apply a macroscopic boundary condition, and have the deformation partitioned in some realistic fashion to the grains in the interior. It will be these 39 co-registered interior grains that we use as a comparison against the experimental data to evaluate the CPFEM model.

Certainly there are a multitude of different schemes that could be used to take the HEDM data (both ff-HEDM and nf-HEDM), and turn it into a finite element model. We chose the simple method outlined above, with the full knowledge that this methodology does carry some disadvantages. For instance, the exact boundary conditions of each of the co-registered grains may not be as accurately represented as possible with the data. Specifically, not all of the nf-HEDM data are utilized, and the Voronoi nature of the ff-HEDM grains is certainly a simplifying assumption. This could have an effect upon the deformation of the entire aggregate. However, we felt that this first simple model was a good test case to do an initial comparison between the experiments and the CPFEM simulation.

Next, we applied boundary conditions matching the experimental conditions, where we fixed one end in the y-direction (along the tensile axis) while we allowed the other end to extend and deflect laterally. This does not correspond to a perfect uniaxial deformation, but we chose these boundary conditions to best match the degrees of freedom of a gage section removed from the experimental test specimen. In addition, the model approximated the displacement control used during the experiment. The parameters for the crystal plasticity model ($h_{o}$, $g_{s0}$, $h_{s}$, $g_{initial}^{\alpha }$, $\dot{\gamma }_{0}$, and m) were initialized in such a manner that the macroscopic stress-strain response from the simulations matched the stress-strain response from the experimental specimen (Figure 2). The model parameters we utilized are shown in Table II below, and we assumed slip occured on the Pyramidal, Basal, and Prismatic families of slip systems. Finally, we utilized the following anisotropic elastic constants: C ₁₁ = 162.4 GPa, C ₁₂ = 92.0 GPa, C ₁₃ = 69.0 GPa, C ₃₃ = 180.7 GPa, and C ₄₄ = 46.7 GPa.[45]

Table II Material Parameters for the Simulation of the Micro-tension Test

To complete the simulation, the model was deformed in tension until it reached the same macroscopic axial stress levels as the experiment (Load 1 (180.9 MPa), Load 2 (339.8 MPa), Load 3 (495.9 MPa)). This is seen in Figure 2, which also shows good yet not perfect agreement between the experiment and simulation loading curves. Just as in the experiments, we simulated the tensile tests by initially overloading past each desired axial load level, and then unloaded approximately 10 pct.[47] This is highlighted in Figure 4, which shows the progression of the simulation, by plotting the effective stress against time. The unloading points are clearly seen, as are two measurement points between the different comparison load levels (between Load 1 and Load 2, and again between Load 2 and Load 3). At these intermediate points, the experiment was interrupted (held at the current displaced position after the 10 pct unloading) to collect DIC images from the surface of the experimental specimen for surface strain reconstruction, though no diffraction was performed at these intermediate load levels. The DIC images were later used to extract an accurate measure of the axial strain along the specimen gage length.

Fig. 4

Progression of the load curve for the experiments and the matching simulations

4 Results

As this was a first ever combined ff-HEDM/nf-HEDM dataset, there are limitations to the data collected. During the experiment, the specimen was held at Load 3 for 48 hours to conduct a room temperature creep test. This limits the extent of the flow curve which can be used to tune the plasticity parameters in the model. We have therefore adopted a crawl before running approach, and future experiments contain the fully developed flow curve to better instantiate the model. However, by examining the elastic response of the material, both in the experiment and the simulations, some significant conclusions can be drawn from the datasets.

4.1 Experimental Results

Figure 5 shows the results of the experimental HEDM measurements mapped onto the co-registered grains. The grains are colored by effective stress, which is a single value as opposed to a distribution. This is because the stress values for each grain come from the ff-HEDM experiment, where a single grain average for the elastic strain tensor is determined from the diffraction data (i.e., a single tensor averaged over the entire grain). This is important to note, as the ff-HEDM measurements, especially when using a box-shaped X-ray beam which covers the entire diffraction volume, do not reveal intragranular strains. The spatial resolution of the strain measurement is on the single grain scale. It does, however, provide a means to examine the distinct and significant intergranular heterogeneity in the deformation.

Fig. 5

Experimental effective stress in MPa plotted onto the 39 co-registered grains for (a) Load 1 (180.9 MPa), (b) Load 2 (339.8 MPa), and (c) Load 3 (495.9 MPa)

Figure 6 provides another method to examine in a more quantitative manner how the stress evolves throughout the tensile deformation. This figure plots the effective stress for each of the 39 co-registered grains, highlighting the heterogeneity at the initial load level (Load 0 @ 23 MPa), as well as how that heterogeneity evolves. The thin horizontal lines in the figure are the macroscopic applied stress values; the deviation in the data from this line at Load 0 is due to the grain-level residual stress. From this figure, it is apparent that the initial Load 0 state contains significant heterogeneity.

Fig. 6

Experimental evolution in effective stress throughout the tensile deformation of the HEDM specimen for the 39 co-registered grains

4.2 Simulation Results

Figure 7 shows the simulation results at each load level, plotted onto the 39 co-registered grains. It is important to note that the CPFEM simulation provides an element-by-element stress, and therefore predicts intragranular stress gradients. In order to best compare with the experiments, we averaged the stresses over the grains and then calculated the effective stress in each grain. Therefore, the simulation results shown here are presented as grain-average quantities.

Fig. 7

Simulation effective stress in MPa plotted onto the 39 co-registered grains for (a) Load 1 (180.9 MPa), (b) Load 2 (339.8 MPa), and (c) Load 3 (495.9 MPa)

Overall, it appears that the CPFEM predictions qualitatively capture the intergranular stress distributions as observed in the experiments. However, by comparing the range of the scale bars of Figures 5 with 7, it is apparent that the model under-predicts the degree of stress heterogeneity. In addition, it appears that the predictions do not exactly match the absolute stress values in certain grains, while others are well predicted. However, these results provide an excellent starting point to discuss the relative strengths and weaknesses of this particular model.

5 Discussion

As outlined in the results section above, there are several points worthy of discussion in regard to the experiments, the simulations, and ultimately the comparison between them. First, Figures 5(a) through (c) illuminate a substantial point about the deformation of the material. These figures show the level of heterogeneity from grain-to-grain under tensile loads that are nominally in the macroscopic elastic regime (180.9 to 495.9 MPa). Load 3 may in fact show evidence of the onset of plasticity as we will discuss further, but these figures each display significant grain-to-grain variation in the effective stress. This clearly highlights that a simple deformation when viewed from the macroscopic scale can in fact be significantly more complex at the microscale. For instance, considering Load 2 (Figure 5(b)), some of the grains experience only 71 pct of the axial load, while others carry as much as 130 pct. Clearly this heterogeneity makes the onset of fatigue and other failure mechanisms plausible even under simple load conditions that would not normally be thought of as creating plastic flow in the material.

The other point that is worthy to consider when viewing Figures 5(a) through (c) is that the grain-to-grain distribution of stresses changes throughout the deformation. Certain grains that initially were high in stress under a lower loading case unload in a relative sense as the deformation proceeds. In other cases, other grains start at a lower nominal stress state and evolve to a relatively higher state when compared to their peers. Again, this points to the complexity of the deformation fields at the microstructural level.

Figure 6 provides insight into this same point, as it highlights the deformation of the material throughout the tensile loading. Even at Load 0, this figure shows that significant heterogeneity exists on the grain-to-grain level. Admittedly, Load 0 has an approximately 23 MPa of axial load due to the sample loading technique, but even with this relatively minor initial load state, some grains exhibit nearly four times that stress. This may well be due to residual stress in the material. The processing route for the Ti-7Al used in this work was chosen to minimize the bulk residual stress; however, the results in Figure 6 suggest that at the length scale of individual grains the initial residual stress state is not insignificant. This is not an entirely unexpected result, as the anisotropic thermal expansion in the material likely creates this residual stress at the grain level.[55,56] To better study this, future experiments will conduct the initial ff-HEDM measurements with only one sample end clamped in the RAMS machine. This will create a completely unloaded state in the sample.

Figure 6 allows another observation supporting the assertion of significant residual stress in the material. When looking at the traces for Load 0 and Load 1, the heterogeneity decreases. This would suggest that the stress from the loading begins to counter the initial residual stress in the material. The same pattern of effective stress exists between Load 1 and Load 2, albeit at a higher average load level, indicating that the specimen finds equilibrium in how the deformation is partitioned among all the different grains. Finally, by Load 3 we see the heterogeneity change significantly, perhaps indicating that some plastic flow has begun. This is supported by the onset of non-linearity in the loading seen in Figure 2.

The first direct comparisons between the model and the simulation come from comparing Figures 5(a) through (c) to 7(a) through (c). These can be thought of as direct comparison points. The simulation also predicts grain-to-grain level heterogeneity in the effective stress averaged over each grain. As pointed out earlier, the simulation predicts a full stress field on an element-by-element basis in each grain, and these elemental predictions are averaged to present the grain averaged results shown in Figures 7(a) through (c). Interestingly, the model does not predict the same evolution in the stress heterogeneity as seen in the experiments. In fact, in the first two loading states (Load 1 and Load 2), the pattern of the intergranular stress distributions is virtually identical, and only begins to evolve in Figure 7(c) (Load 3).

Figure 8 provides a direct comparison between the experiment and the simulation by using Load 2 (339.8 MPa). Here we have re-scaled Figure 7(b) to match that of Figure 5(b), so it is easier to make a direct comparison between the experiment and simulation at this load level. The range of the stress predictions at the grain level of the simulation is smaller than that in the experiment. However, what this figure cannot adequately illustrate is that despite the great pains that were taken to inform the model with the exact structure measured through the combined nf-HEDM/ff-HEDM data, we did not instantiate the model with the initial measured residual stresses.

Fig. 8

Comparison between the effective stress at Load 2 (339.8 MPa) in the (a) experiment and the (b) simulation for the 39 co-registered grains

To further show this, Figure 9 highlights the stress state of both the experiment and the simulation at Load 0. As we have stated earlier, we recognize that the specimen had a 23 MPa axial load at this initial measurement point. In addition, though effort was made to keep the material residual stress free through the processing route, we suspect that there was a significant initial residual stress state at the grain level due to anisotropic thermal expansion. It is impossible to decouple how much these two factors contribute to the combined stress seen in Figure 9(a). As such, it becomes that much more difficult to instantiate the model with the initial residual stress field. To complicate this further, the ff-HEDM measurements, which provide the stress state through measuring the elastic strains in the grains, do so by averaging over each grain. So even if we could instantiate the model with an average stress state in each grain, this grain-level homogenized stress state would likely not be in equilibrium as a starting point. For these reasons, we chose to ignore the residual stress in the model, at least for the scope of the present work. Even with this simplification, Figure 9(b) shows that grain-to-grain heterogeneity develops in the model at a macroscopic load of 23 MPa. However, by choosing to start the model without any initial stress, we may be biasing the predictions at each load level such that they do not develop the same level of heterogeneity as seen in the experiments (Figures 5 and 6).

Fig. 9

Comparison between the effective stress at Load 0 (23 MPa) in the (a) experiment and the (b) simulation for the 39 co-registered grains

Figure 10 makes the same point, but in a more quantitative fashion by plotting out the stress state in the 39 co-registered grains. In this case, the error bars are determined by propagating the ±5.0e⁻⁵ resolution on each strain component[11,42] into a possible set of stress states by knowing the elastic crystal constants. Although we did not use an initial residual stress state before loading the model to the Load 0 point (23 MPa), we see that at least part of the variation in the stress seen in Figure 9(a) for the experiment may be due to experimental uncertainty. However, in 10 of the 39 co-registered grains the predicted stress state from the simulation lies outside the error bars from the experiment. This may provide further proof that the initial residual stress state is at least partially to blame for the imperfect correlation of the simulation to the experiment.

Fig. 10

Graphical comparison between the effective stress at Load 0 (23 MPa) in the experiment and the simulation for the 39 co-registered grains

Extending the insight gained from Figure 10, we turn our attention to a further analysis of Load 2. Using the 39 co-registered grains, we display the stress state in a series of figures which provide a more quantitative look at the situation (Figures 11, 12, and 13). These three figures highlight different aspects of the stress tensor through the effective stress (Figure 11), the hydrostatic stress (Figure 12), and the directionality of the stress through the coaxiality[57–59] (Figure 13).

Fig. 11

Graphical comparison between the effective stress at Load 2 (339 MPa) in the experiment and the simulation for the 39 co-registered grains

Fig. 12

Graphical comparison between the hydrostatic stress at Load 2 (339 MPa) in the experiment and the simulation

Fig. 13

Graphical comparison between the stress coaxiality at Load 2 (339 MPa) in the experiment and the simulation for the 39 co-registered grains

Starting with Figure 11 and considering the uncertainty of the measurements, we see reasonable agreement between the simulation and the experiments. There are, however, still several grains where the predicted effective stress falls outside of the experimental uncertainty. This figure provides a more quantitative manner to examine the simulation results rather than a simple visual comparison between Figures 5(b) and 7(b). While the grain-level predictions of effective stress are not perfect, once we include the experimental uncertainty we realize the simulation did a better job than perhaps thought on first examination. From this figure, we can see that despite not having the initial residual stress state in the simulation, by Load 2 the simulation reasonably predicts the effective stresses on a grain-to-grain basis.

Figure 12 shows a similar plot, but this time for the hydrostatic stress. This component of the stress will not affect plastic flow; however, it does arise in many failure prediction models, including those that examine void nucleation and coalescence as a means to explain fatigue crack initiation. Once again, the simulation does a decent job in predicting the hydrostatic component of the stress on a grain averaged basis, but there are still several grains that fall outside of the experimental uncertainty.

Finally, Figure 13 shows the plot of coaxiality in the stress state between the experiment and the simulation. Stress coaxiality is a scalar measure of the alignment of the stress state in each grain to the macroscopic applied stress state. To evaluate this, we used the stress tensor components in the form of a 6-component vector.[57–59] This is shown in Eq. [4].

$$ \bar{\sigma } = [\sigma_{xx} ,\sigma_{yy} ,\sigma_{zz} ,\sigma_{xy} ,\sigma_{xz} ,\sigma_{yz} ]. $$

(4)

During uniaxial tension, only one component is non-zero. In the case where the y-direction is parallel to the tensile direction, this is written as $\bar{\sigma }_{axial} = [0,\sigma_{yy} ,0,0,0,0]$. We evaluate the stress state for each grain (experiment or simulation) through a comparison of the vectorized grain-level stress with the macroscopic stress applied to the specimen during the tension test. The coaxiality between stress states, ϕ, is an angle formed between two stress vectors, computed using the usual dot-product operation.[58,59]

$$ \varphi = a\cos \left( {\frac{{\bar{\sigma }_{axial} \cdot \bar{\sigma }}}{{\left| {\bar{\sigma }_{axial} } \right|\left| {\bar{\sigma }_{{}} } \right|}}} \right). $$

(5)

This provides a scalar, a single quantitative value of how the stress in each grain differs from the uniaxial applied stress. By this definition, the stress coaxiality does not provide direction in the six-dimensional stress space. Instead, it represents a scalar measure, similar to a distance. This means that two different stress states might have a similar stress coaxiality compared against a pure uniaxial tension. In this manner, a single stress coaxiality value actually is actually a cone of possible stress states around pure uniaxial tension.

Figure 13 exhibits significant differences in the stress coaxiality between the simulation and the experiment. Figures 11, 12, and 13 represent a means to quantifiably compare three-dimensional stress states, and in this case it appears that the simulation does a decent job in capturing the effective stress and the hydrostatic component of the stress; however, it does less well when predicting the directionality of the stress state as defined by the coaxiality. This may in part be due to the fact that the residual stress is not accounted for in the model, and even by Load 2 the effects of this initial residual stress in the experimental sample are not completely overcome by the axial loading.

Although we do not show it here, exploring the evolution of the stress state revealed a similar conclusion to that seen in Figures 11, 12, and 13 for Load 1 and Load 3. However, there are interesting conclusions to draw by examining the evolution of the coaxiality. Figure 14 shows this for both the experiment and the simulation. Looking at Figure 14(a) first, we see that the initial coaxiality for the experiment at Load 0 is quite high, with an average of 52 deg from the macroscopic tensile stress. This is not unexpected, as the loading here is low (23 MPa) and any initial stress state likely did not align with the macroscopic tensile stress. Therefore, this offers more evidence of an initial residual stress state in the material. By the time the experiment reaches Load 1 and then Load 2, the stress state in each grain begins to align with the macroscopic tensile state, as evidenced by the decrease in the coaxiality. This continues through Load 3. The simulation reveals a different trend. Examining Figure 14(b), the coaxiality at Load 0 for the predicted stress states (average coaxiality of 4.1 deg) is much lower than for the experiments. The stress in the simulation is completely due to the loading, as the model incorporates no residual stress states. Therefore, the misalignment of the grain-level stress states relative to the macroscopic stress state occurs because of the deformation partitioning in the polycrystal. Comparing the Load 0 states across Figures 14(a) and (b) provides a decent justification as to why the model misses the prediction of the coaxiality in Figure 13—the model simply does not incorporate residual stress that would account for the range of coaxiality shown at Load 0 in Figure 14(a). Once again, this points to the conclusion that we require some means of instantiating the model with residual stress.

Fig. 14

Evolution of the coaxiality for the (a) experiment and (b) simulation across the 39 co-registered grains

Given that the CPFEM simulation does a decent job in predicting the stress state, even with the shortcomings discussed previously, we sought another method to interrogate the accuracy of the model. In the experiments, the direct measurement is on the spacing of the crystal planes through diffraction, and from this the elastic strain tensor is calculated. Therefore, a comparison of the elastic strain state at the grain level is warranted, and given the earlier complications in the stress comparisons due to the possible effect of the initial residual stress state, we chose to examine the change in elastic strain between load steps. In particular, Figures 15(a) through (c) show the change in strain between Load 2 and Load 0 for the transverse and axial components of the elastic strain tensor. As we can see, the model captures this change in strain extremely well. This indicates that despite the differences in the initial stress states between the experiments and the simulation, the model does partition the deformation in a realistic manner, and we do accurately predict the evolution of grain-average elastic strains. This of course is largely testing out the elastic response in the model, as little plasticity occurs throughout this particular loading. However, predictions at this level are useful as engineering designs are built to stay below the elastic-plastic transition under service loading. Ensuring that we can model the partitioning of a deformation to the underlying microstructure is the first step toward examining cyclic plasticity and the initiation of fatigue cracks, as well as the growth of those cracks which leads to failure.

Fig. 15

Change in the normal components of the elastic strain tensor between Load 2 and Load 0 for (a) ε _xx , (b) ε _yy , and (c) ε _zz for all 39 co-registered grains where the specimen tensile axis is in the y-direction

With the perspective gained in Figure 15, we believe that the current modeling strategy, while still limited in the manner of instantiation with initial residual stresses, does a decent job in capturing the deformation in the polycrystal. So once we have faith in the model, we can use it to explore regions of the deformation where the experimental data are sparse. For instance, by plotting the coaxiality in each grain (determined between the grain stress state and the macroscopic stress state) with the macroscopic stress level, we find another interesting manner to examine the onset of yield and plastic flow. Figures 16(a) and (b) show this plot, where Figure 16(a) shows all 39 co-registered grains.

Fig. 16

Evolution of coaxiality for (a) all 39 co-registered grains, and (b) for three specific grains

What we see in these figures is a means to evaluate when plastic deformation has begun by examining the stress state. More specifically, the evolution of the coaxiality provides a quantitative measure of how the stress state in each grain changes throughout the deformation. Since these figures are calculated from the model, which relies on the rate-dependent version of the faceted yield surface due to the nature of the restricted slip upon specified slip systems,[57] we expect the stress state to evolve as it approaches the yield surface. This is manifested as a change in the coaxiality. We can see in Figure 16(a) that the interesting portion of the simulation occurs between Load 2 and Load 3, which display the first changes in coaxiality with increasing axial loading. Figure 16(b) extracts three different grains (labeled Grain A-C on the figure). These three grains have a very different nature to their coaxiality evolution. Grain A appears to begin plastic flow at a macroscopic axial stress of around 500 MPa, while Grain B appears to begin flow at a lower macroscopic axial stress of ~400 MPa, and Grain C appears to have very little evolution in the coaxiality. This may indicate that Grain C has not yet begun to plastically deform, or that its stress state is perfectly aligned with a stable position on the yield surface and the stress state will not change much even with fully developed plastic flow. This type of information could be incredibly important for developing a better understanding, and then perhaps modeling phenomena such as fatigue crack initiation.

Unfortunately, the experiment did not have the fidelity in terms of the number of measurements through yield to verify this behavior seen in the model. However, this will be the focus of future work as we attempt to use this methodology on experimental data to examine the onset of yield in polycrystalline metals. Figure 16 also provides feedback to the experiments, as it shows where we might need more experimental measurements. Thus, the simulations become a means to steer future experiments, optimizing valuable experimental time. Clearly, performing ff-HEDM measurements at many points between Load 2 and Load 3 would be advisable.

As a final discussion point, Figure 17(a) shows the full effective stress field plotted over the co-registered grains. By this we mean the effective stress is not averaged over the grain volume, but rather is shown on an element-by-element basis. This is from the simulation, and shows the degree that the predicted stress field varies over individual grains. Figure 17(b) displays a single grain from the aggregate. Clearly the stress is not uniform over the grain, and in all likelihood we believe this is also true in the experimental aggregate. While we have attempted to validate the model on the grain level, we did so by using grain averaged quantities. More work could be done to get finer spatial resolution in the experimental stress measurements, allowing even more validation for the model. However, the current work presents a step forward over more traditional validation attempts for CPFEM modeling.[15,16,20,23–25]

Fig. 17

Simulation results displaying the full effective stress fields for (a) the 39 co-registered grains, and (b) a single grain extracted from the co-registered aggregate

6 Conclusion

This work represented a first attempt to model a combined HEDM experiment, merging both ff-HEDM and nf-HEDM data to create a rich description of the microstructure, while also providing data to validate a CPFEM simulation. In general, the simulation showed promise in matching the experimental results. The maps of grain-average stress states revealed that while the simulation appeared to predict the grain-to-grain heterogeneity seen in the experiments, that heterogeneity was less well developed than in the actual specimen. However, when considering the experimental uncertainty, these comparisons are more reasonable. The differences remaining between the experiment and simulation are likely due to the residual stress in the sample which was not accounted for in the model, as the model did an excellent job of predicting the evolution of the elastic strain state. Future work will explore how to incorporate this residual stress state into simulations.

It is important to note that this kind of combined HEDM data could be useful for a variety of different modeling strategies that incorporate microstructural data into the simulations. CPFEM is just one example. In addition, the data shown here do not allow a full evaluation of the CPFEM methodology presented. In particular, we do not have data through the elastic-plastic transition, and into the regime of fully developed plastic flow, whereby we could evaluate the hardening and evolution equations (Eqs. [2] and [3]) in a more robust manner. In actuality, the work presented here does a better job evaluating the partitioning of the deformation in the CPFEM methodology and the constitutive prediction utilizing a linear anisotropic elasticity model (Eq. [1]). Future datasets will consider the transition to fully developed plastic flow in order to evaluate the accuracy of hardening assumptions in our modeling strategy. However, the current data could still be used by other model formulations, such as the Fast-Fourier Transform (FFT) methods,[60,61] which will partition the deformation through a different technique.

Experimental limitations also hindered the goal of providing a robust validation of the CPFEM methodology. Specifically, the experiment included only a few measurement points along the loading curve, and did not contain a steady-state flow curve past the elastic-plastic transition. Future experiments will contain a more resolved measurement path into fully developed plastic flow such that the plasticity parameters in the CPFEM simulation may be better tuned. However, despite this limitation, the simulation did an admirable job of predicting the deformation of the grains in the aggregate. While this is only a portion of a good validation scheme for a CPFEM simulation, it provides great hope as the model is capturing the grain-scale deformation throughout loading before fully developed plastic flow occurs. This is important not just for the validation efforts, but also because we now have a methodology to examine deformation in a polycrystal within the typical stress space for engineering designs.

Future work will also focus on strategies that may allow more engineering materials to be analyzed by the HEDM methodology. The material used in this study, while an ideal material for these experiments, is quite simple when compared to most microstructures of materials used in structural applications. Furthermore, the current setup is designed for 1.0 mm² cross-section samples to be tested at room temperature in uniaxial tension or compression. Current development efforts are underway to expand the experimental capabilities to include larger axial loads (enabling a larger sample cross section), multi-axial loading (tension-torsion), and elevated temperature. The work presented here represents an initial step to examine materials in situ; however, much more work remains before we can analyze advanced engineering materials under application-appropriate thermomechanical test conditions.

Finally, by examining the onset of plasticity in the model, we developed a criterion to see when individual grains began to flow by the rotation of their stress state. Future experimental data, especially with data points more finely resolved throughout the elastic-plastic transition, will be required to fully validate this methodology. However, it could represent a significant criterion for determining the onset of plasticity at the grain level, and further enhance our understanding of phenomena such as fatigue and crack propagation at the microstructural level.