Mechanical Properties Involved in the Micro-forming of Ultra-thin Stainless Steel Sheets

Abstract

The objective of this paper is to characterize the mechanical behavior of an ultra-thin stainless steel, of 0.15-mm thickness, that is commonly used in the manufacturing of miniature connectors. The main focus is the relationship between some microstructural features, like grain size and surface roughness, and the macroscopic mechanical behavior investigated in uniaxial tension and simple shear. In tension, adaptations to the very small sheet thickness, in order to hold the specimen under the grips, are presented. Yield stress, initial elastic modulus, and evolution of the loading–unloading slope with plastic deformation were evaluated. Moreover, the kinematic contribution to the hardening was characterized by monotonic and cyclic simple shear test and reproduced by a mixed hardening law implemented in Abaqus finite element code. Then, the evolution of surface roughness with plastic strain, both in tension and simple shear, was analyzed. It was shown that in the case of an ultra-thin sheet, the stress levels, calculated either from an average thickness or when considering the effect of the surface roughness, exhibit a significant difference. Finally, the influence of surface roughness on the fracture of a tensile specimen was also investigated.

1 Introduction

Due to the trend of miniaturization in high technology fields like micro-electronics, medicine appliances, and energy, ultra-thin metallic sheets are widely used, particularly stainless steel, due to its excellent corrosion resistance, high strength, and good formability,[1,2] and Cu alloys.[3] For instance, the austenitic ultra-thin stainless steel sheets including AISI 304 are currently used for the manufacturing of mobile phone parts, energy devices like film heater, and micro medical devices.[4,5] Fabrication processes of small parts, i.e., having dimensions between 2 and 20 mm,[6] with thin sheet metal, offer attractive characteristics of low production cost and low energy consumption compared to those of larger parts.[7]

The thickness of the material is what determines whether it is called ultra-thin sheet, thin sheet, or even plate. From an industrial point of view, an ultra-thin sheet has usually a thickness ranging from 13 μm up to 200 μm.[8,9] This division depends in fact on the ratio $N = \frac{t}{d}$ between the thickness t and the average grain size d. By investigating the behavior of pure copper with a thickness ranging from 500 μm down to 10 μm, Hoffmann et al.[10] showed that the stress–strain curves for a sheet thickness of 200 μm ($N \simeq 10$) and 500 μm ($N \simeq 25$) have similar shape and level. Specimens thicker than 200 μm were classified as macro scale specimens, while specimens thinner than 200 μm, from 100 μm and $N \simeq 3.3$ down to 10 μm and $N \simeq 0.3$, exhibited a lower stress level typical of ultra-thin sheet. These results are similar to those presented by Furushima et al.[11,12] for pure copper, with $t < 300\,\mu$m and $N < 5$, for pure titanium with $t < 300\,\mu$m and $N < 15$, and also by Miyazaki et al.[13] for steel specimen with $t < 300\,\mu$m and $N<12$. This phenomenon is so called “smaller is weaker.”[14] However, if $N$ further decreases, meaning that only a very few or no grain boundaries are present across the specimen thickness, several authors reported an increase of the flow stress. For instance, tensile test results of 99.999 pct Al performed by Hansen[15] showed an increase in the flow stress as $N$ decreased slightly from 3.9 to 3.2. Similar results were also observed by Xu et al.[16] in the case of the tension of AISI 304 ultra-thin sheet stainless steel, when $N$ changed from 1.13 up to 5.6 ($t \leq 100$ μm) and by Klein et al. when $N$ changed from 2.9 ($d = 35\,\mu$m, $t = 100\,\mu$m) down to 2.6 ($d = 30\,\mu$m and $t = 78\,\mu$m). This phenomenon is so called “smaller is stronger”.[14] From the above findings, ultra-thin sheets can be defined as sheets having a thickness between 13 μm and 300  μm and contains from 2-6 up to 10-15 grains in the thickness. A summary of the effect of $N$ on the flow stress based on the findings reported in the literature is presented in Figure 1.

Fig. 1

Size effect on the flow stress as a function of $N = t/d$. $\sigma _{\text{f}}$ is the flow stress (from Ref. [17])

In the case of ultra-thin sheet metal, the behavior depends not only on the thickness but also on the width of the specimen. To analyze this effect in tension, Hoffmann et al.[10] changed the width for three different thicknesses. It was observed that the conventional initial yield stress was either approximately constant ($t = 200 \,\mu$m) or tended to decrease when the width increased. Such a dependence, in particular at the onset of plastic strain, was also observed in Reference 18 for high purity aluminum (99.999 at. pct). The cutting method, that was either mechanical or laser cutting, influences the edge quality, which in turn leads to a dependance of the yield stress on the sample width. However, except for the effect related to the local hardening of the edge, the sample width should be chosen relatively to the sample length, in order to ensure a uniaxial stress state.

Grain size is not directly related to the sheet thickness, and therefore, from these results, it appears that to understand the influence of thickness on the mechanical properties, the ratio N should rather be considered. A similar conclusion can be drawn regarding free surface roughness, as well as the evolution of surface roughness with plastic strain, which are independent of the specimen thickness.[19] Surface roughness has been the subject of numerous investigations, including both experimental and modeling studies. In the case of tension of Al-8.5 pct Mg alloy, with a thickness of 1 mm and for different grain sizes, Wouters et al.[20] showed a linear evolution of the surface roughness with deformation, with a slope depending on the average grain size, but not on the thickness. This result was also found in References [19,21,22]. Therefore, the ratio of the surface roughness to the thickness may be relatively large for ultra-thin sheet metals.

Not only the stress level is affected by the ratio $N$, but also the fracture strain; indeed, a decrease of the fracture strain was observed for ultra-thin sheets metals.[16,16,19] For large values of $N$, the behavior of the material can be considered as homogeneous up to necking, then inhomogeneous with plastic strain localized in a band and rupture takes place in the necking band, whereas for $N \approx 3$ , there is a rupture prior to the development of a necking band with a surface of rupture perpendicular to the tensile direction.[11,19] Klein et al.[24] explained this size effect on the fracture strain on the basis of different textures; however, such an influence is still not clearly understood. Indeed, the decrease of the fracture strain with decreasing thickness can also be explained by a significant increase of the surface roughness at higher strains[25] and by the decrease of the specimen thickness down to the grain size.[26] On one hand, Mizuto and Mulki[25] showed that at high strains but before crack occurrence, the evolution of surface roughness is no longer linear with deformation. An abrupt increase of the surface roughness was observed in the tensile test of commercial low carbon steel sheets of 0.7-mm thickness. In the case of ultra-thin sheet metal, this abrupt increase may enhance crack development. On another hand, based on the study performed by Fu et al.,[26] the decrease of the fracture strain with the decrease of $N$ can be explained based on the fact that only a few slip systems can be activated to accommodate the deformation process when there is only a few grains in the specimen thickness. Inhomogeneous deformation thus occurs and the distribution of plastic strain becomes non-uniform along the gage length. Surface roughness acts as strain concentrator and therefore induces premature fracture.

Therefore, there are specificities of ultra-thin sheets that demand further investigation of their mechanical behavior.[26] However, from a macroscopic point of view, the mechanical behavior of metallic sheets is usually modeled within a large deformation framework and using elasto-plasticity. During stamping and springback processes of ultra-thin stainless steel 304, the material is affected by various deformation modes such as stretching, bending, and unbending.[7] At the macroscopic scale, this material exhibited a significant Bauschinger effect, and mixed hardening should be considered to represent its mechanical behavior.[27] In order to increase the accuracy of the numerical prediction, in particular for springback, it is also necessary to take into account the evolution of the unloading slope with the equivalent plastic strain.[28] Therefore, a database to determine the mechanical properties of a metallic sheet should include loading–unloading steps in tension as well as loading, reverse loading sequences in simple shear test.[29]

The objective of this study is to characterize the behavior of an ultra-thin stainless steel of 0.15-mm thickness in order to investigate twisting phenomenon by finite element simulation.[30,31] For this objective, conventional tests such as tensile and simple shear tests were performed very carefully and with necessary adaptations due to the small thickness. The influence of the sample width on the stress level and fracture strain was investigated by using two different standards of test specimen, i.e., ASTM E8 and ISO 6892-1. In order to characterize the behavior of the material, the initial elastic modulus and the unloading behavior with increasing plastic deformation were evaluated during dedicated loading–unloading tensile tests. The contribution of the kinematic hardening was determined by inversion of the load in simple shear. Material parameters of a phenomenological elasto-plastic model were identified from tensile and simple shear tests. In parallel, the surface roughness evolution with the equivalent plastic strain as well as the mechanism of the ductile fracture of ultra-thin sheet metal was studied. The evolution of surface roughness during plastic deformation was measured in both tension and simple shear test. Its effect on the ductile fracture behavior and on the stress–strain curve of thin sheet stainless steel was discussed.

2 Material and Experimental Procedure

The material is an austenitic stainless steel provided by the ArcelorMittal company of AISI 304 type (X4CrNi18-9). The material was supplied as cold-rolled sheets of 0.15-mm thickness, in coils of 28 mm width in a shining annealed final state. The specimens for both tension and simple shear tests were cut in the rolling direction (RD), which were aligned with the band length. They were cut by electron discharge machining in the case of tension and by mechanical cutting in simple shear. The chemical composition of the material is given in Table I.

Table I Chemical Composition in Weight Percent of Material AISI 304

2.1 Microscopic Observations

Microstructure plays a leading role in the definition of the behavior of the material, particularly for ultra-thin sheets.[32] The microstructure of AISI 304 stainless steel in the initial state was examined with an Olympus optical microscope. Specimens were directly cut in the sheet at different positions: either near the edge, or in the middle of the band. The grain size, both on the surface and in the thickness of the sheet, was measured after etching using Glyceregia etching solution.[33]

Fig. 2

Microstructure of stainless steel AISI 304 in the initial state: (a) in the sheet plane and (b) in the thickness

The grain size $d$ and the ratio of specimen thickness to grain size (N) were measured according to the E112-10 ASTM standard.[34] An average grain size of approximately 19 μm and average grain surface of 335 μm² were determined (Figure 2). It corresponds to about 8 grains through the thickness of the sheet. This means that this material is expected to exhibit ultra-thin sheet specificities, i.e., scatter of process variables,[15] decrease of the flow stress,[17] occurrence of inhomogeneous deformation,[35] increase of springback,[39] and decrease of formability.[37]

2.2 Strain and Load Measures

Tensile and simple shear tests were carried out using a non-contacting Digital Image Correlation (DIC) system ARAMIS (GOM GmbH). Two cameras were used and 3D correlation was performed, in order to check the out of plane displacements that remain very small during the tests. A white coat of paint was deposited over the specimen surface and then a pattern of black dots. The pixels of the digital cameras were distributed into small groups called facets (Figure 3(a)), and then the software computed the displacement field by calculating the relative movements between the facets (Figure 3(b)). Each facet became a data point. The default facet size was 15 × 15 pixels with a facet step of 13 pixels, which means the facets overlapped each other by 2 pixels. When using a large facet size, there is a spatial averaging of the strain, leading to a smoother evolution; however, any local deformation within the facet is then ignored and a small facet size captures the localized effect better. However, the facet size should not be smaller than the dot size. Moreover, with more pixels overlapping (smaller facet step), more data points are calculated.

Fig. 3

Measurement with the DIC system: (a) Facet field (green) and overlapped area (red) (b) computation of the displacement (c) influence of facet size for ASTM E8 specimen (d) dispersion of strain measure illustrated in the case of loading–unloading slope (Color figure online)

Figure 3(c) presents the evolution of the longitudinal strain component $\varepsilon _{22}$ along three longitudinal sections, for the specimen in tension, using different facet sizes. It shows that the facet size of 0.60 × 0.60 mm² with 0.18 × 0.08 mm² overlapping area in the initial stage captures the evolution of the strain component. This value is a compromise between accuracy and computation time. It is sufficiently small so that the movements between elements can be captured and also large enough to limit the computation time. The dispersion of the DIC measure in the case of a tensile test was then investigated. Three different areas on the same tensile sample were selected for calculating the strain average. The stress–average strain curves corresponding to these areas in the elastic domain are plotted in Figure 3(d) and it shows that the dispersion is $\Delta \varepsilon = 1\times10^{-4}$.

Tensile tests were carried out on Instron 5566 tensile testing machine with a load cell of maximum capacity 10 kN. The load measurement accuracy of this machine is $\Delta \mathrm{F}={\pm }0.4$ pct of reading down to 1/100 of load cell capacity and $\Delta \mathrm{F}={\pm }0.5$ pct of reading down to 1/250 of load cell capacity.[38] In the case of tensile test, with a maximum force of 1310 N for ISO 6892-1 test specimen or 630 N for ASTM E8 test specimen, the error of force is less than 5 N, and the incertitude of Young’s modulus is smaller than ±6 GPa (Figure 3(d)). These results show that the equipment can be used to realize these tests with a good accuracy.

2.3 Uniaxial Tension

2.3.1 Monotonic tests

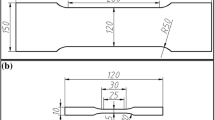
To study the influence of the geometry of the test specimens on the behavior of the material, two types of specimen were prepared according to ISO 6892-1 standard[40] (Figure 4(a)) and ASTM E8 standard[41] (Figure 4(b)). Specimens were cut in the rolling direction. These geometries were chosen in order to obtain a similar ratio between the gage length and width of both specimens (5.3 for ASTM E8 and 4.8 for ISO 6892-1). Before the test, a pre-load corresponding to a stress $\sigma _{0} = 20$ MPa was applied in order to flatten the sample. The tests were performed at room temperature and controlled by the displacement of the grip with a crosshead speed of 3 mm/min, leading to a strain rate around 5.7 × 10⁻⁴ s⁻¹ for ISO 6892-1 and 11.5 × 10⁻⁴ s⁻¹ for ASTM specimen. In this study, strain rate sensitivity was not considered. Each type of test was performed at least three times to ensure a good reproducibility of the experiments. Both longitudinal $\varepsilon _{22}$ and width $\varepsilon _{11}$ strains were recorded during the experiments. Indices are related to the frame defined in Figure 5.

Fig. 4

Specimen of uniaxial tensile test: (a) ISO 6892-1, (b) ASTM E8. The measurement zone is limited to the green (or shaded if printed in black and white) (c) bending of the specimen head under the grips

Because of the very small sheet thickness, the head of specimen was bent two times to ensure an homogeneous clamping and avoid any slip under the grip (Figure 4(c)). The strain was calculated by choosing a measurement zone on the surface of the test specimen. This measurement zone was determined in the vicinity of the fracture and over the entire width of the specimen. The length of this zone was determined by considering the effective length of the specimen (12.5 mm for ISO 6892-1 and 7 mm for ASTM E8, Figure 4). The logarithmic strain was chosen as a measure of deformation.

The strain distribution over all the gage area of the test specimen was also analyzed. Three sections at a different position along the width of the test specimen were used to evaluate the uniformity of the elongation during the test (Figure 5).

Fig. 5

Local strain field measured by the DIC system over the whole sample surface, at the end of the test, before rupture occurred. The three longitudinal sections used to output results are shown in black (section 1), red (section 5), and green (section 9) (Color figure online)

Scanning electron microscopy (SEM) observations, with Jeol 6460 LV microscope, were performed to observe the fracture surface of samples ISO 6892-1 standard. Sample preparation and measurements were done according to Reference 42.

Finally, the surface roughness was measured by contact with TR100 surface roughness tester, along a length of 2.5 mm. The surface roughness $R_{z}$ was then evaluated.[11]

2.3.2 Sequential loading–unloading tests

Testing conditions for the sequential loading–unloading tests were similar to that of monotonic tensile test. Only the specimen corresponding to ISO 6892-1 standard was used. The sequential loading–unloading tensile cycles consisted of four steps: (1) continuous loading to a prescribed pre-strain, (2) interruption by crosshead stop, (3) continuous unloading down to the pre-load, and (4) reloading up to the next cycle. Five different tests were performed in order to check the reproducibility of the results.

Three cycles of loading–unloading were performed in the reversible strain range in order to determine the initial elastic modulus or Young’s modulus E. Then, loading–unloading–reloading sequences were imposed with a control on the load level. The evolution of the loading–unloading slope with the plastic strain was then evaluated with a deformation increment about 0.05 up to failure (Figure 6(a)). The chord modulus $E_{\text{U}}$ was defined as the slope of a straight line connecting the intersection point of unloading curve with loading curve of the next cycle and the end point of the unloading stress–strain curve corresponding to $\sigma _{0} = 20$ MPa, as illustrated in the magnified area displayed in Figure 6(b).[43]

Fig. 6

Loading–unloading–loading cycles: (a) description of the full test (b) definition of the chord modulus $E_{\text{U}}$ on a magnified view

2.4 Simple Shear Test

The simple shear tests were carried out with a dedicated device developed in the laboratory,[44] which was installed on a Instron 8803 testing machine, with the DIC system to measure the strain field. Rectangular specimens of dimensions 28 × 18 mm² were cut directly in the band length. During the shear test, buckling phenomenon can occur in the width of the gage area, caused by the stress perturbations induced by the clamping.[45] In order to minimize this phenomenon, the gage width over thickness ratio h/t should be reduced as much as possible. In the case of ultra-thin sheet metal, with 0.15-mm thickness, this phenomenon occurred when the width of the gage area was above 1.4 mm. This corresponded also to the minimal value for the width that gave enough space to perform strain measure with the DIC system. The specimen size in simple shear test is presented in Figure 7(a). Moreover, buckling was reported for a higher gage width (2.2 mm) as displayed in Figure 7(b).

Fig. 7

Geometry of the specimen in simple shear test (a) dimensions of the specimen in this study with a gage width of 1.4 mm (b) buckling phenomenon with gage width of 2.2 mm. The red arrows indicate the direction of the applied load (Color figure online)

The deformations in the sheet plane were measured by the DIC system (Figure 8). The parameter γ, that describes the kinematics of a simple shear test[29] was calculated from the component $\varepsilon _ {12}$ of Green–Lagrange strain tensor: $\gamma = 2\varepsilon _{12}$. Direction $\overrightarrow{1}$ is parallel to the shear direction and $\overrightarrow{2}$ is perpendicular in the sheet plane as defined in Figure 7(a). The shear stress $\sigma _{12}$ is defined by $\sigma _{12} = F \diagup S_{0}$ with $S_{0}= L_{0}t_{0}$, F the load during the test, $S_{0}$ the initial gage section, $t_{0}$ initial thickness, and $L_{0}$ initial length of the specimen.

Fig. 8

Isovalues of $\varepsilon _{12}$, which is the component of Green–Lagrange strain tensor on the surface of specimen, at the end of the monotonic test. Visualization of the chosen sections, all three being parallel to the shear direction and evenly distributed along the width direction

Monotonic and cyclic tests were both performed in simple shear in order to highlight the Bauschinger effect and to quantify the kinematic hardening contribution. These tests were composed of a loading up to several values of $\gamma$ then unloading followed by a reloading in the opposite direction. Each type of test was performed at least three times to ensure good reproducibility of the results. The tests were carried out at a low strain rate ($\dot{\gamma } = 1.2\times10^{-2}\, {\text{s}}^{-1}$), thus limiting the rise in temperature caused by the plastic deformation. To check the homogeneity of the deformation, three cross sections were selected on the surface of the test specimen (Figure 8).

3 Results and Discussion

3.1 Monotonic Uniaxial Tensile Test

The stress–strain curves for the different types of samples (ISO 6892-1 and ASTM E8) are presented in Figure 9. A good reproducibility of both the initial yield stress (R _p0.2) and the tensile strength (R _m) was observed for both geometries. A total elongation A of 53.1 ± 3 pct was measured; it must be emphasized that it corresponds to an average value over a rather large area and when considering a smaller area of length 1 mm, a maximum longitudinal strain of 0.6 was recorded. The maximum average strain is the same for both types of specimen, although there is a slight dispersion of the results. The behavior of the material does not depend on the geometry of the specimen, when the ratio length over width was kept to a constant value. Moreover, such a value ensures that a uniaxial stress state is applied in the central zone.

Fig. 9

Stress–strain curves for the two geometries, ISO 6892-1 and ASTM E8

Three sections were used to measure the distribution of the deformation according to the specimen width (Figure 5). Figure 10 shows that the strain was homogeneous along the width of the test specimen but varied significantly along the length. The maximum local strain value reached before fracture ($\varepsilon _{\text{max}}$) was 0.61, which was higher than the average value of 0.46 shown in Figure 9. Furthermore, it can be seen that the evolution of the deformation along the length of the test specimen is very close for the three sections.

Fig. 10

Distribution of strain component $\varepsilon _{22}$ along the width and length of the test specimen ISO 6892-1. $\varepsilon _{\text{av}}$ is an average value of the longitudinal logarithmic strain over a central area, whereas $\varepsilon _{\text{max}}$ corresponds to the maximum value reached

The mechanical properties obtained from the stress–strain curves are given in Table II. The measured results were then compared with results obtained for materials with similar chemical composition but different thicknesses.[16] The lower values of both the initial yield stress R _p0.2 and tensile strength R _m of this material confirmed the phenomenon “smaller is weaker” that appears when the thickness of the sheet decreases.[46] Table II also shows the elongation of the specimen.

Table II Mechanical Properties of the Ultra-thin Sheet Stainless Steel AISI 304 Compared with Those Obtained for Thicker Material in Literature

3.2 Simple Shear Test

Figure 11 shows the distribution of γ along the length of the specimen, for three different sections presented in Figure 8. It was found that with a gage width h = 1.4 mm, the buckling phenomenon did not occur and the deformation was homogeneous in the center of the specimen. These results also highlighted the boundary effects near the free edges. Indeed, it was observed that $\varepsilon _{12}$, and then γ, tends to zero close to the free edges of the specimen (Figure 8). Therefore, the deformation $\varepsilon _{12}$ was calculated as an average value in a central region further limited by sections 1 and 3 over the width.

Fig. 11

Distribution of γ along the width and length of the test specimen

Fig. 12

Monotonic and Bauschinger shear tests: magnitude of kinematic hardening. Dotted line corresponds to the straight line when $\sigma _{12} < 0$, but with curves flipped around the unloading point

Figure 12 shows the evolution of $\sigma _{12}$ as a function of γ for monotonic and Bauschinger shear tests. The reverse loading curves corresponding to each Bauschinger test were also flipped around the unloading point in order to highlight the magnitude of the Bauschinger effect. It can be seen that, for both pre-strains, the material exhibits a significant Bauschinger effect: a rounded yield point, a reloading yield stress lower than the one reached during the pre-strain and a softening during reverse flow. For this material, gaps $\Delta _{0.1} = 60$ MPa and $\Delta _{0.2} = 80$ MPa for reverse deformation γ = 0.1 and 0.2, respectively, between monotonic and Bauschinger curves were recorded.

3.3 Plastic Behavior Identified from Tensile and Simple Shear Tests

In order to investigate twisting phenomenon by finite element simulation, an elasto-plastic model based on mixed hardening associated to the von Mises yield criterion was considered. Indeed, Figure 12 shows that this material exhibits a significant kinematic hardening. Moreover, plastic anisotropy coefficients were calculated in the rolling and transverse directions (from specific tensile tests on small length specimen) and similar values, close to 0.9, were obtained. Therefore, the assumption of an isotropic yield criterion seems reasonable.

The model is already implemented in the Abaqus finite element code, within the large transformation framework. A scalar variable R describes the isotropic hardening and is associated to the equivalent plastic strain $\overline{\varepsilon }^{p}$; a second-order tensor ${\varvec{X}}$ describes the non-linear kinematic hardening according to Chaboche-Ziegler model. The yield criterion is written as $\overline{\sigma } \left( \varvec{\sigma }, \varvec{X} \right) = R,$ where $\overline{\sigma }$ is the equivalent stress, $\varvec{\sigma }$ is the Cauchy stress tensor, and $\overline{\sigma } =\sqrt{3/2 \varvec{\sigma } : \varvec{\sigma }}$. The evolution of R with the equivalent plastic strain is represented with a saturating Voce type (Eq. [1]).

$$\begin{aligned} R = \sigma _{0} + Q \left( 1-\exp \left( -b \overline{\varepsilon }^{p}\right) \right) \end{aligned}$$

(1)

with $\sigma _{0}$ the initial yield stress and $Q, b$ scalar material parameters. To fully capture the evolution of the work hardening after strain path reversal, the kinematic hardening ${\varvec{X}}$ is split into two terms ${\varvec{X}}_{1}$ and ${\varvec{X}}_{2}$, the evolution laws of which are given by Eq. [2].

$$\begin{aligned} \varvec{X}&= {} \varvec{X}_{1} + \varvec{X}_{2} \nonumber \\ \dot{\varvec{X}}_{1} &= {} \frac{C_{1}}{\overline{\sigma }}(\varvec{\sigma } - \varvec{X})\dot{\overline{\varepsilon }}^{p} - \gamma _{1}\dot{\overline{\varepsilon }}^{p}\varvec{X}_{1} \nonumber \\ \dot{\varvec{X}}_{2} &= {} \frac{C_{2}}{\overline{\sigma }}(\varvec{\sigma } - \varvec{X})\dot{\overline{\varepsilon }}^{p} - \gamma _{2}\dot{\overline{\varepsilon }}^{p}\varvec{X}_{2}, \end{aligned}$$

(2)

where $C_{i}$ and $\gamma _{i}$ , $i =1,2$ are scalar material parameters and $\dot{\overline{\varepsilon }}^{p}$ is the rate of the equivalent plastic strain.

A finite element model with only one elementary brick element, a cube of side 1 mm, defined in Abaqus software with boundary conditions corresponding either to homogeneous tension or homogeneous simple shear, was used to identify the material parameters. A direct identification of material parameters was performed, based on the trial and error method. As the number of experimental tests is moderate (4), this simple procedure appeared to be very effective, as can be seen in Figure 13. Moreover, concerning the two terms for kinematic hardening, one was chosen to saturate very rapidly (γ ₁) and the second one was imposed a slower evolution with the equivalent plastic strain (γ ₂). It can be seen that the model gives a good description of the mechanical behavior of the material both in tension and simple shear. Parameters of this model are given in Table III. This figure also shows that the kinematic contribution to the hardening is significant, as highlighted by a comparison with a pure isotropic hardening model.

Table III Material Parameters for the Mixed Hardening Model, Identified from Tensile and Simple Shear Tests

Fig. 13

Comparison of the stress–strain curves predicted by the mechanical model with the experiments for uniaxial tensile test, monotonic and Bauschinger simple shear tests. Predictions with an isotropic hardening model are also added, out of comparison’s sake

3.4 Loading–Unloading Tests

Sequential loadings–unloadings in the elastic domain were performed in order to determine Young’s modulus of the ultra-thin sheet metal. However, great care has to be taken on the alignment and the design of the gripping systems. The value of Young’s modulus determined by this procedure in the recoverable range is $E_0 = 206.2$ GPa with a dispersion smaller than 5 pct (Figure 3).

Within the plastic strain range, when the material is unloaded from the stress $\sigma _{\text{U}}$, the unloading curve follows a non-linear path as shown in Figure 6(b). As a result, the total recovered strain during unloading can be divided into two components, namely, linear elastic and non-linear elastic strains,[43] as expressed in Eq. [3].

$$\begin{aligned} \varepsilon _{\text{recovered}} = \varepsilon _{\text{elastic}} + \varepsilon _{\text{non-elastic}} = \frac{\sigma _{U} - \sigma _{0}}{E_0} + \varepsilon _{\text{non-elastic}}, \end{aligned}$$

(3)

where $\sigma _{0}$ is the residual stress after recovery.

Figure 14 shows that the non-linear elastic strain is a more and more important contribution to the total recovered strain. It can reach up to 30 pct of $\varepsilon _{\text{recovered}}$. As this phenomenon can result in the underestimation of springback,[53] the chord modulus is sometimes used in the numerical prediction of forming processes,[28] as a way to compensate for the very small recovered strain predicted by linear elasticity model. Figure 15 shows the evolution of the chord modulus with the equivalent plastic strain. These results are similar to those observed by Yamaguchi et al.[51] and Vrh et al.[52] Such an evolution can be represented by Eq. [4]

$$\begin{aligned} E_{U} = E_{0} - \left( E_{0} - E_{\text{sat}} \right) \left[ 1 - \exp \left( -\xi .\overline{\varepsilon }^{p}\right) \right] \end{aligned}$$

(4)

with $E_{\text{sat}}$ = 147 GPa and $\xi$ = 45.

Fig. 14

Evolution of the recovered, linear elastic, and non-linear elastic strains according to the pre-stress ($\sigma _{\text{U}}$)

Fig. 15

Degradation of chord modulus with the increase of the equivalent plastic strain. The several sets of points represent results for the five tests performed on different samples

Chord modulus evolution was introduced in the finite element model as an evolution of the elastic modulus with the equivalent plastic strain. Figures 16(a) and (b) show the comparison of the predicted tensile stress evolution during loading–unloading–loading sequences with experimental values, when using Eq. [4]. This comparison was performed only to check out that chord modulus evolution associated to the elastic-plastic model described above gave indeed a good prediction of the stress evolution. Figures 16(c) and (d) show then the validation of the model for simple shear. Though the experiments are clearly dispersed within such a small strain area, the taking into account of the decrease of the chord modulus significantly improved the numerical prediction. It can be concluded that mixed hardening associated to the von Mises isotropic yield criterion and chord modulus evolution gives a good representation of the mechanical behavior of AISI 304 ultra-thin sheet material, both in monotonic tension and simple shear as well as cyclic simple shear. Such a model was used in the prediction of 2D springback and twisting.[54]

Fig. 16

Verification and validation of the mechanical model in tension and simple shear. Results presented in (a) and (b) were used in the material parameter identification step, whereas (c) and (d) show a validation of the model in simple shear

3.5 Surface Roughness in Tension and Simple Shear

In the finite element simulation of forming processes, considering both loading and springback steps, the modeling of the mechanical behavior is a key point. When considering ultra-thin sheets, the free surface roughness evolution with the plastic strain may alter significantly the thickness and therefore the stress calculation. This influence is investigated in this section.

Figure 17(a) shows the evolution of the surface roughness R _z with the equivalent plastic strain $\overline{\varepsilon }^{p}$, as measured over the free surface of samples deformed in tension and simple shear. It was found that the surface roughness increased linearly with the equivalent strain during both tests. For the same value of the equivalent plastic strain, the surface roughness in the case of simple shear test was close to that in tension. The surface roughness of this material can be represented with a linear dependence to the equivalent plastic strain, as written in Eq. [5].

$$\begin{aligned} R_z = R_0 + C\overline{\varepsilon }^{p} \end{aligned},$$

(5)

where C = 10.2 or 10.8 μm in tension and simple shear, respectively, and depends on the grain size of the material.[11,20] R ₀ = 1.4 μm is the initial roughness of the sheet.

In the case of simple shear, the thickness remained constant, whereas in tension, the thickness decreased with the increase of the longitudinal strain. The ratio of the surface roughness to the actual thickness $\displaystyle \frac{R_z}{t}$ is interesting to consider in this case. Figure 17(b) shows the relationship between this ratio and the equivalent plastic strain for both tests. This figure shows that this ratio is very close in tension and simple shear. This relationship can be represented by a trend line and expressed by Eq. [6]. This result shows that at $\overline{\varepsilon }^{p} = 0.5$, this ratio can reach up to 6.5 pct, meaning that the surface roughness represents 6.5 pct of the thickness of the material and its influence may not be neglected during the test.

$$\begin{aligned} \frac{R_z}{t} = 0.009 + 0.075 \overline{\varepsilon }^{p} \end{aligned}.$$

(6)

Fig. 17

Evolution of (a) surface roughness $R_{z}$ with $\overline{\varepsilon }^{p}$ and (b) ratio of surface roughness to thickness ${R_{z}}/{t}$ with $\overline{\varepsilon }^{p}$, both in tension and simple shear

The following part of this section is dedicated to a tentative quantification of the influence of surface roughness on the stress level in tension in the case of ultra-thin sheet. The basic idea is that the measured thickness t _m corresponds to a maximum value, e.g., the distance between highest points as illustrated in Figure 18(a). When the thickness decreases down to 0.1 mm, there are usually only a few grains in the thickness. Furushima et al.[11] showed that the concave part formed by grains in the vicinity of the free surface with a lower flow stress in the initial tensile stage became deeper with the deformation (Figure 18(b)). These concavities tended to decrease the effective thickness of the specimen. This decrease is visualized by the hatched area in Figure 18(a). To take this phenomenon into account, it is proposed here to calculate this effective thickness as an average value between the highest and the lowest points on the surface. The details are given below.

During the test, the actual thickness $t_\varepsilon$ can be calculated using the volume conservation assumption:

$$\begin{aligned} t_\varepsilon = \frac{S}{w} = \frac{S_{0}.\exp (-\varepsilon _{l})}{w_{0}.\exp (\varepsilon _{w})}, \end{aligned}$$

(7)

where w stands for the actual width of the specimen and w ₀ its initial value. The effective thickness, defined as an average position between highest and lowest positions on the surface, which is bounded by the two blue (dotted) lines in Figure 18(a), can be calculated with Eq. [8]; this calculation represents an average value in the sense that peaks and depressions over the surface level out around the average level of the oscillations.

$$\begin{aligned} t_{\text{eff}} = t_\varepsilon - 2 \cdot \frac{R_z}{2} = t_\varepsilon - R_z. \end{aligned}$$

(8)

Therefore, the Cauchy stress is given by Eq. [9]:

$$\begin{aligned} \sigma = \frac{F}{w (t_\varepsilon - R_z)}. \end{aligned}$$

(9)

As the surface roughness depends on the grain size d but not on the thickness t of the sheet, Eq. [9] shows that, when $t_\varepsilon \gg R_z$ e.g., for thin sheet or plate, the role of $R_z$ may be negligible, whereas for ultra-thin sheet, this role may become non-negligible. The effective thickness of the specimen deformed in tension can be calculated by combining Eqs. [7] and [8] as

$$\begin{aligned} t_{\text{eff}} = \frac{S_{0}\cdot\exp (-\varepsilon _{22})}{w_{0}\cdot\exp (\varepsilon _{11})} - \left( R_0 + C\cdot\varepsilon _{22} \right). \end{aligned}$$

(10)

The cross section of the test specimen is modified in uniaxial tension, with $\overline{\varepsilon }^{p} = \varepsilon _{22}$:

$$\begin{aligned} S = S_{0}\cdot{\text{exp}}(-\varepsilon _{22})- {w_{0}\cdot{\text{exp}}(\varepsilon _{11})}\cdot\left( R_0 + C\cdot\varepsilon _{22} \right). \end{aligned}$$

(11)

Fig. 18

Relationship between surface roughness and thickness (a) modification of thickness calculation when considering surface roughness (b) change in surface roughness along a profile during deformation[11]

Table IV shows the values of the different thicknesses introduced above, i.e., $t_\varepsilon$ using Eq. [7] and t _eff given by Eq. [10]. Moreover, the experimental value t _m was also measured with a micrometer with an accuracy of 1 μm. For each measure of t _m, a length of 12.5 mm along the sample in the initial state was selected. The deformation of this zone was measured by DIC and the average strain was determined. The thickness of the specimen is therefore the average value throughout the length of this zone. It can be seen that the values of t _m and $t_\varepsilon$ are similar (t _m $\simeq$ $t_\varepsilon$). The values of the effective thickness t _eff are always smaller than t _m and $t_\varepsilon$ (t _eff < t _m, $t_\varepsilon$).

Table IV Variation of the Surface Roughness with the Longitudinal Strain and Values of the Different Thicknesses in Tension

The stress modified by taking into account the surface roughness, via the decrease of the thickness according to Eq. [9], is plotted in Figure 19. Moreover, to confirm the influence of the surface roughness on the mechanical behavior of the ultra-thin sheet, tensile tests performed for a sheet of 0.8-mm thick with a similar chemical composition and grain size were used.[47] The results shown in Figure 19 exhibit a significant deviation when not taking into account the roughness (i.e., using $t_\varepsilon$), whereas the stress level modified by the surface roughness (i.e., using t _eff) is closer to the thicker material flow stress, up to a longitudinal strain around 0.5. It should be emphasized that such a stress calculation does not capture local stresses due to the stress concentrations arising from the surface asperities but an average macroscopic stress over an effective thickness that is lower than the actual measured thickness. Such an assumption should be further investigated with the aid of finite element simulations of grain aggregates, as presented in Reference 11.

The same method was used for the simple shear test. In the case of tension, the deviation between the two curves (with and without taking into account the surface roughness) is significant, whereas in the case of simple shear test, deviation is lower and may be neglected.

Fig. 19

Stress–strain curves in tension and simple shear, either taking into account a thickness decrease due to roughness (W-roughness) or neglecting this effect (W/O-roughness)

3.6 Rupture in Tension

Rupture was investigated in tension only because, in the case of simple shear, it occurred under the grips and therefore did not reflect rupture in simple shear. Moreover, SEM observations were performed only for the ultra-thin sheet sample. Figure 20 shows the fracture of the two types of samples, i.e., ISO and ASTM; after uniaxial tension, It was found that the failure occurred rapidly after necking in the transverse direction and the fracture surface is perpendicular to the tensile direction; this phenomenon seems to be typical for ultra-thin sheets[11] and can be also explained by the decrease of specimen size down to a few grain size[26] and non-linear evolution of the surface roughness at high strains.[25] Figure 10 shows a large strain concentration before fracture, in the specimen center, and this concentration is homogeneous along the width of the test specimen. At concave areas formed by free surface roughening, local deformation occurs before macroscopic necking phenomenon in the sheet plane and leads to premature fracture before reaching the limiting uniform elongation at the maximum tensile stress based on plastic instability theory.[11]

Fig. 20

Fracture of specimen after uniaxial tensile test (a) ISO 6892-1, (b) ASTM E8 specimens

Figure 21 shows a side view of SEM observation of the fracture surface, in the thickness direction, and shows that there is no observable necking in the thickness. Whereas for thin sheets of aluminum alloys of thickness 2.3 mm[55] and 1.6 mm,[56] a continuous slant fracture surface was observed, and it can be seen that for the material of this study, the fracture surface is alternately oriented at $\pm 45$ deg to the tensile direction.

Fig. 21

(a) Orientation of the fracture surface in the thickness (b) orientation at 45 deg to the tensile direction

At a higher magnification (Figure 22), two areas can be clearly identified, the one close to the free surface and the one in the middle, with dimples typical of ductile rupture by void growth and coalescence mechanism. However, it is not possible at this stage to conclude in which area the crack starts. It can therefore be concluded that rupture of ultra-thin sheets in tension exhibits specific features like a fracture surface perpendicular to the tensile direction in the sheet plane and displaying a non-continuous inclination at ±45 deg in the sheet thickness.

Fig. 22

Fracture surface in uniaxial tension of the very thin sheet sample, observed by SEM

4 Conclusions

Tension and simple shear tests were conducted to investigate the mechanical behavior at room temperature and in quasi-static conditions of an ultra-thin stainless steel sheet AISI 304. Monotonic tests as well as loading–unloading–reloading sequences were carried out in uniaxial tension, in order to measure the classical mechanical properties and the chord modulus after prescribed pre-strains. Monotonic and cyclic tests in simple shear were realized to determine the contribution of the kinematic hardening. Material parameters of an elasto-plastic model combining mixed hardening and isotropic yield criterion were identified from the experimental database. The evolution of the surface roughness was studied using both tests, and its influence on the stress level and the fracture of the specimen in tension was investigated. The following conclusions can be drawn.

First of all, conventional tests such as tension and simple shear can be used to determine the mechanical behavior within the small strain range (≤0.2) for ultra-thin sheet materials. Indeed, the ratio of the surface roughness, which evolves linearly with the equivalent strain, to thickness $R_z/t$ was small and its influence can be neglected. However, for large strains, surface roughness tends to decrease the effective thickness, leading to modifications on the stress level.

Secondly, the contribution of the total recovered strain, as linear and non-linear elastic strain, in tension, was considered. The non-linear elastic strain component was proportional to the unloading stress. In order to compensate the classical underestimation of springback, the chord modulus was measured. As plastic strain increased, the chord modulus significantly decreased by as much as around 30 pct from its initial value. A very rapid evolution was observed at low strain levels and saturation occurred after a moderate plastic strain of about 15 pct.

Then, an elastic-plastic model based on a mixed hardening, the von Mises yield criterion and the evolution of the elastic modulus, was used to represent the mechanical behavior of the material both in tension and simple shear. Such a representation gives reliable predictions in the case of finite element simulations of forming processes involving springback.[54]

Moreover, within the large strain range in tension, and according to surface roughness, the conventional stress calculation from the average thickness may not be valid any longer. The surface roughness can reach up to 6.5 pct of the thickness specimen and it leads to a decrease of the actual thickness. This decrease influences the stress level calculation.

Finally, the fracture of the specimen before occurrence of diffuse necking in both the thickness and width was observed. The fracture surface is macroscopically perpendicular to the tensile direction. The evolution of the surface roughness and the material inhomogeneity in the thickness can explain such a premature rupture compared to a thicker material, but further work should be performed to model this phenomenon.