Electrical and thermal conductivity of Earth’s core and its thermal evolution—A review

Abstract

The Earth’s core is composed of iron, nickel, and a small amount of light elements (e.g., Si, S, O, C, N, H and P). The thermal conductivities of these components dominate the adiabatic heat flow in the core, which is highly correlated to geodynamo. Here we review a large number of studies on the electrical and thermal conductivity of iron and iron alloys and discuss their implications on the thermal evolution of the Earth’s core. In summary, we suggest that the Wiedemann–Franz law, commonly used to convert the electrical resistivity to thermal conductivity for metals and alloys, should be cautiously applied under extremely high pressure–temperature (P–T) conditions (e.g., Earth’s core) because the Lorentz number may be P–T dependent. To date, the discrepancy in the thermal conductivity of iron and iron alloys remains between those from the resistivity measurements and the thermal diffusivity modeling, where the former is systematically larger. Recent studies reconcile the electrical resistivity by first-principles calculation and direct measurements, and this is a good start in resolving this discrepancy. Due to an overall higher thermal conductivity than previously thought, the inner core age is presently constrained at ~1.0 Ga. However, light elements in the core would likely lower the thermal conductivity and prolong the crystallization of the inner core. Meanwhile, whether thermal convection can power the dynamo before the inner core formation depends on the amounts of the proper light elements in the core. More works are needed to establish the thermal evolution model of the core.

1 Introduction

Earth’s accretion has been estimated via lead and tungsten isotopes to have started at 4.5 Ga ago (Kleine et al. 2002; Schoenberg et al. 2002; Yin et al. 2002). Subsequently, the core formation and volatile degassing shaped the history of the early Earth (the Hadean). Earth’s magnetic field has existed since 3.45 Ga ago, as indicated by the paleomagnetic records (Biggin et al. 2011; Tarduno et al. 2010), and where the dynamo is supposed to be driven by liquid-core convection. The present-day magnetic field protects our Earth from the hazard of cosmic radiation (Buffett 2000). To generate a self-sustained magnetic field, convection within an electrical current in the metallic liquid outer core (Breuer 2019) is necessary. Liquid core convection can be driven by thermal buoyancy from superadiabatic heat flows (thermal dynamo) across the core-mantle boundary (CMB) (Davies et al. 2015; Driscoll and Bercovici 2014; Nimmo 2015) or by compositional buoyancy from exsolution of the light elements (e.g., O, Si, Mg, and C) in the core (chemical dynamo) (Hirose et al. 2017; O’Rourke and Stevenson 2016). If the CMB is in a subadiabatic condition at the present day, thermal buoyancy is not sufficient to drive the convection in the core. In this case, compositional buoyancy is primarily driving geodynamo. In particular, other driving sources are required to power the Earth’s ancient geodynamo before the birth of the inner core. Moreover, the conductive heat flow from the core provides fundamental control to drive the dynamo, affects the secular cooling rate which determines the inner core’s age, and supplies energy upward to drive mantle convection (Williams 2018).

High pressure–temperature (P–T) experiments suggest that the exsolution conditions of MgO as the core cools is limited and can only power the geodynamo over a limited geological time (Du et al. 2019). Apart from the core dynamo, a silicate dynamo hypothesis in the lowermost basal magma ocean is also proposed if the electrical conductivity of the basal magma is high enough (> 10⁴ S m⁻¹) to generate an Archean paleomagnetic field (Stixrude et al. 2020). The silicate dynamo might explain the mystery of ancient paleomagnetism data. However, the large uncertainty of the thermodynamic state of the core makes it ambiguous to ascertain which mechanism dominates the geodynamo (Driscoll and Du 2019).

The thermal dynamo can be physically activated when the heat flow across the lowermost mantle (Q_CMB) exceeds that conducted along the core adiabat (Q_ad), according to the Schwarzschild criterion for convection (Schatten and Sofia 1981). Thus, thermally driven convection in the core requires that

$$Q_{CMB} > Q_{ad} = 4\pi r^{2}k_{CMB} *dT/dr|_{ad}$$

(1)

where r is the radius at the CMB, k_CMB is the thermal conductivity of the core near the CMB, and dT/dr|_ad is the adiabatic temperature gradient in the core. The temperature gradient (dT/dr|_ad) at the topmost outer core is usually taken from 0.9(0.2) K km⁻¹ (Driscoll and Bercovici 2014; Labrosse 2015). The parameter k_CMB is essential to constrain Q_ad and the heat evolution of the Earth’s core over geological time. Thus, determining the thermal conductivity (k) of the core materials through experiments and calculations becomes vital.

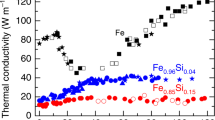
There are overall three ways to obtain the k of the core materials at conditions relevant to the Earth’s core, including electrical resistivity (ρ) measurements (ERM), first-principles calculations (FPC), and direct thermal conductivity (k) measurements (DTCM). The first two methods, ERM and FPC, are commonly used to investigate the core’s thermal conductivity because of the difficulty in performing direct measurements on the thermal conductivity at extreme pressure and temperature conditions (e.g., the Earth’s core environment). The electronic part of the thermal conductivity of metals and alloys can be obtained approximately by the ERM method based on the Wiedemann–Franz law. Although extensive efforts have been paid, there is still a large discrepancy in the core thermal conductivity obtained by different studies. In contrast to the high thermal conductivity (~ 100 Wm⁻¹ K⁻¹) of hcp-iron obtained by indirect methods (e.g., ERM and FPC) (Table 1), the DTCM method shows a smaller k (Konôpková et al. 2016, 33 ± 7 Wm⁻¹ K⁻¹ for hcp-Fe; Hsieh et al. 2020, ~ 20 Wm⁻¹ K⁻¹ for Fe-15Si (at%); Saha et al. 2020, 40 ± 16 Wm⁻¹ K⁻¹ for hcp-Fe). The possible reasons for the discrepancy including (1) The classical laws and theories might not be valid for iron under ultrahigh P–T conditions: specifically, the Wiedemann-Fran law to correlate electrical resistivity with thermal conductivity, the Bloch-Grüneisen formula to describe the relationship between resistivity and temperature, as well as the possible temperature and chemically-induced resistivity saturation due to the Mott–Ioffe–Regel limit; (2) accurate theoretical calculations in modeling the electrons moving in iron are challenging in terms of complex interactions and correlations in electrons and phonons and several other effects on conduction, such as impurity scattering, magnetic change, and electronic structure transition; and (3) direct thermal conductivity measurement at Earth’s core conditions is extremely difficult and has large errors (whether under static-loading or shock compression).

Table 1 Summary of the electrical resistivity and thermal conductivity of the Earth's core

In this review, we will present the development of techniques and methods applied to investigate the core’s transport properties, as well as the updated knowledge on the thermal conductivity of the Earth’s core (pure iron and iron-light element systems). Geophysical implications from the different thermal conductivity levels are discussed, particularly on the thermal evolution of the inner core and the geodynamo throughout Earth’s history.

2 Methods and techniques

We have reviewed three methods (ERM, FPC, and DTCM) that are broadly applied to obtain the thermal conductivity of Fe and Fe–X alloys (X is light elements, such as S, O, Si, C, P, and H) at high P–T conditions. We will explain the methods and techniques developed thus far in the following sections.

2.1 Electrical resistivity measurements of iron and iron alloys at high P–T

The electronic thermal conductivity (k_el) contributed by the electrons in the iron-based materials (Fe, Fe–Ni, and Fe-light element alloys) can be calculated from the corresponding electrical resistivity (its inverse, electrical conductivity) through the Wiedemann–Franz (W–F) law:

$$k_{el} = LT/\rho = LT\sigma$$

(2)

where L and T are the Lorentz number (ideal Lorentz number L₀: 2.445 × 10^–8 WΩK⁻²) and temperature (K), respectively. ρ and σ are electrical resistivity and conductivity, respectively. Hence, direct measurements of the resistivity of the core components at high P–T conditions make it easy to probe the thermal conductivity of the planetary core. The W–F law, however, seems to be invalid under extreme conditions like the Earth’s core because of the deviation of the Lorentz number (de Koker et al. 2012; Pourovskii et al. 2017; Righter 2002). Commonly, phonons (vibrations of atoms) and electrons transport heat in iron, but the phonon conductivity (k_ph) is typically smaller than the electron conductivity (k_el) (de Koker et al. 2012). At ambient pressure, experimental results show that k_ph in liquid iron is estimated to be ~ 3 Wm⁻¹ K⁻¹, far less than its total conductivity of 40.3 Wm⁻¹ K⁻¹ (Touloukian et al. 1970). Thus, the ERM method is a reasonable way to estimate the core’s thermal conductivity.

2.1.1 Resistivity measurement in the multi-anvil apparatus (MAA)

The multi-anvil apparatus (MAA) is commonly used to generate a stable high P–T environment and provides an in-situ way to measure the sample’s resistance, along with a four-terminal method. The electrical resistivity of the sample is then simply computed from the geometry and resistance of the sample through the formula:

$$\rho = 1/\sigma = RA/l = \left( {\Delta U/I} \right) \times A/l$$

(3)

where R is the measured resistance, A is the cross-sectional area of the sample, l is the length of the sample, ΔU and I are the measured voltage change and current, respectively. In particular, the current (I) is set to a constant value, and the voltage change (ΔU) triggered by the samples is measured. The A and l values are obtained from the recovered samples. The four-terminal method is extensively applied to measure the resistivity of pure metals (e.g., Fe, Ni, Co, Zn, Pt, and W) and alloys (e.g., Fe-S, Fe-Si, and Fe–P) at conditions of 1–26 GPa and 300–2500 K (Berrada et al. 2020; Ezenwa 2017; Ezenwa and Secco 2017a, b; Ezenwa and Yoshino 2020a, b; Littleton et al. 2019; Pommier 2018; Silber et al. 2019, 2017; Yin et al. 2019; Yong et al. 2019). To improve the experimental quality, a four-terminal method coupled with a current reversal technique was originally applied and explained in the studies of Ezenwa and Secco (2017a, b) and Ezenwa et al. (2017) who measured the resistivity of Zn, Co, and Cu in a cubic MAA (one-stage press). The current reversal technique has advantages in eliminating the contact resistance and wire resistance and could thus reduce measurement errors. Another helpful strategy to reduce contact resistance is to adopt preheating cycles before actual resistivity measurement (Ezenwa and Secco 2017a, b).

Back in 1985, Yousuf et al. (1985) designed a high P–T cell for electrical resistivity measurements, where they used a Bridgman anvil device along with a graphite heater. They measured the resistivity of Ni and Fe at pressures of 5 and 1.6 GPa, respectively (Yousuf et al. 1986). Soon after, Secco and Schloessin (1989) developed a four-terminal method coupled with a self-heating method and measured the resistivity of Fe in solid and liquid states up to 7 GPa. In recent years, extensive work has been conducted to improve the resistivity measurements in the MAA. Kiarasi (2013) developed H- and Z-shaped configurations and measured the resistivity of Fe and Fe–Si alloys up to 5 GPa in a cubic MAA. Deng et al. (2013) measured the resistivities of Fe at 5, 7, and 15 GPa and high temperatures using the four-terminal method without electrodes in a Walker-type MAA. Ezenwa (2017) developed the thermocouple-resistance mode four-terminal technique in a cubic MAA (Fig. 1a). Besides, Silber et al. (2017) implemented the four-wire technique in an octahedral cell and used tungsten disks to reduce electrode-sample contamination in the electrical resistivity measurements of nickel in an MAA. Very recently, Pommier and Leinenweber (2018) showed how to adopt the four-terminal method along with Fe/Mo electrodes in an MAA to measure the sample’s resistivity. Yong et al. (2019) measured the resistivity of iron at pressures and temperatures up to 24 GPa and ~ 2400 K in octahedral cells using the four-terminal technique.

Fig. 1

modified from Ezenwa and Yoshino (2020b)

Two assembly configurations used in MAA for resistivity measurements of iron at high P–T conditions. a Four-terminal method, a sample assembly used in an octahedral cell by Silber et al. (2017), and the original design is referred to Ezenwa (2017). b Single member wire technique,

To reduce the possible contamination from electrodes during resistivity measurement, Secco and Schloessin (1989) proposed to use the same materials of electrodes as samples (e.g., iron) (Fig. 1b). A similar configuration was then adopted in the resistivity measurements in a diamond anvil cell (DAC) by Gomi et al. (2013) and Ohta et al. (2016). Ezenwa and Yoshino (2020b) followed this design and replaced W electrodes with iron to contact with Fe samples, which in principle have no contact resistance between the samples and electrodes (Silber et al. 2017, 2018; Pommier 2018). Based on this strategy, Ezenwa and Yoshino (2021) measured lower resistivities in iron than that of Yong et al. (2019) at the same P–T conditions.

Given the convenience of the resistivity measurements in an MAA, various features (such as the pressure–temperature-composition induced saturation effect and constant resistivity along the melting boundary) of the resistivity of iron and iron alloys at high P–T conditions have been carefully investigated. Kiarasi and Secco (2015) measured the resistivity of Fe–17Si (wt%) alloys up to 5 GPa, where the data show a trend of pressure-induced resistivity saturation in the Fe–Si system. Moreover, recent studies indicate a constant electrical resistivity along the melting boundary in liquid Fe and Fe–Si (4.5 wt%, 8.5 wt%) alloys at pressures up to 26 GPa (Berrada et al. 2021; Silber et al. 2019, 2018; Yong et al. 2019). Similar behavior was also found in some transition metals with electronic structures similar to iron at high pressure (Co, Ezenwa and Secco 2017b; Ni, Silber et al. 2017). Resistivity measurements for Fe-light element alloys conducted in an MAA have also extended our knowledge of the cores of terrestrial planets (Fe–Si, Berrada et al. 2020; Silber et al. 2019; Fe–S, Littleton et al. 2021, Manthilake et al. 2019, Pommier 2018; Fe–P, Yin et al. 2019). Despite being relatively low pressure and generally below 30 GPa in an MAA, the temperature is homogeneous and easily controlled during the resistivity measurements.

2.1.2 Resistivity measurement in DAC

To generate the P–T conditions relevant to the Earth’s core (> 130 GPa and 3000 K), laser-heated DAC and shock-wave compression (SC) techniques are also commonly used in the lab (e.g., Gomi et al. 2013, 2016; Matassov 1977; Ohta et al. 2016; Zhang et al. 2020). In a DAC, the resistivity measurement strategies overall fall into two groups depending on the sample geometry (Fig. 2): the four-terminal method with a bridge geometry and the four-probe van der Pauw (VDP) method with a Greek cross geometry (e.g., David and Buehler 1977). For a bridge geometry, the sample shape and thickness should be homogeneous, and any sidewall effects are negligible. The Greek-cross geometry could minimize the influence of the sidewall effect and eliminate the voltage contribution from the contact resistance. The theory and strategy of the resistivity measurement used for a bridge geometry in DAC are the same as the four-terminal method used in the MAA. The four-probe VDP method is different but reliable for measuring the resistivity of tiny sheet samples up to over 100 GPa and 4000 K in a laser-heated DAC (Zhang et al. 2020, 2021). This measurement method was well established by van der Pauw (1958) and Buehler and Thurber (1978), where the resistivity of the sample could be computed through the formula:

$$\rho = f\pi R/ln2 = \pi d\left( {R_{ > } + R_{ < } } \right) \cdot f\left( {R_{ > } /R_{ < } } \right)/ln4$$

(4)

where d, R_>, and R_< are the thickness of the sample, the measured higher resistance value, and the measured lower resistance value, respectively. f(R_>/R_<) is a function of the ratio of R_> and R_<. Uncertainties in the resistivity are related to the resistance and thickness of the samples. Four conditions must be satisfied to use this method: (1) the sample must have a flat shape of uniform thickness, (2) the sample must not have any isolated holes, (3) the sample must be homogeneous and isotropic, and (4) all four contacts must be located at the sample edge.

Seagle et al. (2013) performed resistivity measurements for iron and iron-silicon alloys at 300 K and up to 60 GPa via the four-probe VDP method in a DAC. Meanwhile, Gomi et al. (2013) applied a single-member wire (bridge geometry) as an electrode and sample to measure the electrical resistivity of iron and iron-silicon alloys to 100 GPa and 300 K in a DAC. Thereafter, Ohta et al. (2016), Zhang et al. (2020), and Basu et al. (2020) measured the resistivity of iron and iron alloys at high P–T conditions using a laser-heated DAC. The pioneering work by Ohta et al. (2016) developed a method for resistivity measurements at high P–T in a laser-heated DAC, and they observed the resistivity-saturation phenomenon of hcp-iron at ultrahigh temperatures. Zhang et al. (2020) subsequently improved the measurement method and applied a standard four-probe VDP technique in flat-top laser-heated DACs (Fig. 2a), which lowers the temperature gradient and resistivity measurement uncertainties. Meanwhile, Inoue et al. (2020) employed a four-terminal technique in an internally heated DAC (Fig. 2b) to measure the resistivity of iron and iron alloys, which significantly reduces the temperature gradient in the samples.

Fig. 2

modified from Zhang et al. (2020)]; b Schematic diagram of the experimental settings in an internally heated DAC for resistivity measurement under high P–T conditions [modified from Inoue et al. (2020)]

Experimental setups in DAC for electrical resistivity measurement at high pressure and temperature conditions. a Schematic diagram of a standard van der Pauw four-probe configuration for resistivity measurements in a DAC [

2.2 Direct measurements of the thermal conductivity of iron and its alloys

The thermal conductivity of bcc-Fe at ambient conditions was measured to be ~ 80 Wm⁻¹ K⁻¹ (Touloukian et al. 1970). Increase the temperature at ambient pressure, the thermal conductivity of iron drops to 33–35 Wm⁻¹ K⁻¹ upon the melting (Nishi et al. 2003). To date, some techniques have been developed to directly measure the thermal conductivity of iron and iron alloys in laser-heated DACs under high P–T conditions, such as time-dependent finite-element models (Konôpková et al. 2011), pulsed light heating thermoreflectance techniques (Yagi et al. 2010), and ultrafast time-domain thermoreflectance (TDTR, Hsieh et al. 2017).

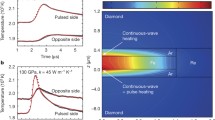
Using time-dependent finite-element models along with a laser-heated DAC, Konôpková et al. (2016) estimated k for pure Fe to vary from 33 ± 7 Wm⁻¹ K⁻¹ under CMB conditions (T = 3800–4800 K, P = 136 GPa) to 46 ± 9 Wm⁻¹ K⁻¹ under ICB conditions (T = 5600–6500 K, P = 330 GPa). In the work of Konôpková et al. (2016), the temperature on the top of the sample varies as a function of time, as derived from time-resolved spectroradiometric measurements, in which a laser pulse impinges on the bottom surface of an iron foil held within the laser-heated DAC (Fig. 3a). The thermal emission is monitored on the top side of the foil and the bottom (laser pulse) surface, to which the pulse has been transmitted by a thermal pulse within the sample (Fig. 3a). Then, using appropriate parameters to fit the curve of the time-dependent temperature variations, the thermal conductivity of the sample could be easily modeled (Fig. 3a). Measuring the thermal diffusivity using the pulsed light heating thermoreflectance technique (Yagi et al. 2010) in a DAC, Ohta et al. (2018) estimated the thermal conductivity of hcp-Fe at 16.0–44.5 GPa and room temperature. By modeling the temperature gradient in a cylindrical iron plate heated by a small heat source at its center in a DAC (Fig. 3b), Saha et al. (2020) estimated the k of solid iron to be 55 ± 22 Wm⁻¹ K⁻¹ at the Earth’s CMB and a likely k of 40 ± 16 Wm⁻¹ K⁻¹ for a liquid iron outer core. Combining ultrafast time-domain thermoreflectance with the DAC technique (Fig. 3c), Hsieh et al. (2020) measured the thermal conductivity of pure Fe (single-crystal and powder) and Fe-Si alloys (powders) up to 120 GPa at room temperature. Their results favor a low estimate of k in the Earth’s outer core of ~ 20 Wm⁻¹ K⁻¹.

Fig. 3

High-pressure thermal conductivity experiments with different measurement techniques in DAC. a Temperature varies as a function of time, as derived from time-resolved spectro-radiometric measurements of iron under 135 GPa [data was from Konôpková et al. (2016)]. b Temperature gradients were detected in a laser-heated DAC and the modeled thermal conductivity from COMSOL commercial simulation software. The computed thermal conductivity of iron at 6, 31, 46, and 60 GPa are at 95, 115, 125, and 75 Wm⁻¹ K⁻¹, respectively [data replotted from Saha et al. (2020)]. c The fitted thermal conductivity at 120 GPa and 300 K, obtained by an ultrafast time-domain thermo-reflectance (TDTR) technique used in a DAC. The best fit of the thermal conductivity is 120 ± 12 Wm⁻¹ K⁻¹ [data originated from Hsieh et al. (2020)]

The abovementioned techniques are direct approaches compared to methods that convert thermal conductivity from electrical resistivity measurements via the W–F law. However, these thermal conductivity measurements rely heavily on numerical models and several estimated physical parameters to derive the thermal conductivity (Konôpková et al. 2011; Saha et al. 2020). Notably, the directly measured thermal conductivity in a laser-heated DAC has a large uncertainty of 40–50%, especially at high temperatures (Konôpková et al. 2016; Saha et al. 2020). Although the data obtained by Hsieh et al. (2020) and Ohta et al. (2018) have high precision at room temperature, the modeling for the thermal conductivity requires the specific heat capacity of iron, which has a large uncertainty at high P–T conditions. In other words, flash heating techniques suffer from non-reproducibility and time-drifting due to chemical degradation of the samples, which requires three-dimensional finite-element modeling of the temperature distribution in the sample chamber (Konôpková et al. 2011). The thermoreflectance method determines very small changes in sample reflectivity due to changes in temperature by a probe laser and is, therefore, a relatively more direct method. In this method, the sample to be tested needs a laser transducer that has an ideal optical surface and is in good contact with the measured materials (Goncharov et al. 2015). Furthermore, the estimated thermal conductivity of diamond and the temperature dependence of the thermal conductivity of the pressure medium and the insulator may also induce significant errors in the modeling sample’s thermal conduction (Saha et al. 2020). In summary, although these methods have systematic uncertainties, they provide an experimental method for constraining the thermal conductivity of iron.

2.3 First-principles calculation of the transport properties of iron and its alloys

Established on the density-function theory (DFT) in the Kohn–Sham scheme, the first-principles calculation is an effective tool for predicting the properties of condensed materials (Hohenberg and Kohn 1964; Kohn and Sham 1965). It is possible to probe the electrical/thermal conductivity of the core materials under conditions of the core of the Earth or super-Earth planetaries via this method. Electrical conductivity and electronic thermal conductivity of metals can be computed through the Kubo–Greenwood (K–G) equation (Greenwood 1958; Kubo 1957), which essentially involves the evaluation of matrix elements of the electron momentum operator. Fortunately, the electron properties of condensed materials can be computed by DFT tools (such as VASP, QE, and ABINIT). In theory, the dynamic Onsager coefficients ${\mathcal{L}}_{ij}$(ω) in the static limit for each ionic configuration in iron and iron alloys can be computed according to the K–G equation:

$$\begin{aligned} \mathcal{L}_{ij} & = \mathop {\lim }\limits_{\omega \to 0} \left( { - 1} \right)^{i + j} \frac{2\pi }{{3V}}\mathop \sum \limits_{{n,m,{\varvec{k}},\alpha }} |\psi_{{n,{\varvec{k}}}} \left| {\nabla_{\alpha } } \right|\psi_{{m,{\varvec{k}}}} |^{2} \left( { \epsilon_{{m,{\varvec{k}}}} - \mu } \right)^{i - 1} \\ &\quad \times \left( { \epsilon_{{n,{\varvec{k}}}} - \mu } \right)^{j - 1} \frac{{f\left( { \epsilon_{{m,{\varvec{k}}}} } \right) - f\left( { \epsilon_{{n,{\varvec{k}}}} } \right)}}{{ \epsilon_{{n,{\varvec{k}}}} - \epsilon_{{m,{\varvec{k}}}} }}\delta \left( { \epsilon_{{n,{\varvec{k}}}} - \epsilon_{{m,{\varvec{k}}}} - \omega } \right) \\ \end{aligned}$$

(5)

where f(ε) is the Fermi–Dirac distribution function, subscripts i and j are equal to 1 or 2, μ is the chemical potential, V is the volume of the simulation cell, with α = x, y, z, and ψ_l,k are Kohn–Sham orbitals (at band l and wave vector k), with corresponding energies ε_l,k (Di Paola et al. 2020). When ε_n,k − ε_m,k goes to zero (the case of intraband transitions and degeneracies), [f(ε_m,k) – f(ε_n,k)]/(ε_n,k – ε_m,k) is replaced with −df(ε_m,k)/dε_m,k, as discussed by Calderín et al. (2017). By DFT computational tools, the Kohn–Sham orbitals, chemical potential, and frequency-dependent dielectric functions used in Eq. 5 can be directly computed. Finally, the σ and k_el can be calculated through the Chester-Thellung formulation (Chester and Thellung 1961) of the K-G equation, which reads:

$$\sigma = {\mathcal{L}}_{11}$$

(6)

$$k_{el} = \frac{1}{{e^{2} T}}\left( {{\mathcal{L}}_{22} - \frac{{{\mathcal{L}}_{12}^{2} }}{{{\mathcal{L}}_{11} }}} \right)$$

(7)

where k_el and T are the electronic thermal conductivity and electronic temperature, respectively.

One route to computing the transport properties of iron and iron alloys at high P–T conditions is to perform first-principles molecular dynamics (FPMD) calculations and use K–G equation to calculate transport properties. First, the electron properties of a unique system can be computed at a limited P–T condition (e.g., the Earth’s core) by an FPMD method. United with the K–G equation, the σ and k_el can be computed theoretically. The thermal conductivities of iron and iron alloys under the Earth’s core conditions were computed by a method of FPMD + K–G equation (de Koker et al. 2012; Pozzo et al. 2012, 2013). For example, compositional models of Fe–S (Wagle et al. 2018), Fe–O–Si–S (Wagle et al. 2019), and Fe–Ni (Li et al. 2021) were investigated to constrain the transport properties of the Earth’s core. Notably, the electron properties computed by FPMD are derived from the self-consistent electronic structure based on the Born–Oppenheimer approximation, and it includes only the electron–phonon scattering (EPS) contribution to the thermal conductivity (k_e–p) but not the electron–electron scattering (EES) contribution (k_e–e) (Xu et al. 2018), where k_el is composed of k_e–p and k_e–e. Nevertheless, the influence of EES on the calculations of thermal conductivity in solids cannot be ignored (Pourovskii 2019). The EES reduces the value of k by approximately 20% (Pourovskii 2019) for solid iron under conditions of the Earth’s core. Moreover, Xu et al. (2018) and Gomi et al. (2016) used a Korringa–Kohn–Rostoker (KKR) plus coherent potential approximation (CPA) method (Ebert et al. 2011) to model the thermal lattice vibrations because the KKR-CPA naturally includes resistivity saturation effects.

Beyond the abovementioned methods, a newly developed methodology of direct nonequilibrium ab initio molecular dynamic simulation coupled with electrostatic potential oscillation (named the “NEAIMD-EPO” method) successfully predicted the thermal conductivity of hcp-iron under the Earth’s core conditions (Yue and Hu 2019). The derived results by this method are comparable to those of the DFT + K–G method. The NEAIMD-EPO method intrinsically includes electron–electron scattering and electron–phonon scattering and can thus compute the electronic and phononic thermal conductivity (Yue et al. 2016). Its advantage is skipping the K–G formula to obtain thermal conductivity and avoiding the deficiencies of the FPMD method that does not include electron–electron scattering. This method only works for pure metal systems but not for complex impurity systems (such as the Fe–X system in the Earth’s core) because it does not theoretically incorporate impurity effects.

3 Transport properties of iron at high P–T conditions

In the following sections, we will discuss the effect of phase transition, pressure–temperature, and resistivity saturation on the electrical resistivity and thermal conductivity of iron.

3.1 Phase transitions

The resistivity changes in iron due to phase transitions are shown in Fig. 4. At room temperature, the resistivity of iron increases a lot (2–3 times) when the iron transforms from a body-centered cubic (bcc) structure to a hexagonal closed-packed (hcp) structure at ~ 13–20 GPa. With increasing pressure (> 20 GPa), the resistivity of hcp-iron gradually decreases and saturates at >  ~ 100 GPa (Fig. 4a). At ~ 136 GPa (CMB pressure) and 300 K, the resistivity of hcp-iron is approximately 5 μΩ cm. At below ~ 13 GPa, sold iron transforms from bcc to face-centered cubic (fcc) structure at high temperature, and the resistivity changes. At 20–100 GPa, solid iron transforms from hcp to fcc structure at high temperatures, and the resistivity changes. The bcc–fcc phase transition in iron increases the resistivity at 1–5 GPa and high temperature (Fig. 4b), and the temperature coefficient of resistivity of bcc-Fe is greater than that of fcc-Fe (Silber et al. 2018; Chu and Chi 1981). Conversely, the resistivity decreases when the iron’s structure changes from hcp to fcc at high P–T conditions (Ezenwa and Yoshino 2021; Fig. 4b). Usually, liquid iron has larger resistivity than solid iron.

Fig. 4

Pressure- and temperature-induced phase transitions and the corresponding changes of iron’s resistivity. a The electrical resistivity of iron as a function of pressure at 300 K. b Temperature-dependence of resistivity in iron at ambient pressure and high pressures up to 26 GPa. Blue dashed line, black dash-dot line, and red dashed line indicate the phase transition of iron from bcc to fcc, hcp to fcc, and fcc to liquid, respectively. References are Se2013-Seagle et al. (2013); Go2013-Gomi et al. (2013); Zh2018-Zhang et al. (2018); Zhang2020-Zhang et al. (2020); Ja2002-Jaccard et al. (2002); Sh2011-Sha and Cohen (2011); Ch1981-Chu and Chi (1981); Si2018-Silber et al. (2018); Yo2019-Yong et al. (2019); Ez2021-Ezenwa and Yoshino (2021); Oh2016-Ohta et al. (2016)

The resistivity of solid Fe as a function of pressure was measured and calculated in many studies, shown in Fig. 4a. The calculated resistivity of bcc-Fe by Sha and Cohen (2011) is consistent with the experiment results by Zhang et al. (2018), and it gradually decreases with increasing pressure from ambient to 15 GPa. The calculated resistivity of hcp-Fe by Gomi et al. (2013) also agrees with the experiment results at 300 K and > 50 GPa (Seagle et al. 2013; Zhang et al. 2020). But, the calculated resistivity of hcp-Fe is lower than the experiment results at ~ 15–50 GPa (Sha and Cohen 2011). The reasons for this disagreement may include: (1) magnetic spin fluctuations may occur in hcp-Fe at relevant pressures (Jarlborg 2002), which may increase the resistivity, but it is absent in the present calculation methods (Gomi et al. 2013); (2) Hcp-Fe undergoes an electronic topological transition at ~ 30–40 GPa (Glazyrin et al. 2013) that was absent in one-electron computations by Sha and Cohen (2011); and (3) the studies of Sha and Cohen (2011) and Gomi et al. (2013) used a perfect crystalline structure without the atom-disorder effect, which affects the computed resistivity of iron a lot (Pourovskii et al. 2020). Thus, more theoretical studies are needed to verify these impactors.

Transport properties of the liquid iron and liquid iron alloys are significant for understanding the thermal conduction in the liquid outer core. The measured resistivity of iron increases by ~ 10% upon melting (from ~ 128 to 141 μΩ cm) from bcc-Fe at ambient pressure (Fig. 4a, Chu and Chi 1981). At high pressures up to ~ 26 GPa, the resistivity increases by 6–20 % when iron melts from the fcc phase (Ezenwa and Yoshino 2021; Ohta et al. 2016; Silber et al. 2018; Suehiro et al. 2020; Yong et al. 2019) (Fig. 4a). However, the resistivity and thermal conductivity of liquid iron are still very difficult to directly measure under conditions relevant to the Earth’s core, and direct experiments that measure the resistivity change upon melting from the hcp-phase at high pressures are unavailable so far. DFT computations show a resistivity increase of ~ 6–10 % upon melting of hcp-iron under Earth’s core conditions (Pozzo et al. 2014, 2012; Xu et al. 2018). The melting of iron can generally be assumed to increase resistivity by ~ 10% and correspondingly decrease thermal conductivity by ~ 10% under high pressure conditions, according to the W–F law. Additionally, the likely occurrence of a continuous paramagnetic-to-diamagnetic transition in liquid iron may also affect the transport properties (Korell et al. 2019). Beyond 18 GPa, Ezenwa and Yoshino (2021) found that the resistivity of pure iron, along with the melting boundary, decreased from ~ 100 to ~ 60 μΩ cm because of the loss of magnetic structure (Fig. 5b). The iron’s invariant resistivity of ~ 60 μΩ cm at the onset of melting is much smaller than the value of ~ 120 μΩ cm (Fig. 5b) measured at 6–26 GPa by Silber et al. (2018) and Yong et al. (2019). This disagreement may be attributed to the different resistivity measurement techniques used in these two studies, where Ezenwa and Yoshino (2021) used a modified four-terminal technique (Fig. 1c), however, Yong et al. (2019) applied a conventional four-terminal technique (Fig. 1a).

Fig. 5

Melting effect on the resistivity of iron at high pressures. a Iron’s resistivity as a function of temperature across the melting point at ambient pressure (Chu and Chi 1981), 5 GPa (Silber et al. 2020), 21 GPa (Ezenwa and Yoshino 2021), and 22 GPa (Yong et al. 2019), respectively; b The resistivity change of Fe upon melting as a function of pressure up to ~ 26 GPa. The solid and open symbols in b represent the resistivity on the solid and liquid sides along the melting boundary, respectively. Dashed lines in a and b are guide lines for the experimental data. References in b are Ch1981-Chu and Chi (1981); Ez2020-Ezenwa and Yoshino (2020b); Ez2021-Ezenwa and Yoshino (2021); Si2018-Silber et al. (2018); Yo2019-Yong et al. (2019); Oh2016-Ohta et al. (2016)

Hcp-iron, the most likely solid structure in the inner core, may show anisotropy in the resistivity and thermal conductivity at high P–T conditions, and the anisotropic property may affect the seismic propagation and heat transfer of the inner core (Deuss 2014; Lin et al. 2010; Wang et al. 2015). In DAC experiments, polycrystalline hcp-Fe can somehow develop lattice-preferred orientations with the c-axis parallel to the compression axis of a DAC due to nonideal hydrostatic compression (Lin et al. 2010; Mao et al. 1998; Wenk et al. 2000). The computed resistivity of hcp-Fe by DFT + K-G equation methods indicates a resistivity ratio of ~ 1.3 across the a-plane and b-plane (ρ_a/ρ_c = 1.3) under the Earth’s core conditions (Gomi et al. 2016; Xu et al. 2018). The average resistivity in the polycrystal hcp-Fe sample can be described by ρ_poly = (1/3)(2ρ_a + ρ_c) ≈ 0.92 ρ_a or 1.2 ρ_c. The recent resistivity measurements performed in a laser-heated DAC did not show a strong texture effect at high P–T conditions as SiO₂ was used as a pressure transmitting medium and Fe samples were annealed at ~ 1500 K for a few minutes, which reduced the deviatoric stress in the sample chamber (Zhang et al. 2020). Moreover, Ohta et al. (2018) reported direct measurements on the thermal conductivity by a thermoreflectance method at high pressures and used wire, foil, and power polycrystalline iron as samples, which are supposed to have different crystallographic preferred orientations. Their results show a variation of ~ 30% in the resistivity of their samples at up to ~ 45 GPa (Ohta et al. 2018), which is generally consistent with the calculation results. Modeling and extrapolating the thermal conductivity of iron (Ohta et al. 2018) on the c- and a-planes to high P–T conditions related to the Earth’s core suggests that k_c is about fourfold higher than k_a. It is argued that the strong anisotropy in hcp iron may explain the thermal conductivity discrepancy between the early reports by Konôpková et al. (2016) and Ohta et al. (2016). We suggest that the extrapolation is incomplete, and its uncertainty is substantial because of limited data at low pressure and temperature.

3.2 Temperature-dependence of resistivity in iron and the Bloch–Grüneisen formula

The phonon vibration in the metal increases with increasing temperature and is inversely proportional to the mean scattering time. So, resistivity generally has a positive relationship with temperature for metals and conductors by ρ ∝ Tⁿ. For the nonmagnetic metals, n is close to 1, whereas, for magnetic metals, n is close to 2 above ambient temperature but below the melting temperature (Kasap et al. 2017). The Bloch-Grüneisen formula can express the resistivity of metals as a function of volume and temperature:

$$\rho_{} \left( {V,T} \right) = \rho_{0} + \rho_{BG} \left( {V,T} \right) = \rho_{0} + D\left( V \right)\left( {\frac{T}{{\theta_{D} \left( V \right)}}} \right)^{n} \mathop \int \limits_{0}^{{\theta_{D} \left( V \right)/T}} \left[ {\frac{{z^{n} }}{{\left( {e^{z} - 1} \right)\left( {1 - e^{ - z} } \right)}}} \right]dz$$

(8)

where ρ₀ is the residual resistivity of the material when all phonons are frozen, and θ_D is the Debye temperature. Parameters D and n are constants and can be yielded by fitting the measured resistivity data at high temperatures. Hcp-Fe is superconducting at near 0 K, so its residual resistivity ρ₀ equals zero (Bose et al. 2003; Shimizu et al. 2001).

Some studies have investigated the temperature-dependence of electrical resistivity of hcp-Fe under high pressure by experiments and calculations (Ohta et al. 2016; Pozzo and Alfè 2016; Xu et al. 2018; Zhang et al. 2020). Ohta et al. (2016) measured the resistivity of hcp-iron at high pressure by a pseudo-four-probe method in an oven-heated DAC (up to ~ 500 K) and a laser-heated DAC (up to ~ 4000 K). They found that the measured resistivity of iron obeys the Bloch-Grüneisen formula at low temperatures between ~ 300 and 500 K (black open circles, Fig. 6a, b). But at the high temperature (> ~ 1000 K), the resistivities are lower than the extrapolated values by the Bloch–Grüneisen formula from the low-temperature data (blue open circles, Fig. 6). They argue that a temperature-induced resistivity saturation happens in hcp-Fe at high temperatures (Ohta et al. 2016). In the study of Zhang et al. (2020), they used a standard four-probe VDP method and a homogeneous flat-top laser beam in a laser-heated DAC, and their results suggest that the resistivity of iron has a quasi-linear relationship with temperature and can be fitted by the Bloch-Grüneisen formula (such as at ~ 82 and 105 GPa, blue closed circles in Fig. 6a, b). A quasi-linear relationship between resistivity and temperature was also observed at ~ 69 GPa in a study using an internally resistive-heated DAC (Suehiro et al. 2019; Fig. 6a).

Fig. 6

Temperature dependence of resistivity in hcp-Fe at high pressures. Temperature-dependent resistivity of hcp-Fe at ~ 69–82 GPa (a) and ~ 100–106 GPa (b). Insert figure in b shows the resistivity in hcp-Fe by a muffle furnace heating up to ~ 450 K (Ohta et al. 2016). The resistivity in hcp-Fe was measured at high temperatures above 1000 K using an internally resistive heated DAC [open triangles are from Suehiro et al. (2019)] and a double-sided laser-heating DAC [black open circles are from Ohta et al. (2016); blue closed circles are from Zhang et al. (2020)]

The measured resistivity of hcp-Fe from ~ 1200 to 3000 K at ~ 100 GPa by Zhang et al. (2020) agrees with the extrapolated data via the Bloch-Grüneisen formula from the results of high-pressure and relatively low-temperature experiment results (up to ~ 500 K) in an oven-heated DAC (Fig. 6b) but is much higher than the data by Ohta et al. (2016). The difference in the resistivities at high temperatures may be due to the differences in sample geometries, temperature gradients, and/or texture effects (Zhang et al. 2020). The calculated resistivity of hcp-Fe at high P–T conditions by the first-principles calculation method (Xu et al. 2018), which included the EES and EPS contributions (red solid squares in Fig. 6b), is universally consistent with the latest experimental results by Zhang et al. (2020).

The resistivity of hcp-Fe gradually decreases with increasing pressure, but the pressure coefficient of resistivity decreases with increasing pressure, such as at 2000 and 3000 K up to ~ 200 GPa, as shown in Fig. 7a. When comparing the recent experimental results with measured resistivity values of hcp-Fe (Keeler and Mitchell 1969; Keeler and Royce 1971) along with the recently determined Hugoniot P–T conditions by shock compressions, we found that the results of static and dynamic compression are also generally consistent (Fig. 7b), although other shock experiments show higher resistivity (Bi et al. 2002). Shock-wave compression experiments need to be reconducted to explain this systematic inconsistency. In addition, the spin-disorder in iron under the Earth’s core conditions may also theoretically play a role of comparable magnitude with EES and EPS on the resistivity (Drchal et al. 2017).

Fig. 7

Measured resistivity of Fe along Hugoniot P–T. a The measured resistivity of hcp-Fe in a laser-heated DAC [Zh2020 is Zhang et al. (2020)]. The grey region in b represents the Hugoniot temperature profile of the shocked iron [Al2002, Li2020, and Tu2021 are Alfè et al. (2002), Li et al. (2020), and Turneaure et al. (2020), respectively]. c The resistivity of hcp-Fe obtained by using the shock-wave compression, DAC, and DFT-calculation methods [Bi2002, KM1969, and KR1971 are Bi et al. (2002), Keeler and Mitchell (1969), and Keeler and Royce (1971), respectively]

3.3 Resistivity saturation

Resistivity saturation is common in some metals or metallic systems when the resistivity reaches a critical value at high temperatures (Gunnarsson et al. 2003). Above the critical value, the temperature coefficient of resistivity can be significantly reduced with a further increase in temperature (Werman and Berg 2016). This saturation effect is well known as the “Mott–Ioffe–Regel limit” in metals when the apparent mean free path of a quasiparticle (l) becomes comparable to or shorter than the lattice parameter (d) (or the electron scattering rate becomes comparable to the Fermi energy). This saturation phenomenon was observed in some elemental metals (e.g., Al, Ni, and Nb; Calandra and Gunnarsson 2001) and alloys (e.g., Nb₃Sb, Fisk and Webb 1976), as shown in Fig. 8. For some metals, the mean free path l is much larger than d, so the resistivity has a linear relation with temperature, for example, the Mott–Ioffe–Regel limit of Cu is as high as ~ 260 μΩ cm (Matula 1979) (Fig. 8). Resistivity saturation at high temperatures is a sign of a breakdown of the Boltzmann theory. However, the Mott–Ioffe–Regel condition can be violated in some strongly correlated materials like alkali-doped fullerenes, cuprates, and itinerant magnets (Calandra and Gunnarsson 2002; Cao et al. 2004), where the resistivity can reach beyond the Mott–Ioffe–Regel limit at high temperatures. Therefore, the temperature-induced resistivity saturation under the Mott–Ioffe–Regel condition is controversial. In other words, resistivity saturation depends on different systems, where weakly correlated transition metals likely agree with the Mott–Ioffe–Regel condition, while a strongly correlated system does not (Calandra and Gunnarsson 2002). Interestingly, the resistivity of solid Pt at 1 bar seems saturated with increasing temperatures (Arblaster 2016) but quasi-linearly increases with increasing temperature under high pressure (e.g., 8 GPa, Ezenwa and Yoshino 2020a), which contradicts the belief that the resistivity of metals should be saturated under high P–T conditions. A possible reason is that the pressure-induced s-d hybridization increases the occupancy of the d-band and leads to the destabilization of magnetism in transition metals (Ezenwa and Yoshino 2020a). Along with the spin disorder saturation by increasing temperature, the resistivity of the paramagnetic close-packed Pt may show a linear temperature dependency in a high P–T environment (Fig. 8). Given the similar electronic structure with paramagnetic Pt, solid hcp-iron may have an identical magnetism reduction behavior at extremely high pressures and a linear T-dependent resistivity under high P–T conditions (Ezenwa and Yoshino 2021).

Fig. 8

Resistivity saturation in metals at high temperatures and the Mott–Ioffe–Regel limit. In hcp-Fe, the saturation resistivity can be estimated assuming the mean free path l = d according to the criterion of the Mott–Ioffe–Regel limit and the determining equation of state. The resistivity data at 1 bar for Cu is from Matula (1979); Ni from Chu and Chi (1981); Nb from Abraham and Deviot (1972); Pt from Arblaster (2016); Nb₃Sb from Fisk and Webb (1976). The resistivity of Pt at 8 GPa is from Ezenwa and Yoshino (2020a). The resistivity of hcp-Fe at ~ 142 GPa was measured by Zhang et al. (2020), and the Mott–Ioffe–Regel limit of hcp-Fe at a similar pressure was calculated by Xu et al. (2018)

The saturation resistivity of hcp-Fe was computed to be ~ 155 and 143 μΩ cm under conditions relevant to the Earth’s outer core (~ 136 GPa) and inner core (~ 360 GPa), respectively, using the criterion mean free path (Xu et al. 2018). The measured resistivity of hcp-Fe increases quasi-linearly with the increasing temperature near CMB conditions (~ 142 GPa and 3500 K, Fig. 8), and it is approximately 70(5) μΩ cm at ~ 3000 K (red line, Fig. 8) (Zhang et al. 2020). This value remains far below the calculated Mott–Ioffe–Regel limit value. So, the temperature-induced resistivity saturation effect may not occur in hcp-Fe under the Earth’s core conditions. But we cannot yet exclude the possibility that the resistivity saturation may become stronger with a further increase in temperature or upon melting of iron.

3.4 Thermal conductivity of Fe at high pressure–temperature

As outlined, direct measurement results hint at low values of the thermal conductivity of iron and iron alloys under the Earth’s core conditions. (Konôpková et al. 2016; Hsieh et al. 2020; Ohta et al. 2018). At room temperature, the thermal conductivity decreases from ~ 80 to 20 Wm⁻¹ K⁻¹ when iron transforms from the bcc to the hcp structure at high pressure and then gradually increases with increasing pressure in hcp-Fe (Ohta et al. 2018; Fig. 9a). A similar trend was also found at the phase transition from bcc-Fe to hcp-Fe by Hsieh et al. (2020) (Fig. 9a). At high temperatures, Konôpková et al. (2016) measured the k of hcp-Fe, determining that it is ~ 30 Wm⁻¹ K⁻¹ at CMB (~ 140 GPa and 4000 K) and decreases with increasing temperature (Fig. 9b).

Fig. 9

Thermal conductivity of iron at high P–T conditions. Measured thermal conductivity of iron as a function of pressure at room temperature (a) and high temperatures at ~ 65 GPa (b); and a comparison of measured thermal conductivity with calculations in hcp- and liquid-Fe (c). The gray shaded area in a is the estimated thermal conductivity of Fe with uncertainties as a function of pressure according to the measured results. References are Oh2018-Ohta et al. (2018), Hs2020-Hsieh et al. (2020), Ko2016-Konôpková et al. (2016), Xu2018-Xu et al. (2018) and de2012-de de Koker et al. (2012)

Figure 9c compares the k values of iron from experiments and calculations. The calculation results of hcp-Fe and liquid Fe are nearly the same in different studies (de Koker et al. 2012; Xu et al. 2018). However, these calculation values are 2–3 times higher than those measured in experiments at 100–200 GPa and 2000–3000 K. The calculated thermal conductivity of iron is ~ 100 Wm⁻¹ K⁻¹ under the CMB conditions, while the measurement is as low as ~ 30 Wm⁻¹ K⁻¹. The difference becomes large with increasing pressure. This discrepancy cannot simply be attributed to computational uncertainties because the current calculation results in resistivity match well with those of experimental results (Zhang et al. 2020). More thermal conductivity experiments are needed to cross-check the measurement results, for example employing new experimental methods.

3.5 Wiedemann–Franz law and its validity under extreme conditions

The W–F law connects the heat conduction and charges transport of the electrons in metallic materials [Eq. (2)]. This law excludes contributions from phonon vibration and inelastic scattering of electrons (Chester and Thellung 1961). It is likely valid at very low temperatures, where elastic scattering by disorder dominates, or valid above the Debye temperature, where scattering by phonons becomes effectively elastic. However, experiments show that the W–F law is invalid for liquid Pb and Sn at high temperatures (Yamasue et al. 2003). No experiments have yet investigated its validity under extremely high P–T conditions.

Based on the measured resistivity (Zhang et al. 2020) and thermal conductivity (Hsieh et al. 2020; Konôpková et al. 2016) by experiments, the Lorentz numbers of hcp-Fe at high P–T conditions can be derived. The experimental value of L is approximately 0.8–1.0 × 10^–8 WΩ/K² at ~ 80–200 GPa and 2000–3000 K, as shown in Fig. 10, showing a significant deviation from the ideal Lorentz value (L₀ = 2.445 × 10^–8 WΩ/K²). In comparison, the experimental value of L is around 1.5–2.3 × 10^–8 WΩ/K² at 32–96 GPa and 300 K (Fig. 10). But, at similar P–T conditions, the L value derived from first-principles calculations is around 2.2–2.4 × 10^–8 WΩ/K², which is slightly lower than the ideal value but much higher than the experiment results (Fig. 10). Nevertheless, the experimental L value derived at room temperature and pressure > 80 GPa is close to the ideal Lorentz value and consistent with calculation results. That is, the L values of hcp-iron only at high P–T conditions differ a lot between experiments and calculations. Hsieh et al. (2020) observed an inflection point in the thermal conductivity of hcp-Fe at ~ 30–40 GPa and 300 K, similar to the changes in the hcp-Fe c/a (hexagonal lattice parameter) ratio and the changes in the Mossbauer center shift detected in experiments (Glazyrin et al. 2013). These distinct peculiarities can be explained by an electronic topological transition (ETT), coming with the appearance of new Fermi-surface hole pockets at a given pressure (Glazyrin et al. 2013). An apparent slope change in the L value for iron at ~ 40 GPa and room temperature is definitely due to the ETT in hcp-iron (Fig. 10). Moreover, because the inelastic scattering rate in the perfect lattice of iron is frequency-dependent, its L value is likely 1.57 × 10^–8 WΩ K⁻², whereas the L value for the iron with thermal-disorder lattice is approximate to the ideal value, such as 2.28 × 10^–8 WΩ K⁻² (Pourovskii et al. 2020). The deviation in L values between experiments and calculations (Fig. 10) cannot be attributed to the shortage in experiments. Indeed, the W–F law appears no longer valid for iron at extremely high P–T conditions.

Fig. 10

The Lorentz number was derived from the measured resistivity and thermal conductivity of iron at high P–T and compared with theoretical calculations. Open and solid circles represent the derived Lorentz number of iron from the high temperature (2000, 3000 K) experiments by Konôpková et al. (2016) and Zhang et al. (2020); diamonds represent the derived Lorentz number of iron from room-temperature (300 K) experiments by Hsieh et al. (2020) and Zhang et al. (2020); triangles and squares represent the computed Lorentz number by Xu et al. (2018) and de Koker et al. (2012), respectively

4 Impurity effect on the core’s electrical resistivity

4.1 Matthiessen’s rule

The impurity effect on the transport properties of iron is critical for evaluating the heat conduction of the Earth’s core due to the presence of light elements in the core (Li and Fei 2014). Physically, impurities can cause an overall increase in the electrical resistivity and a decrease in the thermal conductivity in a solid metal because the conduction electrons in a material can be scattered by impurities, along with lattice defects, grain boundaries, dislocations, and any other deviation in a perfect lattice (Kasap et al. 2017), reducing the mean scattering time.

Commonly, the electron scattering, phonon scattering, and impurity scattering contribute to the total resistivity of iron and iron alloys. In a dilute Fe-light element alloy, these three scatterings are most likely independent, and the total resistivity equals the sum of these individual parts, which is Matthiessen’s rule (Matthiessen and Vogt 1864). It can be defined in the following form:

$$\rho_{Fe - i} \left( {V,T} \right) = \rho_{Fe} \left( {V, \, T} \right) \, + \rho_{i} \left( V \right) \times x_{i}$$

(9)

where i represents the alloying elements, ρ_i (V) is the composition-dependent unit resistivity, x_i is the content of the alloying element in atomic percent (at%), ρ_Fe-i (V, T) is the total resistivity of the iron alloys, and ρ_Fe (V, T) is the resistivity of pure iron as a function of pressure and temperature. The second part, ρ_i (V), is called the impurity resistivity and only depends on the volume (corresponding to pressures). Matthiessen’s rule demonstrates the linear relationship between the alloy element concentration and alloy resistivity under fixed P and T conditions. For example, the resistivity of a Fe–Si or Fe–Ni alloy increases almost linearly with increasing impurity concentration when the impurity content is less than ~ 15 at% at ~ 120 GPa (Fig. 11b). A high concentration of impurities can shorten the electron’s mean free path because of the compositional disorder introduced by alloying light elements, so the Mott–Ioffe–Regel condition is satisfied (Wagle et al. 2019; Wagle and Steinle-Neumann 2018). The chemically induced resistivity saturation in Fe alloys can be described by a parallel resistor model (Gunnarsson et al. 2003; Wagle et al. 2019) or empirical formula by Cote and Meisel (1978).

Fig. 11

Electrical resistivity of binary iron alloys at high pressure–temperature conditions. a Temperature-dependent resistivity of Fe-Ni alloy and Fe-light element (e.g., Si, C, S, N, and O) alloys at ~ 120 GPa. Color curves are the calculated resistivity of Fe-light element alloys from Go2018 (Gomi and Yoshino 2018); solid inverted-triangle, diamond, and triangle are the calculated resistivity of Fe–Si, Fe–S, and Fe–O alloys from Wa2019, respectively (Wagle et al. 2019). Open circle, diamond, and inverted-triangle are the experimental results of pure Fe and Fe-Si alloys (Zh2020: Zhang et al. 2020; Zh2021: Zhang et al. 2021), respectively, which shows a larger temperature-dependence than those of the calculation. b Electrical resistivities of Fe-light elements (Si, Ni, H, C, O, Si, and S) alloys as a function of impurity content (at%). The calculated data in b are obtained at 0 K [Go2016 is Gomi et al. (2016); Zi2020 is Zidane et al. (2020)], and the exhibited experimental data are obtained at 300 K

In addition, impurities in iron can likely change the temperature-dependence coefficient of the resistivity (Gomi and Yoshino 2018), where Fe-light element alloys have a smaller temperature-dependence than those in Fe and Fe–Ni alloys (Fig. 11a). This is so-called chemically induced resistivity saturation in Fe alloys, particularly observed in the case of abundant light elements in iron at high temperatures (Gomi et al. 2016). It is also known as Mooij’s law, which is obeyed by alloys, thin films, and amorphous alloys (Kiarasi and Secco 2015; Mooij 1973).

Additionally, solid iron alloys have ordered and disordered atomic distributions, where the transformation from a disordered solid solution to an ordered iron alloy may affect its transport properties. For instance, ordered Fe-Si alloys (FeSi, Fe₃Si, and Fe₅Si₃) have lower resistivities than disordered Fe-Si solid solutions with the same silicon contents at ambient and high pressures (Suehiro et al. 2019; Tian et al. 2020; Varga et al. 2002). In summary, resistivity saturation most likely occurs in Fe-light element alloys at conditions of abundant light elements in iron, which affects the temperature coefficient of resistivity and breaks down Matthiessen’s rule at high pressure. However, the magnitude of impurity resistivity varies in different Fe-light element alloys, and we will discuss them in the next.

4.2 Nickel

Experiments indicate that nickel has a small effect on the resistivity of iron at high pressure and room temperature conditions (Fig. 11). The impurity effect of nickel varies from 1.93 μΩ cm/at% at 45 GPa to 1.69 μΩ cm/at% at 140 GPa (Fig. 12b). The first-principles calculation indicates that nickel has the smallest impurity resistivity among the Fe-based binary alloys (Fig. 11; Gomi et al. 2018; Zidane et al. 2020). Zhang et al. (2021) measured the electrical resistivity of Fe-10Ni (wt%) alloy at high P–T conditions up to 143 GPa and 3000 K. The results show that the resistivity of Fe-10Ni (wt%) alloy is close to that of pure iron at high P–T (Fig. 11a). More recently, Li et al. (2021) calculated the thermal and electrical conductivity of Fe–Ni liquids throughout the pressure ranges (136–330 GPa) in the Earth’s core using the FPMD + K–G equation approach. They suggested that Fe–Ni liquids have slightly smaller σ and k_el values than those of pure iron under the same conditions. As shown by Pommier (2020), Fe alloys with 5 and 10 wt% Ni present comparable electrical resistivity with pure iron at pressures and temperatures below 8 GPa and 2000 K. To date, all studies agree that nickel slightly affects the resistivity of iron.

Fig. 12

Influence of impurities on the electrical resistivity of iron at high pressures. a Electrical resistivity of Fe–Ni, Fe–Si, Fe–C, and Fe–S alloys as a function of pressure. Fe is from Gomi et al. (2013) (Go2013) and Zhang et al. (2020) (Zh2020); Fe–10Ni (wt%) alloy is from Gomi et al. (2013) (Go2013); Fe–Si alloys are from Gomi et al. (2016) (Go2016) and Seagle et al. (2013) (Se2013); Fe₉₉C₁ (at%) is from Zhang et al. (2018) (Zh2018); Fe–3S–3Si (wt%) alloy is from Suehiro et al. (2017) (Su2017). b Percentage change in electrical resistivity for per atomic percent of an added alloying component from experiments

4.3 Silicon

Si is the most likely light element present in the Earth’s outer core. Seagle et al. (2013) measured the resistivity of Fe–9Si (wt%) alloy at pressures up to ~ 40 GPa and room temperature in a DAC (Fig. 12a). With 9 wt% silicon added to iron, the resistivity increases by 13-fold compared to pure iron at ~ 40 GPa (Fig. 12a). In the case of < 10 at% light elements in solid iron, silicon has a higher impurity resistivity than all other light elements (e.g., C, N, S, and O) at the Earth’s core conditions (Gomi and Yoshino 2018). But dilute iron alloys (~ 1 at% impurity concentration of C, N, O, S, and Si) have impurity resistivities comparable to each other (Gomi and Yoshino 2018). Kiarasi and Secco (2015) measured the resistivity of Fe-17Si (wt%) at 2.2–5.0 GPa and below 600 K. They found that a pressure-induced resistivity saturation occurs in Fe–17Si (wt%) at high P–T conditions. Gomi et al. (2016) found that the concentration and pressure can induce resistivity saturation in Fe–Si alloys at high pressure and room temperature (Fig. 11a). The resistivity of Fe–Si alloys first increases almost linearly with increasing silicon concentration in iron, then the rule breakdown at ~ 20 at% Si (Gomi et al. 2016, Fig. 11b). Berrada et al. (2020) measured the electrical resistivity of various Fe–Si alloys (2, 8.5, and 17 wt% Si) at 3, 4, and 5 GPa and temperatures up to the liquid state. Their results indicate that the impurity resistivity of silicon (Fe–Si alloys) is temperature-dependent, which violates Matthiessen's rule (Berrada et al. 2020). A more recent work suggests that the electrical resistivity of liquid Fe–8.5Si (wt%) alloy seems to remain constant at 127 ± 2 μΩ cm from 10–24 GPa on solid and liquid sides of the melting boundary (Berrada et al. 2021). Inoue et al. (2020) measured the resistivity of Fe–Si (2, 4, and 6.5 wt% Si) alloys up to 117 GPa and 3120 K in a DAC, and they found that Fe–6.5 Si (wt%) alloy has a low temperature-dependency in the electrical resistivity at high temperature, indicating a resistivity saturation. But, when 1.8 wt% silicon was in iron, no distinct resistivity saturation was observed at 138 GPa and ~ 3400 K in the experiments (Zhang et al. 2021). Thus, the failure of concentration-induced resistivity saturation in the case of dilute Fe–Si alloys agrees well with the first-principles calculation results obtained by Gomi and Yoshino (2018).

4.4 Sulfur, carbon, oxygen, phosphorus, and hydrogen

Carbon likely has a stronger alloying effect than other impurities (e.g., Ni, Si, and S), because it is in the interstitial site of the Fe lattice instead of a lattice substitution site for other Fe-light element alloys (Yang et al. 2019). In addition, experiments suggest that carbon has a larger impurity resistivity than silicon under high pressure and 300 K (Zhang et al. 2018). At ~ 120 GPa, each percent (at%) of the impurities Ni, S, Si, and C in iron can increase the resistivity by ~ 1.6, 2.8, 3.8, and 4.0 μΩ cm, respectively (Fig. 12b). Although the experimental result (Zhang et al. 2018) and the calculation result (Gomi and Yoshino 2018) differ, one certainty is that Si and C have large impurity resistivity.

In the more complex systems, Fe–Si–O alloys (Fe–10Si–8O, Fe–8Si–13O, at%) have similar resistivity but slightly smaller electronic thermal conductivity than pure iron, as computed by Pozzo et al. (2012). Increasing the content of Si and O in iron, the electrical conductivity and electronic thermal conductivity will remarkably decrease (de Koker et al. 2012). The impurity resistivity of S measured in DAC experiments is smaller than that of Si (Suehiro et al. 2017) at high pressure and room temperature. However, it seems that the impact of S and Si on the resistivity of iron may be reversed at high-temperature conditions (Wagle et al. 2019). In the case of high pressure (~ 360 GPa) and high sulfur concentration (Fe₃S, 25 at% S), the Mott–Ioffe–Regel condition is satisfied, and the temperature coefficient of resistivity changes from positive to negative in the Fe-S system (Wagle et al. 2018). In systems with a high impurity content, the calculations demonstrate that the mean free path approaches the interatomic Fe–Fe distance in the alloys (Fe₃Si, Fe₃S, Fe₃O, Fe₇Si, Fe₇S, and Fe₇O) with increasing temperature, compression, and impurity concentration (Wagle et al. 2019). Due to the difficulties in sample synthesis, there are few experimental studies for the thermal conductivity of Fe–S alloys at the Earth's core conditions, despite sulfur being a major component in the core. More experiments for the Fe–S system conducted at extremely high P–T conditions are needed to constrain the thermal conductivity of the core.

Hydrogen is also a candidate light element in the Earth’s core. Gomi et al. (2018) modeled the Fe–H system under Earth’s core conditions and estimated the resultant thermal conductivity of the Fe–Si–H alloy to be ~ 100 Wm⁻¹ K⁻¹ and a maximum inner core age of 0.49–0.86 Ga. In addition, Yin et al. (2019) measured the resistivity of Fe–P compounds in a MAA and found that phosphorus has a smaller impurity effect than silicon under the same conditions.

5 Heat budget and thermal evolution of the core

5.1 Present geodynamo and heat budget of the core

The present-day Q_CMB is composed of the radioactive heat production Q_R, secular cooling Q_S, core contraction Q_P, the heat of reaction Q_H, gravitational energy Q_g, and latent heat Q_L released with the growth of the inner core (Li et al. 2021). While the heat production by contraction, reaction and radiation is relatively small (Nimmo 2015), the Q_CMB is thus given by:

$$Q_{CMB} = Q_{S} + Q_{L} + Q_{g}$$

(10)

In particular, Q_S, Q_L, and Q_g are related to the core cooling rate (dT_CMB/d_t). On the other hand, Q_CMB is estimated at ∼10–12 TW based on the thermal conductivity of the Earth’s lowermost mantle materials (∼10–12 Wm⁻¹ K⁻¹) (Ammann et al. 2014; Haigis et al. 2012; Hsieh et al. 2018) and a temperature drop of ∼1300 K across the lowermost ∼190 km of the mantle (Zhang et al. 2018). As shown in Eq. 1, when Schwarzchild’s criterion is satisfied across the CMB (Q_CMB > Q_ad), thermal convection could contribute to the geodynamo. In contrast, subadiabatic conditions across the CMB (Q_CMB < Q_ad), may lead to thermal stratification in the core and stop thermal convection (Driscoll and Bercovici 2014).

Early modeling suggested a low Q_ad of 3–5 TW (Stacey and Loper 2007) based on an estimated thermal conductivity of ~ 30 Wm⁻¹ K⁻¹ in iron alloys (Bi et al. 2002; Matassov 1977), which is consistent with the directly measured thermal conductivity of iron and iron alloys at high P–T (Konôpková et al. 2016; Hsieh et al. 2020). As shown above, the experiments and theoretical calculations suggest a relatively higher conductivity in iron that varied from 70 to 226 Wm⁻¹ K⁻¹, indicating a high Q_ad at 10–16 TW (Davies et al. 2015; de Koker et al. 2012; Gomi et al. 2013, 2016; Gomi and Hirose 2015; Ohta et al. 2016; Pozzo et al. 2012; Pozzo and Alfè 2016; Zhang et al. 2021, 2020). When the value of Q_CMB (~ 10 to 12 TW) is smaller than the highest estimated value of Q_ad (~ 16 TW) derived from the thermal conductivity of pure iron, thermal stratification may occur at the top of the outer core and thus suppress the magnetic field. However, compositional convection could overcome this stratification and mix the excess heat downward, restoring adiabatic conditions everywhere (Loper 1978). Above all, higher electrical conductivity makes it easier for the dynamo to induce a current and magnetic field, but higher thermal conductivity hinders thermal convection that drives the geodynamo (Driscoll and Du 2019). We know that the inner core is growing at present, and the compositional convection can thus help to maintain the geodynamo. However, a “core paradox” has been proposed where the thermal-convection-induced dynamo is unlikely to occur in the core with such high thermal conductivity before inner core formation, but paleomagnetic evidence indicates that the magnetic field (> 3.45 Ga) is much older than the inner core age (Olson 2013).

Figure 13 shows the relationship between the resistivity of core materials, T_CMB, and dynamo energy sources (thermal, compositional, and thermal-compositional) in detail. The liquid core solidifies and forms the solid inner core when T_CMB is less than the inner core nucleation temperature, which is usually assumed to be ~ 4100 K at the CMB (Driscoll and Bercovici 2014). It is noted that the electrical resistivity of pure iron (hcp and liquid) is too low to generate thermal convection in the liquid core and power the early geodynamo (Fig. 13), where the geodynamo crosses into the “no dynamo” regime near T_CMB = 4200 K before inner core nucleation (Fig. 13). With inner core growth, compositional convection becomes effective in driving dynamos. Alloying light elements into iron can increase the resistivity and inversely reduce its electrical conductivity to support thermal convection (Fig. 13, cyan area). The electrical resistivity of Fe–Ni-light element alloys crosses the thermal dynamo regime at ~ 4100 K before the inner core nucleation process and enters into a thermal-compositional dynamo regime (Fig. 13). This implies that thermal convection works continuously before inner core nucleation to the present day, which avoids the “core paradox” proposed by Olson (2013). Q_ad at the top of the present Earth’s outer core is approximately 8.0 TW when the k of the outer core is ~ 50 Wm⁻¹ K⁻¹ (Fe-5Ni-8Si alloy, wt%), the temperature at CMB is ~ 4000 K and the adiabatic temperature gradient is ~ 1.0 K/km (Zhang et al. 2021). Thus, Q_ad is ~ 20% less than the suggested heat flow (Q_CMB) across the CMB (~ 10–12 TW), and thermal-driven geodynamo becomes possible. Given a constant Q_CMB (~ 10 TW) over geological time, Zhang et al. (2021) modeled the buoyancy flux by thermo and composition and concluded that the Earth’s core was superadiabatic until ~ 3.0 Ga ago. Compositional buoyancy contributed ~ 83% of the total buoyancy flux to power the present geodynamo. In summary, thermal convection can drive the geodynamo over geological time, but compositional convection is dominant at present (Zhang et al. 2021).

Fig. 13

Electrical resistivity of the core as a function of CMB temperature (T_CMB) along with different dynamo categories. The geodynamo regimes are divided into four parts by the solid vertical orange line and solid pink curve (updated from Driscoll and Du 2019). The present-day T_CMB is around 4000 K and inner core nucleation is assumed to be ~ 4100 K (solid vertical orange line) of T_CMB. Pink solid curve denotes the lower boundary for purely thermal convection and dynamo action. The dotted and dashed lines represent the experimental estimate of temperature-dependent electrical resistivity in solid-hcp and liquid Fe at ~ 140 GPa, respectively, from Zhang et al. (2020). Cyan region is the potentially temperature-dependent electrical resistivity of Fe–Ni–Si alloys, estimated from Zhang et al. (2021)

On the other hand, if a Fe–Ni-light element fluid has a very low electrical conductivity, the current in the core is too weak to generate strong magnetic fields, which is one of the main limitations in generating self-sustaining dynamos (Driscoll and Du 2019). Therefore, only proper light elements can satisfy the requirements of the geodynamo regime. Recent theoretical studies show that Fe–Ni–Si/C has a lower electrical conductivity than Fe–Ni–O/S (de Koker et al. 2012; Gomi and Yoshino 2018; Pozzo et al. 2012; Wagle et al. 2018; Zhang et al. 2018), but the uncertainties remain large given the species and content of the light elements in the core are unclear.

5.2 The age of the inner core

Once we know the present-day core thermal state, we can estimate the heat evolution history of the Earth’s core. In the parameterized convection model (Labrosse 2015; Nimmo 2015), the time evolution of the CMB heat flow, Q_CMB(t), is

$$Q_{CMB} \left( t \right) = Q_{CMB} {\text{exp}}\left( { - \Delta t/\tau_{D}} \right)$$

(11)

where Q_CMB is the present CMB heat flow, τ_D is the characteristic time (4.5 Ga), and Δt is the time before the present. The growth rate of the inner core (r_i, inner core radius) depends on the cooling rate at the CMB (dT_CMB/dt):

$$\frac{{dr_{i} }}{dt} = \frac{ - 1}{{\left( {dT_{m} /dP - dT/dP} \right)}}\frac{{T_{i} }}{{\rho_{i} g}}\frac{1}{{T_{cen} }}\frac{{dT_{CMB} }}{dt}$$

(12)

where T_m is the melting temperature, T_i is the temperature of the inner core, T_cen is the temperature at the center of the Earth, ρ_i is the density of the inner core, g is the gravitational acceleration, and t is the time since the formation of Earth. The age of the inner core can be calculated from the time evolution of the core radius, r_i(r). The entropy budget of the core (Li et al. 2021) is:

$$E_{\Phi } = E_{s} + E_{{\text{g}}} + E_{L} - E_{k}$$

(13)

where E_Φ is the ohmic dissipation (rate of entropy production, Roberts et al. 2003), E_k is the adiabatic effect, and E_S, E_g, and E_L are entropy expressions for secular cooling, gravitational energy, and latent heat, respectively. E_Φ ultimately determines how quickly the core must cool to maintain the dynamo and thus should be > 0 when the dynamo exists. E_S, E_g, and E_L are related to the core cooling rate (dT_CMB/d_t) and thermal conductivity (k). In particular, the heat conduction entropy (E_k) can be calculated from the k of the core and expressed as

$$E_{k} = \int k\left( {\frac{{\nabla T_{a} }}{{T_{a} }}} \right)^{2} dV$$

(14)

where T_a is the adiabatic temperature in the core, and the volumetric integral is over the outer core (Li et al. 2021). T_a at a radius of r can be expressed as

$$T_{a} \left( r \right) = T_{cen} *{\text{exp}}\left( { - r^{2} /D^{2} } \right)$$

(15)

where D is the lengthscale (Labrosse et al. 2001). The nucleation of the core is strongly associated with the T_CMB and k of the core. Low thermal conductivity corresponds to a small isentropic heat flow and a low cooling rate (dT_CMB/d_t), leading to a low initial T_CMB and T_cen, and thus an old inner core age. For instance, if k at the top of the outer core is ~ 20 Wm⁻¹ K⁻¹, as determined by direct measurement (Konôpková et al. 2016; Hsieh et al. 2020), the minimum initial CMB temperature is estimated to be ~ 4250 K, corresponding to an inner core age as old as ~ 3.3 Ga (Hsieh et al. 2020). In contrast, the high thermal conductivity of the core (> 90 Wm⁻¹ K⁻¹, e.g., Gomi et al. 2013; Ohta et al. 2016; Li et al. 2021) corresponds to a high temperature (5700–7800 K, Labrosse 2015) at the CMB (T_CMB) in the early Earth and hence a young inner core age (< 0.7 Ga, Davies et al. 2015; Ohta et al. 2016; Pozzo et al. 2012). For comparison, observations of the change in the palaeomagnetic field suggest a young inner core between 0.7 and 1.5 billion years old (Biggin et al. 2015; Bono et al. 2019; Landeau et al. 2017).

5.3 Other energy sources of the geodynamo

In addition to the thermal convection driven by primordial heat, other energy sources, including radioactive heat, exsolution of light elements, and precession, can also drive the geodynamo that sustains the paleomagnetic field in the early Earth. To date, many researchers have tried to explain the different contributions of various energy sources to the geodynamo.

There is no consensus on how many radioactive elements (e.g., U, Th, and K) are in the primordial Earth’s core. Some believe that these incompatible radioactive elements have difficulty entering the core (Corgne et al. 2007). Others argue that their abundances in the core are affected by the presence of other elements or extremely high-temperature conditions (Li and Fei 2014). For example, the content of potassium (K) in Fe–S alloy melts increases with increasing temperature (Murthy et al. 2003). The core-mantle partition coefficients of K and Na increase with increasing O and S abundance, so the early core may contain potassium (K) up to hundreds of ppm (Gessmann and Wood 2002). On the other hand, some researches indicate that the concentrations of potassium and uranium in the iron alloys at 20–70 GPa and 3000–5000 K may not be significant (Blanchard et al. 2017; Chidester et al. 2017). It remains debated that whether the radioactive energy in the primordial core is sufficient to provide decay heat under extremely high-temperature conditions.

Moreover, the exsolution of light elements from the core as it cools is promising but remains a debate. The exsolution mechanism requires a strong dependence on the positive correlation between the solubility of these light components in the iron alloys and the temperature under the core conditions. Metal-silicate partition experiments conducted at 34–138 GPa and 3500–5450 K suggest that MgO can dissolve in the core in the P–T conditions of the Earth’s formation and precipitate out into the mantle as the core cools, because of the high solubility of the light composition of MgO at high temperatures, producing high buoyant flux (thus a significant amount of energy) capable of stirring vigorous convection of the geodynamo (Badro et al. 2018, 2016; O’Rourke and Stevenson 2016). Although this conclusion is not supported by later experiments (Du et al. 2019), the latest work by first-principles calculation show a similar positive solubility-temperature correlation of MgO (Liu et al. 2020). Similar to MgO, high P-T experimental results of the Fe–Si–O system indicate that SiO₂ can also dissolve in the core (Hirose et al. 2017). But this conclusion is challenged by first-principles calculation results (Huang et al. 2019). In addition, experimental and theoretical investigations are limited to possible exsolution of a few light elements such as Si, Mg, and O. Hence, it remains equivocal and highly controversial whether light elements (such as S, Si, O, C, H, Mg, K, and Na) and their compounds can enter the core at high temperatures and exsolution as the core cooling.

Numerical and experimental magnetohydrodynamic investigations suggest that precession, a possible type of exogenetic force independent of the energy budget of Earth itself, can stir convection of the core when the Earth’s axis of rotation shifts periodically when it orbits the sun and is thus another plausible driving mechanism of the geodynamo of the early and present-day Earth (Giesecke et al. 2019; Lin et al. 2016; Tilgner 2005). Unfortunately, there are no exact constraints on the orbital dynamics of the early Earth and the early solar system as a whole. The feasibility of precession as a driving force of the early geodynamo remains ambiguous.

In summary, thermal and compositional convection drives the present geodynamo, with the latter contributing predominantly. The moderate thermal conductivity of a Fe–Ni-light element core could support a geodynamo driven by thermal convection over geological time according to the present knowledge of the Earth’s core. Besides the determinations of the electrical and thermal conductivity of the iron and iron alloys themselves, more work is required to precisely constrain the contribution of radioactive elements, exsolution of light elements, precession, and basal magma ocean to the paleomagnetic field of the early Earth.

6 Conclusions and outlook

In this review, we summarized the recent experimental and theoretical studies on the transport properties of iron and iron alloys under extreme pressure–temperature conditions and provided a perspective direction for further work. To date, those studies extend our understanding of the thermal conductivity and thermal evolution of the Earth’s core and geodynamo. The main conclusions are briefly shown as follows:

• (1) Although questions remain, recent studies have intensively investigated the transport properties of iron and iron alloys under the Earth’s core P–T conditions via experiments and calculations. First, pressure- and temperature-induced phase transitions in Fe and Fe alloys can significantly change their transport properties. The phase transition from bcc- to hcp-Fe at ~ 15 GPa can increase the electrical resistivity and decreases the thermal conductivity. Besides, the resistivity may increase by ~ 10% upon the melting of iron. Second, the temperature-dependence of resistivity in hcp-Fe still obeys the Bloch-Grüneisen formula before melting at high pressures. At high P–T conditions of the Earth’s core, the electrical resistivity of solid hcp-Fe is far below the Mott–Ioffe–Regel limit, or saturation resistivity, so it has a quasi-linear relationship with temperature (from room temperature to at least 3500 K at ~ 140 GPa). However, it is dull whether this conclusion can be extrapolated to higher P–T conditions and whether it can be further applied to liquid Fe and Fe-light element alloys. Third, the ideal W–F law (with an ideal Lorentz number) is invalid for iron and iron alloys at extremely high P–T conditions. The Lorentz number varies with changes in P–T conditions and light elements. So far, the derived value of the Lorentz number by experimental measurements disagrees with that of theoretical computation, more theoretical and experimental works are thus needed to resolve this discrepancy. Lastly, in cases of low concentration of light elements in iron, scattering effects from electron, phonon, and impurities can be simply summed. In high impurity concentration scenarios, chemically induced resistivity saturation may occur, thus Matthiessen’s rule is invalid. To completely understand the electrical resistivity and thermal conductivity of iron and iron alloys at extremely high P–T conditions, more experiments are needed to verify the above assumptions.

• (2) The resistivity of hcp-Fe at high P–T conditions measured by experiments is consistent with the result of first-principles calculations that include contributions from both electron–phonon and electron-electron scaterings. The electron–electron scattering contributes ~ 30% to the total resistivity of hcp-Fe in the Earth’s core environment. Based on measured resistivity and the W–F law, the thermal conductivity of iron in the Earth’s core is estimated at ~ 100 Wm⁻¹ K⁻¹. Nevertheless, the direct measurements on the thermal conductivity of iron indicate a conversely low value of < 40 Wm⁻¹ K⁻¹. This discrepancy remains unsolved. Several effects may impede the transport of heat in iron alloys at high P–T, such as spin disorder/local magnetic moments, electron correlations, and impurities (Williams 2018). Thus, first-principles calculations on the thermal conductivity of iron alloys should include all the factors mentioned above to accurately predict the thermal conductivity of the Earth’s core.

• (3) The electrical and thermal conductivity of pure iron is too high to power an early geodynamo through thermal convection. Incorporation of the proper light elements in the Earth’s core is critical, which may efficiently reduce the electrical and thermal conductivity of iron to satisfy the requirements of a thermal-convection-driven geodynamo in the early Earth.

Further work on the direct measurements and calculations of thermal conductivity in solid and liquid Fe–Ni-light element alloys and the lowermost materials under the P–T conditions of the Earth is necessary to further clarify the heat budget, inner core age, and thermal evolution.