Introduction

Coastal areas form dynamic ecosystems at the land–sea interface (Leewis et al. 2012; Gonçalves et al. 2013; Martins et al. 2013). An important feature of these areas is their variability (Dias 2004) in terms of the exposure to many natural and human-made pressures (Nobre and Ferreira 2009). Among several non-structural and structural coast protection methods, the latter have detrimental effects on coastal environment (Fathi-Moghadam et al. 2018).

Slopes far from the ocean, and places behind the dunes are the coastward sheltered areas were coastal forests form. Although the latter do not undergo daily salt spraying, they are affected by storm winds and salts (Temmerman et al. 2013). Coastal forest is commonly used as an effective approach against natural and human-made disturbances (Gaertner-Mazouni and De Wit 2012; Nanko et al. 2019), the capacity of which was not studied in all aspects (Turker et al. 2006). To date, the best known effect of forest in coastal areas is the attenuation of sea waves (Mendez and Losada 2004). Coastal trees as palm (Vanderpuye and Armah 1997), coconut (Rajendra and Sumariati 2018), and pine (Torita et al. 2022; Jalil-Masir et al. 2022) can protect the coast against waves. Vegetation not only reduces wave destructive effects (Leonardi et al. 2018; Möller et al. 2014; Temmerman et al. 2013; Morris et al. 2018) and storm effects (Wamsley et al. 2009) on natural coasts and coastal defense structures (Winterwerp et al. 2020; Mu et al. 2019), but also strengthens the natural habitats (Nordstrom 2014) and provides recreational opportunities (Foster et al. 2013).

Wave-forest interactions were simulated under laboratory-controlled conditions with natural (Tschirky et al. 2001) or artificial vegetation (Huang et al. 2011; Cavallaro et al. 2011; Augustin et al. 2009). Zinke et al. (2011) believed that correct parameterization of flow resistance by vegetation was the most important uncertainty factor. Modeling a tree with a flexible structure (Fathi Moghadam et al. 2018) or with a rigid structure (Akgul et al. 2013; Sundar et al. 2011) is a reason why the real and model specimens differ.

According to studies, palm and coconut trees are effective in reducing the harmful effects of waves in coastal regions (Mascarenhas and Jayakumar 2008). The flexibility parameter is expected to have little influence on wave characteristics owing to the tree structure and, therefore, the flow structure; hence, rigid cylinders are often employed to describe these trees. Thus, the effects of coastal forest on damping of waves were evaluated via the extensive field or wave-flume laboratory studies, and the integrated coast-forest-wave simulation.

To quantify these effects, several field studies were performed in various areas, including salt marshes in the USA (Knutson et al. 1982); tidal areas in the UK (Möller et al. 1999; Möller and Spencer 2002); mangrove coastal forests in Vietnam (Mazda et al. 2006; Quartel et al. 2007; Nguyen and Parnell 2017); shallow lakes in Sweden (Lovsted and Larson 2010); southern coasts of the Pacific Ocean in Indonesia and New Guinea (Hirashi and Harada, 2003; Grilli et al. 2020); and northern coasts of the Arctic Ocean in Norway and Russia (Sinitsyn et al. 2020). Similar results were yielded to reduce the wave height significantly in the areas with forest cover compared with those without forest cover.

Several experimental studies were conducted on the vegetation-caused wave attenuation. Esteban et al. (2020) studied the bed roughness effect on the coastal wave propagation and water level rise; they suggested that such experiments be performed on uneven beds with a Manning coefficient of about 0.06. When waves hit the coast, the turbulence intensity changes (Lou et al. 2018) and the wave velocity falls (Hu et al. 2014). Turbulence plays an important role to describe the physical process of cover-through flow (Zhang et al. 2013; Wang et al. 2015). Chen et al. (2020) studied the changes in wave velocity and turbulence by rigid vegetation and proposed a formula to predict the stem-scale turbulence using velocity, drag coefficient, and vegetation density and diameter. Möller et al. (2014) assessed the energy loss in a reservoir with natural lagoon vegetation under long-wave conditions in the laboratory and came to the conclusion that up to 60% of the observed wave height decrease might be attributable to the vegetation. Yin et al. (2017) found, by experimental studies on coast vegetation, that damping coefficient increased with an increase in the number of rows and in the relative density.

The dependence of wave damping rate on the forest density indicates the forest performance at a certain area, which can be examined by the drag coefficient as a representative of the resistance against the flow (Hirashi and Harada 2003). In fact, the wave energy loss is mainly related to the forest-caused drag force (FD) that can be defined quantitatively by the Morison equation (Dalrymple et al. 1984; Morison et al. 1950). In the vegetation-wave interaction simulation, choosing the appropriate value for the forest drag coefficient (Cd), which has a significant impact on the FD, is crucial for an accurate wave damping prediction (Cao et al. 2015; Maza et al. 2015). This study aims to obtain a relationship capable of predicting the group drag coefficient in terms of tree cover under known wave height conditions. The effect of different characteristics of waves and vegetation was addressed in several studies.. Despite any vegetation diversity, the changes in the wave damping by the coastal forest are significant (Mendez and Losada 2004). Lima et al. (2007) obtained increased wave damping values for forests with higher densities. Porosity effect of vegetation compaction causes waves to reflect and reduce their heights. Although the inertial force leads to the energy loss and reduction of damping capacity of the vegetation, overall, the wave damping is still rising (Suzuki et al. 2019). The damping effect of the wave height was not clearly explained; initial results of a study by Cavallaro et al. (2011) showed that an increase in the inflow wave height increased the wave damping while the observations by Bradley and Houser (2009) estimated less damping increase at more inflow wave heights. This issue is examined. Van veelen et al. (2020) studied the effect of forest flexibility and showed that wave weakening effect of flexible cover is 20–70% less than that of rigid cover due to wave’s passing through the flexible cover. Flexible cover has no impact on the velocity profile, but stiff cover changes it. According to Wang et al. (2019), leaves are more effective than stems in reducing wave transmission and height changes. In actuality, a flexible surface's element's flow energy is lower than a rigid surface's (Toloui et al. 2019). Based on the literature review, most related studies have focused on submerged vegetation or salt marsh and swamp plants rather than on terrestrial coastal forest (TCF) to examine mentioned parameters. This research attempts to fill the gap by emphasizing the role of TCF in significant reduction of destructive effects of coastal waves. However, more empirical and numerical studies are needed to provide the design criteria for coastal vegetation development.

The idea of a flume with knife edge supports and capability of performing freely in any flume under motion threshold conditions so that the contact friction could be kept at a zero level, is first defined and used. The wave force absorbed by the coastal forest is directly measured.

This research attempts to fill the gap by emphasizing the role of TCF in significant reduction of destructive effects of coastal waves. In particular, this study aims to simulate the TCF, measure the force absorbed from long waves by terrestrial coastal forest, and determine the total drag coefficient and wave damping rate based on breaking solitary waves, which denotes waves breaking on the coast before reaching the TCF.

Materials and methods

Dimensional analysis

The parameters that influenced the hydraulics of the phenomenon were included: coast slope (S); coast still water level (d0); fluid density (ρ); fluid viscosity (μ); gravity acceleration (g); tree diameter (D); the width of the TCF parallel to the wave direction (BG); TCF length along the flume width (L); TCF density number (Dv); tree height (hv); absorbed wave force in the presence of the TCF (F), which is assumed to equal the drag force (FD); absorbed wave force in the absence of the TCF (F0); shear stress by the cover (τv); wave propagation velocity (V); wave height (H); and damped wave height (H0):

Parameters effective in such issues as the drag coefficient and cover resistance against flow can be related in the form of Eq. (1).

$$f_{1} \left( {S,d_{0} ,\rho_{w} ,\mu_{w} ,g,D,BG,L,D_{v} ,\tau_{v} , h_{v} ,F_{0} ,F,V,H,H_{0} } \right) = 0$$
(1)

Next, the Buckingham π method (Buckingham 1914) was used to extract dimensionless parameters from Eq. (2):

$$f_{2} \left( {\frac{F}{{ \rho_{w} H^{2} V^{2} }},\frac{{\rho_{w} HV}}{{\mu_{w} }},\frac{{\tau_{v} }}{{\rho_{w} V^{2} }},\frac{V}{{\sqrt {Hg} }},\frac{BG}{L},\frac{H}{{h_{v} }},\frac{H}{D},\frac{{F - F_{0} }}{{F_{0} }},\frac{H}{{H_{0} }},D_{v} ,S} \right) = 0.$$
(2)

The obtained dimensionless parameters were then examined to omit Fr (Froude Number) and Re (Reynolds Number), flow nature and flow turbulence, respectively.

Omitting constant parameters, dimensionless numbers with little effect, and those overlapping with other numbers during the experiment resulted in Eq. (3):

$$C_{{\text{d}}} = f_{3} \left( {\frac{{\tau_{{\text{v}}} }}{{\rho_{{\text{w}}} V^{2} }},\frac{H}{{h_{{\text{v}}} }}} \right).$$
(3)

Based on the studies by Nardin et al. (2016) and Baptist (2005) on investigating the forest cover effects on the flow, Eq. (3) is used to estimate \(\tau_{v}\) presented in Eq. (4):

$$\tau_{{\text{v}}} = \frac{1}{2}\rho C_{{\text{d}}} D D_{{\text{s}}} h_{{\text{v}}} V^{2},$$
(4)

where \(\tau_{v}\) is the shear stress by the cover, \(C_{{\text{d}}}\) is the drag coefficient, D is the tree diameter, \(D_{{\text{s}}}\) is the stem density (number of stems per unit area), \({h}_{v}\) is the cover height, and \(V\) is the flow velocity in the forest.

Then, dimensionless parameters Ft and Kv (Eqs. 5 and 6), obtained through dimensional analyses, were used to study the effects of the TCF on reducing wave force and wave height, respectively. In fact, Ft indicates TCF performance and Kv is used as wave dissipation rate.

$$F_{t} = \frac{{F - F_{0} }}{{F_{0} }}$$
(5)
$$K_{v} = \frac{H}{{H_{0} }}$$
(6)

Drag force theory

The inflow wave gradually turns into an unstable current that expands above the shallow water near the coastline (Fathi-Moghadam et al. 2018). Upon hitting the TCF, this inflow wave exerts two forces on the trees: (1) drag force that is equal to wave absorbed force (the first term in Eq. 7) due to the wave velocity and (2) inertial force (the second term in Eq. 7) due to the flow acceleration; Eq. (7) can be used to estimate the total hydrodynamic force (FTL) (Morison et al. 1950):

$$F_{{{\text{TL}}}} = 0.5 \rho C_{{\text{d }}} A_{{\text{p}}} { }\left| V \right|V + \rho C_{{\text{m}}} \forall \left( {{\raise0.7ex\hbox{${\partial V}$} \!\mathord{\left/ {\vphantom {{\partial V} {\partial t}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\partial t}$}}} \right),$$
(7)

where ρ is the fluid density, Cd is the drag coefficient, AP is the flow-front tree area, V is the wave-induced particle velocity (equal to wave velocity before breaking), Cm is the inertia coefficient, ∀ is the flow-front tree volume, and \((\frac{\partial V}{\partial t})\) is the time-based velocity variations.

The total instantaneous hydrodynamic force exerted on the tree throughout the streamline includes the drag force and the inertia force. Sorensen (2006) believed that since the temporal inertia \((\frac{\partial V}{\partial t})\) is negligible in the shallow water, so is the inertial force equation because it is a function of \((\frac{\partial V}{\partial t})\). This was confirmed by a laboratory study by Hirashi and Harada (2003), in which the pressure difference between the two sides of the vegetation was explained to be mainly due to the drag resistance. This study too neglected the very small \(\left(\frac{\partial V}{\partial t}\right)\) assuming quasi-steady flow (Husrin et al. 2012) and simplified Eqs. (7) to (8). In other words, the total instantaneous hydrodynamic force exerted on the tree through the streamline can be the drag force (Fathi-Moghadam et al. 2018).

$$F_{TL} = F = 0.5 \rho C_{d} A_{P} V^{2}$$
(8)

Using Eq. (9), the drag coefficient can be calculated as follows:

$$C_{d} = \frac{2F}{{\rho A_{p} V^{2} }}.$$
(9)

Experimental detail

Tools and equipment

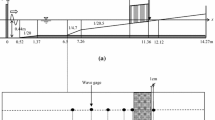
Experiments were performed in a laboratory flume of 8.6 m long, 0.6 m wide, and 0.6 m height composed of a metal floor and Plexiglas walls. Water from the main water pipe was pumped via a connecting pipe into the wave tank in the flume.

The solitary wave theory was used to produce the waves that were the subject of this study. In recent decades, single-wave modeling of tsunami wave impacts and their propagation to coastal regions have drawn a lot of interest (Hsiao and Lin 2010). An important reason for this simulation is the transmission property of solitary waves (Chang and Hwung 2006). Here, two sliding gates were installed in a 2-m distance of the flume to create a reservoir where water could be regulated at different levels and waves with known heights could be created by quick gate opening. This method was first proposed by Russell (1845) and later applied in other studies by Ratnosooriya et al. (2008) and Jalil-Masir et al. (2021).

To measure the force used to the coast, a moving plate was equipped with a 50-kg-capacity dynamic load cell of class C3 measurement accuracy with 0.023% error installed in front of the knife edge flume to transfer the instantaneous wave force exerted to the moveable plate and TCF model to the PM-LD01 electronic display.

To measure the velocity, received information and signals were recorded by a 3D acoustic Doppler velocimeter (ADV) and stored on data logger software on the attached computer system. The wave breaking point was estimated in preliminary experiments according to studied geometry, and the velocimeter was installed on the coastline to record the wave velocity at the breaking moment. Waves can break by changing in either the entrance slope of the shore or the still water depth (Jalil-Masir et al. 2021). Here, the primary slope and still water depth were determined based on previous studies to ensure breaking of waves with different heights reaching the flat shore.

Experiment steps

A 8.6-m-long flume was divided longitudinally into three parts: 2 m for the tank, 3 m for the model, and 3.6 m for the downstream. The tank was created first by placing a Plexiglas plate at the beginning of the flume and then by installing a sliding metal gate 2 m from the plate. The gate was opened using a thread-and-spool mechanism made up of a tow rope and weights. The water depth behind the sliding valve was modified for various pipes with the still water level along the shore set at 7 cm. Meeting the objectives of the present study required the generation of waves broken at the front of the study area. The wave height simulation was performed using a 1:50 scale and the solitary wave theory (Russell, 1845; Ratnasooriya et al. 2008). In the laboratory, behind-the-gate water depths of 25.6, 39.5, and 47 cm from the flume bed could yield wave heights of 6, 9, and 12 cm, respectively, at the front of the coast.

In physical modeling, since the ratio of two forces (surface friction and driving body) increases or decreases, inherent uncertainties are unavoidable, but they can be acceptable in a specific flow condition, if the range of the modeling scale is selected appropriately. Hence for good physical modeling which normally hindered by uncertainties in the selected scale and constraints in the experiments, this research selected the 1:50 scale that lies in the 1:30–1:60 range (accepted for coastal waves modeling; Heller 2011) so that the results are least affected. Considering 10 m as the full-scale height for a tree, which lies in the 8–12 m range and is quite acceptable for a middle age coastal palm tree, this study assumed (based on its selected scale) 0.25 m as the tree height in its modeling. In this research, the wave velocity ranged from 1.30 to 1.5 m/s (full scale: 9–11 m/s, according to the Froude number similarity) and wave height varied in the 0.06–0.12 m range (full scale: 3–6 m). Shafiei et al. (2016) have reported 4–16 m/s and 3–15 m as the ranges of the wave velocity and wave height for a real tsunami, and those of the current study fall within these ranges.

To simulate the coast, a movable plate was placed in the flume and the rigid vegetation was placed on top of it. The load cell was connected to the plate to measure the wave-induced force. For the first time, the maximum wave force absorbed by the coastal forest was measured directly.

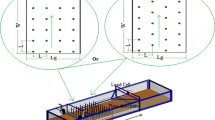
Experiment videos recorded by a high-speed camera were converted into images which were then analyzed to calculate the wave height at each point of the coastline. An ADV was used to measure the velocity at the point before the wave began to break. Experiments were carried out with and without TCF. To model the trees, a structure of 32-cm-high and 9 mm-diameter rigid plastic cylinders was used (Akgul et al. 2013; Sundar et al. 2011; Huang et al. 2011).

Placed 5 × 5, 10 × 10, 15 × 15, and 20 × 20 cm apart on the coast plate in two parallel (P) and staggered (S) arrangements, the TCF cover was 40 and 45 cm long (normal to the flow direction) and 15, 30, 45, and 60 cm wide (extended in the flow direction). Here Dv = \(\frac{Q\times G}{T}\) where \(Dv\) is the density number (stems/m2), \(Q\) is the number of stems/m2 in each arrangement, \(G\) is the number of stems in each experiment (for the width and distance among the trees in each arrangement), and \(T\) is the number of stems per unit width along the TCF cover length in each arrangement. Considering the definition of density, the number of cover rows (normal to the flow) and obtained densities were identical in both arrangements. However, the number of trees and the way they were arranged against the wave were different. Figures 1, 2 and 3 show the experimental setup and TCF arrangements. Table 1 lists the cover placement conditions. In all experiments, the cover increased in the direction of coast.

Fig. 1
figure 1

Side view of the flume with the equipment

Full size image
Fig. 2
figure 2

Experimental setup

Full size image
Fig. 3
figure 3

TCF in staggered and parallel arrangements in 4 widths and shortest inter-tree distance * Flow direction → 

Full size image
Table 1 Cover characteristics
Full size table

Results and discussion

TCF effects on the wave height reduction in the form of damping rate

Figures 4 and 5 show the wave dissipation rate (\(\frac{H}{{H}_{0}}\)) in two arrangements (named P and S). TCF effect on the wave damping was studied by Kv.

Fig. 4
figure 4

\({K}_{v}\) ratio for different pre-cover wave heights in parallel arrangement, (P1–P4)

Full size image
Fig. 5
figure 5

\({K}_{v}\) ratio for different pre-cover wave heights in staggered arrangement, (S1–S4)

Full size image

When a wave hits the coast, it faces a cover-caused drag as a resistive force and loses part of its driving force to resist the drag. Recorded data showed that, in general, the wave height reduction depends on cover features, such as arrangement, inter-tree distance, and cover width.

In fixed tree intervals, increasing the TCF width decreased the post-cover wave height. As wave hits a higher number of trees, the drag resistive force increases and more energy is absorbed by the cover from the wave.

Studies on Kv showed that following an increase in the width and a decrease in the tree distance, the wave damping either increases or, in some cases, remains relatively unchanged. According to the observations, the difference in wave height reduction rate between the highest (13) and lowest (2) number of the TCF rows was 50% at the highest inflow wave height (12 cm).

Table 2 shows Kv based on the inflow wave height for different parallel-mode TCF densities. Considering the results of the present study and those found by Yin et al. (2017) and Lou et al. (2018), who used the post-cover to pre-cover wave height ratio to determine the damping rate, a rise in the row numbers and a fall in the tree cover distance could decrease the wave height and increase its damping rate. TCF interferes with the wave propagation and leads to increased friction, turbulence, wave breaking, and hence, reduced wave energy. However, at low densities where the coast-TCF resistance against the waves is low, the wave height reduction rate decreases and Kv tends to reach zero. The increase in the TCF density from 12 to 273 (stem/m2) reduced the post-cover wave height by 4.62 times. The staggered mode was more effective than parallel mode in wave damping (by 24% averagely). The rate of wave height reduction in terms of the effect on trees (Kv* = 1− \(\frac{{H}_{0}}{H}\)) is presented in Table 2. As shown in Table 2, the TCF effect on the wave energy loss due to reduced wave height was up to 81%. The rate of wave height reduction reported by Ratnasooriya et al. (2008) and Irtem et al. (2009) for coastal vegetation varies in the 40–45% range. Causes of this difference can be such laboratory conditions as the features of coast and coastal forest cover and the wave height or the experiments scale.

Table 2 Damping rate for different TCF densities
Full size table

TCF effects on the wave force absorption

TCF effect on wave force reduction was studied as the cover efficiency to generate drag force against the waves. The absorbed forces were recorded by a dynamometer in with-TCF and no-TCF states. Figures 6 and 7 show the results as the Ft diagram in terms of the inflow wave heights in parallel and staggered modes.

Fig. 6
figure 6

Dimensionless force ratio (Ft), against wave height for the parallel arrangement, (P1–P4)

Full size image
Fig. 7
figure 7

Dimensionless force ratio (Ft), against wave height for the staggered arrangement, (S1–S4)

Full size image

Figures 6 and 7 show the effects of rows (TCF width), spacing, and arrangements on reducing the wave force and show that, in general, the absorbed forces increased compared with no-cover case. In the densest case (width of 60 cm and distance of 5 × 5 cm), with the staggered arrangement and wave heights of 6, 9 and 12 cm, the force damping rate increased 3.22, 3.4 and 4.7 times, respectively. Four different aspects were studied to evaluate the TCF effects on the wave force:

Constant wave height and TCF width and variable distance

In general, a reduced distance increased the load cell-recorded force. Based on Table 3, at maximum cover width and wave height, and in parallel arrangement, the absorbed force increased 0.68, 1.049, and 1.4 times, in the 5 × 5 cm distance compared with 10 × 10, 15 × 15, and 20 × 20 cm distances, respectively. In other widths as well, this tendency persisted. In reality, the greater breadth may absorb more force from the waves because to the higher density number and tree resistance. In all instances, the densest cover in the staggered configuration had the best force-absorbing efficacy (3.76 times more than that of the no-cover case).

Table 3 Absorbed wave force (N); width, 60 cm; wave height, 12 cm; arrangements, P and S
Full size table

Constant tree distance and wave height and variable width

This result shows that at a fixed distance, an increase in width increased the absorbed force because more cover rows against waves can absorb more force. According to Table 4, at the minimum distance (5 × 5 cm) and wave height (6 cm), and in parallel arrangement, the absorbed force increased, in width of 60 cm, 0.287, 0.555 and 0.825 times compared with widths of 45, 30 and 15 cm, respectively. At the maximum 20 × 20 cm distance, although the number of rows and hence number of trees increased, the absorbed force did not increase significantly in each width, possibly in terms of the long inter-row and inter-tree distances (in a row). Since trees lie in the flow path and flow is separated over their bodies, a wake zone is formed behind each tree. When trees are placed in the front tree's wake zone, the latter's effectiveness virtually declines since its real effective absorbing surface is diminished. However, when trees are excessively apart, their group effect is practically reduced and each tree alone, instead of several, stands against the wave causing it to break and not function properly, especially in front rows. It was assumed that the tree does not break or bend against the stream.

Table 4 Absorbed wave force (N); cover distance, 5 × 5(cm × cm); wave height, 6 cm; arrangements, P and S
Full size table

In general, maintaining the optimal inter-tree distance has shown to be of great importance and needs additional studies and experiments for correct determination.

Constant width and tree distance and variable inflow wave height

The results show that an increase in the wave height increased the absorbed force. For instance, in a 60-cm width and a 10 × 10 cm distance, absorbed wave force increased by 3.217 and 0.613 times at 12 cm height compared with 6 and 9 cm, respectively. In fact, a height increase causes the wave to hit the cover faster, more drag force to be created from the cover (because of increased contact surface and hitting velocity), and more force to be absorbed from the waves.

Arrangement effects

Results (Tables 3 and 4) show that the staggered arrangement was more effective in all comparisons than the parallel arrangement reduce the waves force.

The maximum difference in absorbed force between two arrangements was reported to be 29.5% in the density of 147.

TCF effects on the drag coefficient

To study the effects of TCF on drag coefficient, the drag coefficient variations was plotted against the forces absorbed from waves for each parallel (Fig. 8) and staggered mode (Fig. 9).

Fig. 8
figure 8

Drag coefficient versus force for parallel arrangement, (P1–P4)

Full size image
Fig. 9
figure 9

Drag coefficient against force for staggered arrangement, (S1–S4)

Full size image

As seen in Figs. 8 and 9, an increase in rows and cover widths and a decrease in inter-cover distances increased drag coefficient and the force. For instance, at a wave height of 9 cm and a fixed distance of 5 × 5 cm, increasing rows from 4 to 13 increased the drag coefficient by 36.65%. At the same wave height, a fixed cover width (60 cm), and a variable distance, reducing the distance from 20 × 20 cm to 5 × 5 cm, for example, increased the drag coefficient by 27.54%, because more wave force was absorbed and dissipated by the cover due to more number of rows against the wave and more applied resistance. The staggered arrangement was more effective than the parallel arrangement in absorbing the wave force and consequently increasing the drag coefficient. The impact surface against the wave in the staggered state is greater than it is in the parallel state due to the different arrangements of the cover. Hence, when the wave hits the staggered cover, the drag force resistance against the wave passage is higher. As inter-tree distance decreases, the graphs become denser because force variations with the drag coefficient are more scattered at longer distances, to some extent showing TCF inter-tree distance and density effects, as major factors, on the force absorbed from the waves.

TCF width effects on the drag coefficient

Figures 10 and 11 show that reduced cover rows reduced the drag coefficient; the addition of one cover row increased the drag coefficient by averagely 9.7%. Increasing the width and rows increases the cover resistance against the flow, and hence, more force is drawn from the wave causing the drag coefficient to increase. However, drag coefficient increase rate was not a fixed or an absolute increase because after a certain value, known here as the optimal limit, the growth intensity was reduced. In other words, after the optimal limit, the drag coefficient increase rate did not justify the row increase in regard to economic/administrative issues (although no accurate economic calculations were done).

Fig. 10
figure 10

Effects of the cover row increase on the drag coefficient in parallel mode, (P1–P4) *Drag coefficient of smaller tree group: CdS, Drag coefficient of longer tree group: CdL

Full size image
Fig. 11
figure 11

Effects of cover row increase on the drag coefficient instaggered mode, (S1–S4)

Full size image

Drag coefficient increase was addressed in maximum and minimum distances, and the optimal limit was obtained at the highest wave height (12 cm) and for each inter-tree distance. For instance, at a 20 × 20 cm distance in both arrangements, a row increase from 2 to 3 and from 3 to 4 added 7.94 and 16.38% to the drag coefficient, respectively. In fact, a row increase from 2 to 4 caused the drag coefficient to reach from 4.72 to 5.93, which means in the 4-row case, the share of the first 2 rows was 79% and that of the next 2 rows was only 21%.

At a 5 × 5 cm distance, increasing the rows from 4 to 7, 7 to 10, and 10 to 13 increased the drag coefficient by 8.43, 8.02, and 11.89%, respectively. In fact, an increase of 9 rows raised the drag coefficient by 30%, while the first 4 rows increased the drag coefficient by around 70%, causing the rise from 4 to 13 to cause the drag coefficient to reach from 5.41 to 7.06 (in a 13-row arrangement). In 5 × 5 cm inter-tree distance, the drag coefficient intensity reduced for each cover row increase. In 20 × 20 cm distance, the drag coefficient increase rate for each cover row was higher indicating a better cover performance. As mentioned earlier (Sect. 3–2-2), further studies need to be conducted on determining the optimum distance value and to use the wake zone created by each tree as a basis to place the next one.

TCF density effects on the drag coefficient

As shown in Fig. 12, an increase in the density and in the number of rows increased both the drag coefficient and cover resistance against the flow. Increasing the density increased drag coefficient and cover resistance by 62.32 and 54.31%, in staggered and parallel arrangement respectively. Comparing two arrangements (Fig. 12) reveals that the staggered mode was more efficient than the parallel mode (averagely 11.38%) in showing more resistance against the wave.

Fig. 12
figure 12

Drag coefficient against the TCF density (a: Staggered, b: Parallel)

Full size image

Although an increase in the drag force with the TCF density is mainly due to an increase in the area that absorbs the force, scale, wave height and TCF (type, material, density and definition) too affect the drag coefficient considerably. Previous studies have estimated lower values for the drag coefficient because they have defined the force-absorbing area differently and estimated higher force values, which can be attributed to their using of different tree simulation models that, instead of cylinders, used trees with branches and foliage. For instance, Hirashi and Harada (2003) and Huang et al. (2011) have reported drag coefficients in the 1–1.5 range and 1.5–2 range, respectively.

A relationship for estimating the drag coefficient (Cd)

Statistical analyses were used to study the interaction effects of extracted dimensionless parameters on the drag coefficient and to present a mathematical relationship (Eq. 10) to predict the related values as follows:

$$C_{{\text{d}}} = 8.882\left( {H/h_{{\text{v}}} } \right)^{0.702} + 0.152\left( {\frac{{{\uptau }_{{\text{v}}} }}{{{\uprho }_{{\text{w}}} {\text{V}}^{2} }}} \right)^{0.1},$$
(10)

where \(C_{{\text{d}}}\) is the drag coefficient, \(\frac{\mathrm{H}}{{\mathrm{h}}_{\mathrm{v}}}\) is the relative immersion (dimensionless ratio of the wave incident height to the tree height) and dimensionless \(\frac{{\uptau }_{\mathrm{v}}}{{{\uprho }_{\mathrm{w}}\mathrm{V}}^{2}}\). Equation (10) is extracted using 70% of the data recorded from the experiments and then validated using the remaining 30%. The selection of these parameters is based on the sensitivity analysis performed for all independent parameters with the dependent parameters.

As seen in the statistics evaluations (Table 5), the results that calculated via Eq. (10) were acceptably accurate and the predicted value of the drag coefficient was close to experimental results. The correlation coefficient (R square) and efficiency coefficient (CE) of this formula were close to 1 (representing a perfect correlation and a good model), since the NRMSE range is (0, + ∞), and it was near zero here, and the simulation is excellent accurate (< 10%) (Jamieson et al. 1991). Also since P value < 0.05, the proposed formula is acceptable at 95% confidence level. As shown in Fig. 13, the correlation is relatively high because the points are closely scattered around the 45° line.

Table 5 Evaluation statistics of the drag coefficient estimation formula
Full size table
Fig. 13
figure 13

Comparison of the observed drag coefficient with the predicted one by Eq. (10)

Full size image

When laboratories have limitations, relations found in this research can be used in similar cases with the same accuracy. However, this study has used dimensionless ratios effective on the studied phenomenon to maintain the all-inclusiveness of the presented formula; hence, it can be generalized to reality as well. But, using the results under different conditions needs future experiments.

In addition to using statistical and mathematical methods to define a model for predicting the studied parameter, data-based methods can also be used. Machine learning models have been recently used in certain researches on the costal phenomena; hence, we suggest they be used in future studies, too, to find appropriate formula (Ghanbari-Adivi et al. 2022; and Jalil-Masir et al. 2022).

Conclusion

This research addressed the effective contributions of TCF to protection against the long waves in tsunami/storm conditions. By direct measuring of trees drag forces and waves velocities, TCF efficiency to create the resistive forces and in wave force absorption/attenuation was investigated in the form of drag force.

The effects of cover density, distance, width, arrangement, and wave height on wave force absorption were also looked at in order to attain a better drag coefficient. Particularly at higher densities and wider cover widths, more variances were observed. The drag coefficient grew as the number of rows, cover widths, and inter-tree spacing all increased. So that increasing the width of the covered area by 4 times increases the drag coefficient by about 26%, and reducing the inter-tree distance by 75% increases it by about 20%, but it has not highly increased with a decrease in the distance or an increase in the width. Under the smallest/largest inter-tree distances, an increase in the cover rows reduces/increases the drag coefficient. In fact, the inter-tree distance and drag coefficient are inversely related, i.e., for a specified number of trees, a 20 × 20 tree arrangement performs better than other arrangements with smaller inter-tree distances (same No. of trees); among the cases examined in this research, this superiority is estimated to be, averagely, 24%. As reducing the inter-tree distance naturally increases the resistance, but imposes more implementation costs, determining an optimal density including optimal inter-tree distance and optimal width for the cover area is a very important initial step in implementing such plans.

On the other hand, at a given cover width, the effects of the back rows on the total drag were less than those of the front rows. The intensity of increased drag coefficient in a known width with more trees is a highly important factor on enhancing the coastal cover performance against the waves.

Increasing the number of rows of trees from 2 to 4 rows had increased the drag coefficient by about 29%, but increasing the number of rows of trees from 4 to 13 rows only increased the drag coefficient by 33%. Further studies need to be conducted on determining the optimum distance. Since the post-cover wave height reduction has not been significant in small widths and large inter-tree spacing, determining the optimum distance is important to prevent group effect being reduced to a single-tree effect.

Studies showed that the staggered arrangement was shown to be more efficient than the parallel layout. Staggered tree arrangement, compared with the parallel form, has increased the drag coefficient by about 14.5%, averagely.

Explaining the effects of coastal conditions on wave-caused drag force, practically with independent measurable wave-coast variables, enables a better understanding and estimation of drag coefficient to evaluate numerical models. Finally, a relationship with acceptable accuracy was presented to predict the drag coefficient with a correlation coefficient of 0.97.