Introduction

Naturally fractured reservoirs have attracted increasing attention in oil and gas explorations. Analysis and understanding of the distribution law of fracture development are important in exploration and development of fractured reservoirs, since mesoscopic fracture distributions and development degrees control the enrichment of underground oil and gas. Meanwhile, fluid identification in fractured reservoirs has been one of the hot spots of the present researches.

Anisotropy, which is induced by aligned fractures, is a useful attribute for the detection and characterization of fractures. As a consequence of overlying strata compaction and tectonic stress, horizontal or low angle fractures usually disappear, while high angle and near vertical fractures remain. Theoretically, layers with vertical or near vertical aligned fractures could be simplified as transversely isotropic media with a horizontal symmetry axis, namely, horizontal transverse isotropy (HTI) media. Therefore, the basis for prediction of fractured reservoirs is the propagation theory of seismic waves in anisotropic media, especially in HTI media, which has attracted considerable interests in recent years. Fracture-induced anisotropy has notable effects on seismic wave propagation. As fractures in subsurface media are more developed, the azimuth differences of seismic waves are more remarkable. The azimuthal differences between seismic channels can be characterized through a series of seismic attributes, such as amplitude, velocity, travel time, attenuation, and so on. Many conventional seismic techniques that use longitude wave data are available to estimate seismic anisotropy. Detections of azimuthal variations of normal moveout velocities and reflection amplitudes are the most widely adopted methods for characterizing and predicting fractures. Daley and Hron (1977) derived the formula of reflection and transmission coefficients for longitude wave and transition wave in vertical transverse isotropy (VTI) media. Banik (1987) proposed a P-wave reflection coefficient expressed by weak anisotropic parameters on the interface between two transverse isotropy (TI) media with small velocity differences. Schoenberg and Protazio (1992) applied the Zoeppritz equation to anisotropic media and calculated the relationship between reflection coefficient and azimuthal angles. Based on the studies by Banik (1987) and Thomsen (1995), Rüger (1997) derived a more precise approximation expression of longitudinal wave reflection coefficient which could fit relatively larger incident angles. Václav and Ivan (1998) confirmed that P-wave reflection coefficient of weak anisotropic media was close to the accurate value. Macbeth and Lynn (2000) studied the azimuthal changes characteristics of P-wave amplitude associated with fluid.

Fluid recognition using seismic data is commonly relied on the inversion of those abnormal features related to fluid which are called fluid factors. The efficiency of fluid recognition mainly depends on two aspects: the sensitivity of fluid factors and the reliability of seismic inversion. For isotropic media, elastic parameters and combination of AVO (amplitude versus offset) attributes are common fluid factors (Huang et al. 2012). Smith and Gidlow (1987) first proposed the concept of fluid factor and detected gas-bearing layer using weighted stack method; Fatti (1994) used the difference between P-wave impedance and S-wave impedance to detect gas-bearing layers; Goodway et al. (1997) adopted parameters such as λρ, μρ, and λ/μ as fluid factors, and achieved preferable effects; Gray (2002) directly extracted λ and μ by improving the Goodway’s method. Russell et al. (2011) studied the Gassmann fluid term, which could be used to recognize fluid in deep reservoirs. For fractured anisotropic reservoirs, we must choose parameters independent with azimuths to construct fluid factors, such as fracture excess compliance (Chen et al. 2017). Such conventional fluid factors have achieved good results in practical applications, but they ignore the influence of seismic dispersion and attenuation, resulting in low precision and low accuracy.

According to Chapman et al. (2006), velocity dispersion and attenuation greatly affect the AVA (Amplitude Versus Angle) and AVAZ (Amplitude Versus incident Angle and Azimuth) analysis of seismic data for fractured reservoirs. The influence is more considerable when large offset data are available. The reflection coefficient on the interface between the overburden layer and fractured layer is frequency dependent, and is closely related to fracture parameters (e.g., fracture density, fracture size, and fracture aperture) and fluid properties (e.g., bulk modulus and viscosity). The frequency-dependent reflection coefficient contains more information about the reservoir in comparison with the frequency-independent reflection coefficient. Frequency-dependent amplitude versus offset (FAVO) in isotropic media has been studied in-depth. Wilson (2010) proposed a method for calculating dispersion property based on the Smith–Gidlow approximation, and constructed the FAVO inversion frame on the basis of petrophysical theory, spectral decomposition, and amplitude versus offset (AVO) analysis. Wu et al. (2012) applied FAVO to field data using Wigner–Ville distribution, and estimated gas saturation using FAVO analysis (2014). Zhang et al. (2011) derived a frequency-dependent reflection coefficient approximation based on dispersion degree and gradient of longitudinal wave. Cheng and Xu (2012) constructed a series of FAVO attributes to recognize fluid. Zhang et al. (2014) studied the application of dispersion attribute for Gassmann fluid term in fluid identification.

Studies for FAVO in anisotropy media, especially the anisotropy parameters variation with frequency, however, are relatively scarce. Due to wave-induced fluid flow taking place within seismic frequency band, the seismic wave propagation, as well as the anisotropy is frequency dependent, which is conducive for fluid identification. The special theory of squirt flow of Chapman (2003) took mesoscopic fluid flow into account and could explain the dispersion and attenuation of seismic waves reasonably. In this paper, we first analyze the frequency-dependent characteristics of HTI media based on Chapman’s model, and then present a new attribute P-wave anisotropy parameter dispersion gradient (PADG) as the fluid indicator to detect gas in fractured reservoirs. We have analyzed the sensitivity of PADG on fluid type, and discuss its restrictions and adaption capacity. Based on the relationship between PADG and Rüger’s reflection coefficient formula in anisotropy media, the inversion scheme to obtain the PADG attribute using the azimuthal P-wave seismic data after spectral decomposition is established. We use a spectral composition method combining the Orthogonal Matching Pursuit and Wigner–Ville distribution to prepare the frequency-division seismic data. Finally, we apply the method to synthetic seismogram and field data and the results demonstrate its potential for gas identification for reservoirs with meter-scaled fractures.

Methodology

Selection of fluid factor

Squirt-flow model can characterize the dispersion and attenuation due to wave-induced fluid flow in porous media. Squirt flow (Mavko and Jizba 1991) is caused by pressure gradients at the microscopic or mesoscopic scale and in the direction potentially different from that of the wave propagation. Chapman et al. (2002) present a poroelastic model based on squirt-flow theory and calculated the frequency-dependent modulus, considering the fluid exchange between pores and microcracks and between microcracks of different orientations. Then, Chapman (2003) extended the microscale squirt-flow model to a mesoscopic scale by adding a set of aligned mesoscale fractures in porous background media and analyzed frequency-dependent anisotropy caused by fluid flow between fractures, pores, and microcracks.

In Chapman’s mesoscopic squirt-flow model, the radii of the microcracks and the pores are identified with the grain size, whereas the fracture radius is much greater than the grain size but smaller than the wavelength of the seismic waves. Microcracks and pores are interconnected and connected to at most one fracture. Fractures are not connected with other fractures. The random isotropic distribution of microcracks and pores and aligned fractures make the model for fractured porous media possess hexagonal symmetry, and when the fractures are vertical, the model will be HTI media. One of the crucial parameter is the characteristic frequency in “squirt-flow” theory. The model concerns two scales of fluid flow, so there are two timescales (reciprocal of characteristic frequency) τ m and τ f , corresponding to microcracks and fractures. The relationship between the two timescales is

$$\tau_{\text{f}} = \frac{{a_{\text{f}} }}{\varsigma }\tau_{m} ,$$
(1)

where a f is the radius of fracture and ς is the grain size. The frequency-dependent anisotropic elastic tensor is expressed as

$$C = C^{0} - \varphi_{\text{p}} C^{1} - \varepsilon_{\text{c}} C^{2} - \varepsilon_{\text{f}} C^{3} ,$$
(2)

where C 0 is the isotropic elastic tensor for the background medium; C 1, C 2, and C 3 are the corrections to the stiffness tensor of pores, microcracks, and fractures, respectively. φ p is the porosity; ɛ c is microcrack density and ɛ f is the density of the aligned fractures. C 1, C 2, and C 3 in complex expression containing attenuation information are functions of the Lame parameters (λ and μ), fluid properties, fracture length, time-scale parameters, and frequency. The Chapman model is restricted to low porosity case originally. For the cases of high porosity calculation, the stiffness tensor with the grain moduli λ and μ can result in substantial errors (Al-Harrasi et al. 2011). Chapman et al. (2003) proposed a modified parameterization method which overcomes the restriction to low porosity. They suggested using the velocities V 0 p and V 0 s of the unfractured porous rock to calculate λ 0 and μ 0 first as

$$\lambda^{0} = (V_{p}^{0} )^{2} \rho - 2\mu^{0} ,$$
(3)
$$\mu^{0} = (V_{s}^{0} )^{2} \rho ,$$
(4)

where ρ is the density of the saturated rock. The isotropic tensor C 0 needs to be expressed by the measured isotropic velocities at a certain frequency f 0 with the correction from pores and cracks. The new Lame parameters are defined as

$$\varLambda = \lambda^{0} + \varPhi_{{{\text{c}},{\text{p}}}} (\lambda^{0} ,\mu^{0} ,f_{0} ),$$
(5)
$$\varUpsilon = \mu^{0} + \varPhi_{{{\text{c}},{\text{p}}}} (\lambda^{0} ,\mu^{0} ,f_{0} ),$$
(6)

where \(\varPhi_{{{\text{c}},{\text{p}}}}\) is the correction function due to the microcracks and pores. Thus, Eq. 2 becomes

$$C\left( f \right) = C^{0} \left( {\varLambda ,\varUpsilon } \right) - \varPhi_{P} C^{1} \left( {\lambda^{0} ,\mu^{0} ,f} \right) - \varepsilon_{c} C^{2} \left( {\lambda^{0} ,\mu^{0} ,f} \right) - \varepsilon_{f} C^{3} \left( {\lambda^{0} ,\mu^{0} ,f} \right),$$
(7)

where f denotes the frequency. The detailed parameterization process is available in the literature (Chapman 2003).

To single out the fluid identification factor, we first performed a numerical simulation to evaluate the frequency dependence of P-wave-related attributes and their fluid sensitivities. The reference velocities of “unfractured rock” (saturated with brine water, a 10% porosity) are V 0 p  = 4000 m/s, V 0 s  = 2500 m/s, respectively. The fracture density which only influences the degree of anisotropy is set to be 0.05. The average fracture radius is 1 m. The microcrack density is zero for simplicity. In the squirt-flow model, there is a transition zone, where maximum velocity dispersion and attenuation occurs. The central frequency of this transition zone for an unfractured rock is often referred to as the mineral scale “squirt-flow frequency”, ω m (angular frequency), with the associated relaxation timescale, τ m = ω −1m . τ m is usually evaluated from laboratory experiments, but it is found to be proportional to the viscosity of the saturating fluid, and inversely proportional to the permeability of the host rock. Here, the timescale is assumed to be τ m = 4.75 × 10−5s for water saturation and τ m = 9.5 × 10−7s for gas saturation (Al-Harrasi 2011). τ f is calculated through Eq. 1 (ς is assumed to be 200 μm).

After the frequency-dependent stiffness tensor of the complex media including pores and aligned fractures is derived through the Chapman model, the P-wave anisotropic parameter ɛ and ɛ dispersion gradient (PADG) are expressed as

$$\varepsilon = \frac{{C_{11} - C_{33} }}{{2C_{33} }},$$
(8)
$${\text{PADG}} = \frac{\partial \varepsilon }{\partial f}.$$
(9)

The P-wave velocity at normal incidence in HTI media is computed as

$$V_{p} = \sqrt {C_{33} /\rho } .$$
(10)

C 11 and C 33 are the coefficients of the stiffness tensor obtained by Eq. 7. ρ is the density of the saturated rock. As the stiffness tensor derived from Chapman model is complex and frequency dependent, the P-wave velocity from Eq. 10 is also a complex value. The real-phase velocity and inverse quality factor can be calculated as

$$v_{p} = \left[ {\text{Re} \left( {\frac{1}{{V_{p} }}} \right)} \right]^{ - 1} ,$$
(11)
$$Q_{p}^{ - 1} = \frac{{\text{Im} \left( {V_{p} } \right)}}{{\text{Re} \left( {V_{p} } \right)}}.$$
(12)

Figure 1 illustrates the predicted dependence of P-wave velocity (Fig. 1a) and Q −1 p (Fig. 1b) on frequency for water and gas saturation (normal incidence). As real seismic data normally lack the low-frequency information, the frequency band considered in the model is set to 10–100 Hz. We can see that there are obvious differences for the P-wave velocities at gas and water saturation cases, as shown in Fig. 1a. The velocity for gas saturation is slightly frequency dependent, increasing from 3555 to 3575 m/s, while the velocity for water saturation is almost unchanged, so that the transition zone for gas is located in the frequency band we choose. Furthermore, the velocity dispersion gradients for both gas and water saturation are displayed in Fig. 2. The velocity dispersion gradient curve shows the distinction between gas and water more clearly. The velocity dispersion gradient for gas is nonlinear by presenting an initial increase and then a decreasing trend. However, for the case of water saturation, the velocity dispersion gradient quickly drops to 0 in the frequency band 10–100 Hz. The velocity dispersion gradient shows a similar pattern with P-wave attenuation, as shown in Fig. 1b. The P-wave anisotropic parameter ɛ is expected to show an analogous feature with P-wave velocity. Figure 3 shows variations of ɛ (Fig. 3a) and PADG (Fig. 3b) dependent on frequency. Notably, the high value of PADG indicates the occurrence of gas. Therefore, we finalize the PADG as the fluid factor for gas detection in fractured reservoirs.

Fig. 1
figure 1

Variation of velocity (a) and inverse quality factor (b) with frequency for gas and water saturation situation

Full size image
Fig. 2
figure 2

Variation of P-wave velocity dispersion gradient with frequency

Full size image
Fig. 3
figure 3

Variation of ɛ (a) and ɛ dispersion gradient (PADG) (b) with frequency

Full size image

Frequency-dependent AVAZ inversion for PADG

Schoenberg and Protazio (1992) gave explicit solutions for the plane-wave reflection and transmission problem using submatrices of the Zoeppritz equation coefficient matrix. For weakly anisotropic media, simple analytical formulas can be used to compute AVAZ responses at the interface of anisotropic media that can be either VTI, HTI, or orthorhombic. The P-wave reflection coefficient for weakly anisotropic VTI media as limited by small impedance contrast was derived by Thomsen (1993) and corrected by Rüger (1997). For HTI media, Chen (1995) and Rüger (1997, 1998) derived the P-wave reflection coefficient in the symmetry planes for reflections at the interface of two HTI media, which has become one of the most common equations to calculate the AVAZ response and could be written as

$$\begin{aligned} R_{\text{PP}}^{\text{HTI}} (\theta ,\varphi ) & = \frac{1}{2}\frac{\Delta Z}{{\overline{Z} }} + \frac{1}{2}\left\{ {\frac{\Delta \alpha }{{\overline{\alpha } }} - \left( {\frac{{2\overline{\beta } }}{{\overline{\alpha } }}} \right)^{2} \frac{\Delta G}{{\overline{G} }}} \right. \\ & \quad + \;\left. {\left[ {\Delta \delta^{{({\text{v}})}} + 2\left( {\frac{{2\overline{\beta } }}{{\overline{\alpha } }}} \right)^{2} \Delta \gamma } \right]cos^{2} \varphi } \right\}\} sin^{2} \theta \\ & \quad + \frac{1}{2}\left\{ {\frac{\Delta \alpha }{{\overline{\alpha } }} + \Delta \varepsilon^{{({\text{v}})}} cos^{4} \varphi + \Delta \delta^{{({\text{v}})}} \sin^{2} \varphi cos^{2} \varphi } \right\}sin^{2} \theta \tan^{2} \theta \\ \end{aligned} ,$$
(13)

where θ is incident angle and φ is azimuthal angle; α and β are the velocities of longitude wave and shear wave propagating in the isotropic plane, respectively; Z is P-wave impedance; and G = ρβ 2 is the tangential modulus with ρ for density. The symbol Δ denotes the contrast across an interface. Bar over a symbol denotes an average calculation. ɛ (v),δ (v) and γ are the anisotropy coefficients for HTI media proposed by Tsvankin (1997) based on the Thomsen’s result (1995) for VTI media.

From Eq. 13, the reflection coefficient R HTIPP can be divided into two parts: the isotropic part R isoPP (14) dependent on incident angle θ and the anisotropic part R aniPP (15) dependent both on θ and azimuthal angle φ:

$$R_{\text{pp}}^{\text{iso}} = \frac{1}{2}\frac{\Delta Z}{Z} + \frac{1}{2}\left\{ {\frac{\Delta \alpha }{{\overline{\alpha } }} - \left( {\frac{{2\overline{\beta } }}{{\overline{\alpha } }}} \right)^{2} \frac{\Delta G}{{\overline{G} }}} \right\}\sin^{2} \theta + \frac{1}{2}\frac{\Delta \alpha }{{\overline{\alpha } }}\sin^{2} \theta \tan^{2} \theta$$
(14)
$$R_{\text{pp}}^{\text{ani}} = \left( {\frac{{2\overline{\beta } }}{{\overline{\alpha } }}} \right)^{2} \Delta \gamma \cos^{2} \varphi \sin^{2} \theta + \frac{1}{2}\left\{ {\Delta \varepsilon^{(v)} \cos^{4} \varphi + \Delta \delta^{(v)} \sin^{2} \varphi \cos^{2} \varphi } \right\}\sin^{2} \theta \tan^{2} \theta .$$
(15)

To simplify the reflection coefficient expression, a subtraction operation between two reflection coefficients at two orthogonal azimuths φ and φ + π/2 is done. To distinguish the elastic parameters difference between two layers from the reflection coefficient difference, δR PP (θ, φ) is used to denote the difference of the reflection coefficients of two azimuths. After subtraction, we obtain

$$\begin{aligned} \delta R_{\text{PP}} (\theta ,\varphi ) & = R(\theta ,\varphi )_{\text{PP}} - R(\theta ,\varphi + \pi /2)_{\text{PP}} \\ & = \frac{1}{2}\left[ {2\Delta \gamma \left( {\frac{{2\overline{\beta } }}{{\overline{\alpha } }}} \right)^{2} + \Delta \delta^{(v)} } \right]\cos 2\varphi \sin^{2} \theta \\ &\quad+\;\frac{1}{2}\Delta \varepsilon^{(v)} \cos 2\varphi \sin^{2} \theta \tan^{2} \theta . \\ \end{aligned}$$
(16)

Equation 16 can be written as

$$\delta R_{\text{PP}} (\theta ,\varphi ) = a(\theta ,\varphi )\Delta \gamma + b(\theta ,\varphi )\Delta \delta^{(v)} + c(\theta ,\varphi )\Delta \varepsilon^{(v)} ,$$
(17)

where

$$\begin{aligned} a(\theta ,\varphi ) & = \left( {\frac{{2\overline{\beta } }}{{\overline{\alpha } }}} \right)^{2} \cos 2\varphi \sin^{2} \theta \\ b(\theta ,\varphi ) & = \frac{1}{2}\cos 2\varphi \sin^{2} \theta \\ c(\theta ,\varphi ) & = \frac{1}{2}\cos 2\varphi \sin^{2} \theta \tan^{2} \theta . \\ \end{aligned}$$
(18)

There are only three Thomsen style anisotropy parameters and velocity ratio remaining as the longitude wave impedance and tangential modulus have been eliminated. Under certain circumstances, the velocity ratio is often known from well-logging data. Therefore, there are only three unknown quantities in Eq. 17. As mentioned previously, the anisotropy parameters are frequency dependent, and δR PP is considered to vary with frequency in the dispersive media:

$$\delta R_{\text{PP}} (\theta ,\varphi ,f) = a(\theta ,\varphi )\Delta \gamma \left( f \right) + b(\theta ,\varphi )\Delta \delta^{(v)} \left( f \right) + c(\theta ,\varphi )\Delta \varepsilon^{(v)} \left( f \right),$$
(19)

where f represents frequency.

Expand Eq. 19 as a first-order Taylor series around a reference frequency f 0:

$$\begin{aligned} \delta R_{\text{PP}} (\theta ,\varphi ,f) & = a(\theta ,\varphi )\Delta \gamma \left( {f_{0} } \right) + (f - f_{0} )a(\theta ,\varphi )I_{a} \\ & \quad + \;b(\theta ,\varphi )\Delta \delta^{(v)} \left( {f_{0} } \right) + (f - f_{0} )b(\theta ,\varphi )I_{b} \\ & \quad +\; c(\theta ,\varphi )\Delta \varepsilon^{(v)} \left( {f_{0} } \right) + (f - f_{0} )c(\theta ,\varphi )I_{c} , \\ \end{aligned}$$
(20)

where I a , I b, and I c are the derivatives of the anisotropy parameter contrasts with respect to frequency:

$$I_{a} = \frac{d\Delta \gamma }{df},\quad I_{b} = \frac{{d\Delta \delta^{(v)} }}{df},\quad I_{c} = \frac{{d\Delta \varepsilon^{(v)} }}{df}.$$
(21)

A continuation of rewriting Eq. 20 yields

$$\begin{aligned} \delta R_{\text{PP}} (\theta ,\varphi ,f) - \delta R_{\text{PP}} (\theta ,\varphi ,f_{0} ) & = (f - f_{0} )a(\theta ,\varphi )I_{a} \\ & \quad + (f - f_{0} )b(\theta ,\varphi )I_{b} + (f - f_{0} )c(\theta ,\varphi )I_{c} , \\ \end{aligned}$$
(22)

where \(\delta R_{\text{PP}} (\theta ,\varphi ,f_{0} ) = {\text{a(}}\theta ,\varphi )\Delta \gamma \left( {f_{0} } \right) + b(\theta ,\varphi )\Delta \delta^{{ ( {\text{v)}}}} \left( {f_{0} } \right) + c(\theta ,\varphi )\Delta \varepsilon^{{ ( {\text{v)}}}} \left( {f_{0} } \right).\)

To emphasize the azimuthal variation of seismic waves, we keep the incident angle as a fixed value. Accordingly, Eq. 20 with regard to different frequency and azimuthal angle has the form of

$$\begin{aligned} \Delta \delta R_{\text{PP}} (\varphi_{i} ,f_{j} ) & = (f_{j} - f_{0} )a(\varphi_{i} )I_{a} \\ & \quad + (f_{j} - f_{0} )b(\varphi_{i} )I_{b} + (f_{j} - f_{0} )c(\varphi_{i} )I_{c} \\ \end{aligned} ,$$
(23)

where \(\Delta \delta R_{\text{PP}} (\varphi_{i} ,f_{j} ) = \delta R_{\text{PP}} (\varphi_{i} ,f_{j} ) - \delta R_{\text{PP}} (\varphi_{i} ,f_{0} ).\)

Equation 23 can be expressed in matrix form as d = G m. d denotes the data. G is the kernel function. m is the unknown parameters. For the simple circumstance of two layers, two frequencies and three sets of azimuths, the specific form of Eq. 23 is

$$\left[ {\begin{array}{*{20}c} {\Delta \delta R_{1}^{1} } \\ {\Delta \delta R_{2}^{1} } \\ {\Delta \delta R_{3}^{1} } \\ {\Delta \delta R_{1}^{2} } \\ {\Delta \delta R_{2}^{2} } \\ {\Delta \delta R_{3}^{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {(f_{1} - f_{0} )a(\varphi_{1} )} & {(f_{1} - f_{0} )b(\varphi_{1} )} & {(f_{1} - f_{0} )c(\varphi_{1} )} \\ {(f_{1} - f_{0} )a(\varphi_{2} )} & {(f_{1} - f_{0} )b(\varphi_{2} )} & {(f_{1} - f_{0} )c(\varphi_{2} )} \\ {(f_{1} - f_{0} )a(\varphi_{3} )} & {(f_{1} - f_{0} )b(\varphi_{3} )} & {(f_{1} - f_{0} )c(\varphi_{3} )} \\ {(f_{2} - f_{0} )a(\varphi_{1} )} & {(f_{2} - f_{0} )b(\varphi_{1} )} & {(f_{2} - f_{0} )c(\varphi_{1} )} \\ {(f_{2} - f_{0} )a(\varphi_{2} )} & {(f_{2} - f_{0} )b(\varphi_{2} )} & {(f_{2} - f_{0} )c(\varphi_{2} )} \\ {(f_{2} - f_{0} )a(\varphi_{3} )} & {(f_{2} - f_{0} )b(\varphi_{3} )} & {(f_{2} - f_{0} )c(\varphi_{3} )} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {I_{a} } \\ {I_{b} } \\ {I_{c} } \\ \end{array} } \right].$$
(24)

The seismic records can be expressed by convolution of wavelets and reflection coefficients: D = w * R + e, where D represents seismic amplitude, w represents wavelet, R represents reflection coefficient, and e represents the noise term. Therefore, Eq. 24 in a well-known inverse problem form is

$$\Delta \delta d = {\mathbf{G'}}m,$$
(25)

where Δδd is the seismic data difference; G’ = WA, where W is wavelet matrix that is introduced to simplify calculation, and A is the matrix related to azimuthal angles. An extension of Eq. 24 up to n sample points, q azimuths, and k frequencies is

$$\left[ {\begin{array}{*{20}c} {\Delta \delta \varvec{d}_{1}^{1} } \\ {\Delta \delta \varvec{d}_{2}^{1} } \\ \vdots \\ {\Delta \delta \varvec{d}_{q}^{1} } \\ {\Delta \delta \varvec{d}_{1}^{2} } \\ \vdots \\ {\Delta \delta \varvec{d}_{q}^{2} } \\ \vdots \\ {\Delta \delta \varvec{d}_{q}^{k} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\varvec{W}^{1} \varvec{A}_{1}^{1} } & {\varvec{W}^{1} \varvec{B}_{1}^{1} } & {\varvec{W}^{1} \varvec{C}_{1}^{1} } \\ {\varvec{W}^{1} \varvec{A}_{2}^{1} } & {\varvec{W}^{1} \varvec{B}_{2}^{1} } & {\varvec{W}^{1} \varvec{C}_{2}^{1} } \\ \vdots & \vdots & \vdots \\ {\varvec{W}^{1} \varvec{A}_{q}^{1} } & {\varvec{W}^{1} \varvec{B}_{q}^{1} } & {\varvec{W}^{1} \varvec{C}_{q}^{1} } \\ {\varvec{W}^{2} \varvec{A}_{1}^{2} } & {\varvec{W}^{2} \varvec{B}_{1}^{2} } & {\varvec{W}^{2} \varvec{C}_{1}^{2} } \\ \vdots & \vdots & \vdots \\ {\varvec{W}^{2} \varvec{A}_{q}^{2} } & {\varvec{W}^{2} \varvec{B}_{q}^{2} } & {\varvec{W}^{2} \varvec{C}_{q}^{2} } \\ \vdots & \vdots & \vdots \\ {\varvec{W}^{k} \varvec{A}_{q}^{k} } & {\varvec{W}^{k} \varvec{B}_{q}^{k} } & {\varvec{W}^{k} \varvec{C}_{q}^{k} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {I_{a} } \\ {I_{b} } \\ {I_{c} } \\ \end{array} } \right].$$
(26)

In Eq. 26, \(\Delta \delta \varvec{d}_{{i_{{\left( {i = 1,2, \ldots ,q;j = 1,2, \ldots ,k} \right)}} }}^{J}\) represents the column vector of length n for the ith azimuth, jth frequency; \(\varvec{W}^{j}_{{\left( {j = 1,2, \ldots ,k} \right)}}\) is the wavelet matrix corresponding with the jth frequency; \(\varvec{A}_{i}^{j}\), \(\varvec{B}_{i}^{j}\), and \(\varvec{C}_{i}^{j}\) are the diagonal matrixes related to different azimuthal angles. I a , I b, and I c are the frequency dispersion gradient vectors of three anisotropic parameters to be inverted, respectively. Above all, Eq. 26 is a linear system of equations on I a , I b, and I c , under the circumstance of known α/β. We can solve the equations through the damped least squares method. The unknown m = [I a , I b , I c ]T was derived by

$${\mathbf{m}} = \left[ {{\mathbf{G^{\prime}}}^{T} {\mathbf{G^{\prime}}} + \sigma {\mathbf{I}}} \right]{\mathbf{G^{\prime}}}^{\rm T} \delta {\mathbf{d}},$$
(27)

where \({\mathbf{G^{\prime}}}^{\rm T}\) is the transpose matrix of \({\mathbf{G^{\prime}}}\), σ is the damping factor, and I is the identity matrix. \({\mathbf{I}}_{\varvec{c}}\) is the P-wave anisotropy dispersion gradient (PADG) that we focus on treated as the new fluid indicator.

Spectral decomposition

Application of spectral decomposition techniques allows frequency-dependent behavior to be detected from seismic data. Reflections from hydrocarbon-saturated zones can be anomalous in this regard (Castagna et al. 2003). For nonstationary signals, such as seismic record, spectral decomposition techniques transform the signal from the time domain to the frequency domain through time–frequency analysis methods. There are a variety of spectral decomposition techniques, such as the short time Fourier transform (STFT), continuous wavelet transform (CWT), generalized S transformation (GST), Wigner Ville distribution (WVD), and matching pursuit decomposition (MPD). These different techniques have been studied and used for different applications, including layer thickness determination (Partyka et al. 1999), stratigraphic visualization (Marfurt and Kirlin 2001), as well as direct hydrocarbon detection. In this paper, we combined the MPD and WVD methods for adaption to azimuthal seismic data.

Both CWT and GST use the idea of window function, belonging to linear algorithms, so that the resolution is restricted by the uncertainty principle. In other words, time and frequency resolution is a pair of contradictions. However, MPD algorithm overcomes the window function restriction by precisely characterizing the signal according to both time and frequency domains. Mallat and Zhang (1993) proposed the idea of sparse decomposition using over-complete dictionary, and introduced the MPD algorithm. MPD is excellent for analyzing spectrum characteristics of signals due to the superiority of sparse representation. As a type of greedy iteration algorithm, MPD decomposes the seismic record into a series of wavelets. MPD selects an optimal fit wavelet \(m_{{\gamma_{n} }}\) from the wavelet dictionary by matching time–frequency features in each matching process. After N times matching, the seismic signal s(t) could be expressed with N wavelets and the residual as

$$s\left( t \right) = \sum\limits_{n = 1}^{N} {a_{n} m_{{\gamma_{n} }} } + R^{\left( N \right)} f,$$
(28)

where n is the number of matching; a n is the amplitude of the nth wavelet \(m_{{\gamma_{n} }}\); and R (n) f mean the residual after n matchings and R (0) f = s(t). We adopted Morlet wavelet (29) to construct the redundant dictionary due to its high time and frequency resolution:

$$m\left( t \right) = \exp \left( { - 4\ln 2\frac{{f^{2} (t - \tau )^{2} }}{{\sigma^{2} }}} \right)\exp \left[ {i\left( {2\pi f\left( {t - \tau } \right) + \phi } \right)} \right].$$
(29)

In the Morlet wavelet function, there are four parameters: τ standing for time delay, f standing for dominant frequency, σ standing for the attenuative coefficient, and ϕ standing for phase. Thus, the Morlet wavelet can be described by the parameter set γ = {τ, f, σ, ϕ}. The creation of the wavelet set is controlled by three parameters, which are the main frequency, phase and attenuation factor, with fixed range and fine division. Thus, the wavelet set is called complete wavelets.

If the vertical projection of the signal (residual) in selected atoms is non-orthogonal, it will make each matching result suboptimal, rather than optimal. Therefore, extra iterations are needed for convergence. Orthogonal matching pursuit (OMP) can effectively solve the problem using an orthogonal processing on all selected atoms in each step of decomposition for a faster convergence. The difference between OMP and MP is that the residual after each matching in OMP is orthogonal to each atom selected before

$$\langle R^{\left( N \right)} f,\quad m_{{\gamma_{n} }} \rangle = 0,\quad n = 1,2, \ldots ,N.$$
(30)

The symbol 〈·〉 means the inner product operation.

Wigner Villa distribution (WVD) is an effective nonlinear time spectral decomposition method, but there are cross-term interferences in the analysis of composite signals that consist of multiple frequency components. However, the WVD maintains a high resolution in the time and frequency domains simultaneously for Morlet wavelet:

$$W_{{m_{{\gamma_{n} }} }} \left( {t,f} \right) = \frac{1}{2\pi }\int_{ - \infty }^{\infty } {m_{{\gamma_{n} }} \left( {t + \frac{\tau }{2}} \right)} \cdot m_{{\gamma_{n} }} \left( {t - \frac{\tau }{2}} \right) \cdot \exp \left( { - i2\pi f\tau } \right){\text{d}}\tau$$
(31)

where \(W_{{m_{{\gamma_{n} }} }} \left( {t,f} \right)\) is the time–frequency spectrum. Finally, the time–frequency spectrum of seismic signal can be calculated by Eqs. 29 and 31:

$$Af\left( {t,f} \right) = \sum\limits_{n = 0}^{N - 1} {\frac{{a_{n}^{{}} }}{{\left\| {m_{{\gamma_{n} }} } \right\|}}\sqrt {W_{{m_{{\gamma_{n} }} }} \left( {t,f} \right)} } .$$
(32)

Synthetic data example

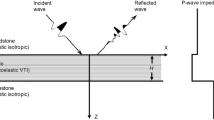
A three-layer numerical model is constructed to test the theory. The model includes an upper isotropic elastic layer with P-wave velocity of 2743 m/s, S-wave velocity of 1394 m/s, a density of 2060 kg/m3, a middle dispersive layer that consists of three parts: two water saturated sandstone layers on two sides, a gas-saturated layer in the middle, and a lower layer with parameters which are as the same as those of the upper layer. The parameters for the dispersive layer are consistent with those introduced in section “Selection of fluid factor”. The density is 2600 kg/m3 under water saturation, and 2540 kg/m3 under gas saturation.

The velocities and anisotropy parameters of the dispersive layer are calculated after the effective stiffness tensor is derived for each frequency (20, 30, 40, and 50 Hz). Then, the synthetic azimuthal gathers for different frequencies are computed using the reflection coefficient Eq. 13 with the corresponding Ricker wavelets as the explosive sources. The incident angle is fixed to 22.5°, and three pairs of azimuthal angles with 90° displacement are chosen to generate azimuthal gathers. Figure 4 displays typical synthetic gathers of two azimuths. To test the robustness of our methods, two kinds of noises have been added to the whole synthetic data, the correlated noises (Fig. 4a) and uncorrelated noises (Fig. 4b). The correlated noise is a sine wave with a frequency of 50 Hz and the uncorrelated noise is a gauss random noise. The signal-to-noise ratio (SNR) for both cases is 20. Since we need to do a subtraction operation between two seismic volumes, the correlated noises will be eliminated. Therefore, we will mainly consider the influence of random noises. The amplitudes for the gas saturation case are apparently less than those for water saturation, as the difference between the synthetic data of two azimuths (Fig. 5a). As a consequence, the strong event unfortunately hides the amplitude variation induced by anisotropy. To address this issue, we replace the absolute difference with relative difference (shown in Fig. 5). The relative difference between azimuthal gathers could prominently reveal the manifestation of seismic anisotropy (Fig. 5b). Finally, the inverted attribute PADG shown in Fig. 6a exhibits significant difference for gas and water. We also show the inversion results for cases SNR is 10 (Fig. 6b) and SNR is 30 (Fig. 6c). We can see that the noise has a great influence on the inversion results. When the SNR is low, we cannot efficiently distinguish gas and water sections just like Fig. 6b, but when the SNR is high, the PADG attribute can clearly indicate the gas section.

Fig. 4
figure 4

Synthetic gathers: a with a 50 Hz sin wave noise and b with Gauss random noise (black line: the azimuthal angle is 27°; red line: the azimuthal angle is 117°)

Full size image
Fig. 5
figure 5

Strong event unfortunately hides the amplitude variation induced by anisotropy in the absolute gather difference (a) and the relative gather difference (b) prominently reveals the manifestation of seismic anisotropy

Full size image
Fig. 6
figure 6

Estimated PADG attribute: a SNR is 20; b SNR is 10; and c SNR is 30

Full size image

Field data application

Real seismic data are derived from a fractured porous reservoir which is a typical carbonate fractured vuggy reservoir characterized by marls, limestones, and dolomites. The fractures existing widely in the area result in strong anisotropy. The imaging logging of well A shows that high angle and near vertical fractures develop in this reservoir (Fig. 7). The lengths of fractures are in the range of 0.4–5 m and the average fracture radius is about 0.8 m which is adaptive for our method. Therefore, we apply the method to the seismic data for gas detection. The inversion based on Eq. 20 requires information about fracture strikes φ f . The azimuthal angle φ in Eq. 13 is actually the combination of survey line azimuth φ s and fracture strike φ f :φ = φ s  − φ f  + π/2. The fracture strike angles are derived from frequency-independent AVAZ inversion. Figure 8 shows the rose diagram of fracture strikes. The fractures mainly develop along two mutually perpendicular directions 30° and 120° (0° indicates the direction of the North).

Fig. 7
figure 7

Imaging logging of well A

Full size image
Fig. 8
figure 8

Rose diagram of fractures

Full size image

Pre-stack seismic data of eight azimuthal angles are available for this area. Figure 7 shows the processed profiles of four pairs of mutually orthogonal survey lines. We can see that the amplitudes of same seismic survey line for different azimuth are nearly the same for basic shape (Fig. 9a). Furthermore, we extract the same seismic trace (Fig. 9b) and select the sample points (Fig. 9c) at the same time for these eight azimuthal gathers. Although the phases seem alike, the amplitudes are apparently discrepant when specific to the sample points.

Fig. 9
figure 9

a Seismic profiles for different azimuths; b seismic azimuthal traces; and c amplitude of the same sample point for different azimuths

Full size image

Seismic data resolution and signal-to-noise ratio have great influences on the structural interpretation, reservoir inversion, and other geophysical methods. The spectrum analysis provides a basis for favorable data, such as the dominant frequency and bandwidth of the seismic data for subsequent seismic data interpretation and stacking velocity inversion. The amplitude spectra of two arbitrary traces from two mutually perpendicular azimuthal data (5° and 95°) are analyzed with fast Fourier transform. As shown in Fig. 10, the dominant frequency is 28 Hz, and the bandwidth is approximately 5–65 Hz. Thus, the overall quality of seismic data with high folds in the study area meets the needs of fine seismic inversion and interpretation. Therefore, we stipulate the reference frequency as 28 Hz and define 20, 30, and 40 Hz as the set of frequencies for the frequency-division data.

Fig. 10
figure 10

Amplitude spectra of the same survey line for azimuths 5° (a) and 95° (b)

Full size image

Figures 11 and 12 show the frequency-division sections of the same survey line from two orthogonal azimuths, namely, 20, 30, and 40 Hz, respectively. As shown, the energy becomes weak when the frequency reaches 40 Hz, especially in the deep layers. Therefore, the wavelet matrix derived from the frequency-division data is needed to balance the spectra. The amplitude anisotropy results in an amplitude spectrum difference for different azimuthal seismic data, which provides a good foundation for the analysis of anisotropic parameters characteristics. Finally, the inversion workflow is performed on the data. The inverted PADG attribute is shown in Fig. 13. The results are consistent with the well-logging interpretation results (the red patch represents gas-bearing layer and the green patch represents water bearing layer). The strong magnitude of PADG at approximately 1900 ms implies the occurrence of gas, while the PADG for water bearing layer at 1750 ms is rather low.

Fig. 11
figure 11

Frequency-division sections: a 20 Hz; b 30 Hz; and c 40 Hz (the azimuthal angle is 5°)

Full size image
Fig. 12
figure 12

Frequency-division sections: a 20 Hz; b 30 Hz; and c 40 Hz (the azimuthal angle is 95°)

Full size image
Fig. 13
figure 13

Estimated PADG attribute

Full size image

Discussion

Model parameter selection

We have presented a new attribute PADG to identify fluid in fractured reservoirs from frequency-dependent AVAZ inversion. In fact, we take advantage of the sensitivity of the characteristic frequency or transition band to fluid type. The microscale characteristic frequency usually lies between the sonic and ultrasonic frequency ranges, which cannot explain the attenuation in seismic frequency band. The squirt flow between mesoscopic fractures and pores proposed by Chapman (2003) makes the characteristic frequency drop into seismic frequency band. Unfortunately, the mesoscopic characteristic frequency is controlled by both fluid type and fracture size, so as the PADG attribute. If the fracture radius keeps unchanged, the characteristic frequency is highest for gas saturation. When the fractures are meter-sized, the characteristic frequency for gas saturation is just located in seismic frequency band, generating a strong dispersion and attenuation while that for oil or water is very low, meaning that the attenuation is close to 0 in seismic frequency band. Therefore, the method has a high accuracy for gas detection for reservoirs with meter-scaled fractures. For larger fractures, the method is not suitable as the transition band becomes low enough beyond the seismic band. For smaller fractures, the PADG attribute becomes remarkable for oil or water saturation in seismic frequency band; that is to say, we can use PADG to identify oil or water when fracture radius is small, for example, millimeter scaled.

The mesoscopic relaxation time is associated with the microscale relaxation time; however, the relaxation time (characteristic frequency) for field rocks is difficult to estimate, so there is some uncertainty in our results. We use τ m from published laboratory data, since we do not have measurements of τ m for the field rocks. Chapman (2001) deduced τ m  = 2 × 10−5 s for brine-saturated sandstone and τ m  = 4 × 10−7 s for gas-saturated sandstone. Chapman et al. (2003) obtained τ m  = 7.7 × 10−7 s for gas-saturated sandstone. Al-Harrasi (2011) used τ m  = 9.5 × 10−7 s for gas-saturated carbonatite, which is adopted in this paper. According to these published data, the microscale relaxation timescales for different rocks are different but in the same order. Therefore, the uncertainty of τ m does influence the characteristic frequency, but the transition band hardly changes. Precise τ m from experiments on the field rock sample will provide more convincing and exact fluid recognition results.

For the issue of patchy fluid or the calibration of degree of saturation, the difficult point is the measurement of τ m and construction of effective fluid. We must consider the dynamic viscosity of the patchy fluid as the fluid shows viscoelastic characteristics. The future work will address these issues.

Weak contrast approximation

The objective function to invert the PADG is derived based on the Rüger equation, which is reformed into a frequency-dependent form. Almost all the approximate formulas based on the Zoeppritz equation are adaptive to the cases of weak contrast approximation. The weak contrast approximation can be expressed as

$$\frac{{\Delta {\rm X}}}{{\bar{\rm X}}} < 1,$$
(33)

where X is the parameter of layer medium which can be velocity, density, and anisotropic parameters, ΔX is the parameter contrast between two layers, and \(\bar{\rm X}\) is the average value of the parameters of two layers. The weak contrast approximation is adaptive for most cases. In the case of dispersion and attenuation, \(\Delta {\rm X}/\bar{\rm X}\) will be frequency dependent. Taking the parameters introduced in section “Frequency-dependent AVAZ inversion for PADG”; for example, we calculate \(\Delta v_{p} /\bar{v}_{p}\) variation with frequency. As shown in Fig. 14, \(\Delta v_{p} /\bar{v}_{p}\) increases with frequency, but is still less than 1. Thus, on most geological conditions, the weak contrast approximation is feasible, and Rüger equation is suitable for the dispersive cases. Furthermore, the anisotropy is weak and the contrast across the interface is also weak in many practical cases. Therefore, our method is doable both in theory and in application.

Fig. 14
figure 14

\(\Delta v_{p} /\bar{v}_{p}\) variation with frequency

Full size image

Conclusions

Fluid-related dispersion and attenuation makes a significant difference on amplitude versus offset and azimuth and give rise to a frequency dependence of reflection coefficients. Furthermore, frequency-dependent anisotropy is sensitive to the fluid type. Through the numerical simulation based on Chapman model, we analyze the frequency dependence of phase velocity, attenuation, and P-wave anisotropic parameter, and choose P-wave anisotropy parameter dispersion gradient (PADG) as the fluid factor. When the aligned fractures in the reservoir are meter-scaled, gas-bearing layer could be accurately identified using PADG attribute. The multi-azimuthal seismic data allow us to analyze the anisotropic characteristic for the fractured reservoirs. In this paper, the target function of inverting PADG using frequency-dependent AVAZ is derived by rewriting the reflection coefficient equation in HTI media. A method combining a high-resolution spectral decomposition technique and least squares inversion is performed to the synthetic data and real data from a fractured reservoir. The results of the synthetic data with noises show that our method needs high-qualified seismic data. When the seismic data are contaminated by noises seriously, the identification results could be unreliable. When seismic data are with high SNR, the results demonstrate that our method is potentially useful for gas detection in reservoirs with meter-scaled fractures.