Introduction

The channel wave seismology was promoted in China by a German company in 2010. Since then, channel wave exploration technology has rapidly developed, with applied research now being actively performed in several coal mines. The channel wave dispersion features of coal seams with different thicknesses have led the Yima Coal Industry Group and other research organizations to achieve remarkable results in exploring coal seam thickness on working faces using channel wave seismograph technology (Hu et al. 2013; Wang et al. 2012a; Le et al. 2013). Dispersion is the clearest characteristic of channel wave signals, wherein the channel wave’s propagation velocity is a function of its frequency (Evison 1955). The channel wave is produced owing to the unique lithology combination of the “roof–coal seam–floor” system (Krey 1963, 1982) and contains valuable information on the coal seam and its surrounding rocks (Buchanan 1978). The accuracy of the dispersion calculation method is the key to the channel wave exploration of coal seam thickness, because it directly affects travel time pickup reliability and channel wave tomography results (Chapman and Pratt 1992). Cheng et al. (2012) and Yang et al. (2010) theoretically obtained the channel wave dispersion curve using forward modeling and analyzed the dispersion characteristics in detail; however, the channel wave computation method has not been sufficiently discussed. In this study, we mainly propose a method for calculating the channel wave dispersion curve. The advantage of this method is that it improves dispersion calculation accuracy using S-transform and coordinate rotation.

The current seismic signal dispersion curve computation method is adapted from surface-wave exploration methods used in ground engineering. Multiple filtering and time–frequency analysis based on single-trace signal processing are the most commonly used methods that conduct filter processing in the frequency and time domains, respectively (Cox and Mason 1988). Other commonly used methods are based on multi-trace signal processing, such as the f–k transformation method (two-dimension Fourier transform), the τ-p transformation method, and the phase shift method (Buchanan and Jaskson 1983; Park et al. 1999). The f–k transformation method requires the same data sampling interval in both the space and time domains; it results in a large error if the sample data have bad traces (Ren et al. 2009; Xia et al. 2004). The τ-p transformation method yields better results for higher order mode dispersion curves, but is inferior for base-order modes in low-frequency ranges (Shao and Li 2010). Although a dispersion extracting method based on multi-trace processing can obtain a more stable dispersion curve than that obtained via single-trace methods, channel wave exploration needs to analyze the dispersion characteristic of each trace. Therefore, it is more practical to generate a more accurate computation method for single-trace methods.

The group velocity and phase velocity of channel wave

Channel waves can be viewed as complex vibration signals formed via the mutual interference of several waves with different frequencies that are propagating in the coal seam. Because of dispersion, channel wave amplitude propagates at an independent velocity. Thus, the propagation velocity of the maximum amplitude in a coal seam is a group velocity, and the signal propagation velocity in the same phase is a phase velocity (Liu et al. 1994). The analysis of channel wave dispersion is basically extracting the group velocity or phase velocity curve from the channel wave signal. Because of the mutual conversion between the group and phase velocities, if one velocity is obtained, the remaining velocity can be converted as follows:

$$u = \frac{d\omega }{d(\omega /c)} = \frac{d(ck)}{dk} = c + k\frac{dc}{dk},$$
(1)

wherein c is the phase velocity; u is the group velocity; and k is the circular wave number.

This formula shows the relation between the group velocity and the phase velocity. Seismic wave energy is proportional to the square of the amplitude; therefore, the seismic energy is mainly concentrated near the maximum amplitude. Consequently, the group velocity is the wave energy’s propagation velocity. Using time–frequency analysis methods, the energy distribution can be acquired from an energy spectrum map. Therefore, the group velocity of the channel wave can be obtained.

The theoretical dispersion curve of channel wave

A channel wave can be subdivided into Love and Rayleigh channel waves (Krey et al. 1982). Because the channel wave seismograph widely used in Chinese coal mines is a SUMMIT II system, the geophone has only two horizontal components and cannot receive vertical components. The Love channel wave is the main signal received by the horizontal two-component geophone, whereas the Rayleigh channel wave is not clear in this seismograph. At present, Chinese mines mainly use Love channel wave dispersion characteristics for coal seam thickness detection. The main objective of this study was the Love channel wave. To test the accuracy of an extracted channel wave dispersion curve, we established a standard theory dispersion curve of the channel wave to compare the methods. For the simple roof–coal seam–floor three-layer model, sources and receivers are set in the center of the coal seam. The Love channel wave is also an SH wave that has particle vibration in the horizontal plane perpendicular to the wave propagation direction. Former studies have given the specific formula for the propagation rule of Love channel waves (Rader et al. 1985); therefore, we do not derive it here but simply state it:

$$\frac{\omega d}{{c_{L} }}\sqrt {\frac{{c_{L}^{2} }}{{\upsilon_{s2}^{2} }} - 1} = \arctan \,\,\left[ {\frac{{\mu_{1} }}{{\mu_{2} }}\frac{{\sqrt {1 - \frac{{c_{L}^{2} }}{{\upsilon_{s1}^{2} }}} }}{{\sqrt {\frac{{c_{L}^{2} }}{{\upsilon_{s2}^{2} }} - 1} }}} \right] + n\pi \,\,\, n \, = \, 0, 1, 2, \ldots$$
(2)

wherein d is the coal seam thickness; v s1 and v s2 are the shear velocities of surrounding rocks and the coal seam, respectively; μ 1 and μ 2 are the shear moduli of surrounding rocks and the coal seam, respectively; ω is the circle frequency; C L is the phase velocity of the Love channel wave; and n is the dispersion order. When v s2 ≤ C L  ≤ v s1 and when n = 0, dispersion is in the base-order mode. Cheng and Zhu (Cheng et al. 2012) demonstrated that the dispersion of channel waves is mainly in the base-order mode (n = 0) when coal seam thickness is less than 5 m. The Love channel wave propagation equation shows that the phase velocity of the coal seam channel wave is affected by coal seam thickness and the seismic source’s excitation frequency. Dispersion results from different frequency components propagating at different speeds. In addition, the waveform length broadens as the propagation distance increases. According to the measured petrophysical data (Table 1) of the coal seam and formulas (1) and (2), the theoretical Love channel wave group velocity dispersion curves were in base-order mode and established with coal seam thicknesses of 1, 3, 5, and 7 m (Fig. 2).

Table 1 Model petrophysical parameters (Wang et al. 2012a)
Full size table

As can be seen in Fig. 1, coal seam thickness significantly influences dispersion. In the frequency range 0–500 Hz, the channel wave main energy distribution interval, thicker coal seams have a faster group velocity change with frequency. The thinner the coal seam, the slower the velocity varied with frequency. Furthermore, the group velocity decreases as frequency increases, and wave velocity tends to be stable close to the shear wave velocity with increasing frequency to a certain extent.

Fig. 1
figure 1

Theoretical dispersion curves for coal seams with different thicknesses

Full size image

The computation method of dispersion curve

We used a time–frequency analysis method based on single traces to calculate the dispersion curve. Time–frequency analysis methods mainly include short-time Fourier transform (STFT), which confines the results to a fixed resolution, and the Wavelet Transform (WT), which has difficultly with scaling corresponding directly to the frequency information. To solve these problems, Stockwell (1996) proposed the S-transform (ST) method based on a previous research. The ST method combines the advantages of the STFT and WT methods, overcoming STFT’s inability to adjust window frequency, having multiple resolutions like WT, and possessing a definite time–frequency concept.

First, we assumed that the channel wave signal can be defined as s(t) and that the general formula corresponding to ST is as follows:

$$\text{ST}(t,f) = \int_{ - \infty }^{ + \infty } {s(\tau )w(\tau - t)} e^{ - j2\pi f\tau } d\tau ,$$
(3)

wherein ST(t, f) is the ST of signal s(t); t and f are time and frequency, respectively; τ is the center of the window function; and w(t) is the window function, which is defined as the Gaussian function that changes with frequency and it is expressed as follows:

$$w(t) = \frac{\left| f \right|}{{\sqrt {2\pi } }}e^{{{ - }\frac{{f^{2} t^{2} }}{2}}} .$$
(4)

Therefore, ST transforms as follows:

$$ST(t,f) = \int_{ - \infty }^{ + \infty } {s(\tau )\frac{\left| f \right|}{{\sqrt {2\pi } }}e^{{{ - }\frac{{f^{2} (\tau - t)^{2} }}{2}}} } e^{ - j2\pi f\tau } d\tau .$$
(5)

Consequently, ST can be considered to use the multi-scale Gaussian window as a filter (Fig. 2). The resolution of the frequency domain can be improved using small-scale window filtering in the low frequencies of the channel wave signal, and the resolution of the time domain can be improved by increasing the frequency domain window width and reducing the time domain window scale for high frequencies. Thus, ST improves the channel wave signal time–frequency analysis accuracy via adaptively modulating the filter window based on signal resolution characteristics.

Fig. 2
figure 2

Schematic diagram of S-transform

Full size image

The Gaussian window function of ST proposed by Stockwell is controlled by frequency and the window width cannot be freely changed. Pinnegar and Mansinha (2003) and Gao et al. (2004) improved the window function via implementing adjustment coefficients, which resulted in a freely changing window width. Because there are different types of transform windows, this is collectively referred to as a generalized S-transform (GST) (Wang et al. 2012b). Based on the idea of GST, this study controls the width of the window via increasing the adjustment coefficient. The redefined window function is expressed as follows:

$$w(t) = \frac{\left| f \right|}{{\sqrt {2\pi } }}e^{{{ - }\lambda (f )\frac{{f^{2} t^{2} }}{2}}} ,$$
(6)

wherein λ(f) is a function of the adjustment coefficients and a linear function of the frequency, defined as follows:

$$\lambda (f) = \alpha + \beta f,$$
(7)

wherein parameters \(\alpha\) and \(\beta\) are constants used to control the ST window width. The Gaussian window adjustment coefficients linearly increase with the increase of \(\alpha\) and \(\beta\) (Fig. 3).

Fig. 3
figure 3

Adjustment coefficients with various parameters

Full size image

The Gaussian window width can be freely controlled via changing the parameters of the adjustment coefficients. \(\alpha\) dictates the range of the Gaussian window width, with larger values creating narrower windows, and \(\beta\) adjusts the Gaussian window boundary slope, with larger values yielding a steeper window boundary (Fig. 4).

Fig. 4
figure 4

Effects of various parameters on the Gaussian window

Full size image

The time–frequency energy scattergram was obtained after the ST on the channel wave. Time can be converted to velocity using Eq. (8), because the relation between velocity and frequency generally needs to be analyzed later when calculating the dispersion curve. According to the above concept of channel wave velocity, this velocity is also the group velocity:

$$u(f) = x/t,$$
(8)

wherein x is the distance from the seismic source to the detector. By combining formulas (6), (7), and (8), and substituting them into formula (3), we obtain the ST formula of velocity–frequency of channel wave signal:

$$ST\left( {\frac{x}{u},f} \right) = \int_{ - \infty }^{ + \infty } {s(\tau )\frac{\left| f \right|}{{\sqrt {2\pi } }}e^{{{ - (}\alpha + \beta f )\frac{{f^{2} \left( {\tau - \frac{x}{u}} \right)^{2} }}{2}}} } e^{ - j2\pi f\tau } d\tau ,$$
(9)

wherein u is the propagation group velocity of the channel wave, and the other variables are defined above. The diagram of the channel wave group velocity and frequency can be obtained if all the data points of single trace are transformed using the above formula. After converting time to velocity using the distance from source to receiver, we note that the original time sampling points are no longer equally spaced in the velocity domain. It is thus necessary to re-interpolate the grid before mapping, and the line of maximum energy is the corresponding dispersion curve.

Dispersion curve computation of the theoretical model

The forward model used dispersion curve data from the 3-m-thick coal seam in Fig. 2. We set the known dispersion curve to \(v(f)\) and assumed that the seismic wavelet exciting by source points can be expressed by the following function (Gaždová and Vilhelm 2011):

$$w(t,f_{i} ) = ae^{ - bt} \sin (2\pi f_{i} t),$$
(10)

wherein a and b are constants representing the amplitude coefficient and damping coefficient, respectively, which control the amplitude and attenuation speed of seismic wavelets.

The velocity, \(v_{i} = v(f_{i} )\), is a function of frequency with the changing frequency. The delay time of the seismic wavelet can be calculated at a different frequency (\(f_{i}\)) when the distance (x) from the source to receiver points is given:

$$\Delta t_{i} = \frac{x}{{v_{i} }}.$$
(11)

The sum of the seismic wavelets of all frequencies can synthesize the dispersion seismic waveform. The formula of the synthetic seismogram (\(s(t,x)\)) is defined as follows:

$$s(t,x) = \sum\limits_{i = 1}^{n} {w\left( {t + \frac{x}{{v(f_{i} )}}} \right)}$$
$$= \sum\limits_{i = 1}^{n} {ae^{{ - b\left( {t + \frac{x}{{v(f_{i} )}}} \right)}} \sin \left( {2\pi f_{i} \left( {t + \frac{x}{{v(f_{i} )}}} \right)} \right)} ,$$
(12)

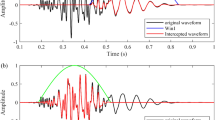
wherein n is the number of all data points of a known dispersion curve and x is the distance from the source to the receiver. Using the dispersion synthetic seismogram formula, we then obtained the forward model (Fig. 5). In addition, source excites on the left and the spacing of seismic traces is 10 m.

Fig. 5
figure 5

Forward model with seismic dispersion. The red trace is used for method test

Full size image

Taking the data of the 15th trace in the synthetic seismic record (Fig. 5) as an example to compute dispersion, different values of α and β could be analyzed via adjusting the coefficients. When we set α to 0.8 and β to 0.01, energy was concentrated in the dispersion diagram (Fig. 6a), and the line linking the maximum points (red zones) was consistent with the theoretical dispersion curve of a 3-m-thick coal seam (Fig. 1). The energy became more distributed in the dispersion diagram when α and β were varied, indicating that the signal dispersion computational accuracy could be controlled via adjusting the Gaussian window.

Fig. 6
figure 6

Dispersion maps with different values for α and β

Full size image

Two-component signal dispersion analysis of channel waves

At present, most channel wave seismographs used in Chinese coal mines rely on a horizontal two-component (x and y) geophone, wherein the x component is parallel to the coal wall and the y component is vertical to the coal wall. Because the azimuth of the seismic wave that propagated from the source to the receiver was different, the channel wave was not clear. To unify the propagation direction of the signal received by a two-component geophone, a polarization filtering method can be used with high precision (Feng et al. 2015); however, this method is complex. We, therefore, adopted the coordinate rotation method to solve the problem in this study. After rotation, the channel wave horizontal propagation is defined as x’ and the vertical propagation is defined as y’. The coordinate rotation formula is given as follows:

$$\left\{ {\begin{array}{*{20}c} {x^{\prime} = x\cos \theta + y\sin \theta } \\ {y^{\prime} = y\cos \theta - x\sin \theta } \\ \end{array} } \right.,$$
(13)

wherein \(\theta\) is the angle of the coordinate rotation, x and y are the original component signals, x’ is the horizontal propagation direction of the channel wave, and y’ is the signal perpendicular to the channel wave’s horizontal propagation direction.

We calculated \(\theta\) using the P-wave propagation energy criterion. In addition to the channel wave, the seismic wave signals received from the coal seam also contained a P wave (refraction wave), which arrives first (Fig. 7). The two-component channel wave signal in Fig. 8 is actual acquisition data. The first received vibration (50–70 ms) recorded in the x and y component received by the geophone was the P wave, and the most obvious Airy phase in the channel wave signal was received at 185–225 ms. The channel wave, the vibration of which is perpendicular to the vertical wave propagation direction, existed in both x and y components, because the relation between particle vibration direction and wave propagation direction was indeterminate.

Fig. 7
figure 7

Channel wave schematic diagram

Full size image
Fig. 8
figure 8

Original signal received by two-component seismic detector. The first signal received was the P wave (50–70 ms), and the most obvious Airy phase was received at 185–225 ms

Full size image

As observed from the P-wave propagation law, vibration direction is consistent with the wave propagation direction, and the P wave has maximum energy in the propagation direction and minimum energy in the direction perpendicular to wave propagation. Seismic wave energy is proportional to the square of amplitude. Therefore, the P-wave energy is defined as \(P_{x} (\theta )\) in the wave propagation direction and \(P_{y} (\theta )\) in the direction perpendicular to wave propagation:

$$\left\{ {\begin{array}{*{20}c} {P_{x} (\theta ) = \sum\nolimits_{i = 1}^{n} {(x^{\prime}_{i} )^{2} = \sum\nolimits_{i = 1}^{n} {(x{}_{i}\cos \theta + y_{i} \sin \theta )^{2} } } } \\ {P_{y} (\theta ) = \sum\nolimits_{i = 1}^{n} {(y^{\prime}_{i} )^{2} = \sum\nolimits_{i = 1}^{n} {(y{}_{i}\cos \theta - x_{i} \sin \theta )^{2} } } } \\ \end{array} } \right.,$$
(14)

wherein n is the number of data points and the azimuth is the angle of the seismic wave, \(\theta\), with regard to the coordinate rotation when \(P_{x} (\theta )\) takes the maximum value and \(P_{y} (\theta )\) takes the minimum value. The objective function \(M(\theta )\) is defined as follows:

$$M(\theta ) = \frac{{\sum\nolimits_{i = 1}^{n} {(y{}_{i}\cos \theta - x_{i} \sin \theta )^{2} } }}{{\sum\nolimits_{i = 1}^{n} {(x{}_{i}\cos \theta + y_{i} \sin \theta )^{2} } }}.$$
(15)

When \(M(\theta )\) takes the minimum value, \(\theta\) correspondingly is the angle to examine. The prerequisite of taking the minimum value is \(\frac{\partial M(\theta )}{\partial \theta } = 0\) and the rotation angle \(\theta\) can be calculated using the following equation:

$$\theta = \frac{1}{2}\arctan \left( {\frac{{2\sum\nolimits_{i = 1}^{n} {x_{i} y_{i} } }}{{\sum\nolimits_{i = 1}^{n} {(x_{i}^{2} - y_{i}^{2} )} }}} \right).$$
(16)

According to formula (16), when using P-wave data, the angle \(\theta\) that the component needs to rotate is 105°. The signal after rotation is shown in Fig. 9, and it can be seen in the diagram that the energy of the P wave is the strongest in the direction parallel to the horizontal component and weakest in the direction perpendicular to the horizontal component. Similarly, the channel wave (SH wave), in which the particle vibration direction is perpendicular to the wave propagation direction, has the strongest energy and most recognizable feature in the direction perpendicular to the horizontal component after rotation.

Fig. 9
figure 9

Seismic signal after coordinate rotation. The original signal is shown in Fig. 8

Full size image

The P-wave signal data points of the x and y components can be marked and linked onto a curve according to the values and symbol of sample points in Cartesian coordinates before and after rotation (Fig. 10). The P-wave vibration direction is consistent with the wave propagation direction in an ideal case without interference, and the path of a particle should be a straight line. However, disturbances produced by random noise mean that this is a very flat ellipse. The angle between the long axis of the ellipse and the x-axis is the angle \(\theta\) between the P-wave particle vibration direction and the x-axis. It can be seen that this angle is approximately 105° before rotation. In addition, the P-wave particle vibration direction is consistent with the x-axis direction (wave propagation direction) after coordinate rotation.

Fig. 10
figure 10

P-wave particle vibration vectorgraph

Full size image

The signal recorded by the y’ component after coordinate rotation is considered to be the Love channel wave, because the particle vibration direction of the Love channel wave is perpendicular to the wave propagation direction. We then calculated the dispersion of signals in the x and y components (Fig. 11a, b) and compared the results before and after coordinate rotation. The relation between the particle vibration direction and wave propagation direction is unclear. The original signal contained several different seismic waves such as a P wave, an S wave, and a channel wave. Consequently, the dispersion rule for the dispersion map was not obvious, and the line linking maximum energy points was divergent and discontinuous. After coordinate rotation, the Love channel wave was mainly concentrated horizontally in the vertical component. Finally, the dispersion characteristic was obvious, and as clearly shown in Fig. 11c, it is consistent with the characteristics of the theoretical dispersion curve (Fig. 1).

Fig. 11
figure 11

Dispersion maps of the channel wave before and after coordinate rotation

Full size image

Conclusions

We gave the dispersion calculation formula of a channel wave with two components in the frequency–velocity domain based on the ST time–frequency analysis method. According to the analysis of dispersion curves in theoretical models and real data, we can draw several conclusions, which are as follows:

  1. 1.

    The calculation accuracy of the dispersion curve of the channel wave signal can be improved using linear adjustment parameters that change the ST Gaussian window width.

  2. 2.

    The P-wave energy distribution criterion in a two-component geophone shows that seismic wave propagation direction and polarization angle can be calculated, and that the Love channel wave signal that horizontally vibrates in the vertical component can be obtained after coordinate rotation.

  3. 3.

    The dispersion characteristics of the channel wave signal were obvious and the channel wave velocity was largely influenced by frequency and coal seam thickness. Furthermore, the channel wave velocity rapidly decreased when the frequency increased.