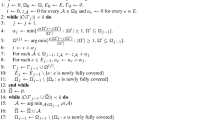Approximation algorithm for minimum partial multi-cover under a geometric setting

Abstract

In a minimum partial set multi-cover problem (MinPSMC), given an element set X, a collection of subsets ${\mathcal {S}} \subseteq 2^X$, a cost $c_S$ on each set $S\in {\mathcal {S}}$, a covering requirement $r_x$ for each element $x\in X$, and an integer k, the goal is to find a sub-collection ${\mathcal {F}} \subseteq {\mathcal {S}}$ to fully cover at least k elements such that the cost of ${\mathcal {F}}$ is as small as possible, where element x is fully covered by ${\mathcal {F}}$ if it belongs to at least $r_x$ sets of ${\mathcal {F}}$. Recently, it was proved that MinPSMC is at least as hard as the densest k-subgraph problem. The question is: how about the problem in some geometric settings? In this paper, we consider the MinPSMC problem in which X is a set of points on the plane and ${\mathcal {S}}$ is a set of unit squares (MinPSMC-US). Under the assumption that $r_x=f_x$ for every $x\in X$, where $f_x=|\{S\in {\mathcal {S}}:x\in S\}|$ is the number of sets containing element x, we design an approximation algorithm achieving approximation ratio $(1+\varepsilon )$ for MinPSMC-US.

1 Introduction

In this paper, we study the minimum partial set multi-cover problem (MinPSMC) in a geometric setting. Given an element set X of order n, a collection of subsets ${\mathcal {S}} \subseteq 2^X$, a cost $c_S$ on each set $S\in {\mathcal {S}}$, a covering requirement $r_x$ for each element $x\in X$, and an integer k, the goal of MinPSMC is to find a sub-collection ${\mathcal {F}} \subseteq {\mathcal {S}}$ to fully cover at least k elements such that the cost of ${\mathcal {F}}$ is as small as possible, where an element x is fully covered by ${\mathcal {F}}$ if it belongs to at least $r_x$ sets of ${\mathcal {F}}$, and the cost of ${\mathcal {F}}$ is $c(\mathcal F)=\sum _{S\in {\mathcal {F}}}c_S$.

This problem was motivated by a monitoring problem in a wireless sensor network and an information propagation problem in a social network [22, 23]. Speaking from the theoretical point of view, MinPSMC contains the minimum k union (MinkU) problem, which was proposed by Chlamtáč et al. [6]. Furthermore, it is a combination of the minimum set (full) multi-cover problem (MinSMC in which $k=n$) and the minimum partial set (single-)cover problem (MinPSC in which $r\equiv 1$), which are important variants of the classic set cover problem.

Although both MinSMC and MinPSC admit approximation algorithms achieving tight ratios matching those for the set cover problem, it was proved in [18] that MinPSMC cannot be approximated within factor $O(n^\frac{1}{2(\log \log n)^c})$ for some constant c under the ETH assumption. Then a natural question arises: can we obtain better approximation when considering geometric setting? In a geometric setting, the element set is a set of points on the plane, denoted as P. Given a set of objects ${\mathcal {O}}$ on the plane, the collection of subsets is ${\mathcal {S}}=\{P\cap O:O\in {\mathcal {O}}\}$ where $P\cap O$ is the set of points contained in object $O\in {\mathcal {O}}$.

In this paper, we consider the MinPSMC problem in which the objects are unit squares. Denote the corresponding problem as MinPSMC-US. As a starting step, we study the case when $r_p=f_p$ for every $p\in P$, where $f_p=|\{S\in {\mathcal {S}}:p\in S\}|$ is the number of objects containing point p. Call this a constrainted MinPSMC problem. Notice that such an constraint is not too artificial since it is equivalent with a geometric MinkU problem (this will be explained in the Related Work section).

1.1 Related works

MinPSMC was formally proposed in [16] to study the minimum partial positive domination set problem, which has its background in information propagation of social network. A greedy algorithm was proposed in [16], and a local ratio algorithm was given in [17]. The MinPSMC problem is a combination of the minimum set (full) multi-cover problem (MinSMC) and the minimum partial set (single-)cover problem (MinPSC). Despite the fact that greedy strategy and local ratio method can achieve tight approximations for MinSMC and MinPSC [1, 15], the approximation ratios obtained by employing them on the MinPSMC problem are very large, which indicates the difficulty of the MinPSMC problem. Such an indication was confirmed by Ran et al. [18]. They showed that if MinPSMC admits a $\gamma$-approximation, then the famous densest k-subgraph problem (DkS) will have a $2\gamma ^2$-approximation. As a corollary of the hardness result of Manurangsi [14] for DkS, MinPSMC cannot be approximated within factor $O(n^\frac{1}{2(\log \log n)^c})$ for some constant c under the ETH assumption. Denote $r_{\max }=\max _{x\in X}r_x$. Assuming that $r_{\max }$ has a constant upper bound, some polynomial time approximation algorithms were proposed in [18, 20, 21, 24]. The barrier of assumption on $r_{\max }$ was finally dropped off by Ran et al. [19] in which a $(4\log ^2n\ln k+2\log n\sqrt{n})$-approximation algorithm was presented.

The minimum k union problem (MinkU) was first proposed by Chlamtáč et al. [6]. Given a hypergraph G with vertex set V and hyperedge set ${\mathcal {H}}$, together with an integer $1\le k\le m$ where m is the number of hyperedges, the goal of MinkU is to select k hyperedges such that the number of vertices in their union is as small as possible. A $2\sqrt{m}$-approximation algorithm was given in [6], which was further improved to $O(m^{1/4+\varepsilon })$ in [8]. MinkU is a generalization of the smallest k-edge subgraph problem [7] to hypergraphs, which is a dual problem of the densest k-subgraph problem.

It was proved in [19] that a MinkU instance $(V,\mathcal H,k)$ can be viewed as a MinPSMC instance $(X,{\mathcal {S}},c,r,k)$ with $X={\mathcal {H}}$, ${\mathcal {S}}=V$, $c\equiv 1$, and $r_x=f_x$ for every $x\in X$, where $f_x=|\{S\in {\mathcal {S}}:x\in S\}|$ is the number of sets containing element x (called frequency of x). So our constrained MinPSMC-US problem can be viewed as a special MinkU problem by taking every vertex to be a unit square, and every hyperedge to be the set of unit squares containing a common point.

Geometric set cover problem (GSC) is an extensively studied topic in computational geometry [10]. For the geometric partial set cover problem (GPSC), Gandhi et al. [9] gave a PTAS in the setting that the objects are unit disks and can be replaced anywhere on the plane. Inamdar and Varadarajan [13] showed that a feasible solution to the the standard linear program for set cover can be rounded to a $(2\beta +2)$-approximation for MinPSC, where $\beta$ is the integrality gap for the set cover LP. Combining this with the result in [3], the minimum weight disk partial cover problem admits a constant-approximation. Inamdar [12] established a local search framework for GPSC, obtaining PTAS for many GPSC problems including partial covering points by halfspaces in ${\mathbb {R}}^3$, partial covering points by r-admissible regions in ${\mathbb {R}}^2$, etc. There are also a lot of works on geometric (full) multi-cover problems (see for example [2, 5]). But we have not seen works on geometric cover problem combining both partial cover requirement and multi-cover requirement.

1.2 Our contributions

Since the MinPSMC problem in a general setting is very difficult, we study the geometric MinPSMC problem in which objects are unit squares, and present a PTAS under the assumption that $r_p=f_p$ for every $p\in P$.

The algorithm employs a strategy of shifted-grids combined with a dynamic programming. First, the whole problem is divided into subproblems on blocks of a grid-partition. For each subproblem, a dynamic programming is designed to obtain an exact local solution in polynomial time. Assembling the local solutions yields a feasible solution to the original problem. Shifting is used to control the error of assembling.

The most challenging part is to design an exact algorithm for the subproblem on a block. The mod-one technique proposed by Chan and Hu in [4] is employed. However, a straightforward employment of this technique on our problem only works for the case when $r_{\max }=\max \{r_p:p\in P\}$ is upper bounded by a constant, because due to the multi-cover requirement, one has to “guess” the depth-one, depth-two, up to depth-$r_{\max }$ envelope-square-sets of a solution, and thus the running time contains a factor of $n^{r_{\max }}$. To overcome such a difficulty, we exploit the speciality of the considered problem. The idea is that under the assumption that $r_p=f_p$ for every $p\in P$, no square in the optimal solution ${\mathcal {O}}^*$ can be completely contained in the envelope of ${\mathcal {O}}{\setminus } {\mathcal {O}}^*$. So, instead of “guessing” ${\mathcal {O}}^*$, we guess the envelope of ${\mathcal {O}}{\setminus } {\mathcal {O}}^*$, which is why the the running time can be brought down.

The paper is organized as follows. Section 2 obtains a PTAS for this constrained MinPSMC-US problem. Section 3 concludes the paper with some discussions.

2 A PTAS for MinPSMC-US

In this section, we give a PTAS for the constrained MinPSMC-US problem, in which the set of objects ${\mathcal {O}}$ consists of unit squares on the plane.

2.1 Outline of the method and some preliminaries

The strategy used in this paper is shifted grids combined with dynamic programming. The whole problem is divided into subproblems on blocks of constant side-length. The crucial step is to design an exact algorithm for the subproblem on a block. For this purpose, we further divide the block into grids with side-length 1. The algorithm will “guess” the envelope of ${\mathcal {O}}{\setminus } {\mathcal {O}}^*$ for each grid point, and then assemble these guesses by a dynamic programming.

First, we introduce some terminologies used in the design and analysis of the algorithm. For a subset of unit squares $\mathcal O'\subseteq {\mathcal {O}}$, denote by ${\mathcal {O}}'_g$ the subset of unit squares in ${\mathcal {O}}'$ containing grid point g, and denote by $U({\mathcal {O}}')$ the union of those unit squares in ${\mathcal {O}}'$.

Definition 2.1

(envelope-set) For a set of unit squares ${\mathcal {O}}'$ containing a common grid point g, the subset of unit squares appearing on the boundary of $U({\mathcal {O}}')$ is called the envelope-set of $\mathcal O'$.

An illustration is given in Fig. 1. The crossing point of the two lines is grid point g, and $\mathcal O''=\{s_1,s_2,s_3,s_4\}$ is the envelope-set of $\mathcal O'=\{s_1,s_2,s_3,s_4,s_5\}$.

Fig. 1

An illustration of envelope-set

For convenience of statement, we call the right-upper corner of unit square s as its position. Notice that a unit square is uniquely determined by its position.

Definition 2.2

(monotone-set [4]) Let ${\mathcal {O}}'=\{s_1,\ldots ,s_t\}$ be a set of unit squares containing a common grid point g, where $s_1,\ldots ,s_t$ are arranged in increasing x-coordinates of their positions. If the positions of $s_1,\ldots ,s_t$ are in increasing y-coordinates, then we say that ${\mathcal {O}}'$ forms a monotone-set for the 2-nd and the 4-th quadrant; if the positions of $s_1,\ldots ,s_t$ are in decreasing y-coordinates, then we say that ${\mathcal {O}}'$ forms a monotone-set for the 1-st and the 3-rd quadrant.

Observe that an envelope-set ${\mathcal {O}}''$ associated with grid point g can be decomposed into four monotone-sets: for $i=1,2,3,4$, the set of unit squares which appear on the boundary of $U({\mathcal {O}}'')$ in the i-th quadrant form a monotone-set. For example, the envelope-set ${\mathcal {O}}''=\{s_1,s_2,s_3,s_4\}$ in Fig. 1 can be decomposed into monotone-sets $\mathcal O''_1=\{s_2,s_1\}$, ${\mathcal {O}}''_2=\{s_2\}$, $\mathcal O''_3=\{s_2,s_3,s_4\}$, and ${\mathcal {O}}''_4=\{s_4,s_1\}$.

Definition 2.3

(mod-one mapping [4]) For a real number z, let $(z\mod 1)=z-\lfloor z\rfloor$. Define mod-one mapping $\psi :{\mathbb {R}}^2\mapsto {\mathbb {R}}^2$ as $\psi (x,y)=\big ((x \mod 1),(y \mod 1)\big )$.

Figure 2 is an illustration of mod-one mapping. The blackened unit square s on the left hand is mapped onto the right-hand unit square, where grid point g is mapped to $g'=(0,0)$, points $q_1,q_2$ are mapped to $q_1',q_2'$, the four rectangles 1, 2, 3, 4 are mapped to $1',2',3',4'$, and the four corners $p_1,p_2,p_3,p_4$ are mapped to a same point $p'$ (which we call as mod-one-position of s). The advantage of mod-one operation is that it can fold a set of unit squares onto one unit square and deal with them simultaneously. Furthermore, since the four corners of unit square s are identified, the left boundary of s coincides with the right boundary of s, which we call as mod-one-boundary of s. So, if we move a vertical sweep line from left to right, then the entering time of s and the leaving time of s are the same (namely when the sweep line goes through the mod-one-boundary of s), and thus there is no need to remember a square using both of its entering time and leaving time, which may avoid repetition in counting a square.

Fig. 2

An illustration for mod-one mapping.

2.2 Dynamic programming for MinPSMC-US in a block

Suppose a block is of size $q\times q$. Assume, without loss of generality, that q is an integer. Divide the block into grids of side-length 1. We assume that the unit squares are in a generic position in the sense that every unit square contains exactly one grid point and no unit squares have the same mod-one-position. The following observation is crucial to the validity of our algorithm.

Observation 2.4

The union of unit squares in ${\mathcal {O}}{\setminus } {\mathcal {O}}^*$ consists of a collection of envelope-sets for the grid points. No point lying in the union of these envelope-sets is fully covered by ${\mathcal {O}}^*$, and ${\mathcal {O}}^*$ is composed of all those unit squares which are not completely contained in the union of these envelope-sets.

The reason for the validity of this observation is as follows: under the assumption that $r_p=f_p$ for every $p\in P$, if point p is fully covered by ${\mathcal {O}}^*$, then all unit squares containing p must be included in ${\mathcal {O}}^*$, hence no unit square in ${\mathcal {O}}{\setminus } {\mathcal {O}}^*$ can contain p. Notice that p belongs to some unit square in ${\mathcal {O}}{\setminus } {\mathcal {O}}^*$ if and only if it lies in the union of some envelope-set $(\mathcal O{\setminus } {\mathcal {O}}^*)_g$ for some grid point g. Then the first part of the observation follows. Also notice that any square $s\in {\mathcal {O}}^*$ must cover some point outside of $U(\mathcal O{\setminus } O^*)$, since otherwise s is useless and can be removed from ${\mathcal {O}}^*$. This leads to the second part of the observation.

Remark 2.5

Observation 2.4 can be restated as follows: a unit square s belongs to $O^*$ if and only if s is not completely contained in the union of the envelope-set of $({\mathcal {O}}{\setminus } O^*)_g$, where g is the unique gird point contained in s.

This remark seems to be stronger than Observation 2.4, because one may ask: is it possible that s is not completely contained in the union of the envelope-set of $({\mathcal {O}}{\setminus } O^*)_g$ (which is only one envelope-set) but it is completely contained in the union of the envelope-sets of ${\mathcal {O}}{\setminus } {\mathcal {O}}^*$ (with respect to all grid points)? The answer is no. In fact, if s is completely contained in the union of the envelope-sets of ${\mathcal {O}}{\setminus } O^*$, then s is useless for coverage and thus belongs to ${\mathcal {O}}{\setminus } {\mathcal {O}}^*$, which implies that s is completely contained in the union of the envelope-set of $({\mathcal {O}}{\setminus } O^*)_g$ where g is the unique grid point contained in s.

By Remark 2.5, to find out ${\mathcal {O}}^*$, it suffices to guess for every grid point g the envelope-set of $(\mathcal O{\setminus } O^*)_g$ and find out all those unit squares of $\mathcal O_g$ which are not completely contained in the union of this envelope-set.

Notice that the number of guesses for the envelope-set at a grid point g is exponential in the number of unit squares containing g. In order that the algorithm can be executed in polynomial time, they should not be guessed once for all. Instead, we track the guesses by a path in an auxiliary acyclic digraph (DAG). The idea is that each vertex of the DAG corresponds to a configuration in which only a constant number of guesses is stored at each grid point, and walking along a path in the DAG can recover all these unit squares. Each configuration will consist of at most four guessed monotone sets at each grid point. Because there are $(q+1)^2$ grid points, the number of guessed unit squares for each configuration is $O(q^2)$, which is a constant since q is a constant.

Assume that there are m unit squares having non-empty intersection with the block under consideration. Let $s_0$ and $s_{m+1}$ be two virtual unit squares whose positions can be regarded at any of the four corners of the mod-one unit square, and can be placed suitably to form monotone-sets of the four quadrants. See Fig. 3 for an example, the four blackened unit squares $s_1,s_2,s_4,s_6$ in (a) are folded into the mod-one unit square in (b), and the four monotone-sets are depicted in (c), with the real unit squares indicated by blackened lines and the two virtual unit squares indicated by blackened dashed lines.

Fig. 3

An illustration for the monotone-sets with virtual unit squares. Also an illustration for the transition of configurations. In (b), the left-bottom shaded area indicates the monotone-set in the 1st quadrant, the right-upper shaded area indicates the monotone-set in the 3rd quadrant. In (b, c), the denser dotted lines indicate $s_5$ and the sparser dotted lines indicate $s_7$

For a unit square s, denote by x(s) and y(s) the x-coordinate and the y-coordinate of the mod-one position of s.

Definition 2.6

(Configuration) A configuration consists of a 3-tuple $(S,\tilde{k},\ell )$, where $S=\bigcup _{g}S(g)$ with g running over all grid points, $S(g)=\bigcup _{i=1}^4S^i(g)$ with $S^i(g)=(s^i_{prev}(g),s^i_{curr}(g))$ being a 2-tuple of unit squares in ${\mathcal {O}}_g\cup \{s_0,s_{m+1}\}$ which form a sub-monotone-set in the i-th quadrant at grid point g; $\ell$ is a vertical line whose mod-one x-coordinate satisfies $x(s_{prev}^i(g))\le x(\ell )<x(s_{curr}^i(g))$ for every g and every i, and $x(\ell )=x(s_{prev}^i(g))$ for some g and some i; and $\tilde{k}$ is an integer no larger than the number of points whose mod-one x-coordinates are smaller than $x(\ell )$.

An intuition of how we track the envelope-set of $\mathcal O{\setminus } {\mathcal {O}}^*$ is given in Fig. 3 (for a clearer understanding of the idea, we only consider one grid point and temporarily ignore mod-one operation). Suppose $\mathcal O^*=\{s_5,s_7\}$. Then ${\mathcal {O}}{\setminus } \mathcal O^*=\{s_1,s_2,s_3,s_4,s_6\}$. Notice that $s_3$ is not on the boundary of $U({\mathcal {O}}{\setminus } {\mathcal {O}}^*)$ and thus is redundant in detecting ${\mathcal {O}}^*$, so what we need to discover the envelope-set of $\mathcal O{\setminus }{\mathcal {O}}^*$, which is $\{s_1,s_2,s_4,s_5\}$ (the blackened unit squares). By following a sequence of 2-tuples $(s_0,s_1),(s_1,s_4),(s_4,s_6),(s_6,s_{m+1})$, we can discover the monotone-set $\{s_1,s_4,s_6\}$ in the first quadrant; by following $(s_0,s_1),(s_1,s_2),(s_2,$ $s_6),(s_6,$ $s_{m+1})$, we can discover the monotone-set $\{s_1,s_2,s_6\}$ in the third quadrant; similarly, we can discover the monotone-set $\{s_1\}$ in the second quadrant by following $(s_0,s_1),(s_1,$ $s_{m+1})$, and discover the monotone-set $\{s_6\}$ in the fourth quadrant by following $(s_0,s_6),(s_6,$ $s_{m+1})$. The union of these four monotone-sets is the envelope-set of ${\mathcal {O}}{\setminus }{\mathcal {O}}^*$. In realizing such an idea, instead of following these sequences of 2-tuples separately, we follow their combinations, which is the idea underlying the definition of 2-tuples in configurations.

The ultimate goal is to detect ${\mathcal {O}}^*$ during the tacking. By Remark 2.5, every unit square $s\in {\mathcal {O}}^*$ protrudes out of the boundary of the envelope-set of $(\mathcal O{\setminus } {\mathcal {O}}^*)_g$, where g is the unique grid point contained in s. If it protrudes out in the i-quadrant, then it can be detected when tracking the monotone-set in the i-the quadrant. For example, unit square $s_5$ in Fig. 3 can be detected when moving from $s_4$ to $s_6$ in the first quadrant. It can also be detected when moving from $s_2$ to $s_6$ in the third quadrant. When a unit square in ${\mathcal {O}}^*$ is detected, its weight is counted. A question is: if a unit square of ${\mathcal {O}}^*$ can be detected multiple times, how to guarantee that its weight is counted only once? This is where mod-one trick comes in. As to the integer $\tilde{k}$ and the vertical line $\ell$ in each configuration, they are used to help counting the number of fully-covered points. The details will be clearer after we introduce some notations and how the DAG is constructed.

Define the detectable region of 2-tuple $(s_{prev}^i(g),s_{curr}^i(g))$ to be

$$\begin{aligned}&DR(s_{prev}^i(g),s_{curr}^i(g)) \\&\quad =\left\{ \begin{array}{ll} \{(x,y):x(s^1_{prev}(g))<x<1,y(s^1_{curr}(g))<y<1\}, &{} \text{ if }\ i=1,\\ \{(x,y):0<x<x(s^2_{curr}(g)),y(s^2_{prev}(g))<y<1\}, &{} \text{ if }\ i=2,\\ \{(x,y):0<x<x(s^3_{curr}(g)),0<y<y(s^3_{prev}(g))\}, &{} \text{ if }\ i=3,\\ \{(x,y):x(s^4_{prev}(g))<x<1,0<y<y(s^4_{curr}(g))\}, &{} \text{ if }\ i=4. \end{array}\right. \end{aligned}$$

A unit square s is detectable by $(s^i_{prev}(g),s^i_{curr}(g))$ if (x(s), y(s)) falls into the detectable region of $(s^i_{prev}(g),s^i_{curr}(g))$. Denote by $DS(s^i_{prev}(g),s^i_{curr}(g))$ the set of unit squares detectable by $(s^i_{prev}(g),s^i_{curr}(g))$. In the first figure of Fig. 4, the blackened solid lines indicate $s^1_{prev}(g)$ and $s^1_{curr}(g)$ in the first quadrant. The right-upper dashed box indicates the detectable region $DR(s^1_{prev}(g),s^1_{curr}(g))$, and $DS(s^1_{prev}(g),s^1_{curr}(g))=\{s_2,s_3,s_4,s_5\}$. The dashed boxes in the latter three figures of Fig. 4 indicate $DR(s^i_{prev}(g),s^i_{curr}(g))$ for $i=2,3,4$, respectively.

Fig. 4

An illustration of detectable unit squares

For a configuration $v=(S^v,\tilde{k}^v,\ell ^v)$, let ${\mathcal {O}}^v$ be the set of unit squares in those 2-tuples of $S^v$, $\mathcal O^v_g={\mathcal {O}}^v\cap {\mathcal {O}}_g$, $DS^v_g=\bigcup _{i=1}^4DS(s^i_{prev}(g),s^i_{curr}(g))$, and $DS^v=\bigcup _gDS_g^v$. The DAG with parameter $k_b$ restricted to a block b is constructed as follows and some explanations are given after the construction.

Definition 2.7

(DAG) The vertex set of the auxiliary digraph $G_{b,k_b}$ in block b with parameter $k_b$ consists of all configurations, a source vertex $u_{src}$, and a sink vertex $u_{sink}$. The arcs in $G_{b,k_b}$ are as follows.

(Arc between two configurations) For two configurations $u=(S^{u},\tilde{k}^{u},\ell ^u)$ and $v=(S^{v},\tilde{k}^{v},\ell ^v)$, there is an arc (u, v) in $G_{b,k_b}$ if only if the following conditions hold:

(i) $x(\ell ^v)=x(s')$ where $x(s')=\min _{g,i}\{x(s_{curr}^{u,i}(g))\}$. By the definition of configurations, $x(\ell ^u)<x(s_{curr}^{u,i}(g))$ for all g and i. So, $\ell ^v$ can be viewed as a sweep line moving from $\ell ^u$ to the right until it touches the first mod-one position of $\{s_{curr}^{u,i}(g)\}_{g,i}$. Let $g'$ be the unique grid point contained in $s'$ and $I'=\{i:s_{curr}^{u,i}(g')=s'\}$.

(ii) $S^u$ and $S^v$ differ in exactly one grid point, namely $g'$, and for each $i\in I'$, $s_{prev}^{v,i}(g')=s'$ (that is, $s_{prev}^{v,i}(g')=s_{curr}^{u,i}(g')$). All the other 2-tuples are the same.

(iii) $\tilde{k}^{v}$ is the sum of $\tilde{k}^{u}$ and the number of points between $\ell _u$ and $\ell _v$ which are covered by $\bigcup _gU(DS^u_g)$ and not covered by $\bigcup _gU(\mathcal O^u_g)$.

The weight on arc (u, v) is set to be $w(u,v)=\sum _{d\in DS^v{\setminus } DS^u}c_d$.

(Arcs from source vertex to configurations) Let $\ell _0$ be the sweep line with $x(\ell _0)=0$. The source vertex $s_{scr}$ is linked to every vertex $u=(S^u,0,\ell _0)$ whose 2-tuples all have the form $(s_0,s_{curr}^i(g))$. The weight on such an arc is $w(s_{scr},u)=\sum _{d\in DS^u}c_d$.

(Arcs from configurations to sink vertex) Let $\ell _{m+1}$ be the sweep line with $x(\ell _{m+1})=1$. A vertex $v=(S^v,\tilde{k}^v,\ell ^v)$ whose 2-tuples all have the form $(s_{prev}^i(g),s_{m+1})$ is linked to the sink vertex $s_{sink}$ only when the sum of $\tilde{k}^v$ and the number of points between sweep lines $\ell ^v$ and $\ell _{m+1}$ which are covered by $\bigcup _gU(DS^v_g)$ and not covered by $\bigcup _g U(\mathcal O^v_g)$ is $k_b$, and the weight on such an arc is set to be $w(v,s_{sink})=0$.

As an illustration, the following is a source-sink path in the DAG for the example in Fig. 3 with $k_b=3$: $u_{scr}u_0u_1u_2u_4u_6u_{sink}$

Table 1 A source-sink path in the DAG for the example in Fig. 3

In this table, $\ell _j$ is the sweep line going through the mod-one position of $s_j$. The arcs have weights $w(u_0,u_1)=c_{s_7}$, $w(u_1,u_2)=c_{s_5}$, and $w(u_{scr},u_0)=w(u_2,u_4)=w(u_4,u_6)=w(u_6,u_{sink})=0$. The weight of this path is $c_{s_5}+c_{s_7}$ which equals the cost of the optimal solution. When the sweep line moves from $\ell _4$ to $\ell _6$, the two points covered by $DS^{u_4}$ are counted, resulting in $\tilde{k}^{u_6}=2$. When the sweep line moves from $\ell _6$ to $\ell _{m+1}$, the point covered by $DS^{u_6}$ is counted. Adding this point onto $\tilde{k}^{u_6}$ results in 3 points fully covered, which is exactly the total covering requirement $k_b=3$, and thus arc $(u_6,u_{sink})$ exists.

The following lemma shows that any source-sink path in G corresponds to a feasible solution of the MinPSMC-US instance whose cost is at most the weight of the path.

Lemma 2.8

Let $Q=u_{scr}u_1\ldots u_tu_{sink}$ be a source-sink path in $G_{b,k_b}$. Then the set of unit squares $\mathcal O'=\bigcup _{i=1}^tDS^{u_i}$ fully covers exactly $k_b$ points. Furthermore, $w(Q)\ge c({\mathcal {O}}')$.

Proof

The first half of the lemma follows from the observation that the existence of arc $u_tu_{sink}$ implies (by the definition of the DAG) that the set of unit squares $\mathcal O'=\bigcup _{i=1}^tDS^{u_i}$ fully covers exactly $k_b$ points. Also by the definition of the DAG, $w(u_{i-1},u_{i})=\sum _{s\in DS^{u_i}{\setminus } DS^{u_{i-1}}}c_s$ for $i=1,\ldots ,t$ and $w(u_t,u_{sink})=0$. So $w(Q)=\sum _{i=1}^t\left( \sum _{s\in DS^{u_i}{\setminus } DS^{u_{i-1}}}c_s\right)$. Because the cost of every unit-square in ${\mathcal {O}}'$ is counted in the summation, the second half of the lemma is proved. $\square$

The next lemma shows that the optimal solution of the MinPSMC-US instance corresponds to a source-sink path in G whose weight is equal to the cost of the solution.

Lemma 2.9

Suppose ${\mathcal {O}}^*$ is an optimal solution to MinPSMC-US restricted to block b. Assume ${\mathcal {O}}^*$ fully covers $k_b$ points of block b. Then there is a source-sink path Q in $G_{b,k_b}$ with $c({\mathcal {O}}^*)=w(Q)$.

Proof

The desired path Q will be constructed by tracking the envelope-sets of $\{({\mathcal {O}}{\setminus } {\mathcal {O}}^*)_g\}_g$. Order the unit squares in the envelope-sets of $\{({\mathcal {O}}{\setminus } {\mathcal {O}}^*)_g\}_g$ as $s_1,s_2,\ldots ,s_T$ such that $x(s_1)<x(s_2)<\cdots <x(s_T)$. For each grid point g, the envelope-set of $({\mathcal {O}}{\setminus } {\mathcal {O}}^*)_g$ can be decomposed into four monotone-sets $\{MS_{g,i}\}_{i=1}^4$. Recall that virtual unit squares $s_0$ and $s_{m+1}$ can be regarded as belonging to every monotone-set. Order unit squares in $MS_{g,i}$ as $\{s_{(g,i),1},\ldots ,s_{(g,i),t_{(g,i)}}\}$, where $0=x(s_0)<x(s_{(g,i),1})<\cdots x(s_{(g,i),t_{(g,i)}})<1=x(s_{m+1})$.

We construct a source-sink path $Q=u_{scr}u_0u_1\ldots u_Tu_{sink}$ as follows, where every $u_j$ has the form $(S^{u_j},\tilde{k}^{u_j},\ell _j)$ and $\ell _j$ is the sweep line going through $x(s_j)$ for $j=0,1,\ldots ,T$ (the idea is to track the envelope-sets by moving the sweep line step by step along the mod-one positions of $s_0,s_1,\ldots ,s_T,s_{m+1}$). Referring to Table 1 for the example in Fig. 3 might be helpful in understanding the construction. Let $u_0=(S^{u_0},0,\ell _0)$, where every 2-tuple in $S^{u_0}$ has the form $(s_0,s_{(g,i),1})$. Then $(u_{scr},u_0)$ is an arc in G. Suppose by inductive hypothesis that we have found a path $u_{scr}u_0\ldots u_{j-1}$ in G. Let $u_j=(S^{u_j},\tilde{k}^{u_j},\ell _j)$ be the configuration with the following structure. Suppose $g_j$ is the unique grid point contained in $s_j$. Let $I_j=\{i:s_{curr}^{u_{j-1},i}(g_j)=s_j\}$. Since $\ell _j$ immediately follows $\ell _{j-1}$ and because $s_j\in MS_{g_j,i}$ for some i, we have $I_j\ne \emptyset$. For every $i\in I_j$, suppose $s_j$ is $s_{(g,i),z}$, let $(s_{prev}^{u_j,i}(g_j),s_{curr}^{u_j,i}(g_j))=(s_j,s_{(g,i),z+1})$. All the other 2-tuples of $S^{u_j}$ remain the same as in $S^{u_{j-1}}$. Let $\tilde{k}^{u_j}$ equal the sum of $\tilde{k}^{u_{j-1}}$ and the number of points covered by $\bigcup _gU(DS^{u_{j-1}}_g)$ and not covered by $\bigcup _gU(\mathcal O^{u_{j-1}}_g)$. By Definitions 2.6 and 2.7, $u_j$ is a valid configuration and $(u_{j-1},u_j)$ is an arc in G. Continuing in this way, we could find a path $u_{scr}u_0u_1\ldots u_T$, and for vertex $u_T$, every 2-tuple in $S^{u_T}$ has the form of $(s_{(g,i),t_{(g,i)}},s_{m+1})$. We have observed that every unit square in ${\mathcal {O}}^*$ protrudes out of some monotone-set, so it belongs to some detectable set of some configuration along the path. Since ${\mathcal {O}}^*$ fully covers $k_b$ points, $(u_T,u_{sink})$ exists in G.

When a unit square enters a detectable set, its weight is counted. Notice that a unit square s can only enter a detectable set associated with the unique grid point contained in s. A crucial observation is that due to the mod-one mapping, when s enters a detectable set, it remains in the collection of detectable sets until it no longer protrudes out of any of the four monotone-sets. So, any unit square in the envelope-set ${\mathcal {O}}^*$ is counted exactly once, namely when it first enters a detectable set. So, $w(Q)=c({\mathcal {O}}^*)$. $\square$

Combining Lemmas 2.8 and 2.9, we have the following result

Theorem 2.10

A shortest source-sink path in the auxiliary digraph $G_{b,k_b}$ corresponds to an optimal solution of the MinPSMC-US instance which fully covers exactly $k_b$ points of block b.

2.3 Assembling local solutions

The algorithm for the original region implements the shifting and partition technique which was first proposed by Hochbaum and Maass [11]. Assume that Q is a square containing all the n points of P. Suppose that Q is of size $q_0\times q_0$ and

$$\begin{aligned} Q=\{(x,y):0\le x\le q_0,0\le y\le q_0\}, \end{aligned}$$

For a constant q which will be determined later, let $N=\lceil q_0/q\rceil$. Extend Q into square

$$\begin{aligned} Q_0=\{(x,y):-q\le x\le Nq, -q\le y\le Nq\}. \end{aligned}$$

Partition $Q_0$ into $(N+1)^2$ blocks of size $q\times q$. We denote this partition of $Q_0$ by $P_0$. Note that the lower-left corner of $P_0$ is $(-q,-q)$. For integer $a\in \{0,\ldots ,q-1\}$, construct a partition $P_a$ for square $Q_a=\{(x,y):-q+a\le x\le Nq+a, -q+a\le y\le Nq+a\}$ by shifting $P_0$ by a vector (a, a). Notice that every $Q_a$ contains all points of P. For each partition $P_a$, the extended square $Q_a$ is partitioned into $(q+1)^2$ blocks. We have to guess the number of points to be fully covered in each block. This can be done by first ordering the nontrivial blocks as $b_1,b_2,\ldots ,b_t$ (a block is nontrivial if it contains some point) and then processing them sequentially using the following status transition formulae: let

$$\begin{aligned} B_0^{k_0}=\left\{ \begin{array}{ll}\emptyset , &{}\quad k_0=0. \\ null, &{}\quad \text{ otherwise },\end{array}\right. \end{aligned}$$

and for $i=1,2,\ldots ,t$,

$$\begin{aligned} B^{k_i}_{i}=\arg \min \{c(U(R_{b_i,k_i-k'_i})\cup B^{k'_i}_{i-1}):0\le k'_i\le k_i\}. \end{aligned}$$

(1)

where $R_{b,k_b}$ is a shortest source-sink path in $G_{b,k_b}$ (if such a path does not exist, then $R_{b,k_b}=null$ and the cost of null is $\infty$). By induction, if $B_{i-1}^{k_i'}$ is a feasible solution to the MinPSMC-US problem confined to the first $i-1$ blocks fully covering $k'_i$ points, and if there exists a source-sink path in $G_{b_i,k_i-k'_i}$, then $U(R_{b_i,k_i-k'_i})\cup B^{k'_i}_{i-1}$ is a feasible solution to the MinPSMC-US problem confined to the first i blocks fully covering $k_i$ points. By guessing $k'_i$ which is the number of points to be fully covered in the previous $i-1$ blocks, operation (1) chooses $B_i^{k_i}$ to be the best one obtained in the above way. Finally, let

$$\begin{aligned} {\mathcal {O}}_a=\arg \min \{c(B^{k_t}_t):k_t\ge k\} \end{aligned}$$

be the solution computed for partition $P_a$. The algorithm will output

$$\begin{aligned} \arg \min \{c({\mathcal {O}}^a):a=0,1,\ldots ,q-1\}. \end{aligned}$$

The following theorem shows the performance of the algorithm.

Theorem 2.11

The dynamic programming computes a feasible solution for the MinPSMC-US problem whose cost is at most $(1+\varepsilon )$ times the optimal value and runs in time $O(\frac{1}{\varepsilon } n^3m^{O(1/\varepsilon ^2)})$ by choosing $q=\lceil 3/\varepsilon \rceil$.

Proof

Let ${\mathcal {O}}^*$ be an optimal solution to the MinPSMC-US instance. For any index $a=0,1,\ldots ,q-1$, and for any block b in $P_a$, let ${\mathcal {O}}^*_{a,b}$ be the set of unit squares in ${\mathcal {O}}^*$ which have nonempty intersections with b. Then ${\mathcal {O}}^*_{a,b}$ covers all points in b. By Lemma 2.9, $w(R_{a,b})\le c({\mathcal {O}}^*_{a,b})$. By Lemma 2.8, $c(R_{a,b})\le w(R_{a,b})$. Hence

$$\begin{aligned} c({\mathcal {O}}_a)\le \sum _{\text{ block }\ b\ \text{ of }\ Q_a}c(R_{a,b})\le \sum _{\text{ block }\ b\ \text{ of }\ Q_a}w(R_{a,b})\le \sum _{\text{ block }\ b\ \text{ of }\ Q_a}c({\mathcal {O}}^*_{a,b}). \end{aligned}$$

(2)

Let ${\mathcal {H}}_a$ (resp. ${\mathcal {V}}_a$) be the set of unit squares in ${\mathcal {O}}^*$ which intersect some horizontal (resp. vertical) grid lines of $P_a$. Observe that a unit square can intersect at most four blocks of $P_a$. So,

$$\begin{aligned} \sum _{\text{ block }\ b\ \text{ of }\ Q_a}c(\mathcal {O}^*_{a,b})\le c({\mathcal {O}}^*)+c({\mathcal {H}}_a)+2c({\mathcal {V}}_a). \end{aligned}$$

(3)

For two different partitions $P_a$ and $P_b$, notice that a unit square can not be in both ${\mathcal {H}}_a$ and ${\mathcal {H}}_b$ for $a\ne b$. Hence

$$\begin{aligned} \sum \limits _{a=0}^{q-1}c({\mathcal {H}}_a)\le c({\mathcal {O}}^*). \end{aligned}$$

(4)

Similarly,

$$\begin{aligned} \sum \limits _{a=0}^{q-1}c({\mathcal {V}}_a)\le c({\mathcal {O}}^*). \end{aligned}$$

(5)

Summing both sides of (2) for $a=0,1,\ldots ,q-1$, making use of (3), (4), (5), and because $c({\mathcal {O}}')=\min _{a=0,1,\ldots ,q-1}c({\mathcal {O}}_a)$, we have

$$\begin{aligned} q\cdot c({\mathcal {O}}')\le \sum \limits _{a=0}^{q-1}c({\mathcal {O}}_a)\le q\cdot c({\mathcal {O}}^*)+\sum _{a=0}^{q-1}c(\mathcal {H}_a)+2\sum _{a=0}^{q-1}c({\mathcal {V}}_a)\le (q+3)c({\mathcal {O}}^*). \end{aligned}$$

It follows that

$$\begin{aligned} c({\mathcal {O}}')\le (1+3/q)c({\mathcal {O}}^*)\le (1+\varepsilon )c({\mathcal {O}}^*). \end{aligned}$$

The approximation ratio is proved.

For the time complexity, notice that for each partition and for each block, there are $O(nm^{O(q^2)})$ configurations, where the factor n comes from the number of choices for $\tilde{k}$. So, the time needed to compute a shortest path in a DAG is now $O(n^2m^{O(q^2)})$. Furthermore, since we have to guess the number of points to be fully covered in each block, the number of shortest paths computed for each block is O(n). Since we consider the partitions $P_{0},\ldots ,P_{q-1}$, the combined time complexity is $O(qn^3m^{O(q^2)})$. Substituting $q=\lceil 3/\varepsilon \rceil$ into the expression, the running time is $O(\frac{1}{\varepsilon } n^3m^{O(1/\varepsilon ^2)})$. $\square$

3 Conclusion and discussion

In this paper, for the geometric MinPSMC problem in which objects are unit squares, under the assumption that $r_p=f_p$ for all $p\in P$, we obtain a PTAS for MinPSMC-US. Dropping out the assumption $r_p=f_p\ (\forall p\in P)$, we can modify the above algorithm to yield a $(1+\varepsilon )$-approximation for MinPSMC-US the running time of which is related with $n^{O(r_{\max })}$, where $r_{\max }=\max \{r_p:p\in P\}$ is the maximum covering requirement. So, when $r_{\max }$ is upper bounded by a constant, it is a PTAS. How to obtain a PTAS (or less ambitious, a constant approximation) for MinPSMC-US without any restriction on $r_p$ is an interesting topic. Notice that mod-one operation can only be used for unit square case. New techniques have to be further explored for the geometric MinPSMC problem with other objects such as unit disks.