A derivative-free optimization approach for the autotuning of a Forex trading strategy

Abstract

A trading strategy simply consists in a procedure which defines conditions for buying or selling a security on a financial market. These decisions rely on the values of some indicators that, in turn, affect the tuning of the strategy parameters. The choice of these parameters significantly affects the performance of the trading strategy. In this work, an optimization procedure is proposed to find the best parameter values of a chosen trading strategy by using the security price values over a given time period; these parameter values are then applied to trade on the next incoming security price sequence. The idea is that the market is sufficiently stable so that a trading strategy that is optimally tuned in a given period still performs well in the successive period. The proposed optimization approach tries to determine the parameter values which maximize the profit in a trading session, therefore the objective function is not defined in closed form but through a procedure that computes the profit obtained in a sequence of transactions. For this reason the proposed optimization procedures are based on a black-box optimization approach. Namely they do not require the assumption that the objective function is continuously differentiable and do not use any first order information. Numerical results obtained in a real case seem to be encouraging.

1 Introduction

Nowadays the Foreign Exchange (Forex) markets produce hundreds of thousands of transactions every day (with an average turnover totaling 1.9 trillion a day [17]), all together can be considered the largest financial market.

The main distinguishing feature of a Forex market is its wild dynamics that implies the use of quite complex trading rules, hard to manage manually. Therefore an algorithmic trading is required.

The aim of this paper is to propose a tool that is able to define the parameter values of a given Forex trading strategy to obtain the highest profit according to the current price movements of the market.

The approach is based on the idea that the information extracted from historical data has a direct influence on the trading rule. The optimized rule is applied to the price time series immediately following the training period. The rationale behind this approach is that the market is sufficiently stable so that a trading strategy that is efficiently tuned in a given period still performs well in the incoming next period.

In the considered optimization approach, the objective function value is the profit obtained over a fixed time period by the trading strategy. Therefore, there is no analytic expression of the objective function but it is only possible to obtain its values by reproducing the trading actions obtained by the particular strategy over a known sequence of security prices. The optimization variables are the trading strategy parameters that can be either continuous or discrete.

In this paper a new local optimization method suitable to tackle both the black-box nature of the problem and the mixed-integer one is first proposed.

Then two global optimization algorithms, which have better properties to approximate global solutions instead of local ones, are described. These two algorithms derive by combining two suitable multistart strategies (one probabilistic and one deterministic) with the previous local procedure.

All the described algorithms are tested on a real case. The obtained results seems to indicate that the proposed approach of finding the trading strategy parameters by an optimization approach and exploting the market stability in the near future can be promising. This early result should be completed with an extended backtesting procedure on a larger dataset to avoid data snooping.

We remark that the aim of the work is to point out that an optimization approach can play a positive role in the algorithmic trading field by improving the performances of any strategy. Therefore, the study was neither intended to propose a particular trading strategy which is the most profitable, nor to define the best optimization procedure for parameters tuning. All of these points can be developed in further studies.

In Sect. 2 we present a literature review. In Sect. 3 we introduce the problem and in Sect. 4 we illustrate some possible approaches for the solution of the optimization problem. Finally in Sect. 5 numerical results are presented and discussed.

2 Literature review

The classical signal models generally fail in describing the underlying nonlinear data structure [7, 30]; on the other hand machine learning and data mining techniques have proven to be suitable for the prediction of market movements, mainly relying on the structural ability of Artificial Neural Networks (ANNs) and Support Vector Machines (SVM) to capture significant information patterns in data. A complete survey on the use of ANN for stock market predictions is given in [8] and the same authors in [9] highlight the superiority of ANN methodology versus the standard time series forecasting. The superiority of soft computing compared to statistical analysis is also addressed in [2]. Furthermore, in [28], it is proved that ANN produce better prediction accuracy than non-linear regression and classification tree models.

Fuzzy neural networks (FNN) approaches have been proposed in [18], while support vector regression methods (SVR) are found in [25] and [31].

In these papers and in the similar relevant literature, the learning techniques are mostly used in order to integrate the decision making process but they do not directly affect the structure of its strategy. A different and parallel approach is proposed in literature to improve the efficiency of the trading by influencing more directly the strategy and/or its structure by using learning or optimization techniques (see for example [24]).

In this paper we follow the idea proposed in this last line of research. Namely our aim is to propose a new methodology to improve the efficiency of a trading strategy by exploiting the information contained in a past trading period in order to get “good” values of its parameters. This approach must not be seen as an alternative to the previous ones proposed in literature but rather as a further tool that can be combined with others to provide efficient strategies to traders.

The tuning of the parameters of the trading strategy is carried out by tackling an optimization problem showing the following difficult features: no first order information can be used (black-box problem); nonsignificant local minima can exist (global optimization problem); some variables are continuous and some variables are integer (mixed integer problem).

In literature, optimization problems showing one or more of the previous features have been tackled by using various methodological approaches. Some examples can be found in: [1, 4, 12] (local derivative-free methods); [14, 19, 26] (global derivative-free methods); [5, 20, 23, 27] (mixed integer derivative-free methods).

For a more extensive review we refer to the references reported in the previous papers and to the recent survey [16].

Finally we recall [6] and [3] where, for the first time, a derivative-free approach was used for the tuning of the parameters of an algorithm.

3 A trading strategy and the optimization problem

In this Section a particular trading strategy is chosen and an optimization approach for computing its parameter values is proposed.

The considered trading procedure is composed of basic rules to show that even for a prototypical strategy, the achievable profits can be significantly improved provided that its parameter are selected by an optimal policy.

3.1 A basic trading strategy

In trading, any tradable asset of every kind is called security. The security price is characterized by resuming its behavior over adjacent time intervals called timeBars $\{t_i\}$. The closing price Cl(i), i.e. the last value within the i-th timeBar, is the value used for trading. A trader starts a transaction by opening a position; the position is long/short if he buys/sells a security. Consequently, the transaction is completed when the trader sells/buys back the security, therefore closing the position. Whatever the position, the profit he realizes is given by the difference between the selling and the buying prices. A trading strategy is strictly characterized by the opening and the closing criteria. In the selected strategy, the conditions for opening a position are defined by considering the momentum factor (MF). At timeBar $t_i$, MF is defined as follows:

$$\begin{aligned} MF(i) = Cl(i) - Cl(i-\Delta ),\quad i>\Delta , \end{aligned}$$

where $\Delta$ is a positive integer parameter that defines a suitable time delay. By using the MF the following opening conditions can be obtained:

The closing conditions are defined in terms of the Target and the Stop price levels. These two levels must be fixed whenever a position is opened:

• the Target price level must ensure a satisfiable profit, if the market moves according to the trend expectation;

• the Stop price level must ensure an acceptable loss, if the market moves against the trend expectation.

Stop and Target price levels are defined both for long and short positions. The simplest way to define Stop and Target is as follows

where $0<p_L,\,p_S,\,q_L,\,q_S<1$ are suitable positive constant parameters. As a matter of fact, the Stop and Target values can be updated by a simple “trend-following” rule to ensure a better profit.

In the previous sketch $\Delta _{\{\cdot \}}$ are further four parameters to be determined. Then the described strategy depends on the values of the following ten variables where eight can assume continuous values and the remaining two can assume discrete values:

$$\begin{aligned} x_c= & {} [p_L,\,q_L,\,p_S,\,q_S,\,\Delta _{Stop_L},\,\Delta _{Target_L},\,\Delta _{Stop_S},\,\Delta _{Target_S}\,]\in \mathbb {R}^8, \end{aligned}$$

(1)

$$\begin{aligned} x_d= & {} [\Delta _L,\,\Delta _S]\in \mathbb {Z}^2, \\ x= & {} [x_c,\,x_d\,]\in \mathbb {R}^{8}\times \mathbb {Z}^{2} \nonumber . \end{aligned}$$

(2)

The profits $\{\Pi (i,x)\}$ over a trading period of N timeBars is computed as follows. If at time $t_i$ no opening condition is satisfied, then $\Pi (i,x)=0$; if a long position is opened then $\Pi (i,x)=-Cl(i)$, if a short position is opened then $\Pi (i,x)=Cl(i)$. If a position is opened, at any successice time $t_{i+k}$ the current price $Cl(i+k)$ is compared to the Stop and Target thresholds. On a long position: if $Stop_L(i+k)<Cl(i+k )<Target_L(i+k)$ then $\Pi (i+k,x)=0$, otherwise $\Pi (i+k,x)=Cl(i+k)$. On a short position: if $Target_S(i+k)<Cl(i+k )<Stop_S(i+k)$ then $\Pi (i+k,x)=0$, otherwise $\Pi (i+k,x)=-Cl(i+k)$. At the end of the trading period the total profit is given by

$$\begin{aligned} \Pi (x)=\sum _{i=1}^N \Pi (i,x). \end{aligned}$$

3.2 Suitable sliding time windows

An efficient procedure can be designed by dividing the trading period into adjacent shorter time intervals. The price time series of a subinterval is used as training data to evaluate the parameter values of the trading strategy that guarantee the best profit over the considered subinterval; these values are used in a trading session during the subsequent interval. Hence, a training period is followed by a trading period that will become a training period in the next iteration.

This strategy strongly relies on the implicit assumption that the market shows a sort of resistance to change over short periods of time, so that the optimal parameter values of the training period remain good enough for the subsequent trading period. This assumption can be related to the predictability of economic and financial market time series, this feature can be measured by estimating the Hurst Exponent (H) from data (see [22]). On the batch of data used for training, this analysis showed that the market resistance hypothesis could be reasonably adopted within a time horizon of 90 min.

3.3 The optimization problem

The rationale behind the proposed approach consists in determining the optimal parameter values of a trading strategy over a training period and in using these values in the subsequent trading period.

According to the Hurst Exponent analysis, training/trading periods of 90 min and timeBars of 1 min, $\{t_i\},\,i=1,\ldots ,90$ are considered.

If a set of price values Cl(i), $i=1,\ldots ,90$ is given then the parameter values that increase the final profit as much as possible can be obtained by solving the following maximization problem:

$$\begin{aligned}&\max _{x\in \mathbb {R}^8 \times \mathbb {Z}^2} \quad \sum _{i=1}^{90}\Pi (i,x)=\Pi (x) \nonumber \\&\text {s.t. } \quad l\le x \le u, \end{aligned}$$

(3)

where l and u are the lower and upper bounds for the variables.

In the numerical experience of Sect. 5 we use the following vectors

$$\begin{aligned} l=[2,0,0,0,2,0,1,1,1,1]^T\qquad u=[30,1,1,1,30,1,10,10,10,10]^T \end{aligned}$$

The values of the lower bounds $l_i$, $i=1,\dots ,10$ were chosen so as to avoid that either the objective function is not defined or the indicators used in the strategy lose their meaning. Instead, the values of the upper bounds $u_i$, $i=1,\dots ,10$ were derived by applying the procedure developed in [10]. This procedure finds reasonable values for the upper bounds by exploiting the information contained on a set of data. In particular in [10] it was used a set of data that preceded the one used in this work.

4 Optimization algorithms

The optimization problem described in the previous sections can be easily formalized as the following general bound constrained mixed variable problem:

$$\begin{aligned} \begin{array}{l} \min f(x)\\ x\in \mathcal{F}, \end{array} \end{aligned}$$

(4)

where

$$\begin{aligned} \mathcal{F}:=\Bigl \{l\le x\le u : \ x_i\in \mathbb {R}, \ i\in I_c=\{1,\dots ,r\},\ x_i\in \mathbb {Z},\ i\in I_d=\{r+1,\dots ,n\}\Bigr \}. \end{aligned}$$

In the following we denote by $x_c\in \mathbb {R}^r$ the subvector of x with components $x_i$, $i\in I_c$, by $x_d\in \mathbb {Z}^{n-r}$ the subvector of x with components $x_i$, $i\in I_d$, by $[x]_\mathcal{F}$ the projection of the point x over $\mathcal{F}$ and by $\mathcal{D}=\{x\in \mathbb {R}^n: l\le x\le u\}$ the box constraints of Problem (4).

In this section we try to define some optimization algorithms able to tackle the Problem (4) in a sufficiently efficient way. As said before, the aim is to understand if an optimization approach can be an interesting tool for the tuning of the parameters of a trading strategy. In particular, we try to combine some approaches proposed in the literature that seem to be promising and efficient to deal with the particular features of Problem (4).

In the class of algorithms using only values of the objective function we consider the ones which exploit derivative-free linesearch techniques. Our choice derives from the fact that they usually showed efficient numerical behaviours both on test problems and on difficult real world problems. The approach described in [20] for solving mixed bound constrained problems is initially considered. However methods proposed in [20] can not efficiently deal with the previous Forex trading strategy optimization problem for these reasons:

• (i) the theoretical convergence properties of such methods rely on the assumption that the objective function is continuously differentiable;

• (ii) under the previous smoothness assumption they are guaranteed to converge to points that satisfy only necessary optimality conditions.

In the following, drawback (i) is overcome by defining a new derivative-free local algorithm for Problem (4) whose global convergence properties towards points that satisfy necessary optimality conditions can be stated under a weaker assumption than the continuous differentiability of the objective function.

As regards drawback (ii), two algorithms are defined by using the new proposed local algorithm within two multistart strategies, one probabilistic and one deterministic. In theory, these algorithms have a better capability to find a global minimum. In practice, they should guarantee that an “efficient good solution” can be found.

In the next two subsections the new local algorithm is first studied, then the two multistart global optimization algorithms are described.

4.1 Local optimization algorithm

This sub-section describes a new derivative-free method for box constrained optimization problems where the objective function can be non smooth and some of the variables are continuous and others are discrete. This algorithm derives by combining the approaches proposed in [20] and [12].

The convergence properties of the new algorithm can be stated by using the following assumption.

Assumption 1

The objective function $f: \mathbb {R}^n\rightarrow \mathbb {R}$ is Lipschitz continuous with respect to the continuous variables $x_i$, $i\in I_c$.

First of all we recall that every local/global minimum point of (4) is a stationary point according to the following definition.

Definition 1

A point $x^*\in \mathcal{F}$ is a stationary point of Problem (4) if it satisfies

$$\begin{aligned} f^\circ (x^*; d) \ge 0,&\quad \text{ for } \text{ all }\ d\in D_c(x^*)\end{aligned}$$

(5)

$$\begin{aligned} f(x^*)\le f(x)&\quad \text{ for } \text{ all }\ x\in \mathcal{N}_d(x^*)\cap \mathcal{F}, \end{aligned}$$

(6)

where

$$\begin{aligned} f^\circ (x; d) = \limsup _{\begin{array}{l}y\rightarrow x, y\in \mathcal{F}\\ t\downarrow 0, y+t d\in \mathcal{F}\end{array}} \frac{f(y+t d) - f(y)}{t}, \end{aligned}$$

(7)

$$\begin{aligned} D_c(x)= & {} \{\ d\in \mathbb {R}^n: \ d_i\ge 0\ ~\text{ if }\ \ i\in I_c \ \ \hbox {and}\ \ x_i = l_i,\ \\& \ \ \ \ d_i\le 0\ ~\text{ if }\ \ i\in I_c \ \ \hbox {and}\ \ x_i = u_i,\\& \ \ \ \ d_i\in \mathbb {R}\ ~\text{ if }\ \ i\in I_c \ \ \hbox {and} \ \ l_i<x_i < u_i,\\&\ \ \ \ d_i=0\ ~\text{ if }\ \ i\in I_d\ \},\\&\mathcal{N}_{d}( x) = \left\{ \bar{x}\in \mathbb {R}^n: \bar{x}_c = x_c,\ \Vert x_d-\bar{x}_d\Vert _2=1 \right\} . \end{aligned}$$

For every $x\in \mathcal{F}$, we note that $f^\circ (x; d)$ is the Clarke-Jahn generalized directional derivative of function f along d (see [13]), $D_c(x)$ is the set of feasible directions with respect the continuous variables, $\mathcal{N}_{d}( x)$ is a neighbourhood of x with respect the discrete variables.

The new algorithm (called LDF) takes into account the mixed integer nature of Problem (4) by performing two different sampling techniques, one for investigating the behavior of the objective function with respect the continuous variables and the other one for the behavior with respect the discrete variables.

The Projected Continuous Search updates the continuous variables by performing a derivative-free linesearches along appropriate search directions.

The sequence of the search directions must be able to approximate eventually any direction. This requirement is formalized in the following the definition.

Definition 2

Let K be an infinite subset of indices. The subsequence of normalized directions $\{s_k\}_K$, with $s_k\in \mathbb {R}^r$, is said to be dense in the unit sphere if for any $s \in \mathbb {R}^r$, such that $\Vert s\Vert =1$, and for any $\epsilon > 0$ there exists an index $k\in K$ such that $\Vert s_k -s\Vert \le \epsilon$.

As regards the discrete variables, the Discrete Search updates these variables by performing a suitable local search along the coordinate directions, $e^{r+1}\ldots e^n$ (Discrete Search).

The convergence properties of Algorithm LDF are described by the following proposition.

Proposition 1

Let $\{x_k\}$ be the sequence produced by Algorithm LDF, let $\bar{x}$ be an accumulation point of $\{x_k\}$ and let $\{x_k\}_K$ be the subsequence such that

$$\begin{aligned} \lim _{k\rightarrow \infty , k\in K}x_k=\bar{x}. \end{aligned}$$

If the subsequence $\{s_k\}_K$ of the search directions used by the algorithm is dense in the unit sphere (according the Definition 2), then the point $\bar{x}$ is a stationary point of Problem (4) (see Definition 1).

Proof

The steps of Algorithm LDF imply that, for all k

$$\begin{aligned} f(x_{k+1})\le f(\tilde{x}_{k})\le f(x_{k}). \end{aligned}$$

The previous inequalities and the compactness of the feasible set guarantee the existence of limit $\bar{f}$ such that

$$\begin{aligned} \lim _{k\rightarrow \infty }f(x_k)=\bar{f},\qquad \lim _{k\rightarrow \infty }f(\tilde{x}_k)=\bar{f}. \end{aligned}$$

These limits allow us to repeat, by minor modifications, the theoretical analyses performed in [20] and [12] to prove the convergence of Algorithm DFL$_{ord}$ and Algorithm DFN$_{simple}$ respectively. In particular, by adapting the reasoning behind the proof of Proposition 2.7 of [12], we can conclude that the point $\bar{x}$ satisfies condition (5). Then, the same arguments of the proof of Proposition 12 of [20] guarantee that $\bar{x}$ satisfies also property (6). $\square$

4.2 Global optimization algorithms

Proposition 1 shows that Algorithm LDF is able to produce sequences of points which converge towards stationary points, namely points that satisfy only the necessary conditions to be a global minimum of Problem (4). In order to better understand the real potential of the optimization approach in the considered Forex problem, we use also optimization algorithms that try to determine the global minimum points of the Forex problem.

By adapting the proof of Theorem 4.1 of [11] and by requiring suitable assumptions, it is possible to ensure the existence of a neighborhood of a global minimum where Algorithm LDF is “attracted”. Namely, if Algorithm LDF starts from a point belonging to the previous neighborhood, it produces a sequence of points which remains in this neighborhood and converges to the global minimum point.

We exploit this property to define two suitable multistart techniques for Algorithm LDF. In particular, we generate the starting points by performing some iterations of two global optimization techniques which generate sets of points (either in a probabilistic or deterministic setting) which tend to be dense in the feasible region as the number of iterations increases. Hence, they are able to produce a point belonging to the “attraction set” of a global minimum point after a finite number of steps if such a set exists, otherwise they are able to find better and better approximations of the global minimum as the number of iterations increases.

4.2.1 Simulated annealing multistart algorithm

The proposed probabilistic multistart algorithm is based on the Simulated Annealing approach (see [15]). In particular, a starting point for Algorithm LDF is chosen at random according to a probability density function proportional to

$$\begin{aligned} e^{-\max [0,f(x)-f(x_{min})]/T} \end{aligned}$$

where $x_{min}$ is an approximation of the global minimum point and T is a parameter called “annealing temperature” which is progressively decreased during the minimization process. The more the temperature decreases, the larger is the probability of accepting points satisfying $f(x)\le f_{min}+\epsilon$ and, hence, also points belonging to a neighborhood of a global solution. This strategy is exploited in the following Algorithm SA.

Concerning the updating rule of the temperature $T_k$, we refer to the updating rule reported in [21]. By using the analysis carried out in [29] and [21] it is possible to prove the following result.

Proposition 2

For every global minimum point $x^*$ of Problem (4) and for every $\epsilon > 0$, with probability one Algorithm SA produces in a finite number of iterations a point $x_k\in \mathcal{F}$ such that

$$\begin{aligned} \Vert (x_k)_c-x^*_c\Vert \le \epsilon ,\qquad (x_k)_d=x^*_d. \end{aligned}$$

4.2.2 DIRECT multistart algorithm

The proposed deterministic multistart strategy is based on the DIRECT algorithm proposed in [14]. The approach of the DIRECT algorithm consists in producing a sequence of partitions $\{\mathcal {H}_k\}$ of the initial set $\mathcal{D}$. More in particular, at iteration k, the partition of the set $\mathcal{D}$ is given by

$$\begin{aligned} \mathcal {H}_k=\{\mathcal{D}^i, i\in I_k\} \end{aligned}$$

where $\mathcal{D}^i=\{x\in \mathbb {R}^n: l^i\le x\le u^i\}, \quad l^i,u^i\in [l,u], \quad \tilde{x}_k^i=(l^i+u^i)/2$.

Then the next partition $\mathcal {H}_{k+1}$ is obtained by selecting and by further partitioning the most “promising” hyperrectangles $\mathcal{P}_k\subseteq \mathcal {H}_{k}$. An hyperrectangle $\mathcal{D}^h$ can be considered “promising” in containing a global minimum point if $f(\tilde{x}_k^h)$ is small or if $\Vert u^h-l^h\Vert$ is large. In particular, given a $\theta \in (0,1)$, the set $\mathcal{P}_k$ consists of potentially optimal hyperrectangles, namely

$$\begin{aligned}&\mathcal{P}_k =\biggl \{\mathcal{D}^h,\ h\in I_k:\ \hbox {a scalar} L^h>0 \hbox { exists such that}\\ \nonumber&f(\tilde{x}_k^h)-L^h\Vert l^h-u^h\Vert \le \min \biggl [\ \theta \min _{i\in I_k} f(\tilde{x}_k^i)\ ,\ \min _{i\in I_k}\bigl [\ f(\tilde{x}_k^i)-L^h\Vert l^i-u^i\Vert \ \bigr ]\ \biggr ]\ \biggr \}. \end{aligned}$$

(8)

From the theoretical point of view, the DIRECT algorithm has the important property that, as the iterations increase, the centroids of the hyperintervals tend to produce a set dense on $\mathcal{D}$.

In the following Algorithm DA we introduce Algorithm LDF in the DIRECT type framework presented in [19]. As concerns the partition technique, we refer to [14] for a complete description. Then the analysis carried out in [14] can be adapted to prove the following result.

Proposition 3

For every global minimum point $x^*$ of Problem (4) and for every $\epsilon > 0$, Algorithm DA produces in a finite number of iterations a point $x_k^{\tilde{h}}\in \mathcal{F}$ such that

$$\begin{aligned} \Vert (x_k^{\tilde{h}})_c-x^*_c\Vert \le \epsilon ,\qquad (x_k^{\tilde{h}})_d=x^*_d. \end{aligned}$$

5 Numerical experiments

The considered simple trading strategy has been applied within the Forex market for the currency pair euro and U.S. dollar (EUR/USD). All the experiments have been performed by using a set of the free data from Dukascopy.com of EUR/USD pair from January 2014 to February 2014, data are aggregated in timeBars of 1 min. A first batch of data was exploited to find the values of the environmental variables (the Hurst exponent from Sect. 3.2 and the lower and upper bounds on x); the remaining batch of data was split into a series of adjacent time windows of 90-min, as suggested by the Hurst analysis. Since the set of data covers a relative wide horizon, the results obtained are less affected by the particular time period considered. Then the three procedures LDF, SA and DA have been applied to optimize the basic procedure parameters on a training window, and then the optimized trading procedure was applied on the adjacent trading window, and finally the profits obtained were recorded. As a matter of fact one run of Algorithm LDF, choosing as starting point the middle points of the feasible region $x_i^0=(u_i-l_i)/{2}$ for $i=1,\ldots ,10$, was executed just to show that even a local algorithm can generate positive profits. Then the two global algorithms SA and DA have been applied for a suitable number of local minimizations. Since the dynamics of the EUR/USD pair is quite quick, the number of local minimizations had to satify a trade-off between the computation time and the obtaining of a good approximation of the global minimum. After a rough tuning, we have chosen to stop Algorithm SA after 15 local minimizations and Algorithm DA after 10 local minimizations. The results reported on Table 1, which describe the profits achieved in the training phase at the end of each month by using the trading parameters given by the three algorithms show that, in the training phase, Algorithm SA and Algorithm DA allow to obtain profits which are significantly better than the ones obtained by the Algorithm LDF alone.

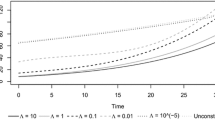
Finally, let us check the analysis of the profits achieved on the trading periods by the strategies with the parameters identified by the different optimization procedures. In Fig. 1 the cumulative profit achieved in the 2-months trading period is reported. The curves show that the DIRECT method performed the best, for the considered set of data: in summary, the parameters obtained by the Algorithm LDF yield a cumulative profit of 0.0247, those obtained by the Algorithm SA yield a cumulative profit of 0.0307 and parameters obtained by the Algorithm DA yield a cumulative profit of 0.0648. In other words, it is possible to gain the $2.47\%$ of the invested capital after 2 months of trading by using Algorithm LDF, the $3.07\%$ by using Algorithm SA and the $6.48\%$ by using Algorithm DA.

These preliminary results indicate that: (i) the local minimization approach by Algorithm LDF is able to find parameters value in the training phase, which yield a positive profit in the successive trading time window; (ii) the global optimization approach by Algorithm SA determines the parameters value that yield higher profits than Algorithm LDF, by performing 15 local minimizations, the differences are significative in the training phase, much less in the trading phase; (iii) the global procedure of Algorithm DA produces parameter values that outperform in terms of profit the ones obtained by both LDF and SA. The differences are significative both in the training phase and in the trading phase. On the other hand Algorithm DA uses 10 local minimizations that, in any case, are less than those used by Algorithm SA.

These results are anyway just indicative, in the effort to support the use of proper optimization procedures in algorithmic trading. To avoid data snooping, a more extensive benchmarking procedure on a larger dataset should be performed. This, along with other issues, is object of a further study.

Table 1 The cumulated profit achieved by the different procedures over the training periods

Fig. 1

The Cumulative Profits achieved applying the different Optimization Algorithms and the single Local Optimization procedure over the whole trading period

6 Conclusions

The aim of the paper is to show that the use of optimization techniques can provide useful tools to final traders. The proposed contribution is to describe an optimization procedure for finding efficient values of the parameters of a trading strategy for the Forex market. The idea is to adopt a sliding time windows scheme for a price time series, to dynamically apply a specific optimization procedure to obtain the best parameters of every time window and, then, to use the optimized trading strategy in the next period. In particular a relatively simple trading strategy is considered and three different minimization algorithms are proposed. The first one, Algorithm LDF, is a local minimization method which tries to take into account the particular structure of the considered optimization problem. The other two are global optimization methods, Algorithm SA and Algorithm DA, and are based on multistart strategies which use LDF Algorithm as local strategy. The numerical experience performed on real data deriving from the trading of the EUR/USD currency pair are promising. All three algorithms are able to obtain values of the trading parameters that guarantee positive global profits on the trading periods. Even the trading parameters given by the local strategy, Algorithm LDF, produce significant profits. Between the two global methods, Algorithm DA produces better profits using less local searches.

The reported results encourage to perform further research on the following topics:

• to apply a similar optimization approach to different (possibly better) trading strategies;

• to define new (possibly more efficient) optimization algorithms;

• to improve (possibly to speed up) the approach by combining it with data mining techniques.

Of course, any improvement deriving from the study of the previous points and a thorough benchmarking, would strengthen further the thesis of this paper.